近年来,较多国内外****围绕管道-流体耦合振动问题已进行了一些研究,多集中在流体瞬变诱发的输流管道振动[1, 2, 3]和充液管道在冲击载荷下的流体振动方面[4, 5, 6],杨超[7]研究了阀门突然关闭时水锤作用对管道轴向振动响应的影响,分析了连接耦合、泊松耦合、结构阻尼等对流体响应的影响规律;Perotti等[8]以充液的复合材料管道为对象,通过实验和仿真研究了管内流体冲击诱发的管道流固耦合振动响应情况,分析了复合材料纤维缠绕角度对流体振动的影响。Kucienska等[9]研究了由阀门突然关闭引发的水锤作用下管道的切应力响应问题,深入分析了切应力响应的变化步骤及其影响因素。Rocha等[10]运用广义线性混合模型(GLIMM)方法数值求解了管道流固耦合轴向振动响应,得到了流体在冲击载荷下的动态响应。Zhu等[11]运用CFD软件仿真研究了三通管内流体压力和流速分布的流动特性,并分析了入口流速、分支管径和分支角度对流体流动特性和管道切应力及变形的影响。
综上,对管道-流体耦合振动的研究中,其振动诱发因素主要来自于流体瞬变引起的水锤作用,如阀门突然关闭、管端受锤击、液体受冲击载荷等[12, 13, 14, 15],但以处于基础振动环境下的输流管道为研究对象,对基础振动诱发的管道-流体耦合振动进行研究鲜见报道。
针对轴向基础振动对液压管道内流体的影响,将液压管道简化为两端受约束的输流管道单元,研究轴向基础振动下流体-管道耦合振动特性,分析系统参数对管道出口流体波动的影响规律,为管道抗振策略的制定提供理论指导。
1 输流管道轴向流固耦合振动模型建立1.1 假设条件①管内流体为无黏性、无内外能量交换的一维流动;②不考虑径向惯性力;③忽略初始应力的影响;④管道材料各向同性;⑤仅研究流体扰动沿轴向的变化;⑥考虑结构阻尼与流体的黏性摩擦力;⑦不考虑流体内部阻尼;⑧在基础振动环境中,安装管道的基础在外界轴向激励作用下做简谐运动。基础振动的表达式为:N1=Nsin ω1t,其中:N为轴向基础振动幅值;ω1为轴向基础振动频率;t为时间。
1.2 轴向振动数学模型考虑轴向基础振动的作用,并结合流固耦合轴向运动4-方程模型[16],得到简谐基础振动下的输流管道流固耦合轴向运动数学模型,即
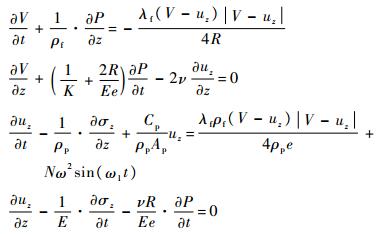
式中:P和V分别为流体的压力和流速;ρf和ρp分别为流体密度和管道密度;λf为流体的摩阻系数;uz和σz分别为管道轴向速度和轴向应力;R和e分别为管道内半径和管壁厚度;K为流体体积压缩模量;E为管道弹性模量;ν为泊松比;Cp为管道材料黏性阻尼系数;z为轴向坐标值;Ap为管道截面面积。
2 耦合模型特征线法求解2.1 特征线方程推导为方便求解,将方程组写成统一矩阵形式:
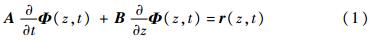
式中:A和B均为方程的系数矩阵;Φ(z,t)为未知变量构成的矢量;r(z,t)为方程右端的组成矢量：
其中:
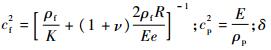为管道厚度。方程式(1)的特征值方程为|B-λA|=0,即:λ4-γ2λ2+cf2cp2=0,其中:λ为特征值;γ2=
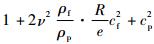。计算得到特征值为
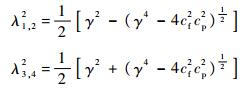
并引入转换矩阵S与变量η(z,t),以对耦合方程进行解耦:Φ(z,t)=Sη(z,t),其中:S=(TA)-1,T的定义为
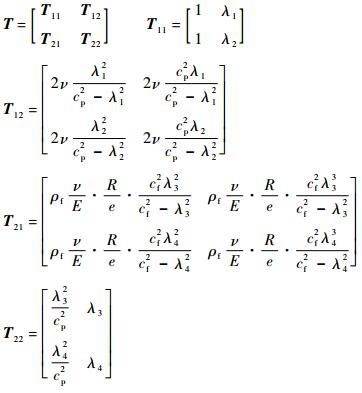
代入式(1):
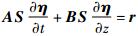，左乘S-1A-1可得
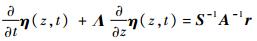其中：Λ=S-1A-1BS,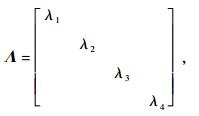
λi为特征方程|B-λA|=0的特征值,i=1,2,3,4。进而得到式(1)的解耦形式为
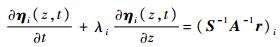
沿特征方向:
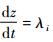将η、S及式(1)中的A代入,得到常微分方程组: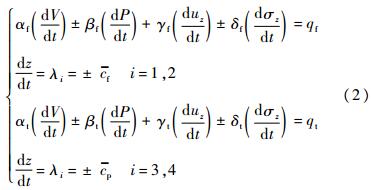
式中:
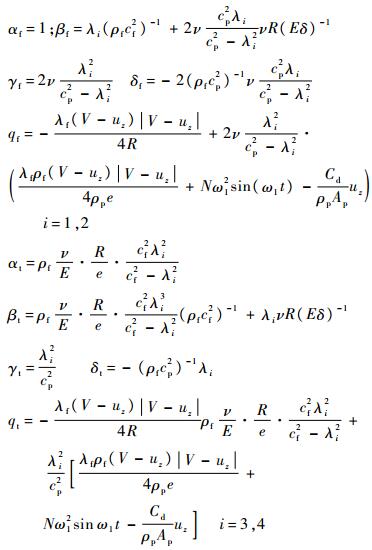
式中：c-f和c-p均为特征线算法计算中的斜率。
将式(2)中的第1个和第3个方程用差分形式表示,并沿各自的特征线积分,得到:
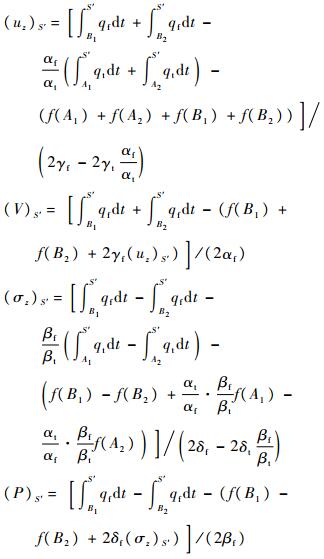
式中:
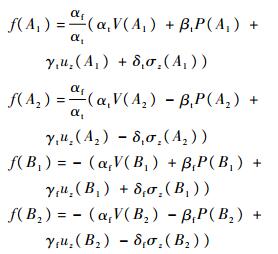
其中：S′、A1、A2、B1和B2为时间空间坐标系内的节点。
求解过程中,沿管道轴向和时间方向按最小波速划分计算网格,由于结构中纵波速度cp和流体中的声波cf不同,特征线与空间坐标轴的交点并不是网格节点,因此如图 1(a)中的A1、A2与图 1(b)中的B1、B2点上的参数值需要插值获得。根据不同空间步长:Δz=cfΔt和Δz=cpΔt划分网格单元,可以分为时间插值计算和空间插值计算2种。由于空间插值在处理边界附近的数据时,要对边界数据进行插值,从而增大了数值计算的误差,而时间插值则可直接获得边界条件数据进行计算,因此采用先空间插值计算,当得到满足时间插值计算的数据时,再采用时间插值计算,即设波速比cp/cf=M+N′,其中M为整数部分,N′为小数部分。从t=0时刻开始,利用初始条件,并结合边界条件,使用空间插值网格计算得到t=Δt,2Δt,…,MΔt时刻线上的参数值,然后从t=(M+1)Δt时刻开始采用时间插值网格求解。
 |
| 图 1 空间插值和时间插值特征线Fig. 1 Spatial interpolation and time interpolation characteristic line |
| 图选项 |
2.2 算例模型和基本参数确定算例模型参照文献[16]的试验装置,如图 2所示,液压系统由变量恒压泵-直管-电磁换向阀组成。油液由油泵送出,经溢流阀、蓄能器流入管道,在管道出口处用流量控制阀调节流量,以设置管道出口流体流速恒定;蓄能器保证管道入口处压力恒定。
 |
| 图 2 算例模型系统简图Fig. 2 System schematic of example model |
| 图选项 |
管道约束模型如图 3所示,管道两端用弹性元件进行固定,当K1或K2为∞时,表示该端固定;当K1或K2为0时,表示该端自由;介于两者之间表示该端弹性约束。基本参数设定如下:管长L=2 m;R=0.019 m;e=0.003 m;E=210 GPa;ρf=890 kg/m3;ρp=7 800 kg/m3;ν=0.3;入口压力Pz=0=10 MPa;出口流速Vz=L=3 m/s;λf=0.023;K=1.488 8 GPa。
 |
| 图 3 管道约束模型Fig. 3 Model of pipe constraint |
| 图选项 |
2.3 初始条件和边界条件推导初始时管道内流速恒定,管道轴向振动速度为零,忽略模型方程式(1)中的时间相关项并对各式积分,在根据管道两端边界条件确定积分常数,得到初始条件为
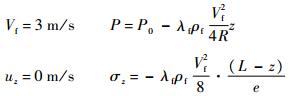
考虑4种不同管道约束方式:① K1=∞,K2=0时,入口固定出口轴向自由;② K1=0,K2=∞时,出口固定入口轴向自由;③ K1=K2=∞时,两端固定;④ K1=∞,K2=k时,入口固定,出口弹性约束。
4种方式中,边界上的4个参数并不都是已知的,对于未知的量要通过式(2)和已知的参数得到。
1) 入口固定出口轴向自由
入口边界条件:
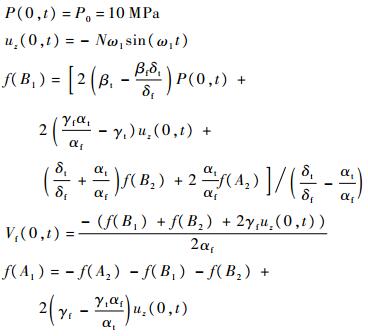
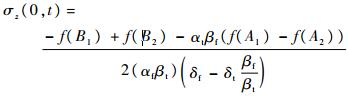
出口边界条件:
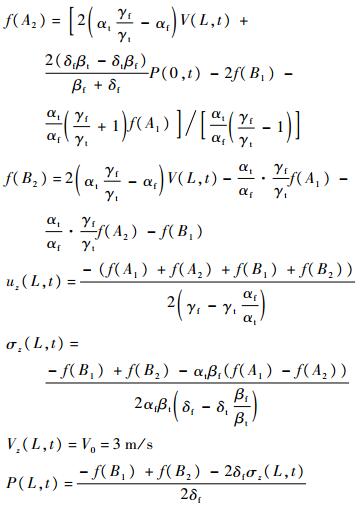
2) 出口固定入口轴向自由
出口边界条件:
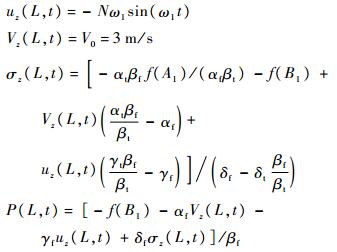
入口边界条件:
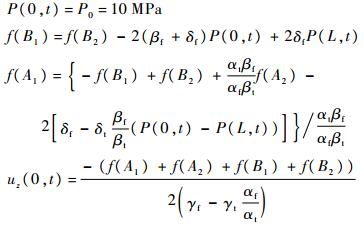
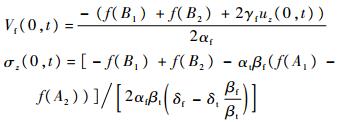
3) 两端固定
入口边界条件:
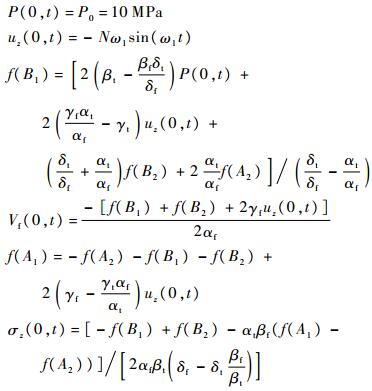
出口边界条件:
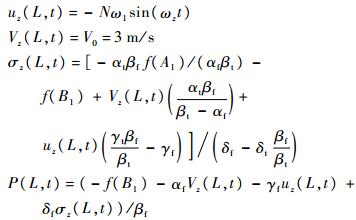
4) 入口固定,出口弹性约束
入口边界条件
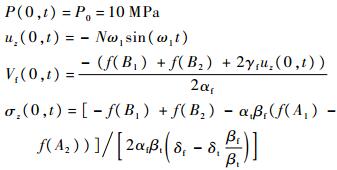
出口边界条件
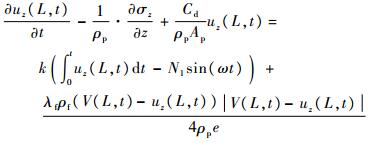
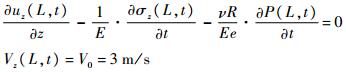
3 系统参数对流固耦合振动特性影响3.1 约束方式对流体振动响应的影响3种不同的管道约束方式的出口流体压力振动响应如图 4所示。
 |
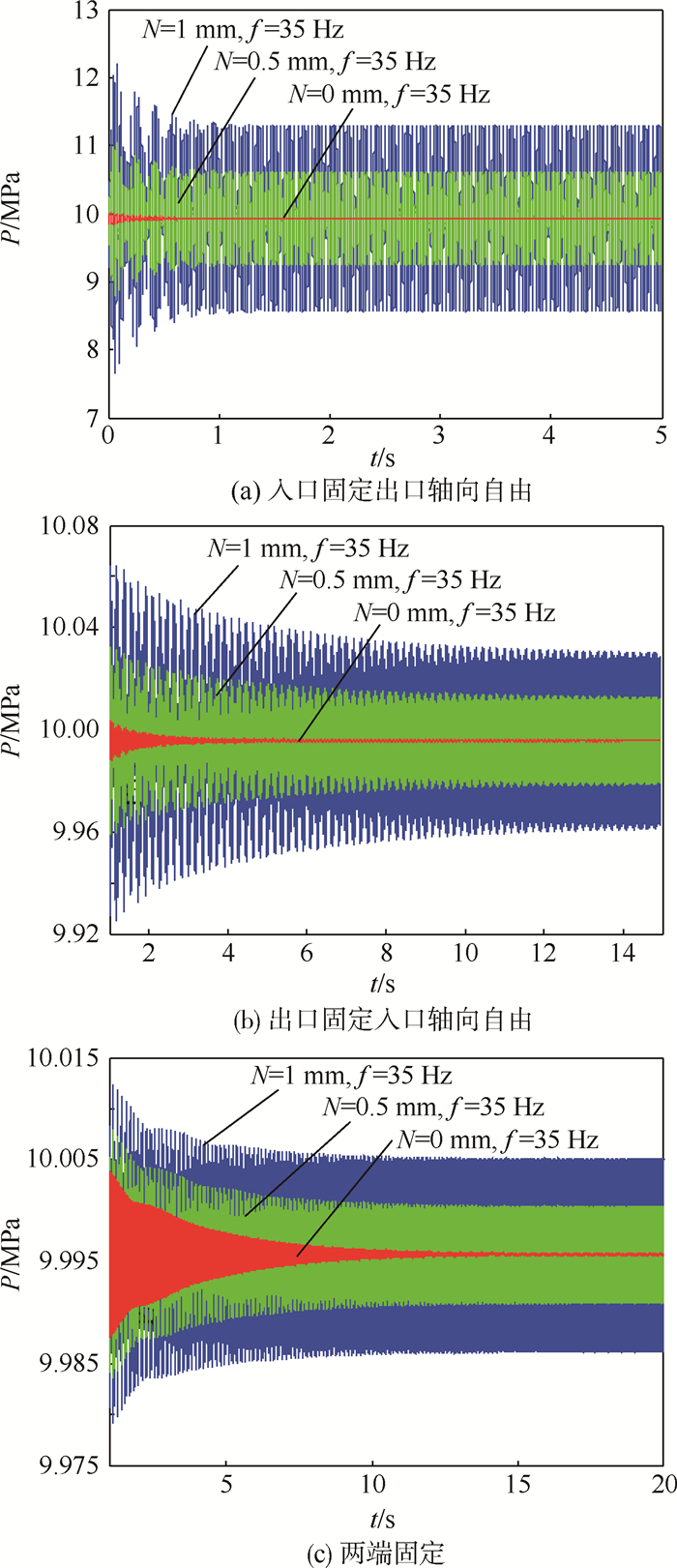| 图 4 入口固定出口轴向自由,出口固定入口轴向自由和两端固定时出口压力的振动响应Fig. 4 Vibration response of outlet pressure with inlet fixed and outlet axial free,outlet fixed and inlet axial free,both ends fixed |
| 图选项 |
由图 4可知,轴向基础振动下,由于流固耦合作用,管道出口流体压力会出现波动,且其平均值会因为压力损失而略小于进口压力值。对于3种不同的管端约束,入口固定出口轴向自由时,管道出口处流体压力波动幅值最大,基础振动幅值为1 mm时其值达到1.32 MPa,入口轴向自由时次之,为0.035 MPa,两端固定时出口压力波动最小,波动幅值只有0.009 MPa,跟两端固定约束方式相比,出口轴向自由和入口轴向自由时出口流体压力波动幅值分别增大了3个和2个数量级,这是因为在基础振动的作用下,管道发生剧烈的轴向振动,并由于流体和管壁之间的相互耦合,使流体产生压力波动,压力波动反过来又影响着管道的振动,彼此间相互作用使振动能量在流体和固体间相互传递。管端轴向自由时,会因管道轴向变形和泊松耦合加剧,流体压能和管壁振动能量之间的转换程度变得更强,更多的基础振动能量流入到流体中,因此压力波动幅值比两端固定约束时大,同时,入口固定出口轴向自由约束时,管道出口附近的管壁轴向运动是轴向基础振动和轴向变形的叠加,在流固耦合中有更多流向流体的转化能量,所以表现出比出口固定入口轴向自由约束时的流体压力波动幅值大。
同时,从同一管端约束的3组不同基础振动来看,基础振动幅值越大,出口流体压力波动越强。单独讨论入口固定出口轴向自由的管道,相同频率(35 Hz)、幅值为1 mm的基础振动作用下的出口流体压力波动幅值是幅值为0.5 mm下波动幅值的1.34倍。这一方面是由于基础振动幅值的增大使管道系统的总振动能量输入增多,从而使传递到流体的振动能量增大,另一方面是因为基础振动幅值的增大加大了流体与管道之间的相对运动,从而加剧了流固耦合的程度,使流体-管道之间的传递能量增多。
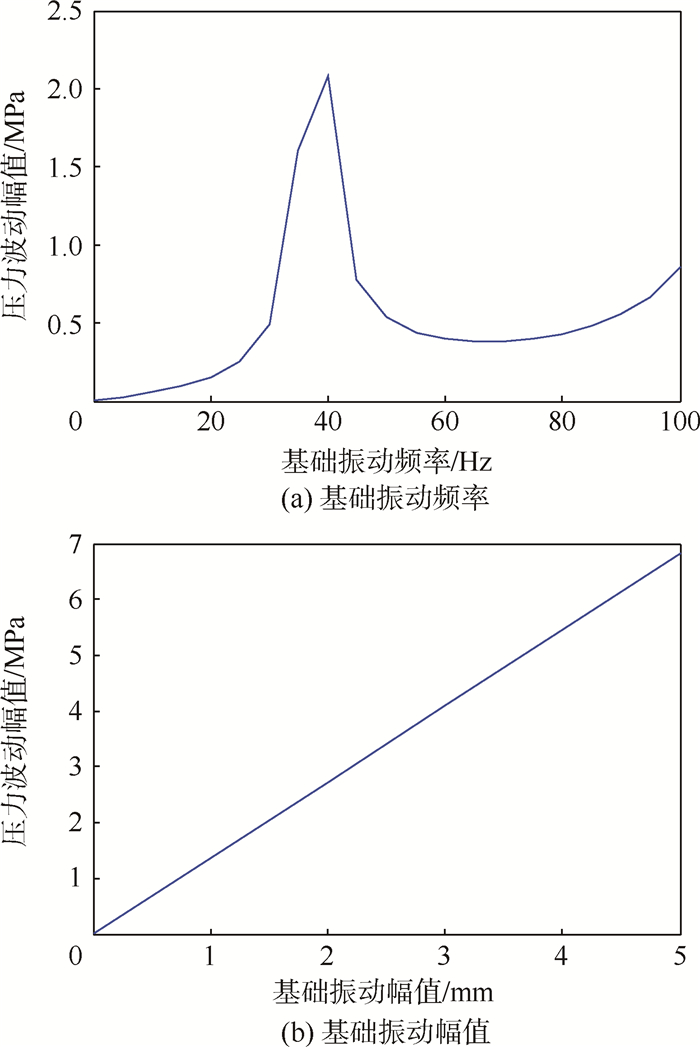
3.2 基础振动对流体振动响应的影响以入口固定出口自由约束管道为例,分析基础振动参数对出口流体压力振动响应的影响规律。图 5(a)和图 5(b)分别给出了出口流体压力波动幅值基础振动幅值和频率的变化规律。
 |
| 图 5 基础振动频率和基础振动幅值对压力波动幅值的影响Fig. 5 Influence of foundation vibration frequency and foundation vibration amplitude on pressure fluctuation amplitude |
| 图选项 |
可以看到,波动幅值随频率的变化先增大后减小,在约40 Hz时达到最大值,此时管道流体出现共振,耦合作用最剧烈。随着频率进一步增大,波动幅值又有增大的趋势,说明基础振动频率越大,管道与流体之间的振动能量传递就越多,大的振动频率不利于流体的稳定性,也表明基础振动频率不仅会因为共振而引起管道振动加剧,从而增大流体波动,还会通过改变流固耦合的作用程度而影响流体波动,另外,压力波动幅值随着基础振动幅值增大而线性增大,35 Hz基础振动频率下,振幅每增大1 mm,压力波动幅值增大1.36 MPa。与2 mm振幅相比,5 mm振幅下的出口压力波动幅值增大了2.43倍。
3.3 约束刚度对流体振动响应的影响以其他参数为定值,改变约束条件为入口固定出口弹性约束(K1=∞,K2=k)时的弹性刚度k,分析约束刚度对管道出口流体波动的影响。
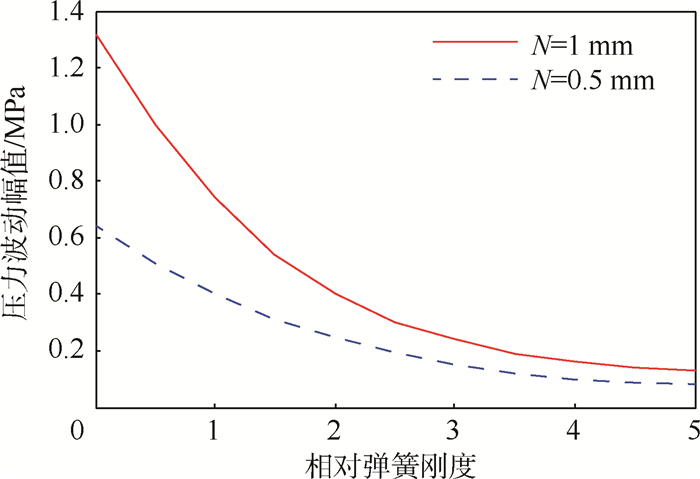
引入相对弹簧刚度k=kL/(EAP),则基础振幅不同时管道出口流体压力波动幅值随相对弹簧刚度k的变化规律如图 6所示。
 |
| 图 6 弹性约束刚度对压力波动幅值的影响Fig. 6 Influence of elastic constraint stiffness on pressure fluctuation amplitude |
| 图选项 |
由图 6可知,随着约束刚度的增大,出口流体压力波动幅值减小,且其减小率越来越小,当相对弹簧刚度k>5时波动幅值基本保持不变,并且越来越接近同一参数设定下两端固定时的值,可认为此时的管道变为两端固定约束。
3.4 结构参数对流体振动响应的影响根据液压管道的实际尺寸范围,以出口固定入口轴向自由管道为例,研究管道长度在1~5 m、厚度在2~10 mm范围内,管道长度和厚度对出口流体压力振动响应的影响,结果如图 7(a)和图 7(b)所示。
 |
| 图 7 管道长度和管道厚度对压力波动幅值的影响Fig. 7 Influence of pipe length and pipe thickness on pressure fluctuation amplitude |
| 图选项 |
结果表明:在1~5 m范围内,随管道长度的增大,压力波动幅值先增大后减小,在约2.5 m处达到最大,这是由于管道约为2.5 m时,管道的固有频率跟仿真时所设定的基础振动频率接近,管道发生共振,使流固耦合程度迅速增强,从而导致流体压力波动幅值显著增大。
随着管壁厚度增加,管道刚度的增大会使管道自由端截面轴向运动速度减小,流固耦合程度和流体-管道之间能量的传递将减小,从而引起出口流体压力波动幅值减小,且厚度越大波动幅值的减小率越小。
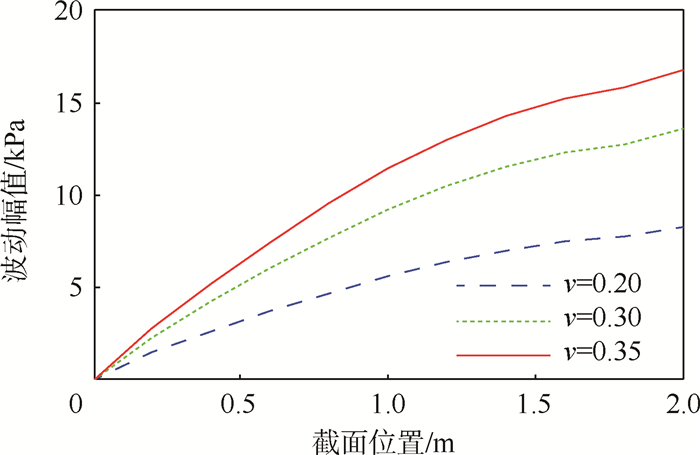
3.5 泊松比对流体振动响应的影响泊松耦合是管道和流体之间能量传递和转换的重要因素,对管道动态特性的影响极为明显;同时流体和固体的耦合长度也会直接影响到流体的动态特性,因此,对于一定长度的管道,其从入口到出口不同截面上的流体受耦合距离的不同,会出现不同的波动幅值,图 8给出了3种泊松比下入口端自由出口端固定约束管道流体压力的波动幅值随不同截面的变化情况。
 |
| 图 8 不同泊松比下各截面位置的压力波动Fig. 8 Pressure fluctuation of each section with different Poisson’s ratio |
| 图选项 |
结果显示,流体流经管道的距离越长,流体压力波动幅值越大,这是因为大的流经长度增加了流体与管道之间的能量转换的时间和空间,流体获得了更多的振动能量,从而加大了流体的波动。但流体的波动幅值随截面位置的变化并非严格的线性增大,而是越接近出口其增长率越小,特别是到出口附近时,受出口边界条件的限制,会使曲线出现小幅度下凹。从不同泊松比的角度来看,泊松比越大,同一截面上流体的波动幅值越大,与泊松比ν=0.20相比,泊松比为0.30和0.35时管道出口处流体压力的波动幅值分别增大了1.74倍和2.15倍,说明泊松耦合对管道的影响不能被忽略。
4 结 论1) 跟两端固定约束相比,出口轴向自由和入口轴向自由时流体出口压力波动幅值分别增大了3个和2个数量级,且出口处约束刚度越大,压力波动幅值越小。
2) 入口端自由出口端固定时,流体流经管道的距离越长,流体波动越剧烈;泊松比越大,同一截面上流体的波动幅值越大,泊松耦合对管道的影响不能被忽略。
参考文献
| [1] | TIJSSELING A S.Water hammer with fluid-structure interaction in thick-walled pipes[J].Computers and Structures,2007,85(1):844-851. |
| Click to display the text | |
| [2] | JEONG H Y,INABA K.Fluid-structure interaction in water-filled thin pipes of anisotropic composite materials[J].Journal of Fluids and Structures,2013,36(2):162-173. |
| Click to display the text | |
| [3] | RIEDELMEIER S,BECKER S,SCHLUCKER E.Measurements of junction coupling during water hammer in piping systems[J].Journal of Fluids and Structures,2014,48(2):156-168. |
| Click to display the text | |
| [4] | HAN J H,KIMA Y J,KARKOY M.Wave propagation modeling of fluid-filled pipes using hybrid analytical/two-dimensional finite element method[J].Wave Motion,2014,51(1):1193-1208. |
| Click to display the text | |
| [5] | 吕海艳.输流管道流固耦合振动的频域分析[D].南京:河海大学,2006:10-18. LV H Y.Anaylsis of fluid-structure interaction eeffct on frequency domain in delviery pipeline[D].Nanjing:Hehai University,2006:10-18(in Chinese). |
| Cited By in Cnki (9) | |
| [6] | 杨超,范士娟.输液管道流固耦合振动的数值分析[J].振动与冲击,2009,28(6):2148-2157. YANG C,FAN S J.Numerical ananlysis of fluidstructure coupling vibration of fluid-conveying[J].Journal of Vibration and Shock,2009,28(6):2148-2157(in Chinese). |
| Cited By in Cnki (25) | |
| [7] | 杨超.非恒定流充液管系统耦合振动特性及振动抑制[D].武汉:华中科技大学,2007:9-16. YANG C.Vibration characteristics of unsteady-fluid-filled pipe system and vibration restrain[D].Wuhan:Huazhong University of Science and Technology,2007:9-16(in Chinese). |
| Cited By in Cnki (22) | |
| [8] | PEROTTI L E,DEITERDING R,INABA K,et al.Elastic response of water-filled fiber composite tubes under shock wave loading[J].International Journal of Solids and Structures,2013,50(7):473-486. |
| Click to display the text | |
| [9] | KUCIENSKA B,SEYNHAEVE J M,GIOT M.Friction relaxation model for fast transient flows application to water hammer in two-phase flow-The WAHA code[J].International Journal of Multiphase Flow,2008,34(1):188-205. |
| Click to display the text | |
| [10] | ROCHA R G,DE FREITAS RACHID F B.Numerical solution of fluid-structure interaction in piping systems by Glimm's method[J].Journal of Fluids and Structures,2012,28(2):392-415. |
| Click to display the text | |
| [11] | ZHU H J,ZHANG W L,FENG G.et al.Fluid structure interaction computational analysis of flow field shear stress distribution and deformation of three-limb pipe[J].Engineering Failure Analysis,2014,42(1):252-262. |
| Click to display the text | |
| [12] | 谢敬华.盾构液压系统流固耦合长管道效应研究[D].长沙:中南大学,2010:12-15. XIE J H.Long pipeline effect of the shield machine based on fluid-structure interaction[D].Changsha:Central South University,2014:12-15(in Chinese). |
| Cited By in Cnki (2) | |
| [13] | 李松,马建中,高李霞,等.水锤引起的管道振动特性分析[J].核动力工程,2008,29(6):25-29. LI S,MA J Z,GAO L X,et al.Analysis of pipeline evirbation induced by water hammer[J].Nuclear Power Engineering,2008,29(6):25-29(in Chinese). |
| Cited By in Cnki (10) | |
| [14] | 李飞,孙凌玉,张广越,等.圆柱壳结构入水过程的流固耦合仿真与试验[J].北京航空航天大报,2007,33(9):1117-1120. LI F,SUN L Y ZHANG G Y,et al.Smiulation and expermient of cylinder shell structure dropping into water based on fluid structure interaction[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(9):1117-1120(in Chinese). |
| Cited By in Cnki (14) | |
| [15] | ARICI M E.Heat transfer analysis for a concentric tube heat exchanger including the wall axial conduction[J].Heat Transfer Engineering,2010,35(2):152-159. |
| Click to display the text | |
| [16] | 何永森,刘邵英.机械管内流体数值预测[M].北京:国防工业出版社,1999:76-85. HE Y S,LIU S Y.Numerical prediction of fluid in mechanical pipe[M].Beijing:National Defense Industry Press,1999:76-85(in Chinese). |
