文献[3]提出了一种基于行为协同和虚拟目标相结合的动态航路规划方法,将规划行为分为局部规划行为和全局规划行为.文献[4]采用部分可观测马尔可夫决策过程引导无人机跟踪地面运动目标.文献[5]采用改进的人工势场法,将相对速度引入势能函数中,使其适用于动态环境.文献[6, 7]采用模型预测控制(MPC)中的滚动优化策略,用局部最优代替全局最优.上述方法虽然能较有效地规划二维动态航路,但扩展到三维复杂飞行环境下,它们的计算效率将大幅降低,无法满足实时性要求.此外,上述方法规划出的航路不够平滑,因此需要额外的航路平滑,影响计算效率.
与上述算法相比,流函数法[8]作为人工势场法的一种变形,由于其快速性与平滑的航路特性,可有效应用在二维动态飞行环境中[9].该方法通过对速度势函数求导获得流线速度,然后对流线速度进行积分即可得到流线,即无人机的规划航路,但该方法在三维环境下往往得不到完整的解析式.文献[10]采用基于流水避石原理的三维航路规划算法,将流体计算与航路规划相结合,规划出具有流体特性且符合无人机约束的航路,该方法具体可分为解析法与数值法.解析法虽然仅能处理球形障碍但计算量很小,因此适用于简单地形下的快速航路规划,数值法计算较繁琐但可处理各种障碍,因此适用于复杂地形下的离线航路规划.因此,文献[11, 12]提出了一种应用于三维环境下的基于流体扰动动态系统的无人机快速避障算法,该算法不会改变原系统的稳定性,可处理多种静态或动态威胁,且计算效率满足动态航路规划的实时性要求,但未考虑运动目标等情况以及动态环境下的路径优化问题.
综合以上分析,针对复杂动态环境下存在运动目标、移动威胁与突发威胁等多种情况,本文提出了基于动态流体扰动算法与滚动优化策略相结合的混合航路规划算法.基于文献[10, 11, 12],本文采用动态流体扰动计算方法,将其与复杂航路规划相结合,处理多种动态情况,保证无人机在跟踪运动目标的同时躲避动态威胁与突发威胁;基于文献[6, 7],本文考虑未来运动态势,加入滚动预测与优化策略,通过滚动优化反应系数进行局部航路寻优,从而保证航路的可飞性与次优性.
1 动态航路规划问题描述无人机动态航路规划问题可看作带约束的实时优化问题.在实际飞行环境中,无人机除躲避地形等静态障碍外,往往还需在跟踪运动目标的同时避开地面雷达车、移动火炮等威胁.由于运动目标、动态威胁等是不断变化的,因此无人机需要根据实时的探测信息进行运动预测,判定未来运动态势.然后,将预测信息与探测信息、飞行任务要求、无人机机动性能等作为约束条件,在线快速生成能满足某种最优指标的可飞航路.给定无人机的规划空间为O-xyz,空间中任意点坐标P=(x,y,z),运动目标的初始位置为Pd0=(xd0,yd0,zd0),目标的最终位置为Pdf=(xdf,ydf,zdf),无人机起始状态即出发点为P0=(x0,y0,z0),无人机到达运动目标点附近时规划结束,无人机最终状态为Pf=(xf,yf,zf)≈Pdf.航路规划的任务就是在规划空间内寻找K个航路点{P1,P2,…,Pk,…,PK},组成最终规划航路,其中满足P1=P0,PK=Pf.
在本文中,为了简化分析,需作如下假设:
假设1 运动目标假定为质点,所有障碍和威胁等均用圆球、圆锥、圆柱、长方体等标准的凸多面体等效[11]:
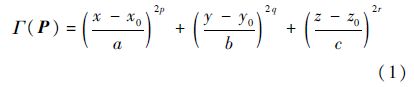
式中:常数a、b、c和p、q、r分别决定凸面体的大小与形状;(xO,yO,zO)表示凸面体的中心;Γ(P)=1即为障碍物表面方程.
假设2 当前时刻的运动目标信息与动态威胁信息可在线获得.
假设3 未来有限时域内,运动目标、移动威胁的位置、速度等信息可通过卡尔曼滤波预测等方法得到[13],本文不再赘述.
假设4 移动威胁的速度ut满足ut<umax,运动目标速度ud满足ud<umax,其中,umax为无人机的最大飞行速度.当无人机与目标点的距离在一定范围内时即认为规划结束,突发威胁在无人机飞入其威胁区域之前探测到.
2 静态环境下的流体扰动算法流体扰动算法可应用于静态环境下的航路规划.静态环境下,在目标点处引入汇流作为初始流场[11],汇流是一种以恒定流速均匀地从四周流入目标点的流体,因此当不存在障碍物或威胁时,无人机以任意一点作为起始点都能沿直线到达目标,如图 1(a)所示.当规划空间中存在静态障碍物时,障碍物的扰动使得初始流场发生改变,但受扰动流场仍具有全局收敛性与稳定性,即流场流线仍能够绕开障碍物并到达目标点,如图 1(b)所示.由此可知,静态环境下的流体扰动算法的关键在于求解扰动后的流场流速.
 |
| 图 1 流体扰动示意图 Fig. 1 Schematic of disturbance of flow |
| 图选项 |
静态环境下的流体扰动算法步骤如下:首先建立初始流场,然后将障碍物对初始流场的扰动影响量化表示,通过修正初始流场流速获得扰动流场流速,最后对其迭代积分,即可得到扰动流场流线即无人机规划航路.
2.1 初始流场以汇流作为初始流场,其流速u(P)定义为
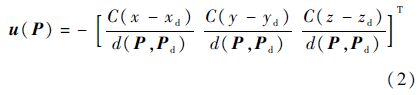
式中:C为汇流速率;d(P,Pd)为无人机位置P(x,y,z)与目标位置Pd(xd,yd,zd)的距离:
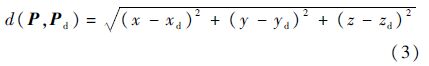
当环境中不存在障碍物时,u(P)作为无人机的飞行速度且满足|u(P)|=C.基于不同无人机飞行速度的差异性,常数C取为无人机巡航速度.
2.2 扰动流场假设环境中有W个障碍物,将障碍物对初始流场的扰动用扰动矩阵$\bar{M}$(P)量化表示[12]:
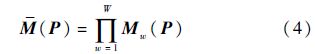
式中:Mw(P)为第w个障碍物的扰动矩阵:
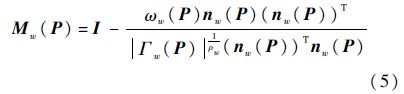
式中:I为单位矩阵;ρw为第w个障碍物的反应系数;Γw(P)为按式(1)获得的第w个障碍物方程;ωw(P)为第w个障碍物的权重系数;nw(P)为第w个障碍物的径向法向量:
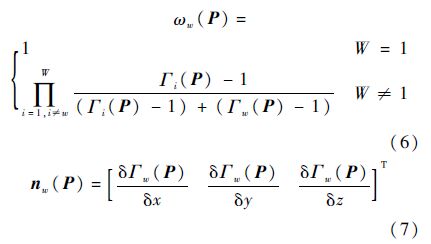
然后修正初始流场流速,得到扰动流场流速:
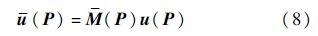
通过积分$\bar{u}$(P),获得下一航路点:
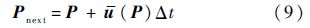
式中:Δt为计算步长.如此迭代求解得到一系列离散点,将其连线即形成扰动流线,即规划航路.
流体扰动算法生成的流线符合流水避石的一般特性:①流线可躲避各种障碍.②流线最终到达目标点.③在障碍物外部不存在局部极小点即$\bar{u}$(P)≠0.④初始阶段无人机距离障碍物较远时,扰动流线沿初始流线方向运动;当逐渐靠近障碍时,流线平滑地趋近障碍物切线方向;远离障碍后,又回到初始流线上.本文不再详细证明.
2.3 扰动流场分析由式(5)可知,当无人机距离障碍物越远时,Γw(P)越大且ωw(P)越趋近于0,Mw(P)越趋近于单位矩阵,当距离足够远时即可忽略该威胁对总扰动流场的影响.因此扰动流场主要受到距离无人机当前位置较近的几个威胁的共同影响.
由式(5)可知,扰动矩阵的选取与各个障碍的反应系数ρw密切相关.通常反应系数越大,该障碍物对流场的扰动作用越大,即流线躲避障碍的时机越早且幅度越大,通过组合调整不同障碍物的反应系数,获得各种形状的扰动流线.当反应系数选取不合适时,威胁的相互作用甚至会导致航路规划停止或在局部区域内徘徊的现象.因此,针对所有威胁(尤其是距离无人机较近的威胁),需选取合适的反应系数,具体见第4节.
此外,由第2.2节知,本文得到的流场符合自然界中的绕流特性,流速大小是实时变化的,因此无人机不再是恒速飞行.为保证$\bar{u}$(P)满足无人机飞行速度约束,也需选取合适的障碍物反应系数,具体分析见第4节.
3 动态流体扰动算法从相对流场的角度出发,将上述静态流体扰动算法改进,使其应用于复杂动态环境下,即为本文的动态流体扰动算法.
若目标点是运动的,在汇流速度的基础上引入目标运动速度,因此当不存在障碍物或威胁时,相对于运动目标,无人机仍沿汇流方向接近目标点.当规划空间中存在移动威胁时,引入威胁运动信息,构建相对初始流场[12].在相对初始流场内,由于移动威胁可等效为静态障碍物,因此可采用静态流体扰动方法计算相对扰动流场,进而得到实际流场,流线仍具有全局收敛性与稳定性.
3.1 相对初始流场无人机跟踪运动目标时,初始流场的定义不仅要考虑目标位置,还需考虑目标运动速度ud:
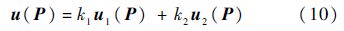
式中:u1(P)为第2.1节中的汇流流速;u2(P)为目标运动速度ud;k1和k2分别为两种速度的权重系数,定义如下:
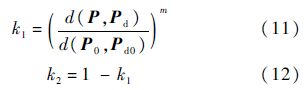
式中:d(P0,Pd0)为无人机初始位置P0与目标初始位置Pd0的距离;m为大于零的常数,它的取值决定了两种速度分量u1(P)和u2(P)的变化快慢,进而影响初始流线形状.当无人机在初始位置时,k1=1,k2=0,u(P)=u1(P);当无人机离目标点较远时,0<k2<k1<1,计算初始流场流速时主要考虑汇流速度;当无人机逐渐靠近目标点时,k1减小而k2增大,流场速度同时考虑了汇流速度与目标运动速度;当无人机足够接近目标点时,0<k1<k2<1,此时主要考虑目标运动速度;若无人机在目标点,k1=0,k2=1,u(P)=u2(P).
假设环境中有W个移动威胁时,依据它们的运动速度、当前位置等信息,计算所有威胁的总参考运动速度[14]为
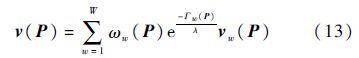
式中:λ为常数,且λ越大,流线躲避威胁的时机越早;vw(P)为第w个威胁的运动速度;ωw(P)为第w个威胁的权重系数.
构建相对初始流场,流速定义为u(P)-v(P).
3.2 相对扰动流场在相对初始流场下,移动威胁可看作是静止的,因此在实时更新移动威胁或突发威胁的位置信息后,可按式(4)~式(7)计算扰动矩阵$\bar{M}$(P).然后,类似于式(8),计算相对扰动流场的流速:

那么实际扰动流场流速为
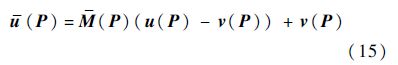
综上所述,动态流体扰动算法的步骤如下.
步骤1 依据运动目标的实时信息,按式(10)~式(12)计算初始流场速度u(P),然后依据移动威胁的运动信息,按式(13)计算参考速度v(P),从而构建相对初始流场,其流速为u(P)-v(P).
步骤2 依据动态威胁或静态障碍的实时位置信息,按式(4)~式(7)计算扰动矩阵$\bar{M}$(P).
步骤3 按式(14)计算相对扰动流场速度$\bar{u}$(P)-v(P),然后按式(15)得到速度$\bar{u}$(P).
步骤4 迭代积分$\bar{u}$(P),获得下一航路点.
步骤5 返回步骤1,直至到达目标点附近.
当无人机到达第w个运动威胁表面时,Γw(P)=1,由式(6)得ωw(P)=1且ωi(P)=0,i≠w,此时v(P)=vw(P),此时相当于无人机躲避单个移动威胁.由于动态流体扰动方法可等效为相对流场下的静态流体扰动算法,而后者规划出的流线具有良好的避障特性,因此该方法能使无人机躲避动态威胁.采用动态流体扰动算法,由于相对于运动目标的初始流场仍为汇流,所以扰动流线最终仍到达目标点.
4 反应系数滚动优化策略动态流体扰动算法仅考虑了当前环境信息,未考虑威胁的未来运动态势,规划轨迹可能会出现大拐角等情况.此外,由第2.3节可知,所有威胁(尤其是距离无人机较近的威胁)的反应系数决定了无人机的避障时机、避障幅度以及飞行速度,而它的选取只依靠经验,因此不能保证航路的最优性,有时甚至会出现不可飞情况.
为解决上述问题,本文借鉴滚动优化原理[7],将滚动优化策略与流体扰动算法结合:设定有限步优化时域,依据实时检测到的动态威胁或目标等信息,预测未来它们的运动状态,采用动态流体扰动算法获得局部航路,然后通过优化反应系数,寻找满足无人机动力学约束与环境约束的局部可飞最优航路;随着预测步数增多,预测精度会降低,影响航路规划的准确性,因此只依局部航路飞行一步,然后重复上述动作,引导无人机完成飞行任务.利用此方法,可以充分考虑未来运动态势,提前确定大致的可靠飞行航路.
假设k时刻,无人机运动到Pk处,用扰动流体算法规划未来N步航路,然后构建航路评价函数J(k)作为航路评估的依据,通常J(k)越小,航路越优.首先考虑无人机的机动能力约束:采用流体扰动算法时,无人机速度不是恒定的,因此需考虑最大与最小飞行速度约束;考虑到无人机的纵向与横侧向机动能力限制,规划航路需满足最大爬升角约束、最大转弯角约束;基于无人机的具体飞行任务,还需设定爬升高度约束.当规划航路超过上述任意约束边界时,无人机是无法飞行的,为体现出这种约束效力,此时直接将J(k)取为无穷大正值.当规划航路满足上述各种约束条件时,才计算目标函数J(k),包括航路长度代价、飞行安全代价、航路跟踪代价:
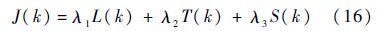
式中:L(k)为航路长度代价;T(k)为飞行安全代价;S(k)为规划航路的跟踪代价;λ1、λ2和λ3分别为3种代价的加权因子且满足λ1+λ2+λ3=1,可根据具体的飞行任务对它们进行赋值.
L(k)不仅要考虑未来N步航路的长度,还要考虑该N步航路之后的航路总长度:
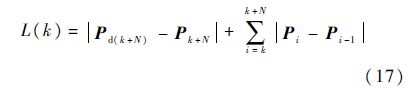
式中:用|Pd(k+N)-Pk+N|粗略表示N步航路之后的航路长度,Pk+N和Pd(k+N)分别为k+N时刻的无人机规划位置与目标预测位置.
假设飞行环境中有W个障碍或威胁,k时刻第w个障碍或威胁的安全代价定义[15]为
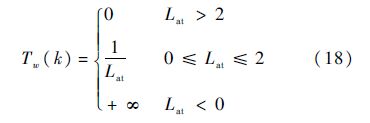
式中:Lat为无人机到障碍物或威胁表面的距离.当无人机在障碍物或威胁的影响范围内即0≤Lat≤2 km时,考虑到无人机的机动性能等因素,将安全代价定义为1/Lat;当无人机落入障碍或威胁的内部区域即Lat<0时,此时安全代价为无穷大的正值,作为安全代价的惩罚项;当无人机距离障碍物足够远即Lat>2 km时,认定无人机是安全的.N步时域内,考虑所有障碍物或威胁的总安全代价为
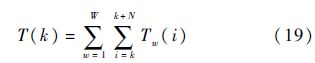
引入S(k),从而提高规划轨迹的平滑性,使得所规划的路径较易跟踪.考虑到路径的平滑性,需减少大机动次数,此时S(k)定义为
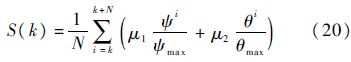
式中:ψi和θi分别为第i段航路的转弯角和爬升角;ψmax和θmax分别为最大转弯角和最大爬升角;S(k)为N步规划航路的平滑度,S(k)越小,表示路径平滑性越好.
然后,通过优化所有威胁(尤其是距离无人机较近的威胁)的反应系数,即得到k时刻的最优反应系数组合:
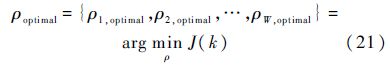
上述反应系数组合对应的N步航路即可作为局部最优航路.类似于MPC控制中的单步控制策略,本文只选取其中的第一个航路点作为下一航路点,到达下一采样时刻后重复以上过程,即可实现滚动规划.
优化时域N的选取是该航路规划算法成败的关键.N过小时,无人机不能充分考虑移动威胁或目标的未来机动特性,航路优化效果不理想;当N过大时,运算时间增长,而且预测信息精度将明显降低.
5 仿真与分析在MATLAB R2011a中进行仿真验证,计算机处理器为Intel Core i5,主频2.5 GHz.设定无人机巡航速度即初始飞行速度C=150 m/s,无人机最大飞行速度为290 m/s,最小飞行速度为60 m/s,爬升角约束范围[-15°,15°],转弯角约束范围[-30°,30°],高度约束范围[0.1,3]km,采样间隔Δt=1 s,加权因子λ1=0.3,λ2=0.5,λ3=0.2,假设任意障碍或威胁的反应系数取值范围为[0.1,10].由于遗传算法等智能优化方法的计算量和存储量太大,不适于在线应用,为提高实时性,采用障碍物反应系数的有限离散集合U={U1,U2,…,U50},寻找次优解.
5.1 静态环境下的航路规划在规划空间内定义18个圆柱形静态障碍,如图 2所示,假设无人机初始位置(0,0,1)km,目标点位置(10,10,1)km,无人机定高飞行,由图可知在规划空间中从目标点到出发点仅存在唯一飞行通道.采用静态流体扰动算法,并通过全局优化调整障碍物反应系数[11],最终获得可飞航路,验证了算法的完备性.
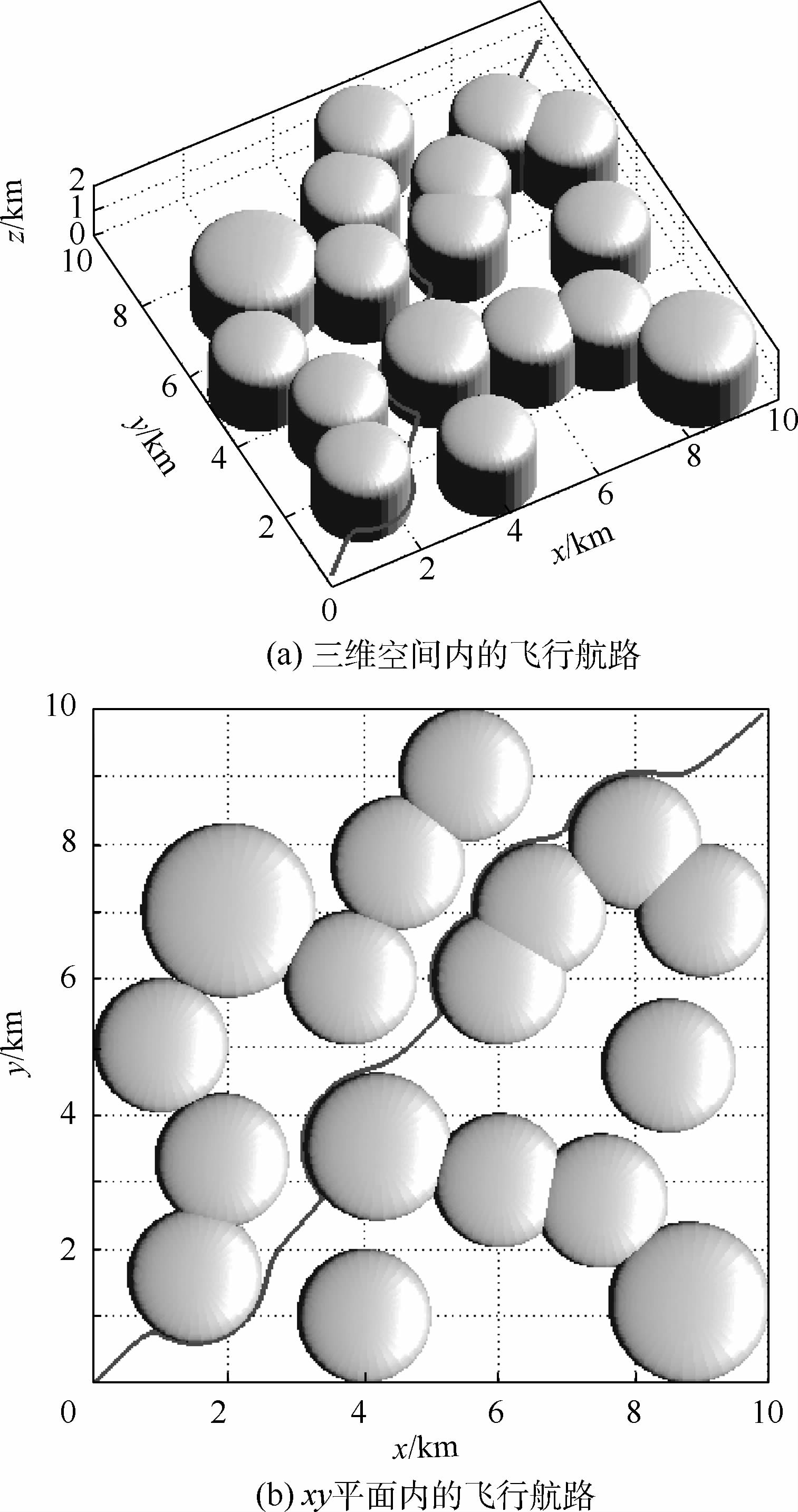 |
| 图 2 静态环境下的无人机航路 Fig. 2 Path of UAV in static environment |
| 图选项 |
5.2 无障碍或威胁时跟踪运动目标的航路规划当环境中不存在障碍物或威胁时,由式(10)确定的初始流线即可作为无人机的飞行航路.假设运动目标的初始位置(0,3,0.5)km,以恒定速度(0.1,0,0)km/s向右移动,无人机起始点为(0,0,0.5)km.m取不同值时的无人机航路与目标轨迹如图 3(a)所示,无人机与目标点的距离如图 3(b)所示,m越小,无人机越早接近目标点,但m过小,会引起航路的振荡,而且航路可能不满足无人机的飞行约束.m=0.5为比较合适的取值,此时无人机较为快速地接近运动目标,而且航路平滑无振荡,满足性能约束.
 |
| 图 3 无障碍情况下的无人机航路与移动目标路径 Fig. 3 Paths of UAV and moving target without obstacles |
| 图选项 |
5.3 目标静止情况下躲避运动威胁的航路规划当目标静止时,将汇流速度作为初始流速.假设球形威胁沿S形曲线移动,无人机的起始点(0,0,0.1)km,目标是静止的,位于(9,9,0.2)km处.图 4(a)为N=3和N=6时的仿真结果,图 4(b)为两种情况下无人机与威胁表面的距离(Lat).当N=3时,无人机飞行过程中与移动威胁表面的最小距离为0.79 km,可避开该威胁;但由于优化时域过小,无人机未充分考虑威胁的运动趋势,所以当动态威胁在65 s左右加速运动时,相应地规划航路在(7.7,5.8,0.13)km附近出现大拐角,很明显是不可飞的.当N=6时,无人机飞行过程中与威胁表面最小距离0.80 km,也能成功避开该威胁;而且,由于优化时域比较合理,充分考虑了未来的运动态势,避障航路较为平滑,满足飞行约束条件.
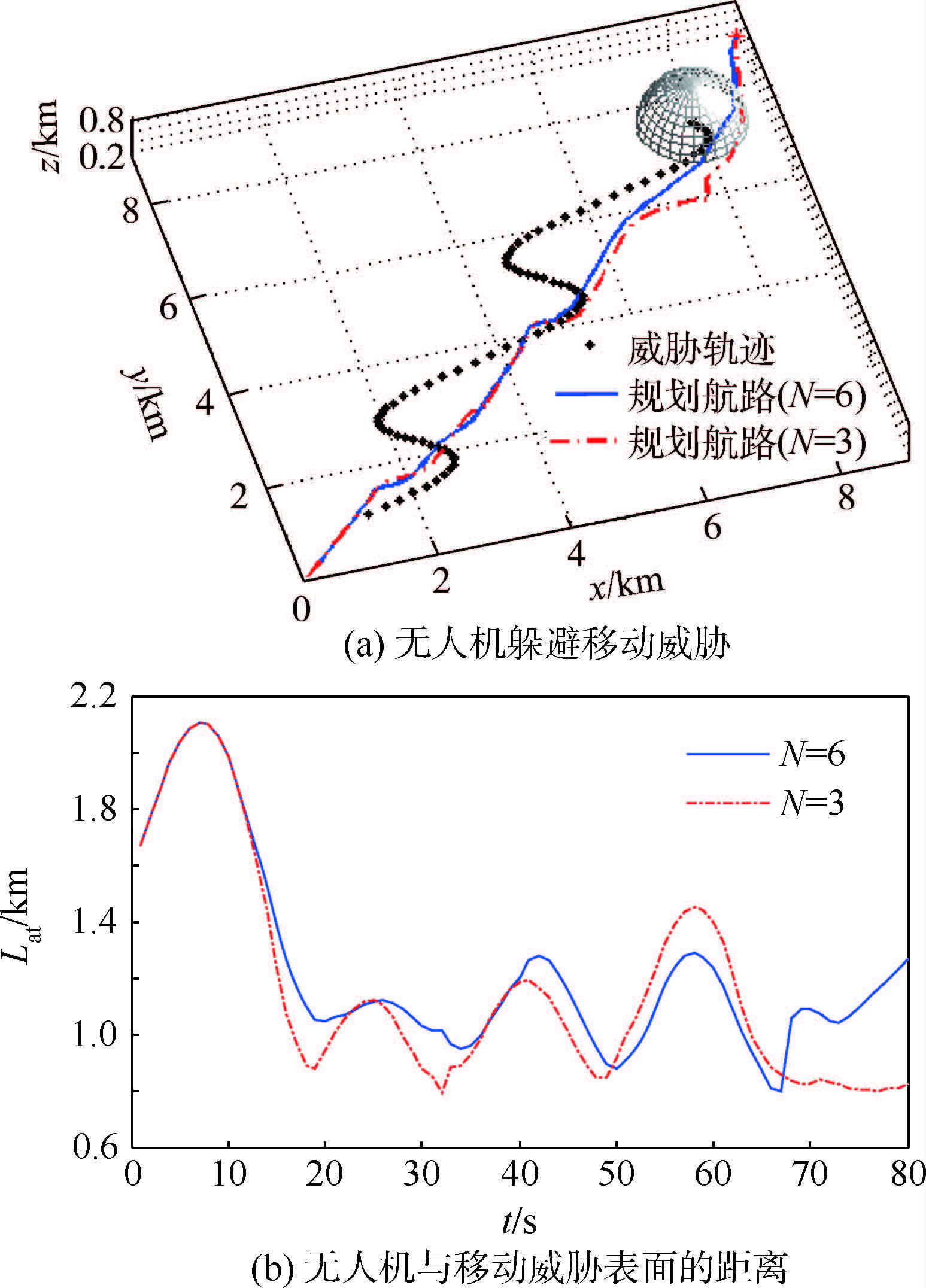 |
| 图 4 目标静止时的无人机航路与运动威胁轨迹 Fig. 4 Paths of UAV and moving threat with static target |
| 图选项 |
5.4 复杂环境下的动态航路规划在11 km×11 km×2 km空间内,随机生成圆锥、圆柱、圆球等固定障碍,同时加入移动球形威胁、突发球形威胁、运动目标等.假设移动威胁在xy平面内沿正弦曲线运动,运动目标沿圆弧线运动,突发威胁1的出现时间为13 s,突发威胁2的出现时间为125 s,优化时域N=5.航路规划过程如图 5所示.图 5(a)规划开始;图 5(b)突发威胁1出现,无人机成功躲避该威胁;图 5(c)由于考虑运动威胁的未来运动信息,无人机成功躲避了该动态威胁,且整个规划过程中无人机到该威胁表面的最小距离为0.32 km;图 5(d)表明无人机跟踪运动目标的同时仍能躲避突发威胁2;图 5(e)规划结束.在该仿真过程中,获得下一航路点的计算时间范围为[0.53,0.76]s,而当前航路点到下一航路点的飞行时间为1 s,因此满足实时性要求.
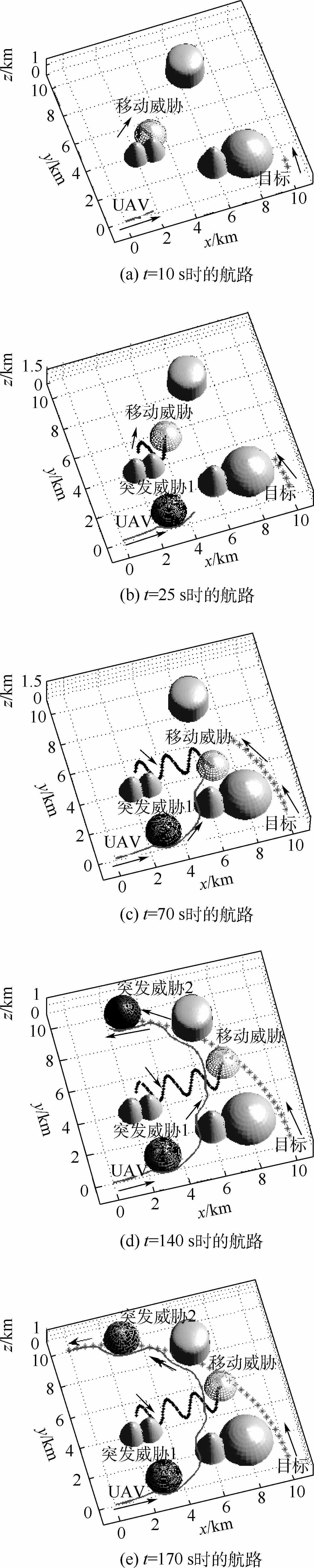 |
| 图 5 复杂动态环境下的无人机航路 Fig. 5 Path of UAV in complex dynamic environment |
| 图选项 |
6 结 论本文将动态流体扰动算法的避障优势与模型预测算法的滚动优化策略相结合,提出一种适用于复杂动态环境下的无人机三维航路规划算法.
1) 静态环境下,流体扰动算法生成的流线即无人机规划航路,符合流水避石现象的一般特性:流线平滑地躲避各种障碍物,并最终到达目标点.
2) 动态流体扰动方法可等效为相对流场下的静态流体扰动算法,因此算法仍具有全局收敛性与稳定性,且适用于动态环境下的无人机多种飞行任务.
3) 考虑到最优性与可飞性要求,利用滚动优化思想,通过优化流体扰动算法中的反应系数,最终可得到满足无人机约束的次优可飞航路.
4) 通过理论分析与实验验证,表明该算法的完备性、有效性与实时性,具有一定的应用价值.
参考文献
| [1] | 柳长安.无人机航路规划方法研究[D].西安:西北工业大学,2003. Liu C A.Study on UAV path planning method[D].Xi'an:Northwestern Polytechnical University,2003(in Chinese). |
| Cited By in Cnki (88) | |
| [2] | Chen M,Wu Q X,Jiang C S.A modified ant optimization algorithm for path planning of UCAV[J].Applied Soft Computing,2008,8(4):1712-1718. |
| Click browse the original | |
| [3] | 武善杰,郑征,蔡开元.基于行为协同和虚拟目标相结合的无人机实时航路规划[J].控制理论与应用,2011,28(1):131-136. Wu S J,Zheng Z,Cai K Y.Real-time path planning for unmanned aerial vehicles using behavior coordination and virtual goal[J].Control Theory & Applications,2011,28(1):131-136(in Chinese). |
| Cited By in Cnki (12) | Click to display the text | |
| [4] | Ragi S,Chong E K P.Dynamic UAV path planning for multitarget tracking[C]//2012 American Control Conference.Piscataway,NJ:IEEE Press,2012:3845-3850. |
| [5] | Ge S S,Cui Y J.Dynamic motion planning for mobile robots using potential field method[J].Autonomous Robots,2002,13(3):207-222. |
| Click browse the original | |
| [6] | 任佳,高晓光,张艳.移动威胁情况下的无人机路径规划[J].控制理论与应用,2010,27(5):641-647. Ren J,Gao X G,Zhang Y.Path planning based on model predictive control algorithm under moving threat[J].Control Theory & Applications,2010,27(5):641-647(in Chinese). |
| Cited By in Cnki (11) | Click to display the text | |
| [7] | 张纯刚.基于滚动窗口的移动机器人路径规划[J].系统工程与电子技术,2002,24(6):63-69. Zhang C G.Mobile robot path planning based on rolling windows[J].Systems Engineering and Electronics,2002,24(6):63-69(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [8] | Sullivan J,Waydo S,Campbell M.Using stream functions for complex behavior and path generation[C]//AIAA Guidance,Navigation and Control Conference and Exhibit.Reston:AIAA,2003:1-9. |
| [9] | 梁宵,王宏伦,曹梦磊,等.无人机复杂环境中跟踪运动目标的实时航路规划[J].北京航空航天大学学报,2012,38(9):1129-1133. Liang X,Wang H L,Cao M L,et al.Real-time path planning to track moving target in complex environments for UAV[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(9):1129-1133(in Chinese). |
| Cited By in Cnki (8) | Click to display the text | |
| [10] | 梁宵,王宏伦,李大伟,等.基于流水避石原理的无人机三维航路规划算法[J].航空学报,2013,34(7):1670-1681. Liang X,Wang H L,Li D W,et al.Three-dimensional path planning for unmanned aerial vehicles based on principles of stream avoiding obstacles[J].Acta Aeronautica et Astronautica Sinica,2013,34(7):1670-1681(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [11] | Wang H L,Lyu W T,Yao P,et al.Three-dimensional path planning for unmanned aerial vehicle based on interfered fluid dynamical system[J].Chinese Journal of Aeronautics,2015,28(1):229-239. |
| Click browse the original | |
| [12] | Yao P,Wang H L,Liu C.3-D dynamic path planning for UAV based on interfered fluid flow[C]//2014 IEEE Chinese Guidance,Navigation and Control Conference.Piscataway,NJ:IEEE Press,2014:997-1002. |
| [13] | 王建东,王亚飞,张晶.基于卡尔曼滤波器的运动目标跟踪算法[J].数字通信,2009(6):53-57. Wang J D,Wang Y F,Zhang J.Moving objects tracking algorithm based on Kalman filter[J].Digital Communication,2009(6):53-57(in Chinese). |
| Cited By in Cnki (25) | Click to display the text | |
| [14] | Khansari-Zadeh S M,Billard A.Realtime avoidance of fast moving objects:A dynamical system-based approach[C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway,NJ:IEEE Press,2012:121-126. |
| [15] | 周锐,成晓静,陈宗基.战术任务规划系统研究[J].控制与决策,2004,19(4):441-447. Zhou R,Cheng X J,Chen Z J.Tactical mission planning systems for modern fighter plane[J].Control and Decision,2004,19(4):441-447(in Chinese). |
| Cited By in Cnki (28) | Click to display the text |
