实际转子结构中,由于加工误差、键槽或者直接采用非圆截面轴等原因,转子系统的弯曲平面刚度在两个主方向上存在最大值和最小值,使转子结构呈现出一定的非线性,从而使系统的稳定性发生极大的改变,对外界激励及其变化相当敏感.目前,对非对称刚度转子系统的瞬态动力响应研究取得了长足的进展.刘占生等[2, 3]采用数值积分,发现刚度各向异性系数会引起系统Hopf分岔、四倍周期分岔和混沌运动甚至失稳.Shu、Nandi、Genta等[4, 5, 6]则发展了有限元法对非对称转子的稳定性进行研究.Darpe、邹剑、Sekhar等[7, 8, 9]针对裂纹引起的刚度非对称分析了转子过临界转速时的瞬态振动,指出裂纹对转子稳定性影响极大.
目前,****们都以薄盘转子为研究对象.鉴于厚盘转子要比薄盘转子多出一个固有频率,为研究这类转子通过临界转速时对不平衡激振力的瞬态响应,采用集中参数法,简化成厚盘转子力学模型,本文将分别计算刚度非对称单、厚盘转子在定角加速度($\ddot \varphi $,常数)和定功率($\dot \varphi $L($\dot \varphi $),常数;其中,$\dot \varphi $为定角速度,L($\dot \varphi $)为轴向外力矩,包括主动力矩、阻力矩及重力引起的附加力矩)条件下穿过两阶临界转速的瞬态振动,以定角加速度加速的模式分析厚盘转子瞬态振动的基本性质,以定功率加速的模式分析厚盘转子与外界能源的非线性耦合效应,对比典型薄盘转子系统,尤其关注分析厚盘转子过高阶临界转速的瞬态振动特性,进而为带厚盘转子系统的旋转机械在设计、运行、维护以及故障诊断等工程实际情况下提供参考.
1 转子的动力学方程本文采用集中参数力学模型如图 1所示.
 |
| Oxyz—固定于惯性空间的静坐标系;Oηξρ—跟随转子一同旋转的动坐标系;η,ξ—非圆截面轴的两个主刚度方向;θ—转子极惯性轴与z轴的夹角;φ—自转角;$\dot \varphi $—自转角速度;Ψ—进动角;β—转动涡动差角;a,b—单盘距左右支点距离;e—偏心距;n—盘平面的法向矢量;S—盘心;S(x,y)—盘心在固定坐标系中的位移;A—转子系统支承左支点;B—转子系统支承右支点;C—盘的质心;x′y′—随盘平动(但不转动)的平动坐标系.图 1 单盘转子系统集中参数力学模型Fig. 1 Mechanical model with lumped parameter of single disk rotor system |
| 图选项 |
本模型考虑了刚度不对称转子,转动惯量的主自由度不一定和刚度的主自由度重合,Jξ、Jη分别为η、ξ方向上的径向转动惯量.根据文献[10, 11]在静止坐标系中表示的单盘转子系统的动能、势能及耗散函数,变换到旋转坐标系中,不考虑材料内阻尼耗散,根据Lagrange方程,在旋转坐标系下表示的单盘转子系统的动力学方程如式(1a)、式(1b)所示.其中,q为旋转坐标系下的广义力;根据材料力学,对于如图 1所示的单跨转子系统,则有:位移对力的刚度为kξ,11=3EIξl(a2-ab+b2)/(a3b3),kη,11=3EIηl·(a2-ab+b2)/(a3b3);位移对盘偏角(或弯矩对力)的刚度为kξ,12=kξ,21=3EIξl(a-b)/(a2b2),kη,12=kη,21=3EIηl(a-b)/(a2b2);弯矩对盘偏角的刚度为kξ,22=3EIξl/(ab),kη,22=3EIηl/(ab),其中:E为弹性模量;Iξ和Iη为惯性矩;l=a+b为轴长.

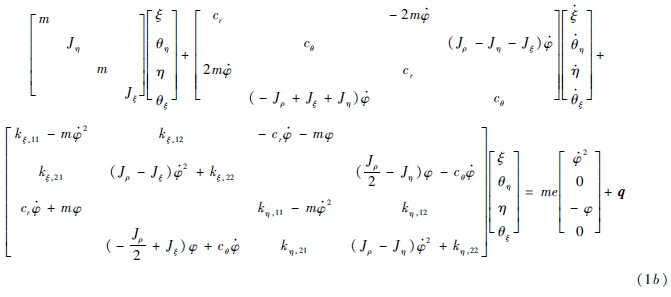
对方程(1a)和方程(1b)无量纲化.定义Jd=(Jξ+Jη)/2,d=(Jη-Jξ)/(Jξ+Jη),则Jξ=(1-d)Jd,Jη=(1+d)Jd;同样地,定义k..=(kξ..+kη..)/2,κ..=(kξ..-kη..)/(kξ..+kη..),则kξ..=(1-κ..)k..,kη..=(1+κ..),k..,..=11,12,22.定义过直径转动惯量的回转半径$\rho {\rm{ = }}\sqrt {{J_{\rm{d}}}/m} ,m$为质量;偏心距与径向回转半径之比$v{\rm{ = }}e{\rm{/}}\sqrt {{J_{\rm{d}}}/m} $;无量纲位移Rξ=ξ/e,Rη=η/e;无量纲角矢量分量分别为Θη=θη/ν,Θξ=θξ/ν;静止固有频率${\omega _n}{\rm{ = }}\sqrt {{k_{{\rm{11}}}}/m} $;无量纲角速度(频率比)$\lambda = \dot \varphi /{\omega _n}$;无量纲角加速度$\alpha = \ddot \varphi /\omega _n^2$;刚度系数${s_1} = {k_{12}}/\left( {{k_{11}}\sqrt {{J_d}/m} } \right),{s_2} = m{k_{22}}/{J_d}{k_{11}}$;位移阻尼比${\zeta _r} = {c_r}/\left( {2\sqrt {m{k_{11}}} } \right)$;偏摆角阻尼比${\zeta _\theta } = {c_\theta }/\left( {2{J_d}\sqrt {{k_{11}}/m} } \right)$;自转角阻尼比${\zeta _\varphi } = {c_\varphi }/\left( {2{J_d}\sqrt {{k_{11}}/m} } \right);{c_r}$为形心运动的位移阻尼;cθ为盘偏摆的偏角阻尼;cφ为转子自转阻尼.
定义无量纲时间τ=ωnt,则$\frac{d}{{dt}} = \frac{1}{{{\omega _n}}}\frac{d}{{d\tau }}$,可得刚性支承单盘转子的无量纲动力学方程式(2)、式(3),其中:$L\left( {\frac{{d\varphi }}{{d\tau }}} \right)$为无量纲轴向扭矩,Q为无量纲广义力.根据方程(3)及文献[1],刚性支承条件、无阻尼单-厚盘偏置转子涡动频率Ω和自转角速度ω的关系曲线,如图 2所示.可见,若工作转速足够高,厚盘转子系统要穿过低阶、高阶临界转速区.


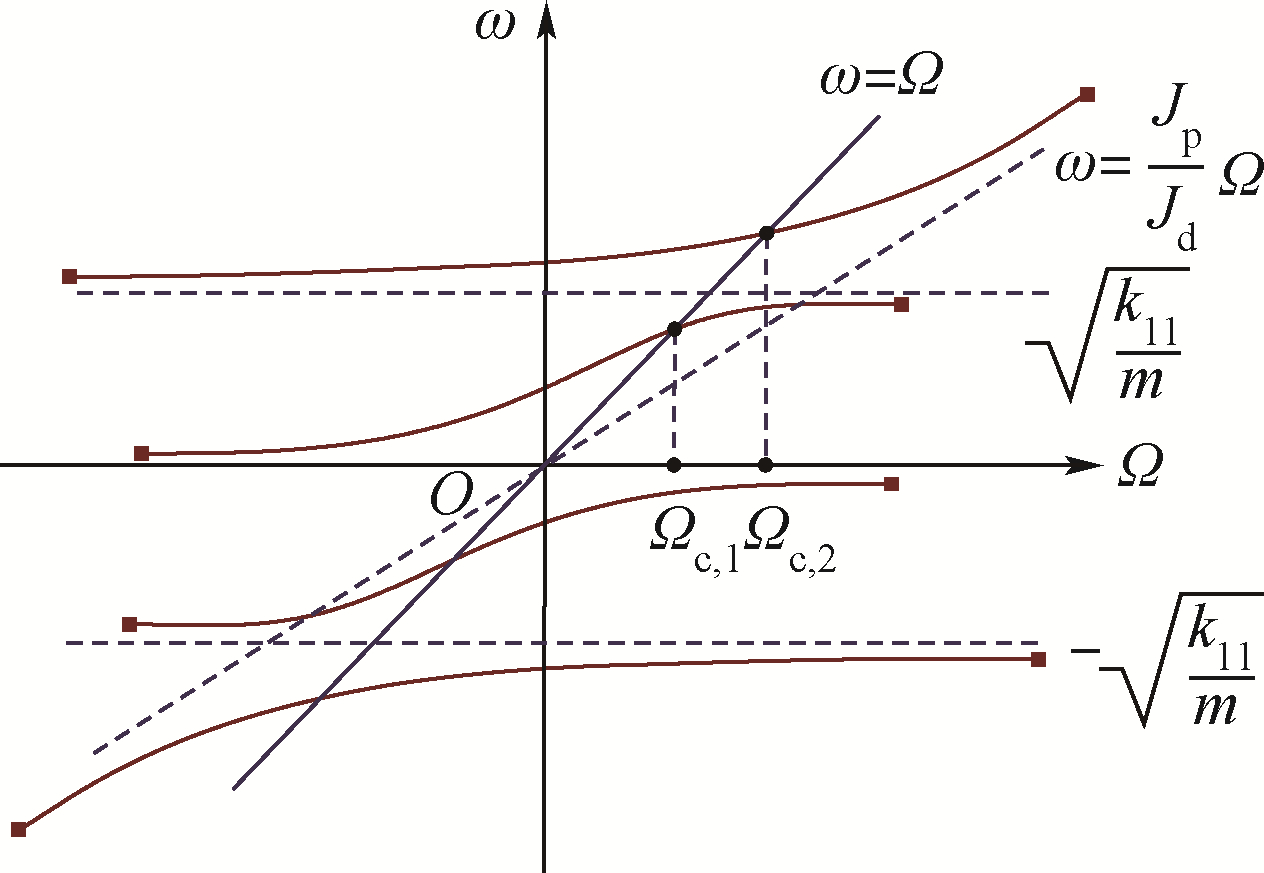 |
| 图 2 刚性支承无阻尼单盘偏置转子涡动频率和自转角速度的关系曲线(μ<1)Fig. 2 Relationship curves between whirl frequency and angular velocity of undamped single disk rotor with rigid support (μ<1) |
| 图选项 |
2 厚盘转子定角加速度过临界转速的瞬态振动特性本节为考察厚盘转子瞬态的基本振动表现,采用定角加速度(φ¨)的直线加速、理想能源模式计算刚度对称厚盘转子的瞬态响应.从零转速状态线性加速,分别通过系统的低阶临界转速和高阶临界转速,分析转子轴的动挠度放大因子、盘的偏摆角放大因子.由于本文建立方程采用旋转坐标系,因此还可以很方便地在旋转坐标系下观察转子形心轨迹,由此判断系统的振动性能和稳定性.可见,转子瞬态响应也是分析系统稳定性的一个重要方法.由于加速度恒定,相当于转子的自转角自由度退化,成为只含有4个广义自由度的系统,方程(2)不参与计算,只需采用Newmark-β法或四阶Runge-Kutta法求解方程(3).为考虑一般单盘转子的回转效应,本文设定盘的位置a=0.4l,l=25rd,rd为盘的半径;采用不同加速比(α=10-4,10-3,4×10-3,10-2),从静止开始加速.对于计及重力效应与否的情况,由于初值不同,将分别予以考虑.
2.1 不计重力的厚盘转子的瞬态振动特性不考虑重力效应的厚盘转子,则单盘转子初值状态为零位移、无偏角.文献[12]对Jeffcott转子过临界转速瞬态振动的分析方法,转子轴的无量纲挠度$\delta = \sqrt {R_\zeta ^2R_\eta ^2} $,则稳态条件下最大临界挠度δmm=1/(2ζr)(同条件下Jeffcott转子发生共振时有阻尼最大挠度),定义动挠度放大因子X=δ/δm;盘的无量纲偏摆角$\Theta = \sqrt {\Theta _\eta ^2 + \Theta _\zeta ^2} $,与转速以及盘在轴上的位置有关,因此取偏摆角放大因子为A=Θ/π.一般地,航空发动机等高精度机械的偏心距与径向回转半径之比在10-3数量级范围内,取ν=10-3;偏摆角阻尼比ζθ和自转角阻尼比ζφ经过无量纲处理后在10-4数量级,取ζθ=ζφ=2.5×10-4,位移阻尼比ζr=0.02.
由图 2可见,厚盘转子的高阶临界转速与μ有极大的关系.为了能迅速观察到转子过高阶临界转速的瞬态振动表现,减小计算时间和计算量,不失一般性,本文采用较小的μ值,分别设定μ=0.07,0.05,0.02作为厚盘参数,计算了厚盘转子过低阶、高阶转速时轴的动挠度和盘的偏摆角,如图 3(a)~图 3(f)所示,分析厚盘转子的瞬态振动特性,不同的线分别表示厚盘转子在转速比
α=10-4、10-3、4×10-3和10-2时的瞬态振动特性曲线.为计算转子的瞬态振动特性,考虑静平衡位置附近形心的振动位移Rξ,0、Rη,0和盘的偏摆角Θη,0、Θξ,0,定义轴的动挠度放大因子为$X = 2{\zeta _r}\sqrt {{{\left( {{R_\zeta } - {R_{\xi ,0}}} \right)}^2} + {{\left( {{R_\eta } - {R_{\eta ,0}}} \right)}^2}} $,盘的偏摆角放大因子为$A = \sqrt {{{\left( {{\Theta _\eta } - {\Theta _{\eta ,0}}} \right)}^2} + {{\left( {{\Theta _\zeta } - {\Theta _{\xi ,0}}} \right)}^2}} /\pi $.
 |
| 图 3 厚盘转子过低阶及高阶临界转速的瞬态振动特性曲线(μ=0.02,0.05,0.07)Fig. 3 Transient vibration curves of thick-disk rotor crossing lower and higher order critical speed (μ=0.02,0.05,0.07) |
| 图选项 |
分析图 3(a)~图 3(f)可知,厚盘转子的两阶临界转速对应于系统的两阶振动模态,低阶振型为转子轴的弯曲,高阶振型为转子盘的偏转.根据图 3(a)、图 3(c)和图 3(f)表现出的厚盘转子在低阶临界转速的振动特征,对比文献[1, 13, 14]关于薄盘转子过临界转速的瞬态动力学特征,厚盘转子服从柔性转子加速通过临界转速的一般振动规律和结论,不再详述.需要指出的是,薄盘转子过临界转速时,其振动峰值在ω>ωn位置处出现,即振动峰值应在横坐标大于1时出现,于厚盘转子而言,以图 3(a)为例,当α=10-4和10-3时,振动峰值在ω<ωn时出现,这是由于厚盘转子回转效应远远明显于薄盘转子,造成系统Ωc,1<ωn,这在图 2中十分形象;另外,在低转速情况下,转子轴的挠曲和盘的偏摆角是同步的,两者随时间的变化规律相同.
根据图 3(b)、图 3(e)和图 4,厚盘转子在高阶临界转速对应于高阶模态,对不平衡力的瞬态响应与低阶临界转速有很大的不同.
1) 在高速条件下,盘的偏转比轴的弯曲对激励要敏感得多.通过高阶临界转速时,主振型为盘的偏转;而且由于当地转速很大,回转效应对转子影响极其显著.
2) 通过高阶临界转速时,产生的瞬态振动响应非常迅速,在极小的时间内即达到最大值,尤其是小加速度转子更为明显.
3) 通过高阶临界转速后,由共振激起的按系统高阶固有频率的自由振动和在当地转速频率下的强迫振动合成很激烈的高频振荡.
4) 通过高阶转速后,线性加速的系统仍然具有稳定性,振动逐渐衰减.这就是柔性转子的自定心效应.但是,小加速度的转子呈指数衰减,大加速度几乎呈线性衰减.
5) 无论低阶还是高阶,过临界转速时的自转角加速度对转子的瞬态振动影响很大;加速度越大,惯性力越大,过临界转速时对振动有一定的抑制作用,产生的瞬态振动振幅越小;但同时,发生瞬态共振后,加速度越大,阻尼对系统的影响就相对较弱,因此衰减也越来越慢.这在过高阶临界转速后的振动中十分明显.
反过来,根据高阶共振发生的转速位置可见,μ值越小,高阶临界转速越靠前;当μ大到一定程度时,实际转子由于能量有限,很难达到高阶临界转速;当μ值大于1时,转子失去高阶临界转速;当μ=2时,即为典型的薄盘转子.
由于旋转坐标系不考虑转子自转对形心运动的干扰,因此可以在旋转坐标系中清晰地观察到形心运动轨迹,这在单转子系统中对比固定坐标系是一个较为明显的优点.以μ=0.05为例,着重分析穿过两阶临界转速过程中的瞬态振动,以此判断转子的稳定性.图 4和图 5给出了厚盘转子形心加速过程中各个阶段在旋转坐标系中的轨迹,图 6(a)和图 6(b)给出了转子穿过高低转速时盘的偏摆角矢尖(盘的单位外法矢量尖)在旋转坐标系中的轨迹,其中图 5(a)和图 6(a)为过低阶临界转速的轨迹,从零初始条件开始到稳定区结束,图 5(b)和图 6(b)为过高阶临界转速的轨迹,从稳定区开始到缓慢衰减结束(其中,加速比α=10-4的转子已经进入高转速稳定区).
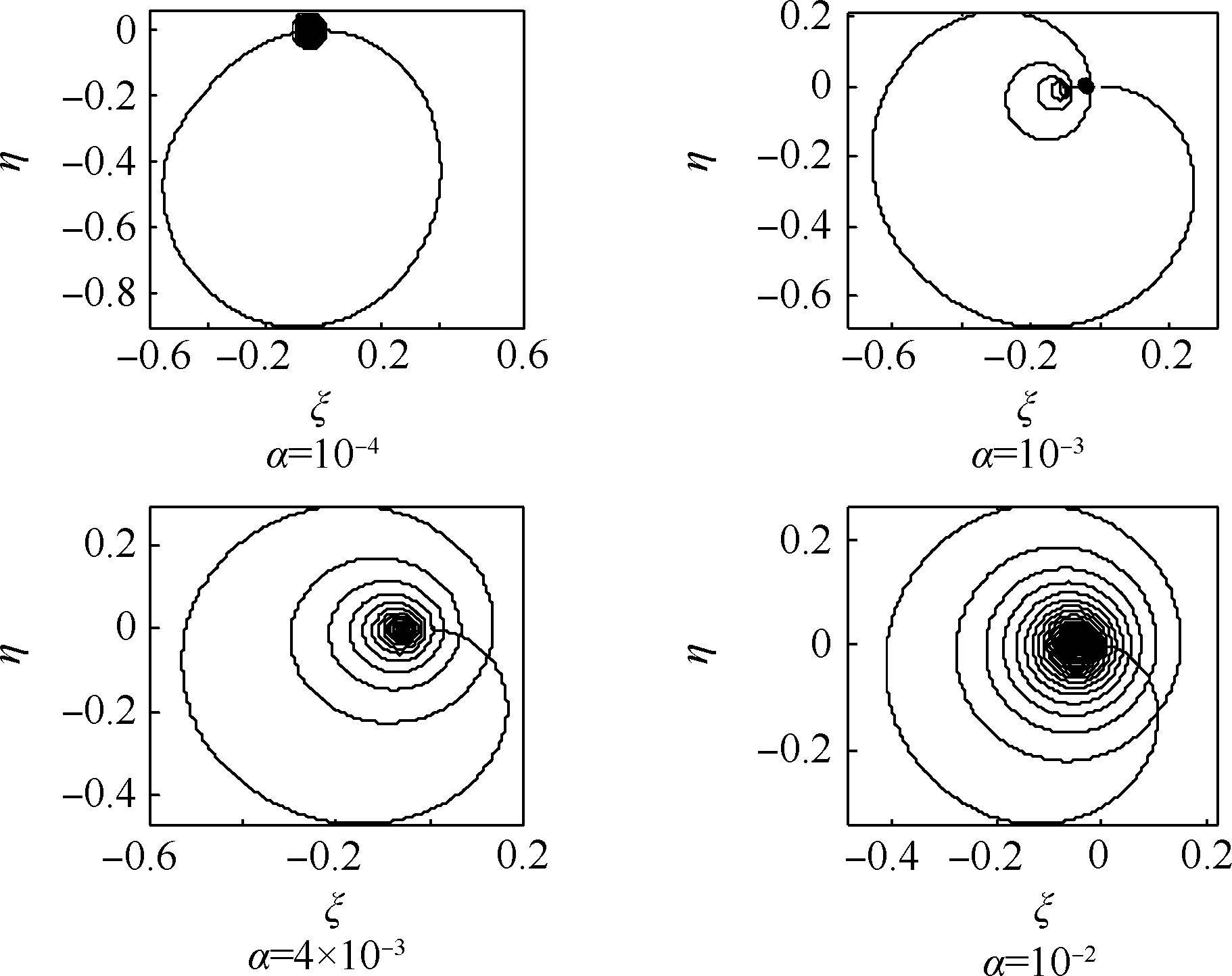 |
| 图 4 整个加速过程形心在旋转坐标系中的轨迹(μ=0.05)Fig. 4 Trajectories of centroid in whole speed-up process in rotating coordinate (μ=0.05) |
| 图选项 |
 |
| 图 5 穿过低阶及高阶临界转速时形心在旋转坐标系中的轨迹(μ=0.05)Fig. 5 Trajectories of centroid crossing lower and higher order critical speed in rotating coordinate (μ=0.05) |
| 图选项 |
 |
| 图 6 穿过低阶及高阶临界转速时盘偏角矢尖在旋转坐标系中的轨迹(μ=0.05)Fig. 6 Trajectories of declination angle vector tip of disk crossing lower and higher order critical speed in rotating coordinate (μ=0.05) |
| 图选项 |
根据图 5(a)和图 6(a)可见,在旋转坐标系中,低转速时转子形心的轨迹和盘偏摆角矢尖的轨迹形状几乎完全相同.这也说明,低转速情况下轴的弯曲和盘的偏转是同步的.注意坐标的数量级,穿过低阶临界转速时,轴的弯曲振动很强烈,而盘的偏摆比较微弱.
当转子超过低阶临界转速后,形心渐进趋近于旋转坐标系中的点(-2ζ,0),表现出的动态螺旋运动过程(图 3为加速过程,方向顺时针).在低阶和高阶临界转速之间,刚度对称的厚盘转子有一段很长的稳定转速区,理论上,由于自定心效应,质心将稳定于(0,0)点,形心稳定于(-2ζ,0).盘偏角矢尖也服从相同的规律,但是在到达高阶临界转速之前,轨迹范围始终处于一个很小的数量级上.
当转子穿过高阶转速时,盘突然偏摆得很剧烈,振动幅值是稳定转速区的上百倍,矢尖在空间高频偏转.不同加速度由于衰减程度不同,形成的轨迹略有不同,但是服从相同的规律.由图 5(b)的α=10-4分图及图 6(b)的α=10-4分图可知,在通过高阶临界转速之后,转子稳定在高转速区,矢尖又在旋转坐标系中稳定于一点.形心则过高阶临界转速表现出微小的高频波动,恰好共振时在旋转坐标系中的速度方向(即从稳定区进入高阶临界转速时轨迹的切线方向)与盘的矢尖在旋转非惯性参考系中的速度方向成180°,除此之外和矢尖轨迹的变化规律相同.
由以上转子的瞬态振动特性分析可知,做正进动的单、厚盘转子系统有两阶模态,其中低阶振型为轴的弯曲,高阶振型为盘的偏摆.在穿过两阶临界转速时,发生由按系统固有频率的自由振动和在当地转速频率下的强迫振动合成的瞬态振动.在有阻尼系统中,单、厚盘转子系统存在稳定转速区.
2.2 考虑重力的厚盘转子瞬态振动特性本节在2.1节基础上,考虑重力对单、厚盘转子过临界转速时的瞬态振动特性的影响.在考虑重力时,转子在零转速时已经具有初始弯曲和偏摆角.根据方程(3),无量纲重力G=g/(eωn2),在100数量级左右,取G=1.0;另外,根据文献[13],存在偏心的转子还受重力对自转轴线的矩-mgecos φ,使得转子在设定的旋转角加速度附近波动,同时存在一个切向惯性力,在固定坐标系中以2倍自转角频率影响系统的稳态和瞬态响应,这就是重力的副临界效应.因此,受无量纲重力作用的转子自转角加速度为
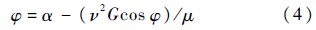
Q=[-Gsin φ,0,-Gcos φ,0]T为广义力,r0=K-1[0,0,-G,0]T为初值(静平衡位移和偏摆角),K为转子的刚度矩阵.
以μ=0.05的转子为例,分析厚盘转子系统受重力与不平衡力作用后的瞬态振动表现.图 7~图 9分别给出了转子线性加速穿过低阶临界转速时的轴的动挠度和盘的偏摆角瞬态振动曲线、形心在旋转坐标系中的轨迹和盘偏角矢尖(盘的单位外法矢量尖)在旋转坐标系中的轨迹.
 |
| 图 7 计重力厚盘转子过低阶临界转速的瞬态振动曲线Fig. 7 Transient vibration curves of thick-disk rotor crossing lower order critical speed with gravity taken into account |
| 图选项 |
 |
| 图 8 计重力过低阶临界转速的厚盘转子形心在旋转坐标中的轨迹Fig. 8 Trajectories of thick-disk centroid crossing lower order critical speed in rotating coordinate with gravity taken into accoun |
| 图选项 |
 |
| 图 9 计重力过低阶临界转速时盘偏角矢尖在旋转坐标中的轨迹Fig. 9 Trajectories of declination angle vector tip of disk crossing lower order critical speed in rotating coordinate with gravity taken into account |
| 图选项 |
对于式(4)中第2项,由于ν值很小,相较于第1项可以忽略,可见对对称厚盘转子而言重力对转速的影响很小.由于方程(3)是线性的,根据叠加原理可知,转子的瞬态振动是由不平衡力和重力叠加激励的结果,因此对比图 3(c),在图 7表示的轴的动挠度和盘偏角出现了叠加在图 3(c)所示的曲线上的次谐波振动.厚盘转子过低阶临界转速的瞬态振动规律与普通单盘转子相同,这些理论已经发展成熟,本文不再讨论.但是,受重力作用的非对称转子的瞬态振动与对称转子有很大的不同,不仅存在副临界转速[13],还可能引起非线性振动[15, 16].
3 刚度非对称厚盘转子瞬态振动特性鉴于国内外****对刚度非对称转子已有研究,本节主要以μ=0.05、刚度非对称系数κ=0.03的单、厚盘转子为例,说明刚度非对称厚盘转子过临界转速时瞬态振动的基本特征,尤其是薄盘转子所不具有的高阶模态.
采用2.1节关于对称厚盘转子的研究方法,设定加速比α=10-4,10-3,4×10-3,10-2,不考虑重力,从零转速、零位移、零偏角的初始条件开始,计算转子μ=0.05、κ=0.03的厚盘转子过低阶、高阶临界转速时的轴的动挠度和盘偏角,如图 10(a)和图 10(b)所示.图 11和图 12分别给出了过低阶、高阶临界转速形心轨迹和盘偏角矢尖轨迹.
 |
| 图 10 不对称厚盘转子过低阶及高阶临界转速的瞬态振动曲线Fig. 10 Transient vibration curves of asymmetric thick-disk rotor crossing lower and higher order critical speed |
| 图选项 |
 |
| 图 11 不对称厚盘转子过低阶及高阶临界转速形心轨迹Fig. 11 Trajectories of centroid of asymmetric thick-disk rotor crossing lower and higher order critical speed |
| 图选项 |
 |
| 图 12 不对称厚盘转子过低阶及高阶临界转速盘偏角矢尖轨迹Fig. 12 Trajectories of declination angle vector tip of disk of asymmetric thick-disk rotor crossing lower and higher order critical speed |
| 图选项 |
对比图 10(a)和图 3(c)可得,在低阶临界转速附近,由于刚度的不对称性,瞬态振动的幅值显著增大,在旋转坐标系中的形心轨迹呈椭圆形;过低阶临界转速后,转子仍然能恢复稳定,保持在较小的振幅.
然而,当厚盘转子过高阶临界转速时,由主振型引起的盘的偏摆急剧增大,轴的动挠度随之发散,系统若以小加速度加速时在高阶临界转速点上迅速失稳,大加速度则能保持有限振幅,穿过临界转速后振动发生近似线性的衰减.
4 厚盘转子定功率过临界转速的瞬态振动特性如第2节所述,线性加速度缺少一个自由度,并不能考虑外界能量与转子系统的相互作用.本节针对具有非对称刚度的厚盘转子结构考虑一种更接近实际的工况:定功率的有限能量模式.
当转子工作于某一稳定转速时,系统的无量纲功率为
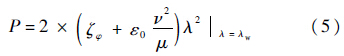
ε0为一修正值,本文取为0.1,则
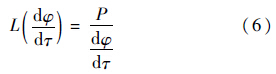
式(5)和式(6)代入方程(2),采用四阶Runge-Kutta法联立求解方程(2)和方程(3).设定工作转速在低、高阶临界转速附近,考察厚盘转子在定功率有限能量模式下瞬态振动的基本特性.下面计算单、厚盘转子过低阶临界转速时的瞬态振动,其中λw=0.8表示工作转速为亚临界转速,λw=1.2,1.6,2.0表示工作转速为超临界转速,在图 13~图 21中给出了对称厚盘转子和非对称(κ=0.05,0.07)厚盘转子时域、频域瞬态振动以及旋转系中形心轨迹.
 |
| 图 13 低阶临界转速附近工作的对称厚盘转子随时间的瞬态振动曲线Fig. 13 Transient vibration curves over time of symmetric thick-disk rotor with working speed near lower order critical speed |
| 图选项 |
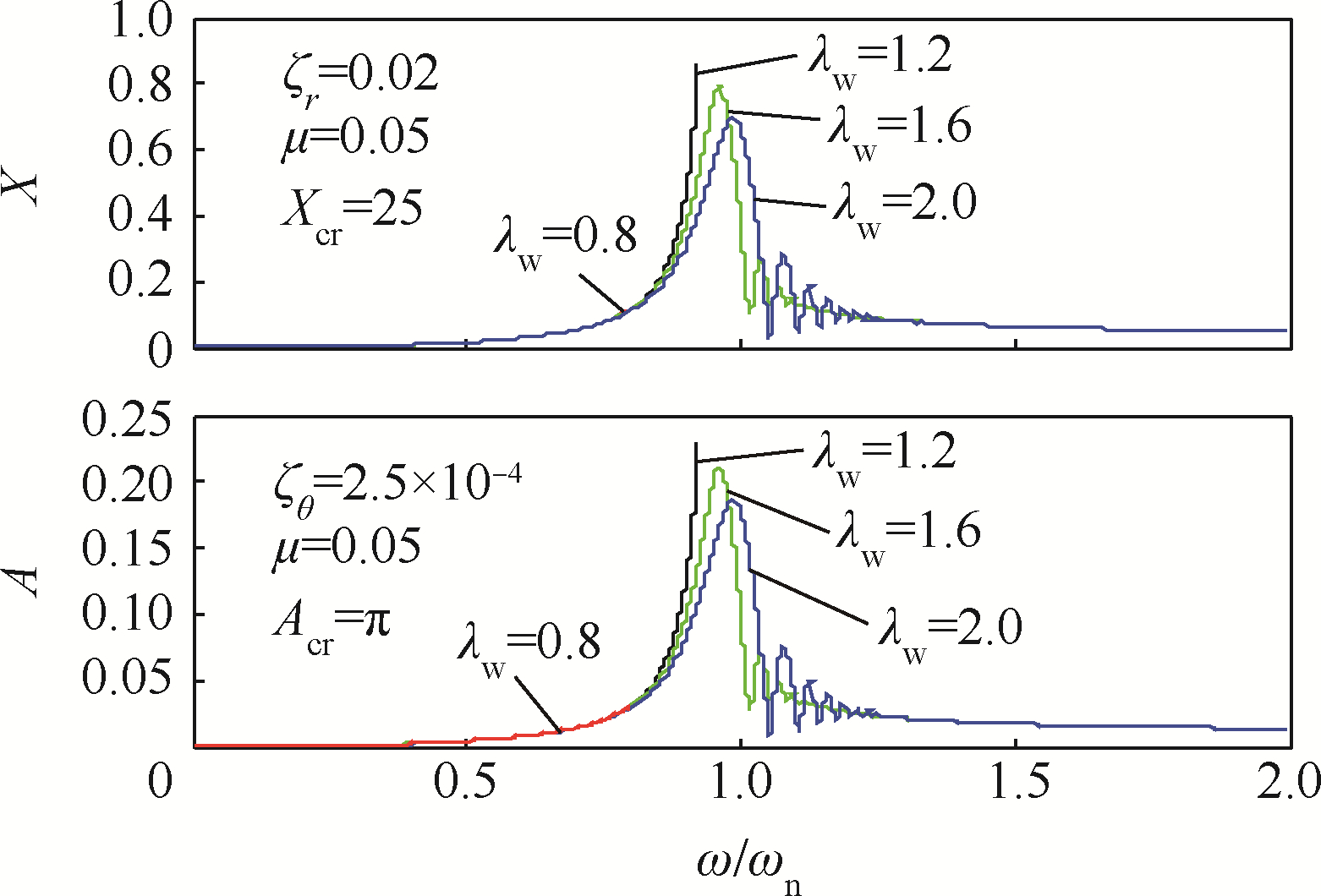 |
| 图 14 低阶临界转速附近工作的对称厚盘转子随转速的瞬态振动曲线Fig. 14 Transient vibration curves over speed of symmetric thick-disk rotor with working speed near lower order critical speed |
| 图选项 |
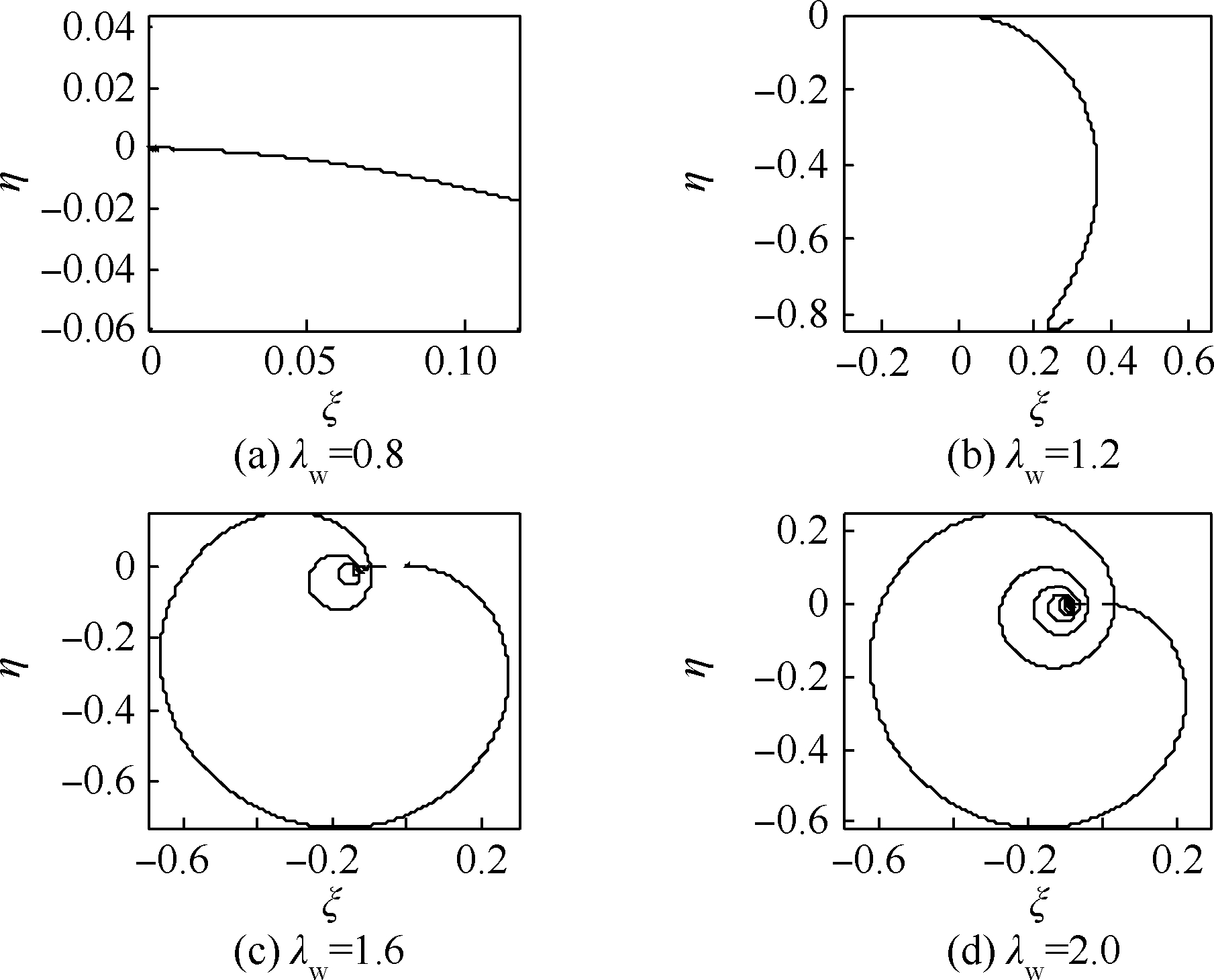 |
| 图 15 低阶临界转速附近工作的对称厚盘转子形心轨迹Fig. 15 Trajectories of centroid of symmetric thick-disk rotor with working speed near lower order critical speed |
| 图选项 |
 |
| 图 16 低阶临界转速附近工作的非对称(κ=0.05)厚盘转子随时间的瞬态振动曲线Fig. 16 Transient vibration curves over time of asymmetric thick-disk rotor (κ=0.05) with working speed near lower order critical speed |
| 图选项 |
 |
| 图 17 低阶临界转速附近工作的非对称(κ=0.05)厚盘转子随转速的瞬态振动曲线Fig. 17 Transient vibration curves over speed of asymmetric thick-disk rotor (κ=0.05) with working speed near lower order critical speed |
| 图选项 |
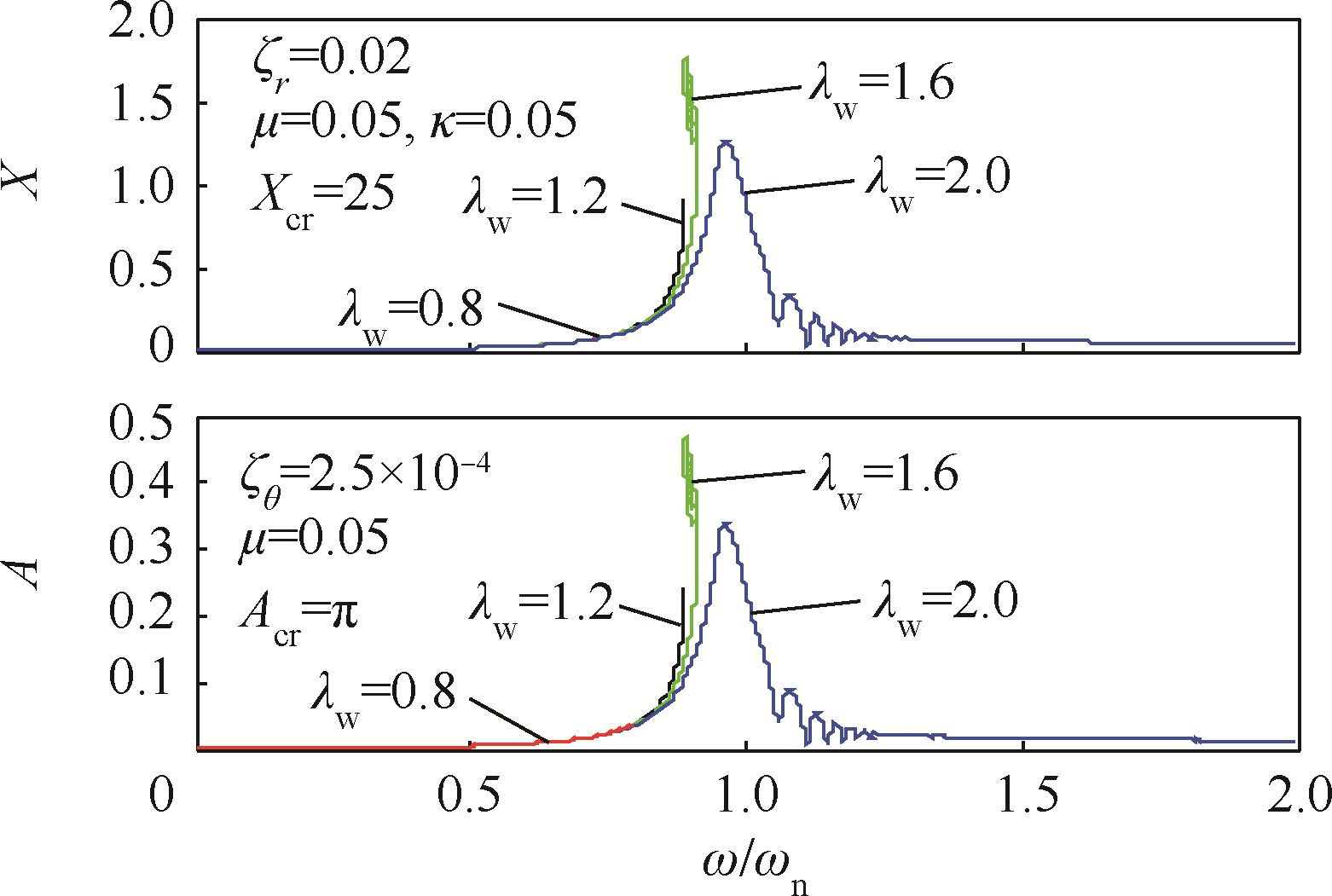
 |
| 图 18 非对称(κ=0.05)厚盘转子在低阶临界转速附近振动的形心轨迹Fig. 18 Trajectories of centroid of asymmetric thick-disk rotor (κ=0.05) with working speed near lower order critical speed |
| 图选项 |
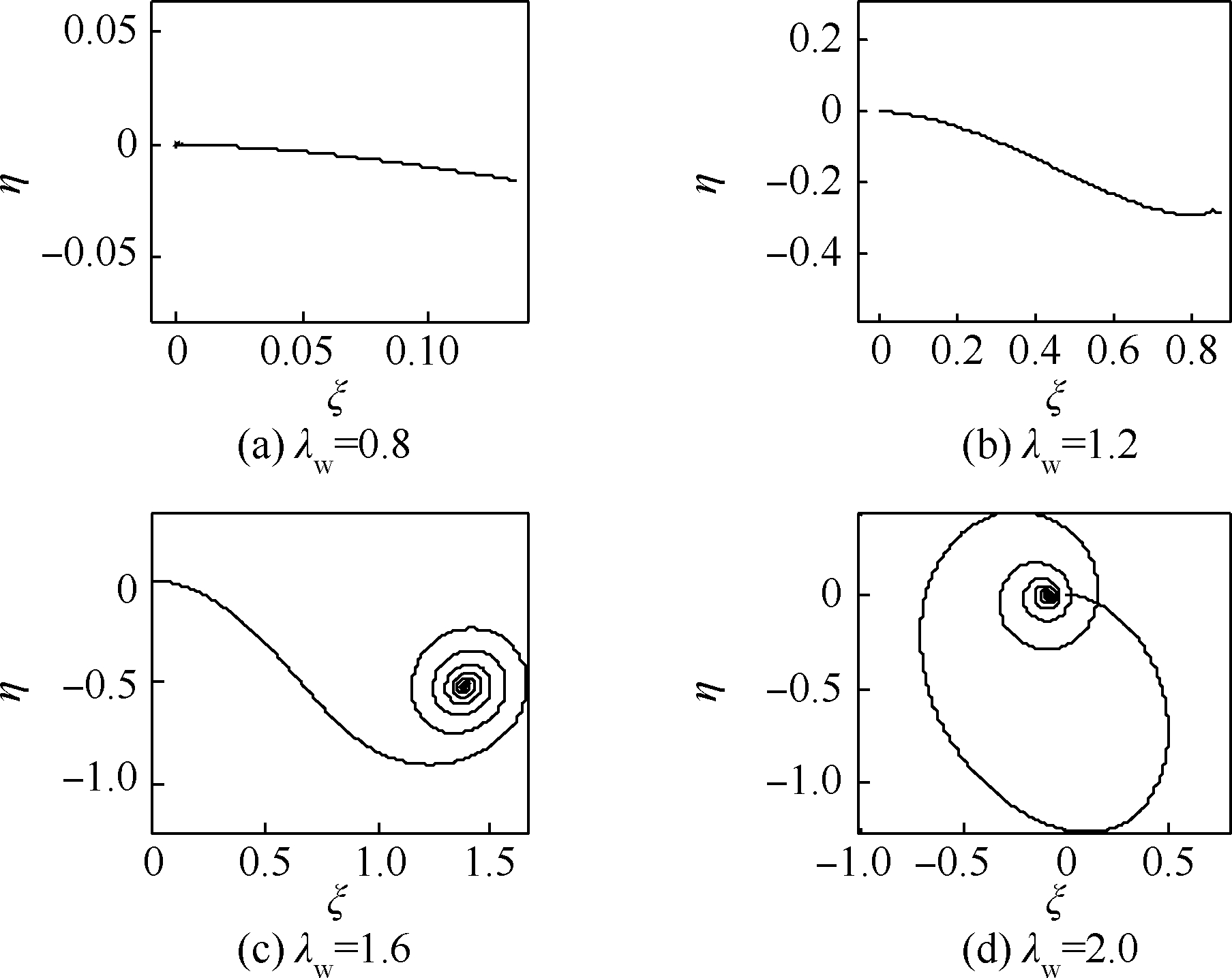
 |
| 图 19 低阶临界转速附近工作的非对称(κ=0.07)厚盘转子随时间的瞬态振动曲线Fig. 19 Transient vibration curves over time of asymmetric thick-disk rotor (κ=0.07) with working speed near lower order critical speed |
| 图选项 |
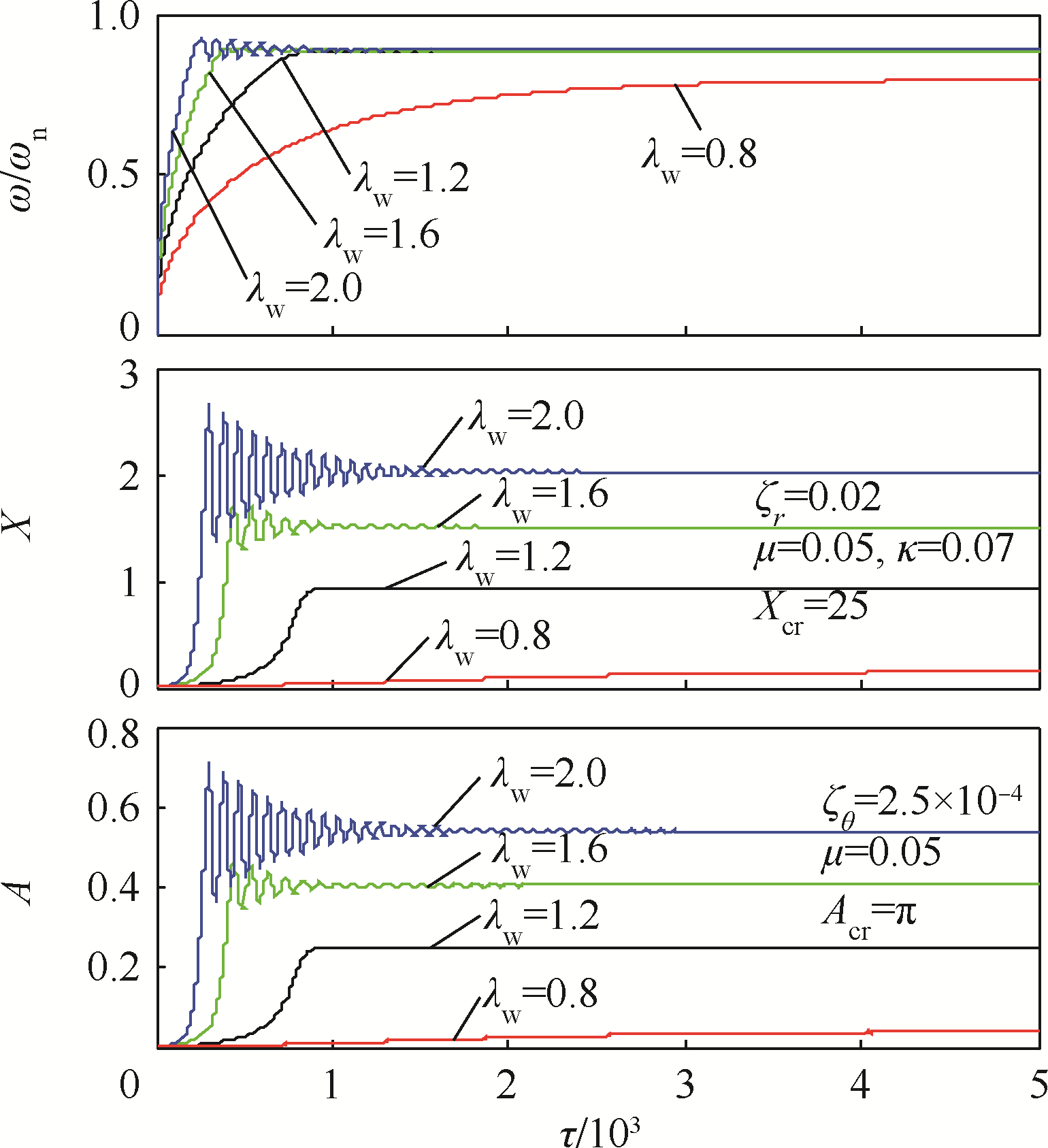
 |
| 图 20 低阶临界转速附近工作的非对称(κ=0.07)厚盘转子随时间的瞬态振动曲线Fig. 20 Transient vibration curves over speed of asymmetric thick-disk rotor (κ=0.07) with working speed near lower order critical speed |
| 图选项 |
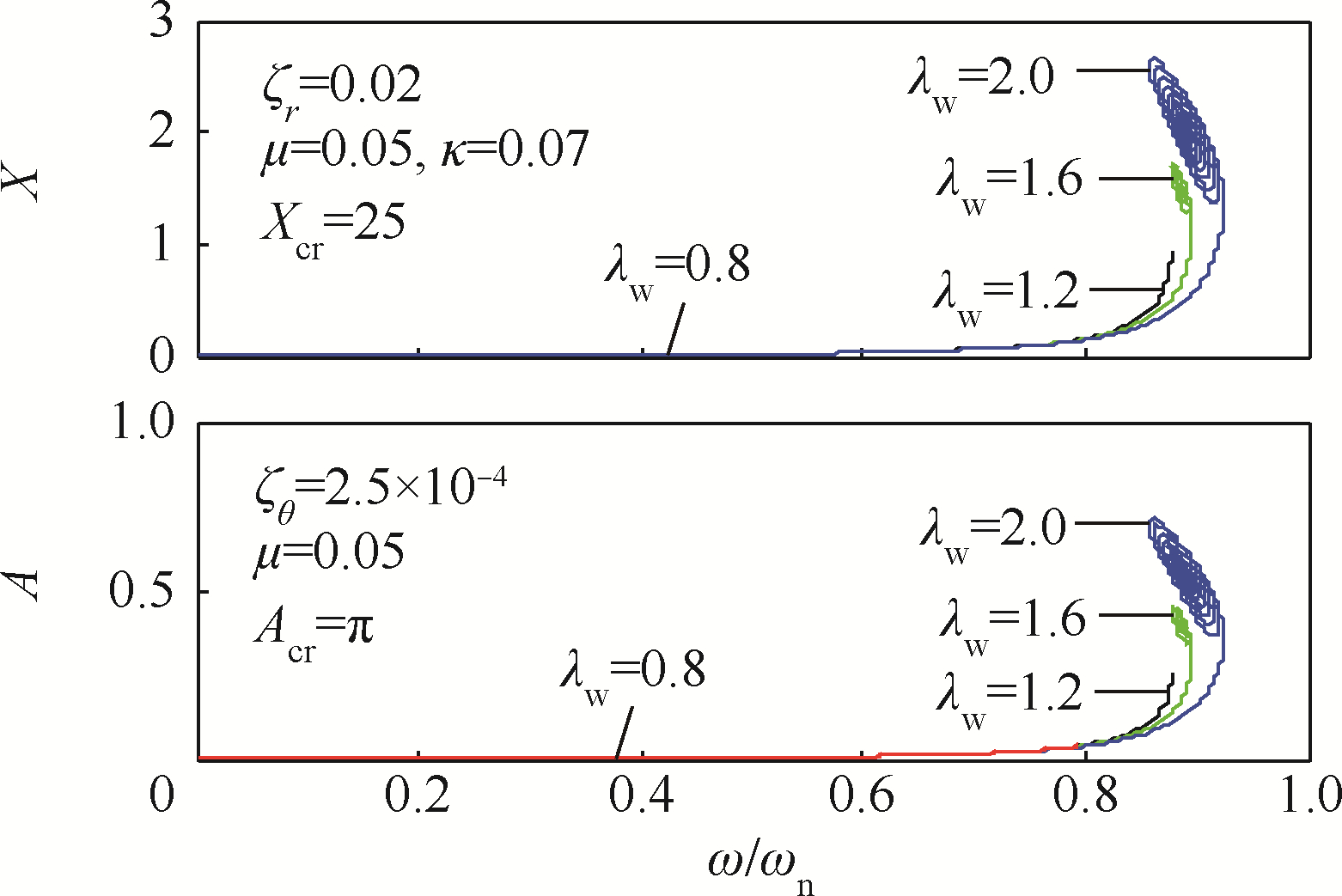
 |
| 图 21 低阶临界转速附近工作的非对称(κ=0.07)厚盘转子瞬态振动的形心轨迹Fig. 21 Trajectories of centroid of asymmetric thick-disk rotor (κ=0.07) with working speed near lower order critical speed |
| 图选项 |
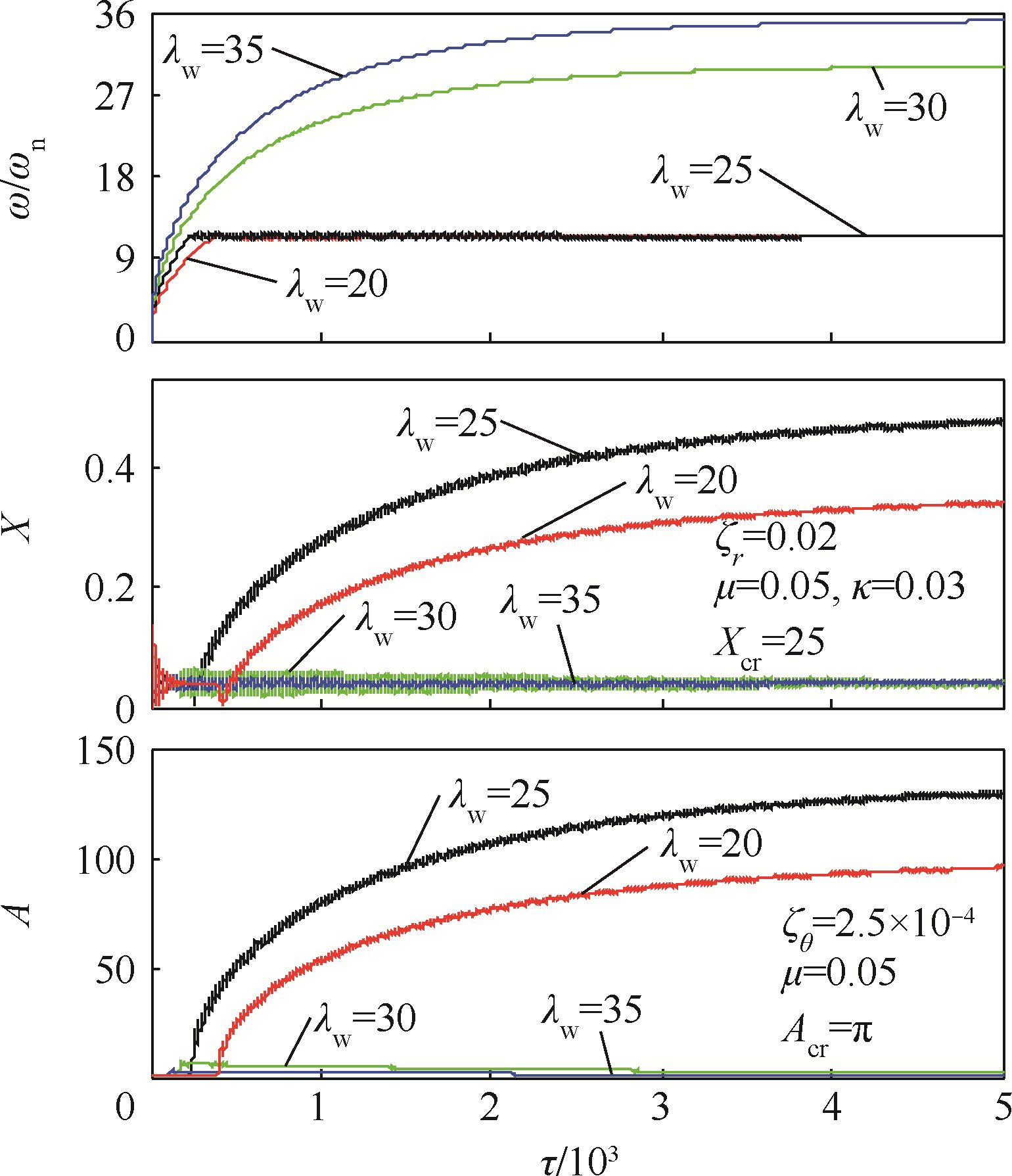
根据λw=0.8的计算结果可知,若工作转速低于临界转速,显然转子的角速度是不能穿过临界转速的,到达工作转速后即发生稳态振动.因此,以亚临界转速工作的厚盘转子不会出现振幅大幅增加的非线性振动.由图 13、图 16和图 19可见,当工作转速高于临界转速,若不发生过临界转速的瞬态振动,则能维持在超临界转速下运行,振动幅值不会剧增.但是,如果外界能源不能向厚盘转子系统提供足够穿越临界转速的能量,自转转速会随着轴的动挠度和盘的偏摆角的瞬态振动而出现波动,造成能量耦合,从而激起系统的非线性振动,发生“失速”现象.这是定功率的有限能量模式区别于定角加速度的理想能源模式最大的特点.进一步,发生“失速”的转速,对同一系统是一个定值,低于临界转速;这时,功率大小只造成非线性瞬态振动的幅值变化,而不能使转子转速继续上升,除非有足够大的功率克服振动引起的阻力矩.“失速”后,外界能源输入的能量被转子系统耗散和转化为势能存储起来.
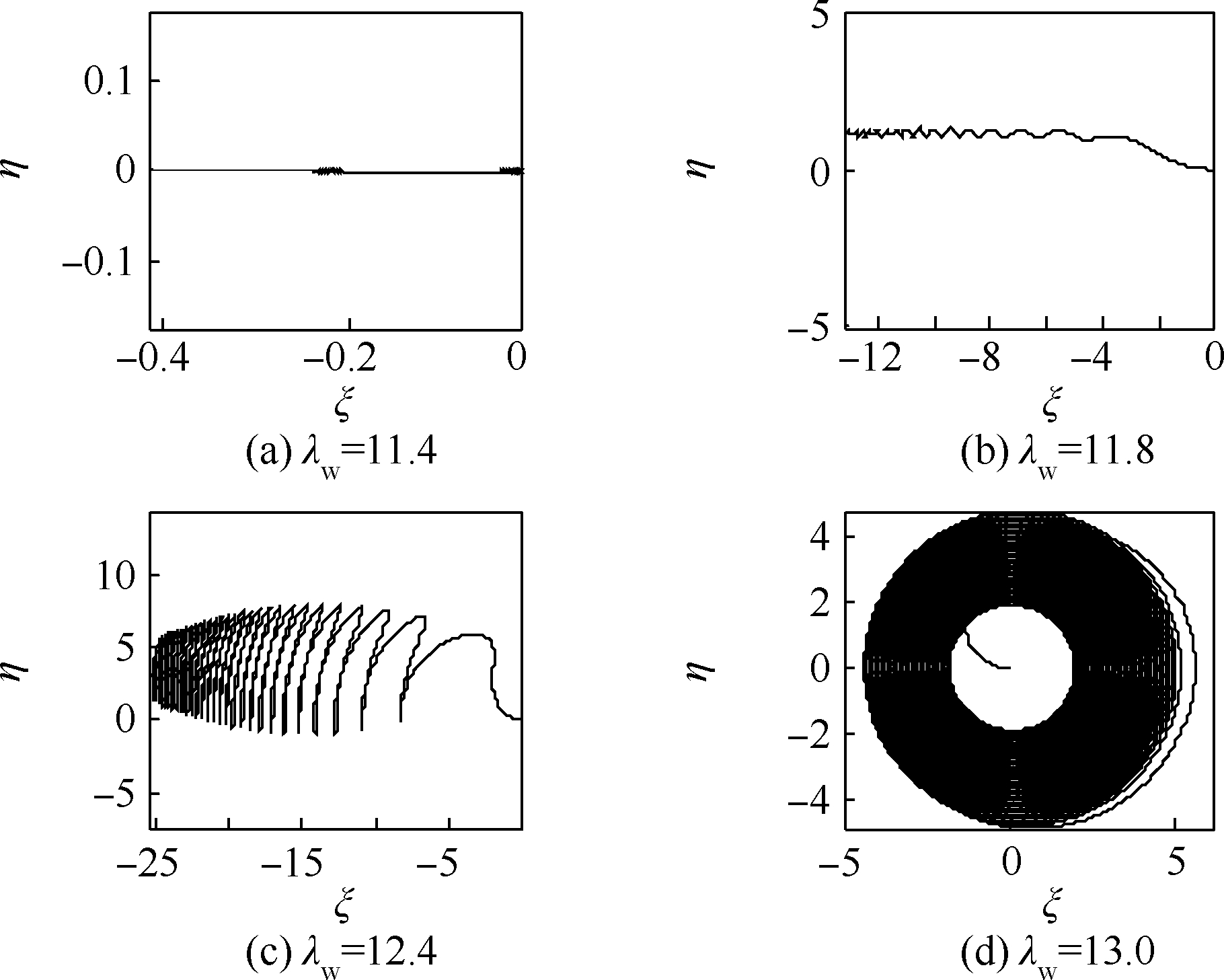
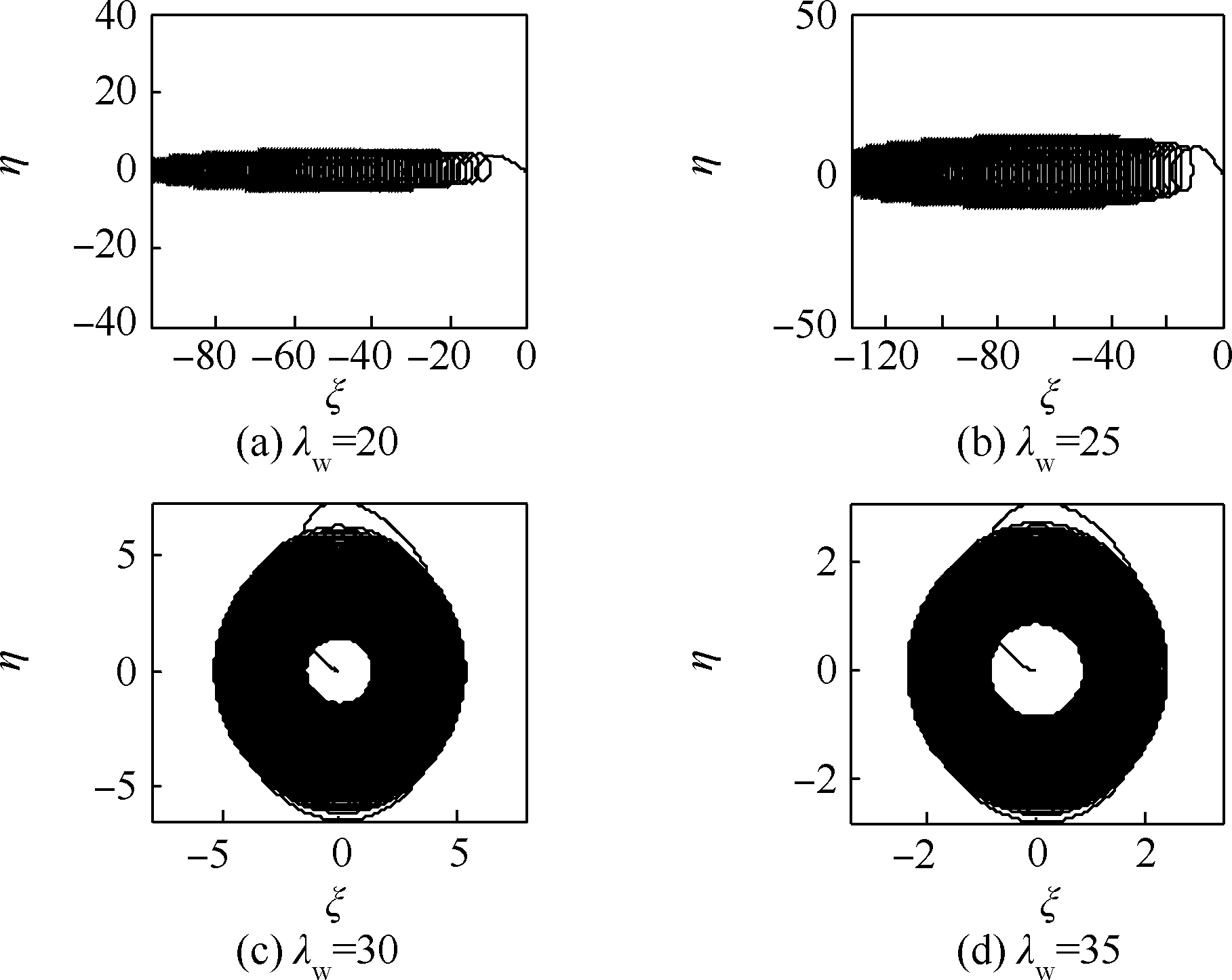
图 22~图 25分别给出了κ=0的对称厚盘转子λw=11.4,11.8,12.4,13.0和κ=0.03的非对称厚盘转子以λw=20,25,30,35过高阶临界转速随时间变化的瞬态振动曲线和盘偏角矢尖(以盘的偏摆表征高阶振动)在旋转坐标系中的轨迹.可以发现,厚盘转子在高阶临界转速附近也存在“失速”现象,盘偏角矢尖轨迹出现分叉,尤其对非对称转子由于非线性振动,要求极高的功率才能顺利通过高阶临界转速.因此,实际工程中的厚盘转子结构是很难在高阶临界转速之上运行.若外界功率足够大,厚盘转子通过临界转速后,瞬态振动衰减,系统仍能保持稳定,这在以盘的偏摆为高阶振型的振动上十分明显.
 |
| 图 22 对称厚盘转子定功率过高阶临界转速时随时间变化的瞬态振动曲线Fig. 22 Transient vibration curves over time of symmetric thick-disk rotor crossing higher order critical speed with constant power |
| 图选项 |
 |
| 图 23 对称厚盘转子定功率过高阶临界转速时盘偏角矢尖轨迹Fig. 23 Trajectories of declination angle vector tip of disk of symmetric thick-disk rotor crossing higher order critical speed with constant power |
| 图选项 |
 |
| 图 24 非对称(κ=0.03)厚盘转子定功率过高阶临界转速时随时间变化的瞬态振动曲线Fig. 24 Transient vibration curves over time of asymmetric thick-disk rotor (κ=0.03) crossing higher order critical speed with constant power |
| 图选项 |
 |
| 图 25 非对称(κ=0.03)厚盘转子定功率过高阶临界转速时盘偏角矢尖轨迹Fig. 25 Trajectories of declination angle vector tip of disk of asymmetric thick-disk rotor (κ=0.03) crossing higher order critical speed with constant power |
| 图选项 |
过临界转速需要的瞬态能量高于相同当地转速条件下稳态的系统能量.而且,非对称转子比对称转子更不稳定,更易发生非线性分叉,穿过临界转速需要的能量也更大.对需要穿过高阶临界转速的对称厚盘转子系统,相较于低阶临界转速,外界能源要提供更高的功率才能克服瞬态振动引起的“失速”;而非对称厚盘转子由于能量有限几乎不能穿过高阶临界转速.
根据本节采用有限能量对厚盘转子瞬态振动的计算,可以得到:
1) 若外界能源的功率不足够克服阻力和振动,反而会与系统耦合,引起振动急剧增大.转速将处于亚临界转速上,不能达到原本在临界转速以上的工作转速,发生“失速”.
2) 若外扭矩功率不足够克服振动,系统将产生非线性瞬态振动,轨迹会出现分叉,如图 15(c)和图 18(c)所示.
3) 随着转子刚度不对称性加强,系统的不稳定区域逐渐扩大.文献[17]采用Floquet理论分析单盘转子,也有同样的结论.
4) 如果外界能源有足够大的功率,使转子产生大自转加速度,即能抑制系统过临界转速的大幅度振动,可以顺利穿过临界转速.且穿过临界转速后,系统仍能保持稳定,瞬态振幅维持在很小的水平.这对于低阶和高阶临界转速都是成立的.这说明,过临界转速的自转角加速度对厚盘转子的瞬态振动的影响很大;发生非线性振动不仅与系统本身的结构有关,还与外界激励有关.
5 结 论本文计算并分析了单、厚盘转子穿过低、高阶临界转速时的瞬态振动,并以转子的形心和盘的偏摆角矢尖在旋转坐标系中的轨迹对有阻尼单、厚盘转子的稳定性进行了分析,得出:
1) 做正进动的单、厚盘转子系统有两阶固有模态,其中低阶振型为轴的弯曲,高阶振型为盘的偏摆;高阶模态是厚盘转子的特有模态.
2) 厚盘转子在穿过两阶临界转速时,发生由按系统固有频率的自由振动和在当地转速频率下的强迫振动合成的瞬态振动;其中过低阶临界转速的瞬态振动服从普通单盘转子的一般规律,过高阶临界转速的瞬态振动则与薄盘转子系统的瞬态振动有很大的不同.
3) 单盘转子的自转角加速度对系统过临界转速时的瞬态影响十分显著.加速度越大,共振时对振幅的抑制越强,但是过临界转速后的振荡衰减越缓慢.
4) 刚度非对称对厚盘转子系统的稳定性影响十分显著.非对称系数κ越大,转子越容易产生非线性振动,不稳定区域扩大,甚至造成转子失稳.
5) 采用定功率的有限能量模式加速的厚盘转子,当外界能源不足够提供转子通过临界转速时,出现了能源与系统的能量耦合的“失速”,造成振动急剧增大,产生了非线性瞬态振动以及分叉.
参考文献
| [1] | 袁惠群.转子动力学基础[M].北京:冶金工业出版社, 2013:64. Yuan H Q.Basic theory of rotor-dynamics[M].Beijing:Metallurgical Industry Press, 2013:64(in Chinese). |
| [2] | Liu Z S, Huang S L, Su J X, et al.Nonlinear dynamic analysis of an unsymmetrical generator-bearing system[J].Journal of Vibration and Acoustics, 2007, 129(4):448-457. |
| Click to display the text | |
| [3] | 刘占生,黄森林,苏杰先,等.非对称柔性转子系统的动力特性分析[J].振动工程学报, 2002, 15(2):210-214. Liu Z S, Huang S L, Su J X, et al.Dynamic analysis of unsymmetrical flexible rotor system[J].Journal of Vibration Engineering, 2002, 15(2):210-214(in Chinese). |
| Cited By in Cnki (22) | Click to display the text | |
| [4] | Shu X D, Chen L P, Wei X H.Analysis of axial deformation of cross wedge rolling asymmetric shaft part based on finite element method[J].Applied Mechanics and Materials, 2011, 101-102:396-399. |
| Click to display the text | |
| [5] | Nandi A, Neogy S.An efficient scheme for stability analysis of finite element asymmetric rotor models in a rotating frame[J].Finite Elements in Analysis and Design, 2005, 41(14):1343-1364. |
| Click to display the text | |
| [6] | Genta G.Whirling of unsymmetrical rotors:A finite element approach based on complex co-ordinates[J].Journal of Sound and Vibration, 1988, 124(1):27-53. |
| Click to display the text | |
| [7] | Darpe A K, Gupta K, Chawla A.Transient response and breathing behaviour of a cracked Jeffcott rotor[J].Journal of Sound and Vibration, 2004, 272:207-243. |
| Click to display the text | |
| [8] | 邹剑,陈进,董广明.裂纹转子过亚临界转速瞬态响应特性[J].上海交通大学学报, 2003, 37(7):1106-1109. Zou J, Chen J, Dong G M.Research on transient response characteristics of a cracked rotor passage through subcritical speed[J].Journal of Shanghai Jiao Tong University, 2003, 37(7):1106-1109(in Chinese). |
| Cited By in Cnki (3) | |
| [9] | Sekhar A S.Transient analysis of a cracked rotor passing through critical speed[J].Journal of Sound and Vibration, 1994, 173(3):415-421. |
| Click to display the text | |
| [10] | 张文.转子动力学理论基础[M].北京:科学出版社, 1990:17. Zhang W.Basic theory of rotor-dynamics[M].Beijing:Science Press, 1990:17(in Chinese). |
| [11] | 方之楚,骆振黄.单盘转子系统过临界转速时的瞬态响应[J].上海交通大学学报, 1987, 21(3):23-36. Fang Z C, Luo Z H.Transient response of single-disk rotor system on passing through critical speed[J].Journal of Shanghai Jiao Tong University, 1987, 21(3):23-36(in Chinese). |
| Cited By in Cnki (4) | |
| [12] | Hassenpflug H L, Flack R D, Gunter E J.Influence of acceleration on the critical speed of a Jeffcott rotor[J].Journal of Engineering for Power, 1981, 103(1):108-113. |
| Click to display the text | |
| [13] | 晏砺堂.结构系统动力特性分析[M].北京:北京航空航天大学出版社, 1989:183-186. Yan L T.Analysis on dynamic characteristics of structure system[M].Beijing:Beihang University Press, 1989:183-186(in Chinese). |
| [14] | 岳聪,任兴民,邓旺群.柔性转子加速过临界瞬态响应特征分析[J].机械科学与技术, 2013, 32(3):395-398. Yue C, Ren X M, Deng W Q.Analyzing transient response of flexible rotor across critical speeds[J].Mechanical Science and Technology for Aerospace Engineering, 2013, 32(3):395-398(in Chinese). |
| Cited By in Cnki (2) | |
| [15] | Xiao X W, Yang S Z, Huang Y Y.1/2 subharmonic resonance of a shaft with unsymmetrical stiffness[J].Chinese Journal of Mechanical Engineering, 2003(1):26-30. |
| Click to display the text | |
| [16] | 林富生,孟光.重力对具有初弯和不对称刚度机动转子特性的影响[J].机械强度, 2002, 24(3):320-326. Lin F S, Meng G.Influence of gravity on the dynamics of a maneuvering rotor with initial bending and asymmetry[J].Journal of Mechanical Strength, 2002, 24(3):320-326(in Chinese). |
| Cited By in Cnki (5) | |
| [17] | 陆鹏,叶黔元.电机转子参数振动的稳定性分析[J].上海海运学院学报, 2001, 22(3):183-186. Lu P, Ye Q Y.The stability analysis of motor-rotor's parameter vibration[J].Journal of Shanghai Maritime University, 2001, 22(3):183-186(in Chinese). |
| Cited By in Cnki (2) |
