对于常规金属构件的疲劳寿命分析,主要方法有名义应力法、局部应力应变法、临界平面法和损伤力学方法.名义应力法[2]是最早出现的一种疲劳寿命估算方法,这种方法在实际工程应用中可以用于设计阶段粗略估算一些应力水平较低、受力状态简单的简单结构的疲劳寿命,不适合解决复杂情况的疲劳问题.局部应力应变法[3, 4]是20世纪60年代中期以后逐步形成的一种疲劳寿命预测方法,它以缺口根部的局部应力应变历程为依据,再结合材料相应的疲劳特性曲线进行寿命估算.这一方法比较适合处理单轴受力状态构件的中、低轴疲劳问题.临界平面法[5, 6]的概念是建立在疲劳裂纹萌生和扩展机理上的,该方法将材料发生最大损伤平面上的应力应变参数作为多轴疲劳损伤参量.但该方法中的疲劳损伤参量物理意义不明确,仍然是一种半经验的方法.损伤力学是近几十年在连续介质力学理论基础上发展起来的一个固体力学分支学科.它是通过引入损伤变量来研究结构材料的力学性能在载荷的作用下逐渐退化,最后导致破坏的规律和机理[7, 8].它的主要优点是数学形式相对较简单,物理意义相对较明确.
然而,由于缺陷的复杂影响,以上研究常规金属构件疲劳问题的方法不能直接用于含缺陷金属构件的疲劳寿命预估.缺陷对金属构件疲劳寿命的影响主要体现在3个方面:①缺陷周围存在残余应力场;②缺陷局部存在塑性损伤;③缺陷局部存在应力集中.
本文基于连续损伤力学理论与方法,研究含刮痕缺陷的7050-T7451铝合金板的疲劳寿命问题.首先,对刮痕的形成进行动力学数值模拟,得到刮痕局部的残余应力场和塑性应变场;其次,根据Lemaitre的损伤力学模型,计算刮痕周围由塑性变形所引起的初始损伤;然后,应用Chaudonneret的多轴疲劳损伤模型,建立有限单元数值解法,计算含刮痕试件的疲劳寿命;最后,进行含刮痕试验件的疲劳试验.通过数值解和试验解的对比,验证上述方法的可行性.
1 理论模型1.1 残余应力分析模型残余应力分析模型需要综合考虑切削变形理论、塑性理论和有限元(Finite Element,FE)理论[9, 10].在刮擦的模拟过程中,由于刮擦物的硬度比结构件的硬度高很多,因此将刮擦物视为刚体,结构件视为弹塑性体,刮痕处的变形根据弹塑性变形理论进行计算.本文采用的塑性准则是分段线性塑性模型,可根据塑性应变定义失效.
在动力学模拟刮擦物沿着结构表面向前运动的过程中,会分离出金属屑,本文采用物理准则作为刮擦过程有限元模拟的分离准则[11].物理标准是以刮擦物前端单元节点的物理量定义的,如应变、应力、应变能等,当单元中所选定物理量的值超过给定材料的相应物理条件时,即认为单元节点分离.采用物理准则使得金属刮擦的有限元模拟研究更接近实际情况.
随着刮擦物的前进,首先在刮擦物的前端面形成很大的应变,然后应变开始沿刮擦物与构件的接触面扩散.刮擦过程完成后,构件表面残存有保持平衡的应力,即为构件表面的残余应力.
1.2 初始塑性损伤分析模型在连续损伤力学的框架中,Lemaitre[12]已经提出了很多基本的概念.对于各向同性材料,用损伤变量D来代表代表性体积单元(Representive Volume Element,RVE)的刚度劣化程度,其表达式为
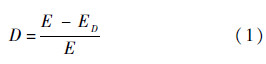
式中:E为无损伤时的RVE弹性模量;ED为有损伤时RVE的等效弹性模量;ED的变化范围为0~E,相应地,D的变化范围为0~1.基于应变等价原理,含损伤的各向同性材料的线弹性本构关系为
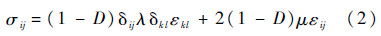
式中:σij为应力分量;εij和εkl均为应变分量;λ和μ为拉梅常数;δij和δkl为克罗内克符号;i、j、k和l为指标.在连续损伤力学中,损伤变量D的计算模型主要有两种:①考虑弹性变形导致的损伤,这部分将在第1.3节中介绍;②考虑塑性变形导致的损伤.根据Lemaitre的塑性损伤计算模型:
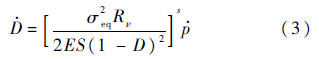
式中:σeq为等效应力;
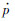为累积塑性应变率;S和s为材料参数; 
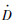为损伤演化率;Rν为三轴度函数.根据式(3)对一个加载过程进行积分,可以得到由于塑性应变而产生的损伤: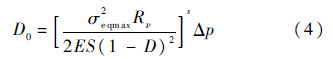 
式中:Δp为一个载荷循环内的累积塑性应变;σeqmax为等效应力最大值;D0为塑性应变而产生的初始损伤.塑性损伤模型中的两个参数S和s是根据疲劳试验数据进行识别的.在采用动力学分析得到刮痕处的塑性应变场后,根据上述计算模型,就可以定量计算刮痕局部的损伤场.
1.3 疲劳损伤分析模型仅考虑一类疲劳载荷情况,即后续疲劳载荷不至使受刮擦后的材料发生新的塑性变形,因此后续的疲劳损伤主要是由弹性变形所导致.
1.3.1 单轴疲劳损伤模型在单轴循环载荷作用下,Chaboche和Lesne[13]提出的疲劳损伤演化模型为
式中:N为循环次数;σmax和σm分别为最大应力和平均应力;α和β为材料常数;M为σm的函数,M(σm)=M0(1－b2σm),M0和b2为材料常数.根据式(5),对D从0到1进行积分,即可得到裂纹萌生时的循环次数:
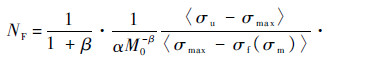
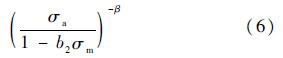
式中:σa为一个载荷循环的应力幅值;σu为强度极限;σf为疲劳极限.1.3.2 多轴疲劳损伤模型在工程应用中,疲劳危险部位的应力和应变多数情况是多轴的,Chaudonneret[14]对Lemaitre[12]和Chaboche[13]单轴疲劳损伤模型进行了扩展,提出了多轴情况下的损伤演化模型:
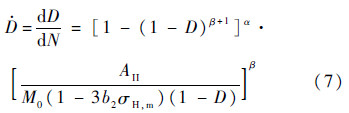
式中:AII为八面体剪切应力幅值;σH,m为平均静水应力,其表达式为
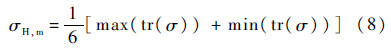
式中:tr(σ)=σ11+σ22+σ33.式(5)中材料常数α的表达式为
式中:σe,max为一个载荷循环内的最大等效应力;a为系数；A*II为Sines疲劳极限准则,表达式为
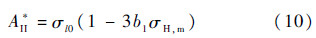
式中:σl0为R=-1时的疲劳极限;b1为材料常数.对式(7),从D=0到D=1积分,得到构件失效时的载荷循环次数为
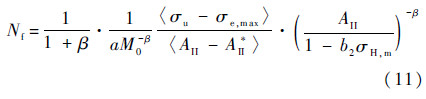
2 7050-T7451铝合金的材质参数标定一共需要标定3类材质参数,分别是刮擦塑性模型中用到的静力性能参数、塑性损伤参数和疲劳损伤参数：①对一组铝合金板进行静力拉伸试验,得到真实应力应变曲线和刮擦塑性模型参数;②进行两组铝合金板的低周疲劳试验,得到材料的塑性损伤参数;③对铝合金板进行高周疲劳试验,得到材料的疲劳损伤参数.
2.1 塑性损伤模型中的材质参数标定首先,根据7050-T7451铝合金板的静力拉伸试验,可以得到其基本的静力力学性能,如表1所示,其中σs为屈服极限,σR为断裂应力.其化学成分如表2所示.根据式(3)可知,塑性损伤方程中有两个参数S和s.在材料手册[15]中,选取两组低周疲劳试验数据点,如表3所示,其中Δεp为塑性应变幅值,Δσ为应力幅值.经计算可得到参数S和s的值,在表4中列出.
表 1 7050-T7451铝合金板的静力力学性能参数Table 1 Static mechanical properties parameters of 7050-T7451 aluminum alloy plate
| 参数 | E/MPa | ν | σs/MPa | σu/MPa | σR/MPa |
| 数值 | 70 | 0.3 | 453 | 511 | 400 |
| 注：ν—泊松比. | |||||
表选项
表 2 7050-T7451铝合金板的化学成分Table 2 Chemcical composition of 7050-T7451 aluminum alloy plate
| 元素 | Zn | Mg | Cu | Zr | Cr | Ti | Fe | Si | Al |
| 质量分数/% | 5.91 | 1.85 | 2.14 | 0.1 | 0.04 | 0.05 | 0.1 | 0.04 | 其他 |
表选项
表 3 两组低周疲劳试验数据点Table 3 Two sets of low cycle fatigue test data
| 组号 | 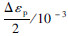 | 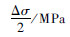 | Nf |
| 1 | 55.34 | 568 | 13 |
| 2 | 0.32 | 404 | 948 |
表选项
表 4 7050-T7451铝合金板的疲劳损伤模型材质参数Table 4 Material parameters of fatigue damage model for 7050-T7451 aluminum alloy plate
| 参数 | β | M0 | b1 | b2 | a | S/MPa | s |
| 数值 | 1.875 3 | 88 132 | 0.001 3 | 0.001 5 | 0.75 | 1.269 | 4.5 |
表选项
2.2 疲劳损伤模型中的材质参数标定为了获得7050-T7451铝合金疲劳损伤演化方程中的材质参数,首先根据材料手册[16]中光滑件和缺口件的疲劳试验数据进行参数识别,然后进行了光滑件在应力比R=0.02情况下的疲劳试验,以验证所得参数的适用性.
在疲劳损伤模型中,一共有5个参数:β、a、M0、b1和b2.首先,根据标准光滑试件的疲劳试验,可以确定4个参数:β、M0、b1和b2.对于单轴疲劳条件下的光滑试件,疲劳寿命预估的闭合形式如式(6)所示.因此,参数β和1/[(1+β)aM-β0]可以直接从R=-1的疲劳试验数据计算得出.然后,通过使用最小二乘法,利用其他应力比下的疲劳试验数据,可以获得参数b1和b2的数值.最后,利用一组R=-1,σmax=81.2 MPa,Nf=1.1×105的缺口件的疲劳试验数据,通过采用损伤力学有限单元[17, 18]方法,可以得到a和M0的数值解.最终,得到的7050-T7451铝合金板的材料参数如表4所示.图1(a)和图1(b)给出了不同应力比(R=－1,0)下拟合的光滑试件的S-N曲线.图1(c)给出了R=0.02时的S-N曲线和疲劳试验数据点.
 |
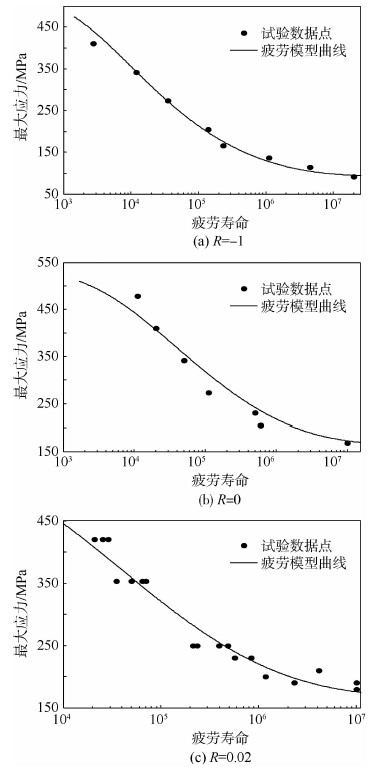| 图 1 R不同时的试验点以及模型预测的光滑试样的S-N曲线Fig. 1 Test points and predicted S-N curves of smooth specimens with different R |
| 图选项 |
3 疲劳寿命预估3.1 计算方案计算流程如图2所示,具体的计算过程为:
 |
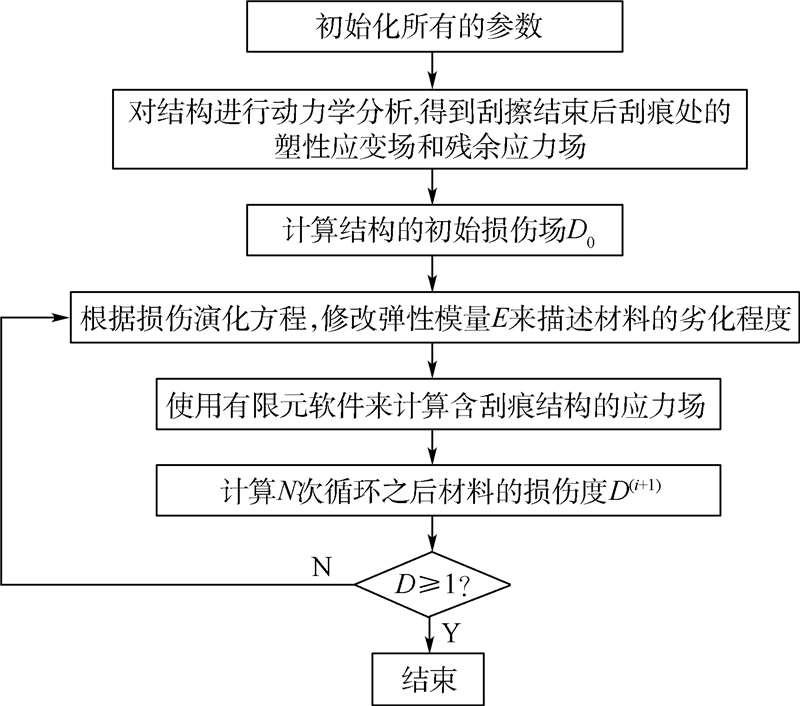| 图 2 简化的FE计算方法流程图Fig. 2 Flow chart of simplified FE computational methodology |
| 图选项 |
1) 初始化所有的参数,将初始损伤度D0的值设为0.
2) 利用Ls_dyna软件对结构进行动力学分析,得到刮痕处的塑性应变场与残余应力场.
3) 根据Lemaitre的塑性损伤分析模型,计算由刮擦过程中产生的塑性变形所导致的初始损伤场.
4) 根据初始损伤度D0,修改每个单元的弹性模量,然后利用ANSYS软件计算应力场(考虑刮痕处的残余应力场),并根据式(12),计算每个单元随着循环载荷的增加而引起的疲劳损伤度的增量为
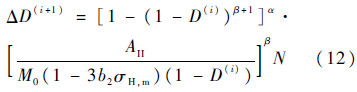
式中:D(i)为载荷循环次数i次后的每个单元的总损伤度，并得到载荷循环次数i+1次后的每个单元的总损伤度为
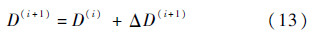
5) 如果任意一个单元的损伤度累积达到了1,就认为疲劳裂纹在这个单元萌生,此时的循环次数即为疲劳裂纹的萌生寿命,如果没有达到1,再利用式(14)重新计算每个单元的弹性模量：
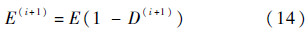
然后,计算下一个循环载荷作用下的应力场和损伤场,直到某一个单元的损伤累积达到1.3.2 疲劳寿命预估过程及结果3.2.1 残余应力分析含刮痕的铝合金板的尺寸如图3所示.刮痕的深度是0.25 mm,刮痕的底部半径是0.2 mm.利用Ls_dyna软件进行刮擦的动力学模拟,考虑到整个模型的对称性,这里只建立了1/2模型.计算时,将刮擦物的材料设为刚体,铝合金板设为弹塑性材料,采用分段线性塑性模型,此模型是根据设定的塑性应变值来定义失效.有限元模型选用8节点的Solid164三维显式结构实体单元,整个模型一共有206 516个单元,224 458个节点,网格的密度决定了数值解的精确度,为了确定合适的网格密度,对原有网格和对加密网格后的模型分别进行了有限元计算,当两次计算的最大轴向应力的差值小于1%时,认为此时的网格密度达到计算精度的要求,划分完网格的有限元局部模型如图4所示.刮擦结束后铝合金板的残余应力分布图如图5所示,可以看到残余应力主要集中在结构的表面层.
 |
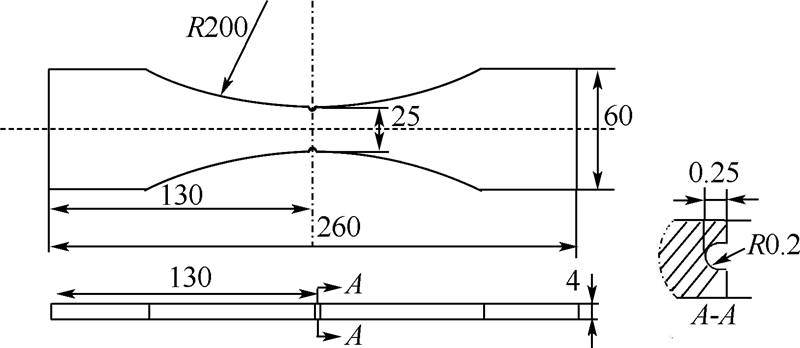| 图 3 含刮痕铝合金板的尺寸图(单位：mm)Fig. 3 Demension figure of scratched aluminium alloy plate specimen (Unit:mm) |
| 图选项 |
 |
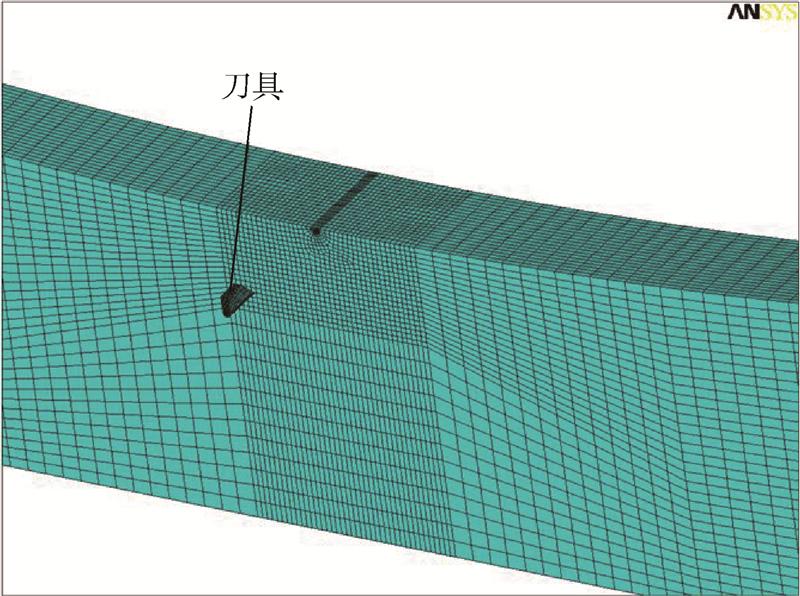| 图 4 有限元局部网格Fig. 4 Local FE model meshing |
| 图选项 |
 |
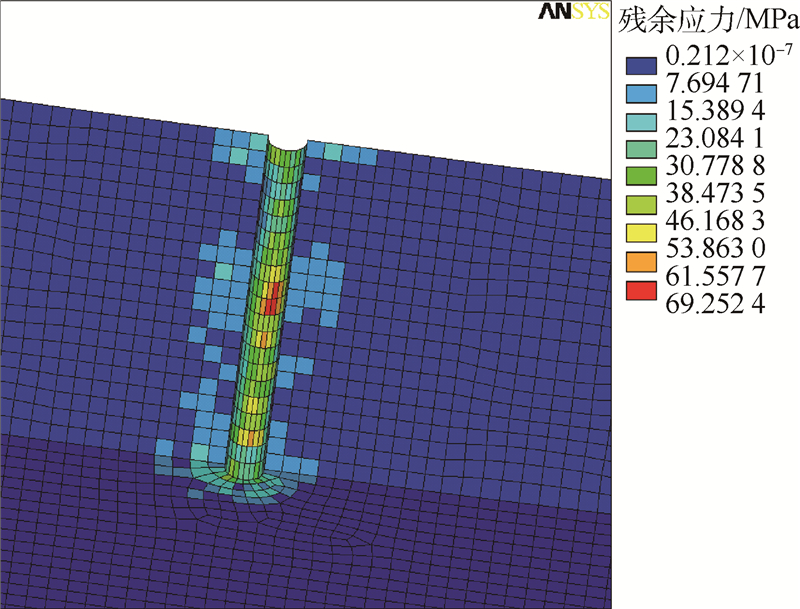| 图 5 刮擦结束后刮痕周围的残余应力分布图Fig. 5 Distribution of residual stress after scratching near scratch |
| 图选项 |
3.2.2 损伤分析以及疲劳寿命预估刮擦结束后,可以得到刮痕处的塑性应变,图6给出了刮痕局部的等效塑性应变分布图.由塑性应变导致的初始损伤可根据式(4)算出.在下面的损伤力学—有限元迭代计算中,初始损伤场和残余应力场将作为初始条件输入.
图 6(Figure 6)
Fig. 6
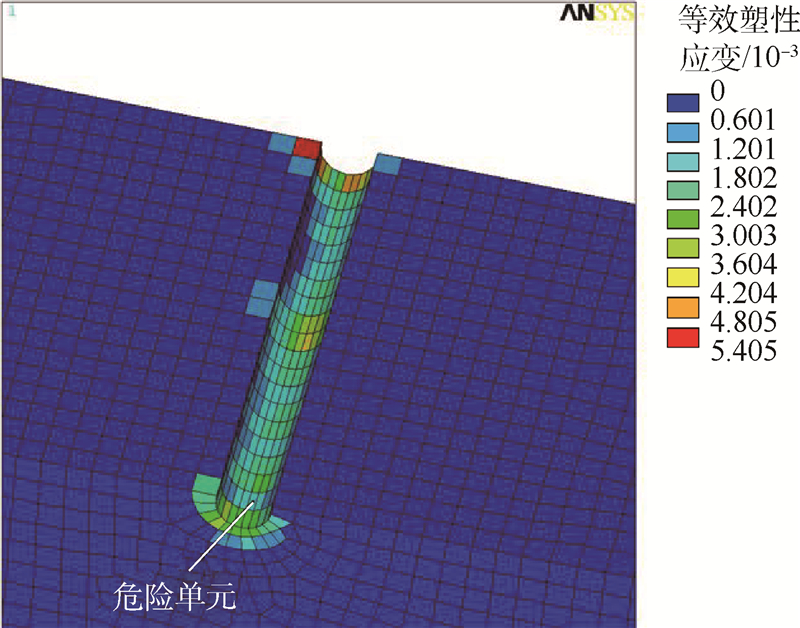 | 图 6 刮痕处的等效塑性应变分布图 Fig. 6 Distribution of equivalent plastic strain |
施加的循环载荷的最大名义应力分别是206 MPa、187 MPa,应力比是0.02.得到的损伤力学有限元数值解在表5中列出.图7给出了两级应力下,编号为447849的危险单元的损伤度随着循环次数的变化趋势图,此单元的位置在图6中标出.
表 5 不同名义应力下的疲劳试验结果与疲劳寿命预估数值解Table 5 Fatigue test results with different nominal stress and numerical solution of fatigue life
| 名义应力/MPa | 数量 | 疲劳寿命 | 中值寿命 | 数值解 | 数值解的误差/% |
| 206 | 7 | 59 900,159 30040 200,81 50032 700,141 00087 500 | 74 395 | 85 000 | 12.48 |
| 187 | 7 | 668 000,250 000165 000,648 000354 000,136 000158 000 | 280 265 | 345 000 | 18.76 |
表选项
 |
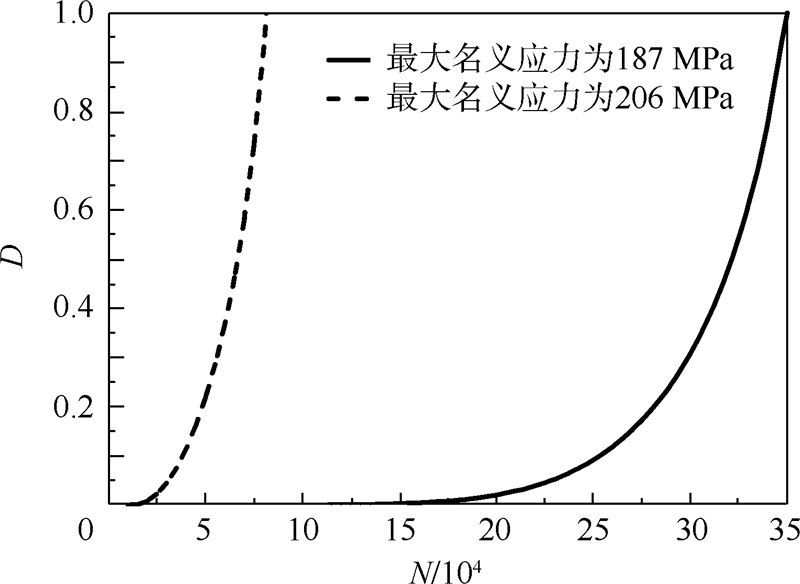| 图 7 损伤度随着循环次数的变化趋势图Fig. 7 Change trend diagram of damage extent versus number of cycles |
| 图选项 |
3.2.3 只考虑刮痕几何形状的铝合金板疲劳寿命预估本节对只考虑刮痕的几何形状的铝合金板进行疲劳寿命预估,并与考虑残余应力场和初始塑性损伤场的计算结果进行对比.刮痕的深度为0.25 mm,底部圆弧半径为0.2 mm.施加的循环载荷分别为206 MPa和187 MPa,应力比为0.02.当载荷为206 MPa时,计算的疲劳寿命为115 000,当载荷应力为187 MPa时,计算的疲劳寿命为410 000.考虑了残余应力场和初始塑性损伤场的铝合金板的疲劳寿命的计算结果如表5所示.可见,与考虑残余应力场和初始塑性损伤场的计算结果相比,计算得到的只考虑刮痕的几何形状的铝合金板的疲劳寿命相对较长.故残余应力场和初始塑性损伤场的存在会在一定程度上缩短铝合金板的疲劳寿命.
3.3 含刮痕铝合金板的疲劳试验首先,采用专用试验装置对铝合金板进行刮擦,保证刮擦后形成的刮痕的尺寸尽量一致.刮擦结束后的铝合金板的疲劳试样如图3所示.然后利用高频疲劳试验机,进行了两级疲劳载荷下的高周疲劳试验,应力比均为0.02.试验结果如表5所示,并与第3.2节得到的疲劳寿命预估结果进行对比.结果表明,在两级应力水平下,预估的疲劳寿命的误差都在20%以内,说明应用以上理论预估的疲劳寿命的结果是可靠的.
3.4 刮痕深度及刮痕底部圆弧半径对疲劳寿命的影响3.4.1 刮痕深度对疲劳寿命的影响本节对含不同深度刮痕的铝合金板进行疲劳寿命预估,分析了刮痕深度对疲劳寿命的影响.刮痕的深度分别是0.35 mm和0.45 mm,刮痕底部的圆弧半径都是0.2 mm.施加的循环载荷最大名义应力分别是140 MPa、125 MPa,应力比是0.02.得到的损伤力学有限元数值解在表6中列出.图8(a)和图8(b)分别给出了动力学模拟刮擦过程结束后的含不同深度刮痕的结构局部的等效塑性应变分布图.图9给出了应力水平为125 MPa时,编号为447968的危险单元的损伤度随着循环次数的变化趋势图,此单元的位置在图10中标出.
表 6 含不同深度刮痕金属板试样的疲劳寿命预估结果Table 6 Fatigue life prediction result for metal plate specimen with different depth of scratch
| 刮痕深度/mm | 刮痕的底部圆弧半径/mm | 名义应力/MPa | 疲劳寿命 |
| 0.35 | 0.2 | 140125 | 100 000175 000 |
| 0.45 | 0.2 | 140125 | 50 00090 000 |
表选项
 |
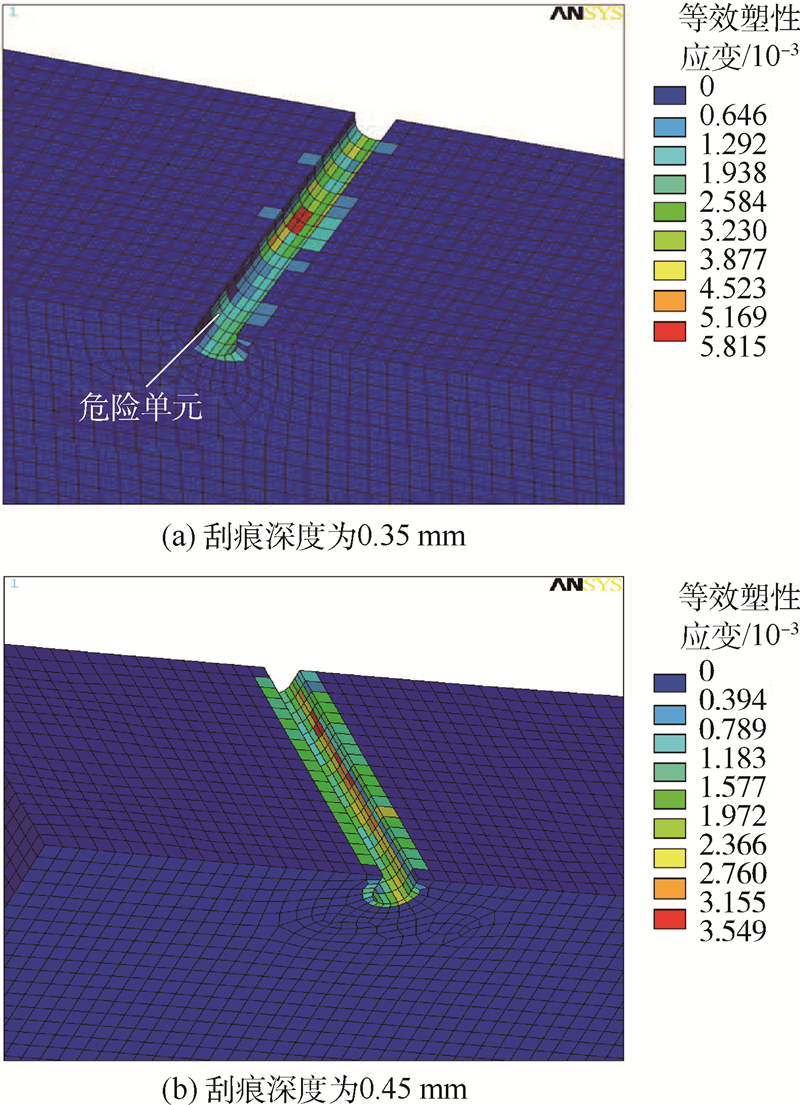| 图 8 含深度为0.35 mm及0.45 mm刮痕试样的等效塑性应变分布图Fig. 8 Distribution diagram of equivalent plastic strain of scratched specimen with depth of 0.35 mm and 0.45 mm |
| 图选项 |
 |
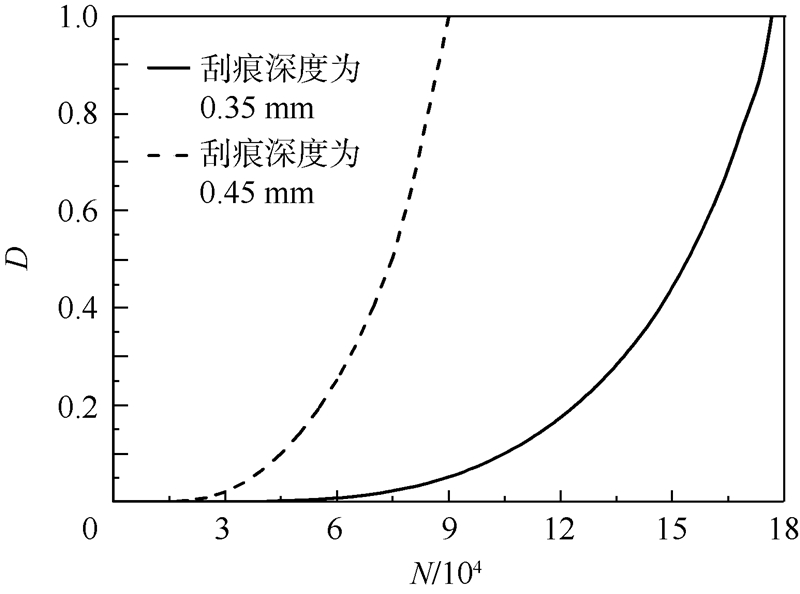| 图 9 含不同深度刮痕的结构损伤度随着载荷循环的变化趋势图Fig. 9 Change trend diagram of damage extent versus number of cycles of specimen with different depth of scratch |
| 图选项 |
 |
| 图 10 含不同圆弧半径刮痕的结构损伤度随载荷循环的变化趋势图Fig. 10 Change trend diagram of damage extent versus number of cycles of specimen with different radius of scratch |
| 图选项 |
通过以上对比看出,在动力学模拟刮擦过程结束后,含不同深度刮痕的结构的等效塑性应变的差别不大,即刮痕深度对刮擦过程结束后刮痕局部的初始损伤场影响较小,但是在同一应力水平下,在刮痕的底部圆弧半径都相同的情况下,刮痕的深度越深,刮痕处结构局部的应力集中越严重,导致其疲劳寿命越短.
3.4.2 刮痕底部圆弧半径对疲劳寿命的影响本节对含不同半径圆弧的刮痕的铝合金板进行疲劳寿命预估,分析了刮痕的底部圆弧半径对疲劳寿命的影响.刮痕的底部圆弧半径分别是0.10 mm和0.25 mm,刮痕的深度都是0.25 mm.施加的循环载荷的最大名义应力分别是120 MPa、100 MPa,应力比是0.02.得到的损伤力学有限元数值解在表7中列出.图10给出了应力水平为120 MPa时的危险单元的损伤度随着循环次数的变化趋势图.
表 7 含不同圆弧半径的刮痕的金属板的疲劳寿命预估结果Table 7 Fatigue life predicted results for metal plate with different radius of scratch
| 刮痕深度/mm | 刮痕底部圆弧半径/mm | 最大名义应力/MPa | 疲劳寿命 |
| 0.25 | 0.10 | 120100 | 85 000200 000 |
| 0.25 | 0.25 | 120100 | 260 000635 000 |
表选项
在动力学模拟刮擦过程结束后,底部圆弧半径为0.1 mm的刮痕附近的最大von Mises等效塑性应变是0.22%,而圆弧半径为0.25 mm的刮痕附近的最大von Mises等效塑性应变为0.61%,可见,刮痕的底部圆弧半径对刮擦过程结束后刮痕局部初始损伤场的影响差别不大.但是在同一应力水平下,在刮痕深度一定的情况下,刮痕的底部圆弧半径越小,刮痕处结构局部的应力集中越严重,导致其疲劳寿命越短.
4 结 论本文基于连续损伤力学理论,对含刮痕缺陷的7050-T7451铝合金板进行了疲劳寿命预估,为考虑含初始缺陷的工程结构疲劳寿命分析提供了一种新的研究方法和手段.
1) 基于非线性有限元方法,对刮擦的过程进行动力学仿真模拟,得到刮痕处的残余应力场与塑性应变场.
2) 基于连续损伤力学理论,根据Lemaitre的塑性损伤计算模型,得到了刮痕处的塑性变形所引起的初始损伤场.
3) 在疲劳损伤分析中,提出了一种对含刮痕结构进行疲劳寿命预估的损伤力学有限单元法,这种方法综合考虑了残余应力、初始塑性损伤以及后续疲劳损伤的共同作用.
4) 进行了含刮痕的铝合金板件的疲劳试验,并通过理论预估结果与试验结果的对比,验证了上述疲劳寿命预估方法的适用性.
5) 对含不同深度和不同圆弧底部半径的刮痕的铝合金板进行疲劳寿命预估,结果发现在刮痕底部的圆弧半径一定的情况下,刮痕的深度越深,刮痕处的应力集中越严重,导致其疲劳寿命越短;在刮痕深度一定的情况下,刮痕的底部圆弧半径越小,刮痕处的应力集中越严重,导致其疲劳寿命越短.
参考文献
| [1] | Schijve J.Fatigue of structures and materials[M].Dordrecht:Kluwer Academic,2001:1-5. |
| [2] | Song J H,Areias P M A,Belytschko T.A method for dynamic crack and shear band propagation with phantom nodes[J].International Journal for Numerical Methods in Engineering,2006,67(6):868-893. |
| Click to display the text | |
| [3] | Ince A,Glinka G,Buczynski A.Computational modeling of multiaxial elasto-plastic stress-strain response for notched components under non-proportional loading[J].International Journal of Fatigue,2014,62:42-52. |
| Click to display the text | |
| [4] | Lim J Y,Hong S G,Lee S B.Application of local stress-strain approaches in the prediction of fatigue crack initiation life for cyclically non-stabilized and non-Masing steel[J].International Journal of Fatigue,2005,27(10-12):1653-1060. |
| Click to display the text | |
| [5] | Chen X,Jin D,Kim K S.A weight function-critical plane approach for low-cycle fatigue under variable amplitude multiaxial loading[J].Fatigue & Fracture of Engineering Materials & Structures,2006,29(4):331-339. |
| Click to display the text | |
| [6] | Susmel L,Taylor D.A critical distance/plane method to estimate finite life of notched components under variable amplitude uniaxial/multiaxial fatigue loading[J].International Journal of Fatigue,2012,38:7-24. |
| Click to display the text | |
| [7] | Chaboche J L.Continuous damage mechanics-a tool to describe phenomena before crack initiation[J].Nuclear Engineering and Design,1981,64(2):233-247. |
| Click to display the text | |
| [8] | Lemaitre J.A course on damage mechanics[M].Berlin:Springer-Verlag,1992:11-19. |
| [9] | 王勖成,邵敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,1997:5-10.Wang X C,Shao M.The basic principle of the finite element method and numerical method[M].Beijing:Tsinghua University Press,1997:5-10(in Chinese). |
| [10] | 徐秉业,刘信声.应用弹塑性力学[M].北京:清华大学出版社,1995:97-112.Xu B Y,Liu X S.Application of elastic-plastic mechanics[M].Beijing:Tsinghua University Press,1995:97-112(in Chinese). |
| [11] | Mamalis A,Horvath M,Branis A,et al.Finite element simulation of chip formation in orthogonal metal cutting[J].Journal of Materials Processing Technology,2001,110(1):19-27. |
| Click to display the text | |
| [12] | Lemaitre J.Mechanics of solid materials[M].Cambridge:Cambridge University Press,1990:442-449. |
| [13] | Chaboche J,Lesne P.A nonlinear continuous fatigue damage model[J].Fatigue & Fracture of Engineering Materials & Structures,1988,11(1):1-17. |
| Click to display the text | |
| [14] | Chaudonneret M.A simple and efficient multiaxial fatigue damage model for engineering applications of macro-crack initiation[J].Journal of Engineering Materials and Technology,1993,115(4):373-379. |
| Click to display the text | |
| [15] | 吴学仁.飞机结构金属材料力学性能手册[M].北京:航空工业出版社,1996:433-434.Wu X R.Handbook of mechanical properties of aircraft structural metals[M].Beijing:Aviation Industry Press,1996:433-434(in Chinese). |
| [16] | Handbook M-5H MIL-HDBK-5H:Metallic materials and elements for aerospace vehicle structures[S].Washington,D.C.:US Department of Defense,1998:3-244. |
| [17] | Zhang M,Meng Q C,Hu W P,et al.Damage mechanics method for fatigue life prediction of pitch-change-link[J].International Journal of Fatigue,2010,32(10):1683-1688. |
| Click to display the text | |
| [18] | Zhang T,McHugh P,Leen S.Finite element implementation of multiaxial continuum damage mechanics for plain and fretting fatigue[J].International Journal of Fatigue,2012,44(2):260-272. |
| Click to display the text |
