基于多个视场的星敏感器设计理念较好地改善了传统星敏感器的性能.与单视场星敏感器对比,多视场星敏感器提高了姿态测量的精度和可靠性,同时兼顾了质量、体积和功耗等方面的要求.国外已经研制出一些多视场星敏感器,如美国德州农工大学参与研制的StarNavⅡ和StarNavⅢ[4, 5, 6, 7, 8],法国EADS Sodern公司研制的HYDRA星敏感器[9, 10, 11],以及美国Space Micro公司研制的SM-MDE13001星敏感器[12]等.国内的多视场星敏感器研究也已经展开[13, 14, 15].
在多视场星敏感器研究设计中,结构参数标定是非常关键且必不可少的一环.目前星敏感器标定的研究主要是针对单视场星敏感器光学系统参数的标定,在轨标定可以大致分为利用外部姿态信息标定的方法[16, 17]和不利用外部姿态标定的方法[18, 19, 20]两类,地面标定主要使用实验室标定[21]和天顶观测法[22],针对多视场星敏感器结构参数标定的研究非常少.本文提出多个视场结构参数标定方法可以有效解决多视场星敏感器结构参数在轨标定和地面标定的问题.
本文提出的多视场星敏感器结构参数标定方法是在假定星敏感器光学参数已经完全标定的基础上,基于星间角距不变原理,利用卫星观测得到的多个星对的星光矢量信息建立目标函数,用欧拉角表示旋转矩阵,然后利用非线性优化算法求解各个视场之间的旋转关系.此方法不依赖外部姿态测量信息,能够精确得到多视场星敏感器的结构参数.
1 结构参数标定模型星间角距不变是星敏感器在标定和姿态确定中常用的原理.角距不变是指两个矢量在不同坐标系中夹角不变,而星间角距不变则是指两个恒星在不同坐标系(如天球坐标系和星敏感器坐标系)下的单位矢量之间的夹角保持不变.恒星在某一坐标系中的单位矢量是指从此坐标系原点到恒星质心的单位化向量.
1.1 星间角距不变法标定的一般原理星敏感器坐标系原点定义为光轴在COMS上的投影中心O,z轴为光轴,x轴和y轴分别为过原点平行于像平面的两直边.星敏感器的图像坐标系是以图像传感器(COMS等)感光面的中心O′为坐标原点,平行于感光面的两直边分别为x轴和y轴的平面坐标系.图 1中,恒星S在图像坐标系中的坐标是(X,Y),Π为图像平面,(α,β)是恒星S在天球坐标系中的赤经和赤纬,f为星敏感器光学系统的主距(焦距).
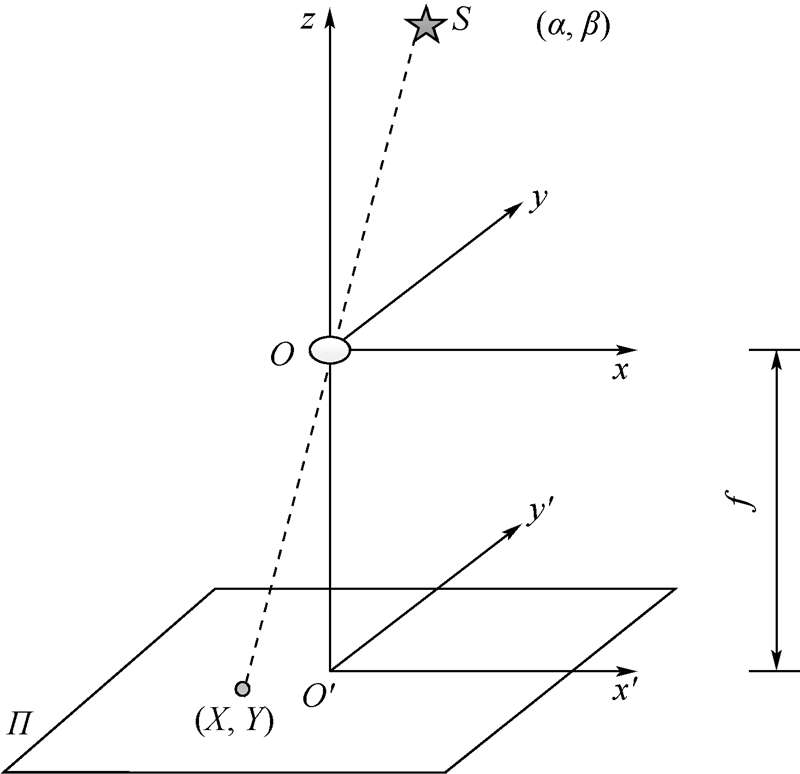 |
| 图 1 星敏感器坐标系和图像坐标系Fig. 1 Sensor reference frame and image reference frame |
| 图选项 |
不失一般性,以两个星敏感器为例,介绍基于星间角距不变的标定原理.图 2为两个镜像敏感器结构参数标定过程示意图. 以星敏感器1坐标系Oc1-xc1yc1zc1为基础建立全局坐标系,Oc2-xc2yc2zc2 为星敏感器2坐标系,O1-x1y1为星敏感器1的图像坐标系,O2-x2y2为星敏感器2的图像坐标系,R 21为星敏感器2坐标系到星敏感器1的旋转矩阵,也就是两个视场之间的结构参数.
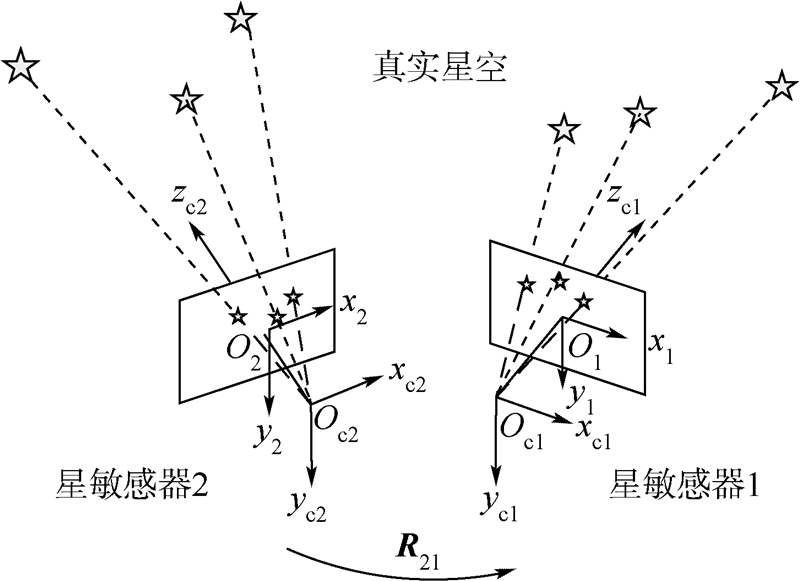 |
| 图 2 两个星敏感器结构参数标定过程示意图Fig. 2 Schematic diagram of structural parameter calibration implementation of two star trackers |
| 图选项 |
若任意一颗被观测到的恒星i的赤经赤纬坐标分别是(αi,βi),它在天球坐标系下的单位矢量 v i 可以用式(1)计算.
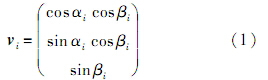
此恒星在图像中星点坐标为(Xi,Yi),主距为f,则在星敏感器坐标系下的单位矢量 w i 可以用式(2)计算:
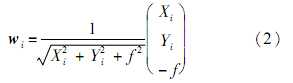
若恒星i、j分别代表星敏感器1、2观测到的任意恒星(i=1,2,…,m,j=1,2,…,n,m、n分别为星敏感器1、2观测到的恒星数目),根据理想小孔成像模型,星点成像星内角距不变,有
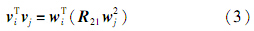
式中: v i、 v j 为它们在天球坐标系下的单位矢量; w i 代表全局坐标系(这里指星敏感器1坐标系)Oc1-xc1yc1zc1中的星光矢量; wj 2 代表星敏感器2坐标系Oc2-xc2yc2zc2中的星光矢量.
将观测得到的恒星数据代入式(3),优化求解,即可获得标定后坐标系Oc2-xc2yc2zc2到坐标系Oc1-xc1yc1zc1的旋转关系(即 R 21),从而实现星敏感器1、2间的结构参数标定.采用相同方法可以实现其他视场的结构参数标定,从而完成整个系统的结构参数标定.
1.2 多视场星敏感器结构参数的表示多个视场之间的结构参数即是多个子视场星敏感器坐标系之间的相互旋转关系.一般地,可以用方向余弦矩阵、欧拉角和姿态四元数等表示坐标系的旋转.
对矢量和坐标系的旋转来说,真正有意义的是包含9个参数的方向余弦矩阵,它也是结构参数在标定计算中的真实表达.但由于方向余弦矩阵参数过多,加之各个参数之间并不独立,所以以方向余弦矩阵的9个参数为优化参数建立目标
函数比较复杂,优化得到 ${\rm{\tilde R}}$要进行正交化才可以得
到真正正交的方向余弦矩阵 R .此外,方向余弦矩 阵表示各个子视场之间的旋转并不直观和明晰.四元数也是如此.
相反地,欧拉角只有3个参数,各个参数物理意义直白,容易理解,而且互相独立,以欧拉角3个参数作为目标函数的待优化参数,不需要外加约束使得旋转矩阵保持正交.
采用3-1-2转动的欧拉角来表示结构参数,将子视场星敏感器坐标系依次沿着z轴、x轴和y轴旋转后与全局坐标系重合,转过的角度分别为ψ、φ和θ,(φ,θ,ψ)即为星敏感器的结构参数.旋转矩阵可以表示成三次坐标转换的乘积:

2 全局结构参数标定方法和步骤在星间角距不变原理的基础上,以四视场星敏感器为例,提出了全局结构参数标定模型.
将4个视场分别记为视场0、视场1、视场2和视场3,对应的星敏感器也依次编号为0、1、2、3.同时建立相应的星敏感器坐标系.以星敏感器0坐标系O-xc0yc0zc0为基础建立全局坐标系,求取其他 3个星敏感器坐标系到全局坐标系的旋转欧拉角.
全局标定方法分为两步进行:首先是利用设计的视轴指向确定结构参数初值;其次使用多个姿态下多个视场的星图进行整体优化,得到精确的结构参数.在标定前,需要采集多组星图,并对它们进行识别,得到观测恒星的图像坐标和天球坐标(赤经和赤纬).
2.1 结构参数初值的确定对于不同的初值,欧拉角优化结果可能不尽相同(这与方向余弦矩阵和四元数不同,对于确定的旋转,他们的表达是唯一的,换言之,对所有初值都收敛到唯一解),欧拉角优化结果会因初值不同而变化,所以选取恰当的初值对采用欧拉角作为优化参数的标定模型来说非常重要.
在设计多视场星敏感器时,各个视场在全局坐标系中视轴指向(即各个子视场视轴在全局坐标系中的投影)是已知的,利用各个视场的视轴指向,可以求出结构参数的初值.
视场0和视场t的姿态转换关系为

式中:t=1,2,3分别为星敏感器坐标系1、2、3; X t-0 为视场t的视轴在全局坐标系即视场0中的投影; R t0 为从星敏感器坐标系t到全局坐标系的旋转矩阵; X t 为视场t的视轴在自身坐标系中的投影,且 X t=[0 0 1]T.
已知 X t-0和 X t 的矢量旋转关系,易求得旋转矩阵 R t0. R t0 采用3-1-2旋转的欧拉角表示(如式(4)所示),记为 R (φ,θ,ψ),然后可以求出结构参数初值(φ,θ,ψ)t.
2.2 结构参数优化由式(3),易推出:
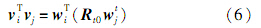
式(6)各元素含义同前文所述.未知参数 R (φ,θ,ψ)(即 R t0),它有3个自由度,则至少需要3个类似于式(6)的方程.
令Vij= v Ti v j,将式(6)变形得到
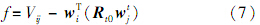
从多组星图中获得多个星对的星光矢量信息,联立n个类似式(7)的方程,得到
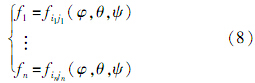
因此式(8)是关于(φ,θ,ψ)的非线性方程组,只需要求解这个方程组,就可以算出星敏感器坐标系t到全局坐标系的旋转角(φ,θ,ψ).
由式(8)建立的目标函数为
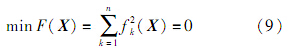
式中: X =(φ,θ,ψ).
由于式(9)的逼近函数的矩阵可能出现奇异或者接近奇异的情况,本文选用了L-M(Levenberg-Marquardt)算法,这一算法的优越性即是在求解非线性方程组时增加了一个正定的对角阵,解决了矩阵奇异的问题.
3 四视场星图仿真及标定结果分析 3.1 四视场星图仿真参数为了验证多视场星敏感器结构参数标定模型,仿真了多组随机且不连续的姿态下4个视场的星图并利用这些星图对结构参数进行了标定.
本文中假定四视场星敏感器的视轴在全局坐标系O-xc0yc0zc0中的指向如图 3所示,各子视场视轴在全局坐标系中投影如表 1所示.
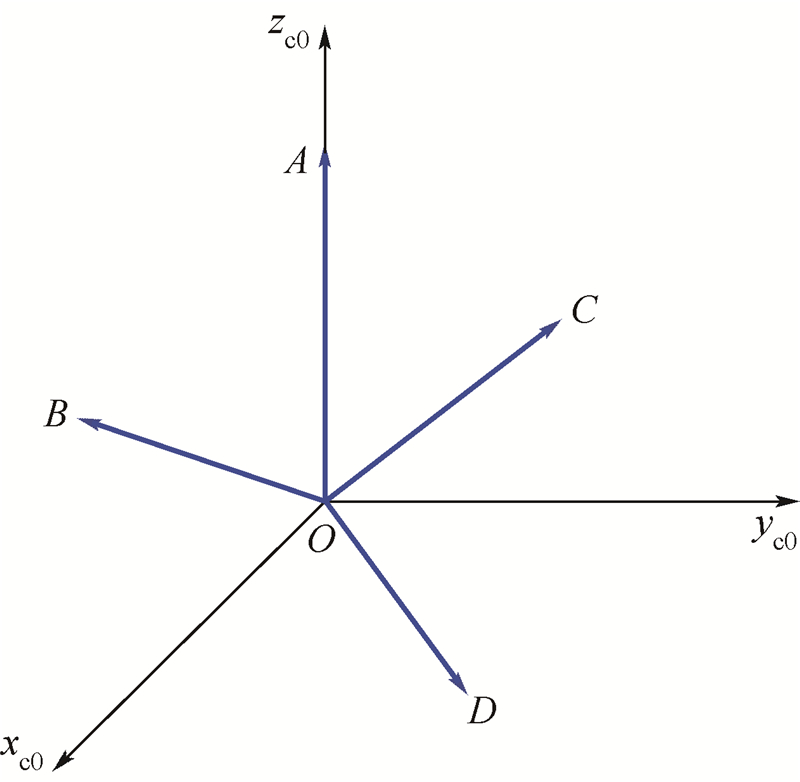 |
| 图 3 四视场视轴的相对关系Fig. 3 Correlative relationship among four FOV boresights |
| 图选项 |
表 1 各个子视场的视轴指向Table 1 Directions of every sub FOV boresight
| 子视场 | 各子视场视轴在全局坐标系中的投影 |
| 第0子视场视轴 | $\mathop {{\rm{OA}}}\limits^ \to $=[0.0 0.0 1.0]T |
| 第1子视场视轴 | $\mathop {{\rm{OB}}}\limits^ \to $=[0.85355 -0.14645 0.5]T |
| 第2子视场视轴 | $\mathop {{\rm{OC}}}\limits^ \to $=[-0.14645 0.85355 0.5]T |
| 第3子视场视轴 | $\mathop {{\rm{OD}}}\limits^ \to $=[0.70711 0.70711 0.0]T |
表选项
星图仿真参数设置如表 2所示.仿真过程不考虑光学镜头的成像变形,仅进行透视投影.
表 2 星图仿真参数设置Table 2 Parameter setting of star image simulation
| 仿真参数 | 数值 |
| 像元分辨率/像素 | 1024×1024 |
| 像元尺寸/mm | 0.0055×0.0055 |
| 主点位置/像素 | (512,512) |
| 焦距/mm | 31.9400 |
| 最大敏感星等/Mv | 6.0 |
| 星点位置噪声均值/像素 | 0.000 |
| 星点位置噪声标准差/像素 | 0.100 |
表选项
3.2 标定结果评价分析3.2.1 结构参数标定结果在全天球随机抽取10个(不连续)姿态,生成10组星图,分别对它们进行识别,然后将这些识别出来的星点信息代入标定模型,计算星敏感器的结构参数,即各个子视场之间的旋转欧拉角.L-M优化方法良好的稳健性保证了目标函数为正定方程组时即可优化得到最优解(单组星图优化即可收敛).但为了避免单幅星图代粗大误差和提高结构参数标定精度,采用10组星图进行优化.
仿真星图各视场视轴夹角的平均值和理论值对比如表 3所示.多组星图整体优化后标定结果和真值偏差如表 4所示.和设定的结构参数(理论真值)相比,结构参数标定结果和真值基本一致.
表 3 视轴之间的夹角Table 3 Angle between two boresights (°)
| 视轴夹角 | 理论夹角 | 平均标定夹角 |
| θ0-1 | 60 | 60.0002 |
| θ0-2 | 60 | 59.9995 |
| θ0-3 | 90 | 90.0001 |
表选项
表 4 4个视场的结构参数真值及标定结果偏差Table 4 True value and deviations of structural parameters of four FOVs
| 4个视场设定的结构参数 |
|
| 视场1到视场0 |
|
| 视场2到视场0 |
|
| 视场3到视场0 |
|
表选项
考虑单星敏感器光学系统初始标定残差,仿真时添加主点标定残差和焦距标定残差(亚像元提取误差,像面倾斜角和畸变的残差已包含到星点位置随机误差中),参考了文献[23]的分析,选取1σ的误差,即1.5像素的主点误差和0.2像素的焦距误差.标定结果和真值偏差如表 4所示.结果表明当单星敏感器光学系统残差在一定范围内时,残差并不会对采用本方法标定多视场星敏感器结构参数结果产生较大影响,标定结果依然有效、可信.
3.2.2 标定结果精度评价结构参数的优化目标函数建立在星间角距不变的基础上,因此采用星内角统计偏差对标定结果进行间接评价.
对于有N颗星点的单视场星敏感器,星内角统计偏差的定义[24]为
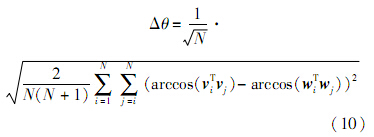
同理,可以推出多视场下结构参数已知的两个子视场之间的星内角统计偏差为
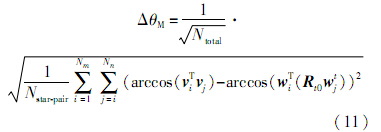
式中:ΔθM为星内角统计偏差;Ntotal为全局视场0和子视场t中的总星点数目;Nstar-pair为代入计算的星对数目(这里的星对必须分别来自全局视场0和子视场t),显然有Ntotal=N0+Nt,Nstar-pair=N0×Nt,N0和Nt分别为视场0和视场t中的星点数目.式(11)利用多组星图整体优化得到的结构参数将子视场t的星点在自身星敏感器坐标系下的单位矢量投影到全局坐标系下,然后再计算两个视场间的星内角统计偏差.10组姿态下所有子视场到全局视场的星内角统计偏差平均值为1.3″,和加入的 0.1像素的星点位置噪声水平相当(易推算出星点位置偏差0.1像素时,星内角偏差为3.55″).
为了验证该标定方法的性能以及结构参数标定对多视场星敏感器姿态测量的影响,比较了多视场星敏感器结构参数标定前后姿态测量精度的变化.随机生成10组仿真星图用于姿态测量(仿真时假设由于噪声引起的星敏感器结构参数变化不超过0.01°).
采用星敏感器坐标系到天球坐标系按3-1-2旋转的欧拉角来表示星敏感器在天球坐标系中的姿态.将子视场1、2和3的星光矢量分别利用未标定的结构参数和标定出来的结构参数投影到全局坐标系下(即第0子视场坐标系),再进行全局姿态解算.
利用未标定的结构参数计算姿态的测量均方根误差为6.5″、8.0″和6.3″,星内角统计偏差的平均值是4.5″.而利用标定后的结构参数计算出来的姿态欧拉角的均方根误差则是3.2″、3.4″和3.9″.对比两者可以看出,结构参数经过标定的多视场星敏感器的姿态测量精度有所提高.
4 外场观星试验标定结果为了进一步验证本方法的实用性,采用课题组研制的三视场星敏感器外场观星拍摄的3组星图作为实验数据,对其结构参数进行了标定.标定结果如表 5和表 6所示.
表 5 外场试验中三视场星敏感器结构参数Table 5 Calibration results of structural parameters of 3 FOV star trackers in outside experiments
| 结构参数 | 欧拉角/rad | ||
| φ | θ | ψ | |
| 视场1到视场0 | 1.58809 | -1.41510 | 1.41213 |
| 视场2到视场0 | -0.01526 | 1.57380 | 0.00869 |
表选项
表 6 外场试验中三视场星敏感器视轴夹角标定结果Table 6 Calibration results of angle between two boresights of 3 FOV star trackers in outside experiments (°)
| 视轴夹角 | 设计夹角 | 平均标定夹角 |
| θ0-1 | 90 | 90.1880 |
| θ0-2 | 90 | 90.2641 |
| θ1-2 | 90 | 90.1248 |
表选项
此三视场星敏感器的结构参数能够被精确标定,将标定出来的结构参数计算结果代入式(11),计算星内角统计偏差,其平均值为6.4″.实际试验的星内角统计偏差均值略大于仿真结果,主要原因是外场观星试验时受到大气折射的影响,且3个视场并不能同时指向天顶.
5 结 论本文通过仿真试验和外场观星试验来测试多视场星敏感器结构参数的标定方法.
1) 在仿真中,比较了仅添加星点位置噪声和添加主点、焦距误差以及星点位置噪声的两种情况下解算出的结构参数和理论值的偏差,对比结果表明一定范围内的光学系统残差对结构参数标定影响很小.
2) 仿真还比较了结构参数标定前后姿态测量精度的变化,对比结果表明多视场星敏感器结构参数标定可以提高姿态测量精度.
3) 外场观星试验中使用本方法也准确地标定了各个视场之间的结构参数.
仿真结果和外场试验结果都表明这种方法能够准确求解多视场星敏感器的结构参数,将标定得到的结构参数用于多视场星敏感器姿态测量,可以精确求解星敏感器天球姿态,具有实用性.
参考文献
| [1] | Jørgensen J L, Liebe C C.The advanced stellar compass development and operations[J].Acta Astronautica,1996,39(9-12):775-783. |
| Click to display the text | |
| [2] | Liebe C C. Accuracy performance of star trackers-a tutorial[J].IEEE Transactions on Aerospace and Electronic Systems,2002,38(2):587-599. |
| Click to display the text | |
| [3] | 王晓东. 大视场高精度星敏感器技术研究[D].长春:中国科学院长春光学精密机械与物理研究所,2003. Wang X D.Study on wild-fleld-of-view and high-accuracy star sensor technologies[D].Changchun:Changchun Institute of Optics,Fine Mechanics and Physics Academia Sinica,2003(in Chinese). |
| Cited By in Cnki (46) | |
| [4] | Mortari D, Romoli A.StarNav III:A three fields of view star tracker[C]//IEEE Aerospace Conference Proceedings.Piscataway,NJ:IEEE Press,2002,1:47-57. |
| Click to display the text | |
| [5] | Mortari D, Pollock T C,Junkins J L.Toward the most accurate attitude determination system using star trackers[J].Advances in the Astronautical Sciences,1998,99(2):839-850. |
| Click to display the text | |
| [6] | Mortari D, Angelucci M.Star pattern recognition and mirror assembly misalignment for digistar Ⅱ and Ⅲ multiple FOVs star sensors[J].Advances in the Astronautical Sciences,1999,102(Pt2):175-1184. |
| [7] | Ju G,Pollock T, Junkins J L.Digistar II micro-star tracker-autonomous on-orbit calibration and attitude estimation[J].Advances in the Astronautical Sciences,2000,103(Pt3):2025-2035. |
| Click to display the text | |
| [8] | Mortari D, Junkins J L.SP-search star pattern recognition for multiple fields of view star trackers[J].Advances in the Astronautical Sciences,2000,103(Pt.3):2127-2143. |
| Click to display the text | |
| [9] | Ludovic B, Nicolas P,Stephen A.New multiple head star sensor (HYDRA) description and status,AIAA-2005-5932[R].Reston:AIAA,2005. |
| Click to display the text | |
| [10] | Ludovic B, Nicolas P,Laurent M.HYDRA multiple heads star tracker based on active pixel sensor and the gyrometer assistance option[C]//AIAA 57th International Astronautical Congress,IAC 2006.Reston:AIAA,2006,6:4187-4195. |
| [11] | Ludovic B, Julien O,Lionel O,et al.High accuracy sodern star trackers:Recent improvements proposed on SED36 and HYDRA star trackers[C]//Collection of Technical Papers-AIAA Guidance,Navigation,and Control Conference 2006.Reston:AIAA,2006:132-138. |
| Click to display the text | |
| [12] | Andrist P, Babbitt A,Ethier V,et al.DEbris capture and orbital manipulation-DECOM[C]//AIAA SPACE Conference and Exposition 2011.Reston:AIAA,2011:97937. |
| Click to display the text | |
| [13] | 张华. 高精度双视场星敏感器关键技术研究[D].武汉:华中科技大学,2011. Zhang H.Research on the key techniques of high precise double-FOV star sensor[D].Wuhan:Huazhong University of Science and Technology,2011(in Chinese) |
| Cited By in Cnki (4) | |
| [14] | 叶生龙,魏新国, 樊巧云,等.多视场星敏感器工作模式设计[J].北京航空航天大学学报,2010,36(10):1244-1247. Ye S L,Wei X G,Fan Q Y,et al.Operation mode design of multi-FOV star sensor[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(10):1244-1247(in Chinese). |
| Cited By in Cnki (9) | |
| [15] | 王真,魏新国, 张广军.多视场星敏感器结构布局优化[J].红外与激光工程,2011,40(12):2469-2473. Wang Z,Wei X G,Zhang G J.Structure optimization for multi-FOV star sensor[J].Infrared and Laser Engineering,2011,40(12):2469-2473(in Chinese). |
| Cited By in Cnki (12) | |
| [16] | Singla P, Griffith D T,Junkins J L.Attitude determination and autonomous on-orbit calibration of star tracker for GIFTS mission[C]//Spaceflight Mechanics 2002.San Diego:AAS,2002:19-38. |
| Click to display the text | |
| [17] | Griffith D T, Singla P,Junkins J L.Autonomous on-orbit calibration of approaches for star tracker cameras[C]//Spaceflight Mechanics 2002.San Diego:AAS,2002:39-57. |
| Click to display the text | |
| [18] | 魏新国,张广军, 樊巧云,等.基于RAC约束的星敏感器在轨校准方法[J].光学精密工程,2008,16(10):2009-2013. Wei X G,Zhang G J,Fan Q Y,et al.On-orbit calibration of star sensor based on radial alignment constraint[J].Optics and Precision Engineering,2008,16(10):2009-2013(in Chinese). |
| Cited By in Cnki (6) | |
| [19] | Samaan M A, Griffith T,Singla P,et al.Autonomous on-orbit calibration star trackers[C]//Core Technologies for Space System Conference.Colorado Springs,CO:Colorado University,2001:1-18. |
| [20] | 申娟,张广军, 魏新国.基于卡尔曼滤波的星敏感器在轨校准方法[J].航空学报,2010,31(6):1220-1224. Shen J,Zhang G J,Wei X G.On-orbit calibration of star sensor based on Kalman filter[J].Acta Aeronautica et Astronautica Sinica,2010,31(6):1220-1224(in Chinese). |
| Cited By in Cnki (7) | |
| [21] | Liu H B, Li X J,Tan J C,et al.Novel approach for laboratory calibration of star tracker[J].Optical Engineering,2010,49(7):073601. |
| Click to display the text | |
| [22] | 李春艳,李怀锋, 孙才红.高精度星敏感器天文标定方法及观测分析[J].光学精密工程,2006,14(4):558-563. Li C Y,Li H F,Sun C H.Astronomical calibration method and observation analysis for high-accuracy star sensor[J].Optics and Precision Engineering,2006,14(4):558-563(in Chinese). |
| Cited By in Cnki (54) | |
| [23] | 孙婷,邢飞, 尤政.高精度星敏感器光学系统误差分析[J].光学学报,2013,33(3):253-261. Sun T,Xing F,You Z.Optical system error analysis of high accuracy star trackers[J].Acta Optica Sinica,2013,33(3):253-261(in Chinese). |
| Cited By in Cnki (5) | |
| [24] | 郝雪涛,张广军, 江洁.星敏感器模型参数分析与校准方法研究[J].光电工程,2005,32(3):5-8. Hao X T,Zhang G J,Jiang J.Star sensor model parameter analysis and calibration method[J].Opto-Electronic Engineering,2005,32(3):5-8(in Chinese). |
| Cited By in Cnki (7) |
