民航领域目前广泛使用的空中交通预警与防撞系统[2](Traffic alert and Collision Avoidance System,TCAS)和广播式自动相关监视系统[3](Automatic Dependent Surveillance Broadcast,ADS-B)都是采用相关飞行间隔规定定义避撞区,并根据实时监测的飞机之间相对位置,向飞行员提供告警信息,最终通过飞行员操纵飞机避免冲突.这类防撞系统虽然无法直接用于无人机的避撞决策,但为无人机避撞系统的设计提供了良好的研究基础.Eric等[4]通过仿真和飞行测试,分析了利用感知与避撞系统和TCAS系统,实现空中无人飞行器自主避撞的可行性.Carbone[5]和Luongo[6]等针对非合作飞行器的避撞问题,分别提出了基于圆球、圆柱碰撞区的三维几何避撞算法.该算法能直接求得所有控制量的改变量,并适用于实时系统.Finley[7]提出了基于不同的碰撞逃避时间划分避撞区域的方法,并在不同避撞区域内采取相应的避撞机动,从而实现无人机自主避撞.Timothy[8]提出了综合考虑飞机位置信息的准确性和跟踪预定航迹的能力等不确定性因素,选取大小不同的距离阈值划分避撞区域的方法.Amirreza等[9]针对多无人机飞行冲突问题提出了基于导航函数的避撞算法,并设计了固定大小的碰撞区、保护区和警戒区.总之,目前主要采用的避撞区是基于固定时间或距离,定义形为圆柱[10, 11]、球[12, 13]的三维避撞区,或者圆[14]、椭圆[7]的二维避撞区.
然而,上述基于固定的时间阈度或安全距离阈度划分避撞区域的方法存在明显的不足.由于未充分考虑无人机和入侵机的相对位置、相对速度、侵入角度等参数的影响,为保证飞行安全,避撞区域定义时往往过于保守.这不仅会导致不必要的避撞机动,而且会造成一定程度的空域浪费,给日益紧缺的空域带来更大压力.
本文针对上述问题,提出了面向空中威胁的无人机动态碰撞区建模方法.首先,基于无人机和入侵机的位置、速度、入侵角,以及无人机的机动约束、最小安全距离等信息,研究了无人机不采取规避机动和采取最大侧向过载规避机动两种情况下,无人机和入侵机会发生碰撞的区域范围,并分别给出了两个碰撞区的解析表达式.在此基础上,提出了一定遭遇条件下的不可规避区(non-escape region)和安全飞行包络的概念.最后,仿真分析了各区域之间的关系,以及主要影响因素.
1 无人机避撞过程和问题的描述无人机的避撞过程可分为3个阶段:碰撞检测、避撞决策和避撞机动.其中,碰撞检测是避撞的前提,避撞决策是避撞的关键.无人机飞行过程中,通过自身携带的传感器或者来自机外其他可信系统(如指挥中心、友机、ADS-B、C4ISR等)获得飞行区域一定范围内的飞行目标运动信息[15],并实时进行碰撞检测.当检测到碰撞的可能时,进行避撞决策并给出规避机动方式和机动时刻.一般而言,当离威胁目标较远有充足的规避时间时,可采取常规的避撞机动方法(如重规划航路),其避撞反应时间较长;而当距离威胁目标较近时则需要以无人机的最大机动能力对威胁进行紧急规避;当和威胁目标接近到一定程度时,无论无人机如何机动都无法避免碰撞的发生.常规的避撞机动对于无人机完成飞行任务的影响较小,而紧急规避机动可能导致无人机偏离预定航路很远的情况发生,是一种不得已的安全措施.避撞决策就是要决定规避机动方式和机动时刻,以尽可能少地影响预定的飞行计划.
根据上述避撞过程的描述,本文通过设计无机动碰撞区来进行碰撞检测,用最大机动碰撞区、不可规避区判断是否该进行紧急规避以及如何进行紧急机动,并通过安全飞行包络为无人机提供全方位的安全性分析.
1.1 碰撞区的描述设t0时刻起无人机、入侵机分别以速度Va和Vm做匀速直线运动,则无机动碰撞区指t0时刻以后两机必将发生碰撞的入侵机t0时刻所有可能位置点的集合.
设t0时刻起无人机以速度Va按最大可用过载做匀速圆周运动,入侵机以速度Vm做匀速直线运动,则最大机动碰撞区指t0时刻以后两机必将发生碰撞的入侵机t0时刻所有可能位置点的集合.
此外,本文将无人机位置点为中心,最小安全距离为半径的圆球叫做禁入区,一旦入侵机进入禁入区,即视为碰撞发生.
1.2 坐标系和投影面假设无人机和入侵机在空中匀速飞行,如图 1所示,点Pa处为无人机,点Pm处为入侵机,DL为两机的最小安全距离;以Pa为球心,DL为半径的红色圆球为无人机的禁入区.设无人机速度为Va,入侵机速度为Vm,将两机的速度矢量在惯性坐标系的三坐标平面内投影,并根据速度矢量的投影值,分别在3个平面上求解各碰撞区的模型.考虑到三坐标平面内碰撞区建模的相似性,本文以xy平面的建模为例来详细阐述建模过程.
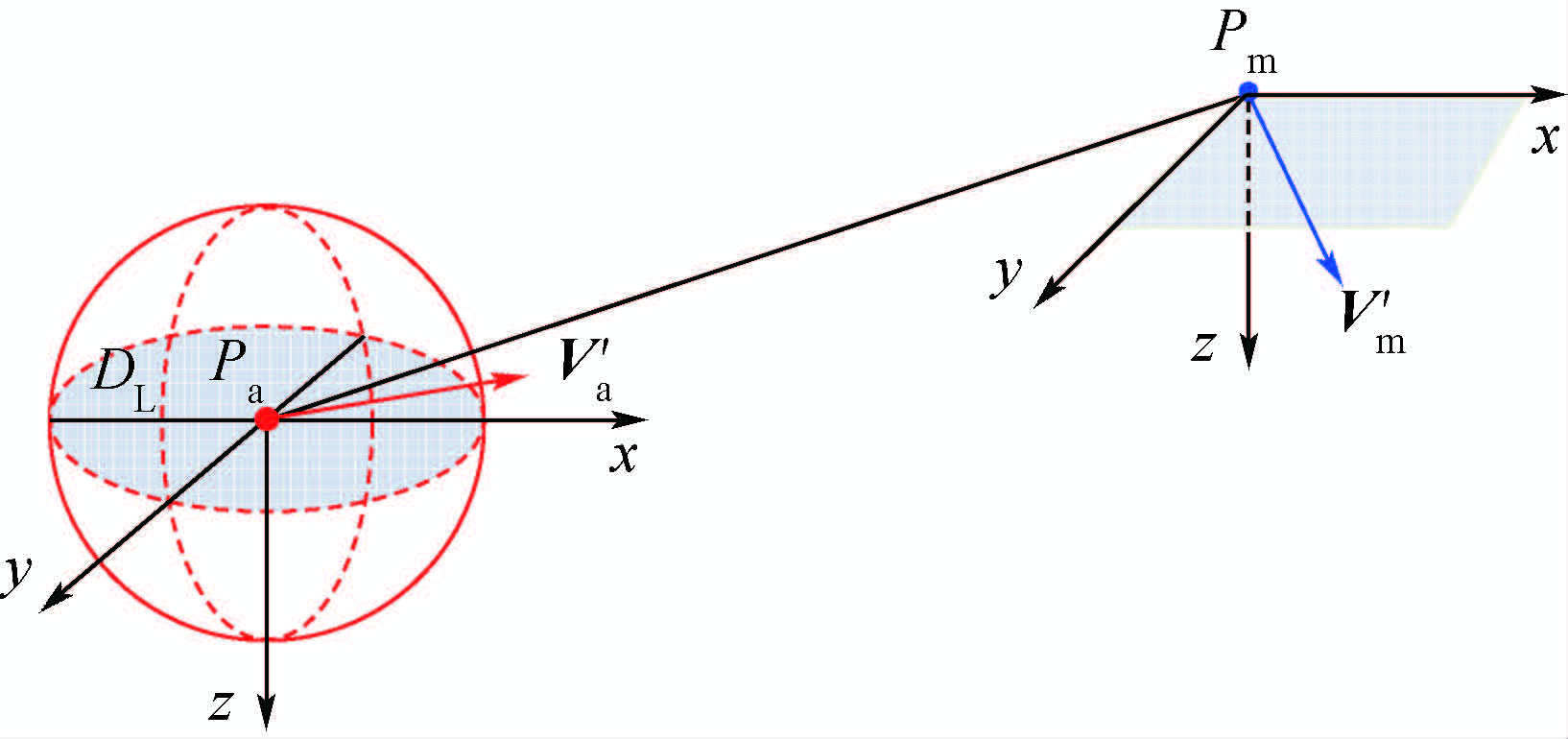 |
| 图 1 无人机与入侵机的碰撞几何关系图Fig. 1 Collision geometric relation diagram between UAV and intruder |
| 图选项 |
2 无机动碰撞区建模根据无机动碰撞区的描述建立其数学模型.如图 2所示,设入侵机速度大小为Vm,航向角为φm,无人机速度大小为Va,航向角为φa(不失一般性,可令φa=0,建立坐标系),两机之间的最小安全距离为DL.将无人机当作参照物,则入侵机以相对速度Vr作匀速直线运动.无机动碰撞区的临界情况是:当入侵机到达离无人机最近点时,两机之间的距离D(t)恰好等于最小安全距离DL,即两机刚好发生碰撞.因此,无机动碰撞区是与相对速度Vr平行,且与无人机的碰撞区相切的两条红色边界线所形成的区域.
 |
| 图 2 无机动碰撞区示意图Fig. 2 Schematic of no-maneuver collision region |
| 图选项 |
取无机动碰撞区边界线上任意一点,设该点处入侵机相对无人机的初始方位角为θ0,初始距离为D0,则t时刻无人机与入侵机之间的距离为
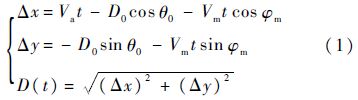
对D2(t)求导数,得
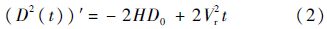
式中:
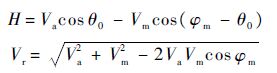
1) 当H≥0时
令(D2(t))′=0,得

此时入侵机到达两机最近点.根据无机动碰撞区的临界条件,可知:
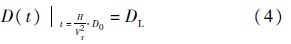
所以
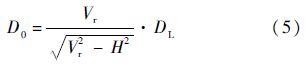
2) 当H<0时
(D2(t))′恒大于零.表明t0时刻无人机与入侵机距离最近;之后,两机之间的距离逐渐增大,即两机互相远离,不会发生碰撞.因此,可规定此时无机动碰撞区的边界值D0=DL,这种情况对应于图 2中的红色半圆弧.
综上,当初始方位角θ0依次在0~2π范围内取值时,可求得无机动碰撞区的所有边界值.因此,无机动碰撞区的解析式为
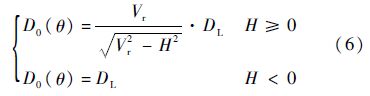
式中:
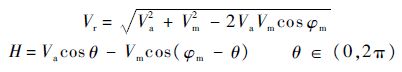
3 最大机动碰撞区建模根据最大机动碰撞区的描述建立其数学模型.最大机动碰撞区的建模思想是:开始时,无人机和入侵机都做匀速直线飞行,当入侵机到达某一位置时,无人机立刻以最大侧向过载向左或向右转弯机动,如果此时恰好可以避免碰撞的发生,则开始转弯机动时入侵机的位置就是最大机动碰撞区的边界点.
以无人机开始进行最大侧向过载转弯机动的位置点为坐标原点、速度方向为x轴正方向,建立直角坐标系.图 3为初始方位角为θ0时无人机与入侵机的运动情形示意图.R为无人机以最大侧向过载nymax飞行的转弯半径,D0为转弯机动开始时刻,两机之间的初始距离,Δφ为转弯机动开始t时间时,无人机速度方向转过的角度,其他符号的意义与图 2相同.
 |
| 图 3 最大机动避撞的运动情形Fig. 3 Flight scenario with maximum maneuverability |
| 图选项 |
最大机动碰撞区的临界情况是:两机距离为D0时无人机开始最大侧向过载转弯机动,当两机到达最接近点时两机距离D(t)恰好等于最小安全距离DL.此时,初始距离D0即为最大机动碰撞区的边界值.
忽略飞行中可能的小侧滑角,则根据xy平面内无人机的侧向动力学方程,可知无人机航向角速度为
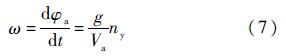
式中:g为重力加速度;ny为无人机侧向过载,其他符号的意义与前文相同.
相应地,无人机的转弯半径为
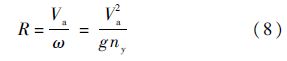
t时刻,无人机与入侵机之间的距离:
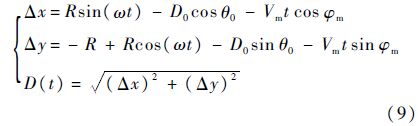
两机到达最接近点时,距离D(t)恰好等于最小安全距离DL,因此可以建立二元方程组:

取ny=nymax,将式(7)~式(9)代入式(10),整理可得
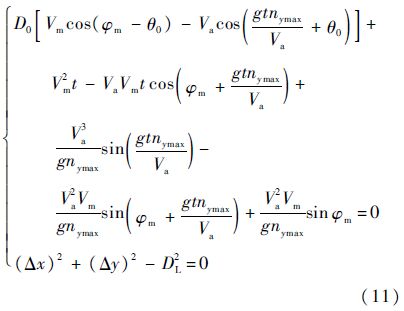
方程(11)中,D0和t为未知量,其他变量均为已知量.因此,通过求解该方程组,可以求得初始方位角为θ0时最大机动碰撞区的边界值D0.然后,其他条件不变,仅使初始方位角θ0依次在0~2π范围内取值,根据方程(11)即可求得无人机和入侵机在该运动状态下,无人机向右转弯的最大机动碰撞区的所有边界值.
同理,取ny=-nymax,可求得当无人机向左转弯机动时,最大机动碰撞区的数学模型,此处不再赘述.
由于最大机动碰撞区模型方程为非线性方程组,因此本文采用数值方法中的二分法[16]进行求解,最终得到未知量t、D0的数值解.同时,由于D0是两机之间的相对距离,因此D0>0.当两机不会发生碰撞时,根据方程组求得的D0<0,不符合D0本身的物理意义,令此时最大机动碰撞区的边界值D0=DL.
4 不可规避区和安全飞行包络设t0时刻起入侵机以速度Vm做匀速直线运动,则不可规避区指无论无人机机动与否,t0时刻以后两机必将发生冲突的入侵机t0时刻可能位置的集合.
根据不可规避区的描述可知,不可规避区是无机动碰撞区与所有可能的向左、向右转弯机动对应机动碰撞区的交集.为简化起见,在实际求取不可规避区的边界时,可用最大侧向过载对应的向左、向右最大机动碰撞区和无机动碰撞区的交集来表示.当入侵机进入无机动碰撞区后,判断其是否同时位于两个方向上的最大机动碰撞区内,即可得知入侵机是否进入不可规避区,因此,建立不可规避区并未增加无人机的在线计算量.
上述不可规避区分别是对应某一入侵机航向角得到的.若令入侵机的航向角φm依次在0~2π范围内取值,则可求得对应不同入侵机航向的不可规避区.取这些不可规避区的并集,得到分布在无人机周围的对应于不同入侵航向角的不可规避区,本文将其外包络定义为安全飞行包络.
安全飞行包络表示了在一定条件下无人机能够规避入侵机威胁的分界线,入侵机处于该包络之外时,无人机可通过某种机动规避碰撞的发生,当入侵机沿相对于无人机汇聚方向进入包络之内时,无人机无论如何机动也无法避免与入侵机的碰撞.安全飞行包络是飞行安全的最后决断线,可为无人机规避方法选择、规避时刻/规避位置的确定等避撞决策提供理论支撑,也可用在有人驾驶飞机上,辅助飞行员处理紧急避撞情形.
上述各区域建模中对于入侵机匀速直线飞行的设定是比较苛刻的.对于比较常见的入侵机按预定航线(该航线不一定是直线)飞行,且机动性不大的情况,无人机可以根据周期性测量的入侵机速度等信息,并假设在一个周期内入侵机的速度大小和方向不变,来计算和更新各碰撞区,并据此调整避撞决策,以实现对这种非匀速直线飞行入侵机的安全避撞.
5 仿真分析与讨论设基本仿真条件为:最小安全距离DL=50 m,无人机飞行速度Va=60 m/s,入侵机飞行速度Vm=120 m/s,无人机航向角φa(0)=0,无人机最大侧向过载nymax=0.8,入侵机航向角φm=240°.在基本仿真条件下,对所建区域进行仿真分析.
5.1 碰撞区仿真分析在基本仿真条件下,根据式(6)计算无机动碰撞区的范围.由图 4可知无机动碰撞区边界与相对速度平行.
 |
| 图 4 无机动碰撞区与相对速度的关系Fig. 4 Relation between no-maneuver collision region and relative velocity |
| 图选项 |
根据最大机动碰撞区的数学模型可求得基本仿真条件下,向右和向左最大机动碰撞区的边界,如图 5所示.
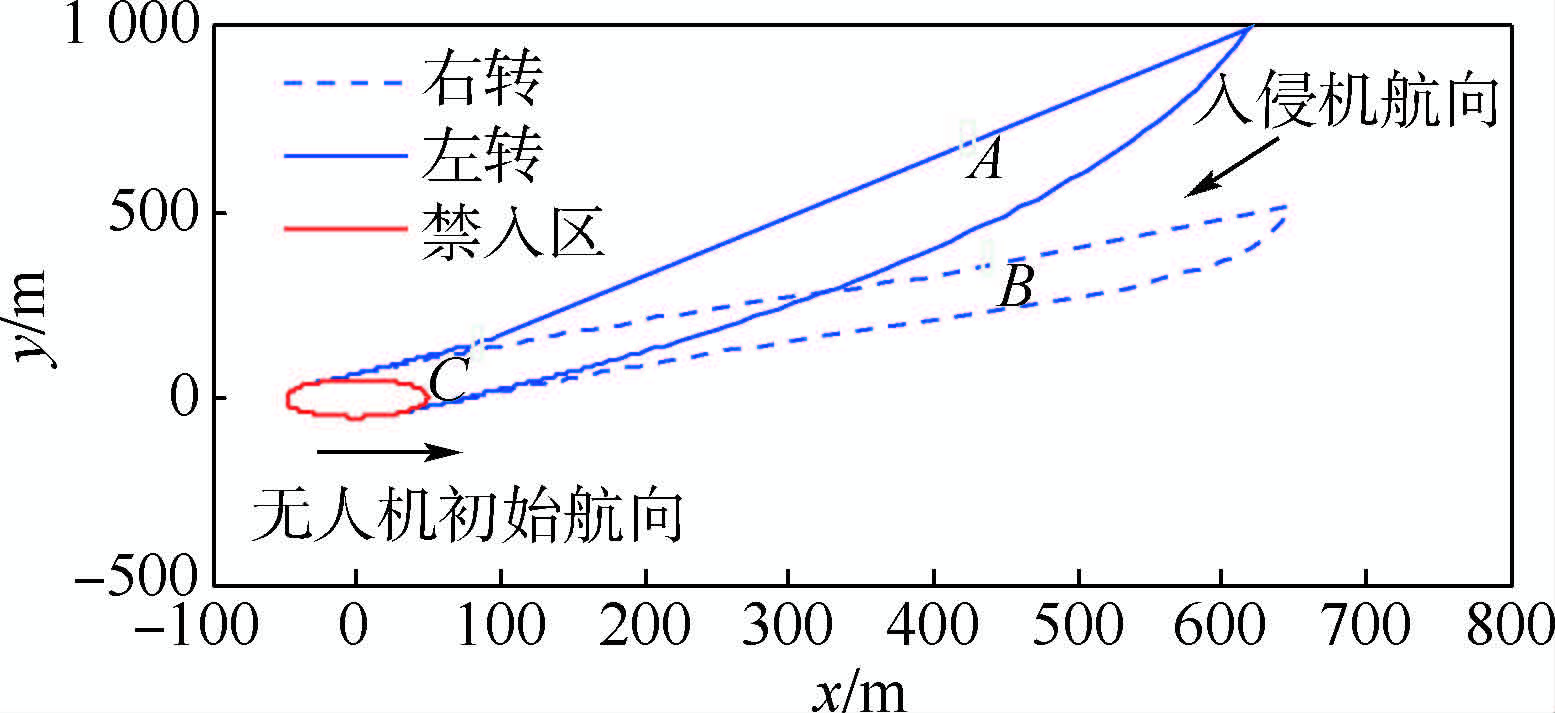 |
| 图 5 向左和向右最大机动碰撞区Fig. 5 Maximum maneuverability collision region (left-and right-turning) |
| 图选项 |
A区和B区分别为向左、向右最大机动碰撞区.当入侵机在A、B区域的边界外时,无人机采取向右和向左最大侧向过载转弯机动均可避免碰撞的发生;当入侵机已进入A或B某一最大机动碰撞区时,无人机采取该方向的最大侧向过载转弯机动无法避免碰撞的发生.当入侵机进入A、B区的交集C区时,无论无人机采取向右或向左最大侧向过载转弯机动都无法避免碰撞发生.
为进一步说明无机动碰撞区、最大机动碰撞区和不可规避区的关系,在基本仿真条件下,当入侵机航向角分别为40°,90°,180°,280°,320°时,各区域的范围如图 6所示.
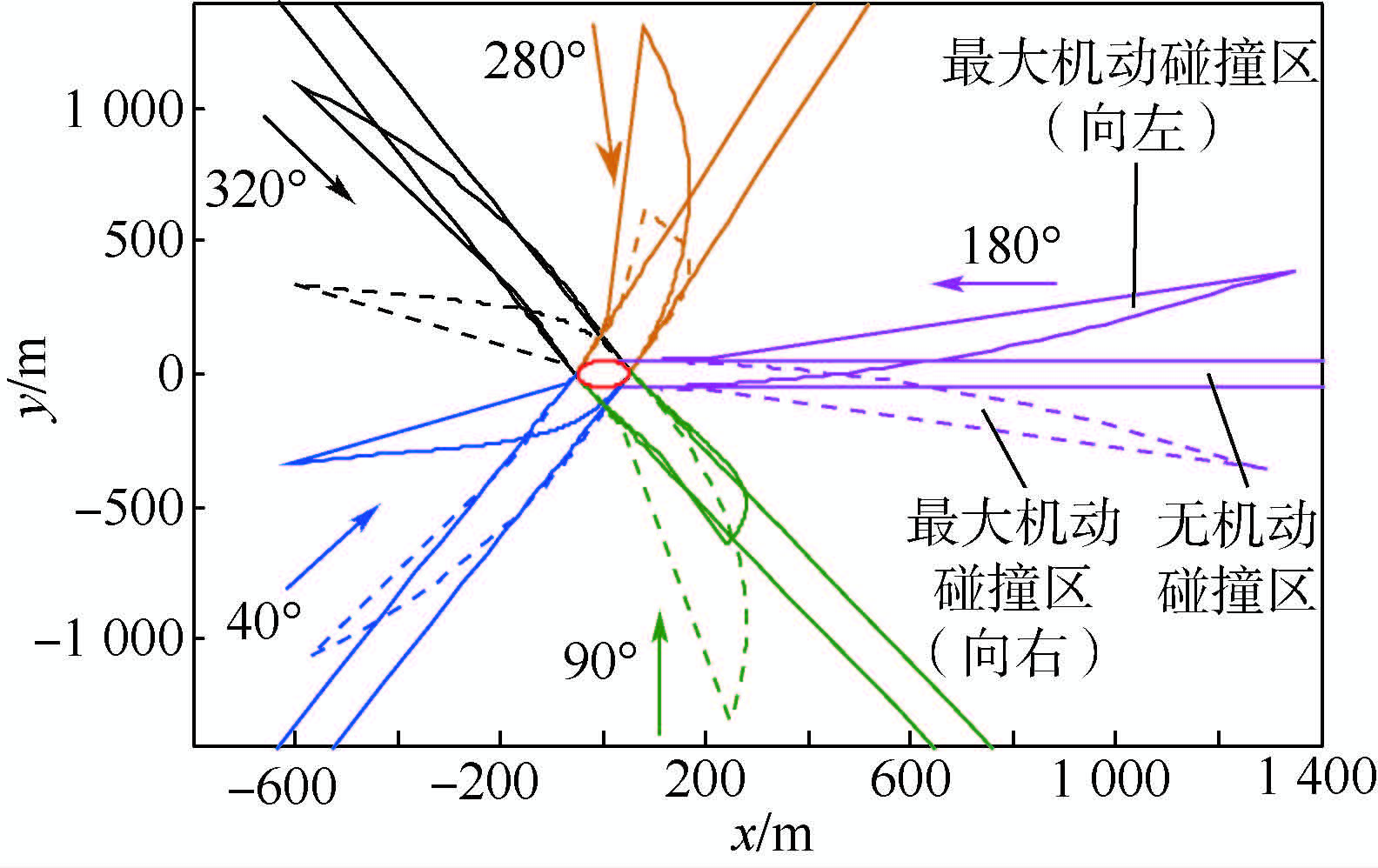 |
| 图 6 不同入侵情况下不可规避区的示意图Fig. 6 Schematic of non-escape region under different intruder’s headings |
| 图选项 |
由图 6可知,当入侵机以航向角40°和90°入侵时,向右最大机动碰撞区的范围大于向左最大机动碰撞区;当入侵机以航向角280°和320°入侵时则结果相反;当入侵机的航向角为180°时,向左和向右最大机动碰撞区的大小相近.同时,无机动碰撞区的分布受相对速度的方向影响,由于图中无人机的初始航向均为0°,因而无机动碰撞区的分布随入侵机航向的变化而偏转.
图 6中向左、向右最大机动碰撞区和无机动碰撞区的相交区域为不可规避区,当入侵机以航向角40°和320°入侵时,相对速度较小,不可规避区的最远点离原点较近;当入侵机以航向角90°和280°入侵时,相对速度较大,不可规避区的最远点离原点较远;当入侵机的航向角为180°时,相对速度最大,因此不可规避区的最远点离原点最远.
在图 6的仿真条件下,安全飞行包络如图 7所示.由图 7可知,由于无人机的初始航向为0°,因此在相对速度较大的区域安全飞行包络的距离较大,即右侧包络距离大于左侧包络距离,其结果与不可规避区的仿真结果一致.
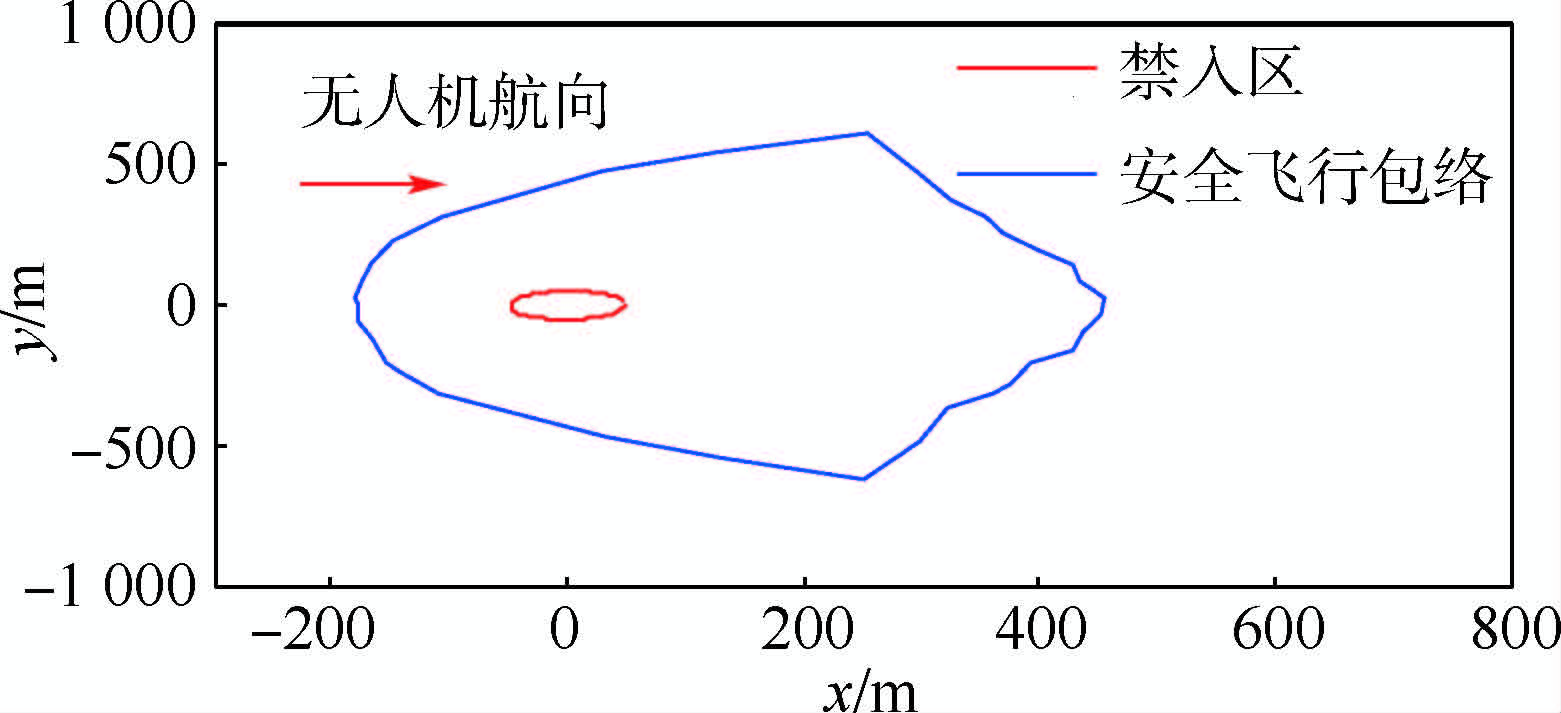 |
| 图 7 安全飞行包络示意图Fig. 7 Schematic of safe flight envelope |
| 图选项 |
5.2 碰撞区影响因素分析对无机动碰撞区来说,其分布范围随相对速度的改变而改变.在基本仿真条件下,改变入侵机速度、无人机速度(如图 8所示)或改变入侵机的航向角(如图 6所示),相对速度都会发生变化,因此无机动碰撞区的范围也都随着相对速度发生偏移.
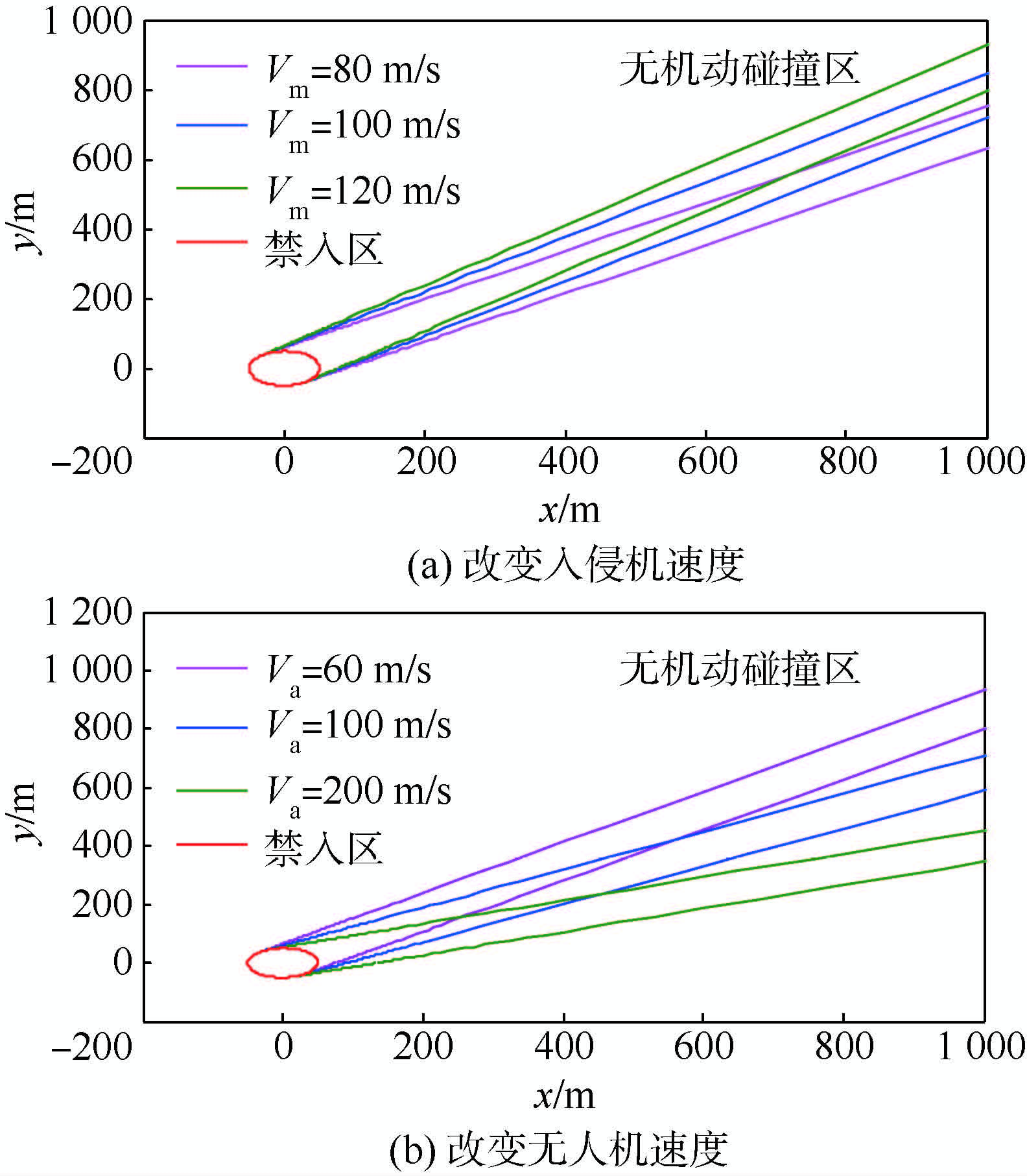 |
| 图 8 速度对无机动碰撞区的影响Fig. 8 Influence of velocity on no-maneuver collision region |
| 图选项 |
对最大机动碰撞区和安全飞行包络来说,增大入侵机速度、增大安全距离,都将使其范围增大(如图 9、图 10所示);相反,则会使其范围减小.同样,改变无人机的速度大小和侧向过载也将影响各碰撞区的分布(类似于图 9),如表 1所示.
 |
| 图 9 入侵机速度对各区域的影响Fig. 9 Influence of intruder’s velocity on proposed regions |
| 图选项 |
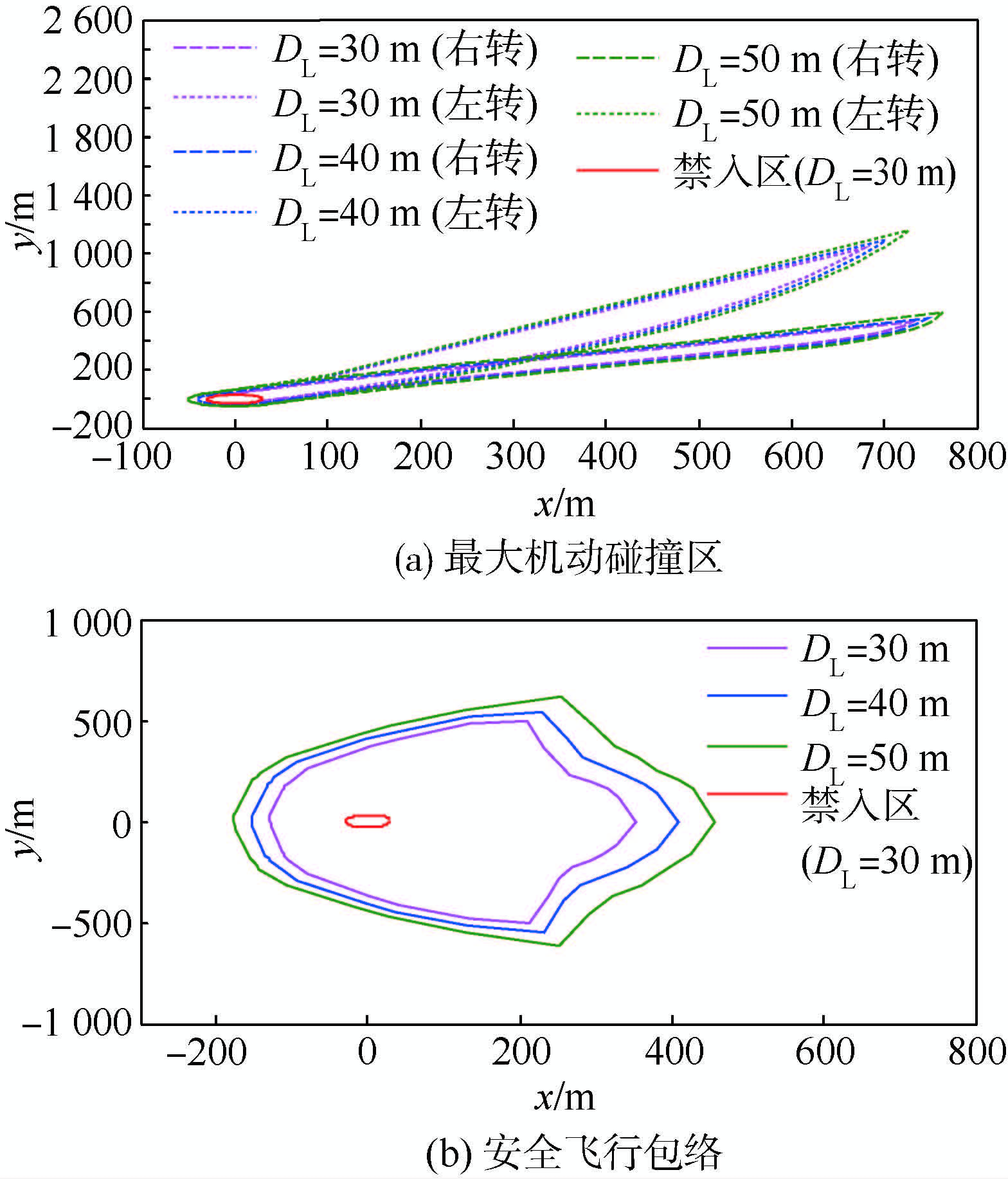 |
| 图 10 安全距离对各区域的影响Fig. 10 Influence of safety distance on proposed regions |
| 图选项 |
表 1 无人机运动对各区域的影响Table 1 Influence of UAV’s motion on proposed regions
| 影响因素 | 无机动碰撞区 | 最大机动 碰撞区 | 安全飞行包络 |
| 无人机速度增大 (60,100,200 m/s) | 偏转 | 增大 | 增大 |
| 侧向过载增大 (0.8,1.0,1.2) | 无影响 | 减小 | 减小 |
表选项
综上可知,相对速度、无人机机动能力和安全距离是所建碰撞区的主要影响因素,其中,无人机的速度是无人机避撞过程中的可控量,因此在设计避撞策略时应考虑对无人机速度的控制.
5.3 基于所建碰撞区的无人机避撞策略由于过早、过晚或者采取不适当的机动方式进行避撞机动,将会导致不必要的机动飞行或无法避开威胁目标.因此,利用所建碰撞区辅助无人机选择避撞机动方式,以及引入时间阈值来决策避撞时机是非常重要的.
根据无人机的机动能力、感知设备的测量误差,以及两机最小安全距离等因素,设定无人机的警戒时间、逃逸时间和最小逃逸时间(如参照文献[7]分别取25、1.5和1 s),用于无人机选择避撞机动方式和机动时机.同时,根据各碰撞区影响因素的仿真分析结果,将无人机速度作为避撞过程中的一个控制量,提出基于所建碰撞区的无人机避撞策略如图 11所示.
 |
| 图 11 基于所建碰撞区的无人机避撞策略Fig. 11 UAV collision avoidance strategy by proposed collision regions |
| 图选项 |
以上避撞策略在综合考虑了避撞时间、机动方式、速度控制等因素的基础上,应用所建碰撞区进行决策判断,可在保证避撞成功的前提下,尽可能少地改变无人机的预定飞行路线.
6 结 论本文针对空中任意角度入侵的突发威胁,研究了无人机动态碰撞区的设计方法.
1) 建立了无机动碰撞区和最大机动碰撞区,并分别给出了两区域的解析表达式.所提出的无机动碰撞区和最大机动碰撞区,可用于进行常规机动和紧急机动的决策,判断是否需要采取最大过载转弯机动,以及选择转弯机动方向.
2) 根据无机动碰撞区和向左、向右最大机动碰撞区的相交区域,提出了不可规避区和安全飞行包络的概念.不可规避区和安全飞行包络是飞行安全的最后决断线,可为无人机避撞决策提供理论支撑,也可辅助有人机飞行员处理紧急避撞情形.
3) 通过理论分析和仿真计算结合的方法分析了各因素对所建区域的影响,验证了建模的正确性;并根据仿真分析结果,提出了基于所建碰撞区的无人机避撞策略.
在后续工作中,将对垂直平面和任意投影面上的碰撞区模型进行研究,进一步推广所提碰撞区的适应性,使其更加符合无人机实际的避撞和决策.
参考文献
| [1] | 蔡志浩,杨丽曼,王英勋,等.无人机全空域飞行影响因素分析[J].北京航空航天大学学报,2011,37(2):175-179. Cai Z H,Yang L M,Wang Y X,et al.Analysis for whole airspace flight key factors of unmanned aerial vehicles[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(2):175-179(in Chinese). |
| Cited By in Cnki (10) | |
| [2] | Thomas W,Ned A S.Development and operation of the traffic alert and collision avoidance system(TCAS)[J].Proceedings of the IEEE,1989,77(11):1735-1744. |
| Click to display the text | |
| [3] | Fairuz I R,Joshua D K,Li L,et al.Impact of automatic dependent surveillance-broadcast(ADS-B)on traffic alert and collision avoidance system(TCAS)performance,AIAA-2008-6971[R].Reston:AIAA,2008. |
| Click to display the text | |
| [4] | Eric P,Alex F,Chen W Z,et al.Sense and avoid (SAA)& traffic alert and collision avoidance system(TCAS)integration for unmanned aerial systems(UAS)AIAA-2007-3004[R].Reston:AIAA,2007. |
| Click to display the text | |
| [5] | Carbone C,Ciniglio U,Corraro F,et al.A novel 3D geometric algorithm for aircraft autonomous collision avoidance[C]//Proceedings of the 45th IEEE Conference on Decision and Control.Piscataway,NJ:IEEE Press,2006:1580-1585. |
| Click to display the text | |
| [6] | Luongo S,Corraro F,Ciniglio U,et al.A novel 3D analytical algorithm for autonomous collision avoidance considering cylindrical safety bubble[C]//Aerospace Conference 2010 IEEE.Piscataway,NJ:IEEE Press,2010:1115. |
| Click to display the text | |
| [7] | Finley B.Autonomous collision avoidance the technical requirements[C]//National Aerospace and Electronics Conference.Piscataway,NJ:IEEE Press,2000:808-813. |
| Click to display the text | |
| [8] | Timothy W R.Algorithms for airborne conflict detection,prevention,and resolution[C]//Digital Avionics Systems Conference.Piscataway,NJ:IEEE Press,2004:3.B.1-1-17. |
| [9] | Amirreza R,Kunihiko K,Takashi T,et al.Multiple UAV deconfliction via navigation functions,AIAA-2008-6626[R].Reston:AIAA,2008. |
| Click to display the text | |
| [10] | James P C,Mykel J K.Analysis of open-loop and closed-loop planning for aircraft collision avoidance[C]//14th International IEEE Conference on Intelligent Transportation Systems.Piscataway,NJ:IEEE Press,2011:212-217. |
| Click to display the text | |
| [11] | 曹红强,费向东,刘宇,等.基于柱体空间的短期冲突告警算法[J].四川大学学报:自然科学版,2009,46(1):65-68. Cao H Q,Fei X D,Liu Y,et al.Short-term conflict alert algorithm based on cylindrical space[J].Journal of Sichuan University:Natural Science,2009,46(1):65-68(in Chinese). |
| Cited By in Cnki | |
| [12] | Manolis A C,Sifis G K.Automatic commercial aircraft-collision avoidance in free flight:The three-dimensional problem[C]//IEEE Transactions on Intelligent Transportation Systems.Piscataway,NJ:IEEE Press,2006:242-249. |
| Click to display the text | |
| [13] | Giancarmine F,Demenico A,Antonio M,et al.Multi-sensor-based fully autonomous non-cooperative collision avoidance system for unmanned air vehicles[J].Journal of Aerospace Computing,Information,and Communication,2008,5(10):338-360. |
| Click to display the text | |
| [14] | Karl D B.A geometric optimization approach to aircraft conflict resolution,AIAA-2000-4265[R].Reston:AIAA,2000. |
| Click to display the text | |
| [15] | 张军.空域监视技术的新进展及应用[J].航空学报,2011,32(1):1-14. Zhang J.New development and application of airspace surveillance technology[J].Acta Aeronautica et Astronautica Sinica,2011,32(1):1-14(in Chinese). |
| Cited By in Cnki (18) | |
| [16] | 颜庆津.数值分析[M].3版.北京:北京航空航天大学出版社,2006:67-68. Yan Q J.Numerical analysis[M].3rd ed.Beijing:Beihang University Press,2006:67-68(in Chinese). |
