基于观测器的故障检测是重要的故障检测方法之一,主要包括残差产生与残差评价两个方面.无人机在飞行过程中将会受到各种未知干扰,如湍流、风切变等大气不稳定因素的影响[5].这些干扰势必造成故障检测过程中产生的残差信号出现偏差[6],严重影响故障检测系统的性能,导致误报和漏报.因此,基于观测器的残差产生器的鲁棒性问题成为了无人机作动器故障检测研究的重点.其中,基于未知输入观测器(Unknown Input Observer,UIO)的故障检测方法多年来一直是研究的热点之一,并取得了大量的研究成果[7, 8].然而,这些方法大多是针对无人机小扰动线性化模型设计的.无人机系统具有非线性、多变量、强耦合等特点[9],线性化过程引入的误差势必会对故障检测结果造成影响.因此,研究无人机系统的非线性鲁棒故障检测方法具有重要的意义.近年来,针对无人机系统的非线性鲁棒故障检测技术研究受到了国内外****的高度重视.文献[10]基于一组无迹卡尔曼滤波器对无人机作动器在线故障检测问题进行了研究;文献[11]采用扩展多模型自适应估计方法对无人机作动器故障实现了快速准确的故障诊断;文献[12]设计了自适应Thau观测器对受模型不确定性以及噪声影响的无人机非线性不确定系统进行故障检测和估计.然而,针对非线性无人机系统的故障检测问题,已有的研究成果大多仅考虑残差对未知输入的鲁棒性设计,而采用非线性未知输入观测器(Nonlinear Unknown Input Observer,NUIO)进行未知输入解耦的故障检测技术还研究的比较少.
近年来,基于NUIO的故障检测方法在非线性系统故障诊断方面取得了一定进展.该方法将系统中未知输入进一步分为未知干扰以及随机噪声,通过配置NUIO系数达到解耦干扰且降低噪声影响的目的.文献[13]通过构造UIO结构消除干扰项,利用扩展卡尔曼滤波(Extended Kalman Filter,EKF)算法求解状态反馈矩阵,增强故障检测系统对干扰、噪声的鲁棒性,但是由于引进了一阶线性化误差,使得在系统存在较强非线性的情况下不能获得理想的故障检测结果.针对这一问题,文献[14]将UIO和CKF算法的优点结合,提出了基于CKF算法的NUIO故障检测方法.该方法具有状态估计精确、收敛速度快、干扰完全解耦等优点,并成功用于化工过程的传感器故障检测.
无人机是典型的非线性系统,实际运行中不可避免地受到未知气流干扰以及环境中随机噪声的影响,可以看出,文献[14]提出的基于CKF的NUIO可用于无人机作动器的故障检测.本文将结合无人机作动器故障检测的实际需求,考虑系统中存在的未知气流干扰以及随机噪声的影响,在文献[14]给出的基于CKF的NUIO设计方法基础上,提出了一种基于NUIO的无人机作动器故障检测方法.最后,利用残差χ2检验方法对残差进行评价,判定故障是否发生.仿真实验验证了该方法的有效性.
1 系统模型及问题描述1.1 系统模型无人机的数学模型是一组复杂的包含12个非线性一阶微分方程的方程组[15],具有强非线性、多变量、强耦合等特点,采用全模型进行故障检测会加大故障传播的范围,使故障检测问题复杂.另外,无人机外形和内部质量分布均对称于中垂平面,并且在飞行过程中大部分处于水平飞行状态,满足水平无侧滑条件,因此,可以把无人机全模型解耦为相互独立的纵向和侧向模型.在实际工程应用中,将无人机纵向运动和横向运动分开进行故障检测方法的研究不仅可以使问题简化,而且可以得到比较满意的故障检测结果.
因此,本文仅针对纵向系统进行作动器故障检测方法研究.为了方便研究,作如下假设:
1) 视飞行器为刚体,且质量为恒定.
2) 选取地面坐标系为惯性坐标系,不考虑离心加速度和哥氏加速度的影响.
3) 忽略地球曲率,将其视为平面.
4) 重力加速度不随高度变化而变化.
5) 机体坐标系的Oxz平面为飞行器的对称平面,即Ixz=Izy=0.
在不考虑大气干扰、随机噪声以及故障情况下,根据合外力与合外力矩对无人机运动的作用,可推导出无人机系统纵向模型[16]为

式中:Vx、Vz分别为x轴与z轴线速度;q为俯仰角速度;θ为俯仰角;g为重力加速度;m为无人机质量;Iy为y轴方向刚体的转动惯量;Sw为机翼面积;ρ为空气密度;c为平均气动弦长;Tx、Tz分别为发动机纵向和垂向推力;Cm、CD和CC分别为俯仰力矩系数、阻力系数和侧力系数,在传统操纵面作动方式情况下可表示为[16]

式中:δe为控制无人机俯仰运动的升降舵偏转角;m*、x*和z*为无人机的气动参数,可由实验得到.迎角定义为

选取状态向量x=[Vx,Vz,q,θ]T,控制输入u=δe,由文献[17]中提出的方法设计控制率实现对飞行姿态的稳定控制.量测输出y=[Vx,Vz,q,θ]T,其中东向线速度Vx和天向线速度Vz由GPS测得,俯仰角θ和俯仰角速度q分别由陀螺地平仪和转弯仪测得.令离散周期T=0.01 s,采用四阶R-K方法对无人机系统纵向模型(1)进行离散化,可得到离散化的系统非线性模型:
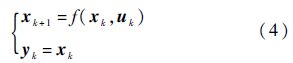
式中:下标k为采样时刻.
1.2 问题描述无人机在飞行过程中不可避免地受到外部扰动的影响,其中最主要的是大气紊流的影响.大气紊流对无人机运动的作用是改变机体与空气间的相对运动,引起无人机绕流的变化,从而产生附加的气动力影响无人机的运动,这种附加气动力的变化可通过无人机运动状态量的等价改变来表示[18].然而,无人机在飞行过程中受到大气不稳定因素影响的同时,不可避免地受到环境中随机噪声的影响,这些都会直接影响到故障检测系统的性能.
本文针对作动器恒偏差故障进行故障检测方法研究,作动器的输入输出关系可由式(5)近似表示:

式中:um,k为实际输出;uk为指令输入.
1) 作动器正常工作时:bk=0.
2) 作动器发生恒偏差故障时:bk为偏差值.
综上,考虑未知气流干扰、随机噪声以及作动器故障,无人机纵向系统可进一步描述为

式中:随机系统噪声为wk~N(0,Qk),随机量测噪声为vk~N(0,Rk);紊流干扰信号为dk=[Vgx Vgy]T,其中Vgx、Vgy分别为x轴、y轴的紊流速度;Ek为干扰分布矩阵,具有如下形式:

其中:干扰参数Cv1~Cv7受到风速、气动系数等影响.
作动器故障检测的重要任务之一是残差产生,本文将文献[14]中构造的NUIO应用于残差产生器设计.其设计问题可描述为:设计基于NUIO的残差产生器,使残差对未知干扰完全解耦,对噪声具有一定的鲁棒性,但对故障又具有较高的灵敏度.考虑如下基于NUIO的残差产生器:
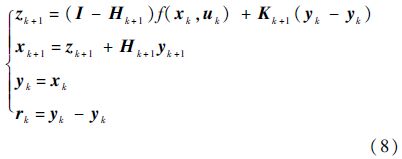
式中:zk+1为观测器状态向量;xk为状态估计值;yk为输出估计值;rk为残差;Hk+1和Kk+1为待设计的参数矩阵.定义ek+1=xk+1-xk+1表示状态估计误差,由式(6)和式(8)得

注意到,残差与作动器故障、未知干扰以及噪声均有关,若不对未知干扰以及噪声进行处理,减小其对系统的影响,将有可能导致误报和漏报.
为了实现残差对未知干扰dk的完全解耦,设计的观测器参数矩阵Hk+1应满足:

根据矩阵的性质可知,存在:

使式(10)成立.
根据需要满足的未知干扰完全解耦条件(10),残差表达式可转化为
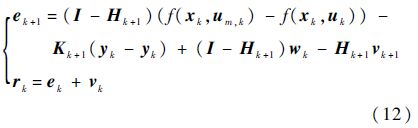
可以看出,此时的残差仍与作动器故障以及噪声均有关.因此,为保证残差对噪声的鲁棒性,所设计的残差产生器应满足状态估计误差的协方差矩阵达到最小,即
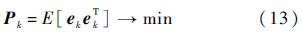
从而可将残差产生器设计问题归结为:在Hk+1阵满足未知干扰完全解耦条件式(10)的情况下,求Kk+1阵,使在无故障时残差产生系统式(12)渐近稳定,并且满足噪声鲁棒性指标式(13).
残差评价是故障检测的另一重要任务.根据残差序列的性质设计有效的评价函数J(rk)和阈值J0,从而可通过如下逻辑关系来检测系统是否发生故障:

2 作动器故障检测2.1 残差产生器设计考虑如下非线性系统:
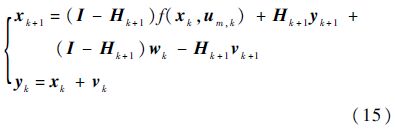
其中:参数矩阵Hk+1由式(11)给出.
将基于NUIO的残差产生器式(8)应用于该系统,定义ek+1=xk+1-xk+1表示状态估计误差,由式(8)和式(15)可得

可以看出,在未知干扰完全解耦的条件下,针对系统(15)产生的残差信号rk与针对系统(6)产生的残差信号rk等价.因此,可将残差产生器设计问题转化为:针对系统(15)设计残差产生器(8),即求增益矩阵Kk+1使残差产生系统(16)渐近稳定,并且满足噪声鲁棒性指标,即
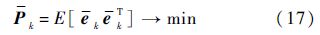
进一步,将残差产生器(8)中观测器方程重新改写为
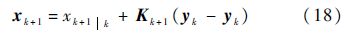
式中:xk+1|k=(I-Hk+1)f(xk,uk)+Hk+1yk+1.
通过比较xk+1|k与系统(15)中xk+1,可以看出将xk+1|k看作状态一步预测,yk-yk看作新息项,增益矩阵Kk+1可通过引入卡尔曼增益来保证系统对噪声的鲁棒性,考虑到Arasaratnam等[19]于2009年提出的CKF算法具有更优的非线性逼近性能、数值精度以及滤波稳定性,本文将UIO与CKF算法的优点结合,将CKF算法用于求解增益矩阵Kk+1.根据上述讨论,可得基于CKF的NUIO的残差产生器的整个设计过程[14]如下:
1) 初始化:
设初始状态均值和方差为x0和P0|0,观测器参数矩阵初始值H0为0.
2) 根据式(11),计算Hk+1.
3) 采用3阶容积规则获得如下的基本采样点和相应权值:
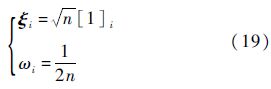
式中:n为系统状态向量的维数,i=1,2,…,2n.
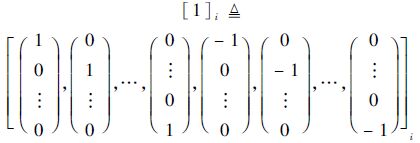
表示构造矩阵中的第i列.
4) 时间更新:
对Pk-1|k-1做Cholesky分解:

计算采样点为
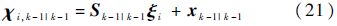
计算经非线性状态方程传递后的采样点:

估计k时刻的状态预测值:

估计k时刻的状态误差协方差预测值:

5) 量测更新:
对Pk|k-1做Cholesky分解:
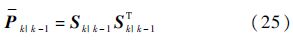
计算采样点:

通过非线性量测方程传递采样点:
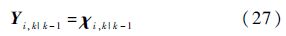
估计k时刻的观测预测值:

估计k时刻的自相关协方差阵:
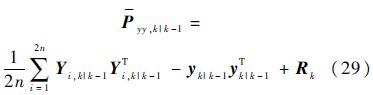
估计k时刻的一步预测互相关协方差阵:
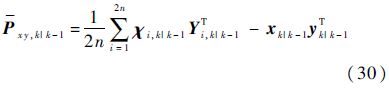
6) 状态更新:
估计k时刻的滤波增益为
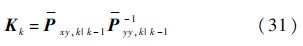
k时刻的状态估计值为
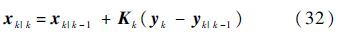
k时刻的状态误差协方差估计值为
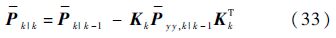
7) 残差产生:

2.2 残差评价本文采用残差χ2检验方法判断系统是否发生故障.如果k时刻系统无故障,残差rk是零均值高斯白噪声,其方差为

定义残差评价函数:
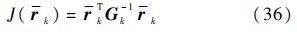
由残差统计特性可知,系统正常工作时,J(rk)是服从自由度为ε的χ2分布,即J(rk)~χ2(ε),ε为系统观测量的维数.如果故障发生,则rk不再服从零均值的高斯分布,J(rk)不再服从自由度为ε的χ2分布.选择适当的误报率σ,满足奈曼-皮尔逊准则:
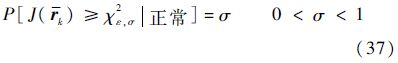
设定阈值J0=χ2ε,σ,因此,基于逻辑决策式(14)可判断系统式(6)是否发生故障.
3 仿真分析考虑某小型固定翼式无人机纵向模型,模型参数如表 1所示[16].
表 1 模型参数Table 1 Model parameters
| 参数 | 数值 | 参数 | 数值 |
| m/kg | 2 000 | m5 | -0.025 5 |
| ρ/(kg·m-3) | 0.037 1 | x1 | 0.714 |
| Sw/m2 | 39.02 | x2 | 0.714 |
| g/(m·s-2) | 9.780 3 | x3 | 0.068 2 |
| Tx/N | 4 864 | x4 | -0.089 6 |
| Tz/N | 212 | z1 | -7.509 5 |
| c/m | 1.98 | z2 | -0.237 5 |
| m1 | -0.789 9 | z3 | 6.573 1 |
| m2 | -0.689 9 | z4 | -0.354 1 |
| m3 | -3.930 0 | z5 | -0.317 5 |
| m4 | -1.862 9 |
表选项
仿真初始条件为

其中:x0、P0|0、Qka和Rka用于NUIO设计,x0、Qkr和Rkr用于产生仿真数据.x0中各元素的量纲分别m/s、m/s、rad/s、rad.
考虑大气紊流在各个方向速度分量值相同,则干扰信号dk和干扰分布矩阵Ek可以表示为

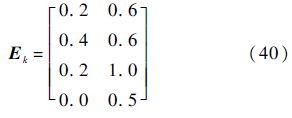
式中:k为步长.
分别采用基于EKF的NUIO和基于CKF的NUIO来构造残差产生器进行作动器故障检测,基于EKF的NUIO算法实现参见文献[20].
在无故障情况下,基于EKF的NUIO与本文采用的基于CKF的NUIO产生的残差信号r1~r4如图 1所示.从图中可以看出,基于CKF的NUIO产生的残差收敛速度快,具有更好的干扰解耦性能.
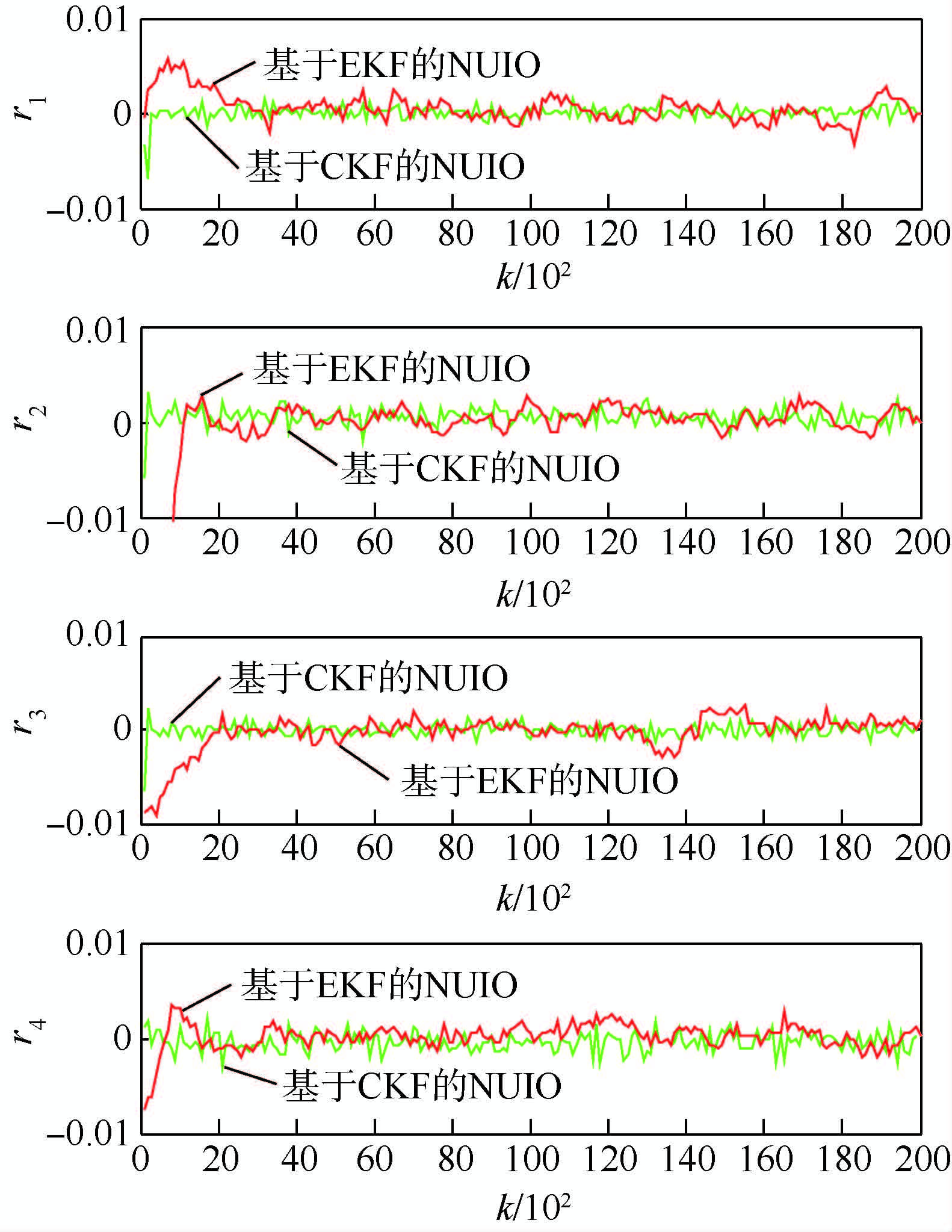 |
| 图 1 无故障时系统的残差信号Fig. 1 Residual signal of system in the fault free case |
| 图选项 |
假设作动器恒偏差故障描述为

选定误报率σ=0.05,根据分布表得到阈值J0(k)=χ4,0.052=9.45,图 2和图 3分别给出了不同条件下,由式(36)计算得到的残差评价函数Jf(k)的变化曲线与阈值J0(k).
 |
| 图 2 Qkr=Qka情况下Jf(k)变化曲线与J0(k)Fig. 2 Evolution of the Jf(k) and J0(k) in the case of Qkr=Qka |
| 图选项 |
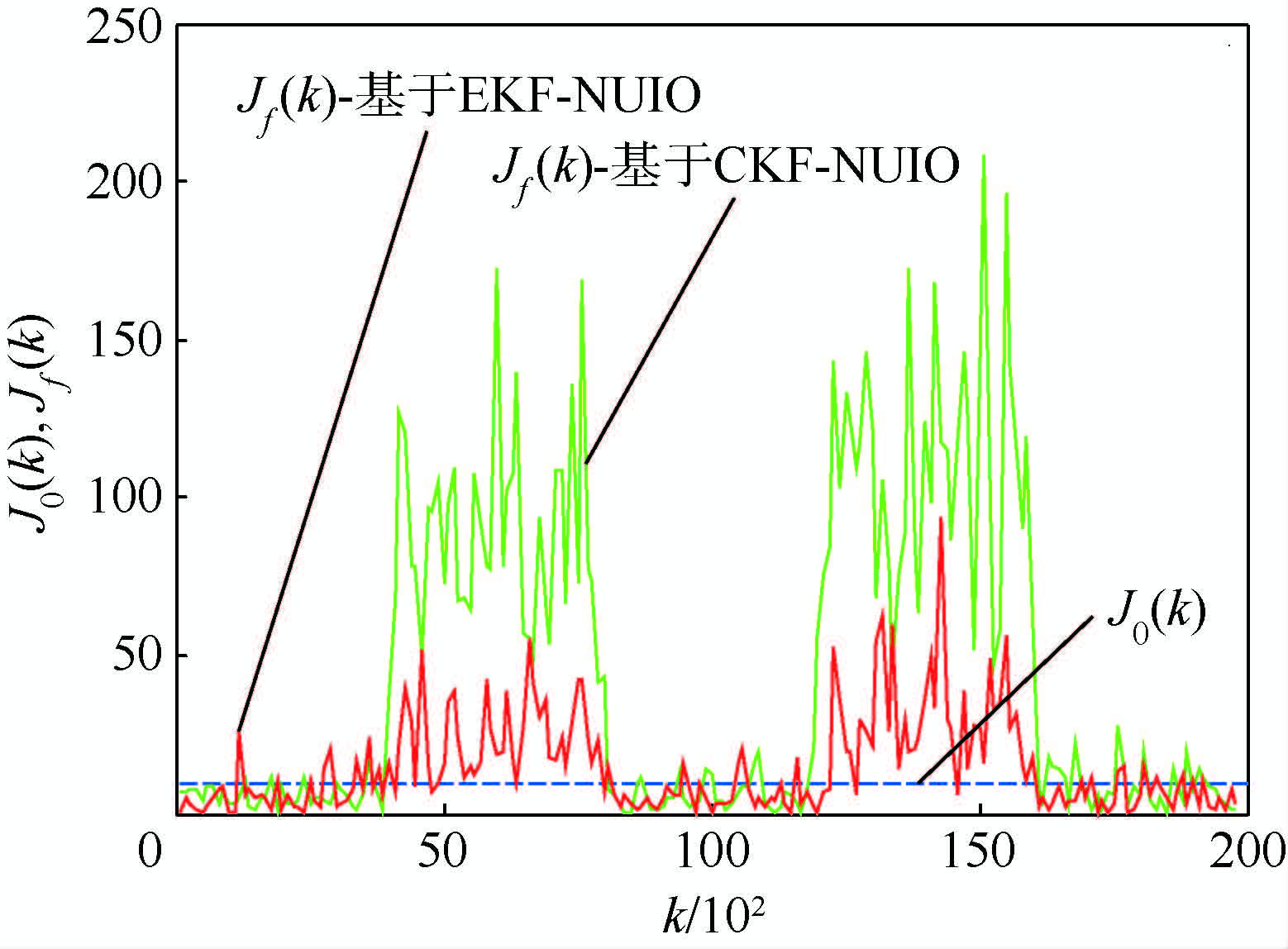 |
| 图 3 Qkr=10Qka情况下Jf(k)变化曲线与J0(k)Fig. 3 Evolution of the Jf(k) and J0(k)in the case of Qkr=10Qka |
| 图选项 |
结果表明:与基于EKF的NUIO故障检测方法相比,在噪声统计特性准确已知的条件下,本文设计的故障检测方法在故障发生时产生的评价函数幅值更大,因而具有更好的故障检测性能.而在过程噪声统计特性不准确的情况下,本文所提出的方法能够准确检测出故障,而基于EKF的NUIO故障检测方法失效.
为了进一步说明离散周期和故障幅值等因素对故障检测方法性能的影响,本文进行了一组对比实验.在噪声统计特性已知的情况下,通过比较不同离散周期与故障幅值情况下,基于CKF的NUIO故障检测方法与基于EKF的NUIO故障检测方法在故障检测的快速性以及微小故障检测能力等方面的差别,进一步说明了本文所提出的方法的有效性,实验结果如表 2所示.从表 2中可以看出,离散周期只引起了检测延时的微小改变,对两种方法的故障检测性能都没有大的影响.而在相同的离散周期与故障幅值下,基于CKF的NUIO故障检测方法具有更小的检测延时.另一方面,基于CKF的NUIO故障检测方法成功检测到了所有的微小故障,而基于EKF的NUIO故障检测方法在故障幅值为0.04时失效.
表 2 故障检测性能对比结果Table 2 Contrast results of foult detection properties
| 离散周期/s | 故障幅值 | 基于EKF的NUIO | 基于CKF的NUIO | ||
| 检测延时/s | 可检测性 | 检测延时/s | 可检测性 | ||
| 0.1 | 0.04 | - | × | 2.1 | √ |
| 0.07 | 0.60 | √ | 0.5 | √ | |
| 0.10 | 0.18 | √ | 0.1 | √ | |
| 0.01 | 0.04 | - | × | 2.0 | √ |
| 0.07 | 0.40 | √ | 0.3 | √ | |
| 0.10 | 0.15 | √ | 0.1 | √ | |
表选项
4 结 论本文提出了一种解决受未知气流干扰与随机噪声影响的无人机作动器故障检测问题的方法.经仿真实验验证表明:
1) 基于CKF的NUIO构造的残差收敛速度快,具有良好的干扰解耦性能.
2) 与基于EKF的NUIO故障检测方法相比,在噪声统计特性准确已知的条件下,该方法在故障发生时产生的评价函数幅值更大,具有更好的故障检测性能.
3) 在过程噪声统计特性不准确的情况下,该方法能够快速、准确地检测出故障,而基于EKF的NUIO故障检测方法失效.
参考文献
| [1] | 蔡志浩,杨丽曼,王英勋,等.无人机全空域飞行影响因素分析[J].北京航空航天大学学报,2011,37(2):176-184. Cai Z H,Yang L M,Wang Y X,et al.Analysis for whole airspace flight key factors of unmanned aerial vehicles[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(2):176-184(in Chinese). |
| Click to display the text | |
| [2] | Hansen S,Blanke M.Control surface fault diagnosis for small autonomous aircraft[C]//Proceeding of the Australian Control Conference.Piscataway,NJ:IEEE Press,2011:185-190. |
| Click to display the text | |
| [3] | Panitsrisit P,Ruangwiset A.Sensor system for fault detection identification and accommodation of elevator of UAV[C]//Proceedings of SICE Annual Conference.Piscataway,NJ:IEEE Press,2011:1035-1040. |
| Click to display the text | |
| [4] | Freddi A,Longhi S,Monteriù A.A diagnostic Thau observer for a class of unmanned vehicles[J].Journal of Intelligent & Robotic Systems,2012,67(1):61-73. |
| Click to display the text | |
| [5] | 朱上翔.大气扰动及其对飞行的影响[J].航空学报,1985,6(2):149-156. Zhu S X.Atmospheric turbulence and the effects on flight[J].Acta Aeronautica et Astronautica Sinica,1985,6(2):149-156(in Chinese). |
| Click to display the text | |
| [6] | Frank P M,Ding X.Survey of robust residual generation and evaluation methods in observer-based fault detection systems[J].Journal of Process Control,1997,7(6):403-424. |
| Click to display the text | |
| [7] | Bateman F,Noura H,Ouladsine M.An actuator fault detection,isolation and estimation system for an UAV using input observers[C]//Proceedings of European Control Conference.Piscataway,NJ:IEEE Press,2007:1805-1810. |
| [8] | Bateman F,Noura H,Ouladsine M.Active fault detection and isolation strategy for an unmanned aerial vehicle with redundant flight control surfaces[C]//Proceeding of the 16th Mediterranean Conference on Control and Automation.Piscataway,NJ:IEEE Press,2008:1246-1251. |
| Click to display the text | |
| [9] | Tousi M M,Khorasani K.Robust observer-based fault diagnosis for an unmanned aerial vehicle[C]//Proceeding of Systems Conference.Piscataway,NJ:IEEE Press,2011:428-434. |
| Click to display the text | |
| [10] | Yang X,Mejias L,Gonzalez F,et al.Nonlinear actuator fault detection for small-scale UASs[J].Journal of Intelligent & Robotic Systems,2014,73(1-4):557-572. |
| Click to display the text | |
| [11] | Guillaume D,Hans P G.Efficient nonlinear actuator fault detection and isolation system for unmanned aerial vehicles[J].Journal of Guidance,Control & Dynamics,2008,31(1):225-237. |
| Click to display the text | |
| [12] | Cen Z H,Noura H,Tri B S.Robust fault diagnosis for quadrotor UAVs using adaptive Thau observer[J].Journal of Intelligent & Robotic Systems,2014,73:573-588. |
| Click to display the text | |
| [13] | Witczak M,Pretki P.Design of an extended unknown input observer with stochastic robustness techniques and evolutionary algorithms[J].International Journal of Control,2007,80(5):749-762. |
| Click to display the text | |
| [14] | Zarei J,Shokri E.Robust sensor fault detection based on nonlinear unknown input observer[J].Measurement,2014,48:355-367. |
| Click to display the text | |
| [15] | 吴森堂,费玉华.飞行控制系统[M].北京:北京航空航天大学出版社,2005:64-70. Wu S T,Fei Y H.Flight control system[M].Beijing:Beihang University Press,2005:64-70(in Chinese). |
| [16] | Miller R H,Ribbens W B.The effects of icing on the longitudinal dynamics of an icing research aircraft,AIAA-1999-0636[R].Reston:AIAA,1999. |
| [17] | Zhai R,Zhou Z,Zhang W,et al.Control and navigation system for a fixed-wing unmanned aerial vehicle[J].AIP Advances,2014,4(3):1306. |
| [18] | Li Z,Ding J.Ground moving target tracking control system design for UAV surveillance[C]//Proceeding of International Conference on Automation and Logistics.Piscataway,NJ:IEEE Press,2007:1458-1463. |
| Click to display the text | |
| [19] | Arasaratnam I,Haykin S.Cubature Kalman filters[J].IEEE Transactions on Automatic Control,2009,54(6):1254-1269. |
| Click to display the text | |
| [20] | Witczak M,Obuchowicz A,Korbicz J.Genetic programming based approaches to identification and fault diagnosis of nonlinear dynamic systems[J].International Journal of Control,2002,75(13):1012-1031. |
| Click to display the text |
