目前,各种数值方法被广泛用来研究弹性波的传播机制,如有限差分方法、有限元方法、边界元方法和离散元法等[2],这里主要采用时域有限差分(Finite Difference Time Domain,FDTD)方法建立数值模型.
在各种数值模拟方法中,有限差分方法是最早,也是目前应用最广泛的一种数值模拟方法.FDTD方法最早用于求解Maxwell方程,由****Yee于1966年提出[3].1970年,Alterman和Loewenthal[4]模拟了爆炸点源在3/4矩形面中的弹性波传播问题,同时分析了矩形长宽比对差分结果精度的影响,开始将FDTD方法应用于求解弹性波动方程问题.随后,Virieux[5]提出了稳定的2阶精度有限差分格式,即速度-应力有限差分方法,该方法适用于任何泊松比的介质,并应用该方法模拟分析了纵波(P波)及竖向横波(SV波)在非匀质介质中的传播问题.1995年,Dai等[6]采用4阶有限差分格式离散网格,同时采用了2阶精度时间差分格式的FDTD方法,推导得到了二维固-液两相介质中的P波传播速度.2002年,Schroder等[7]采用并行算法、交错网格FDTD方法及完全吸收边界条件分析了含有夹杂的弹性波传播问题,同时与实验结果进行了比对.2009年,Jafargandomi和Takenaka[8]采用非标准有限差分方法,求解了二维波动方程,分析研究了P-SV波的传播机制.2012年,Matsuda和Biwa[9]采用FDTD方法分析研究了非线性弹性固体介质中Lamb的传播特性.
FDTD方法被广泛地应用于波动方程的求解,然而在许多波动问题中,空间域通常是无限大的,在研究初期,计算机计算水平有限,无法处理规模较大的数据,因而有****提出了在计算盒边界上引入吸收边界以消除反射.虽然吸收边界条件可以有效地减小计算规模,然而由于吸收边界条件的复杂性,对于震源入射角度、吸收层设计等都有较高的要求[10],同时编译难度较大.
因而,本文采用了在研究区基础上适当扩大计算区域的速度-应力FDTD方法.该方法可以有效避免由于边界存在产生的反射波与研究区域的直达波相干涉,与此同时,为了提高计算速度,在研究区域和扩展区域都满足计算稳定条件和计算精度的前提下,采用不规则交错网格离散格式.同时,对比分析了考虑重力载荷和不计重力影响条件下的瑞利波传播特性,深入研究了瑞利波的传播机制.
1 基本方程1.1 瑞利波速1898年,Bromwich[11]首先考虑了初始应力及重力载荷对固体中弹性波传播性质的影响.1911年,Love[12]研究表明瑞利波的传播特性受到重力场的影响.1999年,Abd-Alla[13]讨论了半空间正交异性弹性材料中重力及初始应力影响下的瑞利波传播波速问题.在经典弹性动力学理论中,研究对象通常是传统材料,其弹性参数通常局限在较小的范围内,重力载荷与外载荷作用相比较小,重力对瑞利波速的影响通常可以忽略不计,然而,随着科学技术的不断发展,新材料的产生,如负泊松比材料和热-弹介质等,重力载荷对于波传播特性的影响是否可以忽略不计,是值得讨论的.因而,本文在运动方程中,考虑了重力载荷对瑞利波传播问题的影响.
首先,假设初应力在重力的作用下达到静水力平衡.在笛卡儿坐标系下,二维形式的动力学方程[14]可以写为

式中:σ11、σ22、σ12分别为x1、x2方向正应力和剪应力;σ11,1、σ22,2、σ12,2、σ12,1分别为σ11对x1、σ22对x2、σ22对x2、σ22对x1求偏导;u1和u2分别为x1和x2方向的位移;u1,1、u2,2、u2,1、u1,2分别为u1对x1、u2对x2、u2对x1、u1对x2求偏导;u1,tt和u2,tt分别为u1和u2对时间t求二次偏导;ρ、λ、μ分别为材料密度、拉梅常数、剪切模量.通过推导,可以得到各向同性弹性材料的瑞利波速方程[13]为

式中:c1、c2和c分别为纵波、横波和瑞利波速;g为重力加速度;k为波数.说明考虑重力影响的瑞利波的波速大小与波数有关,因而可能会发生频散现象.方程左边前2项即为不计重力影响时的瑞利波速方程,第3项是由于考虑了重力影响而附加存在的.c1和c2 的计算公式为

式中:
μ=E/(2+2ν)
λ=νE/[(1+ν)(1-2ν)]
其中:E和ν分别为材料的弹性模量和泊松比.为便于数值分析,将式(2)进行无量纲处理:

式中:

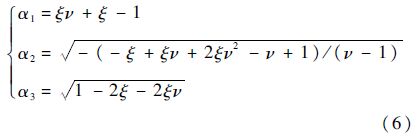
其中:ξ为无量纲处理后的瑞利波速;η为无量纲数,这里暂称为重力影响因子.若不计重力的影响,可以得到解析解,记为ξ0,即
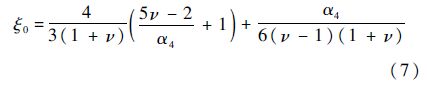
其中:
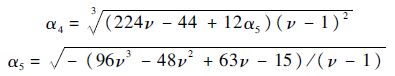
1.2 FDTD方法这里采用的是速度-应力数值有限差分模型[15]及中心有限差分格式近似求解波动偏微分方程.为了便于迭代计算,将重力影响转化到边界条件中[14],方程式(1)可写成1阶双曲函数形式:

式中:v1和v2分别为x1和x2方向的速度;v1,1、v2,2、v2,1、v1,2分别为v1对x1、v2对x2、v2对x1、v1对x2求偏导;v1,t和v2,t分别为v1和v2对t求偏导.x为水平方向,y为竖直方向(即重力加速度所在方向),将波动方程在x-y平面内进行离散,有

式中:Vx和Vy分别为离散网格中速度V的水平和竖直分量;Sxx、Sxy分别为离散网格中应力S的水平、剪应力分量;Vxl+0.5|i+1,j-0.5表示在t=(l+0.5)Δt时刻,坐标为(x,y)=(iΔx,(j-0.5)Δy)的结点在x方向的速度Vx.由方程式(9),推导得到迭代方程:


同理可以得到其他分量的迭代方程[7].为得到较为精确的结果,该差分格式应该满足如下稳定条件[15]:
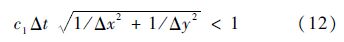
2 数值结果与讨论2.1 理论波速各向同性弹性材料泊松比ν的范围为

图 1为ξ0随泊松比ν变化趋势:曲线1为方程式(7)的数值解,即不计重力影响的无量纲瑞利波速ξ0关于泊松比ν的变化曲线;在传统材料中,瑞利波速与横波波速通常还有如下近似:
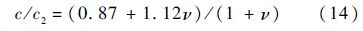
将式(14)按式(5)进行无量纲处理后,得到
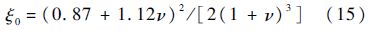
即曲线2.从图 1中可以看出,当ν>0.1时,两条曲线近似重合;ν <0.1时,有较大差异,说明在计算泊松比较小或者负泊松比材料的瑞利波速时,不能再采用式(15)进行近似.
 |
| 图 1 ξ0关于泊松比ν变化Fig. 1 Variation of ξ0 with respect to ν |
| 图选项 |
以η=0时的ξ为基准,即ξ0,图 2为不同量级重力因子影响下,无量纲瑞利波速比值ξ/ξ0随泊松比变化曲线.可以看出,-0.90<ν <0.25时,η量级为10-5~10-1的ξ/ξ0大于1,说明对于该范围内的材料,重力影响理论上会增大瑞利波速,且级数越大影响越显著,ν=-0.30时,差异最明显,η量级小于10-3的数值解ξ与ξ0近似;η量级为100~102时,ξ/ξ0小于1,随着η量级增大,比值增大,差异变小;当η量级数持续增大,ξ/ξ0比值在η量级101的基础上,不会再有显著变化.0.25<ν <0.50时,曲线变化趋势相反.ν=0.25时,各量级ξ/ξ0=1,说明此时方程式(4)中,不含η.
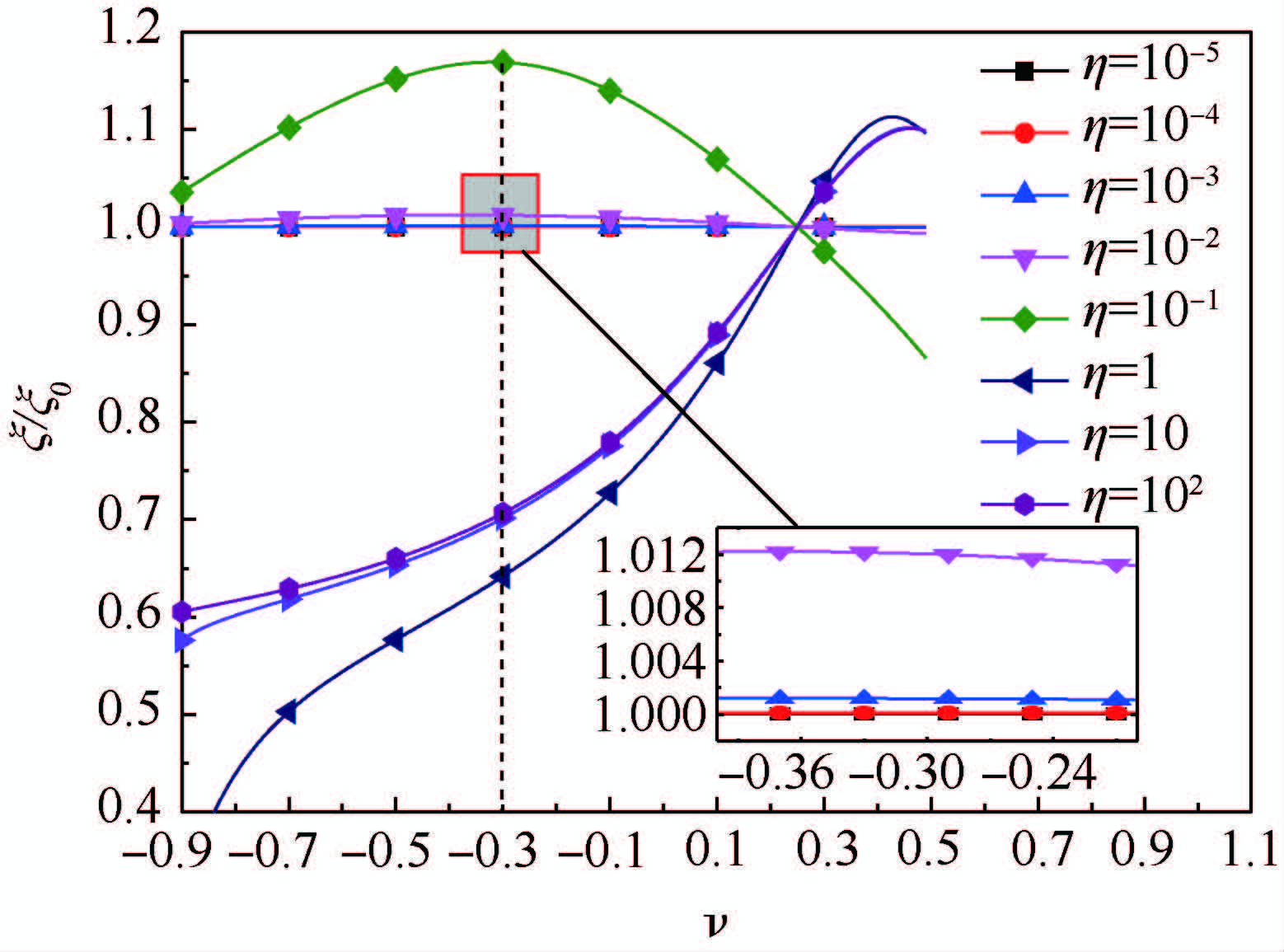 |
| 图 2 考虑重力影响ξ/ξ0随泊松比ν变化Fig. 2 Variation of ξ/ξ0 for different gravity parameters with respect to ν |
| 图选项 |
2.2 算例分析2.2.1 计算模型计算模型材料选为砂土,近似为各向同性线弹性材料,弹性参数[7]为

理论波速为

式中:cg为k=1时含重力因素的参考瑞利波速.
在图 3中计算模型采用交错网格(staggered grid)离散,应用了3套不同的网格系统,即将正应力Sxx和Syy在正常的网格结点上存储和计算,而将速度分量Vx和Vy、剪应力Sxy分别放在两套不同的错位网格上,如图 3所示;该方法可以很好地处理波动方程中速度与应力的耦合关系.图 3中研究区域O为目标计算区域,尺寸为1 200 mm×600 mm,离散方式为

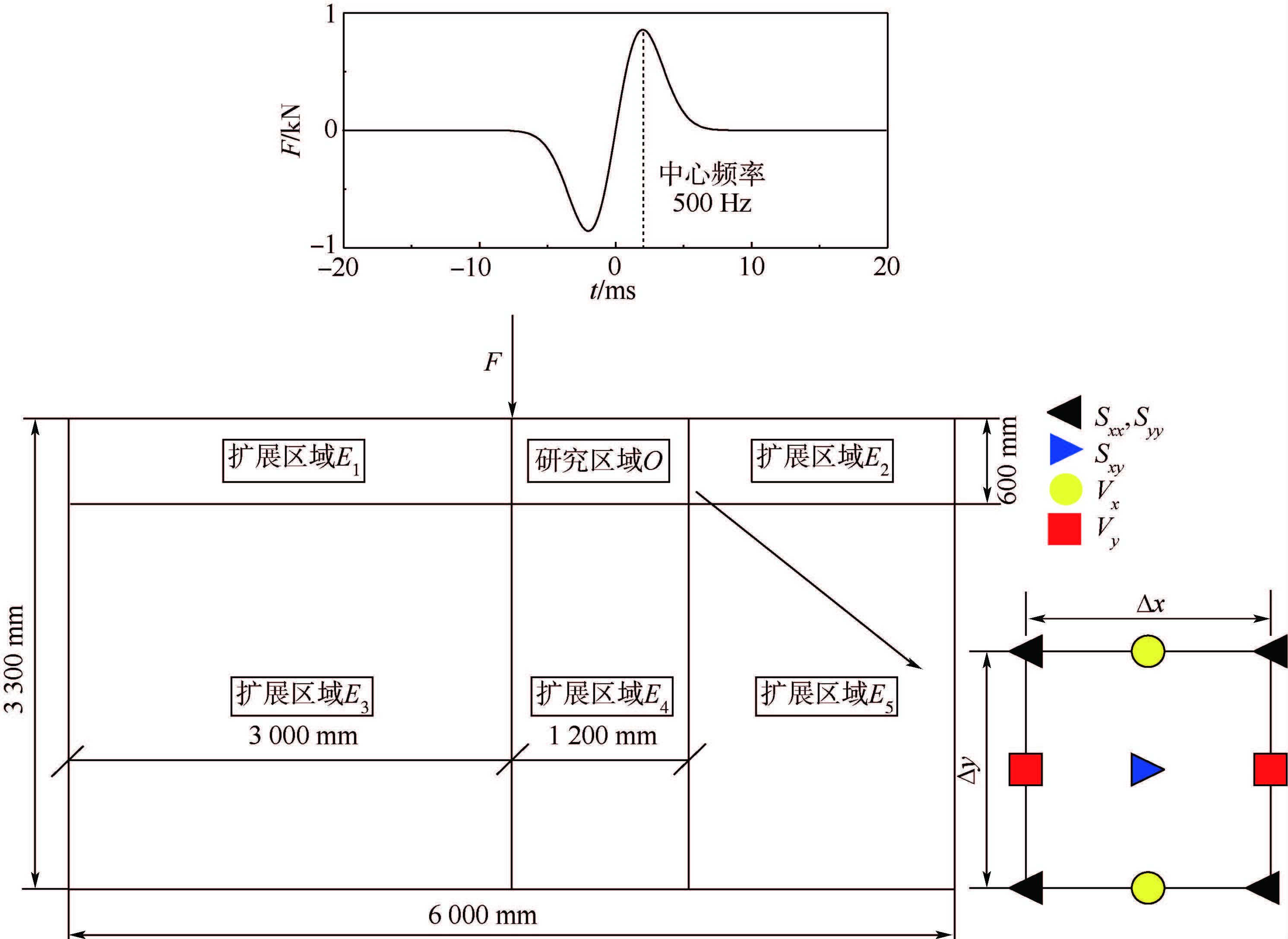 |
| 图 3 模型及激励Fig. 3 Model and excitation |
| 图选项 |
满足FDTD稳定条件,即满足式(12).为使得弹性波在边界上的反射波不影响初始分析结果,适当扩大计算区域,则震源距边界距离L应满足

这里沿x方向的距离L1=3 000 mm,y方向的距离L2=3 300 mm.整个计算区域采用不规则网格离散,扩展区域E1和E2网格尺寸均为50 mm×20 mm,E3和E5为50 mm×50 mm,E4为20 mm×50 mm.激励载荷函数通常选为高斯脉冲(Gaussian Pulse,GP)及1阶微分高斯脉冲(Differentiated Gaussian Pules,DGP)[16],这里选择的是DGP函数:
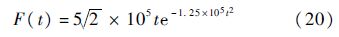
中心频率为500 Hz,持续时间约为7 ms.初始条件,t=0时刻:计算区域内各点应力、速度为0.计算模型四边采用不同的边界条件:左、右及下边界采用Dirichlet边界条件,约束结点的水平、竖向位移[15];上边界,对于不计重力影响情况,采用Neumann自由边界条件,即结点应力为0[15],重力影响下的边界条件[14]为

2.2.2 数值结果在研究区域O内震源右侧每隔200 mm处布置接收点,表 1为相邻两个接收点间计算得到的纵波波速值.表中,第1列为各接收点距震源距离,水平方向(x方向)的起跳位移值设为10-9 mm;第2列为测量得到的各接收点达到起跳位移时的时间;第3列为各接收点实际位移;第4列为通过单位距离(200 mm)所需时间;第5列为计算得到的相邻两个接收点间的纵波波速值.将这5组数据进一步统计平均,得到最终的纵波波速约为260.95 m/s,略大于式(17)中的理论值,但在合理的范围内,与采用吸收边界条件得到的结果相比,更为接近理论值.
表 1 纵波波速Table 1 P-wave velocity
| 距离/mm | 时间/ms | 位移值/(10-6mm) | 时间间隔/ms | 纵波波速/(m·s-1) |
| 200 | 0.52 | 1 | ||
| 400 | 1.24 | 1 | 0.72 | 277.78 |
| 600 | 1.98 | 1 | 0.74 | 270.27 |
| 800 | 2.76 | 1 | 0.78 | 256.41 |
| 1 000 | 3.54 | 1 | 0.78 | 256.41 |
| 1 200 | 4.36 | 1 | 0.82 | 243.90 |
表选项
图 4、图 5分别为含重力影响,表面接收点竖直方向位移uy的三维、二维随时间变化云图,图中LS、SV、R分别表示泄露横波(leaky surface wave)、竖向横波、瑞利波.其中各向同性弹性材料中的LS波速的数学含义为瑞利方程的共轭复数根,只有当泊松比ν>0.263时才出现[17].在图 5中可以清晰地看到LS波的传播路径,其斜率即为其波速,约为193.00 m/s,小于纵波波速,大于横波波速,同理,从该图中可以计算得到S波波速为88.69 m/s.
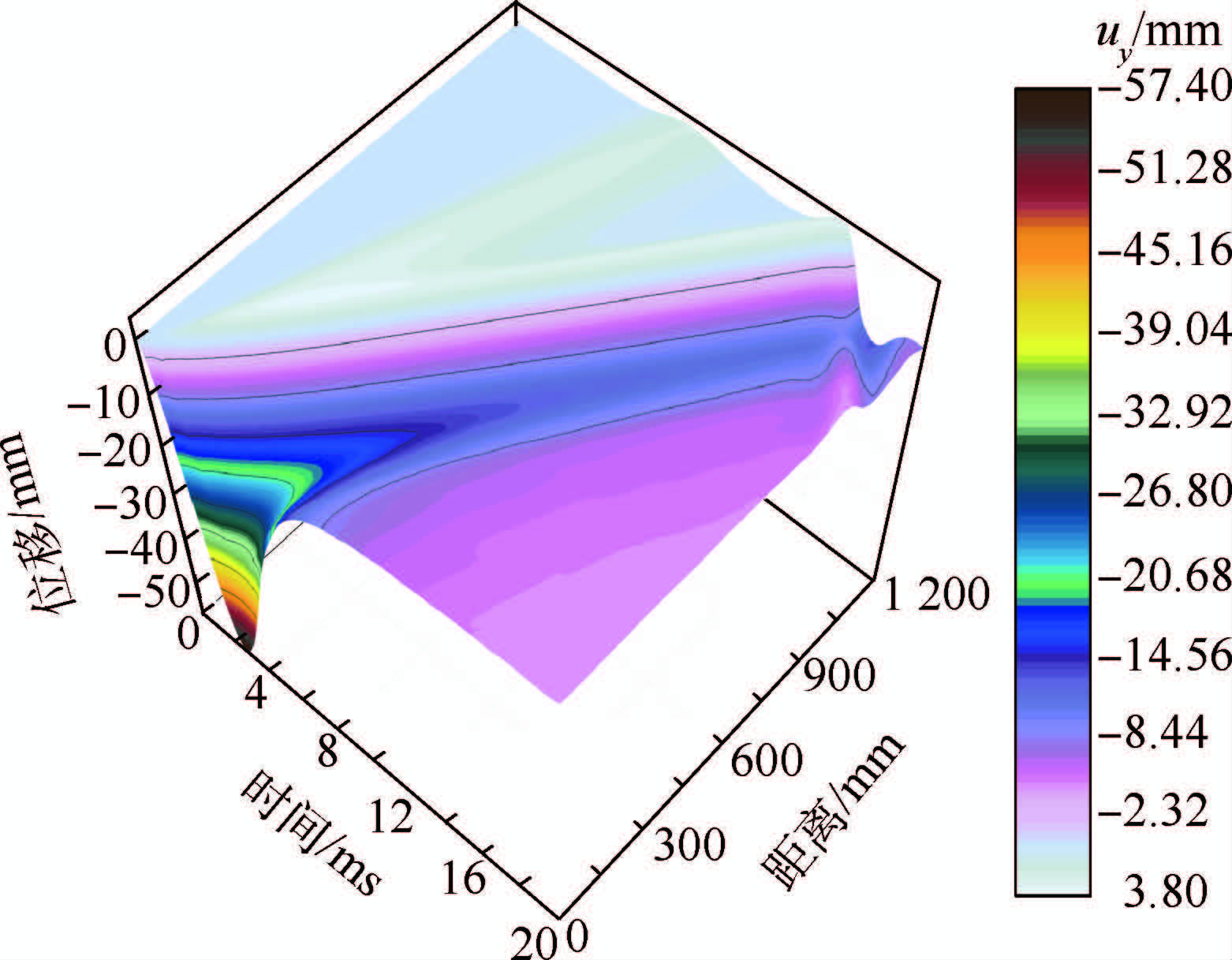 |
| 图 4 接收点竖直方向位移uy变化3D云图Fig. 4 3D contour graph of receivers’ uy |
| 图选项 |
 |
| 图 5 接收点竖直方向位移uy变化2D云图Fig. 5 2D contour graph of receivers’ uy |
| 图选项 |
从图 5中可以看到瑞利波存在的大致区域,然而瑞利波在震源附近并不产生,因而为了从该图中得到瑞利波出现的具体时间,需要进一步分析结点位移变化.图 6为距震源200、400、600、800 mm处接收点竖向位移uy关于水平位移ux的变化曲线,4条曲线可近似拟合为椭圆曲线,然而200~600 mm的近似椭圆短轴与x方向成一定的夹角,说明该位置并不形成R波,只可以形成LS波;800 mm的近似椭圆短轴与x方向平行,说明该处已形成瑞利波.
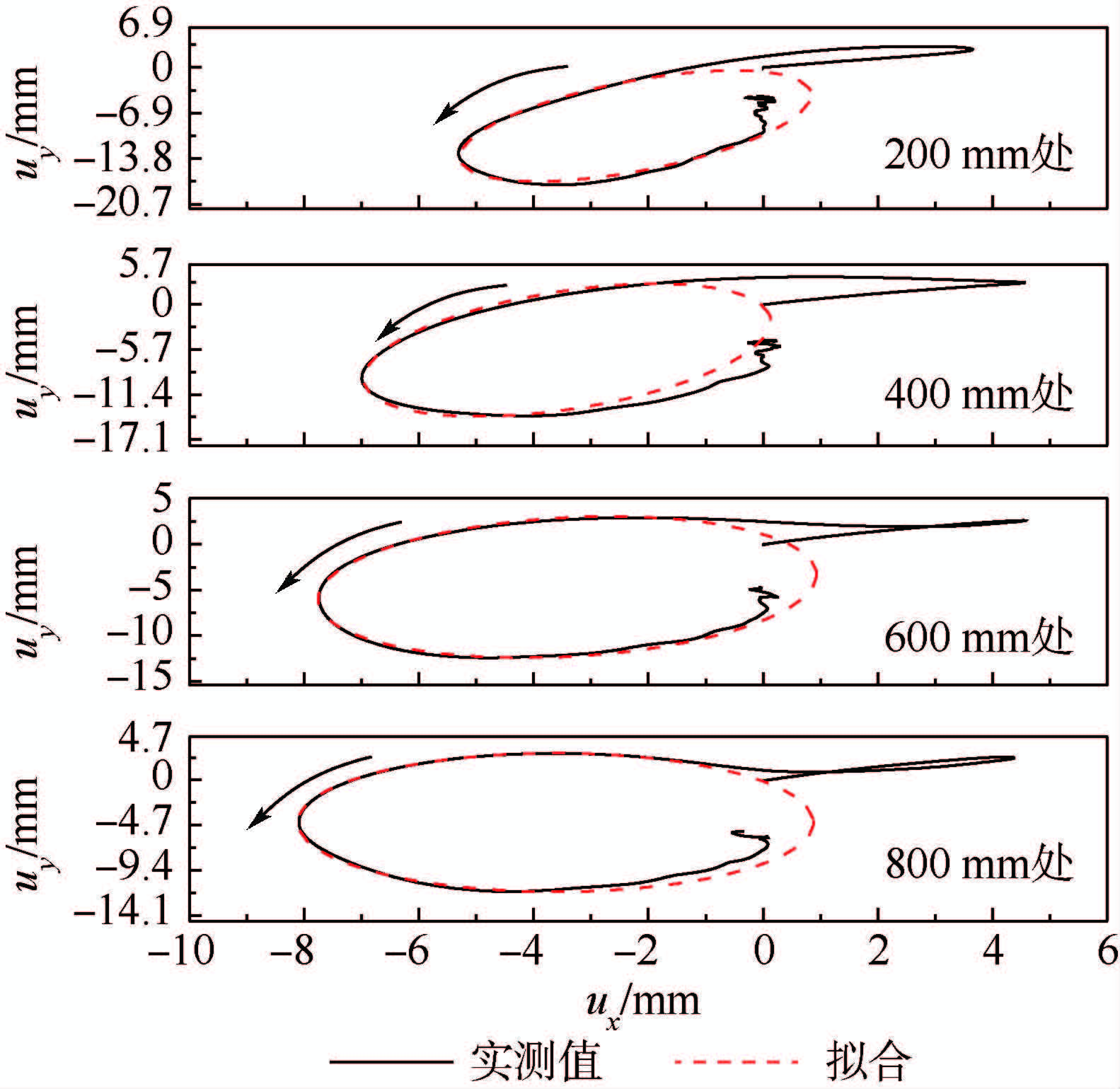 |
| 图 6 uy随ux变化曲线(LS波与R波识别)Fig. 6 uy with respect to ux (LS-wave and R-wave recognition) |
| 图选项 |
图 7为位于800、1 000 mm处的接收点竖向位移随水平位移变化曲线,结点的运动轨迹分别在t=9.80 ms、t=12.14 ms时刻开始呈现椭圆极化,即说明该时刻已形成瑞利波,且随时间呈逆时针变化.可以看出二者差异很小,位移振幅没有显著的变化,验证了瑞利波在水平方向上低衰减率的特性.同时,可以计算得到瑞利波波速约为85.47 m/s,略小于S波波速,但略大于理论值,见式(17).
 |
| 图 7 uy随ux变化曲线(瑞利波识别)Fig. 7 uy with respect to ux (R-wave recognition) |
| 图选项 |
图 8为距震源900 mm处结点位移变化曲线.可以看出重力对水平位移ux不构成影响,与理论预测相一致,验证了该计算模型的有效性;而竖直位移uy曲线略有差异,即可能会影响质点椭圆运动的长轴尺寸,说明重力不仅会影响瑞利波速大小,也会影响其振幅变化.
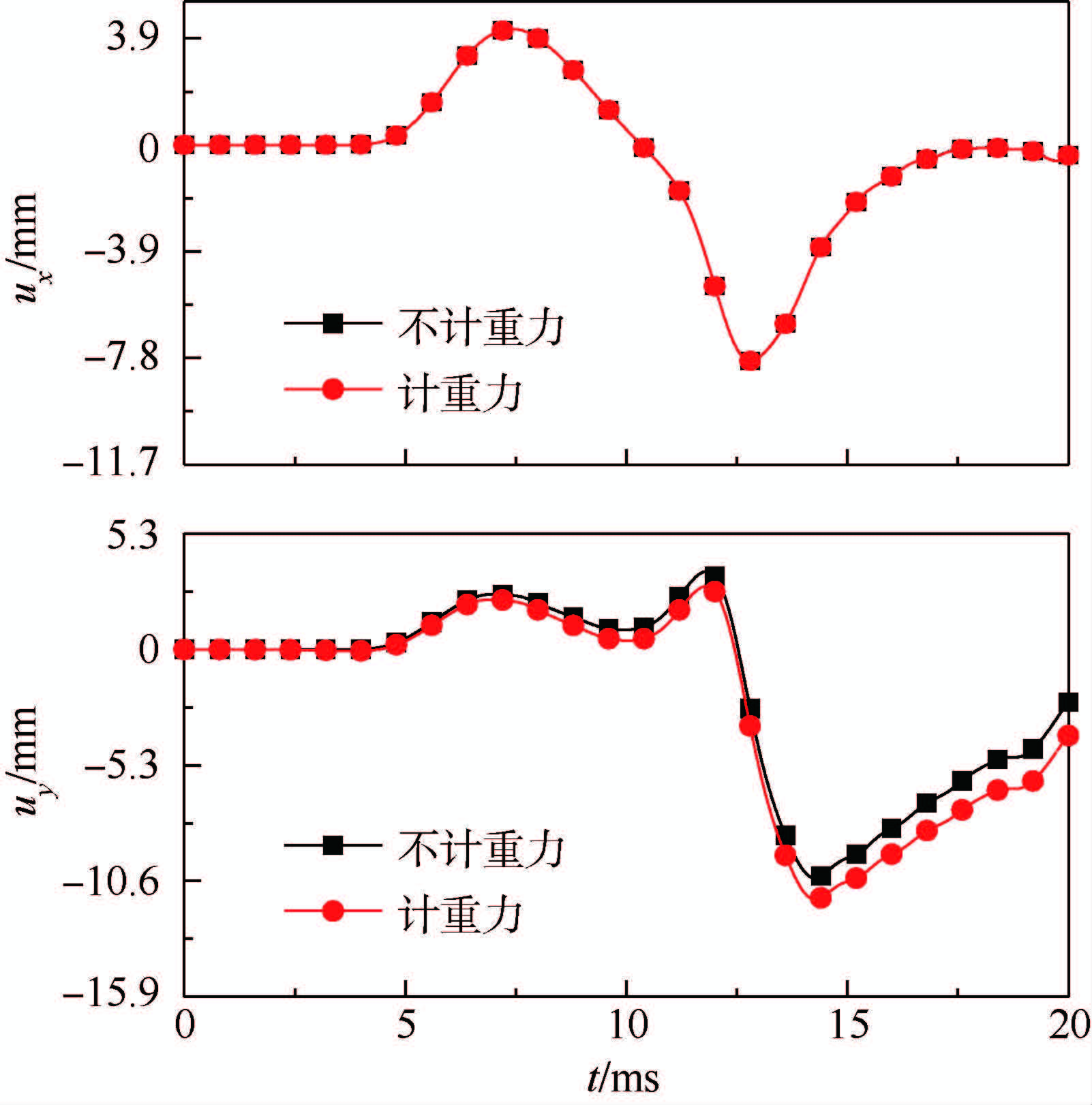 |
| 图 8 位移随时间变化曲线Fig. 8 Variation of displacement with respect to time |
| 图选项 |
为了深入地分析重力的影响,对图 8中的uy曲线进行快速傅里叶变换(Fast Fourier Transform,FFT),见图 9.在FFT中:
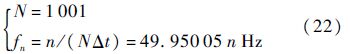
从图 9的振幅曲线中,可以明显观察到3个波峰,波峰所对应的横坐标值即约为该力学模型的前3阶固有频率;重力载荷虽不影响模型固有频率,但对于振幅、相位的影响是显而易见的.表 2为该模型的前5阶固有频率所对应的振幅和相位,可以看出由于重力作用的存在,使得该系统的前5阶频率对于的振幅、相位值都有所提升,振幅增长率分别为11.73%、7.12%、12.44%、19.72%、30.28%.基于考虑重力效应与否对于瑞利波在时域和频域响应都有一定的影响,因而在精细数值模拟中加入重力影响是十分有必要的.
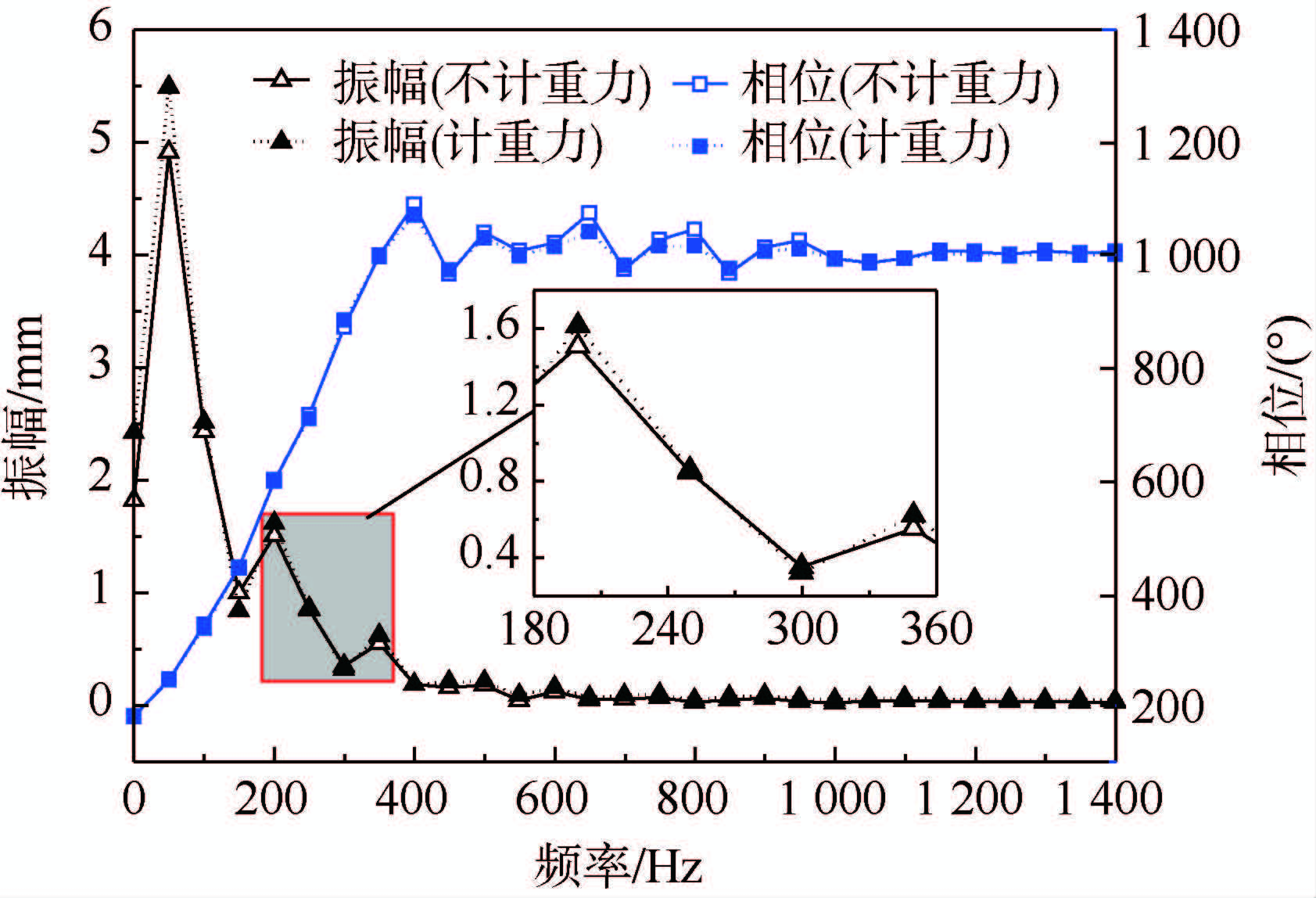 |
| 图 9 uy曲线的FFT变换Fig. 9 Fast Fourier transform of uy curves |
| 图选项 |
表 2 前5阶振幅和相位Table 2 Amplitude and phase of first five order
| 阶数 | 频率/Hz | 不计重力 | 计重力 | ||
| 振幅/mm | 相位/(°) | 振幅/mm | 相位/(°) | ||
| 1阶 | 99.90 | 4.91 | 244.21 | 5.49 | 245.72 |
| 2阶 | 249.75 | 1.51 | 598.24 | 1.62 | 600.42 |
| 3阶 | 399.60 | 0.55 | 999.16 | 0.62 | 998.13 |
| 4阶 | 549.45 | 0.18 | 1 040.31 | 0.21 | 1 030.31 |
| 5阶 | 649.35 | 0.12 | 1 021.98 | 0.16 | 1 014.40 |
表选项
3 结 论1) 对于各向同性线弹性材料,近似波速函数的适用范围为0.1<ν <0.5.
2) 重力影响因子η量级小于10-3时,对于瑞利波速的影响可以忽略不计.
3) η量级大于101时,重力对于瑞利波速的影响也不会再显著增大.
4) ν=0.4有LS波的出现,该模型的LS波速约为193.00 m/s,小于纵波波速,大于横波波速.
5) 验证了R波并不在震源处产生.
6) 重力项的存在会增大R波的振幅和相位,即使对于传统材料,为了真实模拟实验,得到更具有参考价值的研究结果,有必要加入重力影响.
参考文献
| [1] | 寿旋, 夏唐代. 重力对具有表面层的半空间中Rayleigh波的影响[J].振动与冲击, 2011, 30(3): 191-194. Shou X, Xia T D.Rayleigh wave in a half space supporting a layer under influence of gravity[J].Journal of Vibration and Shock, 2011, 30(3): 191-194(in Chinese). |
| Cited By in Cnki | |
| [2] | 曾新吾, 韩开锋, 张光莹.含裂缝介质中的弹性波传播特性[M].北京: 科学出版社, 2013: 7-10. Zeng X W, Han K F, Zhang G Y.Elastic wave propagation characteristics in cracked media[M].Beijing: Science Press, 2013: 7-10(in Chinese). |
| [3] | Yee K S. Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media[J].IEEE Transactions on Antennas and Propagation, 1966, 14(3): 302-307. |
| Click to display the text | |
| [4] | Alterman Z S, Loewenthal D.Seismic waves in a quarter and three-quarter plane[J].Geophysical Journal International, 1970, 20(2): 101-126. |
| Click to display the text | |
| [5] | Virieux J. SH-wave propagation in heterogeneous media: Velocity-stress finite-difference method[J].Geophysics, 1984, 49(11): 1933-1942. |
| Click to display the text | |
| [6] | Dai N, Vafidis A, Kanasewich E R.Wave propagation in heterogeneous, porous media: A velocity-stress, finite-difference method[J].Geophysics, 1995, 60(2): 327-340. |
| Click to display the text | |
| [7] | Schroder C T, Scott Jr W R, Larson G D.Elastic waves interacting with buried land mines: A study using the FDTD method[J].IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(6): 1405-1415. |
| Click to display the text | |
| [8] | Jafargandomi A, Takenaka H.Non-standard FDTD for elastic wave simulation: Two-dimensional P-SV case[J].Geophysical Journal International, 2009, 178(1): 282-302. |
| Click to display the text | |
| [9] | Matsuda N, Biwa S.A finite-difference time-domain technique for nonlinear elastic media and its application to nonlinear Lamb wave propagation[J].Japanese Journal of Applied Physics, 2012, 51(7S): 7G-14G. |
| Click to display the text | |
| [10] | Chew W C. Waves and fields in inhomogeneous media[M].Piscataway, NJ: IEEE Press, 1995: 246-271. |
| [11] | Bromwich T I. On the influence of gravity on elastic waves, and, in particular on the vibrations of an elastic globe[J].Proceedings of the London Mathematical Society, 1898, 1(1): 98-120. |
| Click to display the text | |
| [12] | Love A E H. Some problems of geodynamics: Being an essay to which the Adams prize in the university of Cambridge was adjudged in 1911[M].Cambridge: Cambridge University Press, 1911: 159-194. |
| [13] | Abd-Alla A M. Propagation of Rayleigh waves in an elastic half-space of orthotropic material[J].Applied Mathematics and Computation, 1999, 99(1): 61-69. |
| Click to display the text | |
| [14] | Biot M A.Mechanics of incremental deformations[M].New York: John Wiley & Sons, 1965: 273-281. |
| [15] | Virieux J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method[J].Geophysics, 1986, 51(4): 889-901. |
| Click to display the text | |
| [16] | Uduwawala D. Gaussian vs differentiated gaussian as the input pulse for ground penetrating radar applications[C]//Second International Conference on Industrial and Information Systems.Piscataway, NJ: IEEE Press, 2007: 199-202. |
| Click to display the text | |
| [17] | Schr?der C T, Scott Jr W R.On the complex conjugate roots of the Rayleigh equation: the leaky surface wave[J].The Journal of the Acoustical Society of America, 2001, 110(6): 2867-2877. |
| Click to display the text |
