, 李海1,2 1. 北京科技大学 金属矿山高效开采与安全教育部重点实验室, 北京 100083;
2. 北京科技大学 土木与资源工程学院, 北京 100083
收稿日期：2021-03-15
基金项目：国家自然科学基金资助项目(52004017，52174106)；中国博士后科学基金资助项目(2020M670138)；中央高校基本科研业务费专项资金资助项目(FRF-TP-19-026A1)。
作者简介：孙浩(1992-)，男，安徽阜阳人，北京科技大学讲师，博士;
金爱兵(1974-)，男，江苏兴化人，北京科技大学教授，博士生导师。
摘要：PFC软件中球形颗粒和平行黏结接触模型(PBM)被广泛应用于岩石力学特性模拟研究.然而, 球形颗粒和PBM存在两个明显缺陷: 球形颗粒与岩石材料的晶粒形状相差较大; 无侧限抗压强度与抗拉强度之比(压拉比)偏低.基于此, 以山西吕梁地区典型砂岩为例, 通过Voronoi剖分建立刚性块体数值试样, 并使用软化黏结接触模型(SBM)对砂岩试样进行模拟分析.研究结果表明, 基于刚性块体和SBM的数值模拟相较于传统基于球形颗粒和PBM的数值模拟而言, 主要具有3个优点: 与球形颗粒试样相比, 刚性块体间自锁效应增大, 刚性块体模型间的配位数明显提高, 更能模拟真实砂岩的晶粒形状和晶粒间力学行为; 软化黏结模型能模拟出砂岩更大的压拉比, 更能真实表征砂岩在多应力路径下的力学特性; 采用基于刚性块体和SBM的数值模型能够真实反映砂岩典型的剪切破坏模式.
关键词：砂岩刚性块体Voronoi剖分软化黏结模型压拉比
Study on Mechanical Properties of Sandstone Based on Voronoi Block Model
SUN Hao1,2, CHEN Shuai-jun1,2, JIN Ai-bing1,2
, LI Hai1,2 1. Key Laboratory of Ministry of Education for Efficient Mining and Safety of Metal Mines, University of Science and Technology Beijing, Beijing 100083, China;
2. School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China
Corresponding author: JIN Ai-bing, E-mail: jinaibing@ustb.edu.cn.
Abstract: The spherical particle and parallel bond model(PBM)in PFC(particle flow code) software is widely used to simulate the mechanical properties of rock. However, spherical particles and PBM have two intrinsic drawbacks: the grain shape of spherical particles is quite different from that of rock materials, and the ratio of unconfined compressive strength to tensile strength(UCS/TS)is low. Based on this, taking the typical sandstone in Lüliang area of Shanxi Province as an example, the rigid block numerical specimens are established by Voronoi tessellations, and the mechanical properties of sandstone are studied by using the softe-bond model(SBM). The results show that the scheme has three advantages compared with the traditional numerical simulation based on spherical particles and PBM: compared with the spherical sample, the grain interlocking between the rigid blocks increases, and the coordination number between the rigid block models increases significantly, which can better simulate the grain shape and mechanical behavior of real sandstone. The SBM can simulate the larger unconfined compressive strength to tensile strength ratio of sandstone, which can truly characterize the mechanical properties of sandstone under multiple stress paths. The numerical model based on rigid block and SBM can truly reflect the typical shear failure mode of sandstone.
Key words: sandstonerigid blockVoronoi tessellationssoft-bond modelUCS/TS ratio
隧道、边坡、桥梁和硐室等各种工程施工中遇到的岩石具有不同的力学行为, 而针对岩石力学行为的研究是解决各种工程问题的基础.不同种类岩石力学行为的差异不仅体现在其矿物成分和胶结方式, 岩石中各类微孔隙和矿物结晶亦严重影响岩石的力学特性[1].
物理试验和数值模拟一直是岩石力学特性研究的常用手段.物理试验中, 真实岩样[2]和相似材料试样[3]被广泛应用于岩石力学性质及结构面性质的研究中; 而最新兴起的3D打印试样技术[4]为岩石力学行为研究注入了新的活力.与数值模拟相比, 物理试验具有能反映研究对象物理力学特性的优点, 但也存在控制变量困难、可重复性差以及细观机理研究困难等弊端.数值模拟研究中常用的方法主要包括: 有限单元法(finite element method, FEM)[5]、有限差分法(finite difference method, FDM)[6]、边界元法(boundary element method, BEM)[7]和离散单元法(discrete element method, DEM)[1]等.其中, DEM因其能够直观反映试样内裂纹扩展及贯通过程而被广泛应用.目前, 应用于试样尺度岩石力学细观研究的离散元软件有YADE[8], ESyS- Particle[9]和PFC(particle flow code)[10]等, 均采用球形或球形簇作为基质材料; UDEC(universal distinct element code)[11]软件虽然可生成不规则刚性块体, 但更适用于边坡和地下工程开挖等大变形问题研究.PFC是由Cundall等[12]提出的用于模拟无黏结颗粒材料的细观离散元数值软件, 而在Potyondy等[13]提出黏结模型后, PFC开始逐渐应用于各类岩石力学研究.
利用PFC软件进行试样尺度岩石力学数值试验研究一般分为以下三个步骤: ①建模, 建立基于颗粒体系的岩石试样模型; ②接触模型选择及细观参数匹配, 选择接触模型, 并对墙体、颗粒自身参数以及颗粒-颗粒、颗粒-墙体间接触模型参数的匹配研究; ③数值试验, 开展单轴压缩、三轴压缩和直接剪切等各类岩石力学数值试验研究.上述三步骤模拟的准确性均会影响所研究结果的可靠性.目前, 针对步骤②的接触模型选择及细观参数确定问题, 众多****已分别采用平行黏结模型(parallel bond model, PBM)[10]、平节理模型(flat-joint model, FJM)[2]和伯格斯模型(Burger’s model)[14]等接触模型开展了各类岩石的物理力学特性研究; 针对步骤③, 相关****也已开展了PFC单轴压缩试验[15]、三轴压缩与卸荷试验[2]、巴西劈裂试验[16]以及岩石动荷载试验[17]等各类力学试验的数值模拟研究.本文以山西吕梁地区典型砂岩试样为依据, 从数值模型建立(步骤①)和接触模型选择及细观参数匹配(步骤②)两个方面对现行数值模拟方法进行优化.
首先, 在数值模型构建方面(步骤①), 国内外绝大多数****均采用球形颗粒或球形簇进行岩石力学问题研究.而相关室内试验研究已表明: 矿物组成、粒径尺寸、颗粒形状等因素均对岩石强度具有显著影响[18].含球形和球形簇颗粒模型无法精确模拟岩石结构中的矿物晶粒形状, 致使目前基于PFC的岩石力学问题研究中所构建的数值模型准确性较差.Potyondy等[19]提出了基于PFC2D的细观晶粒模型(grain-based model, GBM), 研究岩石晶粒的非均匀性对其强度和裂纹扩展模式的影响, 但其本质还是采用球形颗粒团簇的方式实现岩石晶粒的模拟, 且晶粒破裂后仍是一个个独立的球形颗粒, 球形颗粒间较小的接触面积与真实岩石晶粒间接触差异较大, 同时, 球形颗粒团簇又大幅增加了模型内颗粒数目, 降低了计算效率.目前, 数值模拟中建模阶段(步骤①)所得数值模型与真实岩石试样误差较大, 且接触模型选择及细观参数匹配(步骤②)的准确性对试样力学性质具有重要影响.因此, 有必要对岩石力学PFC模拟的建模阶段开展优化研究.
在接触模型选择及细观参数匹配(步骤②)方面, 与连续介质方法直接输入室内试验所得宏观物理力学参数不同, PFC中宏-细观参数之间无定量关系.因此, 宏-细观参数的匹配研究是PFC模拟的前提.研究表明: PBM可以模拟岩石的弹性模量、泊松比和无侧限抗压强度[20].但球形颗粒所提供的较小配位数导致球形颗粒间自锁效应偏低, 且基于球形颗粒的PBM不能提供合适的转动阻力[21].因此, 模拟所得无侧限抗压强度与抗拉强度的比值(即压拉比)仅能在3~7范围内波动[13], 小于真实岩石的压拉比(10~20)[22].Scholtès等[23]认为较低压拉比的数值模型在模拟同时存在压缩和拉伸应力路径的问题时误差较大.
综上所述, 在采用球形颗粒和PBM进行岩石力学相关研究时存在两个明显缺陷: ①球形颗粒与岩石材料的晶粒形状相差较大; ②无侧限抗压强度与抗拉强度之比(压拉比)较低.基于此, 本文以山西吕梁地区典型砂岩为例, 通过室内单轴压缩试验和扫描电镜试验获得砂岩的应力-应变关系及微观晶粒图像, 基于Voronoi剖分技术构建刚性块体数值试样, 并利用软化黏结模型(soft-bond model, SBM)开展无侧限压缩和直接拉伸数值模拟研究, 并与传统基于球形颗粒和PBM的数值模拟方法对比, 分析刚性块体数值试样和SBM在模拟典型砂岩晶粒形状不规则性和大压拉比等方面的优势, 研究方法和结果能够提高细观离散元软件PFC在砂岩力学行为数值模拟研究中的适用性与可靠性, 为其他晶粒型结构岩石在多应力路径下的模拟研究提供借鉴.
1 PFC中的Voronoi剖分1.1 3D Voronoi剖分原理3D Voronoi剖分是将三维空间内的某个区域划分为一系列的单元体[24].给定欧几里德空间内有限个点P={p1, p2, …, pN}, 并且P∈ R3, 空间中的每一个点均隶属于一个Voronoi单元体Vi, Vi定义如下:
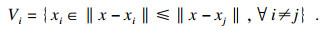 | (1) |
1.2 PFC中刚性块体模型构建在PFC中利用Voronoi剖分原理生成标准试样的步骤如图 1所示.首先生成圆柱形墙体; 其次在圆柱形墙体内生成一定孔隙率和粒径分布的球形颗粒, 并进行静力平衡计算; 最后使用Voronoi剖分命令, 以球心坐标为随机点, 以球半径为欧几里德距离进行Voronoi剖分和正则化, 得到数值试样.采用TESCAN VEGA3扫描电子显微镜(图 2)获得的砂岩试样SEM图像如图 3a所示, 球形颗粒如图 3b所示, 基于Voronoi剖分生成试样的局部放大图如图 3b所示.从图 3中可以看出, 通过Voronoi剖分所建立的块体模型颗粒大小不一、形状各异, 相较于球形颗粒, 更符合砂岩中矿物晶粒分布.
图 1(Fig. 1)
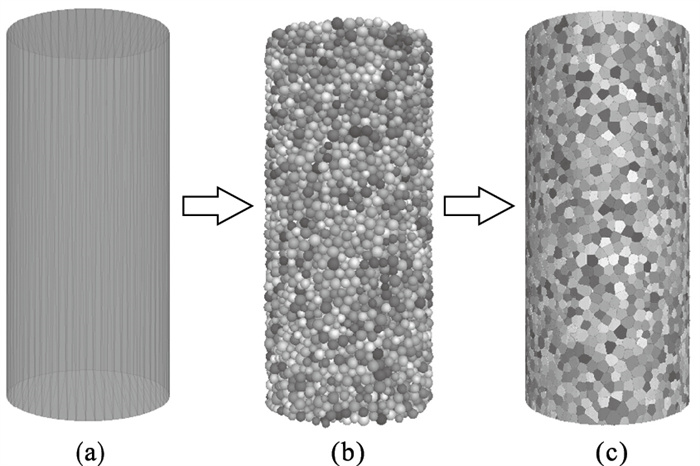 | 图 1 基于Voronoi剖分的PFC刚性块体建模过程Fig.1 Modeling processes of PFC rigid block based on Voronoi subdivision (a)—三维墙体；(b)—球形颗粒试样；(c)—刚性块体试样. |
图 2(Fig. 2)
 | 图 2 TESCAN VEGA3扫描电子显微镜Fig.2 TESCAN VEGA3 scanning electron microscope |
图 3(Fig. 3)
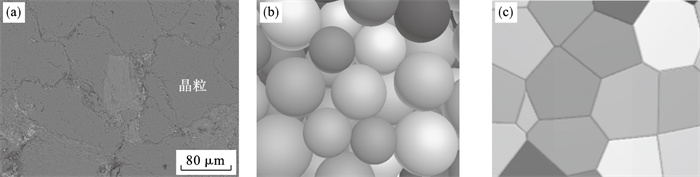 | 图 3 砂岩晶粒结构和两种数值试样颗粒局部图Fig.3 Grain structure of sandstone and partial grain diagram of two numerical samples (a)—砂岩晶粒结构；(b)—球形颗粒试样中颗粒；(c)—刚性块体试样中颗粒. |
研究表明[21], 球形颗粒间的配位数较小, 导致球形颗粒间的自锁效应偏低, 而基于Voronoi剖分原理建立的刚性块体则有效解决了这一难题.以典型四面体刚性块体颗粒为例, 如图 4所示, 在理想情况下, 四面体刚性块体中4个面、6条边和4个顶点均能生成接触, 且每条边和每个顶点又能同时生成多个接触, 而球形颗粒仅能生成4个接触(根据Voronoi剖分原理, 生成Voronoi多面体的面数等于原始球形颗粒的接触个数), 刚性块体间的配位数高于球形颗粒, 导致刚性块体间的自锁效应明显提高.基于Voronoi块体的建模方法是对PFC传统建模方法(Ball, GBM以及Clump)的有力补充, 块体之间的运动和相互作用力均遵循牛顿第二定律.
图 4(Fig. 4)
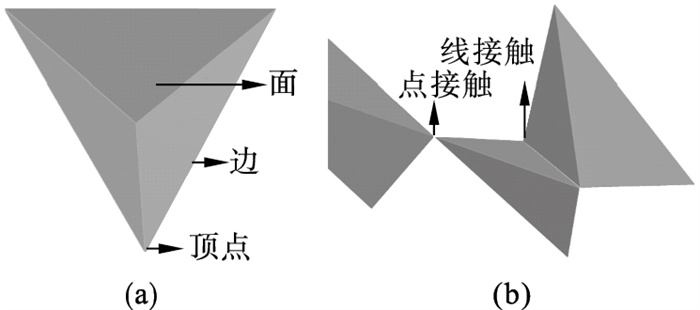 | 图 4 四面体刚性块体Fig.4 Tetrahedral rigid blocks (a)—单个刚性块体；(b)—刚性块体间接触. |
2 基于SBM的刚性块体试样数值模拟2.1 数值模型构建本次研究基于SBM建立刚性块体试样模型.在以往研究中, 球形和球形簇一直作为模拟岩石的基质材料, 通过对墙体施加一定速度的方式对整个试样施加压力, 模拟室内试验中无侧限压缩过程.由于刚性块体之间紧密接触, 孔隙率较小, 软件的算法误差会造成颗粒的局部凸起(图 5), 使试件的上、下表面不平整, 而凸起的块体在用墙体或其他平整面作为加载端时会形成局部的应力集中, 造成试样上下端部的局部破坏, 使模拟结果产生较大误差.因此, 本次数值试验通过建立高度为110mm的数值试样, 设置上下5mm部分刚性块体分别为上下加载端[27].由于加载端和试样一次建模成型, 试样和加载端结合较好, 通过上下加载端匀速运动对试样施加压力的方式模拟无侧限压缩过程.该方法充分考虑了试样和加载端的接触条件, 消除了由于上下端面的不平整带来的误差.刚性块体数值模型试样如图 6所示.
图 5(Fig. 5)
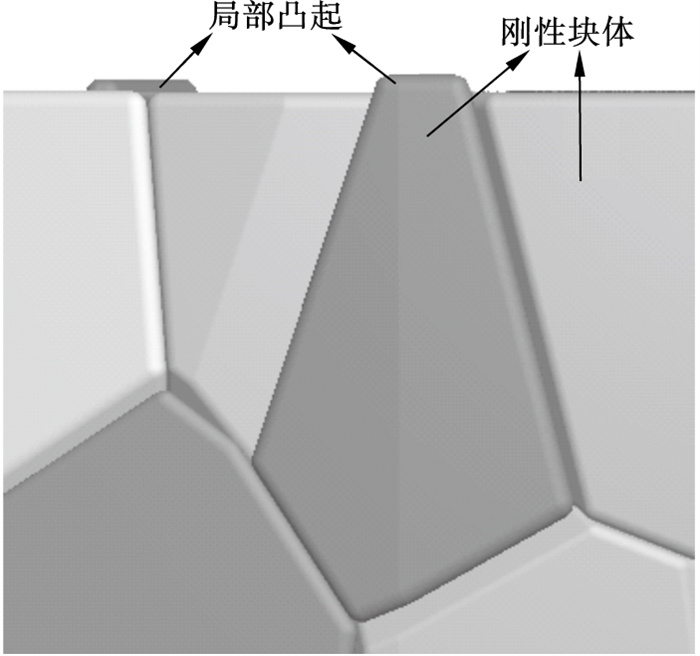 | 图 5 数值试样中刚性块体的局部凸起Fig.5 Local bulge of rigid block in numerical specimen |
图 6(Fig. 6)
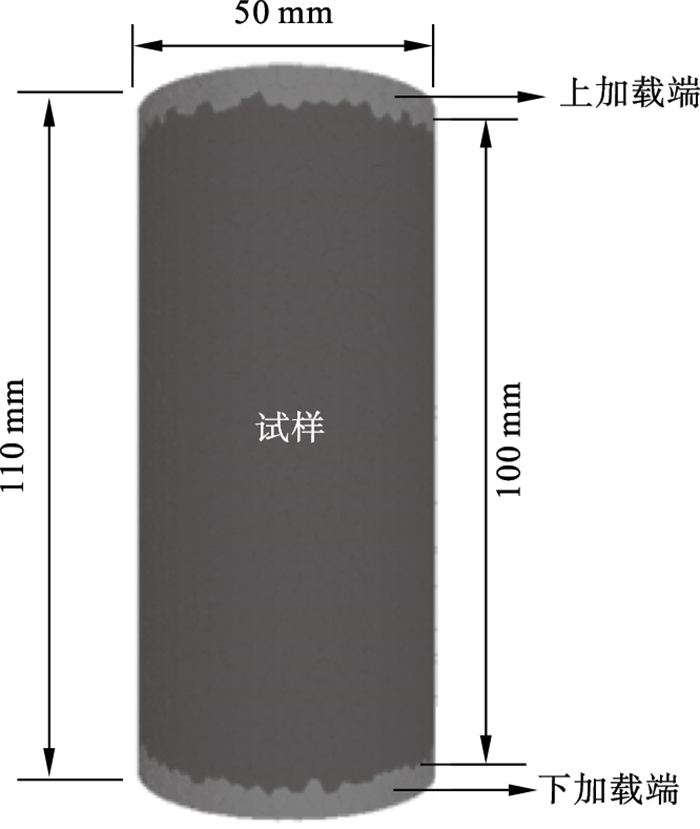 | 图 6 刚性块体数值模型试样Fig.6 Rigid block numerical model specimen |
2.2 SBM原理简介SBM是PFC中开发的接触黏结模型, 可以应用于黏结和未黏结的颗粒[27], 本文主要介绍和使用黏结颗粒.软化黏结模型黏结部分的接触行为如图 7所示, 其中ζ为软化系数, γ为软化抗拉强度系数, σc为抗拉强度, kn为法向刚度, kt为切向刚度, c, ?为内聚力和内摩擦角.
图 7(Fig. 7)
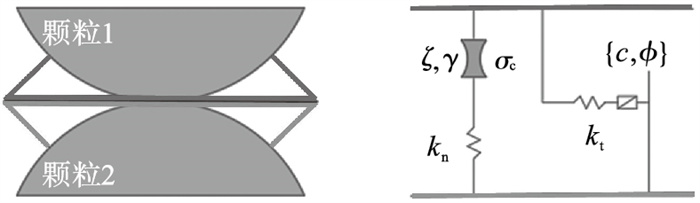 | 图 7 软化黏结模型颗粒间黏结状态和流变组件[27]Fig.7 State and rheological components of the soft bond model[27] |
默认情况下(即软化系数ζ=0), SBM类似于PBM, 而当软化抗拉强度系数γ=1.0时, 黏结键的软化行为也将受到抑制.在ζ≠0和γ≠1.0时黏结键会发生拉伸软化.SBM的软化行为只对拉伸响应起作用, 而对剪切响应无效, 因此, 在抗剪强度超过极限之后黏结键失效破裂.一旦黏结键的拉力超过了黏结键的抗拉强度, 黏结键间的拉力不会像PBM中那样自动设置为0, 而是不断减小, 当拉力小于γ和峰值抗拉强度的乘积时, 黏结键破裂失效.软化速率由软化系数ζ决定, 如果ζ=1, 拉伸软化以与拉力达到峰值抗拉强度相同的绝对速率进行(速率符号相反)[27].
2.3 基于刚性块体的SBM细观参数确定以室内试验力学参数为对照数据, 通过宏-细观参数匹配研究, 获得可靠的软化黏结接触模型PFC细观参数组合.室内试验砂岩岩样取自山西吕梁地区, 加工规格为?50mm×100mm, 采用YAW-600微机控制电液伺服刚性压力试验机(图 8)进行试验获得砂岩试样应力-应变关系.通过构建基于球形颗粒和刚性块体模型的数值试样, 对比探究刚性块体模型模拟砂岩力学特性的可行性.
图 8(Fig. 8)
 | 图 8 YAW-600单轴压力试验机Fig.8 Model YAW-600 uniaxial compression testing machine |
利用PFC3D软件建立高为110mm(上下各5mm作为加载端), 直径?=50mm的三维数值模型, Voronoi剖分前球体颗粒直径为2.0~3.32mm, 生成刚性块体总数目为16142, 刚性块体间采用SBM.与此同时, 建立高度为110mm(上下各5mm作为加载端), 直径φ=50mm的标准圆柱形试样, 试样内球形颗粒尺寸为2.0~3.32mm, 生成球形颗粒总数目为14959, 颗粒间采用传统的PBM.通过不断调整颗粒间黏结的细观参数, 匹配室内试验中砂岩试样的弹性模量、峰值强度、峰值应变和泊松比等参数.数值模拟轴向加载速率为0.05m/s, 终止加载条件为峰值强度的80 %.确定的SBM和PBM细观参数如表 1所示.
表 1(Table 1)
 表 1 SBM和PBM细观参数汇总表Table 1 Summary of SBM and PBM micro-parameters
| 表 1 SBM和PBM细观参数汇总表 Table 1 Summary of SBM and PBM micro-parameters |
真实岩石试样中存在众多微孔隙, 而数值模拟试样中缺少可压缩的微孔隙, 导致离散元数值模拟方法仍无法模拟真实岩石中的微孔隙压密阶段[28].因此, 数值模拟试验中试样的弹性模量略小于室内试验中的弹性模量.球形颗粒和PBM已经在岩石力学领域广泛应用, 并已被证实可以模拟砂岩试样的应力-应变曲线，两种数值模型的应力-应变曲线如图 9所示.从图 9中可以看出, 本文采用的SBM和刚性块体在模拟砂岩应力-应变曲线方面与PBM和球形颗粒并无差异, 即证明了本文中采用SBM和刚性块体数值模拟方法的可靠性.数值模拟与室内试验所得宏观力学参数如表 2所示.由表 2可知，数值模拟所得试样的峰值强度、峰值应变、弹性模量和泊松比等宏观力学参数均与室内试验所得结果较为接近.因此, 认为采用基于刚性块体试样的SBM可以用于砂岩力学行为的数值模拟试验中.
图 9(Fig. 9)
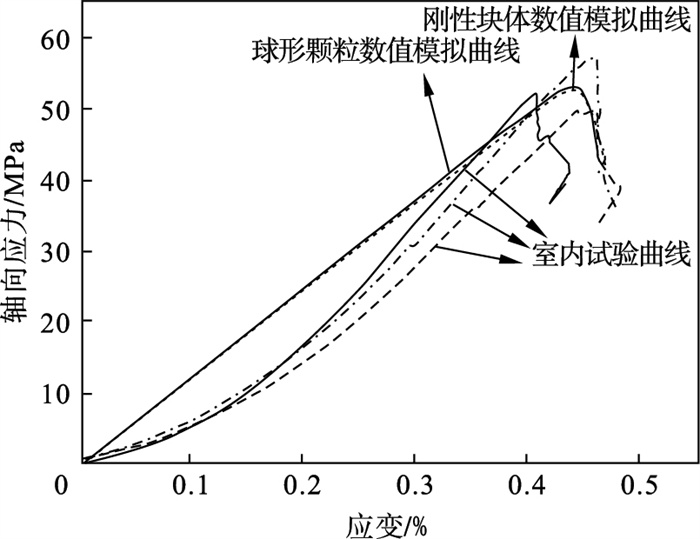 | 图 9 室内试验和数值模拟所得试样单轴压缩应力-应变关系Fig.9 Uniaxial compressive stress-strain curves between laboratory tests and numerical simulations |
表 2(Table 2)
表 2 室内试验和数值模拟所得试样力学参数Table 2 The mechanical parameters of the sample obtained from laboratory test and numerical simulation
| 表 2 室内试验和数值模拟所得试样力学参数 Table 2 The mechanical parameters of the sample obtained from laboratory test and numerical simulation |
2.4 两种数值模型试样无侧限压缩破坏模式对比分析本文从数值模型构建和接触模型选择两个方面对数值模拟过程进行优化, 采用的刚性块体模型与真实砂岩颗粒形状较为接近, 刚性块体间的细观接触行为与真实颗粒间的接触行为近似, 且颗粒间配位数较大, 颗粒自锁效应较大.因此, 宏观数值试样的破坏模式与真实砂岩试样的破坏模式较为接近.图 10为真实砂岩试样和两种数值试样的破坏模式: 刚性块体试样破坏模式为经典岩石力学中常见的剪切破坏, 更符合真实砂岩的破裂模式; 而球形颗粒模型易产生局部破坏, 从而为岩石破裂模式的匹配带来一定困难, 这也是****在利用PFC3D进行岩石力学研究中对完整岩石破裂模式匹配较少的重要原因.因此, 从试样破裂模式可以明显发现刚性块体模型优于传统球形颗粒模型.
图 10(Fig. 10)
 | 图 10 无侧限压缩试样破坏图Fig.10 Schematic diagrams of unconfined compression failure (a)—球形颗粒试样；(b)—砂岩试样；(c)—刚性块体试样. |
2.5 两种数值模型试样拉伸试验模拟结果对比分析本文所采用的软化黏结接触模型通过引入软化系数ζ来改善黏结键的力学行为, 软化系数不仅影响无侧限压缩数值模拟结果, 亦对试样抗拉强度影响较大.图 11为采用刚性块体与SBM数值试样和球形颗粒与PBM数值试样的直接拉伸的应力-应变曲线, 采用球形颗粒与PBM的数值试样抗拉强度为10.53MPa, 采用刚性块体与SBM的数值试样抗拉强度为4.46MPa, 从表 2可知, 球形颗粒与PBM数值试样和刚性块体与SBM数值试样的无侧限抗压强度分别为53.23MPa和52.78MPa.无侧限抗压强度相等情况下, 基于SBM的刚性块体试样抗拉强度较低.
图 11(Fig. 11)
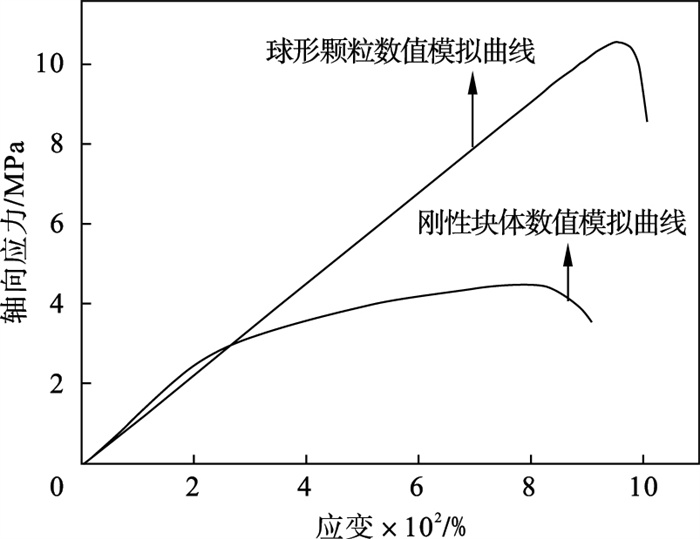 | 图 11 两种数值试样抗拉应力-应变曲线Fig.11 Tensile stress-strain curves of two numerical samples |
通过上述对比分析, 从力学参数和破坏模式等角度探究了基于刚性块体试样的软化黏结接触模型的优越性, 为后续岩石力学数值模拟研究提供一种新型建模方法.
3 基于SBM的刚性块体数值模型研究3.1 基于SBM模型的岩石压拉比分析通常情况下, 岩石的压拉比在10~20之间[22], 表 3为常见的三种典型岩石的无侧限抗压强度和抗拉强度.为了获得两种模型试样的抗拉强度, 分别针对三种典型岩石进行两种模型数值模拟拉伸试验, 每种岩石试样进行2组拉伸数值模拟, 共计6组数值拉伸试验.
表 3(Table 3)
表 3 三种岩石单轴抗压、抗拉强度[29-31]Table 3 Uniaxial compressive and tensile strength of three kinds of rocks[29-31]
| 表 3 三种岩石单轴抗压、抗拉强度[29-31] Table 3 Uniaxial compressive and tensile strength of three kinds of rocks[29-31] |
传统的PBM模型所能达到的压拉比仅仅为3~7[13].SBM模型通过在PBM模型基础上引入软化系数, 可以明显提高数值试样的压拉比.表 4为三种岩石PBM和SBM模型的无侧限抗压强度和抗拉强度数值模拟数据. 从表 4中可以看出, SBM相较于PBM来说, 压拉比明显增大, 更趋近于典型岩石的压拉比, 从而提高模拟结果的准确性.
表 4(Table 4)
表 4 三种岩石的压拉比数值模拟结果Table 4 Numerical simulation results of compressive to tensile strength ratio of three kinds of rocks
| 表 4 三种岩石的压拉比数值模拟结果 Table 4 Numerical simulation results of compressive to tensile strength ratio of three kinds of rocks |
3.2 SBM和PBM压拉比影响机制分析岩石类材料的抗压强度远大于其抗拉强度, 通常情况下, 典型岩石的压拉比在10~20之间[22].对于PBM而言, 其黏结键的抗拉和抗剪强度在黏结键被移除之前始终保持不变, 其黏结键的抗拉力学行为如图 12a所示(抗剪强度类似).随着颗粒间拉力达到黏结键的抗拉强度, 黏结键破裂并被移除, 此时颗粒间表现为无黏结行为.对于采用PBM模型模拟典型岩石的无侧限压缩和抗拉数值试验而言, 颗粒间的黏结强度参数(主要是指黏结抗拉强度和黏结抗剪强度)决定数值模拟试样的无侧限压缩峰值强度和抗拉强度, 这就导致在使用PBM来模拟典型岩石时, 压拉比仅能随着黏结强度参数的变化在3~7范围内波动[13], 不能准确模拟真实典型岩石的压拉比特性.
图 12(Fig. 12)
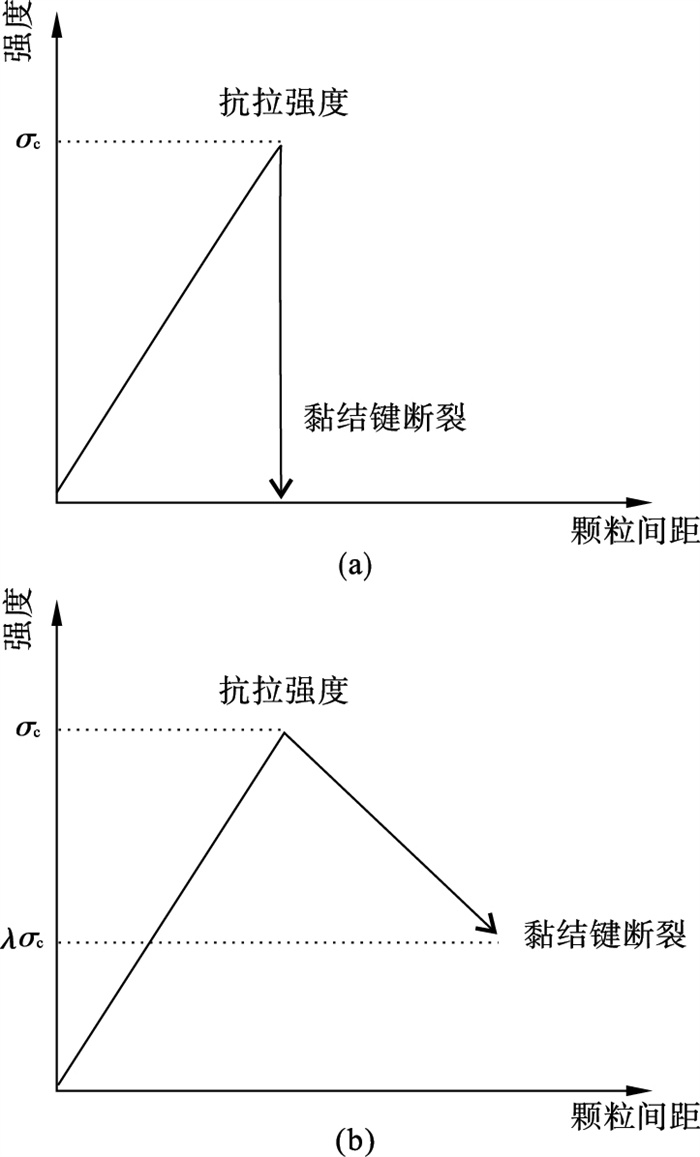 | 图 12 两种黏结键的力学行为[32]Fig.12 Mechanical behavior of two kinds of bonding bond[32] (a)—PBM；(b)—SBM. |
对于SBM来说, 通过引入软化系数, 使黏结键在作用力超过其抗拉强度时并未直接移除, 而是进入一个软化状态(图 12b).这个软化状态使粒间拉力超过黏结抗拉强度时黏结键仍有部分承载力, 其可显著增强试样的抗拉强度和无侧限抗压强度, 使较小的黏结强度参数即可模拟获得较大的无侧限抗压强度和抗拉强度.
无侧限压缩中接触黏结抗拉强度和接触黏结抗剪强度相结合共同支撑试样, 如图 13所示, 而抗拉试验中仅有接触黏结抗拉强度决定试样强度.当PBM试样接触黏结抗剪强度过高时, 在无侧限压缩过程中, 试样的破坏将以拉伸破坏为主, 并不能无限提高试样的抗压强度, 因此, PBM试样的压拉比始终维持在一个范围内.SBM模型则引入软化系数来增强试样抗拉和抗压强度, 但抗压强度增加幅度较抗拉强度大, 进而使试样的压拉比增大.
图 13(Fig. 13)
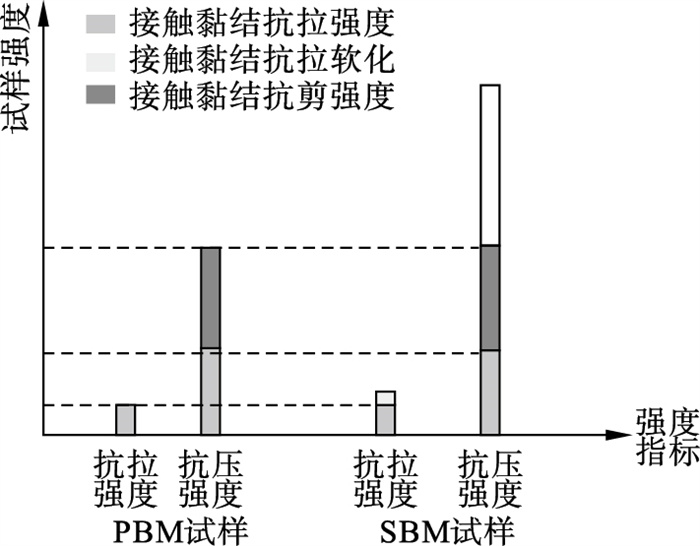 | 图 13 PBM和SBM试样压拉比的影响示意图Fig.13 Schematic of the influence of UCS/TS ratio of PBM and SBM specimen |
由于目前尚未见有关软化黏结接触模型SBM的研究, 且本文并未对细观参数间的复杂作用机理进行深入探究, 因此, 压拉比的范围较小.本文后续将结合典型岩石的无侧限压缩和抗拉试验, 深入研究SBM细观参数对试样力学性质的影响机制, 进一步优化试样压拉比.
3.3 讨论对于PBM模型从细观角度而言, 其黏结键间作用力在超过黏结键的抗拉强度之后会立即跌落至0, 导致黏结失效.对于PBM模型在反映试样宏观力学特性中, 则是达到峰值强度之后应力的迅速跌落, 难以模拟部分软岩应力-应变关系的峰后延性行为.而对于SBM模型而言, 在未激活软化之前, 其表现为PBM的性质, 因此可以模拟典型砂岩应力-应变行为; 激活软化后, 在黏结键间作用力超过其抗拉强度之后, 黏结键间作用力并未直接跌落至0, 而是以一个恒定的速率跌落至某一数值, 软化期间颗粒间应力持续存在, 反映到宏观试样性质上, 在试样应力达到峰值强度之后不会造成应力的突然跌落, 因此, 可模拟部分软岩应力-应变关系的峰后延性行为.
针对李桂臣等[32]研究中所采用的两个泥岩试样, 采用本文中的基于SBM的刚性块体模型和基于PBM的球形颗粒模型进行数值模拟, 所得应力应变关系如图 14所示.从图 14中可以看出, 软化系数的引入可以有效减少试样的峰后脆性破坏模式, 从而使试样从峰后脆性向峰后延性转变.
图 14(Fig. 14)
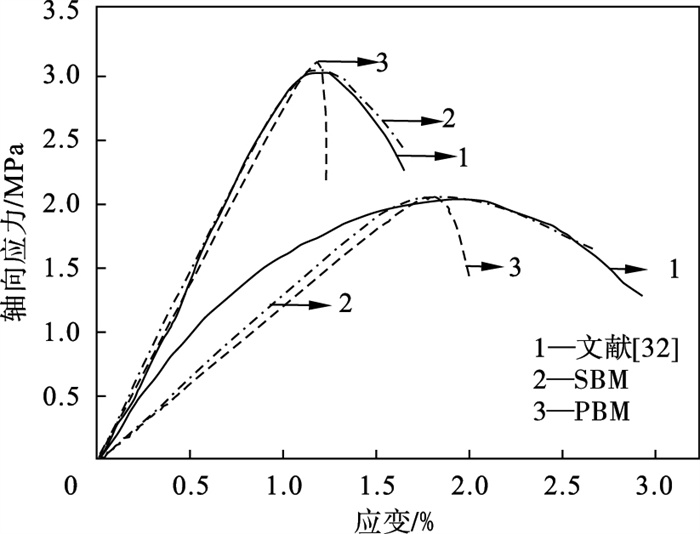 | 图 14 泥岩物理试验和数值模拟应力应变关系Fig.14 Experimental and numerical stress-strain curves of mudstone |
脆性、延性的材料特性最初属于金属材料力学范畴, 随后扩展到岩石材料力学中.脆性、延性性质的差异更多地体现在细观结构构造的差异中, 同时脆性、延性的定义和界定也不仅是峰后, 发生破坏或者达到峰值强度前的变形量相差显著[33].
4 结论1) 相较于球形颗粒试样, 基于Voronoi剖分生成的刚性块体试样颗粒形状各异, 更符合砂岩等含结晶结构岩石中矿物的不规则晶粒形状.
2) 相较于平行黏结接触模型仅能模拟出3~7的压拉比, 软化黏结接触模型能够模拟出砂岩更大的压拉比, 更能真实表征砂岩在多应力路径下的力学特性.
3) 相较于传统的球形颗粒数值模拟方法, 刚性块体间配位数的增加提高了颗粒间的自锁效应, 使颗粒间的接触行为更符合真实砂岩晶粒间的力学行为, 进而能模拟出砂岩典型的剪切破坏模式.
参考文献
| [1] | Li J, Heinz K, Thomas F.H. Voronoi-based DEM simulation approach for sandstone[J]. Rock Mechanics and Rock Engineering, 2017, 50: 2749-2761. DOI:10.1007/s00603-017-1257-4 |
| [2] | 金爱兵, 刘佳伟, 赵怡晴, 等. 卸荷条件下花岗岩力学特性分析[J]. 岩土力学, 2019, 40(sup1): 459-467. (Jin Ai-bing, Liu Jia-wei, Zhao Yi-qing, et al. Mechanical characteristics analysis of granite under unloading conditions[J]. Rock and Soil Mechanics, 2019, 40(sup1): 459-467.) |
| [3] | Yang S Q, Yin P F, Zhang Y C, e t, a l. Failure behavior and crack evolution mechanism of a non-persistent jointed rock mass containing a circular hole[J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 114: 101-121. DOI:10.1016/j.ijrmms.2018.12.017 |
| [4] | 王本鑫, 金爱兵, 赵怡晴, 等. 基于CT扫描的含非贯通节理3D打印试样破裂规律试验研究[J]. 岩土力学, 2019, 40(10): 3920-3927, 3936. (Wang Ben-xin, Jin Ai-bing, Zhao Yi-qing. Fracture law of 3D printing specimen with non-consecutive joints based on CT scanning[J]. Rock and Soil Mechanics, 2019, 40(10): 3920-3927, 3936.) |
| [5] | Abubakar A, Dow RS. Simulation of ship grounding damage using the finite element method[J]. International Journal of Solids and Structures, 2013, 50(5): 623-636. DOI:10.1016/j.ijsolstr.2012.10.016 |
| [6] | Edelbro C. Different approaches for simulating brittle failure in two hard rock mass cases: a parametric study[J]. Rock Mechanics and Rock Engineering, 2010, 43(2): 151-165. DOI:10.1007/s00603-008-0025-x |
| [7] | Chen C S, Pan E, Amadei B. Fracture mechanics analysis of cracked discs of anisotropic rock using the boundary element method[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(2): 195-218. DOI:10.1016/S0148-9062(97)00330-6 |
| [8] | Xu W J, Wang S, Zhang H Y, et al. Discrete element modelling of a soil-rock mixture used in an embankment dam[J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 86: 141-156. DOI:10.1016/j.ijrmms.2016.04.004 |
| [9] | Han Z Y, Weatherley D, Puscasu R. Projected area-based strength estimation for jointed rock masses in triaxial compression[J]. Computers and Geotechnics, 2018, 104: 216-225. DOI:10.1016/j.compgeo.2018.08.020 |
| [10] | Wan W, Liu J, Zhao Y L, e t, a l. The effects of the rock bridge ligament angle and the confinement on crack coalescence in rock bridges: an experimental study and discrete element method[J]. Comptes Rendus Mecanique, 2019, 347: 490-503. DOI:10.1016/j.crme.2018.12.006 |
| [11] | Gui Y L, Zhao Z Y, Zhang C S, et al. Numerical investigation of the opening effect on the mechanical behaviours in rocks under uniaxial loading using hybrid continuum-discrete element method[J]. Computers and Geotechnics, 2017, 90: 55-72. DOI:10.1016/j.compgeo.2017.05.021 |
| [12] | Cundall P A, Strack O D L. A discrete numerical model for granular assemblies[J]. Geótechnique, 1979, 29(1): 47-65. DOI:10.1680/geot.1979.29.1.47 |
| [13] | Potyondy D O, Cundall P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329-1364. DOI:10.1016/j.ijrmms.2004.09.011 |
| [14] | 杨振伟, 金爱兵, 周喻, 等. 伯格斯模型参数调试与岩石蠕变特性颗粒流分析[J]. 岩土力学, 2015, 36(1): 240-248. (Yang Zhen-wei, Jin Ai-bing, Zhou Yu, et al. Parametric analysis of Burgers model and creep properties of rock with particle flow code[J]. Rock and Soil Mechanics, 2015, 36(1): 240-248.) |
| [15] | 李露露, 高永涛, 周喻, 等. 单轴压缩条件下含三叉裂隙类岩石试样力学特性的细观研究[J]. 岩土力学, 2018, 39(10): 3668-3676. (Li Lu-lu, Gao Yong-tao, Zhou Yu, et al. Meso-scale modelling mechanical properties of rock-like material containing trident cracks under uniaxial compression[J]. Rock and Soil Mechanics, 2018, 39(10): 3668-3676.) |
| [16] | 黄彦华, 杨圣奇, 鞠杨, 等. 岩石巴西劈裂强度与裂纹扩展颗粒尺寸效应研究[J]. 中南大学学报(自然科学版), 2016, 47(4): 1272-1281. (Huang Yan-hua, Yang Sheng-qi, Ju Yang, et al. Study on particle size effects on strength and crack coalescence behavior of rock during Brazilian splitting test[J]. Journal of Central South University(Science and Technology), 2016, 47(4): 1272-1281.) |
| [17] | He M C, Miao J L, Feng J L. Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47: 286-298. DOI:10.1016/j.ijrmms.2009.09.003 |
| [18] | Liu H Y, Roquete M, Kou S Q, et al. Characterization of rock heterogeneity and numerical verification[J]. Engineering Geology, 2004, 72(1/2): 89-119. |
| [19] | Potyondy D O. A grain-based model for rock: approaching the true microstructure[C]// Proceedings of the Rock Mechanics in the Nordic Countries. Kongsberg, 2010: 225-234. |
| [20] | Ivars D M, Pierce M E, Darcel C, et al. The synthetic rock mass approach for jointed rock mass modelling[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(2): 219-244. DOI:10.1016/j.ijrmms.2010.11.014 |
| [21] | Wu S C, Xu X L. A study of three intrinsic problems of the classic discrete element method using flat-joint model[J]. Rock Mechanics and Rock Engineering, 2016, 49: 1813-1830. DOI:10.1007/s00603-015-0890-z |
| [22] | Paul M, Evert H. Estimating the geotechnical properties of heterogeneous rock masses such as flysch[J]. Bulletin of Engineering Geology and the Environment, 2001, 60(2): 85-92. DOI:10.1007/s100640000090 |
| [23] | Scholtès L, Donzé F V. A DEM model for soft and hard rocks: role of grain interlocking on strength[J]. Journal of the Mechanics and Physics of Solids, 2013, 61(2): 352-369. DOI:10.1016/j.jmps.2012.10.005 |
| [24] | Ghazvinian E, Diederichs M S, Quey R. 3D random Voronoi grain-based models for simulation of brittle rock damage and fabric-guided micro-fracturing[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2014, 6(6): 506-521. DOI:10.1016/j.jrmge.2014.09.001 |
| [25] | Zhou W, Ji X, Ma G, et al. FDEM simulation of rocks with microstructure generated by Voronoi grain-based model with particle growth[J]. Rock Mechanics and Rock Engineering, 2020, 53: 1909-1921. DOI:10.1007/s00603-019-02014-0 |
| [26] | Chang C S, Misra A, Xue J H. Incremental stress-strain relationships for regular packings made of multi-sized particles[J]. International Journal of Solids and Structures, 1989, 25(6): 665-681. DOI:10.1016/0020-7683(89)90032-2 |
| [27] | Itasca Consulting Group Inc. PFC 6.0 documentation[EB/OL]. (2019-01-01)[2020-11-06]. http://docs.itascacg.com/pfc600/pfc/docproject/index.html. |
| [28] | Huang Y H, Yang S Q, Ranjith P G, et al. Strength failure behavior and crack evolution mechanism of granite containing pre-existing non-coplanar holes: experimental study and particle flow modeling[J]. Computers and Geotechnics, 2017, 88: 182-198. DOI:10.1016/j.compgeo.2017.03.015 |
| [29] | 吴阳春, 郤保平, 王磊, 等. 高温后花岗岩的物理力学特性试验研究[J]. 中南大学学报(自然科学版), 2020, 51(1): 193-203. (Wu Yang-chun, Xi Bao-ping, Wang Lei, et al. Experimental study on physico-mechanical properties of granite after high temperature[J]. Journal of Central South University(Science and Technology), 2020, 51(1): 193-203.) |
| [30] | 许宝田, 张莉萍, 燕晓莹, 等. 空隙特征对砂岩水致劣化规律的影响[J]. 岩土力学, 2019, 40(2): 561-569. (Xu Bao-tian, Zhang Li-ping, Yan Xiao-ying, et al. Effect of void characteristics on deteriorating rules of sandstone due to water[J]. Rock and Soil Mechanics, 2019, 40(2): 561-569.) |
| [31] | 许学良. 脆性岩石抗拉特性及其破裂机制的试验与细观模拟研究[D]. 北京: 北京科技大学, 2017. (Xu Xue-liang. Research on the experiment and meso-simulation of tensile characteristics and its fracture mechanism of brittle rock[D]. Beijing: University of Science and Technology Beijing, 2017. ) |
| [32] | 李桂臣, 孙长伦, 何锦涛, 等. 软弱泥岩遇水强度弱化特性宏细观模拟研究[J]. 中国矿业大学学报, 2019, 48(5): 935-942. (Li Gui-chen, Sun Chang-lun, He Jin-tao, et al. Macro and meso scale simulation study of the strength-weakening property of soft mudstone affected by water[J]. Journal of China University of Mining and Technology, 2019, 48(5): 935-942.) |
| [33] | 朱勇, 周辉, 张传庆, 等. Hoek-Brown准则的脆性不等式及其对GSI取值的限制[J]. 岩石力学与工程学报, 2019, 38(sup2): 3412-3419. (Zhu Yong, Zhou Hui, Zhang Chuan-qing, et al. Brittle inequality of Hoek-Brown criterion and its applicability limit to GSI[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(sup2): 3412-3419.) |
