, 潘恒彦 东北林业大学 交通学院, 黑龙江 哈尔滨 150040
收稿日期：2020-12-18
基金项目：国家重点研发计划项目(2018YFB1600900)；国家自然科学基金重点资助项目(51638004)。
作者简介：裴玉龙(1961-)，男，黑龙江桦川人，东北林业大学教授，博士生导师。
摘要：为提高常规公交的出行服务质量, 建立了考虑车内拥挤状态的公交弹性发车间隔优化模型.通过量化车内拥挤状态, 给出各拥挤状态下的乘车成本; 建立了线路各区间的拥挤状态转移函数.考虑乘客的车内拥挤状态感知, 建立站点乘客随时间的上下车数量的度量模型; 构建乘客出行成本度量模型, 以乘客出行成本与车辆运营亏损之和最小化为目标函数, 建立了公交弹性发车间隔优化模型; 并设计遗传算法对模型进行求解.结果表明: 优化模型能够有效降低出行成本.模型对等待成本有着“补短板”效果, 对乘车成本有着“削峰”效果, 即通过增加乘客到站量小站点的等待成本, 降低乘客到站量大站点的等待成本, 削弱乘车成本峰值的手段, 达到总成本最低的效果.
关键词：交通工程城市公共交通遗传算法弹性发车间隔车内拥挤状态站点等待时间
Optimization of Buses' Flexible Departure Intervals Considering Crowdedness State
PEI Yu-long, YANG Shi-jun
, PAN Heng-yan School of Traffic and Transportation, Northeast Forestry University, Harbin 150040, China
Corresponding author: YANG Shi-jun, E-mail: ysj0826@nefu.edu.cn.
Abstract: In order to improve the travel service quality of conventional bus, an optimization model of buses' flexible departure intervals considering crowdedness state in the bus is established. By quantifying the crowdedness state in the bus, the travel cost under each crowdedness state is given, and the crowdedness state transfer function of each section of the line is established. Considering passengers'perception of the crowdedness state in the bus, the measurement model of the number of passengers getting on and off the bus over time is established; the travel cost measurement model is established, and the optimization model of buses' flexible departure intervals is established with the objective function of minimizing the sum of passenger travel cost and vehicle operating loss; and the genetic algorithm is designed to solve the model. The results show that the optimization model can effectively reduce the travel cost. The model has a "short board filling" effect on the waiting cost, and a "peak cutting" effect on the travel cost. That is, by increasing the waiting cost of the stop with fewer passenger arrivals, reducing the waiting cost of the stop with more passenger arrivals and weakening the peak value of the travel cost, the total cost can be minimized.
Key words: traffic engineeringurban public transportgenetic algorithmflexible departure intervalcrowdedness state in the buswaiting time at the stop
行程时间可靠程度及车内拥挤程度是公交服务水平的重要评价指标, 出行等待时间的长短及在车内的拥挤感受会影响乘客的出行选择.乘客出行过程中, 在站等待的感受及对车内空间舒适度的感受不容忽视.在倡导公共交通出行及绿色出行的当下, 提高公交服务水平、降低乘客的出行成本尤为重要.
在车内拥挤程度分析的相关研究中, Li等[1]对地铁出行乘客的主观车内拥挤感受与实际拥挤程度的差异性展开分析；Wardman等[2]指出地铁的座位占有情况对乘客的出行过程选择产生影响; 王殿海等[3]基于条件价值法, 分析了时间价值与车内拥挤程度的内在关系, 并依据杭州市进行案例分析, 指出拥挤成本随着拥挤程度而增加, 同时给出了各种承载率下的乘客感受; 陈亮等[4]基于乘客车内感知, 建立了发车间隔优化模型, 研究通过引入“出行者收入”变量, 得到不同拥挤程度下乘客的乘车感知价值, 运用“立席密度”将车内拥挤程度分为4个等级; 邵敏华等[5]在调查数据的基础上, 对车内拥挤程度进行分级, 并基于Binary logit模型分析不同拥挤状态对乘客出行抉择的影响, 给出了拥挤程度与时间价值的函数关系.在乘客的候车感知相关研究中, 吕慎等[6]建立了非集计模型对公交候车时间进行服务等级划分, 总结了不同候车时间下乘客的心理与情绪; Soza等[7]考虑公交出行时间、等待时间和乘客舒适度感知, 分析了出行时间可靠性对乘客出行方式选择的影响; Fan等[8]通过调查数据分析, 发现乘客感知候车时间大约是实际等待时长的1.21倍.
公交调度及发车间隔优化方面, Larrain等[9]对公交拥挤以及非拥挤状态下进行车辆调度优化, 求解线路的最优发车频次; Shang等[10]建立了考虑乘客等待成本的公交车辆调度模型; Feng等[11]以公交运营利润最大、乘客换乘等待时间最小及乘客出行费用最小建立了公交线路发车间隔多目标优化模型; Toli等[12]考虑乘客等待时间和满载率, 设计了公交时刻表优化模型.
国内外****在乘客的拥挤感受及在站等待时间感知方面获得了较为显著的成果; 同时在公交调度优化方面也获得了丰富成果, 但将乘客的车内拥挤感受及在站等待感知作为影响因素, 进行公交发车间隔优化的研究相对欠缺.本文在相关研究的基础上, 将车内实际拥挤状态、乘客在站等待时间换算成乘客的实际出行成本, 并将企业运营成本考虑其中, 建立总成本最小的公交弹性发车间隔优化模型.
1 车内拥挤状态转移模型1.1 车内拥挤程度量化承载率LF常用于车内拥挤程度的评价[13], 并作为公交服务水平的划分依据.站立密度为站立乘客数量与可站立面积的比值, 车内乘客对拥挤的最直观感受来自于车内的站立密度, 同时站点侯车乘客也会根据车内站立密度做出是否上车的抉择.参照文献[4]的相关研究结论, 按每个乘客站立面积为0.125 m2计算, 站立密度与承载率LF相互转换的公式如(1)所示, 拥挤服务质量如表 1所示.
表 1(Table 1)
 表 1 拥挤服务质量分类Table 1 Classification of crowd QoS
| 表 1 拥挤服务质量分类 Table 1 Classification of crowd QoS |
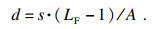 | (1) |
1.2 乘车拥挤成本分析车内拥挤情况下乘客会将自身的乘车成本“夸大”, 感觉在车内的时间较长, 车内的拥挤状态常给乘客带来“额外的出行成本”.文献[5]得出不同承载率LF下的拥挤成本, 假设LF < 0.8时的出行成本为E0, 则不同承载率LF下的出行成本如表 2所示.
表 2(Table 2)
表 2 乘客乘车拥挤成本Table 2 Crowdedness cost of bus passengers
| 表 2 乘客乘车拥挤成本 Table 2 Crowdedness cost of bus passengers |
1.3 拥挤状态转移函数如图 1所示, 假设一辆公交车依次经过行驶线路的站点1, 2, 3, 4, 5, 6.1为始发站, 6为终点站, 则存在5个区间段; 其中qiup为第i个站点上车人数, 终点站无乘客上车; qidown为第i个站点下车人数, 始发站无乘客下车; qise为区间段i的载客人数.则区间段i的载客人数qise如式(2)所示.可知区间i的载客量qise, 可由上区间客流量qi-1se与区间初始站点上、下车人数qiup, qidown决定.车辆载客状态转移方程见式(3)，式(4)为载客量qise与承载率LF的转换关系, 结合式(3)得到车内拥挤状态的转移方程式(5).
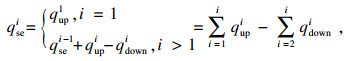 | (2) |
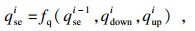 | (3) |
 | (4) |
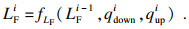 | (5) |
 | 图 1 区间载客量变化示意Fig.1 Schematic diagram of passengers change in the section |
2 弹性发车间隔优化模型构建2.1 车辆到站时间计算车辆在运行时, 途经不同的路段有不同的实时速度.同时, 早高峰、晚高峰及平峰时段公交车辆的营运速度也有差异.图 2为弹性发车间隔下的公交车辆到站时间示意, Gst(1, 2, …, I)为站点集合，I为站点数; Gbu(1, 2, …, J)为某一时段内发车计划集合, J为某一时段内从始发站点发出的公交班次数.以第1班次公交车辆Bus1的发车时刻为时间起点t10=0, 车辆到达第2个公交站的时间为始发时间与路段耗时l1/v11的加和, 第1班次公交车到达第i处公交停靠站的时间为车辆在第i-1处公交停靠站到站时间t1i－1与本段耗时
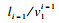
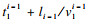
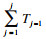
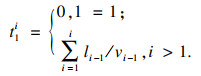 | (6) |
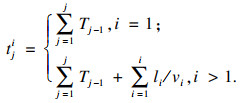 | (7) |
 | 图 2 车辆到站时间示意Fig.2 Schematic diagram of vehicle arrival time |
2.2 考虑弹性发车间隔的站点上下客人数计算2.2.1 站点上客人数文献[5]将SP与RP进行结合, 用一张问卷调查乘客的车内拥挤程度主观感受及选择意愿.本文采用类似的跟车调查方法.乘客根据对车内拥挤的主观感受, 并结合自身的出行时间(高峰或平峰)进行“上车”或“继续等待第2班公交车的选择, 跟车人员记录车内的人数, 估算出调查时刻的乘客站立密度, 基于SP与RP调查的乘客选择统计结果如表 3所示.在平峰时段, 乘客对车内拥挤的忍受程度有所下降, 当出现无座位的现象时, 乘客在QoS=D的上车概率为0.91;在QoS=E时, 上车概率为0.76, 当到达QoS=F时, 上车概率仅为0.52.在早晚高峰时段时, 乘客的时间紧迫感强, 对车内拥挤的忍受程度提高.设站点乘客的上车概率为车内拥挤程度的分段函数, 函数表达见式(8).
表 3(Table 3)
表 3 考虑车内拥挤状态的乘客上车概率统计Table 3 Probability statistics of passengers getting on the bus considering the crowdedness state?
| 表 3 考虑车内拥挤状态的乘客上车概率统计 Table 3 Probability statistics of passengers getting on the bus considering the crowdedness state? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
对于班次j, 各站点上车人数与乘客的到达率呈正比.文献[14]提到站点乘客的到达概率分布, 但本文不做重点考虑.本文假设乘客均匀到达, 若不存在乘客放弃等待, 则随时间的推移, 侯车人数不断增多.到站车辆的拥挤程度会对侯车乘客的上车与否产生影响, 当车内拥挤程度大于自身乘车意愿的阈值时, 乘客会选择放弃上车而二次侯车.结合实际情况, 乘客第二次侯车时对拥挤的忍耐阈值提高, 会选择接受车内的拥挤程度而直接上车, 不再进行第三次等待, “支付”拥挤成本而不再支付额外的“等待成本”.因此本文假设乘客最多侯车2次, 超过2次侯车时, 乘客不受车内拥挤程度的影响, 默认上车.第j班车到达i点时, 上车乘客数由式(9)表示, 本次上车乘客数为可忍受车辆拥挤程度乘客数
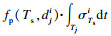
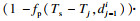
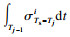
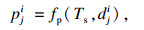 | (8) |
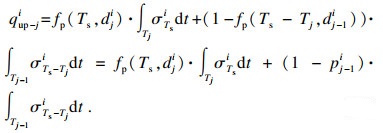 | (9) |
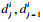
2.2.2 站点下客人数同一公交线路各站点的出行分布随出行时段的不同而变化, 各站点的下车人数与上游站点乘客的出行分布有关.班次j第i个站点的下车人数由两部分构成, 第一部分为本班次j站点i上游站点集合
 | (10) |
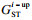
2.3 乘客出行成本计算本文将乘客出行成本分为等待成本与拥挤成本.文献[6]指出, 不同的等待时长会引起乘客心理感受的变化, 侯车时间: 0~6?min, 乘客心态平稳; 6~15?min, 乘客开始焦虑; 15~35?min, 乘客内心焦躁程度增加, 考虑放弃等待; >35?min时, 乘客放弃等待而改变出行方式.假设0~6 ?min侯车时间内, 乘客的等待成本为Ej-0, 则各侯车时长区间乘客的等待成本见表 4.第j班次的乘客等待时间成本见式(11), 前文提到当等待时间>35 ?min时, 乘客会选择放弃等待而改变交通方式.为保证无乘客放弃等待, 本文假设Tj+Tj-1 < 35?min, 即乘客等待两辆公交车的时长不大于35 ?min.乘客的拥挤成本见式(12), 乘客出行总成本为等待成本与拥挤成本之和, 见式(13).
表 4(Table 4)
表 4 公交乘客等待成本Table 4 Waiting cost of bus passengers
| 表 4 公交乘客等待成本 Table 4 Waiting cost of bus passengers |
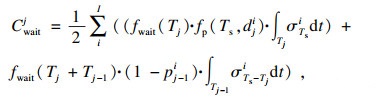 | (11) |
 | (12) |
 | (13) |
2.4 弹性发车间隔优化模型建立本文中的乘客出行成本由站点等待成本及车辆运行过程中的拥挤成本构成, 优化模型要实现乘客出行成本的最小化外, 需考虑公交车辆运营的实际情况, 优化模型如下.式(14)表示以乘客出行成本最小化与公交企业亏损最小化为优化模型; 式(15)表示车辆发车间隔取正整数; 式(16)表示前后两次的发车间隔之和小于35?min, 以保证无乘客放弃等待; 式(17)表示每辆公交车在首末站均能得到30?min的保修时间; 式(18)表示线路运营速度为时间的函数, 高峰与平峰时段的运营速度存在差异.人工成本、燃油成本等直接费用及车辆的折旧成本等间接费用构成了车辆的营运成本[15], 公交事业为社会福利性产业, 国内绝大多数公交企业为亏损运营, 需要国家的资助补贴.班次j的单线亏损量由式(19)所示.
 | (14) |
 | (15) |
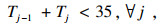 | (16) |
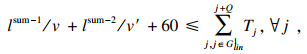 | (17) |
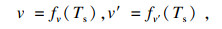 | (18) |
 | (19) |
3 模型求解遗传算法的整体搜索策略与优化搜索方法不依靠梯度信息及其他辅助知识, 仅需要确定影响搜索方向的目标函数与适应度函数.遗传算法为复杂问题的求解提供了一个大的通用框架, 对多种问题具有鲁棒性, 不仅仅局限于某个领域问题的求解.遗传算法在函数优化、组合优化及生产调度优化问题上得到了广泛的应用.遗传算法操作由“选择”、“交叉”及“变异”三个基本遗传算子构成.
3.1 选择“选择”因其“把优化的个体遗传给下一代”或者“通过交叉产生新一代”的特点, 又称为“再生算子”, 选择的过程是建立在个体在群体的适应度评估基础上进行的.本文采用轮盘赌选择法进行选择, 轮盘赌选择法是最常用的选择方法, 假设群体中共n个体, 某一个体i的适应度为fi, 则个体i被选择的概率为
3.2 交叉遗传基因的重组在生物进化过程中起核心作用, 两个父代个体的部分基因相互替代产生新的个体, 进而能够实现适应度函数值的飞跃.本文采用单点交叉的方式进行交叉运算, 在个体遗传中随机产生一个交叉点, 交叉点前后个体的某一部分进行交换, 进而产生新个体.当交叉概率取值过大时, 随机性太大, 会破坏有利基因的保留; 而当交叉概率取值过小时, 不能有效地更新种群.交叉概率一般取值0.4~0.99, 本文取交叉概率为0.7, 并采用实数编码形式, 为保证满足各班次发车间隔加和为60?min的限制条件, 设计具体交叉算法的技术路线如图 3所示, 其中freq为发车总班次.
图 3(Fig. 3)
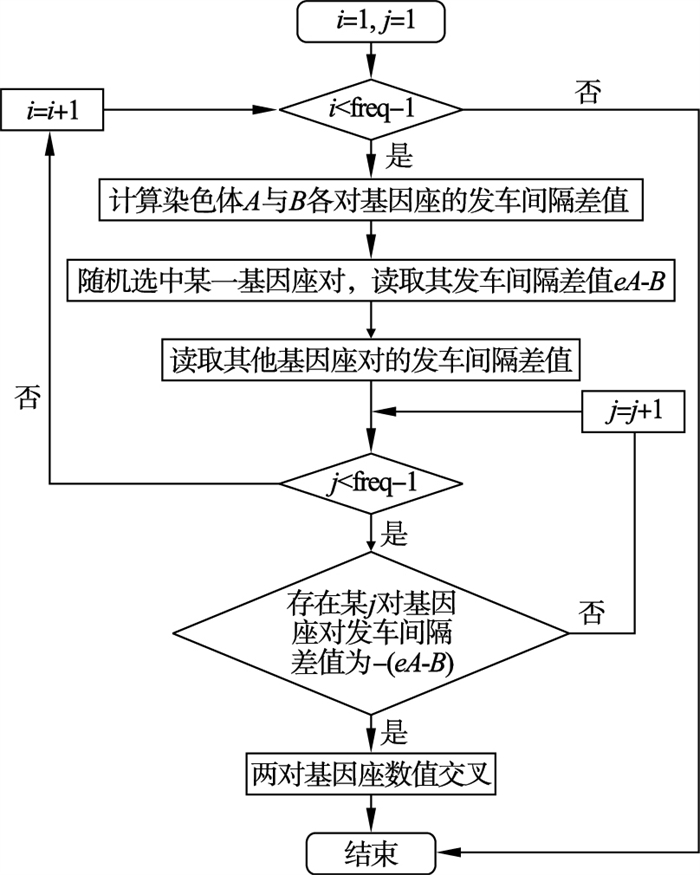 | 图 3 交叉算法技术路线Fig.3 Technical route of crossover algorithm |
3.3 变异变异是对群体中个体的基因值作变动, 从个体码串中随机挑选几个基因座, 并对基因座的基因值做变动.具体操作如下所示, 有“-”下标的为基因发生变异的基因座, 变异概率取值过小, 会造成有利基因的丢失; 而取值过大, 会造成高阶模式被损坏的概率变大.变异概率的取值在0.000?1~0.2, 本文取交叉概率为0.005并采用实数编码形式.为保证各班次发车间隔加和为60?min的限制条件, 设计变异技术路线如图 4所示.
图 4(Fig. 4)
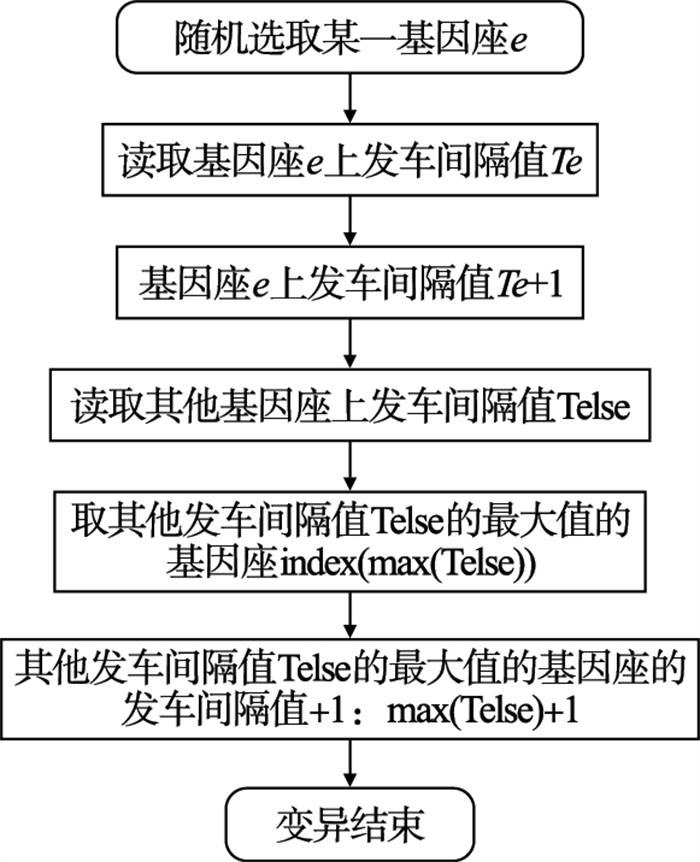 | 图 4 变异算法技术路线Fig.4 Technical route of mutation algorithm |
3.4 终止条件当个体适应度函数值不再提高, 或者达到某种预先设定值时, 遗传算法终止.预设代数一般取100~500代, 本文设定最大迭代数为300，运用遗传算法对弹性发车间隔优化模型进行求解，群体的维度是固定的, 在同一维度下找到最优序列.因此在发车间隔优化模型求解前需确定群体的最优维度, 即在确定的优化时间单元下发车班次数量.计算之前需确定种群的规模, 规模太小会出现因为近代交配而产生携带病态基因的子代, 种群规模太大时, 会造成迭代次数过高, 计算效率低下.本文将种群规模设定为200.优化模型算法技术路线如图 5所示.
图 5(Fig. 5)
 | 图 5 优化模型算法技术路线Fig.5 Technical route of optimization model algorithm |
4 案例分析本文以哈尔滨市16路公交线(省康复中心—通江湿地公交换乘枢纽)为研究对象, 进行发车间隔优化, 通过驻站与跟车调查获取所需数据.线路共29个停靠站点, 每个停靠站安排1位驻站调查人员, 对16路公交车每班次在停靠站的上车人数与下车人数进行统计, 每班次公交车安排2名跟车调查人员, 其中1名调查人员对上车乘客的终点站进行询问并记录, 获取16路公交乘客的出行起讫点, 另外1名调查人员对乘客的上车概率进行询问.调查时间为期2?d, 分别为星期日与星期一, 调查线路有75路、101路、16路、56路等.鉴于调查数据结果的完整性与研究目的, 本文选取星期一16路公交车的调查数据.根据本次调查的公交车辆实际运行情况, 取早高峰时段全部班次车辆的营运速度的均值为早高峰公交线路营运速度, 并设为分析参数进行优化运算, 平峰时段与晚高峰时段的营运速度均以上述方法得到.早、晚高峰营运速度分别取13.5, 15.3?km/h, 平峰取18.0?km/h.
文献[3]中, 根据《杭州市年度交通发展报告》得出居民乘坐公交的平均耗时, 并结合人均工资水平, 折算出小时工资收入, 进而推算出出行时间成本.本文采用相同的方法, 根据哈尔滨市居民人均年收入水平以及出行情况, 取Ej-0=E0≈6.7元/h.以相等的发车间隔为初始条件, 各时段最优的发车班次数以及总成本如图 6所示, 可知7:30-8:30的早高峰时段发车班次取15, 12:30-13:30平峰时段发车班次取8, 16:30-17:30的晚高峰时段发车班次取12.
图 6(Fig. 6)
 | 图 6 各时段最优发车班次数及成本情况Fig.6 Optimal number of departure shifts and cost in each period |
本文对上述3时段的发车间隔进行优化, 线路各站点的乘客到站率如图 7所示.各时段站点客流分布情况如图 8所示.各时段的群体粒子维度分别取15, 8, 12, 即早高峰时段、平峰时段及晚高峰时段发车班次分别取15, 8, 12次.各个时段的迭代结果如表 5所示, 早高峰、平峰、晚高峰时段目标函数最小值分别为: 4?315.5, 2?346.32, 3?900元.结果表明早高峰出行成本>晚高峰出行成本>平峰出行成本.
图 7(Fig. 7)
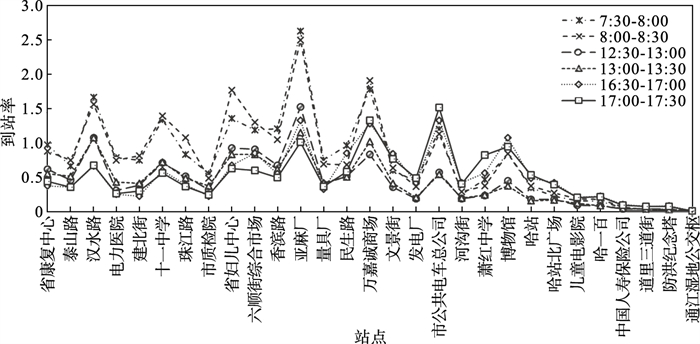 | 图 7 各时段线路站点乘客到站率Fig.7 Passenger arrival rate of the bus stop in each period |
图 8(Fig. 8)
 | 图 8 各时段站点客流分布情况Fig.8 Distribution of passenger flow of the bus stop in each period (a)—早高峰时段；(b)—平峰时段；(c)—晚高峰时段. |
表 5(Table 5)
表 5 各时段最优发车间隔Table 5 Optimal departure interval of each period ?
| 表 5 各时段最优发车间隔 Table 5 Optimal departure interval of each period ? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
各时段的最优解如表 5所示.各时段乘客的出行成本构成如表 6所示, 公交车运营成本经折合单位运营成本取30元/km.对于等待成本, 早高峰的发车间隔相对较短, 但站点乘客到站率高, 导致人均等待成本最低, 总等待成本最高; 平峰时段, 总体等待成本最少, 但由于车辆平均到站间隔较长, 人均等待成本最高; 晚高峰时段的车辆到站间隔相对较长, 乘客到站率相对适中, 使得总等待成本最高.由于早高峰时段的车辆拥挤程度最高, 使得其人均乘车成本最高, 平峰时段乘客的等待成本占比明显提高.
表 6(Table 6)
表 6 各时段总成本构成Table 6 Total cost composition of each period ?
| 表 6 各时段总成本构成 Table 6 Total cost composition of each period ? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
由图 9可以看出, 早高峰时段的发车间隔优化后, 线路前半段等待成本较高的站点(汉水路、十一中学、省妇儿中心), 等待成本下降程度较为明显; 香滨路—哈站区间的乘车成本降低明显, 且乘车成本基数越大, 下降程度越明显, 进而导致香滨路—哈站区间的车站乘客上车率的提高, 使得站点的等待成本有效降低.图 10中, 优化前等待成本较高的站点, 等待成本得到明显改善, 但部分原本等待成本低的站点, 等待成本反而提高, 可以看出: 优化模型通过牺牲部分站点的等待成本去弥补等待成本较高站点, 进而达到平峰时段整体优化, 总成本最低的效果, 由于平峰时段的整体客流量较低, 乘车成本降低的效果较低.图 11中, 晚高峰车内拥挤区间与早高峰不同, 文景街—哈一百区间乘客的乘车成本降低效果明显, 站点的乘客等待成本随之降低.优化模型对等待成本有着“补短板”效果, 对乘车成本有着“削峰”效果, 即通过增加乘客到站量小站点的等待成本, 降低乘客到站量大站点的等待成本, 以及削弱乘车成本峰值的手段, 达到总成本最低的效果.平峰时段(12:30-13:30)客流量少, 线路处于亏损状态或非盈利状态, 总计亏损约4元, 平均每条线路亏损0.5元.其他时段均能够盈利.
图 9(Fig. 9)
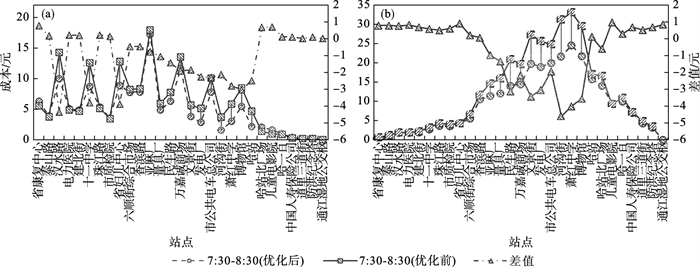 | 图 9 早高峰时段站点及区间优化效果Fig.9 Stop and interval optimization effect in moring peak period (a)—站点等待成本；(b)—区间乘车成本. |
图 10(Fig. 10)
 | 图 10 平峰时段站点及区间优化效果Fig.10 Stop and interval optimization effect in off-peak period (a)—站点等待成本；(b)—区间乘车成本. |
图 11(Fig. 11)
 | 图 11 晚高峰时段站点及区间优化效果Fig.11 Stop and interval optimization effect in evening peak period (a)—站点等待成本；(b)—区间乘车成本. |
5 结论1) 本文根据车内站立密度并结合乘客感受, 对车内的拥挤状态进行量化, 并给出各拥挤程度下的乘车成本以及拥挤成本占比; 构建了基于各站点上下客人数的区段载客量计算模型, 建立了拥挤状态转移函数.
2) 根据弹性发车间隔, 给出各班次车辆到站时间的计算模型; 将乘客对车内拥挤状态的感知考虑其中, 建立各站点的上下车人数的计算模型; 在分析乘客随等待时间而心理变化的前提下, 给出各等待区间下的等待成本.
3) 建立了基于遗传算法求解的弹性发车优化模型.以等发车间隔为初始条件, 得出各时段的群体粒子的维度, 即各时段的最优发车班次; 在此基础上, 运用遗传算法得出各时段的发车间隔序列.
4) 以哈尔滨市16路公交线路(省康复中心—通江湿地公交枢纽)为例, 对其发车间隔进行优化得出: 早高峰、平峰以及晚高峰时段的最优发车班次分别为15, 8, 12;与早晚高峰时段相比, 平峰时段的等待成本占比明显较高; 优化模型对等待成本有着“补短板”效果, 对乘车成本有着“削峰”效果, 即通过增加乘客到站率低站点的等待成本, 降低乘客到站率高站点的等待成本, 并削弱乘车成本峰值的手段, 达到总成本最低的效果.
参考文献
| [1] | Li Z, Hensher D A. Crowding in public transport: a review of objective and subjective measures[J]. Journal of Public Transportation, 2013, 16(2): 107-134. DOI:10.5038/2375-0901.16.2.6 |
| [2] | Wardman M, Murphy P. Passengers' valuations of train seating layout, position and occupancy[J]. Transportation Research Part A, 2015, 74: 222-238. |
| [3] | 王殿海, 叶盈, 朱文韬, 等. 基于条件价值法的公交车内拥挤成本测算模型[J]. 吉林大学学报(工学版), 2016, 46(1): 57-62. (Wang Dian-hai, Ye Ying, Zhu Wen-tao, et al. Estimation of crowding costs in bus based on contingent valuation method[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(1): 57-62.) |
| [4] | 陈亮, 冯柳, 李巧茹. 考虑在车感知价值的公交发车间隔计算模型[J]. 哈尔滨工业大学学报, 2018, 50(3): 150-155. (Chen Liang, Feng Liu, Li Qiao-ru. Bus departure interval model considering on-bus perceived value[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 150-155.) |
| [5] | 邵敏华, 李田野, 孙立军. 常规公交乘客对车内拥挤感知阻抗调查与建模[J]. 同济大学学报(自然科学版), 2012, 40(7): 1031-1034. (Shao Min-hua, Li Tian-ye, Sun Li-jun. Survey method and model of passengers' cost perception of crowding level in bus[J]. Journal of Tongji University(Natural Science), 2012, 40(7): 1031-1034. DOI:10.3969/j.issn.0253-374x.2012.07.012) |
| [6] | 吕慎, 陶流洋, 莫一魁. 通勤出行公交候车时间的服务等级划分和度量[J]. 交通运输系统工程与信息, 2015, 15(3): 190-195, 221. (Lyu Shen, Tao Liu-yang, Mo Yi-kui. Level of service classification and quantification for bus waiting time on commuting trip[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(3): 190-195, 221. DOI:10.3969/j.issn.1009-6744.2015.03.030) |
| [7] | Soza-Parra J, Raveau S, Muoz J C. Public transport reliability across preferences, modes, and space[J]. Transportation, 2021, 1-20. DOI:10.1007/s11116-021-10188-2 |
| [8] | Fan Y, Guthrie A, Levinson D. Waiting time perceptions at transit stops and stations: effects of basic amenities, gender, and security[J]. Transportation Research Part A, 2016, 88(6): 251-264. |
| [9] | Larrain H, Munoz J C, Giesen R. Generation and design heuristics for zonal express services[J]. Transportation Research Part E: Logistics & Transportation Review, 2015, 79: 201-212. |
| [10] | Shang H, Liu Y, Huang H, et al. Vehicle scheduling optimization considering the passenger waiting cost[J]. Journal of Advanced Transportation, 2019(3): 1-13. |
| [11] | Feng J, Ye Z, Wang C, et al. Optimising departure intervals for multiple bus lines with a multi-objective model[J]. IET Intelligent Transport Systems, 2018, 12(8): 809-818. DOI:10.1049/iet-its.2017.0049 |
| [12] | Toli I H, Nyarko E K, Ceder A A. Optimization of public transport services to minimize passengers′ waiting times and maximize vehicles′ occupancy ratios[J]. Electronics, 2020, 9(2): 360. DOI:10.3390/electronics9020360 |
| [13] | Board T. Transit capacity and quality of service manual[M]. 3th ed. Washington DC: TRB, 2013. |
| [14] | Ingvardson J B, Nielsen O A, Raveau S, et al. Passenger arrival and waiting time distributions dependent on train service frequency and station characteristics: a smart card data analysis[J]. Transportation Research Part C: Emerging Technologies, 2018, 90(5): 292-306. |
| [15] | Pena D, Tchernykh A, Nesmachnow S, et al. Operating cost and quality of service optimization for multi-vehicle-type timetabling for urban bus systems[J]. Journal of Parallel and Distributed Computing, 2019, 133: 272-285. DOI:10.1016/j.jpdc.2018.01.009 |
