周静茹, 刘鹏, 夏建业, 庄英萍
华东理工大学 生物反应器工程国家重点实验室，上海 200237
收稿日期：2020-08-10；接收日期：2020-11-16
基金项目：国家重点研究发展计划(No. 2019YFA0904300)，国家自然科学基金(No. 21776082) 资助
作者简介：夏建业??华东理工大学副教授，硕士生导师。兼任上海市微生物学会青委会副主任委员、上海市生物工程学会青委会副主任委员。先后承担“863计划”、科技支撑计划项目子课题、国家自然科学基金青年基金及面上基金等国家级项目。提出流场和生理结合的放大方法在多个企业成功应用。先后获得2011年国家科技进步二等奖、2014年产学研合作成果奖、2019年中国轻工联合会科技进步二等奖，以第一或通讯作者身份发表SCI论文20余篇.

摘要：基因组规模代谢网络模型(Genome-scale metabolic network model，GSMM) 正成为细胞代谢特性研究的重要工具，经过多年发展相关理论方法取得了诸多进展。近年来，在基础GSMM模型基础上，通过整合基因组、转录组、蛋白组和热力学数据，实现基于各种约束的GSMM构建，在基因靶点识别、系统代谢工程、药物发现、人类疾病机理研究等多个方面取得了进一步的发展和理论突破。文中重点综述包括转录组约束、蛋白组约束、以及热力学约束条件在GSMM中的实施方法、相应方法的不足及应用限制等。最后介绍了如何综合运用转录、蛋白及热力学约束，实现GSMM的全整合模型及其细化，并对基于约束的GSMM构建及应用前景进行了展望。
关键词：基因组规模代谢网络模型多组学热力学数学建模约束方法
Advances in the development of constraint-based genome-scale metabolic network models
Jingru Zhou, Peng Liu, Jianye Xia, Zhuang Yingping
State Key Laboratory of Bioreactor Engineering, East China University of Science and Technology, Shanghai 200237, China
Received: August 10, 2020; Accepted: November 16, 2020
Supported by: National Key Research and Development Program of China (No. 2019YFA0904300), National Natural Science Foundation of China (No. 21776082)
Corresponding author: Jianye Xia. Tel: +86-21-64253702; E-mail: jyxia@ecust.edu.cn.

Abstract: Genome-scale metabolic network model (GSMM) is becoming an important tool for studying cellular metabolic characteristics, and remarkable advances in relevant theories and methods have been made. Recently, various constraint-based GSMMs that integrated genomic, transcriptomic, proteomic, and thermodynamic data have been developed. These developments, together with the theoretical breakthroughs, have greatly contributed to identification of target genes, systems metabolic engineering, drug discovery, understanding disease mechanism, and many others. This review summarizes how to incorporate transcriptomic, proteomic, and thermodynamic-constraints into GSMM, and illustrates the shortcomings and challenges of applying each of these methods. Finally, we illustrate how to develop and refine a fully integrated GSMM by incorporating transcriptomic, proteomic, and thermodynamic constraints, and discuss future perspectives of constraint-based GSMM.
Keywords: genome-scale metabolic network modelmulti-omics, thermodynamicsmathematical modelingconstrained methods
代谢工程以基因工程为手段优化细胞的基因及调控过程从而提高细胞生产某特定产物的能力，自1991年由Bailey^[1]首次提出以来，一直探求从定量的角度提高工程化改造菌种的成功率，包括改造靶点的发现及预测等。早期，研究代谢反应速率与细胞表型关系的细胞代谢模型(Metabolic model，MM) 是人们研究细胞代谢特性非常有用的工具。但MM模型一般只以胞外宏观代谢速率的测定作为输入进行胞内代谢反应特性的研究，缺乏对于细胞代谢微观机理的洞察，在指导代谢工程靶点挖掘方面具有局限性。为了更有效地理解工业微生物胞内代谢微观机理，寻找潜在的代谢工程改造靶点，基因组规模代谢网络模型(Genome scale metabolic network model，GSMM)^[2]于“代谢工程”概念提出后的第8年也被提出，距今已有22年的发展历史。1999年，第一个GSMM模型被发表，用于研究流感嗜血杆菌的代谢基因型^[3]。随后，GSMM逐渐成为开展代谢工程的重要工具，包括对大肠杆菌Escherichia coli和酿酒酵母Saccharomyces cerevisiae等微生物的工程菌株设计和表型预测和分析^[4-6]等。2000年，第一个大肠杆菌GSMM发表，用于基因型-代谢表型的研究^[7]；酿酒酵母是第一个建立起GSMM的真菌，其GSMM于2003年首次被发表^[5]，随后经过不断重建和完善^[8-12]，到目前已升级到了Yeast 8.0^[13]，促进了从系统水平理解并促进酿酒酵母代谢工程改造的技术进步。GSMM还进一步被用于动植物细胞的代谢特性研究和药物靶点预测^[14-15]。
GSMM的发展和应用也使生物代谢特性研究逐渐从局部途径研究向整个代谢网络的系统性研究转变，然而由于缺乏对表达调控网络的充分理解，GSMM模型离真实的细胞网络结构还有很大距离，对细胞生理特性的考察还需要对酶功能和热力学机制等的深入挖掘。随着多组学测量技术的发展^[16-21]和针对不同组学或不同生物的多组学数据集的不断积累^[22-28]，建立GSMM基础上的基于约束的代谢建模(Constraint-based model，CBM)^[29]得到发展，包括基于基因表达的转录组约束、基于酶量水平的蛋白组学约束、基于热力学数据的约束GSMM建模理论与方法的出现。目前已经开发了多种计算平台将基于约束的方法应用于GSMM^[30-32]，这种通过数学不等式约束的方式将其他生物学数据与基因组数据集成，加强了模型从机制上对基因-表型关系的洞察与模拟。然而，这些基于各种约束条件的GSMM在模型构建方法和应用限制方面有很多相通之处但又各有特点，为此本文试图通过综述基于各种约束的GSMM的理论基础、构建方法、应用范围、限制条件等作一个梳理，从而为该领域的研究理清线索，为基于各种约束模型的构建提供一些参考。
1 基因组规模代谢网络模型基因组学的发展为生物体的代谢网络模型构建提供了遗传学基础，基因组注释定义了基因、酶及其催化反应之间的关系(即Gene-Protein-Reaction，GPR关系)。随着越来越多菌种基因组的成功注释，准确描述相应菌种GPR关系的基因组规模代谢网络模型相继提出，例如E. coli^{[4, 33]}、S. cerevisiae^[5]、枯草芽孢杆菌Bacillus subtilis^[34]等。这些先后提出的各种微生物的GSMM已在科学发现和工业应用领域得到广泛应用。主要功能可概括为两类：(1) 预测基因操控的有效靶点，从而有针对性地实现对菌株的高效理性设计与改造；(2) 预测细胞生理状态对于特定环境的响应，从工程的角度对菌株最优培养条件进行指导。在设计菌株方面，Yang等^[35]利用大肠杆菌GSMM进行预测，发现酶蛋白(HadA，PhaA) 基因的表达调节可以指导具有不同单体组分芳香族聚酯的生产，该预测结果在实验中得到很好的验证。在指导工业生产方面，GSMM也为不同环境条件下细胞代谢的生理状态变化提供了一个有用的工具，如洞察脂质代谢过程的条件依赖性等^[36]。
GSMM的模型构建与模拟是基于线性规划的相关理论与方法，利用代谢反应网络的计量关系式形成的线性方程组，对细胞内的代谢反应进行建模，从而形成基于代谢反应速率约束的线性规划模型^[37]。目前GSMM普遍基于两个物理假设：首先，要满足质量和电荷守恒，这保证了模型系统产生与消耗的总量相等。其次，系统必须处于代谢稳态(或拟稳态)，这意味着系统内代谢物浓度不随时间变化。这两个假设保证了GSMM的数学解析仍然以通量平衡分析(FBA)为基础，即代谢的数学表示是基于稳态质量平衡方程组(Sv=0) 和线性优化问题(LP)^[38]。基于FBA的GSMM数学模型一般表达为：

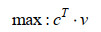(1)

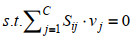(2)

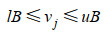(3)

其中S为化学计量矩阵，S_ij代表第i个反应中代谢物j的化学计量系数；v代表反应的通量向量；lB和uB分别代表对反应通量的最小和最大的边界约束；c是由0和1组成的常量向量，1代表该反应被设置为目标函数，通常目标函数设置为菌体(Biomass) 生成反应，并以该反应速率最大化为优化目标，利用有约束的最优化原理来是实现对代谢反应流量的估计。
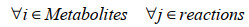2 基因组规模代谢网络模型中的约束条件目前，对代谢网络模型常见的约束条件主要包括化学计量系数、反应通量上下界和反应方向、转录组约束、蛋白酶约束、热力学约束等。质量与电荷守恒对反应化学计量进行约束；反应物或效应物浓度对反应产生动力学约束；相关基因的表达和转录过程指导酶蛋白的翻译与否从而对反应具有开关控制约束；酶蛋白水平对反应产生最大反应速率的约束；热力学则限制了反应的方向性^[39]。将表征这些限制因素的数据引入基因组规模代谢网络模型中能进一步提升模型预测结果的准确性，也更增强了对复杂生化现象进行数学模拟的可靠性。基于约束的GSMM建模的思路及流程如图 1所示。

图 1 基于约束的基因组规模代谢网络模型建模通用流程 Fig. 1 General procedure for constructing a constraint-based GSMM. (A) Generic process for constructing a constraint-based GSMM. (B) Retrieving metabolome information and genome-wide annotation information from various databases, and each data complements, fills and corrects each other. (C) A stoichiometric matrix S is constructed based on the reaction and metabolite information. The columns of the matrix represent metabolites and the rows represent reactions. The elements in the S matrix represent the stoichiometric coefficients of metabolites participating in the reaction. Positive values represent production, and negative values represent consumption. vi composes the vector of reaction flux, which satisfies the mass balance constraint of S·v=0. (D) Various omics and thermodynamic data are retrieved from relevant databases and used to constrain GSMM. (E) Optimization goals are set, and mathematical optimization problems are solved for prediction of metabolic status or for other purposes.

图选项

在进行上述几种约束时，约束条件与模型整合的方式以及相应模型的应用范围都是不同的。在GSMM中，质量和电荷守恒由生化反应方程式给出，体现在反应计量矩阵(公式2中S) 中，是建立代谢网络模型的基础，代谢反应的上下限通量可以对底物、产物等进行约束。除此之外建立的转录组与基因表达约束、蛋白组和酶利用约束以及热力学约束方法在近些年的发展中也在不断地提出、改进并得以完善。以下根据约束种类将相关方法进行了分类总结(图 2)，并列举探讨了各方法的功能及局限性。

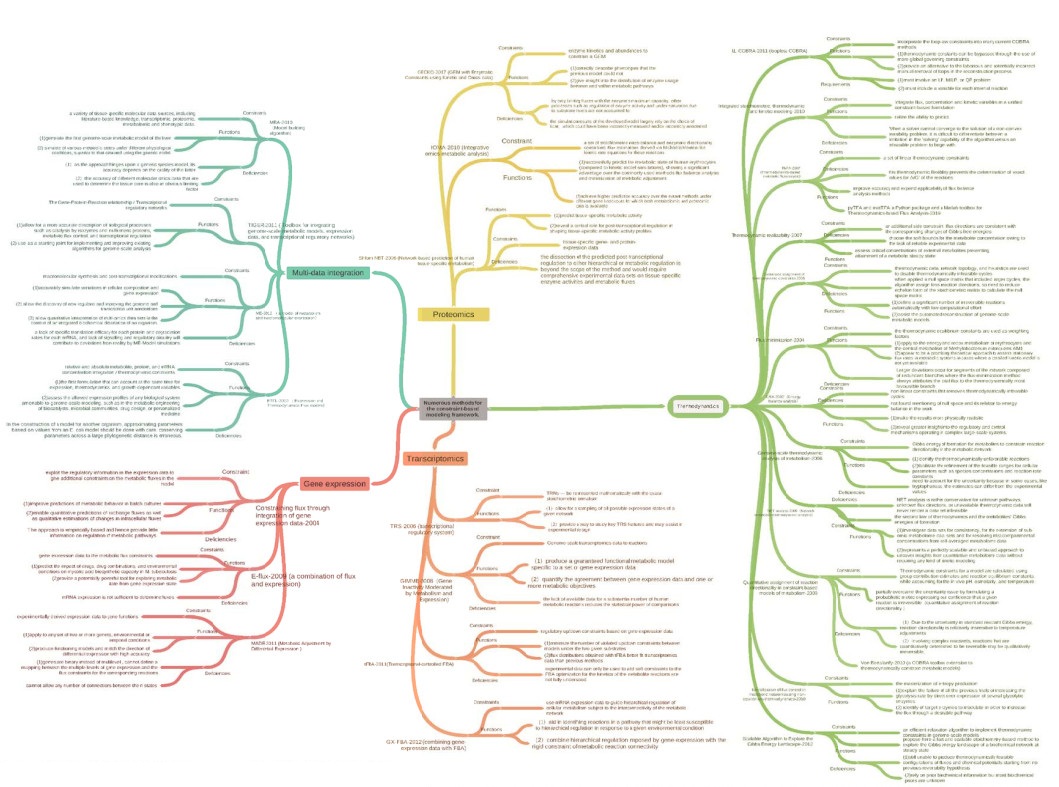图 2 约束条件分类及约束与GSMM整合的实施方法介绍 Fig. 2 Classification of constraints and introduction of methods for integrating constraints with GSMM. GSMM constraints can be divided into transcriptomics and gene expression, proteomics and thermody namics. Multi-data integration is a comprehensive constraint condition. Different methods are used to introduce the above constraints into GSMM. The figure briefly summarizes the functions and deficiencies of the implementation methods.

图选项

2.1 基于转录组数据的约束转录调控与基因表达在细胞功能中起着核心作用，在进行GSMM的构建过程中，需要将转录调控与基因表达对代谢反应速率的影响进行模拟，这是通过向GSMM中加入转录与基因表达约束得以实现的。对于微生物而言，转录调节的主要作用是对环境条件变化的响应，例如微生物会随着胞外营养状况和环境压力而改变基因表达的状态^[40-41]。
因此，细胞的代谢反应受转录调节系统的结构性调控，除了在GSMM中定义代谢物转化的反应之外，还需要对转录调节与基因表达对代谢过程的影响进行系统性数学描述。代谢反应过程受到多个水平的调节，包括对mRNA丰度的转录控制以及各种转录后调节机制，故理论上在构建GSMM时转录调控信息以及信号传导信息都是需要考虑的，单一的转录调控不能完全反映通量信息(转录对代谢的调控如图 3所示)。

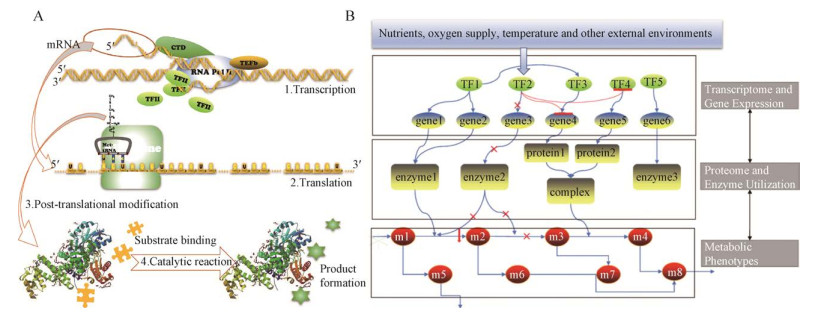图 3 对代谢过程的多组学级联调控 Fig. 3 Cascade regulation of metabolic processes based on multi-omics data. Cellular gene expression status will change in response to the change of extracellular nutritional and environmental conditions. The expression and transcription of relevant genes guide the translation of the enzymes encoded. The activity of enzyme determines the maximum reaction rate of the reaction. By integrating the multi-omics data and the cascade regulation process with GSMM, the global regulation of the metabolic network could be achieved.

图选项

将基因转录信息作为约束用于GSMM构建有两种方法：一种已证明可行的方法是使用表达数据检测未表达的编码基因，将相应的代谢通量实施ON/OFF的严格约束，从而减小了可行求解空间^[42-43]。另一种尝试是基于模型的生长表型和基因表达数据分析，确定新的网络组件及其相互作用，如根据TFs对基因及蛋白质表达的影响来调节代谢反应通量的范围^[44]，如SR-FBA^[45]、E-flux^[46]、tFBA^[47]等方法。这些方法使得GSMM可以更加准确预测通量的变化，解决了传统GSMM中GPR规则无法定量描述转录调控与反应通量关系的问题。
然而，这些方法虽然量化了转录调控在确定代谢通量中的作用，但同时也证明了通量需求与转录调控之间并不完全匹配的关系，因此，逐渐出现一些新颖的表达转录约束方法，MADE^[48]是根据两种或两种以上条件来源的基因表达差异数据来确定最佳的基因状态，可以准确地概括基因表达动力学；IMAT^[49]使用基因表达数据将代谢模型进行分层调节，即把反应分为高表达、适度表达和低表达，这种从表达的不同层面进行代谢调控的方式比单纯ON/OFF模式得到的预测结果更准确。但是转录与基因表达的整合需要更丰富的数据和更系统的方式。在此基础上引入统计学具有进步意义，如PROM^[50]使用概率表示来自大量基因表达数据的基因状态和TF-基因相互作用，并用这些概率自动化制定反应通量约束规则；IDREAM则将统计推断的环境和基因调控影响网络(EGRIN) 模型^[51]与PROM框架相结合，以创建增强的代谢调控网络模型。2019年，Shen等^[52]提出了一种新的整合转录调控与代谢网络的应变设计算法——OptRAM，OptRAM基于IDREAM集成网络框架，采用SA算法优化目标函数，确保目标产物与细胞生长之间的良好耦合。这些方法构建的模型可以更加准确地模拟通量变化，也给人们洞察转录调控与反应通量之间的关系提供了更多的参考，但转录与代谢之间更深层次的关系还需要对细胞代谢反应调控机制更深入的研究。
2.2 基于蛋白组数据的约束转录组中基因的mRNA丰度并不完全代表相应蛋白表达的强度，真正催化反应的主体是蛋白，因此反应的通量实际上是由酶表达水平直接决定的。相对于转录组约束，蛋白组数据为GSMM模型提供更直接更准确的约束。以往的代谢网络模型在预测某种代谢物的生产时，通常只考虑了碳源和供氧的限制，然而代谢通量往往受到其相应酶利用的限制，为了提高预测的精度，越来越多的建模方法考虑到了酶利用约束，特别是随着定量蛋白质组测量技术的发展与蛋白组学数据的丰富，可以从定量蛋白组数据库中搜集到相应菌种各代谢反应利用的酶水平，从而将其以约束形式纳入GSMM中。
最初，对于在GSMM中加入酶约束主要通过转录组数据，通过mRNA水平来表征相应酶蛋白的水平，从而来限制代谢反应^[42]，或是根据胞质空间对酶的总浓度进行约束，如FBAwMC^[53-54]。然而，对代谢反应简单实施ON/OFF约束或酶总浓度约束都不足以表征或描述单个酶的表达量及酶类别与其催化反应的通量之间的关系，所以必须要把动力学和蛋白质分配纳入考量，如整合组学代谢分析(IOMA)^[55]。IOMA是一种酶动力学与GSMM模型相结合来预测代谢通量的新方法，采用一种类似米氏动力学方程的方式进行核心反应通量的估计。该法从动力学角度提供了一个可供参考的表征反应通量与酶量关系的表达方式，该方法成功地预测了人类红细胞基因敲除后的代谢通量。资源平衡分析(RBA) 方法^[56]将蛋白质分配考虑在内进行GSMM的构建，该法利用多个实验数据集来估算酶的表观催化速率，并将估算值作为硬约束(等式) 以预测蛋白质分布，在对枯草芽孢杆菌的模拟中准确、有效地预测了菌体蛋白资源分配。最近，Zeng等^[57]通过将整个细胞蛋白质组划分为4个功能区块的方式，进一步在GSMM中整合了蛋白质组的分配规则。该模型揭示了蛋白组与代谢之间关系：最大比生长速率可能由大量的与生长相关的蛋白质组和其合成成本决定，并且酶和底物之间的亲和能力(米氏常数) 与生长动力学常数(Monod常数) 相关，这取决于细胞的代谢策略。
此外，更灵活的软约束(不等式) 方法也取得了一定进展。2017年，Sánchez等^[58]提出将酶的丰度和周转数(k_cat值) 与反应通量关联的方法——GECKO，该法将酶利用情况与k_cat值用于对反应化学计量矩阵S进行扩展，使得模型可以直接整合定量蛋白质组学数据。对于酶与反应之间的不同关系，GECKO方法进行了考虑和区分，包括同酶催化可逆反应、同工酶、多功能酶和多亚基复合酶催化的反应。此外，作者还提到在缺乏蛋白质组学数据的情况下，利用总蛋白量对缺失的酶总量进行限制。GECKO方法具有灵活性和预测准确性，这在酿酒酵母、枯草芽孢杆菌和大肠杆菌全基因组模型中得到印证^[58-60]。
以上两种将酶蛋白量作为约束条件的GSMM方法都依赖于酶动力学参数的准确获取，然而蛋白数据库中相应参数缺失以及体内(in vivo) 与体外(in vitro) 参数值存在较大差别是在建模时需要考虑的问题。目前来自BRENDA的k_cat值多是基于体外测量。2016，Davidi等^[61]建立了利用组学数据定量分析酶的体外k_cat值和体内最大催化速率之间关系的方法，证明了体外测量的k_cat值与从组学数据推断的体内值之间存在良好的相关性，提供了一种高通量方法来获得反映体内条件的酶动力学常数的方法，可应用于更加准确和完整的GSMM的构建。同年，酶成本最小化(ECM) 方法^[62]也被提出，该方法通过将酶成本作为代谢通量的函数，可描述为一个可进行数据变化的凸优化问题来处理酶相关参数缺失的问题，这里的数据变化主要指ECM根据可用数据的数量允许在不同的细节层次上构建模型，这使ECM更具灵活性。此外，ECM可以根据每单位通量的酶成本总和比较不同途径的优劣，利用该方法解释了酵母和癌细胞在有氧发酵中代谢策略的选择。
2.3 基于热力学基本原理的约束细胞内进行的代谢反应也遵循热力学基本规律，因此将热力学基本原理应用于基因组规模代谢网络模型相关研究也越来越多，热力学约束的加入进一步加深了人们对于生物代谢过程的理解。根据反应吉布斯自由能的变化来判断热力学有利或不利代谢反应，从而在GSMM模型构建中实现热力学约束^[63-64]。
利用热力学原理可对GSMM中反应能否进行实现定性分析。能量平衡分析(EBA) 方法考虑了热力学理论，可用于去除FBA分析结果中热力学不可行的反应^[65]。将热力学引入代谢模型比较经典的是基于热力学的代谢通量分析(TMFA)方法^[66]，它具有在基因组尺度上鉴别热力学可行反应和产生代谢物活性谱的能力。Kümmel等^[67]提出了在基因组规模模型中运用热力学原理自动和系统地分配反应方向的计算方法，解决了手动热力学约束效率低、容易出错的问题。Salvy等^[68]进一步开发了实现TMFA的Python工具包(PyTFA) 和Matlab工具包(MatTFA)，为将热力学约束广泛地应用到各种生物体的GSMM中提供了便捷工具。利用热力学数据还可以对代谢反应方向进行定量分配(图 4B)。如Fleming等2009年就进行了相关研究^[69-70]，他们根据代谢物浓度范围定义了反应的吉布斯自由能范围，进而在模拟时定量预测反应的方向。他们还从数学角度出发，提出了一种符合稳态质量守恒、能量守恒和热力学第二定律的模型，并扩展到涵盖可逆动力学方程式系统，将标准化学势、代谢物及酶浓度和动力学变量进行了归一化处理^[71]。除了对代谢反应引入热力学约束之外，一些研究还着眼于求解GSMM热力学最优解的方法。2012年，Zhu等^[72]基于热力学定律，提出了一种热力学最优解计算方法——热力学最优搜索法(TOS)，该法以热力学最优通量分布替代FBA最优解。该方法实质上是解一个具有质量平衡、能量平衡和最大比生长速率的非线性优化问题，目标函数为最大化单位能量消耗的总熵，求解可得到热力学最优的代谢通量分布。

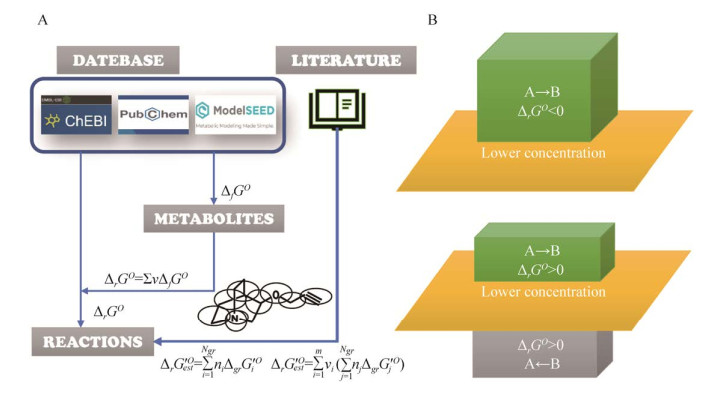图 4 热力学信息搜集和代谢不利反应的识别 Fig. 4 The process of collecting thermodynamic information and identifying adverse metabolic reactions.

图选项

与酶约束需要相关酶参数信息的获取类似，热力学约束也需要获取反应及代谢物的生成吉布斯自由能。虽然一些代谢反应和代谢物质的自由能数据已通过实验得出，可以通过数据库直接检索，但仍然有大部分的数据缺失，故在对GSMM引入热力学约束时需要对一些反应及代谢物的生成吉布斯自由能进行实验获取或估计(图 4A)。1991年，Mavrovouniotis^[73]提出了用于标准吉布斯自由能的估算方法——基团贡献法，该法根据化合物的基团组成估算出化合物的生成吉布斯自由能，把化合物看作成官能团组，各官能团的吉布斯能贡献构成化合物的总吉布斯自由能。在此基础上该方法不断得到更新和改进，如考虑到立体结构相互作用的影响和温度对平衡常数的依赖性等^[74-75]。2010年，Rother等^[76]提出了IGERS法，这是一种根据化学反应相似性推断生化反应的吉布斯能量变化的方法，且相比于基团贡献法具有更好的准确性。鉴于基团贡献法对于存在共轭体系的化合物的估计存在偏差，而IGERS估计范围又不如基团贡献法广泛，伪异构反应物贡献(PRC) 和伪异构基团贡献(PGC) 这两个概念被先后提出，这两种方法的结合可以更好地估计多种化合物在广泛水溶环境下的吉布斯自由能^[77]。基团贡献法已经实现与TMFA的结合，在大肠杆菌GSMM中能准确识别热力学不利的反应和酶，从而进一步提高GSMM的通量预测准确性^[66]。IGERS、PRC与PGC结合法的提出虽然为热力学吉布斯自由能计算提供了更多的参考，但它们与GSMM的结合还需要开展深入的研究。
3 整合多组学和热力学数据的综合代谢网络模型虽然引入酶约束和热力学约束在很大程度上提高了GSMM模型的预测能力，使模型预测值更接近代谢真实值，但生物体是一个极其复杂精密的系统，真实的生物代谢状态不可能只靠单一的酶约束或者热力学约束即可完整地描述，因此有必要研究综合的代谢网络模型。细胞生长代谢重要的两个非线性特征在上述约束中都被忽略了：细胞子代的资源分配与生长稀释。换句话说，真实的细胞会合成细胞成分(代谢物、酶、脂质、DNA) 以形成新的细胞，这些成分的比例与其自身组成相匹配，同时，这些成分的浓度影响新陈代谢和生物合成速率，从而影响生长速度^[78]。而传统代谢模型无法定量描述基因表达，不包含转录和翻译的化学表示，只能将组学数据作为临时约束条件，故建立一个涵盖多组学和热力学数据的综合代谢网络模型是有必要的。
在此背景下，整合多组学数据的综合代谢网络模型得到了快速发展。Jensen等建立了一个基因组规模代谢模型工具箱——TIGER^[79]，该工具箱将基因表达数据、转录调控网络集成于GSMM模型中，利用该工具鉴别出酿酒酵母代谢过程中转录调控与反应通量不一致之处，进而改善酿酒酵母转录调控模型。ME (M代表Metabolism，E代表Expression) 模型^[80]是将基因表达及蛋白翻译的反应过程也加入到GSMM中形成的综合代谢网络模型。ME模型中转录和翻译过程使用代谢产生的原材料和能量来合成组装负责细胞功能的大分子机器，模型集成了代谢物和表达数据，可以在细胞生理学背景下探索基因产物、遗传扰动和基因功能之间的关系。在此基础上Palsson课题组利用蛋白质组学数据，对大肠杆菌ME模型中的关键蛋白质组实现约束，证明了ME模型在代谢预测及揭示蛋白质组分配的基本原则方面的优越性^[81]。
最近，ME模型又取得新进展，Salvy等^[82]建立了将热力学进一步整合到ME模型的方法——ETFL。该法综合考虑了代谢物、酶、核糖体、RNA聚合酶、多肽、mRNA、rRNA、tRNA以及DNA的浓度水平，并结合TMFA方法将热力学引入模型中。具体的约束数学形式可由下式表示：

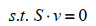(4)

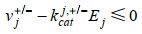(5)

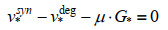(6)

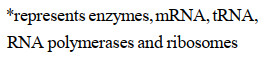(7)

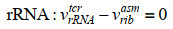(8)

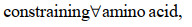(9)

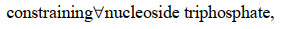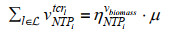(10)

其中，v_*^syn代表合成速率，v_*^deg代表降解速率，μ·G_*是稀释项，这3项对细胞大分子进行了稳态质量平衡约束；多肽和rRNA的约束式由(7)、(8)给出；v_biomass表示通过生物量方程式的通量，η_mi^v_biomass是生物量反应中m_i的化学计量系数，对氨基酸和三磷酸核苷的约束反映在生物量合成反应中，二者比率会随着生长速率而变化。热力学整合体现在对反应方向的限制上。该文献展示了大肠杆菌ETFL模型结果，证明ETFL能够模拟蛋白质组受限的生长，在对mRNA、酶浓度以及必需基因的预测方面也显示出卓越能力。
4 展望近20年来，我们见证了组学检测技术的高速发展，见证了包括表型筛选、基因测序、蛋白质组学、转录组学、代谢组学等生物大数据的积累，描述生命过程的代谢模型经历了MM、GSMM、CBM以及ME-Model这样一个不断精细完善并逐渐向真实代谢状态准确预测靠拢的发展历程，针对包括微生物、人体细胞等相关组学数据的集成算法也不断衍生^[83-88]。借助于数学模型作为分析工具，可以指导科学研究解决科学问题，如利用基因组规模代谢网络模型预测基因缺失后表型以及外源基因插入设计^[89]，进行生物基因组进化预测^[90]、酶功能预测^[91]。而多组学数据作为约束条件的加入，使GSMM规模不断扩大，功能也随之不断完善，在化学品生产^[35]、药物开发与疾病治疗^[92-94]等方面GSMM也展现出积极的指导意义。
但是基于约束的建模仍然存在局限性，如利用IOMA、GECKO法进行酶约束时所需要的体内酶动力学参数的大量缺失，虽然缺失的参数可由实验得到或通过文献检索进行估计，但实施起来并不便捷，且目前关于体内外动力学参数值的差异仍无完备的方案进行评估^[61]。同样地，将热力学约束引入GSMM的实施过程也需要准确的热力学数据，目前这些数据也不完备。相关的吉布斯自由能估计方法也存在其固有缺陷，如在基团贡献法中测量平衡常数的方法、离子强度之间的差异、pH值之间的差异、温度差异等，都会造成估算值的偏差^[74]。要突破这些局限性，需要相关测量技术与数学计算方法的进一步发展。
此外，在对模型微观性和整体性的考虑上也存在局限性，更精细的微观模型需要相关分子结构信息的加入，将分子结构纳入基因组规模代谢模型的重建，将为系统生物学研究开辟新的前景。如2016年Brunk等^[95]介绍的GEM-PRO方法在GSMM基础上考虑了蛋白质结构的影响，证明了生物体之间功能差异不仅来自遗传成分的差异，也来自分子成分之间的物理相互作用。然而，受到实验数据缺乏的限制，存在大量基因不能匹配到实验蛋白质结构信息的问题，只能根据同源性来估计。模型的整体性考虑尤其是在对生物代谢动态性过程的考虑也存在不足。本文中提到的模型及其建模方法都基于稳态假设，这是一种对真实动态代谢状态下的理想化假设，因而生物代谢非稳态模型的建立也是GSMM前进的一个方向。目前已有相关研究着眼于此，如2017年Bordbar等^[96]提出的非稳态通量平衡分析法(uFBA)，以及最近Buchweitz等^[97]开发的GEM-VIS方法，这些研究在对代谢建模的总进程中具有很大的进步意义。随着技术进步与科学发展，GSMM建模不断迎接新的机遇与挑战，人们也因此对生物系统科学和生命背后运行机理的认知不断得到刷新，必将有助于我们利用这些认知改造自然生命、实现更美好的生活！
参考文献

[1]	Bailey JE. Toward a science of metabolic engineering. Science, 1991, 252(5013): 1668-1675. DOI:10.1126/science.2047876
[2]	刘立明, 陈坚. 基因组规模代谢网络模型构建及其应用. 生物工程学报, 2010, 26(9): 1176-1186. Liu LM, Chen J. Reconstruction and application of genome-scale metabolic network model. Chin J Biotech, 2010, 26(9): 1176-1186 (in Chinese).
[3]	Edwards JS, Palsson BO. Systems properties of the Haemophilus influenzae Rd metabolic genotype. J Biol Chem, 1999, 274(25): 17410-17416. DOI:10.1074/jbc.274.25.17410
[4]	Orth JD, Conrad TM, Na J, et al. A comprehensive genome-scale reconstruction of Escherichia coli metabolism--2011. Mol Syst Biol, 2011, 7: 535. DOI:10.1038/msb.2011.65
[5]	Forster J, Famili I, Fu P, et al. Genome-scale reconstruction of the Saccharomyces cerevisiae metabolic network. Genome Res, 2003, 13(2): 244-253. DOI:10.1101/gr.234503
[6]	Lee KH, Park JH, Kim TY, et al. Systems metabolic engineering of Escherichia coli for L-threonine production. Mol Syst Biol, 2007, 3: 149. DOI:10.1038/msb4100196
[7]	Edwards JS, Palsson BO. The Escherichia coli MG1655 in silico metabolic genotype: its definition, characteristics, and capabilities. Proc Natl Acad Sci USA, 2000, 97(10): 5528-5533. DOI:10.1073/pnas.97.10.5528
[8]	Herrg?rd MJ, Swainston N, Dobson P, et al. A consensus yeast metabolic network reconstruction obtained from a community approach to systems biology. Nat Biotechnol, 2008, 26: 1155-1160. DOI:10.1038/nbt1492
[9]	Dobson PD, Smallbone K, Jameson D, et al. Further developments towards a genome-scale metabolic model of yeast. BMC Syst Biol, 2010, 4: 1-7. DOI:10.1186/1752-0509-4-1
[10]	Heavner BD, Smallbone K, Barker B, et al. Yeast 5-an expanded reconstruction of the Saccharomyces cerevisiae metabolic network. BMC Syst Biol, 2012, 6: 55. DOI:10.1186/1752-0509-6-55
[11]	Heavner BD, Smallbone K, Price ND, et al. Version 6 of the consensus yeast metabolic network refines biochemical coverage and improves model performance. Database (Oxford), 2013, 2013: bat059.
[12]	Aung HW, Henry SA, Walker LP. Revising the representation of fatty acid, glycerolipid, and glycerophospholipid metabolism in the consensus model of yeast metabolism. Ind Biotechnol (New Rochelle N Y), 2013, 9(4): 215-228.
[13]	Lu H, Li F, Sánchez BJ, et al. A consensus S. cerevisiae metabolic model Yeast8 and its ecosystem for comprehensively probing cellular metabolism. Nat Commun, 2019, 10(1): 3586. DOI:10.1038/s41467-019-11581-3
[14]	Duarte NC, Becker SA, Jamshidi N, et al. Global reconstruction of the human metabolic network based on genomic and bibliomic data. Proc Natl Acad Sci USA, 2007, 104(6): 1777-1782. DOI:10.1073/pnas.0610772104
[15]	de Oliveira Dal'Molin CG, Quek LE, Palfreyman RW, et al. AraGEM, a genome-scale reconstruction of the primary metabolic network in Arabidopsis. Plant Physiol, 2010, 152(2): 579-589. DOI:10.1104/pp.109.148817
[16]	Heather JM, Chain B. The sequence of sequencers: the history of sequencing DNA. Genomics, 2016, 107(1): 1-8. DOI:10.1016/j.ygeno.2015.11.003
[17]	LaFramboise T. Single nucleotide polymorphism arrays: a decade of biological, computational and technological advances. Nucleic Acids Res, 2009, 37(13): 4181-4193. DOI:10.1093/nar/gkp552
[18]	Wang Z, Gerstein M, Snyder M. RNA-Seq: a revolutionary tool for transcriptomics. Nat Rev Genet, 2009, 10(1): 57-63. DOI:10.1038/nrg2484
[19]	Ludwig C, Gillet L, Rosenberger G, et al. Data-independent acquisition-based SWATH-MS for quantitative proteomics: a tutorial. Mol Syst Biol, 2018, 14(8): e8126.
[20]	Nassar AF, Wu T, Nassar SF, et al. UPLC-MS for metabolomics: a giant step forward in support of pharmaceutical research. Drug Discov Today, 2017, 22(2): 463-470. DOI:10.1016/j.drudis.2016.11.020
[21]	Beale DJ, Pinu FR, Kouremenos KA, et al. Review of recent developments in GC-MS approaches to metabolomics-based research. Metabolomics, 2018, 14(11): 152. DOI:10.1007/s11306-018-1449-2
[22]	Kanehisa, M, Sato Y, Kawashima M, et al. KEGG as a reference resource for gene and protein annotation. Nucleic Acids Res, 2016, 44(D1): D457-D462. DOI:10.1093/nar/gkv1070
[23]	Jeske L, Placzek S, Schomburg I, et al. BRENDA in 2019: a European ELIXIR core data resource. Nucleic Acids Res, 2019, 47(D1): D542-D549. DOI:10.1093/nar/gky1048
[24]	Sayers EW, Beck J, Brister JR, et al. Database resources of the National Center for Biotechnology Information. Nucleic Acids Res, 2020, 48(D1): D9-D16. DOI:10.1093/nar/gkz899
[25]	Magrane M, UniProt C. UniProt Knowledgebase: a hub of integrated protein data. Database (Oxford) 2011, 2011, bar009.
[26]	Krieger CJ, Zhang P, Mueller LA, et al. MetaCyc: a multiorganism database of metabolic pathways and enzymes. Nucleic Acids Res, 2004, 32(Database issue): D438-D442.
[27]	DeJongh M, Formsma K, Boillot P, et al. Toward the automated generation of genome-scale metabolic networks in the SEED. BMC Bioinformatics, 2007, 8: 139. DOI:10.1186/1471-2105-8-139
[28]	Ren Q, Chen K, Paulsen IT. TransportDB: a comprehensive database resource for cytoplasmic membrane transport systems and outer membrane channels. Nucleic Acids Res, 2007, 35(Database issue): D274-D279.
[29]	Bordbar A, Monk JM, King ZA, et al. Constraint-based models predict metabolic and associated cellular functions. Nat Rev Genet, 2014, 15(2): 107-120. DOI:10.1038/nrg3643
[30]	Becker SA, Feist AM, Mo ML, et al. Quantitative prediction of cellular metabolism with constraint-based models: the COBRA Toolbox. Nat Protoc, 2007, 2(3): 727-738. DOI:10.1038/nprot.2007.99
[31]	Schellenberger J, Que R, Fleming RM, et al. Fleming RM, et al. Quantitative prediction of cellular metabolism with constraint-based models: the COBRA Toolbox v2.0. Nat Protoc, 2011, 6(9): 1290-1307. DOI:10.1038/nprot.2011.308
[32]	Heirendt L, Arreckx S, Pfau T, et al. Creation and analysis of biochemical constraint-based models using the COBRA Toolbox v.3.0. Nat Protoc, 2019, 14(3): 639-702. DOI:10.1038/s41596-018-0098-2
[33]	Feist AM, Palsson BO. The growing scope of applications of genome-scale metabolic reconstructions using Escherichia coli. Nat Biotechnol, 2008, 26(6): 659-667. DOI:10.1038/nbt1401
[34]	Oh YK, Palsson BO, Park SM, et al. Genome-scale reconstruction of metabolic network in Bacillus subtilis based on high-throughput phenotyping and gene essentiality data. J Biol Chem, 2007, 282(39): 28791-28799. DOI:10.1074/jbc.M703759200
[35]	Yang JE, Park SJ, Kim WJ, et al. One-step fermentative production of aromatic polyesters from glucose by metabolically engineered Escherichia coli strains. Nat Commun, 2018, 9(1): 79. DOI:10.1038/s41467-017-02498-w
[36]	Osterlund T, Nookaew I, Bordel S, et al. Mapping condition-dependent regulation of metabolism in yeast through genome-scale modeling. BMC Syst Biol, 2013, 7: 36. DOI:10.1186/1752-0509-7-36
[37]	Feist AM, Herrgard MJ, Thiele I, et al. Reconstruction of biochemical networks in microorganisms. Nat Rev Microbiol, 2009, 7(2): 129-143. DOI:10.1038/nrmicro1949
[38]	Orth JD, Thiele I, Palsson BO. Palsson BO. What is flux balance analysis?. Nat Biotechnol, 2010, 28(3): 245-248. DOI:10.1038/nbt.1614
[39]	Lewis NE, Nagarajan H, Palsson, B O. Constraining the metabolic genotype-phenotype relationship using a phylogeny of in silico methods. Nat Rev Microbiol, 2012, 10(4): 291-305. DOI:10.1038/nrmicro2737
[40]	Herrgard MJ, Covert MW, Palsson BO. Reconstruction of microbial transcriptional regulatory networks. Curr Opin Biotechnol, 2004, 15(1): 70-77. DOI:10.1016/j.copbio.2003.11.002
[41]	Wyrick JJ, Young RA. Deciphering gene expression regulatory networks. Curr Opin Genet Dev, 2002, 12(2): 130-136. DOI:10.1016/S0959-437X(02)00277-0
[42]	Akesson M, Forster J, Nielsen J. Integration of gene expression data into genome-scale metabolic models. Metab Eng, 2004, 6(4): 285-293. DOI:10.1016/j.ymben.2003.12.002
[43]	Becker SA, Palsson BO. Context-specific metabolic networks are consistent with experiments. PLoS Comput Biol, 2008, 4(5): e1000082. DOI:10.1371/journal.pcbi.1000082
[44]	Herrgard MJ, Lee BS, Portnoy V, et al. Integrated analysis of regulatory and metabolic networks reveals novel regulatory mechanisms in Saccharomyces cerevisiae. Genome Res, 2006, 16(5): 627-635. DOI:10.1101/gr.4083206
[45]	Shlomi T, Eisenberg Y, Sharan R, et al. A genome-scale computational study of the interplay between transcriptional regulation and metabolism. Mol Syst Biol, 2007, 3: 101. DOI:10.1038/msb4100141
[46]	Colijn C, Brandes A, Zucker J, et al. Interpreting expression data with metabolic flux models: predicting Mycobacterium tuberculosis mycolic acid production. PLoS Comput Biol, 2009, 5(8): e1000489. DOI:10.1371/journal.pcbi.1000489
[47]	Van Berlo RJ, De Ridder D, Daran JM, et al. Predicting metabolic fluxes using gene expression differences as constraints. IEEE/ACM Trans Comput Biol Bioinform, 2011, 8(1): 206-216. DOI:10.1109/TCBB.2009.55
[48]	Jensen PA, Papin JA. Functional integration of a metabolic network model and expression data without arbitrary thresholding. Bioinformatics, 2011, 27(4): 541-547. DOI:10.1093/bioinformatics/btq702
[49]	Zur H, Ruppin E, Shlomi T. iMAT: an integrative metabolic analysis tool. Bioinformatics, 2010, 26(24): 3140-3142. DOI:10.1093/bioinformatics/btq602
[50]	Chandrasekaran S, Price ND. Probabilistic integrative modeling of genome-scale metabolic and regulatory networks in Escherichia coli and Mycobacterium tuberculosis. Proc Natl Acad Sci USA, 2010, 107(41): 17845-17850. DOI:10.1073/pnas.1005139107
[51]	Bonneau R, Facciotti MT, Reiss DJ, et al. A predictive model for transcriptional control of physiology in a free living cell. Cell, 2007, 131(7): 1354-1365. DOI:10.1016/j.cell.2007.10.053
[52]	Shen F, Sun R, Yao J, et al. OptRAM: In-silico strain design via integrative regulatory-metabolic network modeling. PLoS Comput Biol, 2019, 15(3): e1006835. DOI:10.1371/journal.pcbi.1006835
[53]	Beg QK, Vazquez A, Ernst J, et al. Intracellular crowding defines the mode and sequence of substrate uptake by Escherichia coli and constrains its metabolic activity. Proc Natl Acad Sci USA, 2007, 104(31): 12663-12668. DOI:10.1073/pnas.0609845104
[54]	赵欣, 杨雪, 毛志涛, 等. 基于酶约束的代谢网络模型研究进展及其应用. 生物工程学报, 2019, 35(10): 1914-1924. Zhao X, Yang X, Mao ZT, et al. Progress and application of metabolic network model based on enzyme constraints. Chin J Biotech, 2019, 35(10): 1914-1924 (in Chinese).
[55]	Yizhak K, Benyamini T, Liebermeister W, et al. Integrating quantitative proteomics and metabolomics with a genome-scale metabolic network model. Bioinformatics, 2010, 26(12): i255-i260. DOI:10.1093/bioinformatics/btq183
[56]	Goelzer A, Muntel J, Chubukov V, et al. Quantitative prediction of genome-wide resource allocation in bacteria. Metab Eng, 2015, 32: 232-243. DOI:10.1016/j.ymben.2015.10.003
[57]	Zeng H, Yang A. Bridging substrate intake kinetics and bacterial growth phenotypes with flux balance analysis incorporating proteome allocation. Sci Rep, 2020, 10(1): 4283. DOI:10.1038/s41598-020-61174-0
[58]	Sánchez BJ, Zhang C, Nilsson A, et al. Improving the phenotype predictions of a yeast genome-scale metabolic model by incorporating enzymatic constraints. Mol Syst Biol, 2017, 13(8): 935. DOI:10.15252/msb.20167411
[59]	Massaiu I, Pasotti L, Sonnenschein N, et al. Integration of enzymatic data in Bacillus subtilis genome-scale metabolic model improves phenotype predictions and enables in silico design of poly-gamma-glutamic acid production strains. Microb Cell Fact, 2019, 18(1): 3. DOI:10.1186/s12934-018-1052-2
[60]	Ye C, Luo Q, Guo L, et al. Improving lysine production through construction of an Escherichia coli enzyme-constrained model. Biotechnol Bioeng, 2020, 117(11): 3533-3544. DOI:10.1002/bit.27485
[61]	Davidi D, Noor E, Liebermeister W, et al. Global characterization of in vivo enzyme catalytic rates and their correspondence to in vitro kcat measurements. Proc Natl Acad Sci USA, 2016, 113(12): 3401-3406. DOI:10.1073/pnas.1514240113
[62]	Noor E, Flamholz A, Bar-Even A, et al. The protein cost of metabolic fluxes: prediction from enzymatic rate laws and cost minimization. PLoS Comput Biol, 2016, 12(11): e1005167. DOI:10.1371/journal.pcbi.1005167
[63]	Henry CS, Jankowski MD, Broadbelt LJ, et al. Genome-scale thermodynamic analysis of Escherichia coli metabolism. Biophys J, 2006, 90(4): 1453-1461. DOI:10.1529/biophysj.105.071720
[64]	Hoppe A, Hoffmann S, Holzhutter HG. Including metabolite concentrations into flux balance analysis: thermodynamic realizability as a constraint on flux distributions in metabolic networks. BMC Syst Biol, 2007, 1: 23. DOI:10.1186/1752-0509-1-23
[65]	Beard DA, Liang SD, Qian H. Energy balance for analysis of complex metabolic networks. Biophysical J, 2002, 83(1): 79-86. DOI:10.1016/S0006-3495(02)75150-3
[66]	Henry CS, Broadbelt LJ, Hatzimanikatis V. Thermodynamics-based metabolic flux analysis. Biophys J, 2007, 92(5): 1792-1805. DOI:10.1529/biophysj.106.093138
[67]	Kümmel A, Panke S, Heinemann M. Systematic assignment of thermodynamic constraints in metabolic network models. BMC Bioinformatics, 2006, 7: 512. DOI:10.1186/1471-2105-7-512
[68]	Salvy P, Fengos G, Ataman M, et al. pyTFA and matTFA: a Python package and a Matlab toolbox for thermodynamics-based flux analysis. Bioinformatics, 2019, 35(1): 167-169.
[69]	Fleming RM, Thiele I, Nasheuer HP. Quantitative assignment of reaction directionality in constraint-based models of metabolism: application to Escherichia coli. Biophys Chem, 2009, 145(2-3): 47-56. DOI:10.1016/j.bpc.2009.08.007
[70]	Fleming RM, Thiele I. von Bertalanffy 1.0: a COBRA toolbox extension to thermodynamically constrain metabolic models. Bioinformatics, 2011, 27(1): 142-143. DOI:10.1093/bioinformatics/btq607
[71]	Fleming RM, Thiele I, Provan G, et al. Integrated stoichiometric, thermodynamic and kinetic modelling of steady state metabolism. J Theor Biol, 2010, 264(3): 683-692. DOI:10.1016/j.jtbi.2010.02.044
[72]	Zhu Y, Song J, Xu Z, et al. Development of thermodynamic optimum searching (TOS) to improve the prediction accuracy of flux balance analysis. Biotechnol Bioeng, 2013, 110(3): 914-923. DOI:10.1002/bit.24739
[73]	Mavrovouniotis ML. Estimation of standard gibbs energy changes of biotransformation. J Biol Chem, 1991, 266(22): 14440-14445. DOI:10.1016/S0021-9258(18)98705-3
[74]	Jankowski MD, Henry CS, Broadbelt LJ, et al. Group contribution method for thermodynamic analysis of complex metabolic networks. Biophys J, 2008, 95(3): 1487-1499. DOI:10.1529/biophysj.107.124784
[75]	Du B, Zhang Z, Grubner S, et al. Temperature-dependent estimation of Gibbs Energies using an updated group-contribution method. Biophys J, 2018, 114(11): 2691-2702. DOI:10.1016/j.bpj.2018.04.030
[76]	Rother K, Hoffmann S, Bulik S, et al. IGERS: inferring Gibbs energy changes of biochemical reactions from reaction similarities. Biophys J, 2010, 98(11): 2478-2486. DOI:10.1016/j.bpj.2010.02.052
[77]	Noor E, Bar-Even A, Flamholz A, et al. An integrated open framework for thermodynamics of reactions that combines accuracy and coverage. Bioinformatics, 2012, 28(15): 2037-2044. DOI:10.1093/bioinformatics/bts317
[78]	De Groot DH, Hulshof J, Teusink B, et al. Elementary Growth Modes provide a molecular description of cellular self-fabrication. PLoS Comput Biol, 2020, 16(1): e1007559. DOI:10.1371/journal.pcbi.1007559
[79]	Jensen PA, Lutz KA, Papin JA. TIGER: Toolbox for integrating genome-scale metabolic models, expression data, and transcriptional regulatory networks. BMC Syst Biol, 2011, 5: 147. DOI:10.1186/1752-0509-5-147
[80]	Lerman JA, Hyduke DR, Latif H, et al. In silico method for modelling metabolism and gene product expression at genome scale. Nat Commun, 2012, 3: 929. DOI:10.1038/ncomms1928
[81]	Yang L, Yurkovich JT, Lloyd CJ, et al. Principles of proteome allocation are revealed using proteomic data and genome-scale models. Sci Rep, 2016, 6: 36734. DOI:10.1038/srep36734
[82]	Salvy P, Hatzimanikatis V. The ETFL formulation allows multi-omics integration in thermodynamics-compliant metabolism and expression models. Nat Commun, 2020, 11(1): 30. DOI:10.1038/s41467-019-13818-7
[83]	Schultz A, Qutub AA. Reconstruction of tissue-specific metabolic networks using CORDA. PLoS Comput Biol, 2016, 12(3): e100480.
[84]	Agren R, Bordel S, Mardinoglu A, et al. Reconstruction of genome-scale active metabolic networks for 69 human cell types and 16 cancer types using INIT. PLoS Comput Biol, 2012, 8(5): e1002518. DOI:10.1371/journal.pcbi.1002518
[85]	Jerby L, Shlomi T, Ruppin E. Computational reconstruction of tissue-specific metabolic models: application to human liver metabolism. Mol Syst Biol, 2010, 6: 401. DOI:10.1038/msb.2010.56
[86]	Wang YL, Eddy EJ, Price ND. Reconstruction of genome-scale metabolic models for 126 human tissues using mCADRE. BMC Syst Biol, 2012, 6: 153. DOI:10.1186/1752-0509-6-153
[87]	Agren R, Mardinoglu A, Asplund A, et al. Identification of anticancer drugs for hepatocellular carcinoma through personalized genome-scale metabolic modeling. Mol Syst Biol, 2014, 10: 721. DOI:10.1002/msb.145122
[88]	Blais EM, Rawls KD, Dougherty BV, et al. Reconciled rat and human metabolic networks for comparative toxicogenomics and biomarker predictions. Nat Commun, 2017, 8: 14250. DOI:10.1038/ncomms14250
[89]	Orth JD, Palsson BO. Systematizing the generation of missing metabolic knowledge. Biotechnol Bioeng, 2010, 107(3): 403-412. DOI:10.1002/bit.22844
[90]	Papp B, Notebaart RA, Pal C. Systems-biology approaches for predicting genomic evolution. Nat Rev Genet, 2011, 12(9): 591-602. DOI:10.1038/nrg3033
[91]	Oberhardt MA, Zarecki R, Reshef L, et al. Systems-wide prediction of enzyme promiscuity reveals a new underground alternative route for pyridoxal 5'-phosphate production in E. coli. PLoS Comput Biol, 2016, 12(1): e1004705. DOI:10.1371/journal.pcbi.1004705
[92]	Huthmacher C, Hoppe A, Bulik S, et al. Antimalarial drug targets in Plasmodium falciparum predicted by stage-specific metabolic network analysis. BMC Syst Biol, 2010, 4: 120. DOI:10.1186/1752-0509-4-120
[93]	Bidkhori G, Benfeitas R, Elmas E, et al. Metabolic network-based identification and prioritization of anticancer targets based on expression data in hepatocellular carcinoma. Front Physiol, 2018, 9: 916. DOI:10.3389/fphys.2018.00916
[94]	Marin de Mas I, Aguilar E, Zodda E, et al. Model-driven discovery of long-chain fatty acid metabolic reprogramming in heterogeneous prostate cancer cells. PLoS Comput Biol, 2018, 14(1): e1005914. DOI:10.1371/journal.pcbi.1005914
[95]	Brunk E, Mih N, Monk J, et al. Systems biology of the structural proteome. BMC Syst Biol, 2016, 10: 26. DOI:10.1186/s12918-016-0271-6
[96]	Bordbar A, Yurkovich JT, Paglia G, et al. Elucidating dynamic metabolic physiology through network integration of quantitative time-course metabolomics. Sci Rep, 2017, 7: 46249. DOI:10.1038/srep46249
[97]	Buchweitz LF, Yurkovich JT, Blessing C, et al. Visualizing metabolic network dynamics through time-series metabolomic data. BMC Bioinformatics, 2020, 21(1): 130. DOI:10.1186/s12859-020-3415-z