全文HTML
--> --> --> 空气中颗粒物易引发慢性鼻咽炎和慢性支气管炎等呼吸系统疾病,从而影响人群健康[1]。房屋拆迁、土方工程和结构工程等施工过程产生的扬尘是大气颗粒物的重要来源之一[2]。因此,研究施工阶段扬尘的空间扩散特性及相应的管理控制措施,对于改善城市环境空气质量具有重要意义[3]。近年来,国内外****从扬尘化学元素特征[4-5]、扬尘空间扩散[6-8]、扬尘排放因子[9-10]、扬尘排放特征[11-13]、扬尘健康损害评估[14-15]和扬尘控制措施[16-17]等角度,对施工扬尘扩散进行了研究。田刚等[8]对建筑施工扬尘空间扩散模型进行了研究,结果表明,二次幂函数模型同时适用于描述水平和垂直方向的扬尘扩散规律;此外,还提出了四维通量法施工扬尘排放模型[9]。也有****将烟羽扩散高斯模型应用于扬尘扩散研究[16, 18]。随着计算机技术的发展,数值模拟逐渐被广泛应用于对空气污染物分布及扩散的研究[19-20],为扬尘空间扩散模型及监测控制提供了更多研究途径。然而,现有数值模拟研究大多是对比分析风速、围挡距离以及围挡高度等因素对扬尘污染的影响,鲜有结合工地实测扬尘数据来分析扬尘空间扩散模型的研究,而对相应分级控制措施的研究则更加有限。
本研究利用多个城市施工工地的现场监测数据,详细探讨了工地周围扬尘在水平和垂直方向的扩散规律,并以北京某工地实测数据为例,利用数值模拟Fluent软件,重现了工地周围区域扬尘颗粒的分布情况,并提出了综合评价施工扬尘污染程度的分级方法及管理控制措施,以期为有效解决施工扬尘问题提供参考。
1.1. 扬尘浓度监测指标
大气污染物主要包括降尘(dust fall,DF)和总悬浮颗粒物(total suspended particulate,TSP)等,分别表示大气中直径大于10 μm和小于100 μm的颗粒物。DF和TSP浓度存在线性相关关系[12],即DF浓度越高,TSP浓度越大[21]。1.2. 扬尘扩散规律数学模型
扬尘扩散幂函数模型[8]表明,在相同高度或水平位置下,扬尘浓度随离工地水平距离或离地高度均呈2次幂衰减。该一维模型表达式见式(1)。式中:x为自变量,表示水平距离或离地高度,m,;f为施工扬尘浓度,表示DF时单位为t·(km2·d)?1,表示TSP时单位为μg·m?3,测定扬尘浓度时需扣除背景扬尘浓度;a和b为拟合参数。
该模型应用于垂直方向扬尘浓度分布拟合时,参数b等于0,而参数a受现场施工条件和气候等因素影响,变化较大。应用于水平方向时,参数b表示等效逸散初始距离(单位为m),与施工区域沿扩散方向的长度成正相关,对于特定的施工区域为常数;参数a的取值变化很大,与施工现场的扬尘污染强度线性相关。
将烟羽扩散高斯模型用于描述扬尘空间扩散规律[18],其一维模型表达式见式(2)。
式中:x和f的含义与式(1)相同;a和b为拟合参数,参数b表示扬尘沿x方向的扩散系数,m?2。
由于扬尘的空间扩散主要受风的影响,即主要由空间风速大小决定,而不同地貌条件对于风速的减缓或加速效应有所区别。部分国家的对于风速地形修正系数的建议公式中,引入了指数律模型描述地形修正系数[22]。如美国的规范中对于地形修正系数中的K3建议取值为



式中:x为水平距离,m;y为离地高度,m;a、b和c为拟合参数,其中参数b和c分别表示扬尘沿x和y方向的扩散系数,m?1。
1.3. 扬尘扩散规律模型评估指标
数学模型实际应用时需利用评估指标确定其适用程度,常用的回归模型误差评估指标包括和方差(sum of squares for error,SSE)、均方差(mean squared error,MSE)、均方根误差(root mean squared error,RMSE),以及判定系数(R-square,R2)等。其中,SSE、MSE和RMSE 3者的评估效果基本一致。本研究采用RMSE误差和R2指标综合评估,RMSE值越小,R2越接近1,表示该数学模型回归效果越好。1.4. 扬尘扩散数值模拟
扬尘颗粒扩散是气-固两相运动,以空气为连续介质,扬尘颗粒为离散相。通过建立连续相流场,可计算流场中颗粒受力状态及运动轨迹,进而模拟扬尘扩散过程。模拟计算中,假定空气是不可压缩流体,故控制方程见式(5)~(6)。式中:xi(i=1,2,3)分别为x、y、z笛卡尔坐标;ui为i方向的速度分量,m·s?1;P为压强,Pa;t为时间,s;




利用湍流模型对上述方程进行求解时,常用模型包括标准k-ε模型、RNG k-ε模型和Realizable k-ε模型。其中,标准k-ε模型的应用最为广泛[7],k和

式中:k为湍动能,m2·s?2;








由式(5)~(9)求得整个区域的风速和压强等流场数据,再结合扬尘颗粒的粒径、位置和速度等,计算每个颗粒的运行轨道。考虑到颗粒对连续相介质的反作用及颗粒之间的耗散,模拟时引入双向耦合算法和随机轨道模型[23-24]。
1.5. 工程概况
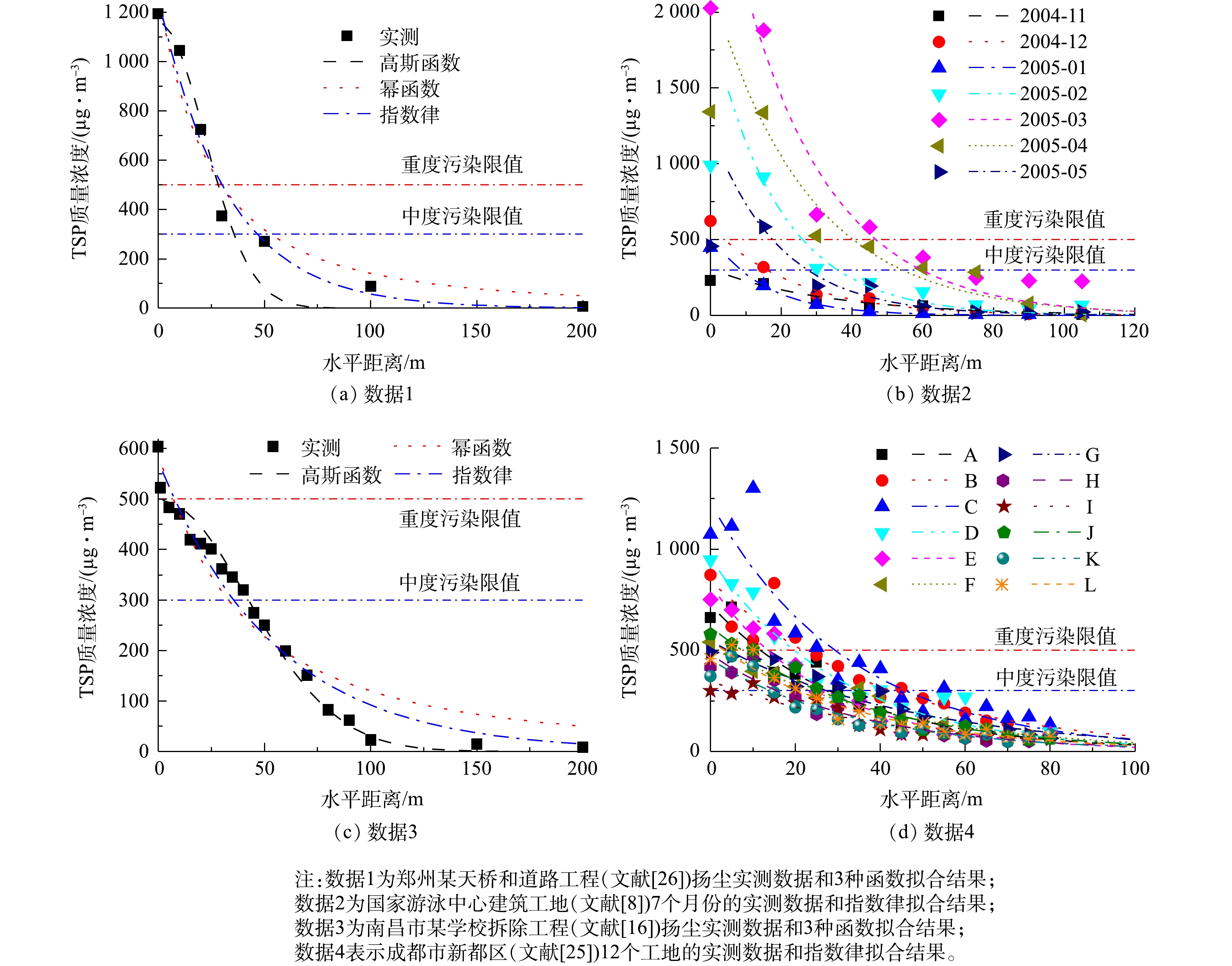
为对比各扬尘扩散数学模型的准确性,选取多个工地及施工阶段(拆除旧建筑、土方施工和主体结构施工等)水平和垂直方向扬尘监测数据[8, 16, 25-26]进行综合分析,结果见表1。表中数据来源广泛,可保证模型验证结果的可靠性与普遍性。2.1. 扬尘在水平方向的扩散规律
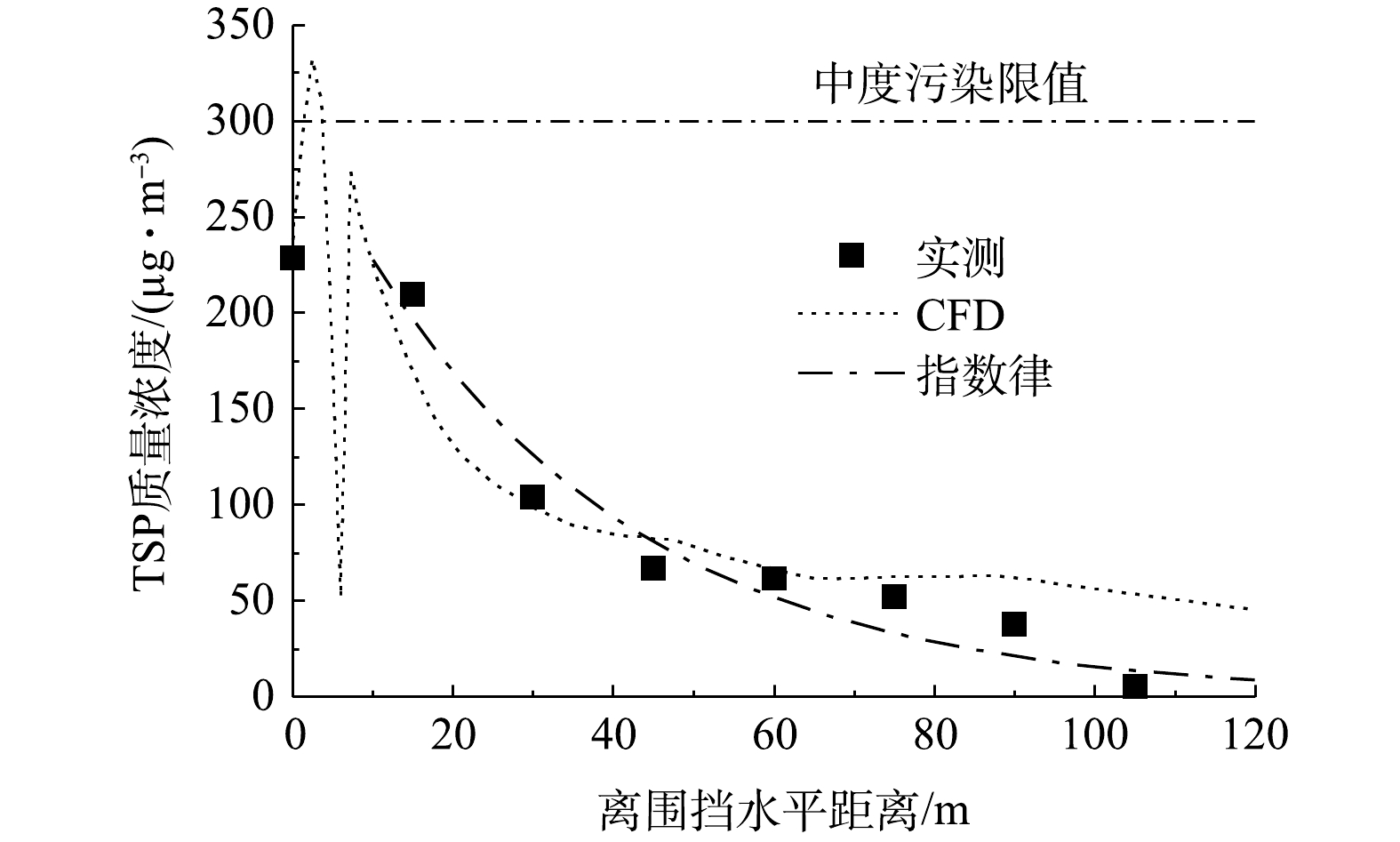
根据表1第2栏中数据1~4,应用模型(1)~(3)对比分析了特定气象要素和施工条件下施工扬尘沿水平方向的扩散规律。为便于分析,以扬尘健康损害评估指标TSP浓度为基准[28],将扬尘浓度监测数据统一。其中,数据1、3、4为TSP浓度,无需变换;数据2为DF浓度,可根据TSP与DF的关系式[21]进行变换。其可行性是由于变换模型由北京市6个工地实测数据拟合得到,且数据2所在工地位于拟合区域内;另外,变换基于线性关系式,故不会影响扬尘浓度衰减曲线,若DF浓度满足指数律衰减形式,变换后仍满足指数律衰减。为便于分级管控,将扬尘TSP浓度为500 μg·m?3和300 μg·m?3设定为限值,超过相应限值分别表示重度和中度污染区域。由第2栏数据1~4得到的水平方向扬尘浓度扩散拟合结果如图1所示。其中,由于数据量较大,数据2和4只显示指数律拟合结果。由图1可知,扬尘浓度随水平距离的增加呈衰减趋势,基本在100 m左右趋于稳定。因此,指数律扩散模型可较准确地描述扬尘浓度在水平方向的扩散规律。
第2栏数据1~4包含15个工地的21组扬尘监测数据,可用于3种扩散模型的综合对比分析。图2为模型误差对比箱线图。由图2可知,幂函数和指数律模型拟合得到的RMSE误差波动较小,且均值均小于60 μg·m?3,R2的均值大于0.93;高斯模型拟合得到的RMSE误差较大,且R2的均值远小于1,效果较差。综上所述,高斯模型不适于模拟水平方向的扬尘扩散规律,而幂函数和指数律模型更适于描述扬尘浓度在水平方向的扩散规律,且稳定性更好。
2.2. 扬尘垂直方向扩散规律
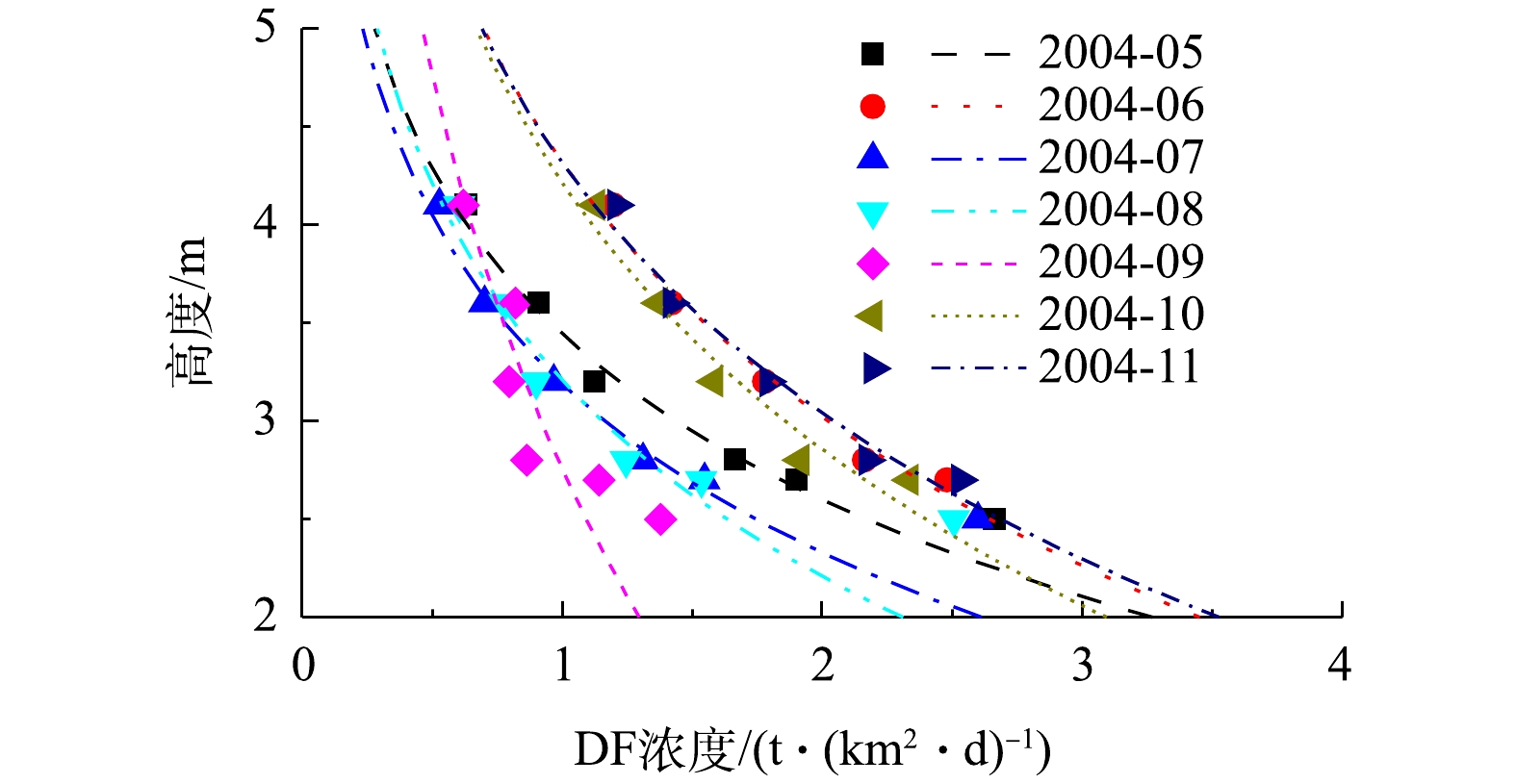
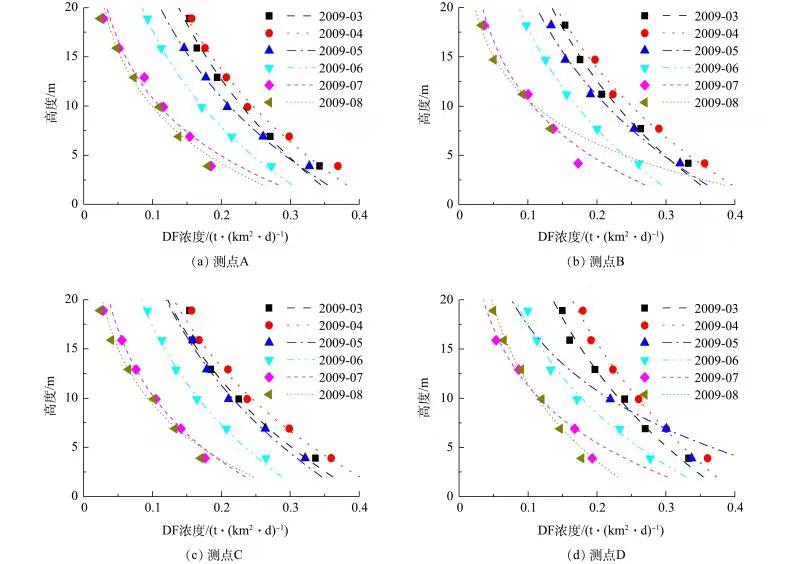
根据表1中第2栏数据5~6,应用模型(1)~(3)对比分析特定气象要素和施工条件下施工扬尘沿垂直方向的扩散规律,结果见图3~4。指数律模型表明,扬尘浓度随水平高度增加逐渐衰减,达到稳定所需高度与具体施工强度和高度等因素相关[8]。图3表明,2004年5—6月的土方施工期间,车辆的往来运输导致近地面扬尘浓度最高;而图4表明,相同月份时4个测点的垂直向扬尘浓度分布基本相同,表明扬尘在该监测点水平方向较均匀。相同高度下,3—5月扬尘浓度最高,6月次之,7—8月最低。这是由于不同月份对应的施工内容不同:3—5月为土方回填和基坑开挖阶段,车辆来往运输频繁,产生扬尘量最多;6月为主体施工阶段,木模板加工产生的扬尘较多,且无法扩散;7—8月为水电安装阶段,产生扬尘最少。不同阶段扬尘浓度不同,达到稳定所需高度亦不同,但沿高度衰减的速率基本一致,故相同施工阶段下,施工区域垂直向扬尘扩散规律基本一致。综上所述,不同施工阶段,施工区域的垂直向扬尘浓度不同,土方施工时最大,主体施工时次之,装修阶段最小,然而各阶段的衰减速率相差不大。第2栏数据5~6包含2个工地的36组扬尘监测数据,各模型误差对比结果见图5。由图5可知,指数律模型拟合的RMSE误差波动较小,且均值小于0.03 t·(km2·d)?1,R2均值大于0.97;高斯函数和幂函数模型拟合RMSE误差较大,且波动性大。因此,幂函数和高斯函数模型对于垂直方向扬尘扩散规律的适用性较差,而指数律模型的适用性与稳定性均较好。
2.3. 扬尘空间扩散规律
指数律模型适用于描述扬尘水平和垂直方向一维扩散规律,幂函数模型仅适用于水平方向,高斯函数模型则均不太适用。为验证指数律模型在扬尘空间扩散规律上的准确性,得到式(4)形式的空间扩散数学模型,选取2004年11月国家游泳中心建筑工地的扬尘监测数据[8]进行数值模拟分析,模拟扬尘颗粒空间扩散的整个过程。该工地数据可靠性较高,相关实验参数清晰具体,便于进行数值模拟。2.3.1. 数值模拟计算域及参数设置
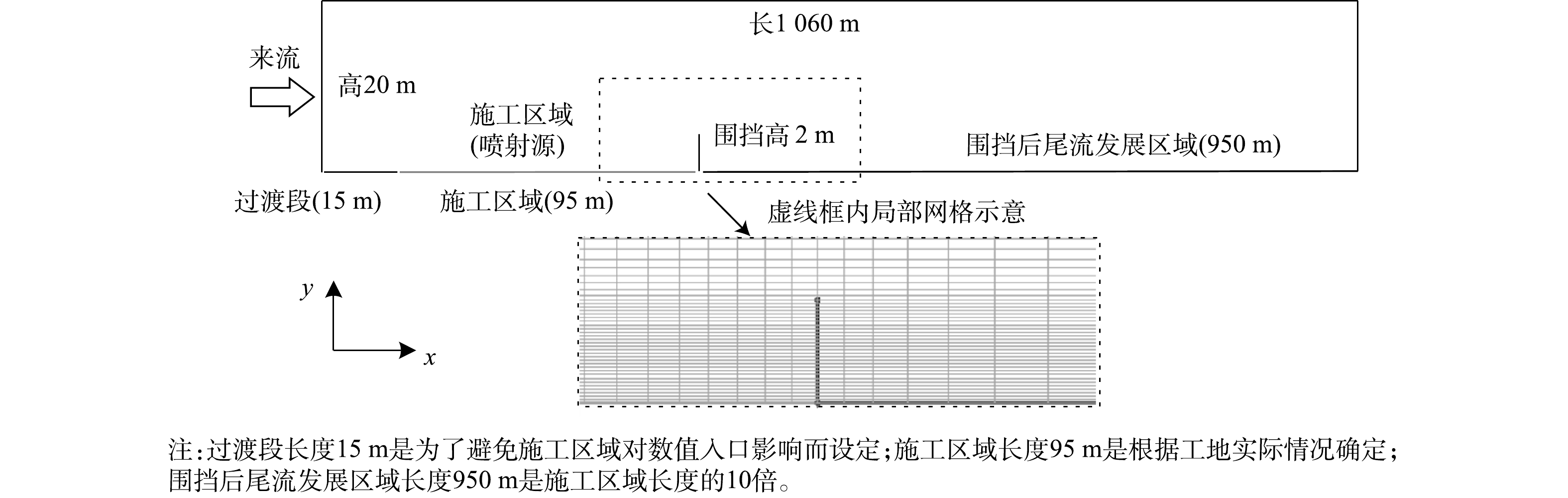
用Fluent软件对该工地的数据进行数值建模,截取该工地中间面得到简化的二维模型[29-30](结果见图6)。工地顺风向长度约为95 m,围挡高2 m。为避免数值边界的影响,在施工区域迎风口设定15 m的过渡区域,在围挡后设定10倍施工区域长度(950 m)的尾流发展区;设定计算域高度为10倍围挡高度。因此,计算域尺寸x × y为1 060 m × 20 m,其中x为顺风向,y为竖向,沿x、y方向分别划分205、88个网格,计算域网格数总计1.8×104。从气象数据网(http://data.sheshiyuanyi.com/WeatherData/)得到北京市海淀区气象站(气象站点编号54511)2004年11月的日平均风速,得到月平均风速为2.2 m·s?1,风力等级为2级(1.6~3.3 m·s?1)。该气象站测点距离地面31.3 m,根据建筑结构荷载规范(GB 50009-2012)[31],该工地所处地貌为B类标准地貌,入口边界条件定义见式(10)~(13)[32-33]。
式中:yr=31.3 m,Ur=2.2 m·s?1,


出口边界设定为压力出口,顶部边界为对称边界,入口为速度入口,地面除施工区域外均设定为无滑移的固壁,围挡为固壁;施工区域设定为扬尘粒子的面喷射源,边界条件为速度入口。扬尘颗粒粒径分布采用Rosin-Rammler分布曲线[34],计算模型及扬尘颗粒相关参数见表2[7]。为保证结果的稳定性,模拟共进行8 000步,选择后1 000步的扬尘浓度模拟结果取其平均值。
2.3.2. 数值模拟结果的验证
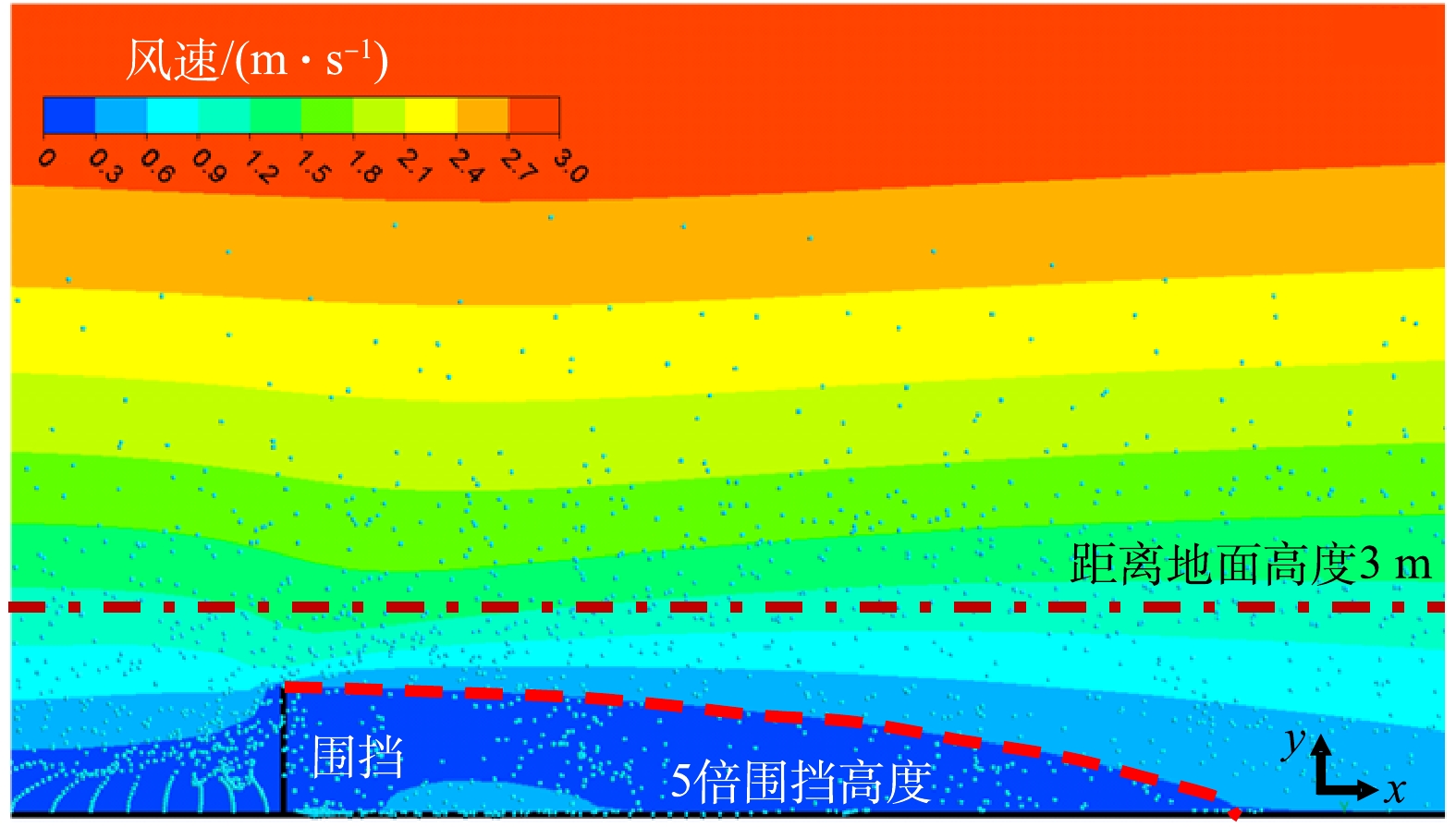
为验证数值模拟结果的准确性,将扬尘浓度CFD模拟结果与实测结果进行了对比(结果见图7)。由图7可知,CFD模拟能较好预测扬尘浓度的空间分布,与实测结果吻合较好,具有一定的可靠性。然而,由于实测数据布置测点水平间距过大,无法精确得到0~15 m范围内的扬尘浓度,但CFD模拟能准确预测其变化趋势。另外,由于围挡的阻挡效应,围挡后面0~2 m内扬尘颗粒大量集中,扬尘浓度较高;2~6 m内,因扬尘颗粒重力作用及相互之间的湍流影响,扬尘浓度急剧下降;6~10 m内,风迁移作用使扬尘浓度升高;距离大于10 m后,扬尘颗粒受重力作用主导,浓度逐渐衰减至稳定。围挡高度为2 m,扬尘浓度在5倍围挡高度之后不再受围挡影响。图8为数值模拟下扬尘颗粒的空间分布图。扬尘颗粒基本集中在3 m高度范围内,特别是围挡后的区域聚集的扬尘颗粒物最多。根据前面的分析结果及平均风速云图,围挡的影响范围约为5倍围挡高度之内,在大于该范围的区域,扬尘颗粒的分布主要受重力作用影响。
2.3.3. 扬尘空间扩散模型验证
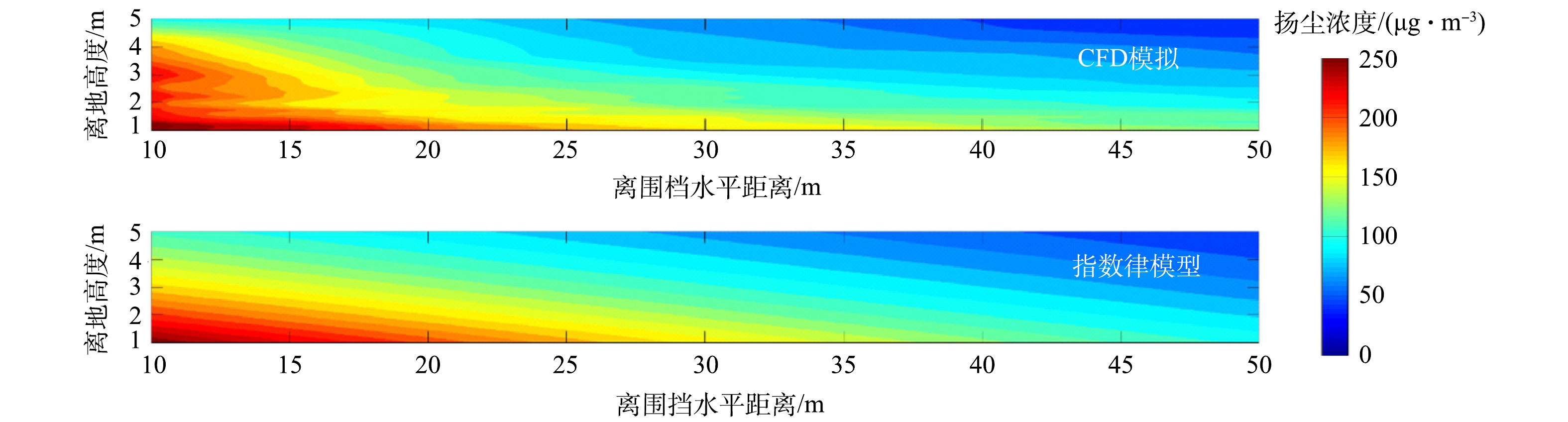
为验证指数律模型(4)在描述扬尘空间扩散上的准确性与适用性,将CFD模拟的扬尘浓度分布结果拟合得到模型(4)。由2.1节可知,扬尘浓度在离工地水平距离100 m左右基本趋于稳定,为避免围挡影响并考虑人类的呼吸高度范围,取CFD模拟结果在围挡后水平范围为[10 m,100 m]、高度范围为[1 m,5 m]进行拟合,对比结果如图9所示。CFD模拟得到的扬尘浓度空间分布与指数律形式基本一致,拟合得到的指数律模型见式(14)。该模型的拟合误差RMSE仅为11.3 μg·m?3,R2为0.933。因此,研究所提出的指数律模型(4)可用于描述扬尘空间扩散规律,适用范围为离围挡水平距离为5H~100 m(H为围挡高度)、高度距离为呼吸高度1~5 m构成的区域,其中的指数律模型参数a、b和c取值与施工阶段、施工强度、风速、空气温度、空气湿度等相关,详细关系有待进一步研究。
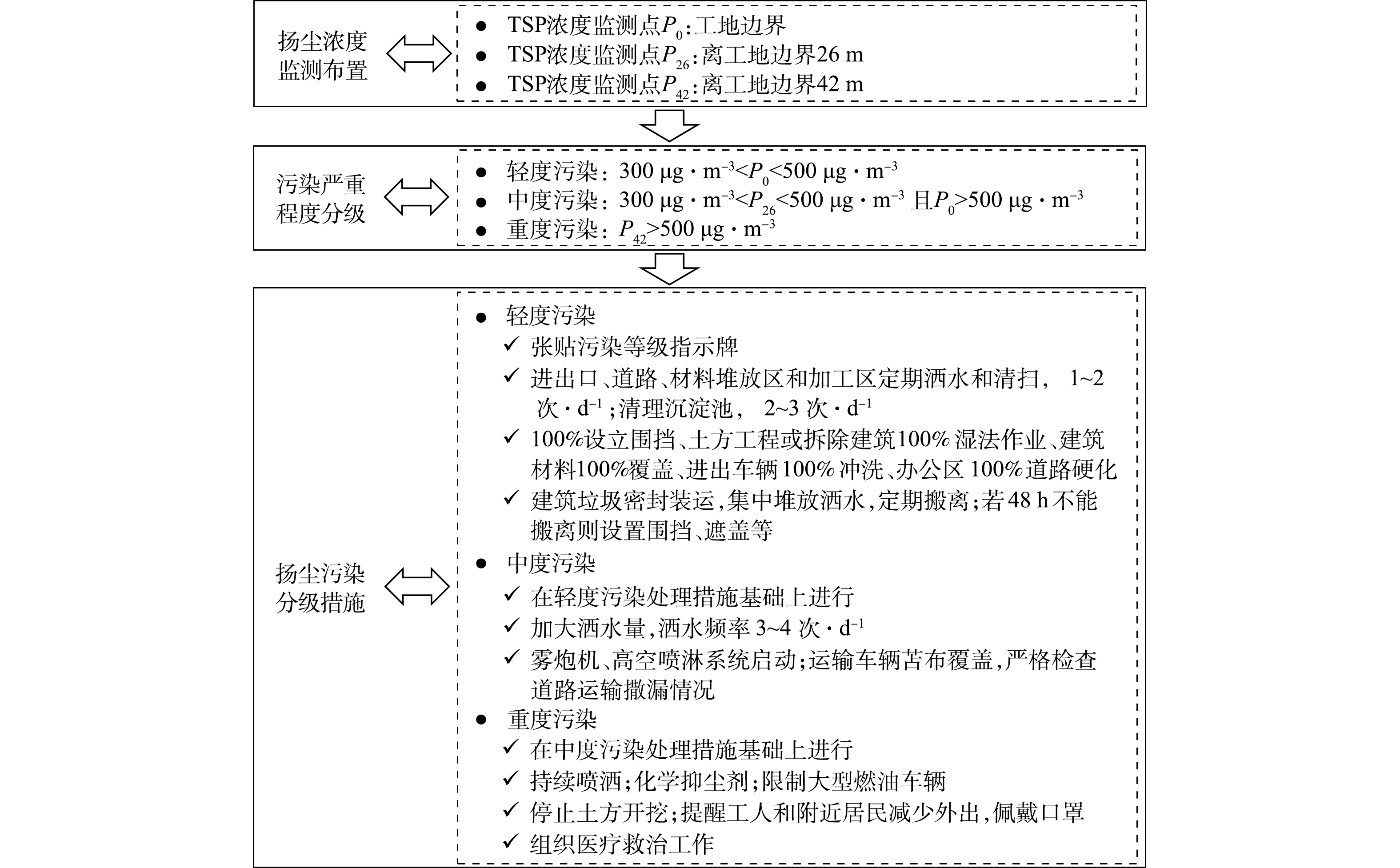
为明确施工扬尘污染程度分级标准,根据水平方向上扬尘浓度在呼吸高度范围内的大小,将工地周围区域划分功能区,并分别设置监测点,以多个监测点的扬尘浓度为评估指标,确定施工扬尘污染等级。根据《环境空气质量标准》(GB 3095-1996)[35]将环境空气质量功能区分为3类:第1、2和3类分别为自然保护区、居住区和特定工业区,对应TSP质量浓度限值分别为120、300和500 μg·m?3。2012年的新标准[36]将第3类环境空气质量功能区取消,保持其他2类功能区不变。由于建筑施工区域通常位于居住区,同时考虑扬尘污染强度精细划分,将扬尘质量浓度进行分为3类:1)重度污染——TSP质量浓度超过500 μg·m?3;2)中度污染——TSP质量浓度在300 μg·m?3和500 μg·m?3之间;3)轻度污染——TSP质量浓度小于300 μg·m?3。
由2.1可知,施工扬尘最远影响水平距离为100 m左右,超出此范围的区域可认为完全不受施工扬尘影响。根据2.3.3中的结果,施工区域围挡的水平影响距离约为围挡高度的5倍数值,在此范围内可认为受到施工扬尘的影响最严重,为重度污染区;另外,根据规定围挡高度不得低于1.8 m[37],即重度污染区至少为围挡水平距离9 m范围内。根据以上条件,基于表1第1栏数据1~4进行污染区域分级结果,整理得到图10。
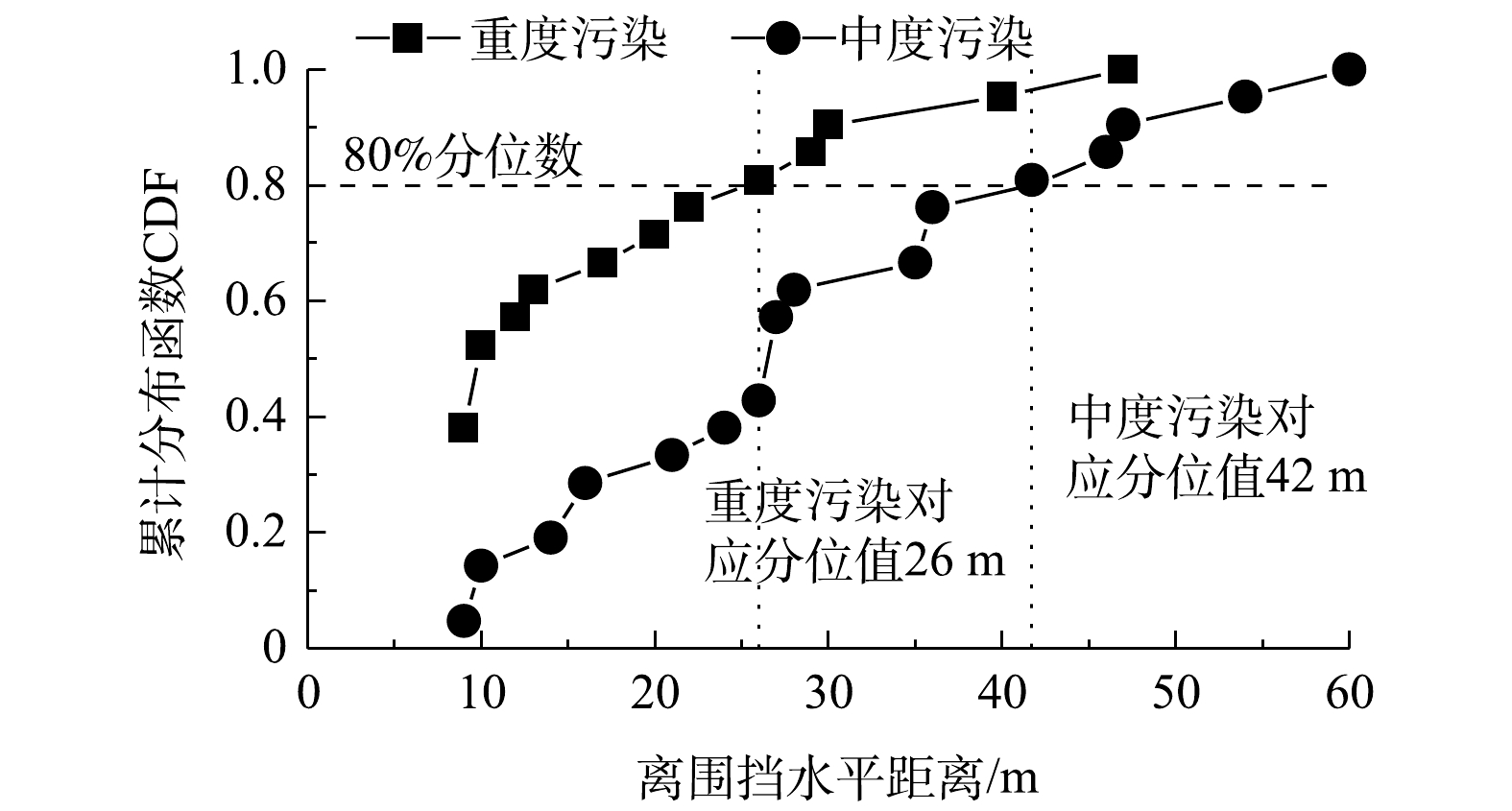
由图10可知,对于表1第2栏数据1~4的21组数据,重度污染影响最远水平距离为9~46 m,中度污染影响最远为9~60 m。若取80%分位数[38]作为相应影响区域的评判标准,则重度污染最远距离为26 m,中度污染最远距离为42 m,即离围挡水平距离为0~26 m、26~42 m和42~100 m分别对应重度、中度和轻度污染区域。因此,在这3个区域布置相应测点,根据其扬尘浓度综合评估空气污染严重程度等级,并采取对应降尘控制措施,具体实施步骤见图11。该方法依据扬尘污染严重程度进行分级管控,可缩减抑尘成本,提高控尘效果。此外,扬尘防治工作还应组织开展防止空气污染对人体健康影响的知识宣传,指导健康防护及空气污染控制措施,帮助公众提高防尘意识和手段,最大程度降低施工扬尘造成的危害。
2)围挡对扬尘浓度的水平影响距离约为5倍围挡高度;CFD模拟结果验证了提出的施工扬尘指数律空间扩散模型的准确性,发现目标工地扬尘TSP质量浓度=397.2exp{?0.023x?0.204y};模型参数与施工阶段、施工强度、风速、空气温度和空气湿度等因素有关,变化较大。
3)根据施工扬尘影响程度,将施工区域周围划分为重度污染区(<26 m)、中度污染区(26~42 m)和轻度污染区(42~100 m);提出了综合评估扬尘污染严重程度的方法,并详细阐述了相应的扬尘分级管理控制措施,以最大程度提高环境空气质量,改善居民居住和出行环境。
参考文献
 下载:
下载: 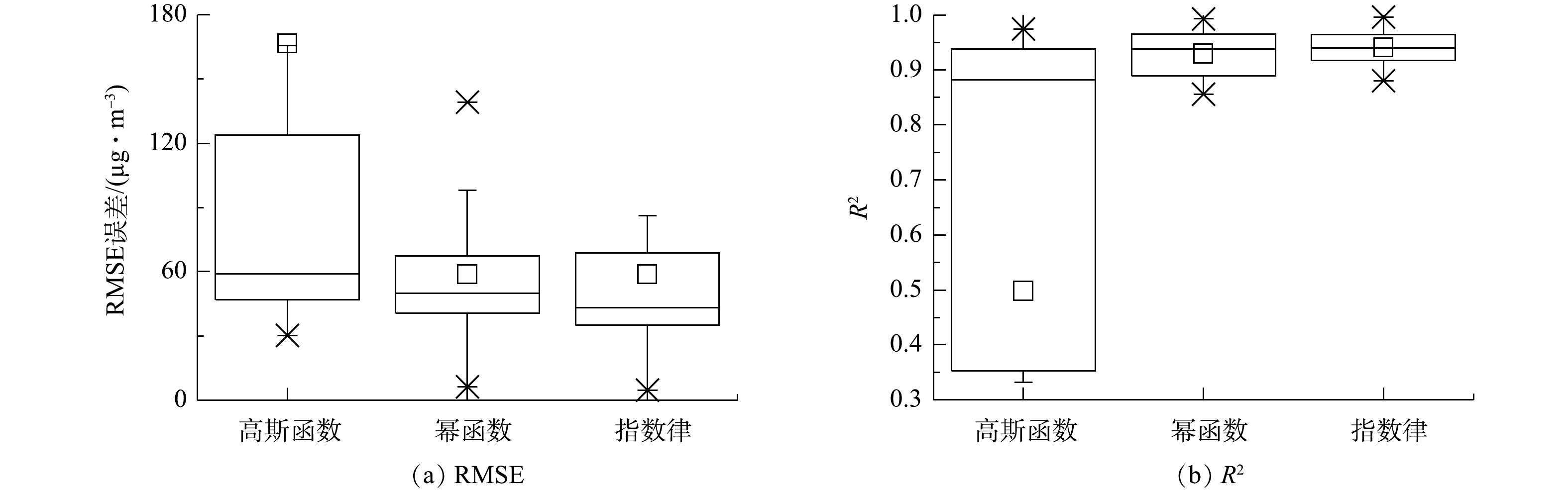

 点击查看大图
点击查看大图