任赫, 陈平()

北京师范大学中国基础教育质量监测协同创新中心, 北京 100875

收稿日期:2020-06-04出版日期:2021-09-25发布日期:2021-07-22
通讯作者:陈平E-mail:pchen@bnu.edu.cn

基金资助:国家自然科学基金面上项目(32071092);中国基础教育质量监测协同创新中心基础教育质量监测科研基金项目(2019-01-082-BZK01);中国基础教育质量监测协同创新中心基础教育质量监测科研基金项目(2019-01-082-BZK02);中国基础教育质量监测协同创新中心自主课题(BJZK-2019A2-19003)

Two new termination rules for multidimensional computerized classification testing

REN He, CHEN Ping()

Collaborative Innovation Center of Assessment for Basic Education Quality, Beijing Normal University, Beijing 100875, China

Received:2020-06-04Online:2021-09-25Published:2021-07-22
Contact:CHEN Ping E-mail:pchen@bnu.edu.cn

摘要/Abstract

摘要： 计算机化分类测验(Computerized Classification Testing, CCT)由于具备分类的功能, 目前在职业资格考试、健康与护理问卷等以分类为目的的测验中得到广泛应用。作为CCT的重要组成部分, 终止规则不仅决定测验停止的条件而且直接影响分类准确率及测验效率。然而, 目前少有研究对多维CCT (Mulitidimensional CCT, MCCT)的终止规则进行探索。针对已有MCCT终止规则的不足, 提出两种新的MCCT终止规则(即基于马氏距离的多维序贯似然比规则Mahalanobis-SPRT和随机缩减的多维广义似然比规则M-SCGLR), 并开展模拟研究在不同实验条件下(比如, 不同的题库结构、能力维度间相关及分界函数)考查它们的表现。结果表明：(1)在使用补偿性分界函数的条件下, Mahalanobis-SPRT规则具有较高的分类精度和与同类方法相近的测验长度; (2)在几乎所有实验条件下, M-SCGLR规则不仅在测验精度上大幅优于已有的多维随机缩减规则, 而且具有较短的测验长度。

图/表 7

图1二维情境下某名被试的能力估计值随作答题数的变化图
图1二维情境下某名被试的能力估计值随作答题数的变化图


表1研究1中各参数的描述统计表

统计量	题库1(题目内多维)				题库2(题目间多维)				被试(ρ=0)		被试(ρ=0.5)		被试(ρ=0.8)
	a1	a2	d	c	a1	a2	d	c	θ1	θ2	θ1	θ2	θ1	θ2
平均数	1.103	1.098	0.086	0.200	0.830	0.833	0.131	0.200	-0.010	0.021	0.022	0.006	-0.016	-0.025
标准差	0.428	0.414	4.348	0.000	0.839	0.842	3.336	0.000	0.998	0.996	1.011	0.991	0.999	1.000
最小值	0.038	0.040	-9.327	0.200	0.000	0.000	-6.281	0.200	-3.331	-3.125	-3.614	-3.196	-4.016	-3.267
最大值	2.285	2.065	8.873	0.200	2.196	2.329	7.220	0.200	3.252	3.332	4.269	3.071	3.264	3.712
相关系数矩阵	1	-0.782	-0.011	—	1	-0.981	-0.001	—	1	-0.002	1	0.486	1	0.803
	0.782	1	0.009	—	-0.981	1	0.004	—	-0.002	1	0.486	1	0.803	1
	-0.011	0.009	1	—	-0.001	0.004	1	—	—	—	—	—	—	—

表1研究1中各参数的描述统计表

统计量	题库1(题目内多维)				题库2(题目间多维)				被试(ρ=0)		被试(ρ=0.5)		被试(ρ=0.8)
	a1	a2	d	c	a1	a2	d	c	θ1	θ2	θ1	θ2	θ1	θ2
平均数	1.103	1.098	0.086	0.200	0.830	0.833	0.131	0.200	-0.010	0.021	0.022	0.006	-0.016	-0.025
标准差	0.428	0.414	4.348	0.000	0.839	0.842	3.336	0.000	0.998	0.996	1.011	0.991	0.999	1.000
最小值	0.038	0.040	-9.327	0.200	0.000	0.000	-6.281	0.200	-3.331	-3.125	-3.614	-3.196	-4.016	-3.267
最大值	2.285	2.065	8.873	0.200	2.196	2.329	7.220	0.200	3.252	3.332	4.269	3.071	3.264	3.712
相关系数矩阵	1	-0.782	-0.011	—	1	-0.981	-0.001	—	1	-0.002	1	0.486	1	0.803
	0.782	1	0.009	—	-0.981	1	0.004	—	-0.002	1	0.486	1	0.803	1
	-0.011	0.009	1	—	-0.001	0.004	1	—	—	—	—	—	—	—

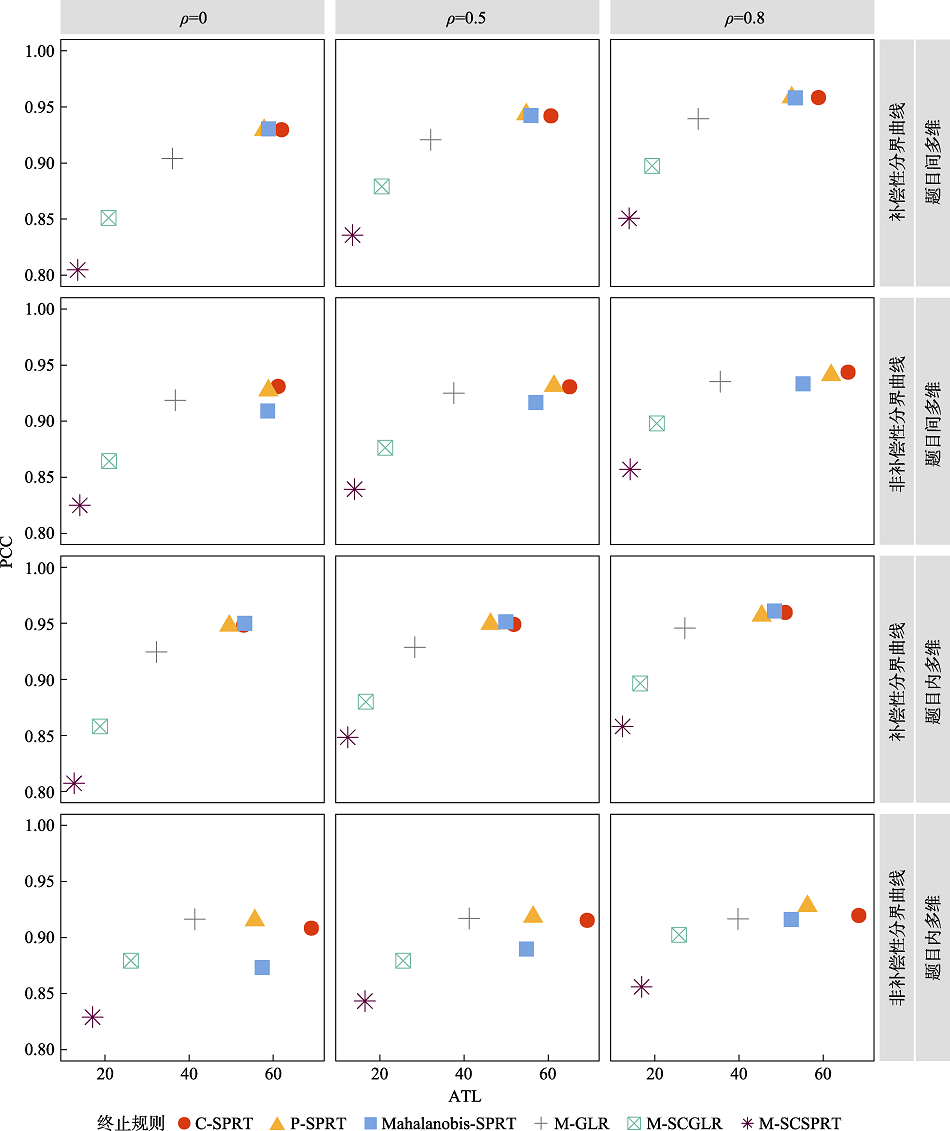
图26种终止规则在各种测验情境下的结果对比图
图26种终止规则在各种测验情境下的结果对比图



图36种终止规则在各种测验情境下的标准化平均损失变化图
图36种终止规则在各种测验情境下的标准化平均损失变化图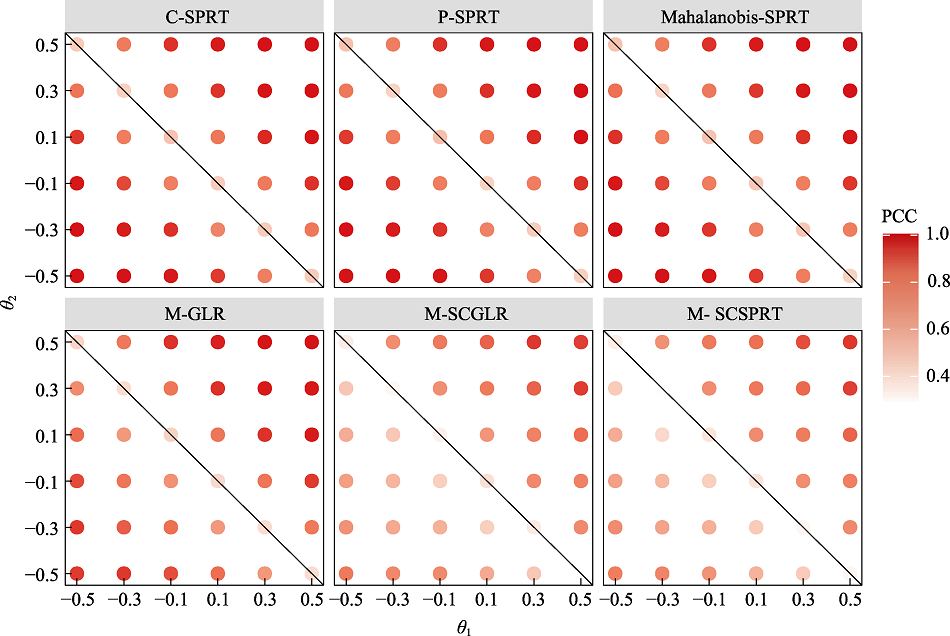



图4能力为各种特定值的被试在补偿性边界下6种终止规则的PCC结果
图4能力为各种特定值的被试在补偿性边界下6种终止规则的PCC结果



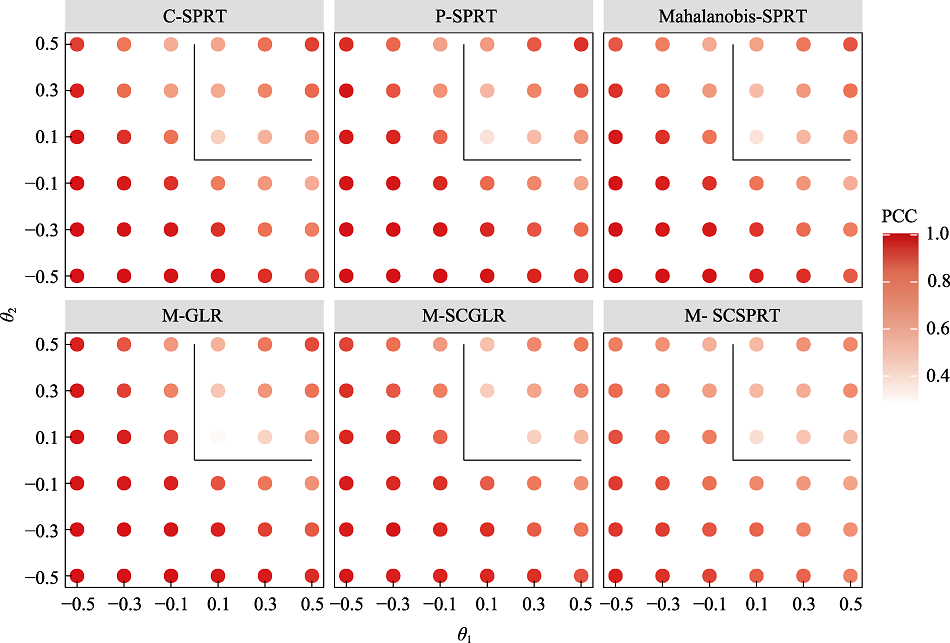
图5能力为各种特定值的被试在非补偿性边界下6种终止规则的PCC结果
图5能力为各种特定值的被试在非补偿性边界下6种终止规则的PCC结果


附表2图2所对应的模拟结果

相关	分界曲线	题库结构	终止规则	PCC	ATL
ρ=0	补偿性	题目内多维	C-SPRT	0.948	52.959
			P-SPRT	0.948	49.541
			Mahalanobis-SPRT	0.950	53.216
			M-GLR	0.924	32.241
			M-SCGLR	0.858	18.849
			M-SCSPRT	0.807	12.649
		题目间多维	C-SPRT	0.930	61.981
			P-SPRT	0.929	57.835
			Mahalanobis-SPRT	0.930	58.876
			M-GLR	0.904	36.016
			M-SCGLR	0.851	20.848
			M-SCSPRT	0.805	13.504
	非补偿性	题目内多维	C-SPRT	0.908	69.070
			P-SPRT	0.915	55.622
			Mahalanobis-SPRT	0.873	57.369
			M-GLR	0.916	41.331
			M-SCGLR	0.879	26.151
			M-SCSPRT	0.829	17.048
		题目间多维	C-SPRT	0.931	61.163
			P-SPRT	0.927	58.847
			Mahalanobis-SPRT	0.909	58.686
			M-GLR	0.919	36.718
			M-SCGLR	0.864	20.974
			M-SCSPRT	0.825	14.012
ρ=0.5	补偿性	题目内多维	C-SPRT	0.949	51.839
			P-SPRT	0.949	46.301
			Mahalanobis-SPRT	0.951	49.922
			M-GLR	0.929	28.306
			M-SCGLR	0.880	16.641
			M-SCSPRT	0.848	12.333
		题目间多维	C-SPRT	0.942	60.648
			P-SPRT	0.943	54.795
			Mahalanobis-SPRT	0.942	55.901
			M-GLR	0.921	32.052
			M-SCGLR	0.879	20.429
			M-SCSPRT	0.836	13.478
	非补偿性	题目内多维	C-SPRT	0.915	69.277
			P-SPRT	0.918	56.422
			Mahalanobis-SPRT	0.890	54.840
			M-GLR	0.917	41.205
			M-SCGLR	0.879	25.501
			M-SCSPRT	0.843	16.417
相关	分界曲线	题库结构	终止规则	PCC	ATL
ρ=0.5	非补偿性	题目间多维	C-SPRT	0.931	65.105
			P-SPRT	0.931	61.374
			Mahalanobis-SPRT	0.917	57.084
			M-GLR	0.925	37.549
			M-SCGLR	0.876	21.250
			M-SCSPRT	0.839	13.966
R	补偿性	题目内多维	C-SPRT	0.960	50.987
			P-SPRT	0.957	45.382
			Mahalanobis-SPRT	0.961	48.457
			M-GLR	0.946	27.139
			M-SCGLR	0.896	16.513
			M-SCSPRT	0.858	12.313
		题目间多维	C-SPRT	0.958	58.903
			P-SPRT	0.958	52.540
			Mahalanobis-SPRT	0.958	53.414
			M-GLR	0.939	30.312
			M-SCGLR	0.897	19.343
			M-SCSPRT	0.851	13.860
	非补偿性	题目内多维	C-SPRT	0.920	68.485
			P-SPRT	0.928	56.274
			Mahalanobis-SPRT	0.916	52.433
			M-GLR	0.917	39.755
			M-SCGLR	0.902	25.742
			M-SCSPRT	0.856	16.835
		题目间多维	C-SPRT	0.944	65.928
			P-SPRT	0.941	61.900
			Mahalanobis-SPRT	0.933	55.232
			M-GLR	0.935	35.541
			M-SCGLR	0.898	20.446
			M-SCSPRT	0.857	14.111

附表2图2所对应的模拟结果

相关	分界曲线	题库结构	终止规则	PCC	ATL
ρ=0	补偿性	题目内多维	C-SPRT	0.948	52.959
			P-SPRT	0.948	49.541
			Mahalanobis-SPRT	0.950	53.216
			M-GLR	0.924	32.241
			M-SCGLR	0.858	18.849
			M-SCSPRT	0.807	12.649
		题目间多维	C-SPRT	0.930	61.981
			P-SPRT	0.929	57.835
			Mahalanobis-SPRT	0.930	58.876
			M-GLR	0.904	36.016
			M-SCGLR	0.851	20.848
			M-SCSPRT	0.805	13.504
	非补偿性	题目内多维	C-SPRT	0.908	69.070
			P-SPRT	0.915	55.622
			Mahalanobis-SPRT	0.873	57.369
			M-GLR	0.916	41.331
			M-SCGLR	0.879	26.151
			M-SCSPRT	0.829	17.048
		题目间多维	C-SPRT	0.931	61.163
			P-SPRT	0.927	58.847
			Mahalanobis-SPRT	0.909	58.686
			M-GLR	0.919	36.718
			M-SCGLR	0.864	20.974
			M-SCSPRT	0.825	14.012
ρ=0.5	补偿性	题目内多维	C-SPRT	0.949	51.839
			P-SPRT	0.949	46.301
			Mahalanobis-SPRT	0.951	49.922
			M-GLR	0.929	28.306
			M-SCGLR	0.880	16.641
			M-SCSPRT	0.848	12.333
		题目间多维	C-SPRT	0.942	60.648
			P-SPRT	0.943	54.795
			Mahalanobis-SPRT	0.942	55.901
			M-GLR	0.921	32.052
			M-SCGLR	0.879	20.429
			M-SCSPRT	0.836	13.478
	非补偿性	题目内多维	C-SPRT	0.915	69.277
			P-SPRT	0.918	56.422
			Mahalanobis-SPRT	0.890	54.840
			M-GLR	0.917	41.205
			M-SCGLR	0.879	25.501
			M-SCSPRT	0.843	16.417
相关	分界曲线	题库结构	终止规则	PCC	ATL
ρ=0.5	非补偿性	题目间多维	C-SPRT	0.931	65.105
			P-SPRT	0.931	61.374
			Mahalanobis-SPRT	0.917	57.084
			M-GLR	0.925	37.549
			M-SCGLR	0.876	21.250
			M-SCSPRT	0.839	13.966
R	补偿性	题目内多维	C-SPRT	0.960	50.987
			P-SPRT	0.957	45.382
			Mahalanobis-SPRT	0.961	48.457
			M-GLR	0.946	27.139
			M-SCGLR	0.896	16.513
			M-SCSPRT	0.858	12.313
		题目间多维	C-SPRT	0.958	58.903
			P-SPRT	0.958	52.540
			Mahalanobis-SPRT	0.958	53.414
			M-GLR	0.939	30.312
			M-SCGLR	0.897	19.343
			M-SCSPRT	0.851	13.860
	非补偿性	题目内多维	C-SPRT	0.920	68.485
			P-SPRT	0.928	56.274
			Mahalanobis-SPRT	0.916	52.433
			M-GLR	0.917	39.755
			M-SCGLR	0.902	25.742
			M-SCSPRT	0.856	16.835
		题目间多维	C-SPRT	0.944	65.928
			P-SPRT	0.941	61.900
			Mahalanobis-SPRT	0.933	55.232
			M-GLR	0.935	35.541
			M-SCGLR	0.898	20.446
			M-SCSPRT	0.857	14.111

参考文献 28

[1]	Ackerman T.A. (1994). Creating a test information profile for a two-dimensional latent space. Applied Psychological Measurement, 18(3), 257-275. doi: 10.1177/014662169401800306URL
[2]	Bartroff J., Finkelman M., & Lai T.L. (2008). Modern sequential analysis and its applications to computerized adaptive testing. Psychometrika, 73(3), 473-486. doi: 10.1007/s11336-007-9053-9URL
[3]	Chang H.-H., & Ying Z.L. (1996). A global information approach to computerized adaptive testing. Applied Psychological Measurement, 20(3), 213-229. doi: 10.1177/014662169602000303URL
[4]	Chen P. (2016). Two new online calibration methods for computerized adaptive testing. Acta Psychologica Sinica, 48(9), 1184-1198. doi: 10.3724/SP.J.1041.2016.01184URL
	[ 陈平. (2016). 两种新的计算机化自适应测验在线标定方法. 心理学报, 48(9), 1184-1198.]
[5]	Chen P., & Wang C. (2016). A new online calibration method for multidimensional computerized adaptive testing. Psychometrika, 81(3), 674-701. doi: 10.1007/s11336-015-9482-9URL
[6]	Chen P., Wang C., Xin T., & Chang H.-H. (2017). Developing new online calibration methods for multidimensional computerized adaptive testing. British Journal of Mathematical and Statistical Psychology, 70(1), 81-117. doi: 10.1111/bmsp.12083URL
[7]	Finkelman M. (2003). An adaptation of stochastic curtailment to truncate Wald’s SPRT in computerized adaptive testing (CSE Report 606). Los Angeles, CA: National Center for Research on Evaluation, Standards, and Student Testing.
[8]	Finkelman M. (2008). On using stochastic curtailment to shorten the SPRT in sequential mastery testing. Journal of Educational and Behavioral Statistics, 33(4), 442-463.
[9]	Finkelman M.D. (2010). Variations on stochastic curtailment in sequential mastery testing. Applied Psychological Measurement, 34(1), 27-45. doi: 10.1177/0146621609336113URL
[10]	Finkelman M.D., He Y.L., Kim W., & Lai A.M. (2011). Stochastic curtailment of health questionnaires: A method to reduce respondent burden. Statistics in Medicine, 30(16), 1989-2004. doi: 10.1002/sim.4231pmid: 21520454
[11]	Guo L., Zheng C.J., & Bian Y.F. (2015). Exposure control methods and termination rules in variable-length cognitive diagnostic computerized adaptive testing. Acta Psychologica Sinica, 47(1), 129-140. doi: 10.3724/SP.J.1041.2015.00129URL
	[ 郭磊, 郑蝉金, 边玉芳. (2015). 变长CD-CAT中的曝光控制与终止规则. 心理学报, 47(1), 129-140.]
[12]	Hartig J., & Höhler J. (2008). Representation of competencies in multidimensional IRT models with within-item and between-item multidimensionality. Journal of Psychology, 216(2), 89-101.
[13]	Huebner A.R., & Fina A.D. (2015). The stochastically curtailed generalized likelihood ratio: A new termination criterion for variable-length computerized classification tests. Behavior Research Methods, 47(2), 549-561. doi: 10.3758/s13428-014-0490-ypmid: 24907003
[14]	Kang C.H., & Xin T. (2010). New development in test theory: multidimensional item response theory. Advances in Psychological Science, 18(3), 530-536.
	[ 康春花, 辛涛. (2010). 测验理论的新发展: 多维项目反应理论. 心理科学进展, 18(3), 530-536.]
[15]	Lewis C., & Sheehan K. (1990). Using Bayesian decision theory to design a computerized mastery test. Applied Psychological Measurement, 14(4), 367-386. doi: 10.1177/014662169001400404URL
[16]	Li X., Zhang J.M., & Chang H.-H. (2020). Look-ahead content balancing method in variable-length computerized classification testing. British Journal of Mathematical and Statistical Psychology, 73(1), 88-108. doi: 10.1111/bmsp.v73.1URL
[17]	Nydick S.W. (2013). Multidimensional mastery testing with CAT (Unpublished doctoral dissertation). University of Minnesota.
[18]	Reckase M.D., & McKinley R.L. (1982). Some latent trait theory in a multidimensional latent space. Iowa City, IA: American College Service.
[19]	Segall D.O. (1996). Multidimensional adaptive testing. Psychometrika, 61(2), 331-354. doi: 10.1007/BF02294343URL
[20]	Siegmund D. (1985). Sequential analysis: Tests and confidence intervals. Springer-Verlag.
[21]	Smits N., & Finkelman M. (2013). A comparison of computerized classification testing and computerized adaptive testing in clinical psychology. Journal of Computerized Adaptive Testing, 1, 19-37.
[22]	Thompson N.A. (2010, June). Nominal error rates in computerized classification testing. Paper presented at the first annual conference of the International Association for Computerized Adaptive Testing, Arnhem, the Netherlands.
[23]	Thompson N.A. (2011). Termination criteria for computerized classification testing. Practical Assessment, Research, & Evaluation, 16(4), 1-7.
[24]	Wald A. (1947). Sequential analysis. John Wiley.
[25]	Wald A., & Wolfowitz J. (1948). Optimum character of the sequential probability ratio test. The Annals of Mathematical Statistics, 19(3), 326-339.
[26]	Wang C., Chen P., & Huebner A. (2020). Stopping rules for multi-category computerized classification testing. British Journal of Mathematical and Statistical Psychology, 74(2), 184-202. https://doi.org/10.1111/bmsp.12202 doi: 10.1111/bmsp.v74.2URL
[27]	Wang T.Y., & Hanson B.A. (2005). Development and calibration of an item response model that incorporates response time. Applied Psychological Measurement, 29(5), 323-339. doi: 10.1177/0146621605275984URL
[28]	Wang W.C., & Chen P.H. (2004). Implementation and measurement efficiency of multidimensional computerized adaptive testing. Applied Psychological Measurement, 28(5), 295-316. doi: 10.1177/0146621604265938URL

相关文章 6

[1]	汪文义; 宋丽红;丁树良. 复杂决策规则下MIRT的分类准确性和分类一致性[J]. 心理学报, 2016, 48(12): 1612-1624.
[2]	詹沛达;陈平;边玉芳. 使用验证性补偿多维IRT模型进行认知诊断评估[J]. 心理学报, 2016, 48(10): 1347-1356.
[3]	郭磊;郑蝉金;边玉芳. 变长CD-CAT中的曝光控制与终止规则[J]. 心理学报, 2015, 47(1): 129-140.
[4]	杜文久;肖涵敏. 多维项目反应理论等级反应模型[J]. 心理学报, 2012, 44(10): 1402-1407.
[5]	刘红云,骆方,王玥,张玉. 多维测验项目参数的估计：基于SEM与MIRT方法的比较[J]. 心理学报, 2012, 44(1): 121-132.
[6]	涂冬波,蔡艳,戴海琦,丁树良. 多维项目反应理论：参数估计及其在心理测验中的应用[J]. 心理学报, 2011, 43(11): 1329-1340.

PDF全文下载地址:

http://journal.psych.ac.cn/xlxb/CN/article/downloadArticleFile.do?attachType=PDF&id=5045