 ), 毕向阳4(
), 毕向阳4( )
) 1. 广州大学心理系
2. 广州大学心理测量与潜变量建模研究中心
3. 广东省未成年人心理健康与教育认知神经科学实验室, 广州 510006
4. 中国政法大学社会学院, 北京 102249
收稿日期:2017-03-04出版日期:2018-12-15发布日期:2018-10-30通讯作者:王孟成,毕向阳E-mail:wmcheng2006@126.com;necessity@126.com基金资助:*国家自然科学基金(31400904);广州大学“创新强校工程”青年创新人才类项目(2014WQNCX069);广州大学青年拔尖人才培养项目(BJ201715)Regression mixture modeling: Advances in method and its implementation
WANG Meng-Cheng1,2,3( ), BI Xiangyang4(
), BI Xiangyang4( )
) 1. Department of Psychology, Guangzhou University
2. The Center for Psychometric and Latent Variable Modeling, Guangzhou University
3. The Key Laboratory for Juveniles Mental Health and Educational Neuroscience in Guangdong Province, Guangzhou University, Guangzhou 510006, China
4. School of Sociology, China University of Political Science and Law, Beijing 102249, China
Received:2017-03-04Online:2018-12-15Published:2018-10-30Contact:WANG Meng-Cheng,BI Xiangyang E-mail:wmcheng2006@126.com;necessity@126.com摘要/Abstract
摘要: 近来以个体为分析对象的方法日益受到研究者的重视, 其中潜类别和潜剖面模型最为流行。研究者在潜类别和潜剖面模型建模时往往需要进一步探讨协变量与潜分组之间的关系(即带有协变量的潜类别模型)。例如, 哪些变量预测个体类别归属, 以及个体的类别归属对结果变量的预测。本文对近年来研究者提出的各种方法进行了回顾和比较。包括当结果变量是分类变量的LTB法; 当结果变量是连续变量时的BCH和稳健三步法。在此基础上, 文章为应用研究者提供了Mplus软件示例, 并在最后对当前研究存在的问题和未来研究趋势进行了简要评价。
图/表 15
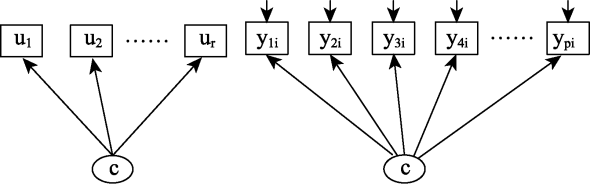
图1LCA和LPA示意图
 图1LCA和LPA示意图
图1LCA和LPA示意图
图2回归混合模型示意图
 图2回归混合模型示意图
图2回归混合模型示意图
图3简单三步法的分析流程
 图3简单三步法的分析流程
图3简单三步法的分析流程
图4稳健三步法分析流程图(Asparouhov&MuthÉn, 2014)
 图4稳健三步法分析流程图(Asparouhov&MuthÉn, 2014)
图4稳健三步法分析流程图(Asparouhov&MuthÉn, 2014)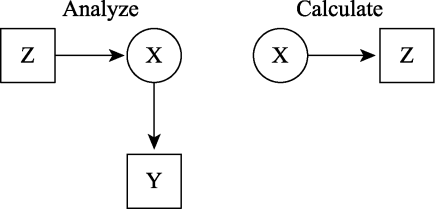
图5LTB法分析示意图
 图5LTB法分析示意图
图5LTB法分析示意图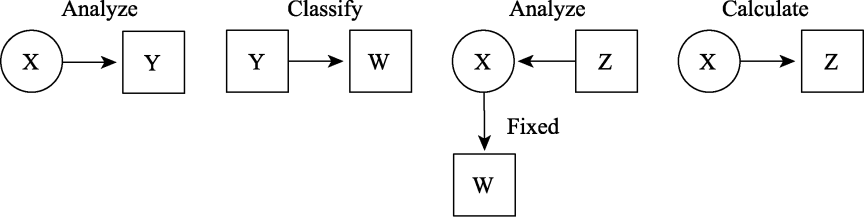
图6修正的LTB法示意图
 图6修正的LTB法示意图
图6修正的LTB法示意图表1各种情况处理方法汇总表
| 适用情况 | 方法 | Mplus语句: Auxiliary=() | 评价 | |
|---|---|---|---|---|
| 结果变量 | 分类 变量 | 单步法 | 无单独语句 | 直接将类别结果变量作为LCA的测量指标; 这种做法显然会影响测量模型; 纳入不同的结果变量会造成测量模型结果的差异, 因此不推荐使用。 |
| LTB | DCAT | 是处理类别结果变量最好的方法之一, 推荐使用。 | ||
| 连续 变量 | 单步法 | 无单独语句 | 非正态时表现不佳。 | |
| BCH | BCH | 是处理连续结果变量最好的方法之一, 在 DU3STEP不报告结果时使用。 | ||
| 稳健三步法:类别方差不等 | DU3STEP | 在结果变量类别内正态分布, 方差不等时表现佳。但会出现类别顺序变化的不足。 | ||
| 稳健三步法:类别方差相等 | DE3STEP | 在结果变量类别内正态分布, 方差相等时表现佳。 | ||
| LTB | DCON | 对假设前提比较敏感, 当假设违反时会扭曲估计结果, 不推荐使用 | ||
| PC method | E | 精确性较差, 不推荐实际使用 | ||
| 预测变量 | PC method | R | 结果有偏, 不推荐使用。 | |
| 单步法 | 无单独语句 | 表现良好, 当变量较多时使用不便。 | ||
| 稳健三步法 | R3STEP | 表现良好, 操作方便, 推荐使用。 | ||
表1各种情况处理方法汇总表
| 适用情况 | 方法 | Mplus语句: Auxiliary=() | 评价 | |
|---|---|---|---|---|
| 结果变量 | 分类 变量 | 单步法 | 无单独语句 | 直接将类别结果变量作为LCA的测量指标; 这种做法显然会影响测量模型; 纳入不同的结果变量会造成测量模型结果的差异, 因此不推荐使用。 |
| LTB | DCAT | 是处理类别结果变量最好的方法之一, 推荐使用。 | ||
| 连续 变量 | 单步法 | 无单独语句 | 非正态时表现不佳。 | |
| BCH | BCH | 是处理连续结果变量最好的方法之一, 在 DU3STEP不报告结果时使用。 | ||
| 稳健三步法:类别方差不等 | DU3STEP | 在结果变量类别内正态分布, 方差不等时表现佳。但会出现类别顺序变化的不足。 | ||
| 稳健三步法:类别方差相等 | DE3STEP | 在结果变量类别内正态分布, 方差相等时表现佳。 | ||
| LTB | DCON | 对假设前提比较敏感, 当假设违反时会扭曲估计结果, 不推荐使用 | ||
| PC method | E | 精确性较差, 不推荐实际使用 | ||
| 预测变量 | PC method | R | 结果有偏, 不推荐使用。 | |
| 单步法 | 无单独语句 | 表现良好, 当变量较多时使用不便。 | ||
| 稳健三步法 | R3STEP | 表现良好, 操作方便, 推荐使用。 | ||
附表1潜类分析Mplus语句
| Title: Lantent Class Analysis Data: File is older_survey.dat ; Variable: Names = C2A C2B C2C C2D C2E C2F C2G C2H C2I C2J C2K C2L C2M C2N C2P C2Q ifold age gds agesq11(11 年龄平方项(/100)); USEVARIABLES = C2A-C2Q; MISSING are all (-9999) ; CATEGORICAL = C2A-C2Q; CLASSES = C (2); Analysis: TYPE = MIXTURE; Starts = 50 3; PROCESSORS = 4; !根据电脑情况指定 PLOT: TYPE = PLOT3; SERIES = C2A-C2Q (*); Savedata: file is older_survey.txt ; save is cprob; output: tech11 tech14; |
附表1潜类分析Mplus语句
| Title: Lantent Class Analysis Data: File is older_survey.dat ; Variable: Names = C2A C2B C2C C2D C2E C2F C2G C2H C2I C2J C2K C2L C2M C2N C2P C2Q ifold age gds agesq11(11 年龄平方项(/100)); USEVARIABLES = C2A-C2Q; MISSING are all (-9999) ; CATEGORICAL = C2A-C2Q; CLASSES = C (2); Analysis: TYPE = MIXTURE; Starts = 50 3; PROCESSORS = 4; !根据电脑情况指定 PLOT: TYPE = PLOT3; SERIES = C2A-C2Q (*); Savedata: file is older_survey.txt ; save is cprob; output: tech11 tech14; |
图7两类别在选项3上的条件概率
 图7两类别在选项3上的条件概率
图7两类别在选项3上的条件概率附表2加入预测变量回归混合模型的Mplus语句
| Title: Regression Mixture Modeling with Predictive Variable Data: File is older_survey.dat ; Variable: Names = C2A C2B C2C C2D C2E C2F C2G C2H C2I C2J C2K C2L C2M C2N C2P C2Q ifold age gdsagesq; USEVARIABLES = C2A-C2Q; MISSING are all (-9999) ; CATEGORICAL = C2A-C2Q; CLASSES = C (2); AUXILIARY = age (R3STEP);!选择稳健三步法 Analysis: TYPE = MIXTURE; PROCESSORS = 4; PLOT:TYPE = PLOT3; SERIES = C2A-C2Q (*); Savedata: file is older_survey.txt ; save is cprob; output: tech11 tech14; |
附表2加入预测变量回归混合模型的Mplus语句
| Title: Regression Mixture Modeling with Predictive Variable Data: File is older_survey.dat ; Variable: Names = C2A C2B C2C C2D C2E C2F C2G C2H C2I C2J C2K C2L C2M C2N C2P C2Q ifold age gdsagesq; USEVARIABLES = C2A-C2Q; MISSING are all (-9999) ; CATEGORICAL = C2A-C2Q; CLASSES = C (2); AUXILIARY = age (R3STEP);!选择稳健三步法 Analysis: TYPE = MIXTURE; PROCESSORS = 4; PLOT:TYPE = PLOT3; SERIES = C2A-C2Q (*); Savedata: file is older_survey.txt ; save is cprob; output: tech11 tech14; |
附表3加入预测变量回归混合模型输出结果(部分)
| TESTS OF CATEGORICAL LATENT VARIABLE MULTINOMIAL LOGISTIC REGRESSIONS USING THE 3-STEP PROCEDURE Two-Tailed Estimate S.E. Est./S.E. P-Value C#1 ON AGE 0.153 0.014 11.219 0.000 Intercepts C#1 -12.935 1.031 -12.541 0.000 |
附表3加入预测变量回归混合模型输出结果(部分)
| TESTS OF CATEGORICAL LATENT VARIABLE MULTINOMIAL LOGISTIC REGRESSIONS USING THE 3-STEP PROCEDURE Two-Tailed Estimate S.E. Est./S.E. P-Value C#1 ON AGE 0.153 0.014 11.219 0.000 Intercepts C#1 -12.935 1.031 -12.541 0.000 |
附表4加入分类结果变量回归混合模型的Mplus语句
| Title: Regression Mixture Modeling with categorical outcome variable Data: File is older_survey.dat ; Variable: Names = C2A C2B C2C C2D C2E C2F C2G C2H C2I C2J C2K C2L C2M C2N C2P C2Q ifold age gdsagesq; USEVARIABLES = C2A-C2Q; MISSING are all (-9999) ; CATEGORICAL = C2A-C2Q; CLASSES = C (2); AUXILIARY = ifold (DCAT);!选择DCAT法 Analysis: TYPE = MIXTURE; PROCESSORS = 4; LRTSTARTS = 2 1 80 16; PLOT: TYPE = PLOT3; SERIES = C2A-C2Q (*); Savedata: file is older_survey.txt ; save is cprob; output: tech11 tech14; |
附表4加入分类结果变量回归混合模型的Mplus语句
| Title: Regression Mixture Modeling with categorical outcome variable Data: File is older_survey.dat ; Variable: Names = C2A C2B C2C C2D C2E C2F C2G C2H C2I C2J C2K C2L C2M C2N C2P C2Q ifold age gdsagesq; USEVARIABLES = C2A-C2Q; MISSING are all (-9999) ; CATEGORICAL = C2A-C2Q; CLASSES = C (2); AUXILIARY = ifold (DCAT);!选择DCAT法 Analysis: TYPE = MIXTURE; PROCESSORS = 4; LRTSTARTS = 2 1 80 16; PLOT: TYPE = PLOT3; SERIES = C2A-C2Q (*); Savedata: file is older_survey.txt ; save is cprob; output: tech11 tech14; |
附表5加入分类结果变量回归混合模型输出结果(部分)
| EQUALITY TESTS OF MEANS/PROBABILITIES ACROSS CLASSES IFOLD Prob S.E. Odds Ratio S.E. 2.5% C.I. 97.5% C.I. Class 1 Category 1 0.265 0.033 1.000 0.000 1.000 1.000 Category 2 0.735 0.0337 2.133 0.389 1.492 3.049 Class 2 Category 1 0.435 0.016 1.000 0.000 1.000 1.000 Category 2 0.565 0.016 1.000 0.000 1.000 1.000 |
附表5加入分类结果变量回归混合模型输出结果(部分)
| EQUALITY TESTS OF MEANS/PROBABILITIES ACROSS CLASSES IFOLD Prob S.E. Odds Ratio S.E. 2.5% C.I. 97.5% C.I. Class 1 Category 1 0.265 0.033 1.000 0.000 1.000 1.000 Category 2 0.735 0.0337 2.133 0.389 1.492 3.049 Class 2 Category 1 0.435 0.016 1.000 0.000 1.000 1.000 Category 2 0.565 0.016 1.000 0.000 1.000 1.000 |
附表6加入连续结果变量回归混合模型的Mplus语句
| Title: Regression Mixture Modeling with continuous outcome variable Data: File is older_survey.dat ; Variable: Names = C2A C2B C2C C2D C2E C2F C2G C2H C2I C2J C2K C2L C2M C2N C2P C2Q ifold age gdsagesq; USEVARIABLES = C2A-C2Q; MISSING are all (-9999); CATEGORICAL = C2A-C2Q; CLASSES = C (2); AUXILIARY = gds (BCH);!选择BCH法 Analysis: TYPE = MIXTURE; PROCESSORS = 4; LRTSTARTS = 2 1 80 16; !配合tech14 PLOT: TYPE = PLOT3; SERIES = C2A-C2Q (*); Savedata: file is older_survey.txt ; save is cprob; output: tech11 tech14; |
附表6加入连续结果变量回归混合模型的Mplus语句
| Title: Regression Mixture Modeling with continuous outcome variable Data: File is older_survey.dat ; Variable: Names = C2A C2B C2C C2D C2E C2F C2G C2H C2I C2J C2K C2L C2M C2N C2P C2Q ifold age gdsagesq; USEVARIABLES = C2A-C2Q; MISSING are all (-9999); CATEGORICAL = C2A-C2Q; CLASSES = C (2); AUXILIARY = gds (BCH);!选择BCH法 Analysis: TYPE = MIXTURE; PROCESSORS = 4; LRTSTARTS = 2 1 80 16; !配合tech14 PLOT: TYPE = PLOT3; SERIES = C2A-C2Q (*); Savedata: file is older_survey.txt ; save is cprob; output: tech11 tech14; |
附表7加入连续结过变量回归混合模型输出结果(部分)
| EQUALITY TESTS OF MEANS ACROSS CLASSES USING THE BCH PROCEDURE WITH 1 DEGREE (S) OF FREEDOM FOR THE OVERALL TEST GDS Mean S.E. Class 1 4.540 0.211 Class 2 2.903 0.075 Chi-Square P-Value Overall test 52.233 0.000 |
附表7加入连续结过变量回归混合模型输出结果(部分)
| EQUALITY TESTS OF MEANS ACROSS CLASSES USING THE BCH PROCEDURE WITH 1 DEGREE (S) OF FREEDOM FOR THE OVERALL TEST GDS Mean S.E. Class 1 4.540 0.211 Class 2 2.903 0.075 Chi-Square P-Value Overall test 52.233 0.000 |
参考文献 16
| 1 | 邱皓政 . ( 2008). 潜在类别模型的原理与技术. 北京: 教育科学出版社. |
| 2 | 张洁婷, 焦璨, 张敏强 . ( 2010). 潜在类别分析技术在心理学研究中的应用. 心理科学进展, 18( 12), 1991-1998. |
| 3 | Asparouhov, T., &MuthÉn, B. ( 2014). Auxiliary variables in mixture modeling: Three-step approaches using M plus. Structural Equation Modeling, 21( 3), 329-341. doi: 10.1080/10705511.2014.915181URL |
| 4 | Asparouhov, T., &MuthÉn, B(2015 ).Auxiliary Variables in Mixture Modeling: Using the BCH Method in Mplus to Estimate a Distal Outcome Model and an Arbitrary Secondary Model.Mplus Web Notes: No.21. Retrieved from |
| 5 | Bakk Z., Oberski D. L., &Vermunt J. K . ( 2016). Relating latent class membership to continuous distal outcomes: Improving the LTB approach and a modified three-step implementation. Structural Equation Modeling, 23( 2), 278-289. doi: 10.1080/10705511.2015.1049698URL |
| 6 | Bakk Z., Tekle F. B., &Vermunt J. K . ( 2013). Estimating the association between latent class membership and external variables using bias-adjusted three-step approaches. Sociological methodology.43( 1), 272-311. |
| 7 | Bakk, Z., &Vermunt, J.K. ( 2016). Robustness of stepwise latent class modeling with continuous distal outcomes. Structural Equation Modeling, 23( 1), 20-31. doi: 10.1080/10705511.2014.955104URL |
| 8 | Bauer, D.J., &Curran, P.J . ( 2003). Distributional assumptions of growth mixture models: Implications for overextraction of latent trajectory classes. Psychological Methods, 8( 3), 338-363. doi: 10.1037/1082-989X.8.3.338URLpmid: 14596495 |
| 9 | Bolck A., Croon M., &Hagenaars J . ( 2004). Estimating latent structure models with categorical variables: One-step versus three-step estimators. Political Analysis, 12( 1), 3-27. doi: 10.1093/pan/mph001URL |
| 10 | Clark, S.L., &MuthÉn, B . ( 2009). Relating latent class analysis results to variables not included in the analysis. Retrieved from |
| 11 | Collins, L.M., &Lanza, S.T . ( 2010). Latent class and latent transition analysis: With applications in the social, behavioral, and health sciences . New York: Wiley. |
| 12 | Lanza S. T., Tan X., & Bray B. C . ( 2013). Latent class analysis with distal outcomes: A flexible model-based approach. Structural Equation Modeling, 20( 1), 1-26. doi: 10.1080/10705511.2013.742377URLpmid: 4240499 |
| 13 | Morin A. J. S., Morizot J., Boudrias J-S., &Madore I . ( 2011). A multifoci person-centered perspective on workplace affective commitment: A latent profile/factor mixture analysis. Organizational Research Methods,14( 1), 58-90. doi: 10.1177/1094428109356476URL |
| 14 | Sterba, S.K. ( 2013). Understanding linkages among mixture models. Multivariate Behavioral Research, 48( 6), 775-815. doi: 10.1080/00273171.2013.827564URLpmid: 26745595 |
| 15 | Vermunt, J.K. ( 2010). Latent class modeling with covariates: Two improved three-step approaches. Political Analysis, 18, 450-469. doi: 10.1093/pan/mpq025URL |
| 16 | Wang C-P., Brown C. H., &Bandeen-Roche K . ( 2005). Residual diagnostics for growth mixture models: Examining the impact of a preventive intervention on multiple trajectories of aggressive behavior. Journal of the American Statistical Association, 100( 471), 1054-1076. doi: 10.1198/016214505000000501URL |
相关文章 5
| [1] | 陈冠宇, 陈平. 解释性项目反应理论模型:理论与应用[J]. 心理科学进展, 2019, 27(5): 937-950. |
| [2] | 王孟成, 邓俏文, 毕向阳. 潜变量建模的贝叶斯方法[J]. 心理科学进展, 2017, 25(10): 1682-1695. |
| [3] | 陈宇帅;温忠麟;顾红磊. 因子混合模型:潜在类别分析与因子分析的整合[J]. 心理科学进展, 2015, 23(3): 529-538. |
| [4] | 冯成志;贾凤芹 . 双眼竞争研究现状与展望[J]. 心理科学进展, 2008, 16(2): 213-221. |
| [5] | 彭正敏,林绚晖,张继明,车宏生. 情绪智力的能力模型[J]. 心理科学进展, 2004, 12(6): 817-817~823. |
PDF全文下载地址:
http://journal.psych.ac.cn/xlkxjz/CN/article/downloadArticleFile.do?attachType=PDF&id=4530
