,?State Key Laboratory of Nuclear Physics and Technology, Institute for Heavy Ion Physics, School of Physics, Peking University, Beijing 100871, ChinaCorresponding authors: ? E-mail:tsfan@pku.edu.cn
Received:2019-01-10Online:2019-04-1
| Fund supported: |
Abstract
Keywords：
PDF (1002KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Zhi-Ming Wang, Wen-Jie Zhu, Xin Zhu, Chun-Lai Zhong, Tie-Shuan Fan. 236U Multi-modal Fission Paths on a Five-dimensional Deformation Surface *. [J], 2019, 71(4): 417-420 doi:10.1088/0253-6102/71/4/417
1 Introduction
Multi-modal fission has been convinced by both theor-ists[1-6] and experimentalists[7-8] since the discovery of fission. Several experimental evidences, such as fission yields, TKE distribution, and neutron multiplicity, suggested that there exist at least two kinds of fission modal, symmetric and asymmetric modes. The fission path can be generally defined in two ways: the static least-energy fission path and the dynamic least-action fission paths.[9-12] They are sometimes very different. In this article, we limit our discussion to the static least-energy fission path.In the first theoretical discovery of multi-model fission,[5] Brosa it et al. found that there are three or more fission modes named by pre-scission shapes existing on the PES and those different paths can better explain the experimental results on fission fragments mass distributions for actinide isotopes. The super-short and super-long channels are always of symmetric deformation and standard channels are asymmetric. However, their path search process reduced the dimension of PES and might introduce unreal channels due to some kind of ambiguity, as pointed out in Ref. [6]. There is no straightforward way to reveal saddle points on a multidimensional PES. M?ller[6,13-14] et al. have stated why commonly used "minimization" techniques always failed. The immersion method[6] uses full degrees of freedom (does not reduce dimensions of PES) and allows the unambiguous identification of the lowest saddle point between two local minima.
Here, we develop a new static least-energy fission path search algorithm, which also consider full degrees of freedom, which is extended from two-dimensional image processing to multi-modal search algorithm for the first time. Using this multi-modal path search algorithm, we find at least two different paths, a symmetric and an asymmetric path, for $^{235}(n,f)$, which can be examined by the fission yield data and reaction cross section data.
2 Model and Multi-Modal Path Search Algorithm
2.1 PES Model
We use the macroscopic-microscopic (MM) model to calculate the PESs in a 5D deformation space. The nuclear shape is described by a 5D generalized Lawrence realistic parameterization.[5,15] The macroscopic model is Lublin-Strasbourg Drop (LSD) model.[16] And the microscopic model is Strutinsky correction method.[17-18] To calculate the single particle levels, we use folded-Yukawa model[19] as the single particle potential, and calculate the Hamiltonian on double center oscillator bases.[20] Considering the pairing effect, we use SBCS model.[21]2.2 Optimal Search Algorithm
Our search technique is the watershed algorithm, which is inspired by the geographic concept of drainage basin, plus depth first algorithm.[15] The watershed algorithm was first used in image processing for image division.[22] To make the watershed algorithm more understandable, we illustrate it on a two-dimensional contour plot as shown in Fig. 1.Fig. 1
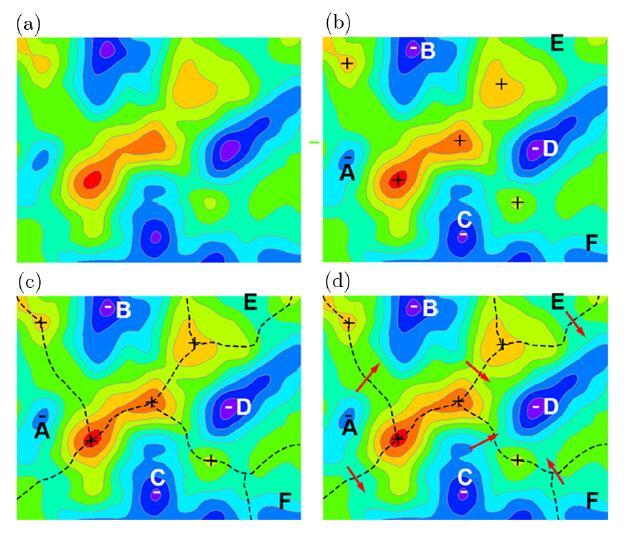New window|Download| PPT slideFig. 1(Color online) Two-dimensional schematic surface for optimal search strategies. The plus symbols indicate the local maxima, and the minus symbols represent the local minima. The energy height on the contour plot decreases from red to purple. The uppercase letters are the tags of the basins. Dashed lines are the watershed of these basins, and red arrows on the dashed lines represent the locations of saddle points.
(i) Initially, we only have the contour plot shown in Fig. 1(a)
(ii) The first step of watershed algorithm is to find the local minimum. In this step, we need to scan all the grids on the PES. Suppose that (a) there is a rainfall on a 5D surface and that (b) a rain drop flows along the steepest descent line which is recorded for each grid using linked list. The definition of a basin is the area in which the rainfall flows to the same minimum. After this step, we can divide the surface into different basins according to different minima as shown in Fig. 1(b).
(iii) Then, based on the definition of a basin, the watersheds can be defined as an area, where there is a point having a neighboring point, which does not belong to the same basin as the former point does. Thus, both points are on the watershed. After this step, watershed can be found on the surface as the dashed lines shown in Fig. 1(c).
(iv) Finally, the saddle point is defined as the point of the smallest value of the potential energy height on the watershed of the two connected basins. Red arrows on Fig. 1(d) show the location of saddle points. The steepest descent lines (stored in Step 2) connecting the basins and the saddles on the 5D surface will produce the whole path.
Compared with immersion algorithm,[6] our algorithm shares one similarity with immersion algorithm, which is the consideration of full-degree of freedom with no minimization. There are also some differences between those two algorithms: (i) Immersion algorithm considers the surface as a whole while we divide it into different areas. (ii) Immersion algorithm raises the water (energy level) step-by-step to see at which energy the exit point gets wet, which might be time consuming, while our algorithm just searches the saddle height on the watershed, a limited area.
After applying the watershed algorithm on surface division, we can simplify the 5D surface into a graph with nodes and edges for further depth-first search algorithm. The edges mentioned here is a concept in graph theory. On the edges, we have the saddle point height of two connected basins. The root node is the ground state. To choose which minimum represents the ground state, geometric deformation should be a criterion as many experiments show that ground-state shapes of heavy elements are almost spheroids. So a minimum with a compact spheroid deformation should be chosen as the root node.
2.3 Scission Criterion
Path search algorithm should know where the starting point is and where the path ends. The starting point is the ground state, which is much easier to be determined than the final state (or the scission "line'' on the PES). The grids on the PES which satisfy both conditions are realy rare. But where the scission happens is hard to be found.In the framework of the MM model, we need to calculate the macroscopic energy by liquid drop model (LDM) as the background and add microscopic correction on it. But when the neck of the deformation nucleus becomes thinner, only few nucleons are in neck region. The hypothesis of the LDM is challenged[23-24] because it will lose physical meaning when the radius of the neck becomes comparable with the distance between the nucleons. The PES with constrains of zero neck cannot be precisely calculated in the MM model. So an alternative criterion should be that the nucleus scissions when its neck size is smaller than a critical value or equivalently its elongation is larger than another critical value. Some of the criteria are shown in Table 1.
Table 1
Table 1Different scission criteria used by theorists. $R^{\rm crit}$ and $D^{\rm crit}$ are the critical values of neck and elongation, respectively. $R_0$ is the radius of a spherical nucleus. ${l}$ and ${r}$ in the third row are the shape parameters, which represent for the semi-length and radius of the deformed nucleus, respectively.
 |
New window|CSV
Rayleigh criterion is from hydrodynamics[30-31] to describe the rupture of cylindrical column of an incompressible liquid. With the LDM hypothesis, Rayleigh criterion can be naturally migrated into fission study with some modifications.[5]Table 1 lists three different criteria, which can be seen as equivalent, due to the volume conservation law. Rayleigh criterion is used in our optimal path search algorithm.
So the final state is a local minimum, which satisfies the Rayleigh criterion. Many local minima can be treated as potential final states, and there are also different paths ending at those minima. But only one path has the lowest fission barrier, which is the optimal fission path, and the corresponding minimum is the final state. With Rayleigh criterion, we reproduce the fission barriers of U and Pu isotopes, and most probable fission fragment mass splitting of U, Pu, Th and Cm even-even isotopes. Those results are consistent with experiments and evaluated data.
2.4 Multi-Modal Path Search Algorithm
To find other fission paths beyond the optimal one as mentioned above, we should first make clear what is the definition of another fission path. The second optimal fission path should have a different fission barrier, which is higher than the optimal one. And the second-optimal path should end at a different final state. An addition neccesary condition is that these two paths are well separated on the PES.According to the above-mentioned conditions, the basins connecting the barrier basin and the final state basin should be removed from the candidates before the searching of the second-optimal path, because a fission path will follow the optimal path once it is intersect with the optimal one. This removement would ensure that the search algorithm leads to a total different path. A constraint, the path can only contain one final state, should be added on the search algorithm. For the third-optimal fission path, we should continue to remove the basins connecting the barrier basin and the final state on the second-optimal path, until there is no way on the PES.
The division of the PES is sensitive to the noise, which might cause the over-division. A major improvement to overcome this problem is to set the threshold of the saddle height between two connected basins. Two connected basins with lower saddle height than the threshold should be considered as one basin. In this process, we merge the basins of blur identity into one larger basin with explicit identity. The threshold used here is a quite low barrier height of 0.3 MeV, lower than M?ller's[6] 0.5 MeV. After this process, the paths are well separated.
3 Multi-Modal Fission Path Results and Discussion
Figure 2 shows two fission paths of $^{236}$U for 13 million different shapes in the 5D deformation space. The asymmetric path is double-hump and the nucleus scissions at the most probable mass splitting with 141/95. The symmetric path is also double-hump and the nucleus scissions at the most probable mass splitting with 118/118. The fission barrier of asymmetric channel is obviously lower than the excitation energy (Q value) line, and the fission barrier of symmetric channel is larger than that line, which means that for the thermal neutron induced fission the symmetric fission is a quantum tunnelling effect. It is consistent with the experiment that the fission mass yield is dominated by asymmetric fission. From the view of prescission shape of these two fission modes, the asymmetric mode is the standard channel and the symmetric mode is the super-long one.From Fig. 2, we can see that both fission channels share the same inner barrier and deviate at the point of second-minimum. The neck appears from the second-minimum to the outer barrier. From the symmetric path, we can see that the shape develops into symmetric one near the scission point.
Fig. 2
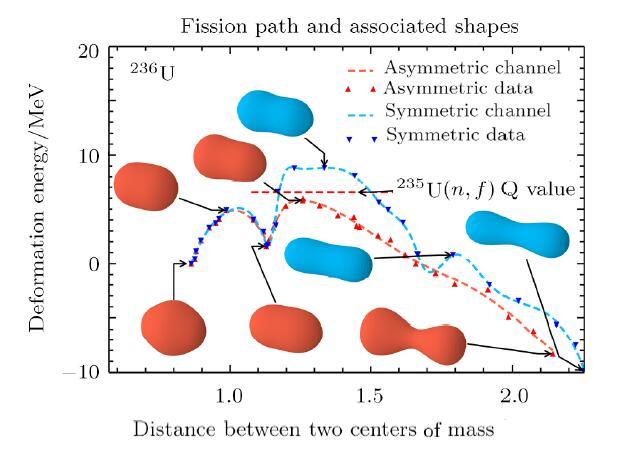New window|Download| PPT slideFig. 2(Color online) Symmetric and asymmetric fission channels of $^{236}$U. The horizontal red line is the excitation energy (Q value) of the $^{235}U(n,f)$ reaction. The triangles are the original data from the search algorithm on the PES.
To illustrate our search result more clearly, we project those two fission channels on a two-dimensional (${l}$ and ${r}$ of generalized Lawrence shape parameters) surface (Fig. 3). The contour plot is the projection of our calculated PES for $^{236}$U. The projection is based on the equation
Fig. 3
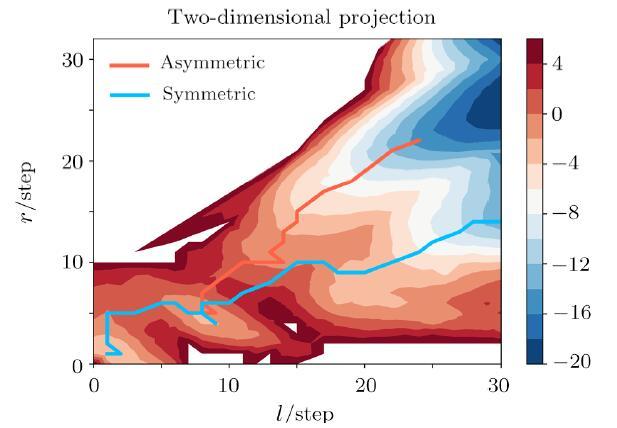New window|Download| PPT slideFig. 3(Color online) Two dimensional projection of the PES for $^{236}$U on ${l}$ and ${r}$ in generalized Lawrence shape parameterization. The symmetric (blue line) and asymmetric (red line) fission channels of $^{236}$U are projected on the same dimension. The label of $x$-axis and $y$-axis is the step of ${l}$ and ${r}$. Larger $x$ means a longer nucleus and larger $y$ means smaller a neck size.
and the $\min_{z,c,s}$ means that varying ${z}$, ${c}$, and ${s}$ to find the minimum $E_{\rm def}$ for the constants ${l}$ and ${r}$.
The projection of the PES show two well separated fission channels with the height of the ridge near 4 MeV, which means that these two fission channels are rarely intervened. The fission channels in Fig. 2 locate exactly in these two valleys and almost follow the line of steepest descent. The longer deformation of symmetric shape is consistent with the dent appearing in contour plot of (TKE,A), because longer deformation means lower TKE.
4 Conclusion
A new path search algorithm, which considers all the degrees of freedom is developed. Asymmetric and symmetric fission paths and barriers are obtained theoretically on the five-dimensional PES of $^{236}$U for 13 million different nuclear shapes. Fission yield and TKE distribution can be explained qualitatively by the lower barrier height of asymmetric path and the higher barrier height of symmetric path compared with reaction energy (Q) and longer elongation of symmetric path, respectively.Acknowledgments
We also acknowledge that computations in this work were performed in Tianhe-2 located at Guangzhou, Guangdong Province, ChinaReference By original order
By published year
By cited within times
By Impact factor
DOI:10.1103/PhysRev.84.52URL [Cited within: 1]
DOI:10.1103/PhysRev.129.2239URL
Measurements with a semiconductor detector system and a two-dimensional analyzer have yielded information on the mass distributions and the details of the kinetic energy release from a series of charged particle-induced fission reactions. The fissioning compound nuclei range from thallium for which the mass distributions are symmetric, to plutonium for which the fission is predominantly asymmetric. In an intermediate region, the charged particle-induced fission of Rayields comparable contributions of symmetric and asymmetric fission. All of the results are quantitatively consistent with a two-mode hypothesis for the fission process and indicate that within each mode the distance between the charge centers of the two fragments at the scission point is approximately the same for all mass divisions. The results show a lower total kinetic energy release from symmetric fission than from asymmetric fission, indicating that the distance between the charge centers at the scission point is about 10% greater for the symmetric mode than for the asymmetric mode.
DOI:10.1016/0022-5088(86)90443-1URLPMID:10033155
We measured the mass and kinetic-energy partitioning in the spontaneous fission of Fm, Md, Md, No, and ]. All fissioned with mass distributions that were symmetric. Total-kinetic-energy distributions peaked near either 200 or 235 MeV. Surprisingly, these energy distributions were skewed upward or downward from the peak in each case, except for ], indicating a composite of two energy distributions. We interpret this as a mixture of liquid-drop-like and fragment-shell directed symmetric fission, although theory had not anticipated this phenomenon.
DOI:10.1016/0375-9474(71)90884-0URL
The potential energy of a nucleus at large (scission) deformation is calculated by the shell-correction method due to Strutinsky. The shape of the nucleus in the zeroth-order approximation is taken to be the Cassinian ovaloid, the deviation being expanded in a series of Legendre polynomials. Asymmetric shapes of the nucleus are studied; a definition of the Woods-Saxon type nuclear potential is given; the single-particle spectrum, shell correction, liquid-drop energy and total potential energy are calculated. It is shown that the transuranium nuclei are symmetric at the first barrier and in the second minimum of the potential energy. The second saddle point is situated at a large asymmetric deformation. The nuclear asymmetry near the scission point is in qualitative agreement with experimental data on the asymmetry in the mass distribution of the fission fragments. The agreement between the theoretical results and experimental data on the fission barriers is improved when the asymmetry is taken into account
DOI:10.1016/0370-1573(90)90114-HURL [Cited within: 3]
[Cited within: 6]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
DOI:10.1103/PhysRevLett.92.072501URL [Cited within: 1]
DOI:10.1103/PhysRevC.61.047602URL [Cited within: 1]
no abstracts in English
DOI:10.1088/0253-6102/62/3/18URL [Cited within: 2]
Potential energy surfaces of uranium nuclei in the range of mass numbers 229 through 244 are investigated in the framework of the macroscopic-microscopic model and the heights of static fission barriers are obtained in terms of a double-humped structure. The macroscopic part of the nuclear energy is calculated according to Lublin trasbourg-drop(LSD) model. Shell and pairing corrections as the microscopic part are calculated with a folded-Yukawa single-particle potential. The calculation is carried out in a five-dimensional parameter space of the generalized Lawrence shapes. In order to extract saddle points on the potential energy surface, a new algorithm which can effectively find an optimal fission path leading from the ground state to the scission point is developed. The comparison of our results with available experimental data and others' theoretical results confirms the reliability of our calculations.
DOI:10.1103/PhysRevC.67.044316URL [Cited within: 1]
Nuclear liquid-drop model is revisited and an explicit introduction of the surface-curvature terms is presented. The corresponding parameters of the extended classical energy formula are adjusted to the contemporarily known nuclear binding energies and fission-barrier heights. Using 2766 binding energies of nuclei with $Z>~8$ and $N>~8$ it is shown that the performance of the new approach is improved by a factor of about 6, compared to the previously published liquid-drop model results, in terms of the masses (new rms deviation $〈\ensuremath{\delta}M〉=0.698\mathrm{MeV})$ and the fission barriers by a factor of about 3.5 (new rms deviation of the fission barriers of isotopes with $Z>70$ is $〈\ensuremath{\delta}{V}_{B}〉=0.88\mathrm{MeV}).$ The role of the nuclear surface-curvature terms and their effects on the description of the experimental quantities are discussed in detail. For comparison, the parameters of the more ``traditional'' classical energy expressions are refitted, taking into account the nuclear masses known today and the performances of several variants of the model are compared. The isospin dependence in the new description of the barriers is in a good agreement with the extended Thomas-Fermi approach. It also demonstrates a good qualitative agreement with the fission lifetime systematics tested on the long chain of Fermium isotopes known experimentally. The new approach offers a very high stability in terms of the extrapolation from the narrower range of nuclides to a more extended one\char22{}a property of particular interest for the contemporary exotic beam projects: the corresponding properties are illustrated and discussed. The new description of the fission barriers being significantly improved, in particular, the new calculated barriers being lower, flatter, but stiffer against high-multipolarity deformations. The chances for ``extra'' stabilization of the hyperdeformed minima at high spin increase, thus calling for the new total energy Strutinsky-type calculations.
DOI:10.1016/0375-9474(67)90510-6URL [Cited within: 1]
Nuclear shells correspond to an inhomogeneous distribution of nucleons in phase space, whereas the distribution in quasi-classical phenomenological models (the liquid in phase space, is supposed to be homogeneous. Starting from this point, Nilsson's level scheme is used to calculate the shell-model correction to the “liquid drop energy” of the nucleus as a function of the occupation number and deformation. A strong correlation between the shell correction and nucleon level density at the Fermi energy was observed. In magic and mid-shell nuclei the calculated deformation energy oscillates around the LDM value. Discussion of problems related to the deformation energy such as nuclear deformations, shell effects in nuclear masses, in deformed nuclei and in nuclear fission, etc. is presented. The role of nucleon pairing is discussed.
DOI:10.1016/0375-9474(68)90699-4URL [Cited within: 1]
[Cited within: 1]
[Cited within: 1]
DOI:10.1016/j.nuclphysa.2006.11.052URL [Cited within: 1]
We perform nuclear ground-state pairing calculations with the monopole pairing interaction. The particle number fluctuations are taken into account by the particle number projection method, with variation after projection. The pairing-correction energies obtained in this approach are compared to the BCS-model results. We discuss extensively how to properly incorporate different pairing models in global macroscopic icroscopic nuclear mass calculations. A method to calculate the smoothly changing part of the particle number projected energy is developed based on the Strutinsky procedure, making it possible to extract a pairing-shell energy. The behavior of the different pairing models is investigated in detail in the nuclei 164Er and 165Tm. Calculations are then performed along the -stability line and for several isotope and isotone chains from the proton drip-line to the neutron drip-line. The single-particle energy levels used are obtained from two different single-particle potentials: the folded-Yukawa and the modified-harmonic oscillator potentials. The pairing calculations in the two potentials differ slightly in the fine-structure but the overall results are very similar. When comparing the particle number projected model and the BCS model it is found that the pairing-shell energy is quite insensitive to which microscopic pairing model is used.
[Cited within: 1]
DOI:10.1016/j.nuclphysa.2007.11.002URL [Cited within: 1]
DOI:10.1103/RevModPhys.44.320URL [Cited within: 1]
DOI:10.1016/0029-5582(63)90635-7URL
Results of the calculation of the symmetrical nuclear equilibrium shapes are presented. An integro-differential equation for equilibrium shapes is solved by an iteration method described in sect. 3.
DOI:10.1103/PhysRevLett.106.132503URLPMID:21517377
Although nuclear fission can be understood qualitatively as an evolution of the nuclear shape, a quantitative description has proven to be very elusive. In particular, until now, there existed no model with demonstrated predictive power for the fission-fragment mass yields. Exploiting the expected strongly damped character of nuclear dynamics, we treat the nuclear shape evolution in analogy with Brownian motion and perform random walks on five-dimensional fission potential-energy surfaces which were calculated previously and are the most comprehensive available. Test applications give good reproduction of highly variable experimental mass yields. This novel general approach requires only a single new global parameter, namely, the critical neck size at which the mass split is frozen in, and the results are remarkably insensitive to its specific value.
[Cited within: 1]
[Cited within: 1]
