V. Yu. Denisov ^1,2,3,
, O. A. Belyanovska ^2,
, V. P. Khomenkov ^1,2,4,
, I. Yu. Sedykh ^5,
, K. M. Sukhyy ^2,
, 1.Institute for Nuclear Research, Prospect Nauki 47, 03028 Kiev, Ukraine
2.Ukrainian State University of Chemical Technology, Prospect Gagarina 8, 49005 Dnepr(Dnepropetrovsk), Ukraine
3.Faculty of Physics, Taras Shevchenko National University of Kiev, Prospect Glushkova 2, 03022 Kiev, Ukraine
4.National Technical University of Ukraine "Igor Sikorsky Kyiv Polytechnic Institute", Prospect Peremogy 37, 03056 Kiev, Ukraine
5.Financial University, Leningradsky Prospect 49, 125993 Moscow, Russia
Received Date:2018-09-11
Available Online:2019-01-01
Abstract:A simple approach is proposed to describe the experimental data for the widths of the fission-fragment mass yields in ¹⁹⁷Au and ²⁰⁹Bi at low and intermediate energies. The approach is based on the expressions for the temperature dependence of the width of the fission-fragment mass yield and the mass of the most probable fragment. The expression for the width of the fission-fragment mass yield depends on the mass of the most probable fragment, the surface terms of the energy level density parameter, the temperature and the stiffness parameter of the potential related to mass-asymmetric degree of freedom. It is shown that the contribution of the surface term of the energy level density parameter is important for describing the experimental data in a wide range of energies.

HTML

--> --> -->

The mass yield of fission fragments is the most studied feature of nuclear fission [1-35]. The mass yield is often described by the several Gaussians [6, 9, 22, 23], which have the corresponding widths σ². The width of the fission-fragment mass yield is a very important quantity of the fission process [3-6, 9-11, 13-20, 23, 24, 26, 29, 31, 32, 35].
Neuzil and Fairhall proposed a simple empirical relationship for the width of the fission-fragment mass yield [3]. Strutinsky found that in the framework of statistical model, the width of the fission-fragment mass yield is proportional to the temperature T of the fissioning system at the saddle point, the square of the number of nucleons A², and inversely proportional to the stiffness parameter C of the potential related to the mass-asymmetric degree of freedom [4]. Nix showed that the width in very low-energy fission is strongly influenced by the zero-point motion of the corresponding quantum oscillators [5]. The zero-point motion is important only in the very low temperature limit, where the values of the width evaluated using the Nix expression are larger than those obtained by the Strutinsky formula. However, the results of Strutinsky and Nix are the same for high temperatures. The numerical studies of the width in the framework of the diffusion model of fission are reported in Refs. [10, 11, 32].
The mass distribution of the fission-fragments of highly-excited fissioning nucleus with the number of nucleons A ? 220 is related to the two-body saddle point [33]. Recently, we found a simple expression for the width of the fission-fragment mass yield at moderate and high excitation energies of the fissioning system in the framework of the statistical approach [35]. In contrast to previous results [4, 5, 9] we take into account both the volume and surface terms of the energy level density parameter [36]. As a result, the temperature dependence of the width is modified due to the contribution of the surface term of the energy level density parameter. However, our expression for the width reduces to the Strutinsky formula in the low temperature limit. Note that we consider temperatures at which the zero-point motion of the corresponding quantum oscillators is negligible. The difference between our and Strutinsky formulas increases with the temperature of the fissioning nucleus and becomes important at temperatures T ? 1 MeV. The width of the fission-fragment mass yield evaluated by using the volume and surface terms of the energy level density parameter is smaller than the one obtained for the same values of parameters and using the volume term only [35].
In this paper, we discuss the energy dependence of the widths of the fission-fragment mass yields in the photo-fission of ¹⁹⁷Au and ²⁰⁹Bi in a wide energy interval. The energy dependence of the width was measured in the photo-fission of ¹⁹⁷Au target by bremsstrahlung with end-point energies of 300-1100 MeV in Ref. [13]. The data for the widths obtained in the photo-fission of ²⁰⁹Bi target by bremsstrahlung with end-point energies of 40-1100 MeV are given in Refs. [14-18]. These data have not been analyzed up to now using the expressions for the width proposed in Refs. [4, 35]. We also take into account the effect of neutron evaporation on the width of the fission-fragment mass yields and apply the expressions for the width from Refs. [4, 35].
The paper is organized as follows. The expressions for the fission width proposed in [4, 35] are shortly described in Sec. 2. A discussion of the results and conclusions are given in Sec. 3.

As pointed out in the introduction, the mass yields of the fission fragments are often described by several Gaussians [6, 9, 22, 23]. The width σ² describes the yield of a fission fragment with mass A₁ for the symmetric fission of a nucleus with A nucleons, exp[-(A₁?A/2)²/σ²] [6, 22, 35].
The width of the mass distribution of the fission fragments obtained in Ref. [35] is given by

$\begin{eqnarray}{\sigma }^{2}=\frac{2{A}^{2}T}{C+2\kappa {A}^{2/3}{T}^{2}}.\end{eqnarray}$

(1)

Here, A is the number of nucleons of the fissioning system at the two-body saddle point, T is the temperature of the system, which is related to the excitation energy E^?=a_s(A)T² of the system of two identical fission fragments at the saddle point, C is the stiffness parameter of the potential related to the mass-asymmetric degree of freedom at the saddle point, and

$\begin{eqnarray}\kappa =\frac{4\cdot {2}^{1/3}}{9}\beta, \end{eqnarray}$

(2)

$\begin{eqnarray}{a}_{{\rm{sp}}}(A)=\alpha A+{2}^{1/3}\beta {A}^{2/3}, \end{eqnarray}$

(3)

is the asymptotic value of the energy level density parameter of a system of two identical nuclei formed by fission of a nucleus with A nucleons. The asymptotic value of the energy level density parameter of a nucleus with A nucleons has the volume and surface contributions related to coefficients α and β, respectively, and is written as [36]

$\begin{eqnarray}(a)(A)=\alpha A+\beta {A}^{2/3}.\end{eqnarray}$

(4)

The values of these coefficients obtained in the framework the back-shifted Fermi gas model are α=0.0722396 MeV^?1 and β=0.195267 MeV^?1 [36]. For β=0, Eqs. (2) and (3) reduce to

$\begin{eqnarray}\kappa =0, \end{eqnarray}$

(5)

$\begin{eqnarray}{a}_{{\rm{sp}}}(A)=\alpha A.\end{eqnarray}$

(6)

As a result, the expression for the width is written in this case as

$\begin{eqnarray}{\sigma }_{{\rm{S}}}^{2}=\frac{2{A}^{2}T}{C}.\end{eqnarray}$

(7)

This expression was obtained by Strutinsky [4]. (Note that the expression for the width obtained in Ref. [4] has a different numerical coefficient, because a different definition of the asymmetry of the fission fragments is used.)
From Eq (1), the fission-fragment width ${\sigma }^{2}\propto \frac{2{A}^{2}T}{C}={\sigma }_{{\rm{S}}}^{2}$ increases linearly with temperature in the low temperature limit 2κA^2/3T² ? C. The width σ² has a maximum at C=2κA^2/3T². In the limit of extremely high temperatures 2κA^2/3T² ?C, the width ${\sigma }^{2}\sim\frac{{A}^{4/3}}{\kappa T}$ is inversely proportional to temperature. The influence of the surface energy level density parameter on the width of the fission-fragment mass yield increases with the number of nucleons of the fissioning nucleus and with the temperature. In contrast, the width ${\sigma }_{{\rm{S}}}^{2}$ increases linearly with temperature in all temperature ranges.

The bremsstrahlung spectrum is continuous; therefore, the nucleus can be excited by γ-quanta of different energies in an experiment using bremsstrahlung. However, the γ-fission cross-section strongly increases with energy [7]. Therefore, we consider that the excitation energy of a fissioning compound nucleus ${E}_{{\rm{cn}}}^{\star }$ is very close to the end-point energy of bremsstrahlung.
The excitation energy of the fissioning compound nucleus ${E}_{{\rm{cn}}}^{\star }$ and the excitation energy of the fissioning system at the saddle point ${E}_{{\rm{sp}}}^{\star }$, associated to the formation of the mass yield, are related by the equation [33, 35]

$\begin{eqnarray}{E}_{{\rm{cn}}}^{\star }={E}_{{\rm{sp}}}^{\star }+{V}_{{\rm{sp}}}-{Q}_{{\rm{fiss}}}={E}_{{\rm{sp}}}^{\star }[1+({V}_{{\rm{sp}}}-{Q}_{{\rm{fiss}}})/{E}_{{\rm{sp}}}^{\star }].\end{eqnarray}$

(8)

Here, Q_fiss is the Q-value of the fission reaction in two symmetric fragments, and V_sp is the height of the saddle point which defines the yield of symmetric fission fragments. The values of V_sp and Q_fiss are similar [33]. As a result, $({V}_{{\rm{sp}}}-{Q}_{{\rm{fiss}}})/{E}_{{\rm{sp}}}^{\star }\ll 1$ for a highly-excited nucleus, and ${E}_{{\rm{cn}}}^{\star }\approx {E}^{\star }$. Therefore, the temperature of the fissioning compound nucleus

$\begin{eqnarray}{T}_{{\rm{cn}}}=\sqrt{{E}_{{\rm{cn}}}^{\star }/a(A)}=\sqrt{{E}_{{\rm{cn}}}^{\star }/(\alpha A+\beta {A}^{2/3})}\end{eqnarray}$

(9)

is close to the temperature of a two-fragment system at the saddle point

$\begin{eqnarray}T=\sqrt{{E}_{{\rm{sp}}}^{\star }/{a}_{{\rm{sp}}}(A)}=\sqrt{{E}_{{\rm{sp}}}^{\star }/(\alpha A+{2}^{1/3}\beta {A}^{2/3})}.\end{eqnarray}$

(10)

The ratio of these temperatures for the same excitation energy, and for A?200, is in the range

$\begin{eqnarray}0.96\le \frac{T}{{T}_{{\rm{cn}}}}=\sqrt{\frac{\alpha +\beta {A}^{-1/3}}{\alpha +{2}^{1/3}\beta {A}^{-1/3}}}\le 1.\end{eqnarray}$

(11)

The differences between the excitation energies ${E}_{{\rm{cn}}}^{\star }$ and ${E}_{{\rm{sp}}}^{\star }$, and the temperatures T_cn and T, are negligible. Nevertheless, small differences between the excitation energies and temperatures should be considered in a careful analysis.
The evaporation of neutrons from the fissioning nuclei with A ? 220 is a very important process at high excitation energies [13-18, 20, 21], because, as a rule, the values of the fission barrier in these nuclei are larger than the values of the neutron separation energy. Due to evaporation of many neutrons, the most probable mass of the experimental fragment mass distribution A_prob is significantly smaller than A/2 at excitation energies higher than the fission barrier [13-18, 20, 21]. For example, A_prob for photo-fission of ¹⁹⁷Au by bremsstrahlung with end-point energy of 1100 MeV is 92 [13], which is smaller than A/2=197/2=98.5. This means that the fission occurs after evaporation of about 13 neutrons. Note that the number of evaporated neutrons is a statistical average. Due to neutron evaporation the number of nucleons in the fissioning system at the saddle point is close to 2A_prob. Therefore, we should use A=2A_prob in Eqs. (1) and (7). The experimental values of A_prob depend on the excitation energy and are extracted from an analysis of the experimental fragment mass distributions [13-18, 20, 21].
The excitation energy of the fissioning system is reduced due to the emission of pre-fission neutrons. Therefore, the average excitation energy of the nucleus at the moment of scission can be written as

$\begin{eqnarray}{E}_{{\rm{eff}}}^{\star }\approx {E}_{{\rm{sp}}}^{\star }-(A-2{A}_{{\rm{prob}}}){\mathop{E}\limits^{\sim }}_{{\rm{n}}}.\end{eqnarray}$

(12)

Here, ${\mathop{E}\limits^{\sim }}_{{\rm{n}}}$ is the average energy removed by a neutron from the fissioning nucleus during evaporation of A ? 2A_prob neutrons. The value of ${\mathop{E}\limits^{\sim }}_{{\rm{n}}}$ has two contributions related to the neutron binding energy and the average kinetic energy of the evaporated neutron

$\begin{eqnarray}{E}_{{\rm{kin}}}\approx \frac{3}{2}{T}_{{\rm{eff}}}\approx \frac{3}{2}{({E}_{{\rm{eff}}}^{\star }/a(2{A}_{{\rm{prob}}}))}^{1/2}.\end{eqnarray}$

(13)

As a result, ${\mathop{E}\limits^{\sim }}_{{\rm{n}}}$ can be approximated as

$\begin{eqnarray}{\mathop{E}\limits^{\sim }}_{{\rm{n}}}\approx \frac{BE(A, Z)-BE(2{A}_{{\rm{prob}}}, Z)}{A-2{A}_{{\rm{prob}}}}+\frac{3}{2}{T}_{{\rm{eff}}}, \end{eqnarray}$

(14)

where BE(A, Z) is the binding energy of nucleus with A nucleons and Z protons [37]. Using Eqs. (12)-(14) we find the effective temperature

$\begin{eqnarray}\begin{array}{ll}{T}_{{\rm{eff}}}&=\left[\frac{{E}_{{\rm{sp}}}^{\star }-(BE(A, Z)-BE(2{A}_{{\rm{prob}}}, Z))}{a(2{A}_{{\rm{prob}}})}\right.\\ &{\left. +{\left(\frac{3(A-2{A}_{{\rm{prob}}})}{4a(2{A}_{{\rm{prob}}})}\right)}^{2}\right]}^{1/2}-\frac{3(A-2{A}_{{\rm{prob}}})}{4a(2{A}_{{\rm{prob}}})}, \end{array}\end{eqnarray}$

(15)

which should be used in Eqs. (1) and (7).
The values of 2A_prob and T_eff can be evaluated in the framework of complex statistical codes, which take into account the competition between emission of neutrons and fission. However, using 2A_prob and T_eff, instead of A and T, in Eqs. (1) and (7) is very useful and significantly simplifies the application of these equations. Moreover, we can compare the values of the stiffness parameter C obtained for various reactions. The effect of neutron emission on the values of A and E is not taken into account in Ref. [35].
The width of the fission-fragment mass yield evaluated using Eqs. (1) and (7) in our approach are compared with experimental data for ¹⁹⁷Au and ²⁰⁹Bi in Figs. 1 and 2, respectively. The experimental data for the width and A_prob for ¹⁹⁷Au, obtained for bremsstrahlung end-point energies of 300, 350, 400, 450, 500, 600, 700, 800, 900, 1000, and 1100 MeV, are taken from Refs. [13, 18]. The corresponding experimental data for ²⁰⁹Bi, for bremsstrahlung end-point energies of 40, 65, 85, 600, and 700 MeV, are taken from Refs. [14-18], and data for bremsstrahlung end-point energies of 450, 500, 600, 700, 800, 900, 1000, and 1100 MeV are from Ref. [18]. (Note that the width of the fission-fragment mass yield was also measured in the photo-fission of ²⁰⁹Bi target by bremsstrahlung with end-point energy of 2500 MeV in [19]. The excitation energy per nucleon after absorption of such a high-energy gamma-quantum is larger than the binding energy per nucleon in ²⁰⁹Bi. As the formation of fission fragments in such a case is affected by various pre-equilibrium and non-equilibrium effects, we ignore this data point in our analysis.)
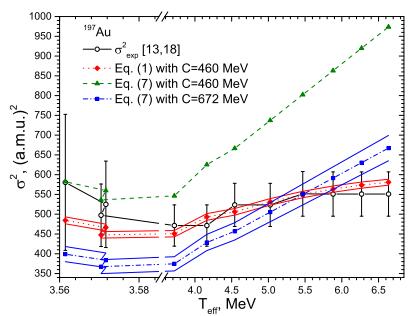Figure1. (color online) The temperature dependence of the fission-fragment width σ² for nuclei ¹⁹⁷Au evaluated by using Eqs. (1) and (7) for various values of the stiffness C. The thin lines show the range of uncertainty of the width induced by uncertainty of C. The experimental data are taken from Refs. [13, 18].

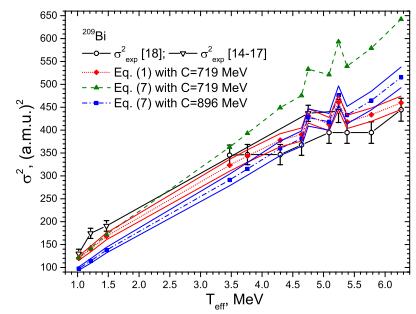Figure2. (color online) The temperature dependence of the fission-fragment width σ² for nuclei ²⁰⁹Bi evaluated by using Eqs. (1) and (7) for various values of the stiffness C. The thin lines show the range of uncertainty of the width induced by uncertainty of C. The experimental data are taken from Refs. [14-18].

The experimental data points from the different references and the theoretical results, shown in Figs. 1 and 2, are connected by lines. The data are ordered according to increasing bremsstrahlung end-point energy. As a rule, the temperature and the width of the fission-fragment mass yield increase with bremsstrahlung end-point energy. The most probable fragment masses A_prob for fission of ¹⁹⁷Au at bremsstrahlung energies of 300, 350, and 400 MeV are 97, 95, and 93 [13-18]. The corresponding effective temperatures T_eff at the saddle point are 3.561, 3.572, and 3.570 MeV. Due to such values of A_prob and T_eff, the width of the fission-fragment mass yield decreases with bremsstrahlung end-point energy in the range of 300÷400 MeV [13-18]. Such a dependence is outside the common trend, and we propose additional experimental studies of fission of ¹⁹⁷Au for bremsstrahlung end-point energies of 300, 350, and 400 MeV.
The values of the stiffness parameter of the potential related to the mass-asymmetric degree of freedom at the saddle point, C=460±10 MeV for ¹⁹⁷Au and C=719±20 MeV for ²⁰⁹Bi, are found by fitting the experimental data with Eq. (1). The uncertainties in C are evaluated using the experimental uncertainties of σ and A_prob given in Refs. [13-18]. The uncertainties in C lead to a range of values of the fission-fragment widths shown by thin lines in Figs. 1 and 2. The value of C for ¹⁹⁷Au is close to C = 382.5 MeV obtained for the slightly heavier nucleus ²⁰¹Tl for temperatures 0.9 MeV ?T?1.4 MeV in Ref. [35]. However, the value of C for ²⁰⁹Bi obtained in our analysis is higher than the one found in an analysis of the particle-induced fission of the nearest nuclei ²⁰⁹Bi and ²¹⁰Po in the range 0.8 MeV ?T?1.4 MeV in Ref. [35]. Note that the wider temperature interval and experimental data for 2A_prob used here lead to a more accurate determination of the stiffness.
The energy dependence of the width of the fission-fragment mass yield evaluated using Eq. (1) agrees well with experimental data, as seen in Figs. 1 and 2. If we substitute the above stiffness values in Eq. (7), then the calculated widths significantly overestimate the data at high energies. We recall that Eqs. (1) and (7) lead to very similar widths for small temperatures and the same stiffness parameter C, see Fig. 2.
The quality of fit of the width can be estimated by using the relation

$\begin{eqnarray}S=\frac{1}{N-1}\displaystyle \sum _{i=1}^{N}{(\frac{{\sigma }_{i{\rm{theor}}}^{2}-{\sigma }_{i{\rm{\exp }}}^{2}}{\Delta {\sigma }_{i{\rm{\exp }}}^{2}})}^{2}, \end{eqnarray}$

(16)

where ${\sigma }_{i\, {\rm{theor}}}^{2}$ and ${\sigma }_{i\, {\rm{\exp }}}^{2}$ are the theoretical and experimental values of the width for a data point i, while $\Delta {\sigma }_{i\, {\rm{\exp }}}^{2}$ is the error of the experimental value ${\sigma }_{i\, {\rm{\exp }}}^{2}$. The values of S for ¹⁹⁷Au are 0.194 and 18.4 when using Eqs. (1) and (7), respectively. The corresponding values for ²⁰⁹Bi are 1.99 and 26.4.
We also find the values of C by fitting the experimental data with the help of Eq. (7). The values of C obtained for ¹⁹⁷Au and ²⁰⁹Bi are 672±32 MeV and 896±41 MeV, respectively. These values are larger than those obtained previously. The uncertainties in C, leading to uncertainties in the corresponding widths, are shown in Figs. 1 and 2. The values of S for ¹⁹⁷Au and ²⁰⁹Bi are in this case 1.80 and 7.76, respectively, and are considerably larger than the ones found using Eq. (1).
Comparing the values of S obtained by different approaches and the results presented in Figs. 1 and 2, we conclude that Eq. (1) for the width describes the data in a wide range of temperatures of the fissioning nuclei. In contrast, Eq. (7) cannot describe the data in such a wide range of temperatures. As we have pointed out, the uncertainties in C lead to uncertainties in the corresponding widths. Taking into account the uncertainties in the calculated values of the widths shown in Figs. 1 and 2, we conclude that in the framework of the proposed approach, application of Eq. (1) leads to a better description of the widths than Eq. (7).
In conclusion, Eq. (1) for the temperature dependence of the width of the fission-fragment mass yield describes well the data for bremsstrahlung fission of ¹⁹⁷Au and ²⁰⁹Bi for intermediate energies. The difference between our results and those of Strutinsky occurs at high temperatures. The width of fission-fragment mass yield evaluated by using the volume and surface terms describes better the data for high excitation energies than the one obtained for the same values of parameters and using the volume term only. The substitutions of A for 2A_prob and T for T_eff in Eq. (1) are very useful for application of this equation in the case of emission of pre-fission neutrons.