摘要:盐度是海洋学中重要的物理参量之一, 其对生物学研究、气候模拟、天气预报以及飓风路径预测都具有极其重要的意义. 在基于拉曼光谱的海洋盐度遥感探测中, 由于拉曼光谱同时与盐度及海水温度相关, 因此反演盐度时, 需要参数假设, 从而降低探测精度. 为实现对盐度的高精度遥感探测, 本文提出了融合水体布里渊散射与拉曼散射光谱的盐度精细反演方法. 文中根据拉曼光谱的低频部分与高频部分的面积比值与水体温度和盐度有定量的关系, 利用最小二乘方法, 建立拉曼光谱与温度和盐度的二元函数方程. 由于布里渊频移量的大小与介质中的声速相关, 而声速变化是由温度和盐度的变化引起, 因此布里渊频移量的大小也同时与盐度及海水温度相关. 激光雷达遥感探测方法可以同时探测拉曼光谱和布里渊频移这两个参量, 因此利用拉曼光谱和布里渊频移与盐度和温度之间的关系, 建立了盐度高精度反演模型, 并分析了探测结果的误差, 得到盐度的反演误差小于0.47‰.
关键词: 海水盐度/
拉曼散射/
布里渊散射/
激光雷达

English Abstract

全文HTML

--> --> -->

盐度是海洋学中重要的物理参数之一^[1]. 盐度的变化与海洋环境和气候变化具有强烈的内在联系, 盐度在海洋学中的分布是揭示海洋物理和生物行为特征的重要指标. 其决定了氧溶解度, 进而影响动植物的初级生产和分配. 因此, 盐度探测对生物学研究、气候模拟、天气预报以及飓风路径预测都有极其重要的意义^[2]. 目前, 盐度探测的主要方法包括采样分析、浮标探测、卫星遥感和激光遥感等^[3]. 采样分析通常使用温盐深仪(conductivity temperature depth profiler, CTD)^[4]; 浮标探测主要采用阿尔戈(Array for Real-time Geostrophic oceanography, Arog)浮标^[5], 然而该方法实现海水大面积盐度探测困难, 且获得的盐度数据分辨率较低; 美国NASA针对Goddard航天中心研制的被动微波辐射计(Electronically Scanned Thinned Array Radiometer, ESTAR)是首台星载海面盐度遥感探测辐射计, 其后土壤湿度和海洋盐度(Soil Moisture and Ocean Salinity,SMOS)卫星的发射进一步推进了卫星遥感海面盐度的发展^[6], 然而卫星遥感只能获得海洋表层的温度和盐度; Artlett和Pask^[7], Burikov等^[8]以及Wall和Hornig^[9]利用激光遥感方法研究了水体拉曼(Raman)散射光谱与盐度的关系, 该方法可满足海洋学中大海域盐度高分辨率、快速、连续廓线监测的探测需求, 然而Raman光谱同时与盐度及海水温度相关, 反演盐度时, 需要参数假设, 这样会降低盐度探测精度.
为实现对盐度的高精度遥感探测, 本文提出了融合水体布里渊(Brillouin)散射与Raman散射光谱的盐度精细反演方法. Brillouin散射是指入射到介质的光波场与介质内的弹性声波场发生相互作用而产生的一种光散射现象. Brillouin频移量的大小与介质内的声速相关, 而声速变化是由温度和盐度的变化引起的, 因此Brillouin频移量也受温度和盐度的影响^[10]. Raman散射光谱强度受温度和盐度变化的影响, 散射光谱低频部分与高频部分的面积比值与温度和盐度变化具有定量的函数关系. 由于激光雷达遥感探测方法可以同时探测Raman光谱和Brillouin频移这两个参量, 融合Raman散射光谱和Brillouin频移与盐度和温度之间的关系, 建立海水盐度的高精度反演模型. 该模型的建立使得盐度反演不需要参数假设, 提高了盐度反演精度, 为研究海洋学的发展提供更可靠的数据支持.

2

-->

2.1.Raman散射理论

Raman散射是由分子振动或固体中晶格振动引起的光散射现象. 在整个的4π立体角范围对各方向的平均的单个分子n←m振动跃迁的总散射截面σ_mn是^[11]:

$ \begin{split}{\rm{\sigma} }_{mn}=\;&\frac{{I}_{mn}}{{I}_{0}}=\frac{{2}^{3}\pi }{{3}^{2}{\varepsilon _0^2}}{v}_{0}{({v}_{0}-{v}_{mn})}^{3}\\&\times gf(T){\left|{\displaystyle \sum\limits_{\rho \sigma }{\alpha }_{\rho \sigma }({v}_{0})}\right|}^{2} ,\end{split} $

式中, I_mn是n←m振动跃迁的Raman散射强度, I₀和v₀是激发光束的强度和频率, v_mn是Raman模的振动频率. g是初态m的简并度因子, f(T)是初态的热分布的玻尔兹曼权重系数. α_ρσ(v₀)是激发频率下对分子所有方向进行平均的Raman极化率张量ρ, σ分量.
在90°散射方向上进行Raman测量, 此时激发光偏振方向垂直于散射平面, 微分Raman散射截面公式如下^[12]:

$ \begin{split}\sigma ({\nu }_{0})=\;&\frac{{\rm{π}}^{2}}{\rm{45}\times {\varepsilon }_{0}^{2}}{b}^{2}g\frac{L({\nu }_{0}){\left({\nu }_{0}-{\nu }_{mn}\right)}^{4}}{1-\mathrm{exp}(-hc{v}_{mn}/kT)}\\&\left[45{\left({\alpha }_{}'\right)}^{2}+7{\left({\gamma }_{}'\right)}^{2}\right] ,\end{split}$

式中, b是零点振幅, b = (h/8π²cv_mn)^1/2, α^′2是极化率张量的平均值不变量, γ^′2是极化率张量的有向性不变量, h是普朗克常数, c是光速, k是玻尔兹曼常数, T是绝对温度, L(v₀)是局域场修正因子, 它的表达式如下:

$ L({v_0}) = ({n_{\rm{s}}}/{n_0}){(n_{\rm{s}}^{\rm{2}} + 2)^2}{(n_0^2 + 2)^2}/81 , $

式中, n_s和n₀是在(v₀ – v_mn)和v₀处样品折射率.
根据(2)式和(3)式可以看出, Raman散射截面是一个与温度、激发频率和溶液浓度(与盐度相关)等相关的函数.
2 -->

2.2.Brillouin散射理论

Brillouin散射是指入射到介质的光波场与介质内的弹性声波场发生相互作用而产生的一种光散射现象. 散射光的频率相对于入射光的频率发生了变化, 而且这种变化和散射角以及散射介质内的声波场的特性有关. 海水Brillouin频移表示为^[13-16]

$ {v_{{B}}} = \pm \frac{{2n(S,t,\lambda )V(S,t)}}{\lambda }\sin \left(\frac{\theta }{2}\right) , $

式中, n为海水折射率, S为海水盐度, V为海水声速, t为海水温度, λ为入射波波长, θ为散射角.
海水折射率n与声速V均与海水温度和盐度相关, 因此在已知入射波长时, 海水Brillouin频移是与海水温度和盐度相关的二元函数. 目前利用Brillouin散射探测海水参量, 主要是用于探测海水温度. 根据Brillouin频移随温度和盐度变化的规律, 利用最小二乘原理, 获得海水温度反演公式如下^[17-21]:

$ \begin{split}t(S,{\nu _{\rm{B}}}) =\;& {w_0} + {w_1}\left( {{v_{\rm{B}}} - 7.5} \right) + {w_2}{\left( {{v_{\rm{B}}} - 7.5} \right)^2} \\&+ {w_3}{\left( {{v_{\rm{B}}} - 7.5} \right)^3} + {w_4}{\left( {{v_{\rm{B}}} - 7.5} \right)^6} \\&+ S\big[ {w_5} + {w_6}\left( {{v_{\rm{B}}} - 7.5} \right) \\& + {w_7}{{\left( {{v_{\rm{B}}} - 7.5} \right)}^2} + {w_8}{{\left( {{v_{\rm{B}}} - 7.5} \right)}^3} \big], \end{split} $

式中, w_i为拟合系数, 数值可参照文献[18]

图1给出了海水盐度探测激光雷达分光系统光路工作原理. 为降低海水对入射光的衰减, 采用532 nm的Nd:YAG脉冲激光器作为光源. 包含Raman和Brillouin散射的回波信号经过分束镜(BS₁)分为两束光, 透射光经过滤光片(IF)后, 利用Princeton Instruments SP2500I光谱仪探测Raman散射光谱信号, 获得Raman散射光谱与海水温度和盐度之间的关系. 反射光经过反射镜(M₁)反射后由分束镜(BS₂)分为两束. 经过BS₂的透射光通过分束镜(BS₃)再次分为两束光, 经过BS₃的透射光通过透镜(L₃)聚焦, 利用光电倍增管1(PMT₁)探测一路信号; 经过BS₃的反射光通过反射镜(M₂)反射, 透镜(L₄)聚焦后, 利用光子计数的光电倍增管2(PMT₂)探测一路信号; PMT₁和PMT₂交替接收受激Brillouin散射回波信号, 再通过光子计数器(photon counter)单光子计数后输入自相关系仪(autocorrelation instrument), 获得散射光强的时间自相关函数. 根据动态光散射与受激Brillouin散射谱宽的自相关性, 获得受激Brillouin散射斯托克斯分量谱宽. 经过BS₂的反射光通过分束镜(BS₄)分为两束光, 经过BS₄的透射光通过反射镜(M₃)反射后形成与BS₄反射光平行的光束, 两束光输入具有两个透射通道的法布里-珀罗标准具(Fabry-Perot Etalons，FPE), 实现双边缘探测受激Brillouin散射谱. 通过改变在同一基板上FPE的两个腔(Cavity₁和Cavity₂)的镀膜厚度来实现透射中心频率的差, 分别利用Cavity₁和Cavity₂的下降边缘和上升边缘检测受激Brillouin散射谱, 由于温度和盐度变化会造成Brillouin光谱产生频移, Cavity₁和Cavity₂探测获得光强相反的变化, 因此利用双边缘探测技术可以增加频移的探测范围, 并且频移探测灵敏度是单边缘探测的两倍. 通过FPE的光束经过透镜(L₁)和透镜(L₂)聚焦, 由PMT₃和PMT₄探测到能量信号, 由数据采集卡采集.
图 1 海洋温盐探测高光谱激光雷达分光系统光路原理图
Figure1. Experimental setup for filter system of ocean temperature and salinity detection high-spectral-resolution-lidar.

2

-->

4.1.基于Raman散射的水体温盐反演

Raman散射光谱法探测海水温度或盐度, 是利用探测到的散射光谱建立与海水温度或盐度之间的函数关系. Haltrin和Kattawar^[22]将常温下纯水的伸缩振动Raman光谱分解为3250, 3425, 3530, 3625 cm^–1四个模再发射过程, 并给出了对应的Raman散射光谱重分配函数为:

$ {I}_{\rm{R}}=d{\displaystyle \sum\limits_{i=1}^{4}{a}_{i}}\cdot \mathrm{exp}\left[\frac{{\left({10}^{7}/{\lambda }_{\rm{E}}-{10}^{7}/{\lambda }_{\rm{R}}-\Delta {v}_{i}\right)}^{2}}{2{\sigma }_{i}^{2}}\right] , $

式中, d是常数, λ_E是激发光波长, λ_R是散射光波长, a_i, Δv_i和σ_i是振动Raman频率重分配参数, 数值可参照文献[22].
利用(6)式, 计算获得不同温度下纯水的Raman散射光谱如图2所示. 从图2可以看出, 水分子的Raman散射光谱范围在3000—3800 cm^–1.
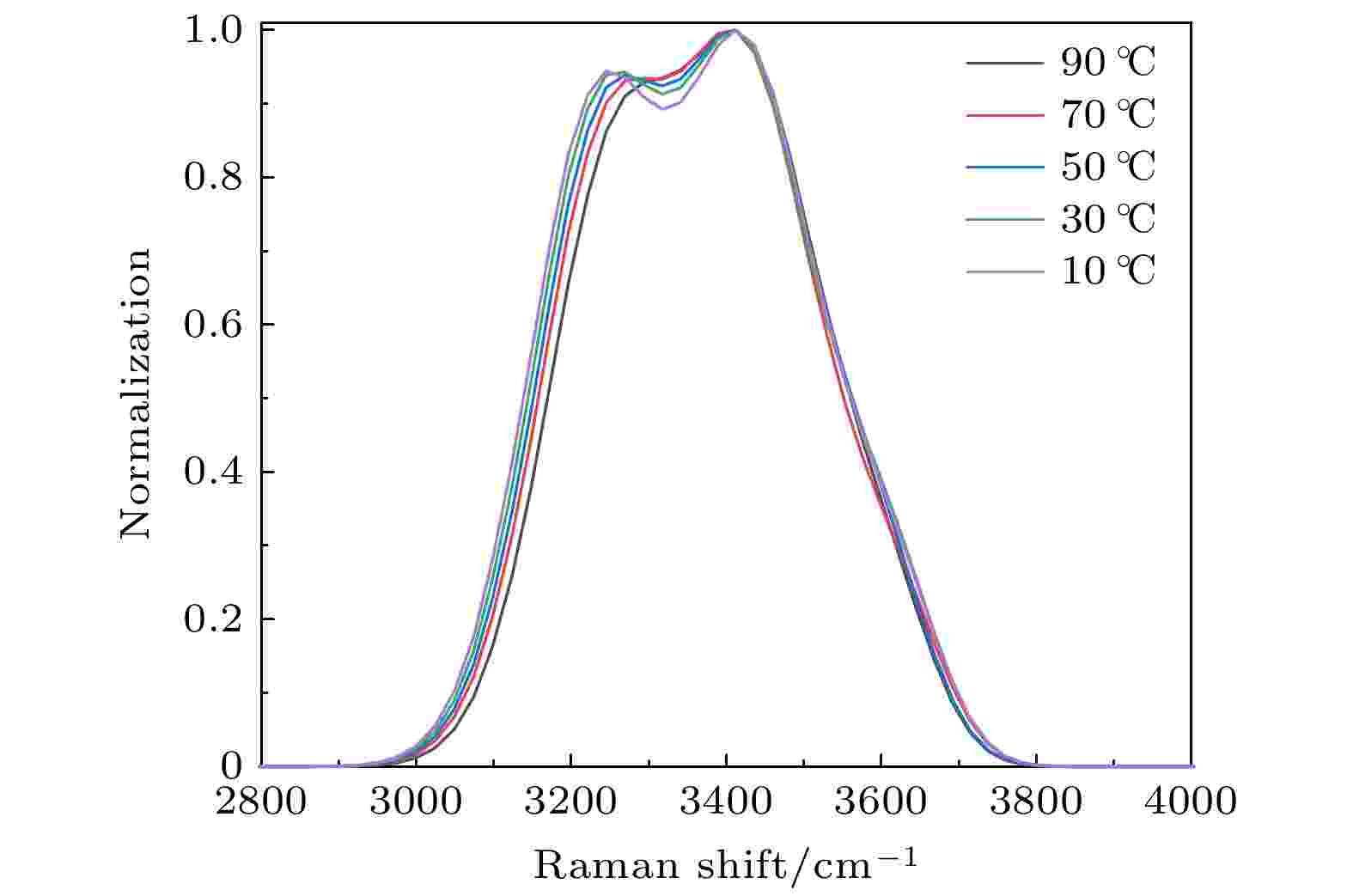图 2 不同温度下纯水的拉曼散射光谱
Figure2. Raman scattering spectra of pure water at different temperatures.

水分子有两种存在形式, 一种是独立的单个水分子, 另一种是多个水分子形成的簇团. 单个水分子的Raman散射频率较高, 多个水分子簇团的Raman散射频率较低, 当水温升高时, 水分子的热运动加强, 水中单分子的浓度增多, 多分子簇团的浓度减少, 使得高波数Raman散射光谱强度增大, 低波数Raman散射光谱强度减弱. 依据光谱随温度变化的情况, 可以建立温度与Raman散射光谱之间的关系. 在散射光谱最大峰值位置, 将光谱分为两部分, 低频部分是包含氢键的振动光谱(HB), 高频部分是非氢键的振动光谱(NHB). 分别对HB部分和NHB部分进行积分, 并对积分结果取对数, 可以得到温度和散射光谱低、高频面积比的关系.
由于溶质对水的振动Raman散射光谱影响机制较为复杂, 可通过实验数据定量建立Raman散射光谱与海水盐度的函数关系. 海水是一种化学成分复杂的混合溶液, 主要含有的阴阳离子有Cl^1–, SO${}_4^{2-} $, Na¹⁺, K¹⁺, Mg²⁺和Ca²⁺等, 因此本文以海水中所含的主要成分NaCl和MgCl₂两种单介质溶液, NaCl, MgCl₂和Na₂SO₄三种介质的混合溶液为实验样品. 在恒定温度下, 分别探测它们在不同盐度下的Raman散射光谱. 图3(a)—图3(c) 分别给出了NaCl溶液、MgCl₂溶液和NaCl, MgCl₂和Na₂SO₄三种介质的混合溶液的散射光谱.
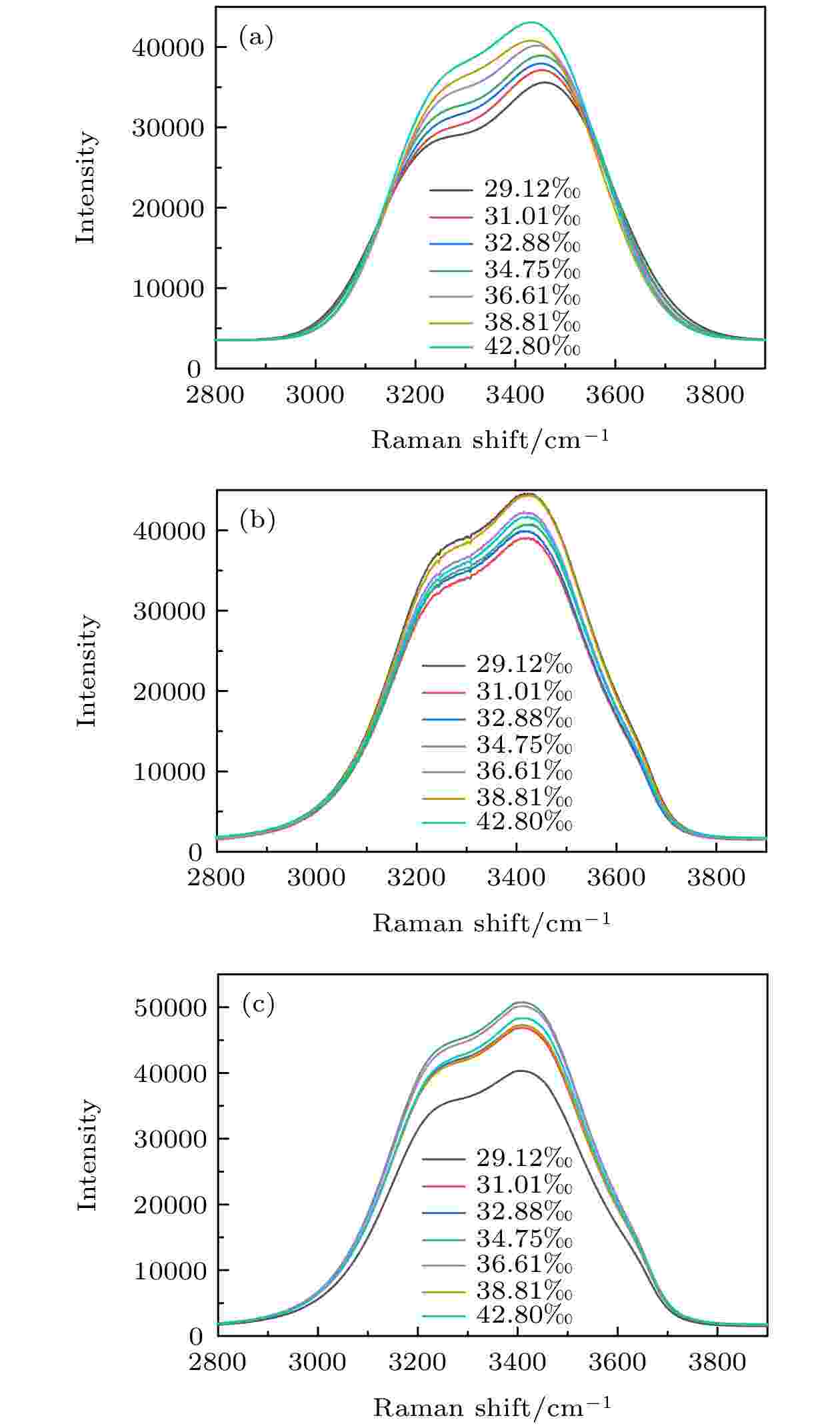图 3 不同盐度溶液的Raman散射光谱　(a) NaCl溶液; (b) MgCl₂溶液; (c) NaCl-MgCl₂-Na₂SO₄三种介质混合溶液
Figure3. Raman scattering spectra of different salinity solutions: (a) NaCl solution; (b) MgCl₂ solution; (c) NaCl-MgCl₂-Na₂SO₄ three media mixture solutions.

根据单介质溶液和混合介质溶液的Raman散射光谱数据, 利用最小二乘原理, 建立Raman散射光谱与海水温度和盐度之间的函数关系, 如下式:

$ \begin{split}\;&\mathrm{ln}\left(\frac{{S}_{\rm{HB}}}{{S}_{\rm{NHB}}}\right) =n(S,t,\lambda )\left[{a}_{0}+{a}_{1}S+{a}_{2}{S}^{2}+{a}_{3}{S}^{3}\right.\\&~~~~~~~~\left.+t({a}_{4}+{a}_{5}S+{a}_{6}{S}^{2})+{t}^{2}({a}_{7}+{a}_{8}S)\right] ,\\[-12pt] \end{split}$

式中, S为海水盐度, t为海水温度, n(S, t, λ)为海水折射率, 系数a₀ = 0.5097, a₁ = –0.002182, a₂ = 4.356 × 10^–7, a₃ = –3.098 × 10^–8, a₄ = –0.003939, a₅ = –5.417 × 10^–5, a₇ = 4.356 × 10^–7, a₇ = 4.876 × 10^–7, a₈ = 3.736 × 10^–6.
海水折射率n(S, t, λ)与海水温度和盐度相关, 它们之间的关系如下式^[13]:

$\begin{split}n(S,t,{\rm{\lambda}} ) =\;& {n_0} + S({n_1}t + {n_2}{t^2} + {n_3}{t^3}) + {n_4}{t^2} \\&+ \frac{{{n_{^5}} + {n_6}S + {n_7}t}}{{\rm{\lambda}} } + \frac{{{n_8}}}{{{{\rm{\lambda}} ^2}}} + \frac{{{n_9}}}{{{{\rm{\lambda}} ^3}}},\end{split}$

式中, n_i为拟合系数, 数值可参照文献[13].
根据海水所含成分占比, 配制海水样品. 在恒定温度下, 利用实验探测不同盐度下海水的Raman散射光谱, 探测结果如图4所示.
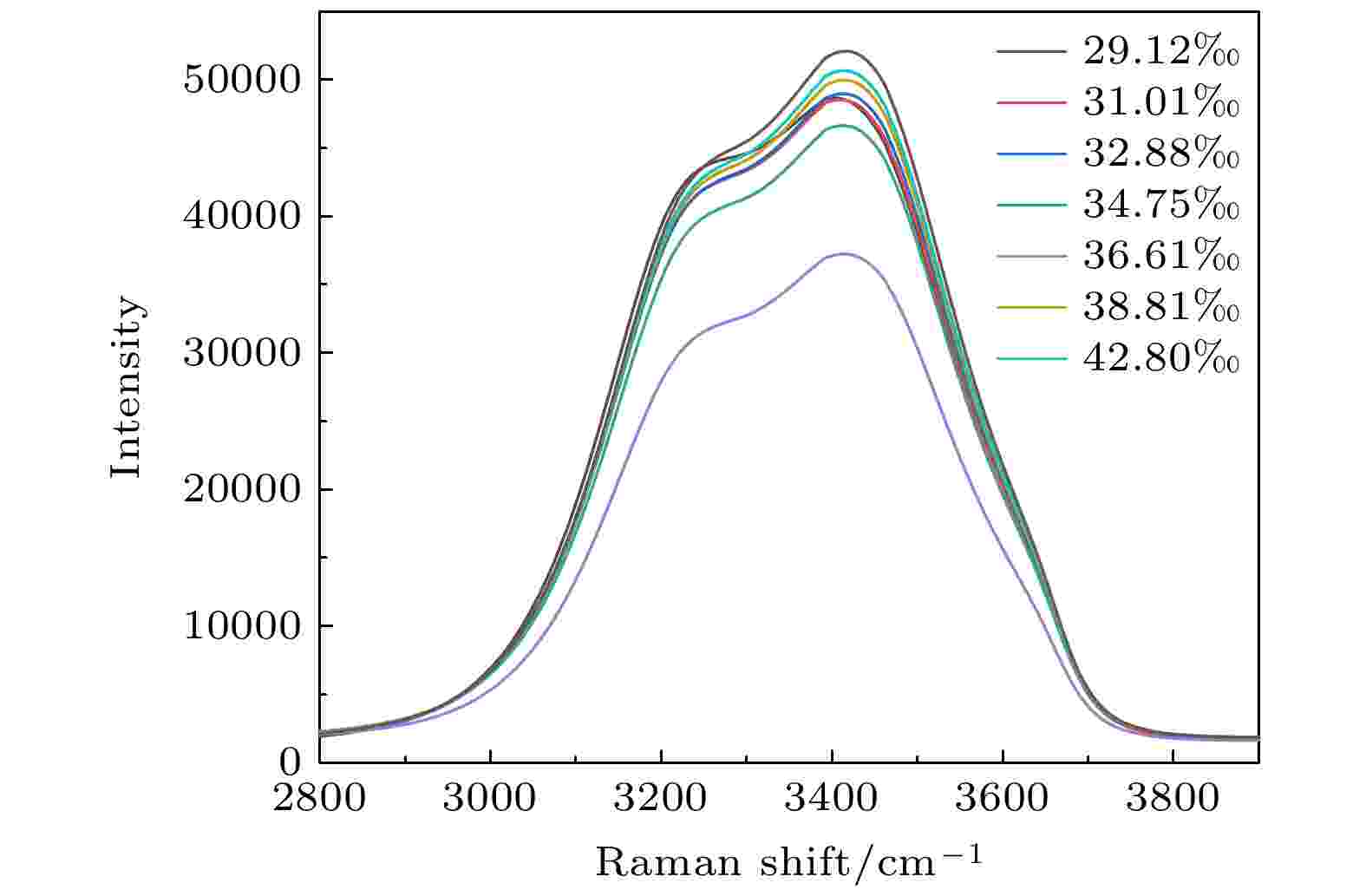图 4 海水的Raman散射光谱
Figure4. Raman scattering spectrum of seawater.

根据海水Raman散射光谱探测结果, 计算出不同盐度下散射光谱的低、高频面积比的对数值. 由于已知海水温度, 将散射光谱低、高频面积比的对数值结果代入(7)式, 可以反演获得海水盐度. 实验数据计算结果与函数关系计算结果如图5所示, 图中点表示实验探测结果, 直线为函数关系计算结果.
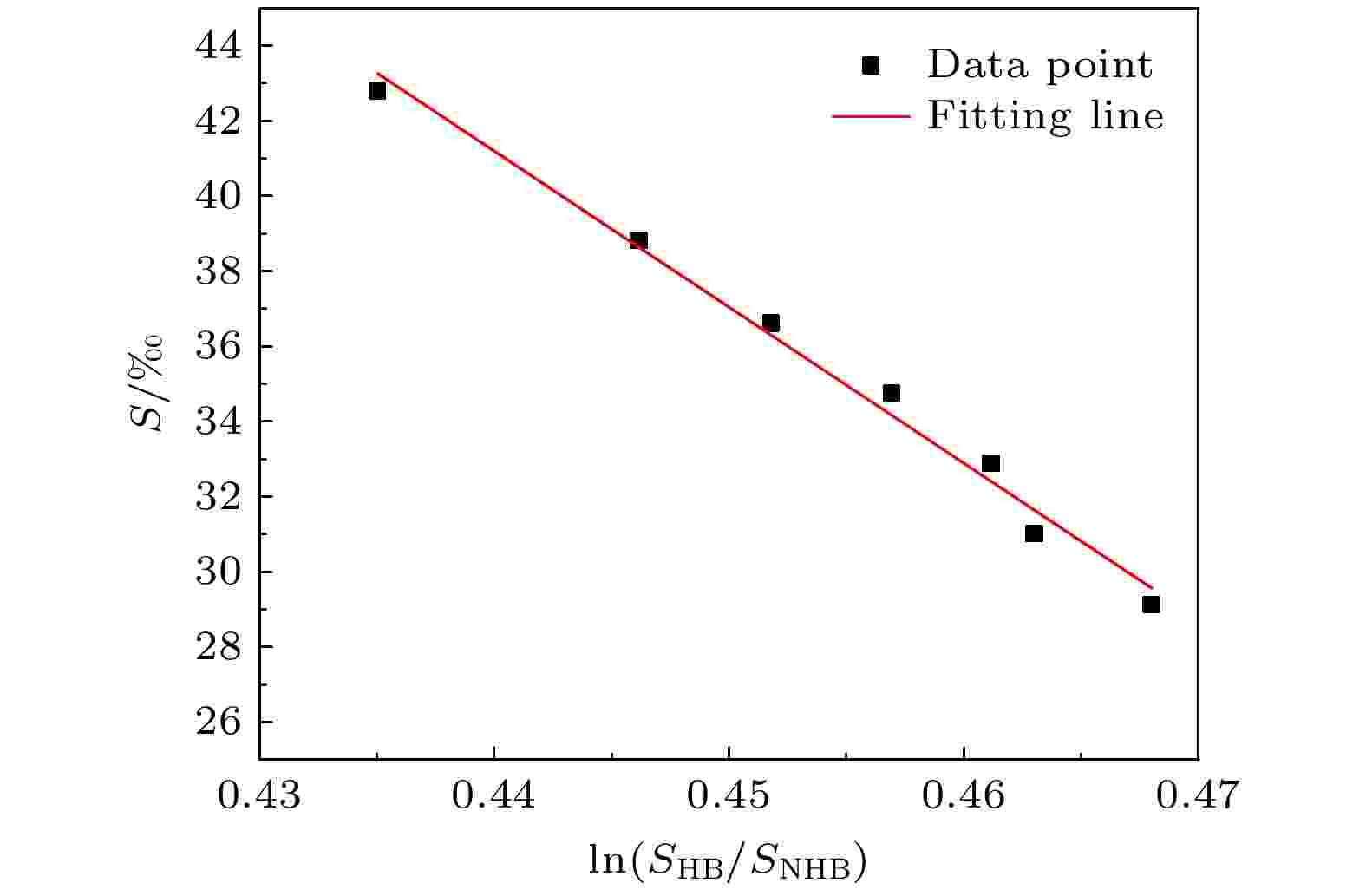图 5 海水Raman散射光谱数据处理结果
Figure5. Data processing results of seawater Raman scattering spectrum.

2 -->

4.2.激光雷达探测Brillouin频移

依据Brillouin散射理论, 图6给出了盐度为35‰时Brillouin的散射光谱. 当温度从20 ℃变为30 ℃, Brillouin频移变化量Δv_B = 0.1142 GHz. 因此在已知海水盐度时, 可以通过激光雷达探测海水Brillouin频移, 利用频移探测结果, 使用(5)式反演获得海水温度.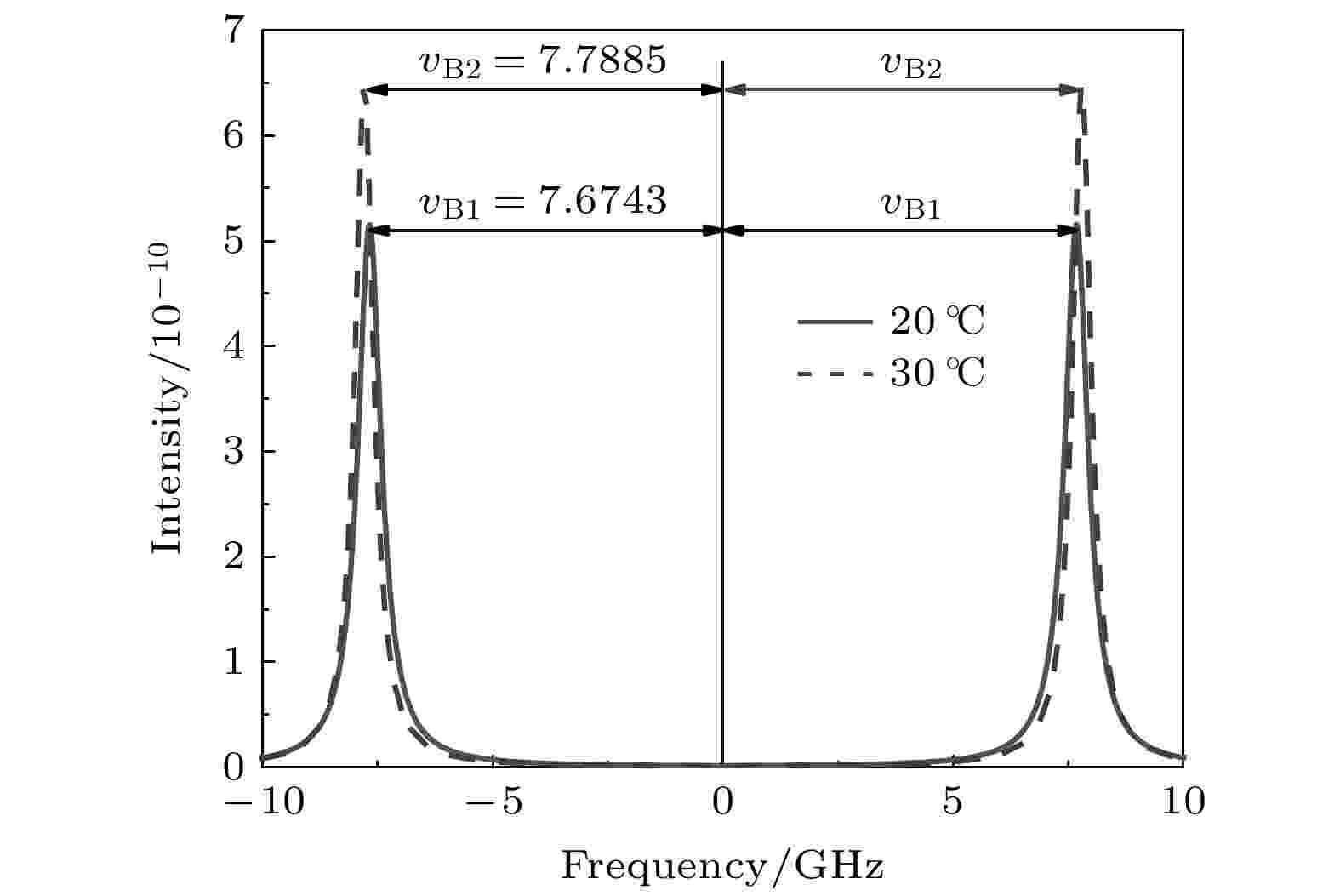
图 6 盐度值为35‰时不同温度下海水Brillouin散射光谱
Figure6. Brillouin scattering spectra of seawater at different temperatures with salinity of 35 ‰.

激光雷达遥感方法探测海水Brillouin频移的方法是, 利用边缘探测技术, 探测得到Brillouin回波信号的能量. 回波信号能量受到Brillouin频移和谱宽两个参量的影响. 其中Brillouin谱宽可以利用光子相关光谱技术探测到, 因此可以利用探测的回波信号能量和Brillouin谱宽计算获得频移. Brillouin频移计算公式如下:

$\begin{split}\;&{v_{\rm{B}}}(I,{\varGamma _{\rm{B}}}) = \sum\limits_{i = 0}^5 {{a_{i1}}} {I^i} + \sum\limits_{i = 1}^4 {{a_{i2}}\varGamma _{\rm{B}}^i} + \varGamma \sum\limits_{i = 1}^4 {{a_{i3}}I_{\rm{B}}^i}\\&~~~~~~~~~ + {\varGamma ^2}\sum\limits_{i = 1}^3 {{a_{i4}}{I^i}} + {\varGamma ^3}\sum\limits_{i = 1}^2 {{a_{i5}}{I^i}} + {a_{06}}\varGamma _{\rm{B}}^4I ,\end{split} $

式中, Γ_B为Brillouin光谱的谱宽, I为探测能量信号, 系数a₀₁ = 8.36826, a₁₁ = –12.98, a₂₁ = 60.01, a₃₁ = –106.9, a₄₁ = 65.78, a₅₁ = 3.109, a₁₂ = –5.179, a₂₂ = 3.643, a₃₂ = –1.296, a₄₂ = 0.1778, a₁₃ = 46.94, a₂₃ = –152.1, a₃₃ = 205.8, a₄₃ = –94.84, a₁₄ = –26.59, a₂₄ = 56.89, a₃₄ = –29.92, a₂₅ = 7.278, a₃₅ = –7.101, a₀₆ = –0.7173.
利用(9)式获得恒定盐度下, 不同温度的Brillouin散射谱宽和能量的结果如表1所列.

t	S	ΓB	I	vB
5	30	1.2732	0.2053	7.38705
10	30	0.9424	0.244	7.48328
15	30	0.7375	0.2859	7.56755
20	30	0.6130	0.3278	7.64070
25	30	0.5376	0.3674	7.70355
30	30	0.4883	0.403	7.75694

表1恒定盐度下, 不同温度Brillouin线宽、能量和频移计算结果
Table1.Calculation results of Brillouin spectrum width, energy and frequency shift at different temperatures under constant salinity.

2 -->

4.3.海水盐度的联合反演与误差分析

依据(5)式和(7)式, Brillouin频移和Raman散射光谱均是与海水温度及盐度相关的二元函数. 因此联立两个函数关系可以得到海水盐度与Brillouin频移和Raman散射光谱低、高频面积比的对数值ln(S_HB/S_NHB)之间的函数关系如下式:

$ S\left( {\ln \left( {\frac{{{S_{{\rm{HB}}}}}}{{{S_{{\rm{NHB}}}}}}} \right),{v_{\rm{B}}}} \right) = \frac{{\sum\limits_{i = 0}^5 {{a_{i1}}\ln {{\left( {\dfrac{{{S_{{\rm{HB}}}}}}{{{S_{{\rm{NHB}}}}}}} \right)}^i}} + \sum\limits_{i = 1}^3 {{a_{i2}}v_{\rm{B}}^i} }}{{\sum\limits_{i = 0}^4 {{a_{i3}}\ln {{\left( {\dfrac{{{S_{{\rm{HB}}}}}}{{{S_{{\rm{NHB}}}}}}} \right)}^i}} }} , $

式中, 系数a₀₁ = 221.928072, a₀₂ = –2069, a₀₃ = –1.8818 × 10⁴, a₀₄ = 1.97 × 10⁴, a₀₅ = –8133, a₁₂ = –11.317912, a₂₂ = 1.5443208, a₃₂ = –0.07678968, a₀₃ = 1.973, a₁₃ = –18.5, a₂₃ = 64.63, a₃₃ = –99.92, a₄₃ = 57.76.
由于海水Brillouin频移和Raman散射光谱的低、高频面积比的对数值ln(S_HB/S_NHB)均是用于反演海水盐度的参量, 因此它们的误差会影响海水盐度反演精度. 海水盐度反演的误差计算方法由下式给出:

$ {\rm{\delta}} S = {\left[ {{{\left( {\frac{{\partial S}}{{\partial \ln \dfrac{{{S_{{\rm{HB}}}}}}{{{S_{{\rm{NHB}}}}}}}}{{{\rm{\delta}} }}\ln \dfrac{{{S_{{\rm{HB}}}}}}{{{S_{{\rm{NHB}}}}}}} \right)}^2} + {{\left( {\dfrac{{\partial S}}{{\partial {v_{\rm{B}}}}}{\rm{\delta}} {v_{\rm{B}}}} \right)}^2}} \right]^{1/2}} . $

海水盐度S关于Brillouin频移的偏导结果如(12)式所示, 偏导结果表示频移量误差为1 MHz时, 会导致盐度产生0.4639‰的误差.

$ \left(\frac{\partial S}{\partial {v}_{\rm{B}}}\right)=0.4639‰/{\rm{MHz}} . $

海水盐度S关于Raman散射光谱的低、高频面积比的对数值ln(S_HB/S_NHB)的偏导结果如(13)式所示, 结果表明Raman光谱低、高频面积比的误差为0.001时, 会导致盐度产生0.6592‰的误差.

$ \left(\frac{\partial S}{\partial \mathrm{ln}\left( {{S}_{\rm{HB}}}/{{S}_{\rm{NHB}}}\right)}\right)={\rm{0}}.6592‰/0.001 . $

海水盐度反演的误差计算, 需要获得Raman散射光谱低、高频面积比的对数值ln(S_HB/S_NHB)和海水Brillouin频移的误差. 其中Brillouin频移的误差结果如图7所示, 拟合关系计算出的频移与理论计算结果之间的误差为 ± 0.8 MHz.
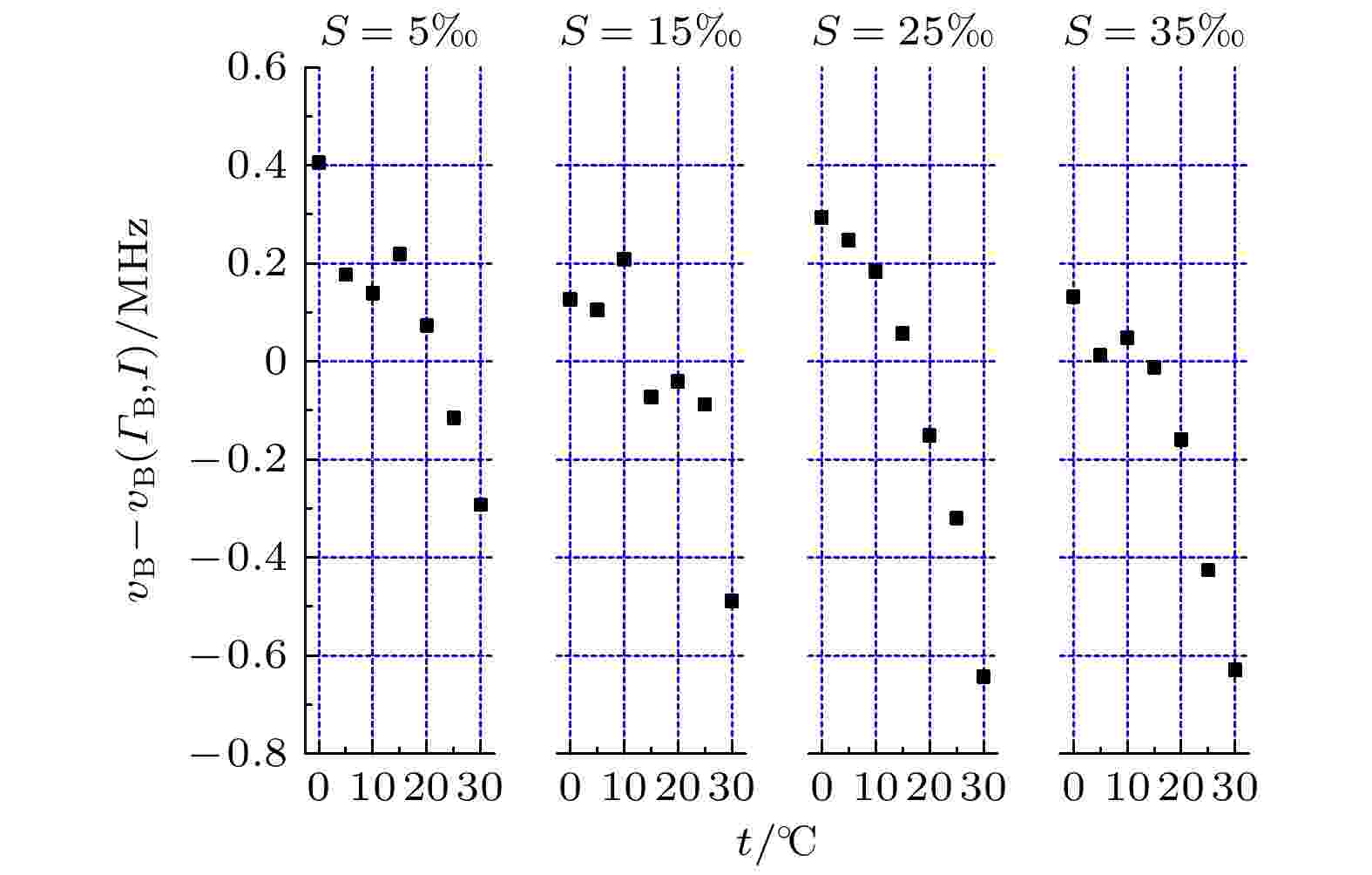图 7 Brillouin频移拟合关系v_B (I, Γ_B)与理论计算结果误差
Figure7. Difference between fitted Brillouin frequency shift v_B (I, Γ_B) and theoretical value.

Raman散射光谱低、高频面积比的对数值ln(S_HB/S_NHB)的误差计算结果如图8所示. 拟合函数关系计算结果与实验结果之间的误差为 ±0.0018. 最终根据Raman散射与Brillouin散射的误差计算结果, 利用(11)式计算海水盐度反演的误差为 ±0.47 ‰.
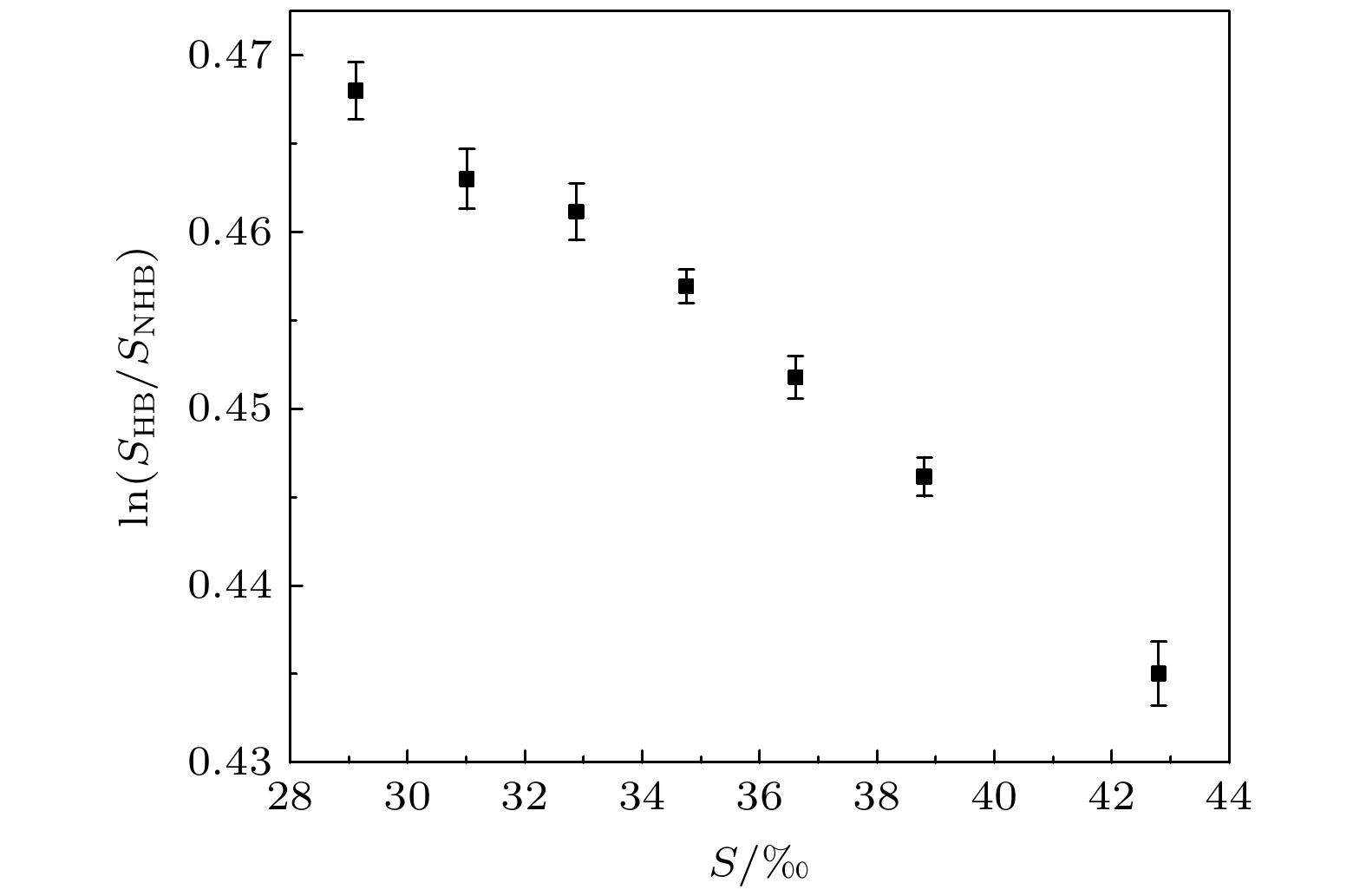图 8 Raman光谱低、高频面积比的拟合结果与实验结果之间的误差
Figure8. The error between the fitting results of low and high frequency area ratio of Raman spectra and the experimental results.

2 -->

4.4.实验误差分析

海水盐度反演需要探测的参量包括: Raman散射光谱、Brillouin散射谱宽和Brillouin散射回波信号能量. 由于海水温度变化对探测结果有影响, 因此样品海水温度控制精度为 ± 0.2 ℃. 控温误差对Raman散射光谱的低、高频面积比的对数值ln(S_HB/S_NHB)造成的影响如图9所示, 温度误差对散射光谱低、高频面积比的对数值ln(S_HB/S_NHB)造成的误差小于0.001.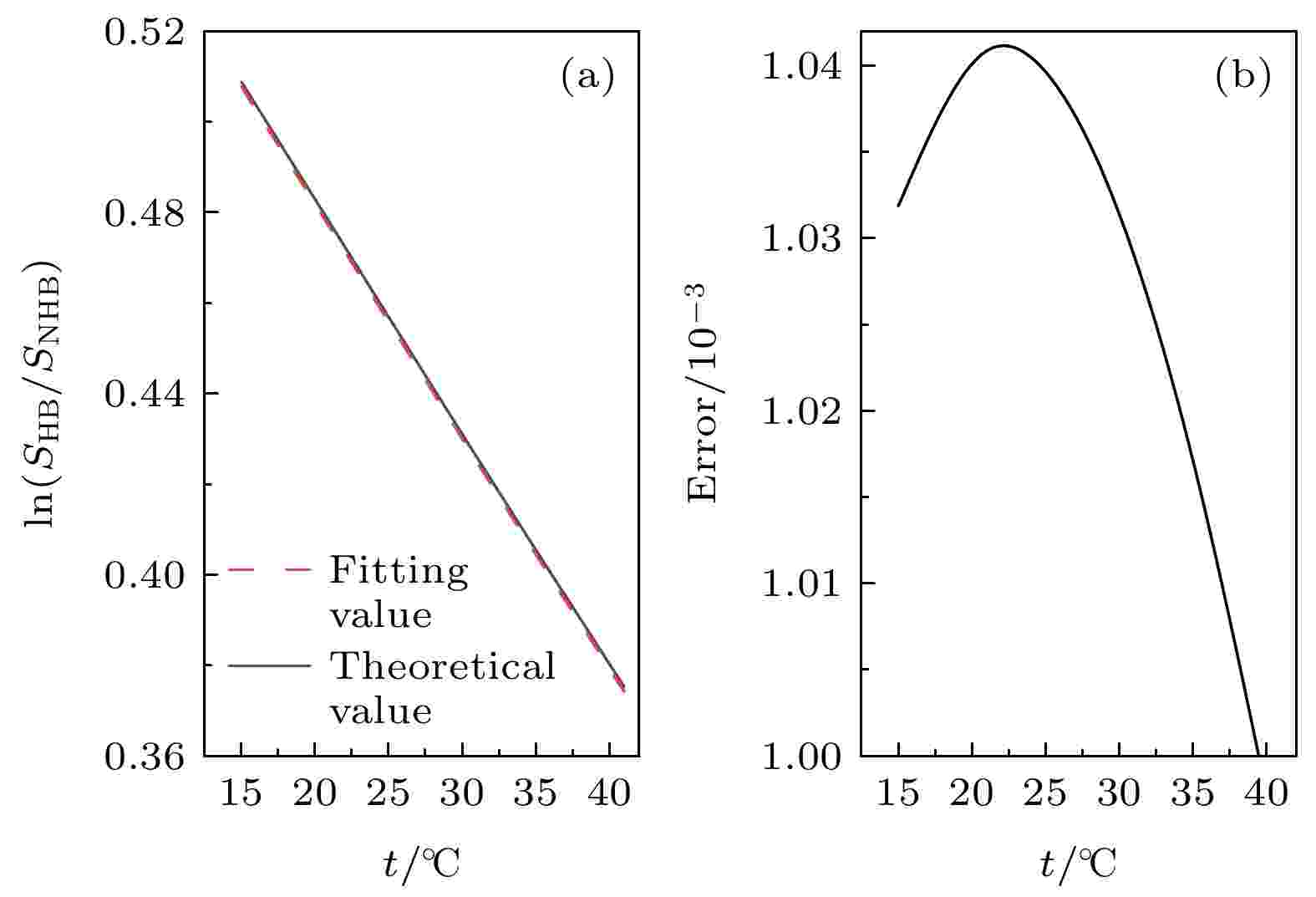
图 9 温度误差对Raman散射光谱低、高频面积比的对数值ln(S_HB/S_NHB)造成的影响　(a) 恒定盐度, 不同温度下对数面积比理论值与拟合值; (b) 温度误差导致对数面积的误差
Figure9. Effect of temperature error on the logarithmic value of the low and high frequency area ratio of Raman scattering spectra: (a) theoretical value and fitting value of log area ratio under constant salinity and different temperatures; (b) error of log area caused by temperature error.

实验中温度误差对Brillouin散射探测的影响结果如图10所示, 其中图10(a)和图10(b)表明在温度误差范围内, 对Brillouin谱宽探测结果造成的误差小于5 MHz; 图10(c)和图10(d)表明在温度误差范围内, 对Brillouin散射探测能量造成的误差小于0.0016.
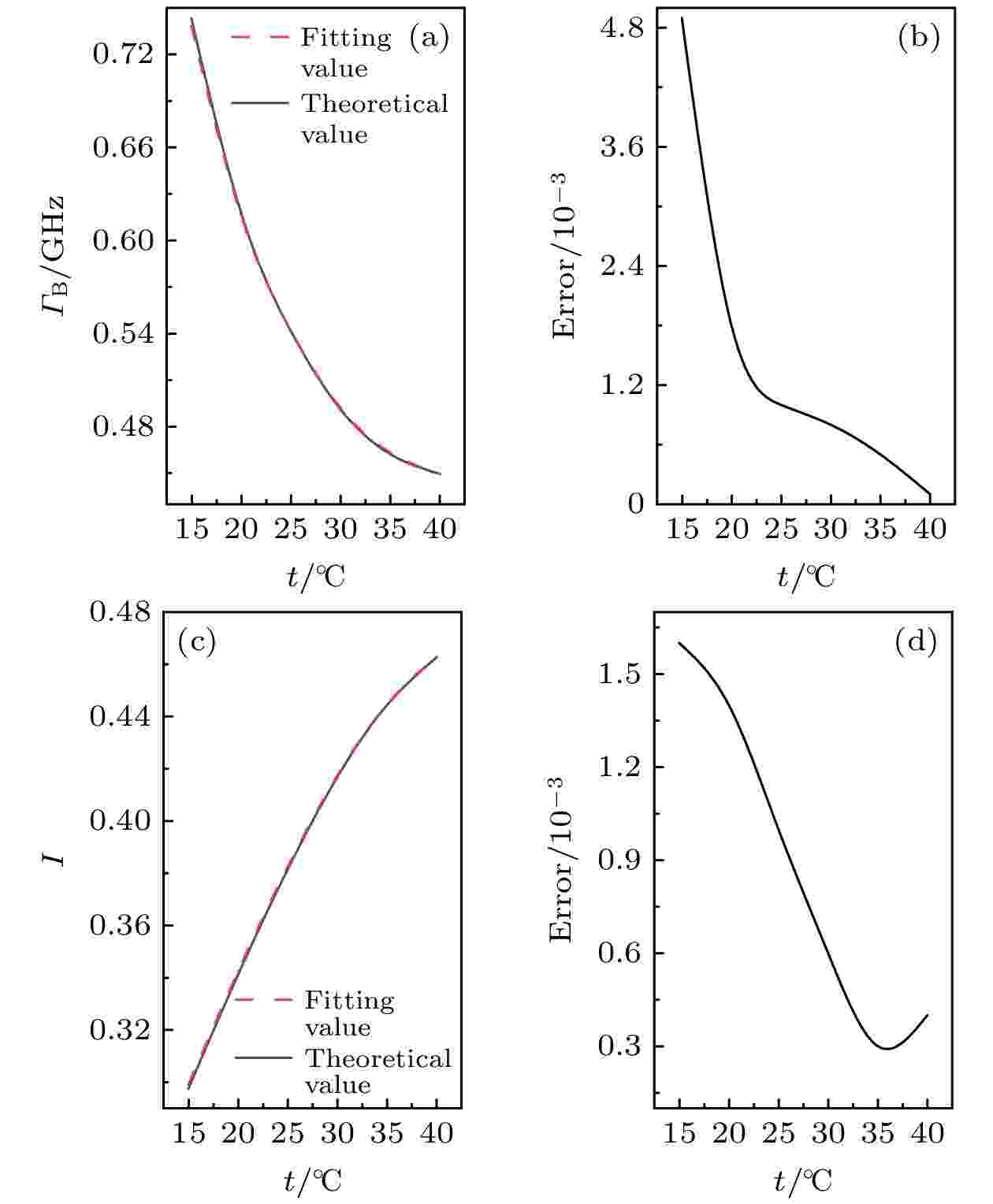图 10 温度误差对Brillouin散射探测造成的影响　(a) 恒定盐度, 不同温度下谱宽理论值与拟合值; (b) 温度误差导致谱宽探测误差; (c) 恒定盐度, 不同温度下探测能量理论值与拟合值; (d) 温度误差导致能量探测误差
Figure10. Effect of temperature error on Brillouin scattering detection: (a) Theoretical and fitting values of spectrum width at different temperatures under constant salinity; (b) temperature error leads to spectrum width detection error; (c) theoretical and fitting values of detection energy at different temperatures under constant salinity; (d) temperature error leads to energy detection error.

温度误差对Raman散射光谱、Brillouin散射谱宽和能量探测造成的影响, 会使得海水盐度反演产生误差. 其中Raman散射光谱探测结果得到的低、高频面积比的对数值ln(S_HB/S_NHB)的误差, 对盐度反演结果的影响如图11所示, 在低、高频面积比的对数值的误差范围内, 海水盐度反演误差小于0.91‰.
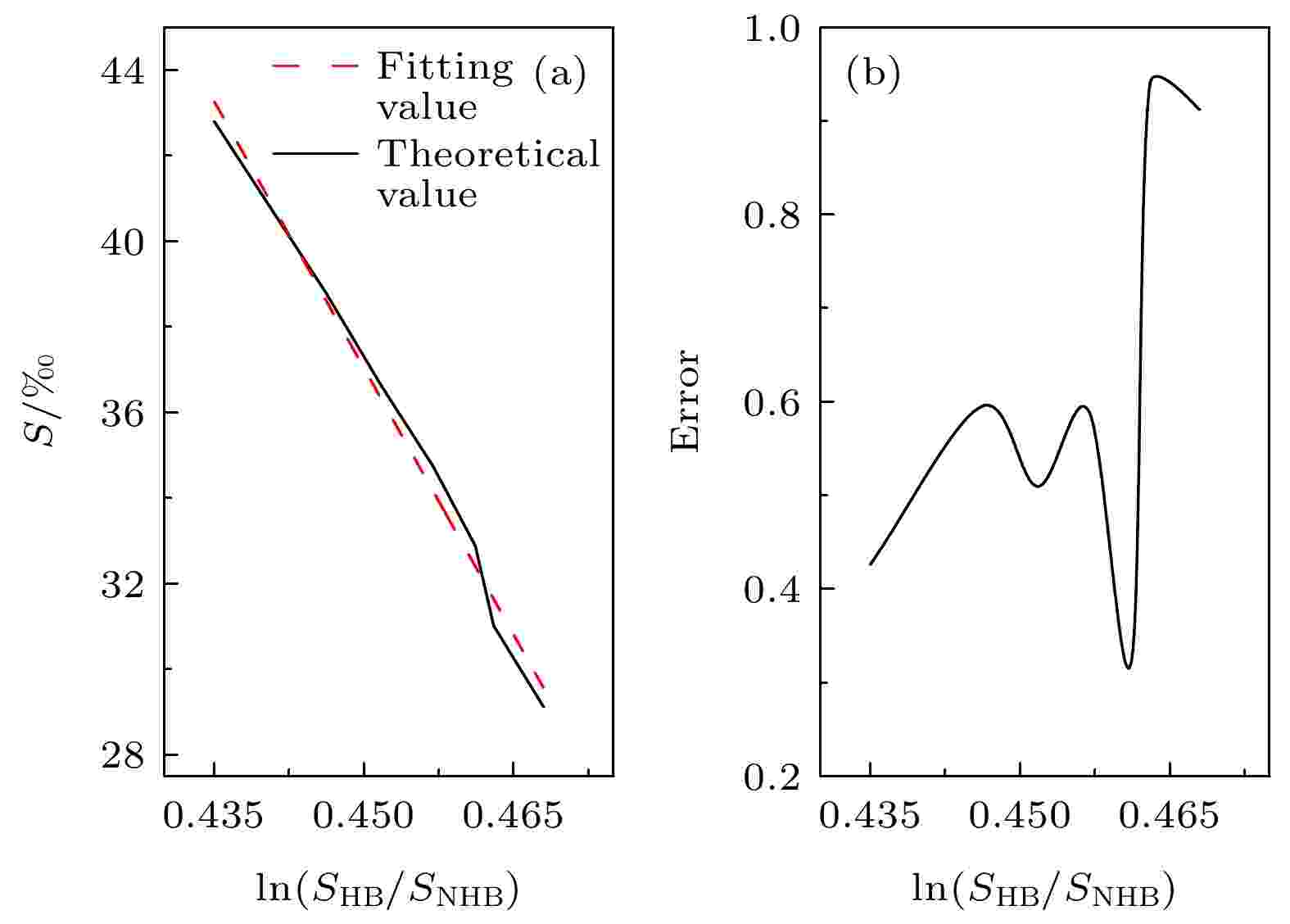图 11 Raman光谱探测误差对盐度探测结果的影响　(a) 盐度反演结果理论值与拟合值; (b) 盐度反演误差结果
Figure11. Effect of Raman spectral detection errors for salinity detection results: (a) theoretical value and fitting value of salinity inversion results; (b) salinity inversion error results.

Brillouin散射探测的误差对海水盐度的反演结果造成的影响如图12所示. 其中图12(a)和图12(b)给出了Brillouin谱宽探测误差对盐度反演的影响, Brillouin谱宽的误差范围内, 海水盐度的反演误差小于0.82 ‰; 图12(c)和图12(d)给出了Brillouin探测能量误差对盐度反演结果的影响, 在探测能量误差范围内, 海水盐度反演误差小于1.34‰.
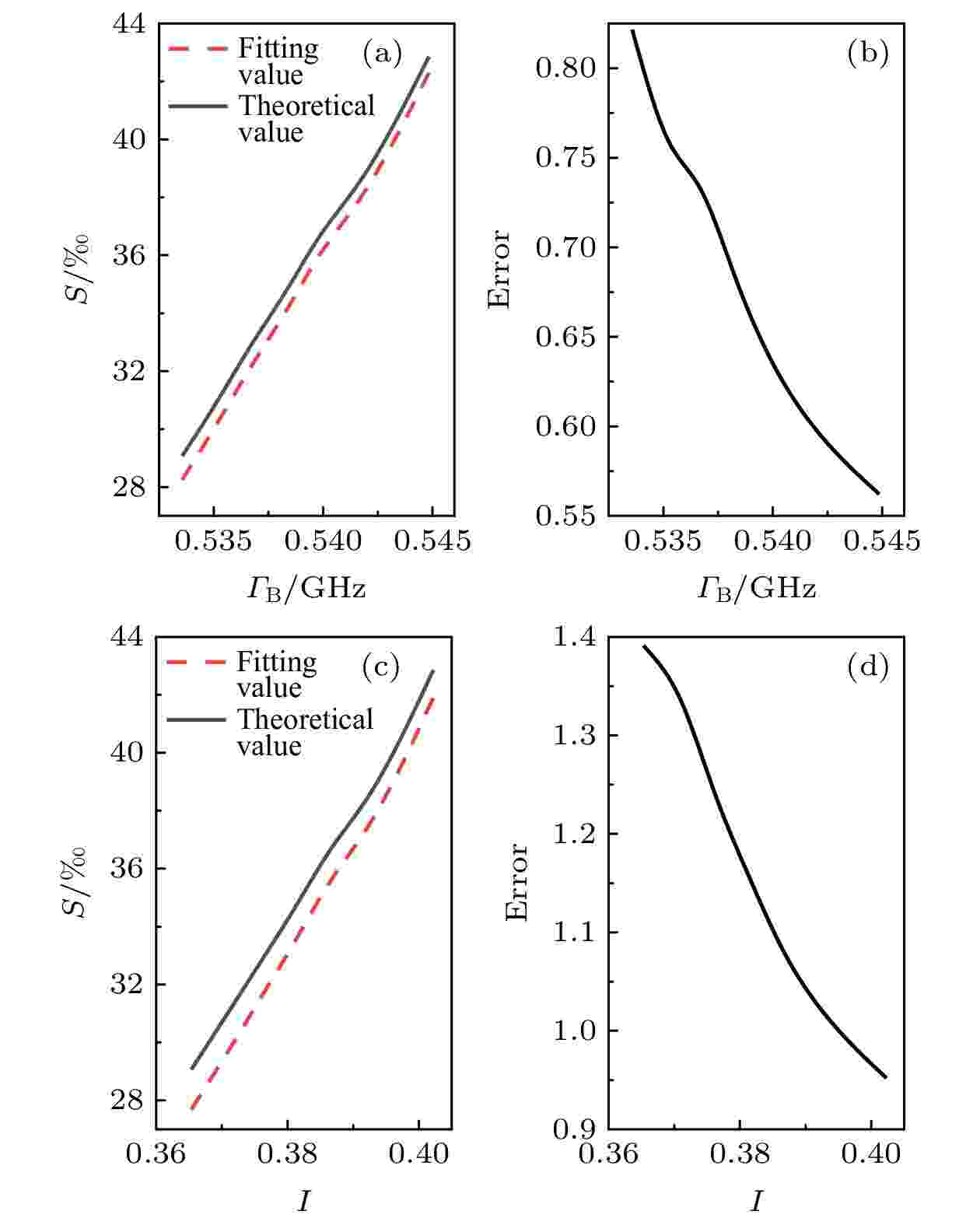图 12 Brillouin散射探测结果对盐度反演的影响　(a) 谱宽改变时, 盐度反演结果理论值与拟合值; (b) 谱宽误差导致盐度反演结果误差; (c) 能量改变时, 盐度反演结果理论值与拟合值; (d) 能量误差导致盐度反演结果误差
Figure12. Influence of Brillouin scattering detection results on salinity inversion: (a) Theoretical value and fitting value of salinity inversion results when the spectral width changes; (b) error of spectral width leads to the error of salinity inversion results; (c) theoretical value and fitting value of salinity inversion results when the energy changes; (d) error of energy leads to the error of salinity inversion results.

针对海水盐度的探测, 本文提出了基于Raman-Brillouin散射方法精确反演海水盐度. 通过实验方法探测不同介质以及海水的Raman散射光谱, 由于光谱受温度和盐度变化的影响, 建立了Raman散射光谱与海水温度和盐度的二元函数关系. 结合海水温度、盐度与Brillouin频移之间的关系, 建立基于Raman-Brillouin散射的海水盐度求解模型. 本方法的提出, 为探究不同环境温度下精确探测海水盐度提供了解决方案. 该研究为改善海洋环境、海洋灾害预警和海洋气象预报准确度等方面提供了可靠的数据支持, 具有重要的研究价值和显著的社会效益.