摘要:相干衍射成像是一种对光源相干性要求非常高的无透镜计算成像技术. 相干性包括时间相干性和空间相干性两方面, 在很多实际场合具有理想相干性的光源很难获得. 导致空间部分相干的因素主要有光源发光区域内各部分不同步的发光机制、检测器像素有限大小引起的非零宽度点扩散函数以及样品的不稳定性; 而时间部分相干则是由光源的能量扩散引起, 表现为扩展的发射光谱带宽. 空间和时间相干性退化的直接结果是衍射图样的清晰度和可见度的降低, 导致相干衍射成像中基于全相干模型构建的重构算法无法实现准确的物体波前重构. 解决方法包括改良实验装置来直接提高光束的相干性, 和通过优化相位恢复算法来补偿相干性退化的影响. 基于Wolf的相干模表示方法和Nugent等建立的部分相干衍射成像理论框架, 针对不同相干衍射成像技术中低相干性问题的各种解决办法相继被提出, 总体历经了从需要提前测出照明光的空间相干特征 (相干长度或者复相干因子) 或者时间相干特征(光谱分布) 到不需要任何已知光源相干特征的发展过程. 本文重点介绍相干衍射成像的部分相干性理论、以及部分空间和部分时间相干光衍射成像中重构算法的研究进展.
关键词: 相干衍射成像/
部分时间相干性/
部分空间相干性

English Abstract

全文HTML

--> --> -->

相干衍射成像(coherent diffraction imaging, CDI)是一种高分辨率、定量相位成像技术, 可广泛应用于纳米尺度生物材料结构测量^[1]、纳米尺度化学组分空间分布测定^[2]以及集成电路芯片结构^[3,4]和表面形貌无损测量^[5]等领域. 其中基于CDI的集成电路芯片逆向工程测量法能够对芯片的内部结构进行无损高清晰成像, 并且将来还有望实现快速的大规模批量探测. 瑞士Paul Scherrer Institute的科研人员先后发展了两种最具潜力的CDI集成电路成像技术, 具体为叠层X射线计算断层成像技术(ptychographic X-ray computed tomography, PXCT)^[3]和叠层X射线分层摄影术(ptychographic X-ray laminography, PyXL)^[4]. PXCT能够在任意投影方向上均实现14.6 nm的空间分辨率, 在成像过程中, 需要先将样品处理成横截面半径约为10 μm的圆柱体, 圆柱体的旋转轴须垂直于光波的传播方向^[3]; 而PyXL则不需要提前对样品进行切割, 这是目前能实现芯片非破坏性逆向工程的唯一方法. 对于40 μm直径的圆形成像区域, PyXL数据采集时间是60 h, 可实现分辨率是18.9 nm, 相对于PXCT的16.5 nm分辨率和23 h采集时间实现的成像体积大了16倍. 在PyXL的实验中, 裸芯片首先被抛光到20 μm的厚度, 然后将其放置在倾斜61°的扫描位移台上, 将X射线聚焦到芯片上, 旋转芯片, 再由光子计数相机来采集不用旋转角度的衍射图样, 最后通过相位恢复算法计算出结构分布.
CDI的成像过程分为两步: 首先通过图像传感器记录物波的衍射强度信息, 其次采用相位恢复算法重构出成像物体的复振幅信息. CDI不依赖于高质量的成像透镜, 在简化硬件装置的同时, 还能避免透镜像差和数值孔径对成像分辨率的限制. 在X射线和电子显微领域, 实现完美的“透镜”目前仍然面临许多制作工艺技术挑战. 另一方面, 与传统显微镜只能获得样品定性的相位衬度不同, CDI可以定量地重构出样品的相位信息. 因此CDI不仅能以较高的分辨率重构出样品的空间结构, 还能作为强大的工具来定量地研究与样品厚度和折射率波动有关的动力学问题.
CDI的概念最初是由Sayre^[6]提出. 1952年Sayre^[6]从香农采样理论的观点思考晶体衍射问题, 提出如果可以同时测量晶体布拉格峰之间的衍射强度, 就有可能唯一地反演求解出物体的结构. 1980年, Sayre ^[7]将这个想法扩展到非周期孤立物体. 非周期物体可以产生连续的X射线衍射图样, 这样通过记录衍射强度并采用数值算法获得晶体结构的X射线晶体学思想便能扩展到非晶样品领域, 衍生出了新的无透镜相干衍射成像方法(CDI). 相对于干涉式的成像^[8-10]而言, CDI不需要参考光波来产生干涉条纹, 因而极大地降低了对系统的稳定性要求. 1999年华人****Miao等^[11]在同步辐射光源上首次成功地实验验证了CDI技术, 完成了对非晶样品的纳米尺度成像测量, 该工作极大地激发了研究人员对CDI技术的兴趣, 在随后的20多年里不同系统结构和不同相位恢复算法相继被提出, CDI技术取得了快速的发展.
CDI最初多采用透射式结构, 系统设置为平行光照明样品, 由放置在样品后面的检测器来记录物波的远场衍射强度信息. 在透射光路下, 以传统CDI为基础发展出的变体有菲涅尔CDI^[12,13], 叠层成像(ptychograohy) ^[14-16], 傅里叶域叠层成像 ^[17,18], 和相干调制成像 ^[19-23]等. 此外, 反射式CDI^[24,25]和布拉格CDI (Bragg CDI) ^[26,27]也相继被提出. 反射式CDI多用于物体形貌定量测量和物体表面缺陷检测. Bragg CDI最初是由Robinson等^[26]于2001年提出, 其能够以小于10 nm的三维空间分辨率来研究纳米晶体的晶格位错, 以及较高的应变灵敏度(<10^–4)来定量表征纳米晶体的应变. 这些技术的成像维度也由二维发展到三维^[28]甚至是四维^[29] (加入了时间维度以实现超快成像). 所采用的相干辐射源包括电子和太赫兹、可见光、极紫外(extreme ultraviolet, EUV)、X射线等不同频谱范围的光子.
相位恢复算法是CDI的核心, 包括迭代投影算法和确定性(也称为解析或者直接)算法. 维格纳分布去卷积(Wigner distribution deconvolution, WDD)算法^[30]和TIE (transport intensity equation)方法是比较典型的直接相位恢复算法. WDD用于叠层成像时, 通过对四维数据(二维衍射图样和二维扫描位置)以扫描位置为变量做傅里叶变换直接计算出样品的相位分布. TIE技术通过记录多个轴向位置的平面上的光强分布和计算光强轴向微分直接获取物体的相位信息^[31]. TIE方法需要做傍轴假设, 只适用于薄样品, 无法应用到一般复杂物体出射波的情况. 迭代相位恢复算法最初由Gerchberg 和Saxton^[32,33]在1971年研究电子显微成像中的相位问题时提出, 故也称为Gerchberg-Saxton算法(简称为G-S算法). 在G-S算法迭代投影思想的基础上, 混合输入-输出(hybrid input-output, HIO)算法^[34]、误差下降 (error reduction, ER)算法^[35]、杨-顾(YG)算法^[36]、松弛平均交替反射(relaxed averaged alternating reflection, RAAR)算法^[37]、PIE (ptychographic iteration engine)算法^[38]、差异映射(difference map, DM)算法^[39]和ePIE (extended ptychographic iterative engine)算法^[40]等相继被提出以改善相位图像恢复的质量和算法的收敛性能. 随着人工智能的发展, 基于神经网络的算法也被应用到求解相位恢复的问题上, 对特定的应用, 表现出了更低的硬件要求和更好的性能^[41-44].
一切衍射成像的本质都是干涉效应, 而形成稳定的干涉需要衍射波具有较高的相干性. 在CDI中, 照明光源的相干性越高, 所记录衍射图样对应的波前不同部分的相位关系越明确稳定, 因此高相干性要求是CDI研究中1个关键性问题. 提高相干性的最直接方法是通过硬件进行改善, 例如使用单色器提高时间相干性; 使用光阑形成二次光源提高空间相干性; 提高系统的机械和电磁稳定性以及降低样品的振动来减弱导致相干性退化的外部因素等. 但是完全基于硬件的方法提高了系统成本, 而且带来其他性能的损失, 比如光通量的降低. 在集成电路的三维测量中^[3,4], 其成像中的数据采集速度、样品体积和空间分辨率均受制于目前的同步辐射光源所能实现的相干X射线通量. 尤其是为了跟上摩尔定律的步伐, 空间分辨率必须进一步提升, 才能对越来越微小的芯片结构进行无损探测. 有限的硬件性能一般很难完全消除CDI重构中光源的部分相干性对成像质量的影响. 除了基于硬件的方法, 数据测量过程存在的部分相干问题可以在相位重构计算过程中进行补偿. 本文系统地回顾了CDI研究中针对低相干性问题的相关成果和最新进展. 首先介绍CDI中的部分相干性基本理论, 随后综述低相干CDI解决方法的研究进程, 各方法的要点和取得的成果, 最后对现存问题以及今后的研究方向进行展望.

相干性一般分为时间相干性和空间相干性. 前者描述传播光场在空间某一点不同时刻波前分布的相关程度, 也称为纵向相干性; 后者描述光场中在光的传播路径上波前上横向间隔的两点在同一时刻光振动的相关程度, 因此又称为横向相干性. 简单来讲, 如果对一束时空变化波场以时间为变量做傅里叶变换得到时间频率谱, 或者以空间坐标为变量做傅里叶变换得到空间频率谱, 二者频谱带宽越窄、成分越单一, 则表明光源的相干性越好. 通常可以在光路中加入狭缝或小孔光阑来增加空间相干性, 采用单色仪来提高时间相干性. 在波的叠加的一般讨论中, 人们往往假定波是完全相干或者完全不相干两种特殊情况. 对于实际光源, 光波的相干性多处于这两者之间, 即部分相干. 例如, 在强激光技术中, 很难获得理想的完全空间相干的基模高斯光束. 针对不同类型的入射波, 衍生出了不同的描述部分相干光的数学物理模型, 比如高斯-谢尔模光束^[45-47]以及部分相干贝塞尔-高斯光束^[48-50]等. 2010年, Gbur和Visser^[51]对经典光学相干性的研究发展历程做过详细的总结, 包括相干性理论研究的起源, 现代光学相干性理论的发展, 部分相干性的空间域-频率域表示, 测量空间相干性的实验, 部分相干模的表示和应用, 以及部分相干波的应用等.
Wolf^[52]提出的相干模表示方法对解决CDI中部分相干性起到了至关重要的作用, 该方法是将部分相干波的交叉谱密度 (cross-spectral density) 函数扩展为一系列正交模的对角化表示, 其中交叉谱密度函数是对互相干函数(mutual coherence function)以时间为变量做傅里叶变换计算得到的. Wolf等所倡导的现代相干性理论就起源于互相干函数的研究. 交叉谱密度是一种非负定的厄米特函数, 是将Mercer’s定理^[53]推广到厄米特函数上的结果, 将交叉谱密度函数$ W({{\boldsymbol{r}}_1}, {{\boldsymbol{r}}_2}, {\omega} ) $扩展为n个相干模^[52,54]:

$ W({{\boldsymbol{r}}_1},{{\boldsymbol{r}}_2},{\omega} ) = \sum\limits_n {{\lambda _n}(\omega )} \cdot {{\boldsymbol{\phi}} _n}({{\boldsymbol{r}}_1},\omega ) \cdot {\boldsymbol{\phi}} _n^*({{\boldsymbol{r}}_2},{\omega} ) , $

其中r₁和r₂代表波场中不同的两个位置; ω是波的时间圆频率; $ {\lambda _n}({\omega} ) $和$ {{\boldsymbol{\phi}} _n}({\boldsymbol{r}}, {\omega} ) $分别为$ W({{\boldsymbol{r}}_1}, {{\boldsymbol{r}}_2}, {\omega }) $的特征值和特征向量, $ {\lambda _n}({\omega} ) $为非负实数, *表示复共轭. 不同的模$ {{\boldsymbol{\phi}} _n}({{\boldsymbol{r}}_1}, {\omega }) $在给定域内两两正交互不相关, 并可在光学系统中独立传播. 这些模是亥姆霍兹微分方程(Helmholtz differential equation)和弗雷德霍姆积分方程(Fredholm integral equation)的共同解^[54]:

$ ({\nabla ^2} + {k^2}){{\boldsymbol{\phi}} _n}({\boldsymbol{r}},{\omega} ) = 0 , $

$ \int {W({{\boldsymbol{r}}_1},{{\boldsymbol{r}}_2},{\omega} )} \cdot {{\boldsymbol{\phi}} _n}({{\boldsymbol{r}}_2},{\omega} ){\rm{d}}{r_2} = {\lambda _n}({\omega} ) \cdot {{\boldsymbol{\phi}} _n}({{\boldsymbol{r}}_1},{\omega} ) \text{, } $

其中$ {\nabla ^2} $为拉普拉斯算子; k为波数, k = ω/c, c为真空光速. 这种相干模分解的方法不仅适用于二维空间, 而且也可以应用于三维空间.
CDI技术的理论基础建立在照明光是完全相干的假设上. 对于实际光源的部分相干性对重构质量的影响, 不同CDI技术对相干性要求的差异, 以及降低相干性要求的可能方法, ****们进行了一系列详细的研究. Quiney^[54]和Nugent^[55]曾分别对其做过一些较为具体的综述.
早在Miao等^[11]用实验首次验证CDI之前就有许多****对部分相干性对衍射强度的影响做过详细的研究^[56,57]. 其中, Sinha等^[56]针对菲涅尔和夫琅禾费衍射的情况做了综合的理论分析; Lin等^[57]提出可以用横向相干传播的统计光学公式来模拟部分横向相干波的衍射, 其实验研究结果表明可以通过狭缝组合和聚焦镜对同步辐射光源的空间相干性进行调控. Vartanyants等^[58]详细地研究了部分相干性对小晶体X射线成像中图像重构质量的影响, 结果表明在部分相干光情况下, 重构图像中会出现局部高强度亮斑. 2004年Spence等^[59]根据香农采样定理对孤立样品的CDI技术的相干性要求做了研究总结, 结论为: 1)空间相干性-相干长度不能低于物体横向尺寸的两倍; 2)时间相干性-检测器阵列的单边像素个数决定了光源的相对频谱宽度(能量扩散).
1991年开始 Nugent^[60]和Williams等^[61]建立起非周期样品部分相干衍射成像的理论框架. 他们研究发现样品的重构十分依赖于照明场源的相干性, 少量的相干度降低就会导致结果和基于完全相干假定建立的物体出射波和其远场衍射强度的数学关系产生较大的偏差. 为此, 他们构建了1个理论模型来表示部分相干照明场源, 并且对球面和平面光波两种照明情况进行对比, 指出曲面波照明更有利于克服部分相干性带来的不良影响, 而平面波照明对相干性的要求就比较苛刻. 对于如图1(a)所示的平面和曲面波照明情况, 他们构建了互光强(mutual optical intensity, MOI)函数, 并用此来分别表示平面波和球面波照明情况下的远场衍射强度. 以图1(b)所示的实验系统模型为例对其进行描述. 假设透镜放置在z = 0处, 三维坐标系统表示为(r, z), 其中r = (x, y)是一个垂直于光轴的二维坐标矢量, z沿着光轴方向, 样品放置在距离透镜焦点一倍焦距的地方. 以$ {J_z}({{\boldsymbol{r}}_1}, {{\boldsymbol{r}}_2}) $来表示距离样品z处光场的MOI. 首先根据广义斯涅耳模型构建的MOI来表示入射到透镜的光场^[61],
图 1 用于研究部分相干CDI的照明方式和成像系统^[61]　(a)平面波和球面波照明示意图, 透镜会引入额外的相位曲率, 假设透镜是理想的并且在物平面的相干长度是相同的; (b)实验系统模型示意图
Figure1. Schematics of the two illumination conditions and experimental system for investigating partially coherent CDI^[61]: (a) Illumination by planar and curved component waves, respectively. Assuming an ideal perfect lens, both have identical intensities and coherence lengths at the sample plane. However, the illumination with a lens has an additional phase curvature by the focal length of the lens; (b) the experimental system being modeled and the coordinate system used.

$ {J_0}({{\boldsymbol{r}}_1},{{\boldsymbol{r}} _2}) = \psi ({{\boldsymbol{r}}_1}){\psi ^*}({{\boldsymbol{r}}_2})g({{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2}) , $

其中相干因子$g({{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2})$的特征宽度即为一般定义的相干长度. 这里光场假定为准单色光, 波数为k ₀ = 2π/λ, 因此只考虑了空间部分相干性. 对于一束空间部分相干光s(r_s), 在距离z处的平面内则有^[61]

$ \psi ({\boldsymbol{r}}) = \frac{{\text{i}}}{{\lambda z}}\exp \left({\text{i}}{k_0}\frac{{{{\boldsymbol{r}}^2}}}{{\lambda z}}\right) , $

$ g({{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2}) = {\left( {\frac{{{k_0}}}{{2{\text{π}}}}} \right)^2}\int {s({r_{\text{s}}})} \exp [ - {\text{i}}{k_0}({{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2}) \cdot {{\boldsymbol{r}}_{\text{s}}}]{\text{d}}{{\boldsymbol{r}}_{\text{s}}} . $

这即为范西特-泽尼克定理(van Cittert-Zernike theorem). 从物理的角度看, 这是一组互不相干的球面波的叠加, 其角度由光源的物理形状决定. (4)式将此概括为任意波的非相干叠加, 从而能够通过一个光学系统或者其他的折射/反射介质进行传播.
光波通过焦距为f的透镜之后, MOI可以表述为^[61]

$\begin{split}&{J_{0 + }}({{\boldsymbol{r}}_1},{{\boldsymbol{r}}_2}) = \psi ({{\boldsymbol{r}}_1}){\psi ^*}({{\boldsymbol{r}}_2})\\&\times\exp \left( - {\text{i}}{k_0}\frac{{{{\boldsymbol{r}}_1}^2 - {{\boldsymbol{r}}_2}^2}}{{2f}}\right)g({{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2}) .\end{split}$

简单起见, 假设入射波分量为强度均匀分布的平面波, 振幅为A₀, 则^[61]

$ \psi ({\boldsymbol{r}}) = {A_0} . $

将相干因子由相干长度l_c来表示, 即^[61]

$ g({{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2}) = \exp \left( { - \frac{{{{\left| {{{\boldsymbol{r}}_1}^2 - {{\boldsymbol{r}}_2}^2} \right|}^2}}}{{2l_{\text{c}}^2}}} \right) . $

那么(7)式则可以表示为^[61]

$ \begin{split}&{J_{0 + }}({{\boldsymbol{r}}_1},{{\boldsymbol{r}}_2}) \\=\;& A_0^2\exp \left[ { - \left( {\frac{{{{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2}}}{{2l_{\text{c}}^2}} + {\text{i}}{k_0}\frac{{{{\boldsymbol{r}}_1} + {{\boldsymbol{r}}_2}}}{{2f}}} \right) \cdot ({{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2})} \right] .\end{split}$

光波通过透镜再传播任意距离z后, 依据标准傍轴部分相干光传播规律可得到^[61]

$\begin{split}&{J_z}({{\boldsymbol{r}}_1},{{\boldsymbol{r}}_2})\\=\;& {A^2}(z)\exp \left[ { - \left( {\frac{{{{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2}}}{{2l_{\text{c}}^2(z)}} + {\text{i}}{k_0}\frac{{{{\boldsymbol{r}}_1} + {{\boldsymbol{r}}_2}}}{{2R(z)}}} \right) \cdot ({{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2})} \right] \text{, }\end{split}$

其中

$ \begin{split} & {l_{\text{c}}}(z) = \left| {\frac{{f - z}}{f}} \right|{l_{\text{c}}}, \\ & R(z) = f - z,\\ &{A^2}(z) = {\left( {\frac{f}{{f - z}}} \right)^2}A_0^2 . \end{split} $

需要注意的是, 相干长度是位置的函数, 随着光束的收缩变小, 在焦点处变为零, 然后随着光束的发散而逐渐增加. 在焦点处的零相干长度是在假设透镜完美且无限大时的结果. 样品到透镜距离为z_s = 2f时, 样品平面的相干长度变为入射到透镜处的相干长度. 下面对平面波和发散波照明的对比研究就将z_s选为样品位置. 为避免发散光照明中振幅调制引起的复杂情况, 下面的对比也仍然保留透镜无限大的假设.
在透镜无限大的假设下, 在样品平面的MOI为^[61]

$\begin{split}&{J_{{z_{\text{s}}}}}({{\boldsymbol{r}}_1},{{\boldsymbol{r}}_2}) \\=\;& A_0^2\exp \left[ { - \left( {\frac{{{{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2}}}{{2l_{\text{c}}^2}} - {\text{i}}{k_0}\frac{{{{\boldsymbol{r}}_1} + {{\boldsymbol{r}}_2}}}{{2f}}} \right) \cdot ({{\boldsymbol{r}}_1} - {{\boldsymbol{r}}_2})} \right] .\end{split}$

这里假设样品为薄散射物体, 其透过率函数为σ(r). 照明光通过样品后的物光波前可以表示为

$ J_{{z_{\text{s}}}}^{{\text{sc}}}({{\boldsymbol{r}}_1},{{\boldsymbol{r}}_2}) = {J_{{z_{\text{s}}}}}({{\boldsymbol{r}}_1},{{\boldsymbol{r}}_2})\sigma ({{\boldsymbol{r}}_1}){\sigma ^ * }({{\boldsymbol{r}}_2}) . $

在检测器平面所记录的远场强度分布则为

$ I_\infty ^{{\text{sc}}}({\boldsymbol{s}}) = \iint {J_{{z_{\text{s}}}}^{{\text{sc}}}({\boldsymbol{r}},{\boldsymbol{r}}{\text{ + }}\boldsymbol{x})\exp( - {\text{i}}{k_0}{\boldsymbol{s }}\cdot {\boldsymbol{x}}){\text{d}}{\boldsymbol{x}}{\text{d}}{\boldsymbol{r}}} \text{, } $

其中r ≡ r₁, x ≡ r₂ – r₁, s是检测器平面的二维矢量.
当采用部分相干发散曲面波照明时, 薄物体的远场衍射强度为^[61]

$ \begin{split} I_\infty ^{{\text{sc}}}({\boldsymbol{s}}) = \;&A_0^2\iint \sigma ({\boldsymbol{r}}){\sigma ^*}({\boldsymbol{r}} + {\boldsymbol{x}})\exp \left( { - {\text{i}}{k_0}\frac{{{\boldsymbol{r}} \cdot {\boldsymbol{x}}}}{f}} \right){\text{d}}{\boldsymbol{r}}\\ &\times \exp ( - \mu {{\left| {\boldsymbol{x}} \right|}^2})\exp( - {\text{i}}{k_0}{\boldsymbol{s}} \cdot {\boldsymbol{x}}){\text{d}}{\boldsymbol{x}} \text{, } \\[-10pt] \end{split} $

其中

$ \mu \equiv \frac{1}{{2l_{\text{c}}^2}} + {\text{i}}\frac{{{k_0}}}{f} . $

当采用部分相干平面波照明时, f →$\infty $ (近似为照明光的曲率半径无限大), 薄物体的远场衍射强度为^[61]

$ \begin{split} I_\infty ^{{\text{sc}}}({\boldsymbol{s}}) =\;& A_0^2\iint \sigma ({\boldsymbol{r}}){\sigma ^*}({\boldsymbol{r}} + {\boldsymbol{x}}){\text{d}}{\boldsymbol{r}}\\ &\times\exp \left( { - {\text{i}}{k_0}{\boldsymbol{s}} \cdot{\boldsymbol{ x}} - \frac{{{{\left| {\boldsymbol{x}} \right|}^2}}}{{2l_{\text{c}}^2}}} \right){\text{d}}{\boldsymbol{x}} . \end{split} $

在相干长度l_c→$\infty$时, 衍射强度分布就变成了散射物体自相关函数的傅里叶变换, 这也就是照明光完全相干时的情形. (18)式本质上是衍射场的卷积积分, 所以部分相干性的表现形式可认为是将相干的衍射图样和复相干因子g(x)的傅里叶变换进行了卷积^[62].
相比于平面波照明, 球面波远场衍射图样中多了exp(–μ|x|²)这一项. exp(–μ|x|²)是球面照明波振荡项和部分相干性引起的指数衰减项的乘积. 如果f足够小, μ的虚部会使这个指数项振荡得非常快, 只有|x|接近0的区域的积分才对远场衍射强度有显著的贡献. 在这种情况下, 所测量的衍射强度就会接近完全相干的情况, 从而CDI方法就会给出比较好的成像结果. 为了克服部分相干性的不利影响, 球面照明波的曲率半径或者说透镜的焦距需要满足: $f \ll 2{l_{\text{c}}^2}/\lambda$^[62].
(4)式将部分相干光概括为任意波的非相干叠加, 根据Wolf的部分相干性理论^[52], $ J({{\boldsymbol{r}}_1}, {{\boldsymbol{r}}_2}) $具有正定性, 可以将样品平面的照明光表示为有限个标准正交而且互不相关的模态的叠加, 即^[63]

$ J({{\boldsymbol{r}}_1},{{\boldsymbol{r}}_2}) = \sum\limits_{n = 1}^N {{\mu _n}} {\psi _n}({{\boldsymbol{r}}_1})\psi _n^*({{\boldsymbol{r}}_2}) , $

其中ψ_n(r)表示正交且互不相干的模态, 非负实数μ_n为第n个模态所占的权重. 远场衍射图样则可以描述为N个模态对应的远场衍射强度I_n(s)的叠加:

$ I_\infty ^{{\text{sc}}}({\boldsymbol{s}}) = \sum\limits_{n = 1}^N {{\mu _n}} {I_n}({\boldsymbol{s}}) . $

部分相干模分解的理论框架也适用于对CDI中时间部分相干性的讨论. Abbey等^[64]利用已知光谱分布信息的宽带X射线作为光源, 利用相干模叠加的迭代重构算法(PolyCDI), 在实验上实现了连续宽带波CDI.

2

-->

3.1.相干长度已知的部分空间相干情况

在2007年和2008年, Williams等^[61]和Whitehead等^[65]分别从理论和实验上论证了部分空间相干光照明对CDI重构质量具有重要的影响. 此后, ****们便采用各种方法计算出照明光的复相干度, 并且尝试着从算法上补偿弱相干性, 从而实现高质量的CDI相位恢复. 2009年Flewett等^[66]根据MOI部分空间相干光理论框架提出了1种可以恢复出照明光的相干模函数以及各个模所占比重的方法. 他们分别采用数值模拟和X-ray实验对所提方法进行了验证, 其中模拟以高斯-谢尔模型来构建MOI, 而实验结果表明相干性越高, 最主要的模态在照明光中所占能量比重越大. Whitehead等^[63]则从实验上实现了部分空间相干光的CDI相位成像. 他们提出了一种多模迭代算法(multimodal algorithm), 证明可以将部分相干光分解为少量的若干个空间相干模态来提高成像质量. 该算法核心流程为^[63]
1)在光源的部分相干性特征提前被测量出的情况下, 根据(19)式来估计部分相干光穿过样品后的物波;
2)用(20)式来描述物波传播到检测器上后所记录的衍射强度;
3)在傅里叶变换域对所有相干模态的波场总和施加模值约束, 即保持各模态波场的相位不变, 仅调整各个模态的振幅;
4)将所占能量比重最大的1个模态由检测器平面反向传播到样品平面;
5)在样品平面对计算得到的物波施加实空间约束, 比如有限非零区域约束.
其中, 步骤4)中可以利用任何1个模态, 而采用占比最大的模态, 是因为其包含照明光中更多的能量.
图2(a)所示为照明光低相干时, 采用上述多模算法重构的物波强度信息. 作为对比如果仍然使用完全空间相干的假设(单模算法)进行重构, 结果重构失败, 如图2(b)所示. 为了进行更进一步的对比, 将低相干照明实验中使用的525 μm宽狭缝变窄为5 μm来提高照明光的空间相干性. 在高相干性情况下, 初始给定一个不准确的相干长度信息, 使用多模算法恢复的结果如图2(c)所示, 而采用单模算法重构的结果如图2(d)所示. 这些结果表明, 多模算法能够有效地提高部分空间相干照明情况下的重构质量.
图 2 低空间相干光照明时, 采用文献[63]多模算法(a)和单模算法(b)分别重构的物波强度信息; 在高空间相干光照明但已知相干长度信息不准确的情况下, 采用文献[63]多模算法(c)和单模算法(d)分别重构的物波强度信息^[63]
Figure2. Reconstruction of the magnitude of the wave leaving the sample. At the low-spatial coherent illumination, the reconstruction using the known coherence information (a) and assuming perfect spatial coherence (b). In the high-spatial coherent condition, reconstruction utilized the known coherence information (c) and full-spatial coherence assumption (d) ^[63]

这些部分相干CDI技术都需要提前测量出照明光的相干性特征, 并将其作为已知先验信息包含在迭代算法中. 可以用来测量空间相干性的方法包括杨氏双缝干涉^[67]、数字微镜装置^[68]、剪切干涉^[69]、等离子体干涉^[70]、2D相位光栅干涉^[71]、环形光栅干涉^[72]、相空间断层成像法^[73,74]、自参考全息^[75]方法等. 其中杨氏双缝实验测量^[67]是最典型的方法, 需要注意的是, 杨氏实验中时间相干性和空间相干性对干涉强度都有影响. 零光程差处的条纹包络表征空间相干性效应, 而条纹包络在光程差变大时逐渐减小至消失则是时间相干性效应的表征. 但是要想测量到亚波长尺度的相干长度, 两个缝或两个孔的大小和距离需要小于等于入射光波长, 这就限制了传统杨氏实验测量法的适用性. 采用表面等离激元干涉技术能在入射光波长为550 nm的情况下, 测量到约330 nm的空间相干长度^[70]. 和传统双缝干涉不同的是, 双缝中的1个缝被替换为1个15 μm长、大约100 nm宽、20 nm深的凹槽, 凹槽能将入射的一部分光波转化为表面等离激元并传播到相邻的缝处, 这样就形成了1种相位延迟机制. 到达缝和沟槽之间的光波之间的空间相干性的变化将导致条纹可见度的测量差异^[70]. 相空间断层成像法已经从测量一维光束(由一维狭缝产生)所对应的的复相干度^[73]发展到了二维光场的情况, 能够完整的测量二维光波的四维相干函数^[74].
2 -->

3.2.相干长度未知的部分空间相干情况

在部分空间相干CDI技术发展初期都需要提前测量出照明光的部分相干性特征, 将已知的部分相干性特征作为先验信息代入重构算法中. 2011年Clark和Peele^[76]提出了一种不需要已知相干性信息的算法, 该算法能够同时重构出样品的复振幅传递函数以及空间相干特性. 之前的相干模分解重构算法在检测器平面进行强度限制(modulus constraint)时, 采用测量的衍射图样来调整所有互不相干模态的振幅而保持相位不变; 而在Clark的方法中, 检测器平面的衍射强度不再表示为一系列互不相干模态叠加后的模值平方, 而是用单个相干波和复相干函数傅里叶变换的卷积来表示, 不再进行相干模分解. 以往的方法只能用于二维物体, Clark等^[77]在2012年又提出了一种能够同时重构出照明光部分相干特性和三维物体的技术, 并指出物体的傅里叶变换和互相干函数对衍射图样各有不同的影响, 前者决定条纹间距及其相对位置, 后者影响可见度和衬度. 该方法适用于各种迭代式CDI, 包括同步辐射光源、自由电子激光、电子二维和三维成像, 也适用于ptychography. 上述方法虽然不用提前测量出照明光的空间相干长度, 但是需要已知部分相干光的数学物理模型. Floating mode方法则可以在不准确知道部分相干光的数学物理模型的情况下重构出可靠的样品和相干长度信息, 即使照明光会随着时间变化也能成功地进行重构^[78].
对于部分空间相干CDI, 一般通过两个方面来提高成像质量和成像分辨率, 一方面为改进重构算法来缓解部分相干照明的影响, 另一方面改进实验装置来对照明光进行滤波改善其空间相干性. 在2014年, Parks等^[79]对此进行了详细的对比研究. 研究结果表明, 成像质量的改善程度取决于样品的相位结构复杂度. 部分相干重构算法对重构图像质量的改进仅仅对弱相位物体有效; 随着物体相位复杂度的提升, 即便是提前测量出空间相干性的情况下, 采用Clark和Peele ^[76]提出的部分相干光投影 (PC projection)的方法进行重构时恢复质量会越来越差; 对于复杂相位物体, 从实验装置上提高照明光的空间相干性仍然是必需的. 远场CDI和近场CDI对部分空间相干性的鲁棒性也不相同. Hagemann和Salditt^[80]的研究表明相对于远场CDI, 近场CDI对部分空间相干光照明的鲁棒性更高.
传统的CDI只能对尺寸受限的孤立样品进行成像, ptychography打破了这种限制, 可以对扩展型样品成像. 通过二维移动照明探针或者样品, 并保证相邻扫描区域之间具有一定照明重叠, 能同时实现大视场范围和高空间分辨率的定量相位成像. Burdet等^[81]和Cadenazzi等^[82]的研究表明ptychography的重叠式扫描引入的大量数据冗余/重叠限制(overlap constraint)使其相对于传统的CDI具有对低空间相干性更高的鲁棒性, 并且鲁棒性也会随着照明光的复杂度即照明探针的相位多样性以及相邻扫描区域之间的交叠率的增大而提升. Ptychography也和传统CDI一样可以通过增加照明光的曲率来提高在部分空间相干情况下的重构精确度, 并且同样地随着物体相位复杂度的增加, 对相干性的要求也越高^[82]. Ptychography是一种扫描式成像, 需要一次性采集数十到成百上千幅衍射图样来重构样品的复振幅信息, 对成像硬件有较高的要求, 除了需要高亮度和高相干性的光源之外, 还需要考虑数据采集过程中样品和光学元件的振动引起的相干性降低, 比如在曝光时间内需要尽量保持样品处于静止稳定状态或者使用短脉冲光源. 类似传统CDI, ptychography在相位重构过程中可以采用一些补偿机制来降低部分相干性的影响. 其中使用最广泛的是混合模态分解(Mixed-state decomposition)算法, 该算法充分利用了ptychography数据的高冗余度来补偿低空间相干性造成的成像质量退化现象^[83].
混合模态(mixed states)的产生原因总的来说可以归结为三方面, 如图3所示: 照明光的低相干性 (图3(a)), 成像物体的模态混合(曝光时间内样品的变化) (图3(b)), 以及检测器的点扩散(图3(c)). 其中检测器的点扩散函数造成的退相干可以由考利互惠原理(Cowley’s reciprocity principle) ^[84]转化为照明光的属性, 那么混合模态就可以简化为照明和样品两种模态来处理. 在X-ray衍射成像中, 除了样品动力学之外, 样品的异质性也会造成相干性的退化, 尤其是在3D XFEL成像技术中^[85]. 这些退相干现象都会降低所采集的衍射条纹的可见度或者衍射斑的锐利度, 如图3(d)所示. 混合模态分解算法的提出可以有效地放松对严苛实验条件的要求, 降低对实验误差的敏感度. 由于该算法能够补偿照明探针的低相干性, 因此可以允许实验中采用高通量但低相干的照明光, 这样能极大地降低检测器的曝光时间; 而采集时间的大幅度减少又能降低对实验装置长时间稳定性的要求.
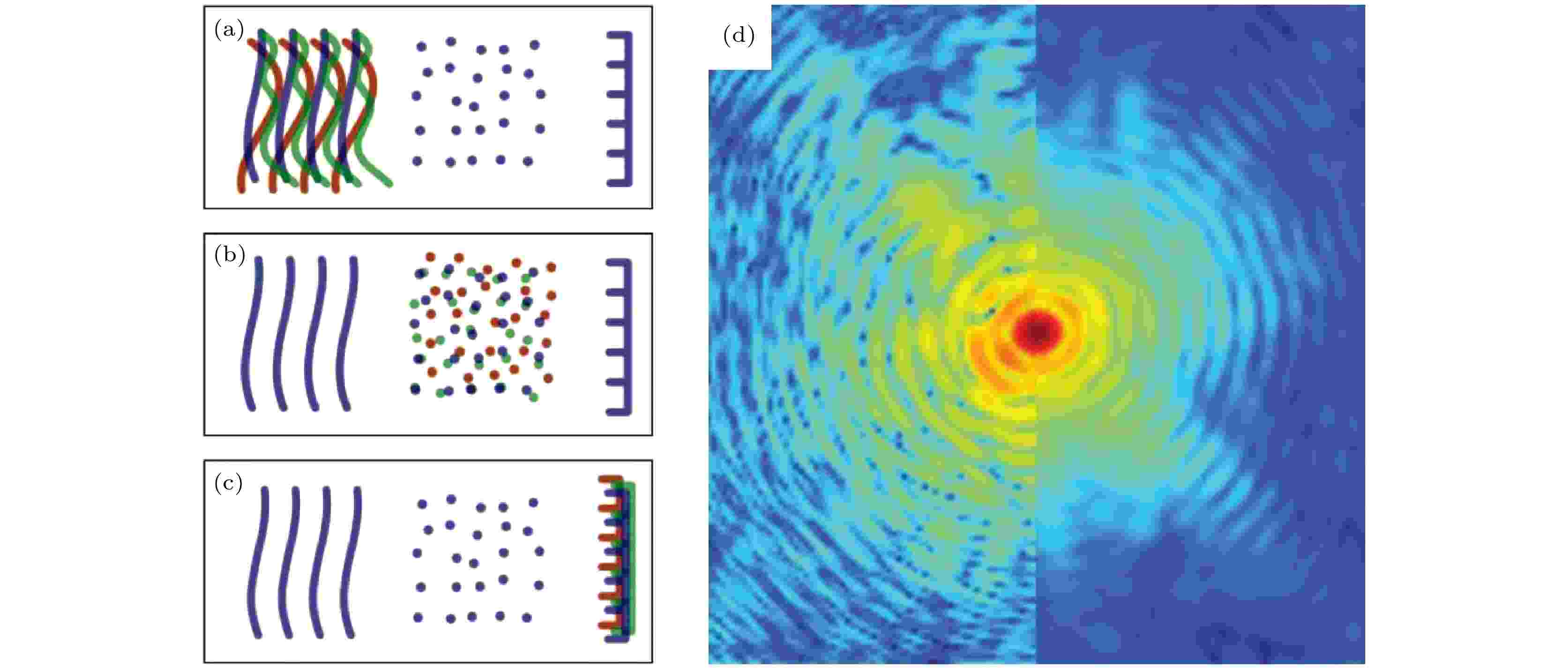图 3 散射实验中的退相干现象^[83]　(a)由照明探针的横向相干性和有限的带宽引起的模态混合; (b)样品中的混合模态, 包括量子混合态和快速平稳随机过程, 如振动、开关或稳定流; (c)检测器的点扩散造成的模态混合; (d)对于远场衍射, 退相干会造成散射强度分布的可见度降低. 图(d)右半边是模拟样品振动给衍射图样带来的影响
Figure3. Decoherence in scattering experiments^[83]: (a) Mixed states within the probing radiation may include all sources of mixing that manifest themselves as transverse partial coherence or finite bandwidth; (b) mixed states in the object of interest may occur from quantum mixtures and fast stationary stochastic processes such as vibrations, switching or steady flows; (c) mixed states caused by the detector point spread; (d) the signature of decoherence in far-field diffraction is a decrease in visibility of the scattered intensity distribution. Here the right half of the simulated diffraction pattern shows the effect of sample vibration.

混合模态分解算法的本质是分别将照明探针函数和物体函数都分解为多个互不相干的模. 照明光模态分解一方面可以提高成像质量和分辨率, 另一方面可以通过重构出多个照明光模态来精确地计算出照明光的复相干度. 物体模态的分解能够用于表征一些广义平稳的动力学过程如连续的样品运动、随机均衡波动、稳定的流动、周期性变化等. Thibault和Menzel^[83]在他们的文章中验证了由重构出的模态计算得到的复相干度和实验测量的结果相吻合. 此外, 他们还采用模拟对伊辛模型进行成像, 验证了物体模态分解方法研究样品动力学的可行性. 伊辛模型是一类描述物质相变的随机过程模型^[83]. 在该模拟的重构过程中假设照明探针为1个相干模态, 样品被分解为16个互不相干的模态, 如图4(a)所示, 表示样品混合模态的密度矩阵足以描述整个实验的统计特征. 在这16个模态中, 4个占据主要能量的模态如图4(b)所示. 由于对称性, 任何自旋的期望值均为零. 尽管如此, 由于量子点涨落会引起退相干, 该重构仍然可以可靠地对每个量子点成像. 而且, 在长度尺度上小于照度的点之间的相关性被编码在了衍射数据之中. 当对两个相邻自旋进行正交化处理时, 这些短程相关便能被很好地重构, 如图4(c)和图4(d)所示. 所得到的相对功率与铁磁和反铁磁耦合定量一致. 除了磁性系统, 该混合模态分解方法在自旋密度波域、量子振荡器模式和纳米流体中稳定流的直接成像中也具有应用潜力.
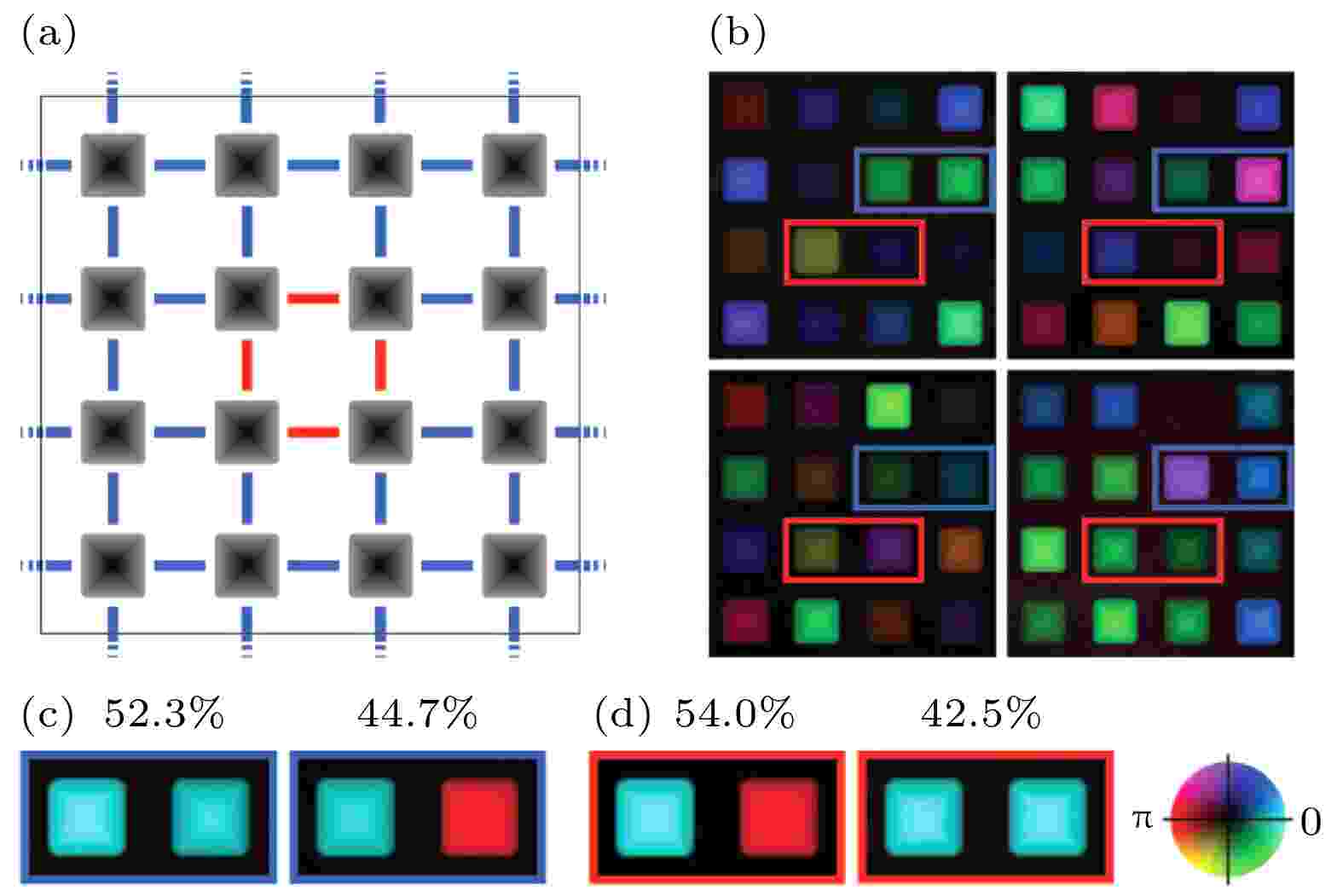图 4 伊辛模型成像模拟^[83]　(a) 在样本的布局中, 灰色方块代表每个自旋, 在照明光上产生±π/2的相移. 蓝色线条表示铁磁耦合, J = –1, 红色线条表示反铁磁耦合, J = +1; (b) 减去平均值后的4个主要物体模态. 相邻自旋正交化的结果, 在(b)中用蓝色和红色框勾勒出铁磁键(c)和反铁磁键(d), 相对模态的振幅与期望值非常吻合
Figure4. Imaging a simulated Ising model^[83]. (a) In the sample layout, grey squares mark individual spins, which incur a ±π/2 phase shift on the illumination. Blue lines represent ferromagnetic couplings, J = –1, red lines antiferromagnetic ones, J = +1. (b) The four dominant modes after subtraction of the mean. (c) and (d) The results of orthogonalization of neighbouring spins, outlined by blue and red frames in panel (b), for a ferromagnetic bond (c) and an antiferromagnetic bond (d). The relative mode amplitudes are in good agreement with expected values.

在曝光时间内样品全局移动和样品横向振动造成的退相干现象均可以等同为移动照明探针的影响. 利用该特性, Clark等^[86]提出了样品连续扫描(飞扫)的叠层扫描相干衍射成像技术(fly-scan ptychography). 不同于传统的ptychography, fly-scan ptychography中样品的移动和数据采集是同时进行的, 样品持续不断的运动, 因此每张衍射图样均为在检测器曝光时间段内许多幅子衍射图样的叠加, 如图5(a)—(c)所示. 他们的研究表明, 这种样品连续运动下的数据采集等价于照明光空间相干性的退化, 因此对照明探针进行混合模态分解能够缓解这种退相干现象, 从而弥补成像质量和分辨率的损失, 如图5(d)—(f)所示. 得益于混合模态分解算法的使用, fly-scan ptychography能够在不明显牺牲成像分辨率的情况下显著地缩短数据采集时间, 现有实验结果已证实在不明显牺牲分辨率的情况下, 可见光^[87]和X-ray^[88]实验条件下所需的采集时间分别能减少五分之四和七分之六. 这不仅能降低对装置稳定性的要求, 而且还有利于进行动态和原位实验^[87-89]. 此外, Clark等^[90]还用实验证明了在每个扫描位置的曝光时间内样品具有横向振动时, 样品的振动可以等效为探针的多个模态, 并且该等效性也表明可以通过对样品施加振动来定量地调控相干性.
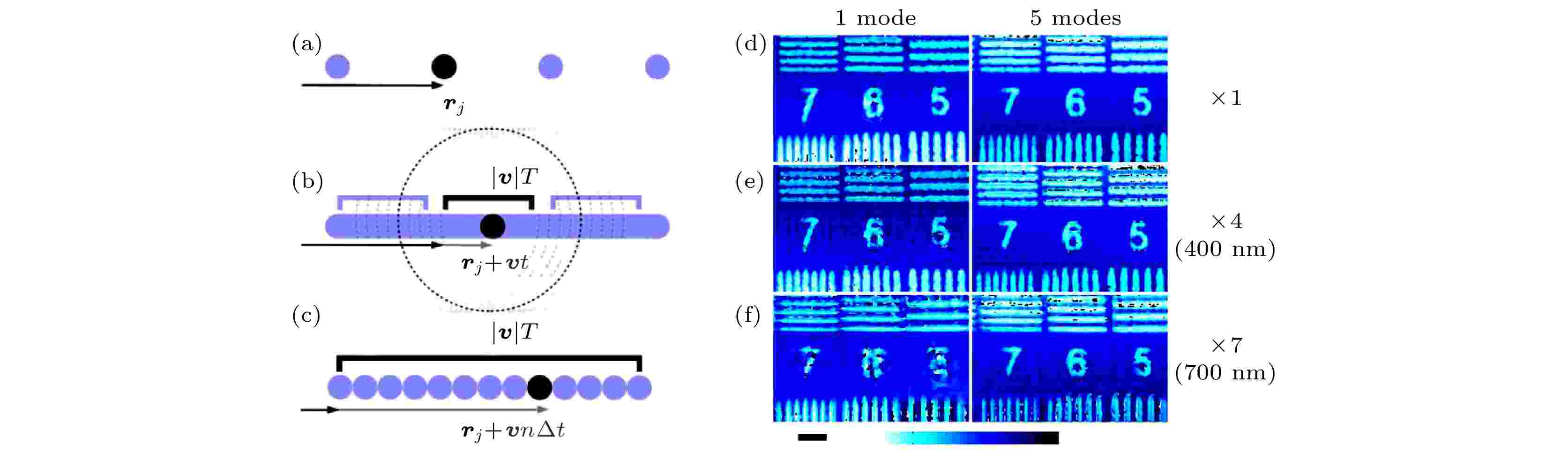图 5 (a)传统ptychography收集数据的模式, 即每移动距离r_j到1个位置静止后, 检测器才开始曝光进行数据的采集^[86]; (b) 样品以速度v进行连续运动时的数据采集模式, 每个r_j位置的衍射图样都是由在检测器曝光时间T内的$ \left| v \right|T $个位置的物波光子的叠加而得^[86]; (c) 样品以速度v进行连续运动时的数据采集模式可以被离散化, 即$ \left| v \right|T $可以离散化为n个小距离$ v\Delta t $^[86]; (d)—(f)样品相位的重构结果(左边1 mode是假设完全相干的情况, 右边5 modes是假设部分相干而将照明探针分解为5个模态的情况): (d)由原始采集数据直接重构的结果; (e)将相邻4个位置(总横跨距离是400 nm)采集的衍射图样叠加后重构的结果, 这里用相邻扫描位置对应衍射图的叠加来近似样品的连续运动^[86]; (f)将相邻7个位置(总横跨距离是700 nm)采集的衍射图样叠加后重构的结果^[86]
Figure5. (a) Conventional ptychography uses data collected with discrete translations r_j ^[86]; (b) for a continuously scanned sample with constant velocity v, the diffraction data will be made up of the positions that occupy a length $ \left| v \right|T $ around the scan positions r_j due to an integration time of T ^[86]; (c) the continuous scan can be discretized with steps separated by a small distance $ v\Delta t $^[86]; (d)?(f) reconstructed object phase (1 mode assuming full coherence, left and 5 modes assuming partial coherence, right): (d) Reconstruction for the original data^[86]; (e) reconstruction using new positions that consist of summing four adjacent positions (over 400 nm horizontally), approximating a continuously scanned sample^[86]; (f) reconstruction for a larger (seven positions, 700 nm) level of summing, which would be equivalent to an increased scanning speed^[86].

目前, 无论对于X射线同步辐射光源, 还是电子显微镜, 亦或是可见光成像装置, 都无法保证照明探针是完全相干的, 也不能保证长时间数据采集过程中样品是绝对静态的, 或者检测器不受点扩散函数的影响. 近年来基于混合模态分解算法的ptychography技术不仅已经广泛应用于高分辨X射线厚样品成像^[91]和三维断层成像^[92]等领域, 而且EUV测量^[93]和电子显微成像中也展现了显著的作用. Cao等^[94]研究表明物质波也能通过混合模态分解算法分解成一系列独立的正交模, 将照明探针分解为对应于密度矩阵特征值的模态, 普适于物质波相干性的描述. 他们还指出electron ptychography测量数据的多样性和高冗余度能够为重构部分相干特征提供充足的信息, 因此将electron ptychography和混合模分解结合能够有效地重构出部分相干电子波的特征, 而不用提前已知照明光的波前分布和空间相干特性. Chen等^[95]通过大量实验对比了electron ptychography在不同电子剂量和不同扫描步长下分别使用单模重构和混合模态重构的结果, 表明在低剂量和大扫描步长实验条件下, 混合模态分解重构方法相对于传统的ptychography重构算法具有更高的鲁棒性, 如图6所示. 其中当扫描步长为0.85 ?, 电子剂量不低于3300 e·?^–2时, 采用混合模分解可实现的空间分辨率最低为0.9 ?.
图 6 (a)—(h)单层WS₂样品在不同电子剂量条件(58000和3300 e·?^–2)下ptychography重构的结果; (i)—(p)单层WS₂样品在不同扫描步长(0.85和5.08 ?)下ptychography重构的结果; (a), (b)和(i), (j)分别分解为3个模态和2个模态重构的结果; (e), (f)和(m), (n)为不使用模态分解方法重构的结果; (c)和(d), (g)和(h), (k)和(l)以及(o)和(p)分别为对应于(a)和(b), (e)和(f), (i)和(j)以及(m)和(n)的衍射花样^[95]
Figure6. Ptychographic reconstructions of a monolayer WS₂ sample in different illumination dose (58000 and 3300 e·?^–2, (a)?(h)) and different scan step size (0.85 and 5.08 ?, (i)?(p)) conditions^[95]: Mixed reconstructions from datasets using three ((a), (b)) and two ((i), (j)) probe modes, respectively; ((e), (f)) and ((m), (n)) single mode reconstructions; ((c), (d)), ((g), (h)), ((k), (l)) and ((o), (p)) corresponding diffractograms of ((a), (b)), ((e), (f)), ((i), (j)) and ((m), (n)).

混合模态分解方法虽然行之有效, 但需要大量的扫描点数来引入更多的数据冗余信息. 即使可以采用一系列的修正算法在后期数据处理中对ptychography的部分空间相干性进行补偿, 但仍不如使用更高相干性的照明光^[96]. 在使用部分相干光照明时, 仅仅通过增加光剂量对重构结果没有明显的提升, 反而会对剂量敏感型样品带来严重的辐照损伤. Gardner等^[97]利用散射介质实现了空间非相干光ptychography. 一方面, 散斑相关成像可以显著地降低ptychography对相干性的要求; 另一方面, ptychography的局域照明特性使得每次扫描的照明区域可以同时满足散射介质的记忆效应范围和检测器的性能限制, 从而能够打破散斑成像对样品尺寸和相位复杂度的限制.

在CDI重构过程中, 除了假设照明光只有单一空间频率之外, 往往也假设其时间频率也是单一的, 即照明光波的波长是唯一的. 在实际情况中, 光源能量的不稳定等因素往往导致光波具有一定的光谱带宽, 此时所采集到的衍射图样则是许多波长所对应衍射强度的叠加. 通常使用单色仪或者滤波片就能有效地减小光谱带宽, 但是这同时也会大幅度降低光强度. CDI技术所实现的空间分辨率和入射光通量直接相关^[98]. 为了提高其空间分辨, 则需要更长的曝光时间或者提高成像技术对光谱带宽的容忍度. 采用由高空间分辨率的菲涅尔波带片和折射透镜组成的消色差菲涅尔光学器件(Achromatic Fresnel optic, AFO)可以显著地提高光子利用率, 并能够将可容许的消色差带宽(Δλ/λ)提高至少两个数量级(当λ = 13.5 nm且折射透镜材料为Si时, 消色差带宽可以从小于0.01%提升至0.97%)^[99]. 对于CDI技术, 也能通过改进算法或者成像系统来提高光谱带宽容忍度.
2

-->

4.1.光谱带宽已知的部分时间相干CDI

在2009年Multiwavelength CDI^[100]和 Two-step CDI^[101]先后被提出, 并采用高次谐波光源(high-harmonic generation sources, HHG)从实验上成功验证了方法的可行性. 在实验中不使用单色仪, 照明光包含若干个谐波成分. 入射波的波谱需要事先测量出来, 这可以通过对杨氏双缝实验产生的条纹进行最大熵法分析获得^[102], 这种方法也可以同时测量出照明光波的空间相干长度. 其中Multiwavelength CDI方法可以将可用的光通量提高至少一个数量级, 并获得了约160 nm的空间分辨率^[100]. Two-step CDI方法能从复色光波衍射数据中提取出1个单色波所对应的数据成分, 这样就能不对传统的CDI重构算法做任何的修改^[101]. 但是这两种方法都只适用于具有离散光谱的光源, 而不能应用于连续光谱照明的情况.
2011年Abbey等^[64]提出了可同时适用于连续和离散光谱的技术, 称为PolyCDI. 这种方法相对于准单色光成像的情况可以将数据采集的曝光时间降低60倍, 并且能够达到(150 ± 5) nm的空间分辨率, 这几乎和完全相干情况下的阿贝衍射分辨极限117 nm相一致. 照明光中部分时间相干的存在不仅会减弱有效的光强度, 而且会降低衍射图样的清晰度, 如图7(a)所示. 使用由较长的曝光时间获得的清晰准单色衍射数据重构结果, 如图7(b)所示. 如果直接采用模糊的衍射图而不使用其他先验信息作为支撑约束时, 完全不能重构出样品的任何信息, 如图7(c)所示. 但是若采用由图7(b)所得的样品尺寸信息作为初始先验信息, 进而作为支撑约束, 就能明显提升重构结果, 如图7(d)所示. 最后当采用PolyCDI算法对模糊的复色数据进行重构时, 且不用使用任何由图7(b)获得的先验信息就能得到和图7(b)一样高的重构质量, 如图7(e)所示.
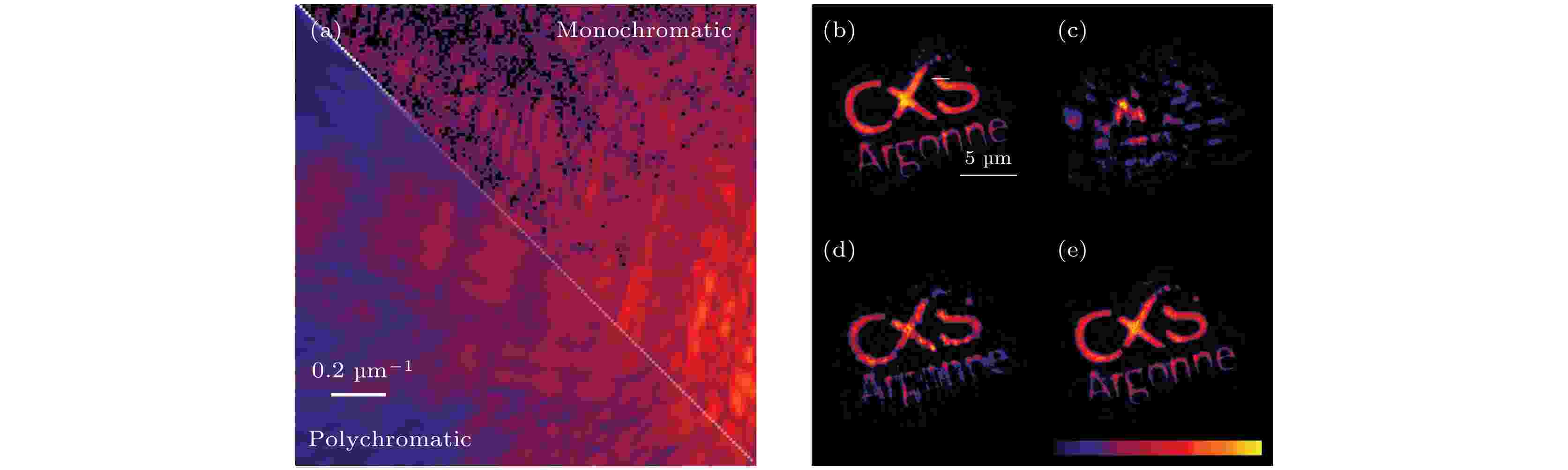图 7 (a) 准单色光(右上)和宽带光(左下)照明所对应的部分衍射强度数据^[64]; (b)—(e) 重构的待测样品幅值信息(空间相干长度已知): (b) 准单色数据重构结果, 数据采集曝光时间为500 × 3 s, 重构时假设照明光完全相干^[64]; (c) 复色数据重构结果, 数据采集曝光时间为500 × 50 ms, 重构时假设照明光完全相干^[64]; (d) 复色数据重构结果, 重构时假设照明光完全相干, 但是采用从图(b)获得的物体精确尺寸作为初始支撑^[64]; (e) 复色数据重构结果, 采用和图(b)和(c)相同的重构过程, 但是重构算法为复色光衍射算法(polychromatic diffraction algorithm, PolyCDI) ^[64]
Figure7. (a) Comparison of the quasi-monochromatic (upper right) and broadband (lower left) data ^[64]. (b)?(e) Reconstructed amplitude of the sample (all reconstructions presented here use known spatial coherence information): (b) Reconstruction from quasi-chromatic data, collected with 500 × 5 s exposures, assuming full temporal coherence ^[64]; (c) reconstruction from polychromatic data, collected with 500 × 50 ms exposures, assuming full temporal coherence ^[64]; (d) reconstruction from polychromatic data assuming full temporal coherence but using the exact dimensions of the object (obtained from panel (b)) as the initial support ^[64]; (e) reconstruction from polychromatic data using an identical procedure to panel (b) and (c) but using the polychromatic diffraction algorithm (PolyCDI) ^[64].

PolyCDI算法本质上是将一束平面波${\psi _\lambda }({{\boldsymbol{r}}_i}, {z_i})$的交叉谱密度分解为一系列互不相干的正交模^[50]. ${\psi _\lambda }({{\boldsymbol{r}}_i}, {z_i})$在自由空间传播距离$ {z_{ij}} = {z_j} - {z_i} $后得到${\psi _\lambda }({{\boldsymbol{r}}_j}, {z_j})$的远场近似可描述为^[64]

$ \begin{split} & {\psi _\lambda }({{\boldsymbol{r}}_j},{z_j}) \\ =\;& - \frac{{\text{i}}}{{\lambda z}}\exp \left( {\frac{{2{\text{πi}}{z_{ij}}}}{\lambda }} \right)\exp\left( {\frac{{{\text{πi}}r_j^2}}{{\lambda {z_{ij}}}}} \right) \\ &\times \iint {{\psi _\lambda }({{\boldsymbol{r}}_i},{z_i})}\exp\left( { - \frac{{2{\text{πi}}{{\boldsymbol{r}}_i} \cdot {{\boldsymbol{r}}_j}}}{{\lambda {z_{ij}}}}} \right){\rm{d}}{{\boldsymbol{r}}_i} \\ = \;& - \frac{{\text{i}}}{{\lambda z}}\exp \left( {\frac{{2{\text{πi}}{z_{ij}}}}{\lambda }} \right)\exp\left( {\frac{{{\text{πi}}{\boldsymbol{r}}_j^2}}{{\lambda {z_{ij}}}}} \right)\Im \left[ {{\psi _\lambda }({{\boldsymbol{r}}_i},{z_i})} \right] ,\end{split} $

其中λ为波长; r_i和r_j分别表示在物平面和检测器平面上且垂直于光传播方向的位置矢量; $ \Im $为傅里叶变换算子. 在检测器平面宽带波的衍射强度分布为整个波段对应的${\psi _\lambda }({{\boldsymbol{r}}_j}, {z_j})$模的平方乘以该波长对应的权重$ {\xi _\lambda } $之后的和^[64]:

$ I({{\boldsymbol{r}}_j},{z_j}) = \int {{\xi _\lambda }} {\left| {{\psi _\lambda }({{\boldsymbol{r}}_j},{z_j})} \right|^2}{\rm{d}}\lambda . $

将波谱的两个相邻采样点之间的波长差定义为$ \Delta \lambda $, 如果$ \Delta \lambda $足够小的话, 那么根据1个特定波长的强度分布的物理尺度就足以获得相邻波长对应的强度分布. 例如, 如果根据(21)式用最大的波长采样间隔$ {\lambda _{\max }} $来传输光场, 那么对应于$ {\lambda _{\max }} $和下一个最小波长的强度分布之间的变化可以通过对r_j进行尺度变换(${{{{\boldsymbol{r}}_j}\left( {{\lambda _{\max }} - \Delta \lambda } \right)} \mathord{\left/ {\vphantom {{{r_j}\left( {{\lambda _{\max }} - \Delta \lambda } \right)} {{\lambda _{\max }}}}} \right. } {{\lambda _{\max }}}}$)来获得^[64]. 在此之前Chen等^[100]采用高次谐波发生源对多波长衍射成像的实验进行研究, 发现单个衍射峰包含HHG源产生的各个谐波所对应的衍射峰, 也就是说衍射图样是所有谐波所对应的衍射强度的非相干叠加.
根据阿贝定理, 对于完全相干的CDI, 最高分辨率为$\varGamma = {\lambda \mathord{\left/ {\vphantom {\lambda {sin\theta }}} \right. } {\sin\theta }}$, 其中θ是物体出射波相对于衍射图样的最大探测半角^[103]. 在傍轴近似的情况下, 对于有限纵向相干的CDI, 分辨率受到最大可干涉路径长度的限制, 即

$ \varGamma = \frac{{\bar \lambda D}}{{2{l_{\text{c}}}}} \text{, } $

其中D是物体的最大特征尺寸, $ \bar \lambda $是入射波的中心波长, l_c是纵向相干长度^[64]. 根据入射波的半高全宽可以将纵向相干长度定义为$ {l_{\text{c}}} = {{{{\bar \lambda }^2}} \mathord{\left/ {\vphantom {{{{\bar \lambda }^2}} {\Delta \lambda }}} \right. } {\Delta \lambda }} $^[64]. 那么$\varGamma = {{0.5 D \cdot \Delta \lambda } \mathord{\left/ {\vphantom {{0.5 D \cdot \Delta \lambda } \lambda }} \right. } \lambda }$, 可见带宽(?λ/λ)越小, 可实现的空间分辨率越高. 在Abbey等^[64]的实验中, 在准单色光的假设下进行CDI重构时最大可允许的带宽是1.4 × 10^–2, 但是1个全波谐波的带宽约为3.7 × 10^–2, 因此需要采用补偿机制弥补分辨率的损失.
PolyCDI迭代算法的具体实施步骤如下^[64].
1) 根据已知的光谱分布信息, 对样品的出射波进行猜测: $ \psi ({{\boldsymbol{r}}_i}, {z_i}) $.
2) 根据(21)式将中心波长对应的$\psi ({{\boldsymbol{r}}_i}, {z_i})$传播到远场并获得其光场分布${\psi _{\rm{c}}}({{\boldsymbol{r}}_j}, {z_j})$, 然后通过位矢缩放因子将其缩放到最大波长对应的出射波$\psi {({{\boldsymbol{r}}_j}, {z_j})_{{\lambda _{\max }}}}$.
3) 对于其他采样波长, 也通过对r_j进行缩放, ${{{{\boldsymbol{r}}_j}\left( {{\lambda _{\max }} - \Delta \lambda } \right)} \mathord{\left/ {\vphantom {{{r_j}\left( {{\lambda _{\max }} - \Delta \lambda } \right)} {{\lambda _{\max }}}}} \right. } {{\lambda _{\max }}}}$, 然后将最大波长对应的衍射强度内插到由r_j缩放定义的新点集上, 就可以计算出每个采样波长所对应的衍射图样.
4) 将所有采样波长所对应的强度分布进行加权求和获得总强度$I({{\boldsymbol{r}}_j}, {z_j})$, 如(22)式所示.
5) 利用采集的衍射强度$I{({{\boldsymbol{r}}_j}, {z_j})_{{\rm{meas}}}}$对中心波长所对应的出射波${\psi _{\text{c}}}({{\boldsymbol{r}}_j}, {z_j})$进行约束, 其相位保持不变, 仅对振幅进行更新

${\left| {{\psi _{\text{c}}}({{\boldsymbol{r}}_j}, {z_j})} \right| \cdot \dfrac{\sqrt {I{{({{\boldsymbol{r}}_j}, {z_j})}_{{\rm{meas}}}}} }{\sqrt {I({{\boldsymbol{r}}_j}, {z_j})} }}.$

6) 将更新后的出射波逆衍射到样品平面, 并在样品平面对其进行支撑约束.
7) 重复1)—6)这个过程直到重构误差满足要求, 重构误差定义为

$ {\chi ^2} = {{{{\left( {\sqrt {I{{({{\boldsymbol{r}}_j},{z_j})}_{\rm meas}}} - \sqrt {I({{\boldsymbol{r}}_j},{z_j})} } \right)}^2}} \mathord{\bigg/ {\vphantom {{{{\left( {\sqrt {I{{({{\boldsymbol{r}}_j},{z_j})}_{meas}}} - \sqrt {I({{\boldsymbol{r}}_j},{z_j})} } \right)}^2}} {I({{\boldsymbol{r}}_j},{z_j})}}} } {I({{\boldsymbol{r}}_j},{z_j})}} . $

重构过程首先是采用100次的ER迭代, 然后再进行50次的HIO迭代, 重复4次上述迭代过程, 这时PolyCDI算法就基本收敛了, 接下来再采用ER算法在固定的支撑约束下进行至多1000次的迭代. 对于照明光中存在的部分空间相干性采用文献[104]所提出的相干模分解方法进行处理. 这就需要在重构之前同时测出照明光的空间相干长度和光谱分布. 相对于传统的CDI重构算法, 在迭代重构过程中进行时间相干模分解也使PolyCDI算法在一定程度上增加了重构计算量.
Huijts等^[105]跳出了时间相干模分解的框架, 其思想类似于Dilanian等^[101]提出的Two-step CDI方法, 都是首先从探测的远场衍射强度图样中提取出1个波长所对应的单色衍射图样. Huijts等^[105]采用的是一种数值的方法直接对连续宽带光所对应的衍射图样进行单色化, 可容忍的光谱带宽可以超过10%, 并且也适用于硬X-ray的能量范围. 由于检测器的积分时间远大于照明光的相干时间, 宽带光衍射图样则是所有角频率分量的非相干叠加. 如果能找出不同角频率分量所对应的衍射图样之间的关联, 就能将模糊的宽带光衍射图样进行数值单色化. 对于远场CDI, 不同波长对应的物波远场分布可以通过缩放进行相互转化. 当样品距离检测器的夫琅禾费衍射距离为z, 光波角频率为w时, 远场衍射强度分布的缩放因子为w/(cz). 根据这一特征可以构建1个尺度缩放矩阵C, 通过求解方程${{ {\boldsymbol{b}} = {\boldsymbol{Cm}}}}$来得到单色化的衍射图样m, 其中b是测量的宽带光衍射图样, 如图8所示. 仅利用照明光波的光谱信息, 就能从宽带光衍射图样中提取出宽带光的中心波长所对应的衍射图样. 这种衍射图样单色化的方法独立于迭代相位重构之外, 后续不用对相位重构算法做任何改变, 可以灵活地应用于多种单次曝光的CDI或者ptychography.
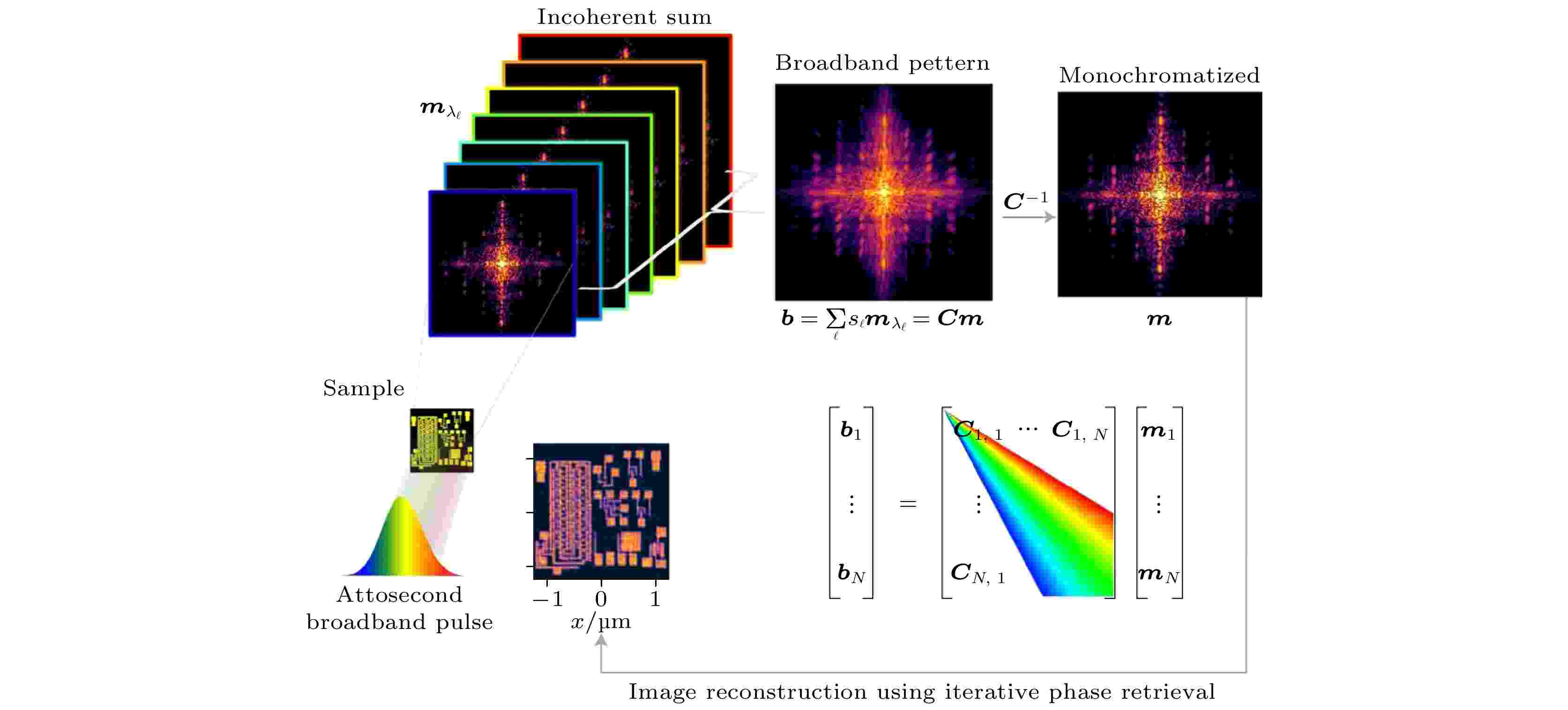图 8 衍射图样数值单色化的原理图^[105]. 传统的CDI假设照明光源是单色的. 对于阿秒宽带光源, 衍射图样是所有波长所对应的单色衍射图样的加权叠加. 这些单色的衍射图样可以认为只有几何缩放的差别. 这种缩放是数值可逆的, 由矩阵C来表示该缩放矩阵. 确定了C之后, 就可以通过求解矩阵向量问题b = Cm从宽带光衍射图样b中提取出单色化的衍射图样m (图中右下部分所示为对应于一维衍射图样的简化情形). 然后就能直接将m代入到传统的相位恢复算法中重构出样品的复振幅信息. ?是复色光所包含的离散化光波的波长个数
Figure8. Principle of the numerical monochromatization^[105]. Conventional CDI assumes a monochromatic source. In the case of an attosecond broadband source, the diffraction pattern is the incoherent, spectrally weighted sum of the monochromatic diffraction patterns corresponding to all wavelengths presents in the sources. These monochromatic patterns are identical except for a geometric scaling. In the presented method this scaling is numerically inverted, and the scaling matrix is denoted by matrix C. The monochromatization method consists in the inversion of the matrix-vector problem b = Cm in order to retrieve the monochromatic diffraction pattern m from the broadband measurement b (The lower right part of the figure shows the simplified case for 1D diffraction pattern). Then m can be directly put into the conventional phase retrieval algorithm. ? is the index that corresponds to the spectral discretization.

近几年对低时间相干性CDI的研究多集中在ptychography上. 2014年Enders等^[106]提出减小照明探针来提高对于低时间相干性的鲁棒性, 照明探针的尺寸D应满足要求$ D < 2\zeta _l/\sin \alpha $, 其中$ {\zeta _l} $为照明光的纵向相干长度, α是携带衍射信息的衍射光波最大立体角, 但是这样会显著地增加扫描次数以获得较大的视场范围. 他们采用混合模态分解的方法在宽带X-ray实验中得到了可靠的重构结果, 但是照明探针的尺寸满足上述要求. 如果将照明光带宽进一步增大或者将照明探针的尺寸增大, 使其不再满足上述要求, 那么这种基于单色光模型的混合模态分解方法将不再适用. 2015年Odstrcil等^[107]首次将PolyCDI的方法用到ptychography中, 在EUV波段实验验证了该方法的可行性. 在2016年, Pradier等^[108]又将PolyCDI方法扩展到了X-ray ptychography, 用来探测薄膜的厚度分布. 同年, Baksh等^[109]提出了一种能同时适用于EUV和X射线波段的大光谱带宽ptychography技术, 该技术仍是采用高次谐波光源, 其重构算法是将ePIE和PolyCDI结合. Yao等^[110]将Mixed-state decomposition^[83]和Multi-wavelength^[108]方法相结合, 可以同时处理低空间和时间相干的问题^[106], 并且不必精确地测出具体的照明光谱, 光谱信息粗略已知即可. 在使用Multi-wavelength方法时, 他们考虑到宽带光能量扩散的问题, 不同波长所对应的探针在样品平面应该具有不同的尺寸和分布, 于是在重构之前采用可变焦的菲涅尔波带片进行独立衍射传播, 生成若干个不同波长所对应的探针来完成探针模态的初始化, 这样更贴合实际的物理模型^[110].
2 -->

4.2.光谱带宽未知的部分时间相干CDI

上述解决部分时间相干性的方法都需要提前测量出光谱的分布, 而在2013年Parsons等^[111]提出了一种可以不用测出光谱分布的宽带光CDI技术. 该技术采用一种类似低通滤波shrinkwrap的方法^[112], 仅保留颜色图样中有用的信息. 虽然该技术可以将允许的带宽提高20%, 但是却由于没有将光谱成分分开而不能用于解决相位问题, 只能重构出样品的振幅信息.
在2014年, Witte等^[113]提出了一种可以进行高分辨相位成像的双脉冲超宽带光谱CDI技术, 不需要提前测量光谱分布而且不受光谱带宽限制. 该技术采用两个具有一定时间延迟的空间相干脉冲作为照明光, 所记录的一系列的衍射图样为以时间延时为变量的函数, 再结合傅里叶光谱法就能从记录的衍射图样中获得光谱信息. 但是这种成像技术不适用于非脉冲式光源的成像系统, 例如电子显微成像系统和其他采用不可调谐的普通激光光源的系统.

本文综述了CDI技术中存在的部分相干性问题, 包括部分相干理论和部分相干重构方法. 虽然在实验装置上加入狭缝或者使用单色仪可以非常直接地提高照明光的空间或时间相干性, 但是这会大幅度的减弱照明光通量. 近年来对于CDI中时间相干性和空间相干性问题的研究主要依据Wolf所提出的相干模分解理论, 即部分相干光可以表示为一系列互不相干的单模态相叠加的结果. 这些单模态可以独立传播互不干扰. 部分空间相干和部分时间相干的CDI重构技术都经历了从需要提前测量出照明光的相干特性(空间相干长度, 相干模型或者是光谱带宽)到不用已知相干性特征的发展过程. Nugent等建立的部分相干CDI理论框架对解决部分空间和时间相干性问题均起到了奠基性的作用, 在部分相干照明情况下的记录的衍射图样都可以看做是一系列正交且互不相干模态所对应的衍射强度的叠加.
对于部分空间相干CDI, 大部分的研究是基于模态分解的方法, 相比于传统的CDI, ptychography利用自身具有大量冗余衍射强度信息的优势不仅可以对照明光进行模态分解, 还可以对物体进行模态分解, 能够在照明光相干长度和相干光数学物理模型完全未知的情况下同时缓解由照明光源, 探测器的点扩散函数和物体的不稳定性引起的退相干现象带来的影响. 对于部分时间相干CDI, 表1列出了最具代表性的方法. Multiwavelength CDI和Two-step CDI只能应用于离散光谱照明情况, 之后提出的PolyCDI和衍射图样数值单色化的方法则可以应用于大带宽连续光谱. PolyCDI是在算法迭代过程中在探测平面进行不同波长衍射强度的叠加, 来求解中心波长所对应的样品信息, 理论上可容忍的光谱带宽能达到11%; 而衍射图样数值单色化的方法则是在迭代重构之前将中心波长所对应的衍射图样计算出来, 避免了在迭代相位重构时增加计算量, 可见光和X-ray实验均验证了该方法的可容忍光谱带宽可以超过10%. 但上述这些部分时间相干CDI技术需要提前测量出照明光的光谱分布, 少数不用提前已知光谱信息的重构技术还不完善. 因此, 未来的一个重要的方向是光源空间和时间相干性特性完全未知情况下的复振幅图像重构技术, 这将大幅度地降低对实验装置的苛刻要求以及复杂度, 同时进一步提高实际系统的成像质量和分辨率.

方法	是否需要光谱信息	可适用的波的类型	最大带宽	实验结果
				中心波长/nm	空间分辨率
Multiwavelength CDI[100]	Yes	Discrete	Several harmonics	(35 ± 1)	(165 ± 5) nm
Two-step CDI[101]	Yes	Discrete	Several harmonics	810	1 μm
PolyCDI[64]	Yes	Continuous	11%	0.888	(150 ± 5) nm
Numerical monochromatization[105]	Yes	Continuous	>10%	710	2.5 μm
Two-pulse imaging[113]	No	Continuous	No limitation	47	6.7 μm

表1不同部分时间相干CDI方法的比较
Table1.Comparison of different methods of partially temporal-coherent CDI.