摘要: 为了让摩尔定律能够延续下去, 降低功耗是很多研究者关注的问题, 铁电负电容效应的发现为其提供了一种解决方案. 应变工程作为调控铁电薄膜物理性能的有效手段已经被广泛研究. 但是应变对铁电负电容调控的相关机理并不清楚. 本文通过Landau-Khalatnikov方程模拟了应变场和温度场对PbZr
0.2 Ti
0.8 O
3 铁电薄膜负电容的影响. 研究表明, 瞬态负电容的产生伴随着极化的翻转, 在一定温度下压应变有助于铁电负电容的稳定, 而在张应变下铁电极化翻转较快, 负电容效应持续时间较短. 但是, 增加的压应变会导致对应的矫顽电压增大, 需要更大的外电压才能使极化翻转, 从而产生负电容. 此外, 在恒定的应变下, 温度越低, 负电容效应越显著. 本工作对未来负电容微纳器件的设计具有一定的指导意义.
关键词: 铁电材料 /
负电容效应 /
失配应变 /
畴演化 English Abstract Strain tuning of negative capacitance in epitaxial PbZr0.2 Ti0.8 O3 thin films Lin Cui 1 ,Bai Gang 1,2,3 ,Li Wei 1 ,Gao Cun-Fa 3 1.College of Microelectronics, College of Electronic and Optical Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210023, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 51602159)Received Date: 27 April 2021Accepted Date: 19 May 2021Available Online: 07 June 2021Published Online: 20 September 2021Abstract: In order to continue Moore’s Law, the reducing of power consumption is concerned by many researchers, and the discovery of ferronegative negative capacitance effect (NCE) provides a solution. Strain engineering has been widely studied as an effective means to regulate the physical properties of ferroelectric thin films. But the relevant mechanism of strain to ferroelectric negative capacitance regulation is not clear. Recently, the experimental results have shown that it is possible to stabilize the transient NCE in resistance-ferroelectric networks. In this work, we use the Landau-Khalatnikov theory to study the microscopic domain evolution and the influence of strain and temperature on NCE in a ferroelectric film. It is shown that compressive strain enhances NCE while NCE becomes weaker under a tensile strain. However, a larger compressive strain will give rise to a higher coercive voltage that hinders the NCE from forming. In addition, under a certain strain, the NCE becomes stronger at lower temperature. This work provides the theoretical basis for designing the negative capacitance devices and scaling towards nanoscale dimensions in future.Keywords: ferroelectric materials /negative capacitance effect /misfit strain /domain evolution 全文HTML --> --> --> 1.引 言 随着半导体技术的飞速发展, 晶体管尺寸变得越来越小, 集成密度越来越高, 这将使芯片的功耗增加, 因此降低器件的功耗, 让“摩尔定律”延续下去成为人们密切关注的焦点问题. 1965年, 戈登·摩尔(Gordon E. Moore)[1 ] 指出集成电路中可容纳器件的密度将以固定的时间间隔增加一倍, 而在一颗很小的芯片上就有可能存在上亿个器件, 单凭人类的肉眼是看不见的. 自引入摩尔定律以来, 集成电路技术飞速发展, 摩尔定律不断得到补充、修改和发展, 也推动了半导体的研究和芯片的制造与发展[2 ] . 快速增长的晶体管密度, 不仅推动了芯片成本的降低, 还促使了芯片运算速度的提升以及功耗的下降[3 ] . 对于传统场效应晶体管 (metal-oxide-semiconductor field-effect transistors, MOSFETs), 由于载流子玻尔兹曼分布的限制[4 ] , 室温下的亚阈值摆幅无法降低到 60 mV/dec以下. 因此, 突破玻尔兹曼极限, 探寻降低晶体管的亚阈值摆幅的方法, 对于促进晶体管特征尺寸的进一步减小具有重要的意义, 也是下一阶段集成电路产业发展必须攻克的难点之一.[3 ] . 2008年, 加州大学伯克利分校的Salahuddin和Datta[5 ] 提出铁电负电容场效应晶体管概念. 这种新型的晶体管是将传统MOSFETs的栅极氧化介质层替换成铁电材料介质层, 从而放大栅压对沟道的作用效果, 降低栅电容与沟道电容的比值, 原理上可以把晶体管的亚阈值斜率降低到60 mV/dec以下, 实现具有低功耗的器件, 从而克服“Boltzmann暴政”[6 ] . 对于这种现象, 他们称之为铁电的负电容效应, 相应的场效应晶体管称之为铁电负电容场效应晶体管, 该设想的实现进一步提高了人们对铁电负电容效应的兴趣. 2015年, Khan等[7 ] 通过构造电阻-铁电电容(resistance-ferroelectric capacitor, R-FEC)串联电路并监测铁电薄膜的电压动态来演示单晶铁电薄膜中的负微分电容. 两年后, 他们又在纯无源元件的组合, 即铁电电容器与普通介电电容器串联电路中, 直接测量了差分电压放大[8 ] . 2016年, Hoffmann等[9 ] 首次对简单的R-FEC串联电路施加电压脉冲, 并在多晶铁电HfO2 电容器中直接观察到瞬态负电容, 该电路类似于Khan等[7 ] 构造的结构模型. 铁电畴形成和动力学对负电容效应的影响对实际器件的应用至关重要, Hoffmann等[10 ] 又在2018年报道了关于铁电电容器在开关过程中的畴动力学, 演示了铁电极化翻转的动态过程. 西安电子科技大学的郝跃院士团队[11 ] 将铁电负电容集成在锗和锗锡晶体管上, 研究发现利用铁电负电容层降低了器件的亚阈值摆幅, 并且降低了器件的栅漏电流.1–x Tix 3 (PZT)铁电材料是由PbZrO3 和PbTiO3 组成的具有钙钛矿结构的连续性固体, 具有优异的介电、压电和铁电性能, 在铁电存储器[12 ] 、能量收集器[13 ] 、传感器[14 ] 、光电器件[15 ] 等领域中应用颇广. 当铁电材料沉积在衬底上时会产生失配应变, 这种失配由铁电薄膜材料与衬底间晶格常数的差异、薄膜和衬底间热膨胀系数的差异以及与相变相关的自应变这三部分组成[16 ] . 此外, 界面/表面以及类似于氧空位和位错等缺陷也可能有贡献. 因此, 铁电体材料和相应的薄膜材料在性能上有很大的差异. 事实上, 不是所有的应变都可以提升铁电性能, 但通过选择合适的衬底、温度以及生长参数, 科学利用应变是可以在一定程度上提升铁电薄膜的指定性能的, 将这种利用应变来调控材料性能的行为称为“应变工程”. 目前, 大量的研究表明, 应变可以有效调控铁电薄膜的结构[17 ] 、热释电系数[18 ] 、铁电-顺电相变及介电响应[19 -23 ] 、铁电-半导体耦合性能[24 ] 等.0.2 Ti0.8 O3 铁电薄膜诱导的等方双轴错配应变对瞬态负电容效应的调控. 本文的第2 部分介绍具体的研究方法, 第3 部分介绍具体的仿真结果和分析, 最后一部分对工作进行总结, 并对未来的研究进行展望.2.热力学理论 电容是电子器件最基本的组成部分之一, 是一个重要的物理量, 理想线性电容器的电容常用C 表示, 并且用$ Q = CV $ 将电容上的电压和电荷联系起来. 电容进一步将存储在电容器中的电能U 与其电荷联系起来, 通常用$ U = {Q^2}/(2 C) $ 表示, 电容还可被定义为$ C=({\text{d}}^{2}U/\text{d}{Q}^{2}{)}^{-1} $ . 另一方面, 像铁电体这样的非线性电容器由于铁电电荷$ {Q_{\text{F}}} $ 与$ {V_{\text{F}}} $ 之间的非线性关系而不具有恒定的电容$ {C_{\text{F}}} $ , 表示为${C_{\text{F}}}({Q_{\text{F}}}) = \dfrac{{{\text{d}}{Q_{\text{F}}}}}{{{\text{d}}{V_{\text{F}}}}}$ , 也可表示为${C}_{\text{F}}({Q}_{\text{F}})= ({\text{d}}^{2}U/\text{d}{Q}_{\text{F}}^{2}{)}^{-1}$ . 虽然电容具有许多非平凡的性质, 但最引人注目的是负电容效应. 当${C}_{\text{F}}({Q}_{\text{F}})= $ $ ({\text{d}}^{2}U/\text{d}{Q}_{\text{F}}^{2}{)}^{-1} < 0$ 时, 电容$ {C_{\text{F}}}({Q_{\text{F}}}) $ 又称为负微分电容, 简称为负电容. 到目前为止, 在对于铁电负电容效应的研究中, 通过间接或直接方式观察到的铁电负电容以两种形式存在. 一种称为静态负电容, 另一种称为瞬态负电容, 而本文主要研究的是瞬态负电容, 对静态负电容不做过多介绍. 为了直接显示瞬态负电容, 在开关过程中必须测量铁电材料上的电压降. 为了测量这种电压降, 大量的研究都集中于铁电电容与电阻串联构成的R-FEC电路上[7 ,9 ,10 ,25 ,26 ] , 模型和等效电路如图1 所示, 结果表明瞬态负电容效应源自于铁电材料的经典开关机制[10 ] .图 1 铁电负电容瞬态响应模型及其等效电路图Figure1. Transient response model of ferroelectric negative capacitance and its equivalent circuit diagram.0.2 Ti0.8 O3 生长在表面平行于(001)取向的立方衬底上, 相互密合的薄膜与衬底之间诱导等方双轴错配应变. 考虑(001)方向的极化($ {P_1} = {P_2} = 0 $ , $ {P_3} \ne 0 $ )以及极化梯度项$ k{(\nabla P)^2} $ , 根据朗道-金兹堡-德文希尔唯象热力学理论, 等方双轴错配应变下铁电薄膜的热力学势如下:$ {P}_{i}\,(i=1, 2, 3) $ 是沿着不同方向的极化分量, $ {s_{lm}} $ 是弹性顺度系数, $Q_{lm}$ 是电致伸缩常数, S m 表示应变. $ {a_1} $ 以及$ {a_{ij}} $ 和$ {a_{ijk}} $ 是介电刚度以及高阶介电刚度系数, $ {E_3} $ 是铁电薄膜中电场E 的分量. 高阶介电刚度系数$ {a_{ij}} $ 和$ {a_{ijk}} $ 可以作为温度无关的参数, 而铁电薄膜中的温度依赖性主要取决于介电刚度${a_1} = (T - $ $ {T_0})/(2{\varepsilon _0}C)$ ($ {T_0} $ 是居里外斯温度, $ {\varepsilon _0} $ 是真空介电常数, C 是常数). $ k{(\nabla P)^2} $ 为畴壁能项. 因为在畴壁处, 极化是非均匀变化. k 为梯度能系数, 反映了畴壁能的大小.[27 ,28 ] , 该方法也直接反映了极化$ {P_3} $ 的动态演化. LK方程为$ \rho $ 是动力学系数, 描述了极化对驱动力的响应速度. 极化$ {P_3} $ 的空间导数是通过有限差分法在x-y 平面上的均匀正方形网格上计算得到的. 网格上的每个点具有局部能量密度$ {u_{\left( {i, j} \right)}} $ 、极化$ {P_{3(i, j)}} $ 和动力学系数$ {\rho _{(i, j)}} $ , 而平均极化$ {\bar P_3} $ 等于各点极化相加除以总的格点数, 用公式表示为$ {N_x} $ 和$ {N_y} $ 分别表示x 方向和y 方向格点的个数. 由于$ {Q_{\text{f}}} = A({\varepsilon _0}E + {P_3}) $ , 所以铁电电容上的总电荷$ {Q_{\text{f}}} $ 表示为A 为铁电电容的总面积, $ {\varepsilon _0} $ 为真空介电常数, N 为总格点数. 由于极化${\bar P_3} \gg {\varepsilon _0}E$ , 所以(6 )式近似成立. 此外, 由于$ \Delta x = \Delta y $ , 所以每个格子单元面积为$ A/N = {(\Delta x)^2} $ , 换言之$ \Delta x = \sqrt {A/N} $ .$ {V_{\text{S}}} $ 定义如下:R 是外部串联电阻, $ {i_{\text{R}}} $ 是流过外部电阻的电流, $ {V_{\text{f}}} $ 是铁电电容上的电压. 换言之, $ {V_{\text{f}}} = {V_{\text{S}}} - {i_{\text{R}}}R $ , 铁电电容的电场$ {E_{\text{f}}} $ 可以表示为$ {t_{{\text{FE}}}} $ 为铁电材料的厚度. 在不考虑寄生电容$ {C_{\text{P}}} $ 的情况下, 电流$ {i_{\text{R}}} $ 可以表示为$ {Q_{\text{f}}} $ 是铁电电容上的总电荷.3.结果与讨论 为了研究铁电薄膜在应变调控下的极化动态翻转过程, 选取厚度为$ {t_{{\text{FE}}}} $ 的铁电材料PbZr0.2 Ti0.8 O3 , 并在其构成的R-FEC电路中施加电压脉冲$ {V_{\text{S}}} $ : $ - 14\;{\text{V}} \to 14\;{\text{V}} \to - 14\;{\text{V}} $ [7 ] , 其材料参数见表1 [29 ,30 ] . 其中, 梯度能系数k 参考Qiu等[31 ] 使用的系数. 参考的梯度能系数${k_{{\text{ref}}}} = \dfrac{1}{2}{g_{11}} = 1.675 \times {10^{ - 9}}\;{{\text{m}}^3}/{\text{F}}$ 对应的畴壁宽度为2 nm, 而本文中$\Delta x = \Delta y = $ $ 150\;{\text{nm}}$ , 远远大于文献[31 ]中的畴壁宽度, 所以本文中梯度能系数应当是参考系数$ {k_{{\text{ref}}}} $ 的75倍, 其值为$ k \approx 1.26 \times {10^{ - 7}}\;{{\text{m}}^3}/{\text{F}} $ , Hoffmann等[10 ] 也利用同样的方法来确定对应的梯度能系数. 动力学系数$\rho = \rho ' \times \dfrac{A}{{{t_{{\text{FE}}}}}}$ , 而$ \rho ' $ 可以看成是铁电电容的内阻[7 ] , 在本文中$\rho ' = 70\;{\rm{k}} \Omega$ .Coefficients PbZr0.2 Ti0.8 O3 Units Reference a 1 3.44(T – 729.5) 105 C–2 ·m2 ·N [29 ] a 11 –3.050 107 C–4 ·m6 ·N [29 ] a 111 2.475 108 C–6 ·m10 ·N [29 ] s 11 8.2 10–12 m2 /N [29 ] s 12 –2.6 10–12 m2 /N [29 ] Q 12 –0.0245 m4 /C2 [30 ] $ {t_{{\text{FE}}}} $ 60 nm [7 ] A 302 ${\text{μ}}{ {\text{m} }^2}$ [7 ] R 50 ${\rm{k } }\Omega$ [7 ] k $ 1.26 \times {10^{ - 7}} $ $ {{\text{m}}^3}/{\text{F}} $ ${\rho{'} }$ 70 ${\rm{k } }\Omega$ $ \Delta x $ $ 150 $ $ {\text{nm}} $ $ \Delta y $ $ 150 $ $ {\text{nm}} $ $ {N_x} $ 200 $ {N_y} $ 200 $ \Delta t $ $ 5 $ $ {\text{ns}} $
表1 PbZr0.2 Ti0.8 O3 材料的相关系数(温度T 的单位为K)Table1. Correlation coefficient of PbZr0.2 Ti0.8 O3 material (The unit of temperature T is K).$ {S_{\text{m}}} = - 0.011 $ 和室温$ T = 300\;{\text{K}} $ 下观察了铁电极化翻转过程, 不同时间段的铁电极化状态如图2 所示. 图2(a) 给出了在外加脉冲$ {V_{\text{S}}} = 14\;{\text{V}} $ 时, $ {V_{\text{f}}} $ 与时间t 的局部关系图, 图2(b) —(f) 描述了不同时间点极化翻转过程中整个铁电电容区域的空间极化分布. 在翻转过程开始阶段, $ t = 0.545\;\text{μ}{\rm{ s}} $ 时, 图2(b) 给出了电容区域随机分布成核的极化分布, 此时不存在极化翻转, 铁电电容总电荷$ {Q_{\text{f}}} $ 为负. 随着时间的推移, 当$t = 4.85\;\text{μ}{\rm{ s}}$ 时, 如图2(c) 所示, 此时逐渐形成反向畴, 极少部分极化翻转, 因此$ {Q_{\text{f}}} $ 仍为负, 而$ {V_{\text{f}}} $ 达到1个极大值点. 当$t = 11.0\;\text{μ}{\rm{ s}}$ 时, 如图2(d) 所示, 新的反向畴在继续增多, 而原有的反向畴几乎可以不受阻碍地横向生长, 将近一半的畴已经完成翻转, 此时铁电电容电荷$ {Q_{\text{f}}} $ 逐渐趋于零. 在图2(e) 中, 即$t = 14.3\;\text{μ}{\rm{ s}}$ 时, $ {V_{\text{f}}} $ 停止减小并开始随时间的推移而增大, 此时大部分畴已经翻转, $ {Q_{\text{f}}} $ 为正. 当$t = 16.5\;\text{μ}{\rm{ s}}$ 时, 如图2(f) 所示, 此时只剩下极少数的畴还未翻转, 电容器上正电荷逐渐积累且趋于最大. 因此, 负电容效应主要发生在图2(c) —(e) 过程中. 换言之, 外加电压为正的情况下, 当铁电电容器中出现反畴成核, 并且畴生长时, 铁电电容总电荷$ {Q_{\text{f}}} $ 由负变为正的区间中, 铁电材料处于负电容状态.图 2 (a)在T = 300 K, S m = –0.011, 外加脉冲$ {V_{\text{S}}} = 14\;{\text{V}} $ 下$ {V_{\text{f}}} $ 与时间t 的局部关系图; (b)—(f)不同时间段的铁电极化分布($ t = 0.545 $ , $ 4.85 $ , $ 11.0 $ , $ 14.3 $ , $16.5\;{\text{μ} }{\rm{ s}}$ )Figure2. (a) Local relationship diagram with time under applied pulse; (b)–(f) ferroelectric polarization distribution in different time periods ($ t = 0.545 $ , $ 4.85 $ , $ 11.0 $ , $ 14.3 $ , $16.5\;{\text{μ} }{\rm{ s}}$ ).$ {S_{\text{m}}} = 0.011 $ 以及$ {V_{\text{S}}} = 14\;{\text{V}} $ 和$ {V_{\text{S}}} = $ $ 10\;{\text{V}} $ 的电压脉冲下, 不同温度时铁电材料PbZr0.2 Ti0.8 O3 与时间相关的电学性能如图3 所示. 图3(a) 和图3(b) 表示铁电电容上的电压$ {V_{\text{f}}} $ 与时间t 的关系, 图3(c) 和图3(d) 表示流经铁电电容上的电流$ {i_{\text{R}}} $ 与时间t 的关系, 图3(e) 和图3(f) 表示铁电电容上的电荷$ {Q_{\text{f}}} $ 与时间t 的关系. 以铁电材料PbZr0.2 Ti0.8 O3 在恒定应变${S_{\text{m}}} = 0.011$ 、恒定温度$T = 100\,{\text{K}}$ 以及电压脉冲$ {V_{\text{S}}} = 14\;{\text{V}} $ 的情况为例, 对铁电瞬态负电容现象做1个简单的解释, 如图3(a) 、图3(c) 和图3(e) 中红色曲线所示. $ {V_{\text{S}}} $ 从–14 V跳变至14 V后, $ {V_{\text{f}}} $ 一直增加, 直至竖直虚线A. 随后, $ {V_{\text{f}}} $ 下降至竖直虚线B. 在AB段时间内, 铁电层上存储的电荷$ {Q_{\text{f}}} $ 的变化趋势与$ {V_{\text{f}}} $ 刚好相反, 意味着$ {{{\text{d}}{V_{\text{f}}}} \mathord{\left/ {\vphantom {{{\text{d}}{V_{\text{f}}}} {{\text{d}}{Q_{\text{f}}}}}} \right. } {{\text{d}}{Q_{\text{f}}}}} < 0 $ , 也暗示着铁电极化穿过了不稳定区域. 与此同时, $ {i_{\text{R}}} $ 从竖直虚线A上升至竖直虚线B, 这一趋势与$ {V_{\text{f}}} $ 相反, 与$ {Q_{\text{f}}} $ 一致. 同样, 当$ {V_{\text{S}}} $ 从14 V跳变到–14 V时, $ {V_{\text{f}}} $ 在到达竖直虚线C之前一直下降, 而从竖直虚线C开始上升, 直至竖直虚线D. 在CD段内, $ {Q_{\text{f}}} $ 和$ {i_{\text{R}}} $ 的变化趋势均与$ {V_{\text{f}}} $ 相反, 表现出与AB段同样的负电容特性. 除此以外, 每隔100 K将温度升高, 并对其做了同样的仿真. 随着温度升高, 负电容的范围缩小, 当温度达到400 K时, $ {V_{\text{f}}} $ 和$ {i_{\text{R}}} $ 在一段时间内几乎保持不变, 也就意味着$ {{{\text{d}}{V_{\text{f}}}} \mathord{\left/ {\vphantom {{{\text{d}}{V_{\text{f}}}} {{\text{d}}{Q_{\text{f}}}}}} \right. } {{\text{d}}{Q_{\text{f}}}}} \approx 0 $ , 负电容开始消失. 当温度继续升高达到500 K时, 负电容完全消失. 此时, $ {V_{\text{f}}} $ 随着$ {Q_{\text{f}}} $ 的增加(减小)而持续增加(减小), 也就意味着$ {{{\text{d}}{V_{\text{f}}}} \mathord{\left/ {\vphantom {{{\text{d}}{V_{\text{f}}}} {{\text{d}}{Q_{\text{f}}}}}} \right. } {{\text{d}}{Q_{\text{f}}}}} > 0 $ , 表现出常见的正电容. 但是, 较$ {V_{\text{S}}} $ 刚跳变时增加(减小)的幅度相比, 幅度放缓. 如图3(e) 所示, 随着温度的升高, 铁电电容上的总电荷$ {Q_{\text{f}}} $ 在稳定之后, 无论是正电荷还是负电荷都相应减小. 因此, 低温更有利于瞬态负电容的产生. 铁电材料PbZr0.2 Ti0.8 O3 在恒定应变$ {S_{\text{m}}} = 0.011 $ 以及电压脉冲$ {V_{\text{S}}} = 10\;{\text{V}} $ 的情况下, 温度对负电容效应的调控如图3(b) 、图3(d) 和图3(f) 所示. 在恒定应变以及电压脉冲$ {V_{\text{S}}} = 10\;{\text{V}} $ 下, 温度对负电容效应的调控表现出与$ {V_{\text{S}}} = 14\;{\text{V}} $ 相似的特性. 不同的是, 电压越大对R-FEC电路的驱动力也越大, 极化翻转更快, 所以相比于$ {V_{\text{S}}} = 14\;{\text{V}} $ , 在$ {V_{\text{S}}} = 10\;{\text{V}} $ 的情况下负电容效应持续的时长增长.图 3 恒定应变$ {S_{\text{m}}} = 0.011 $ 以及不同温度下, (a), (c), (e)外加电压$ {V_{\text{S}}} = 14\;{\text{V}} $ 时铁电材料PbZr0.2 Ti0.8 O3 的${V_{\text{f}}} \text{-} t$ 关系图、${i_{\rm R}} \text{-} t$ 关系图、${Q_{\text{f}}} \text{-} t$ 关系图; (b), (d), (f)外加电压$ {V_{\text{S}}} = 10\;{\text{V}} $ 时铁电材料PbZr0.2 Ti0.8 O3 的${V_{\text{f}}} \text{-} t$ 关系图、${i_{\rm R}} \text{-} t$ 关系图、${Q_{\text{f}}} \text{-} t$ 关系图Figure3. Under constant strain $ {S_{\text{m}}} = 0.011 $ and different temperatures, (a), (c), (e) the ${V_{\text{f}}}\text{-} t$ relationship diagram, ${i_{\rm R}} \text{-} t$ relationship diagram and ${Q_{\text{f}}} \text{-} t$ relationship diagram of ferroelectric materials PbZr0.2 Ti0.8 O3 when the applied voltage $ {V_{\text{S}}} = 14\;{\text{V}} $ , respectively; (b), (d), (f) the ${V_{\text{f}}} \text{-} t$ relationship diagram, ${i_{\rm R}} \text{-} t$ relationship diagram and ${Q_{\text{f}}} \text{-} t$ relationship diagram of ferroelectric materials PbZr0.2 Ti0.8 O3 when the applied voltage $ {V_{\text{S}}} = 10\;{\text{V}} $ , respectively.${S_{\text{m}}} = ({{d - {d_0}}})/{{{d_0}}}$ , 其中d 是衬底有效晶格常数, $ {d_0} $ 是薄膜的晶格常数. 也就是说, 当$ {S_{\text{m}}} < 0 $ 时, 薄膜受到压应变; 当$ {S_{\text{m}}} > 0 $ 时, 薄膜受到拉应变. 外加脉冲$ {V_{\text{S}}} = 14\;{\text{V}} $ , 恒温$ T = 300\;{\text{K}} $ 时, 在不同的错配应变下, 对铁电材料PbZr0.2 Ti0.8 O3 的与时间相关的电学性能进行了仿真, 如图4(a) 、图4(c) 和图4(e) 所示. 铁电薄膜材料在压应变的调控下表现出更显著的负电容效应, 这跟Liu和Wang[32 ] 的研究结论是一致的. 而且, 压应变的强度越大, 负电容效应越显著. 相比于压应变, 拉应变下铁电极化翻转速度更快, 而且拉应变强度越大, 极化翻转速度越快, 从而负电容效应持续的时长越短. 当负电容效应最显著时, 也就是在最大压应变${S_{\text{m}}} = $ $ - 0.011$ 时, 铁电电容表面的总电荷也达到最大.图 4 恒定温度$ T = 300\;{\text{K}} $ 以及不同应变下, (a), (c), (e)外加电压$ {V_{\text{S}}} = 14\;{\text{V}} $ 时铁电材料PbZr0.2 Ti0.8 O3 的${V_{\text{f}}} \text{-} t$ 关系图、${i_{\rm R}} \text{-} t$ 关系图、${Q_{\text{f}}} \text{-} t$ 关系图; (b), (d), (f)外加电压$ {V_{\text{S}}} = 10\;{\text{V}} $ 时铁电材料PbZr0.2 Ti0.8 O3 的${V_{\text{f}}} \text{-} t$ 关系图、${i_{\rm R}} \text{-} t$ 关系图、${Q_{\text{f}}} \text{-} t$ 关系图Figure4. Under constant temperature $ T = 300\;{\text{K}} $ and different strains, (a), (c), (e) the ${V_{\text{f}}} \text{-} t$ relationship diagram, ${i_{\rm R}} \text{-} t$ relationship diagram and ${Q_{\text{f}}} \text{-} t$ relationship diagram of ferroelectric materials PbZr0.2 Ti0.8 O3 when the applied voltage $ {V_S} = 14\;{\text{V}} $ , respectively; (b), (d), (f) the ${V_{\text{f}}} \text{-} t$ relationship diagram, ${i_{\rm R}} \text{-} t$ relationship diagram and ${Q_{\text{f}}} \text{-} t$ relationship diagram of ferroelectric materials PbZr0.2 Ti0.8 O3 when the applied voltage $ {V_{\text{S}}} = 10\;{\text{V}} $ , respectively.0.2 Ti0.8 O3 在恒定温度$T = 300\,{\text{K}}$ 以及电压脉冲$ {V_{\text{S}}} = 10\;{\text{V}} $ 的情况下, 应变对负电容效应的调控如图4(b) 、图4(d) 和图4(f) 所示. 除$ {S_{\text{m}}} = - 0.011 $ 的情况, 在恒温且$ {V_{\text{S}}} = 10\;{\text{V}} $ 的条件下, 应变对负电容的调控表现出与$ {V_{\text{S}}} = 14\;{\text{V}} $ 相似的特性. 在$ {V_{\text{S}}} = 14\;{\text{V}} $ 以及$ {S_{\text{m}}} = - 0.011 $ 的条件下表现出显著的负电容效应, 在$ {V_{\text{S}}} = 10\;{\text{V}} $ 下消失, 这是因为矫顽场随压应变的增加而增大[33 ] . 简单地来讲, 在具有瞬态负电容效应的情况下, 对应的电滞回线会呈现“S”形, 而在$ {V_{\text{S}}} = 10\;{\text{V}} $ , $ {S_{\text{m}}} = - 0.011 $ 的情况下, 极化无法通过“S”的两个弯, 也意味着${V_{\text{S}}} = 10\,{\text{V}}$ 小于所需的矫顽电压. 换句话来说, 较大的压应变反而会使得极化无法翻转, 因此在较大的压应变下, 为了获得负电容效应需要确定外加电压是否大于矫顽电压. 此外, 无论是恒定应变还是恒温条件, 相比于$ {V_{\text{S}}} = 14\;{\text{V}} $ , 在$ {V_{\text{S}}} = 10\;{\text{V}} $ 时负电容效应持续的时长增长, 主要原因是电压降低使极化翻转的驱动力减弱, 极化完全翻转所需的时间增长, 因而负电容效应的持续时间增长. 因此, 在保证负电容效应存在的前提下, 减小电压既延长了负电容效应的时长, 又降低了功耗.图5 所示. 其中, 图5(a) 给出了在恒定应变$ {S_{\text{m}}} = 0.011 $ 时不同温度下的自由能能量势阱曲线, 图5(b) 给出了在恒定温度$ T = 300\;{\text{K}} $ 时不同应变下的自由能能量势阱曲线. 瞬态负电容的消失伴随着自由能曲线由双势阱变为单个极小值的抛物线, 而在恒定应变$ {S_{\text{m}}} = 0.011 $ 的调控下, T = 500和600 K对应单个能量极小值, 此时瞬态负电容效应消失. 在$ T = 300\;{\text{K}} $ , 压应变$ {S_{\text{m}}} = - 0.011 $ 的调控下, 能垒最大, 表现出最显著的瞬态负电容效应, 而在拉应变$ {S_{\text{m}}} = 0.011 $ 的调控下, 能垒最小, 瞬态负电容效应最弱.图 5 自由能U 与极化P 的关系图 (a)恒定应变$ {S_{\text{m}}} = 0.011 $ , 不同温度下$U \text{-} P$ 图; (b)恒温$ T = 300\;{\text{K}} $ , 不同应变下$U \text{-} P$ 图Figure5. Relationship between free energy U and polarization P : (a) $U\text{-} P$ diagram with constant strain $ {S_{\text{m}}} = 0.011 $ at different temperatures; (b)$U \text{-} P$ diagram with constant temperature $ T = 300\;{\text{K}} $ at different strains.4.结 论 应变是调控铁电材料性能的重要手段之一, 充分利用该方法可以使材料展现出更优良的性能. 本文利用Landau-Khalatnikov理论研究了等方双轴错配应变以及温度对铁电薄膜中瞬态负电容效应的影响. 研究表明, 瞬态负电容的产生伴随着极化的翻转, 当铁电材料处于低温和压应变的条件下时, 负电容效应更显著, 持续时间更长. 但是, 过大的压应变会导致对应的矫顽电压增大, 从而极化无法翻转, 所以需要选择合适大小的压应变才能达到预期的目的. 与此同时, 研究发现, 当外加电压大于矫顽电压时, 无论是在恒温还是恒定应变的条件下, 减小电压都可以延长负电容效应持续的时长. 在实际应用中, 为了达到降低功耗的目的常常采用比较低的外加电压, 对于低压下的瞬态负电容效应还需做更多的研究. 
图 1 铁电负电容瞬态响应模型及其等效电路图
图 2 (a)在T = 300 K, Sm = –0.011, 外加脉冲
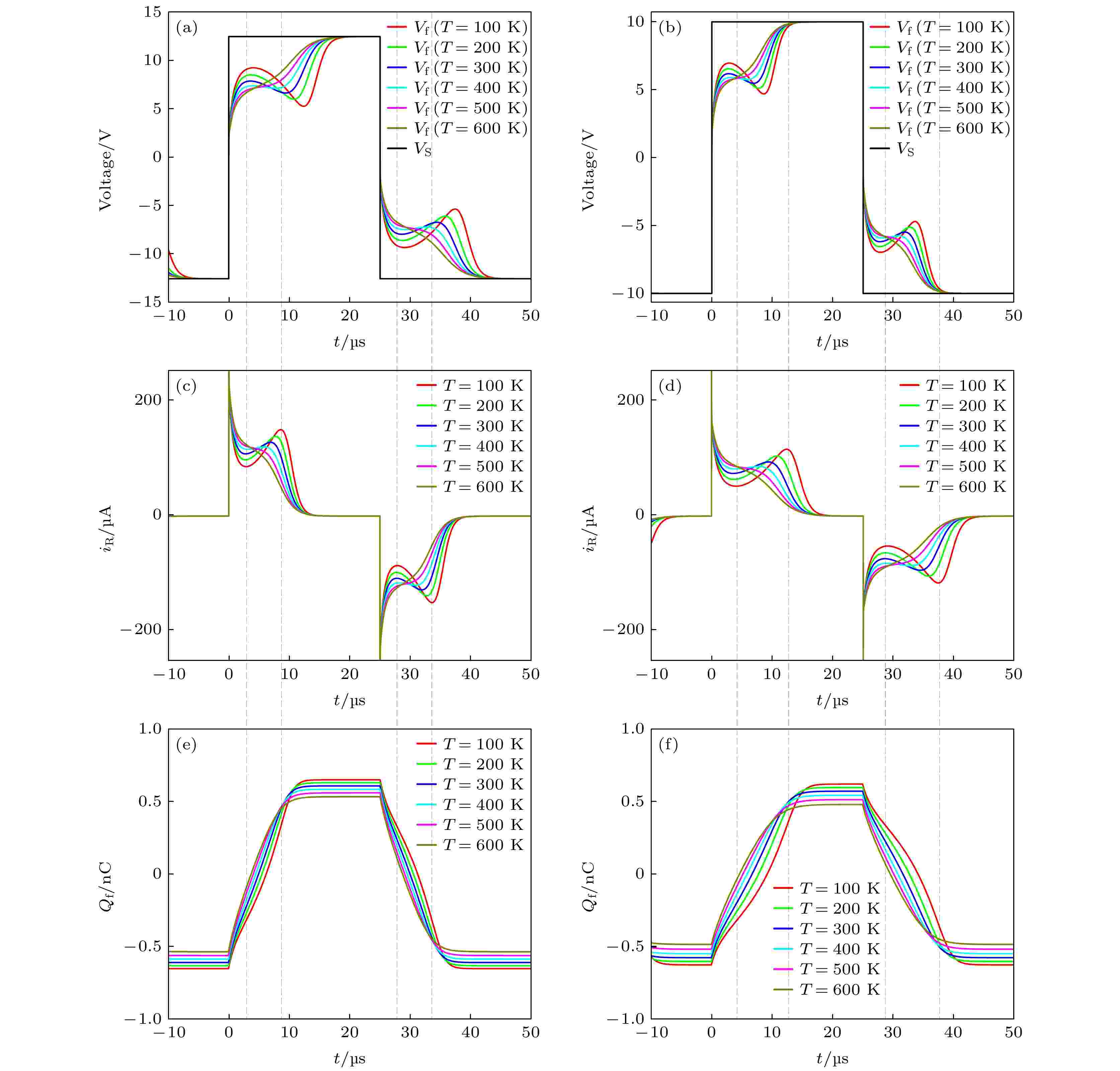图 3 恒定应变
图 4 恒定温度
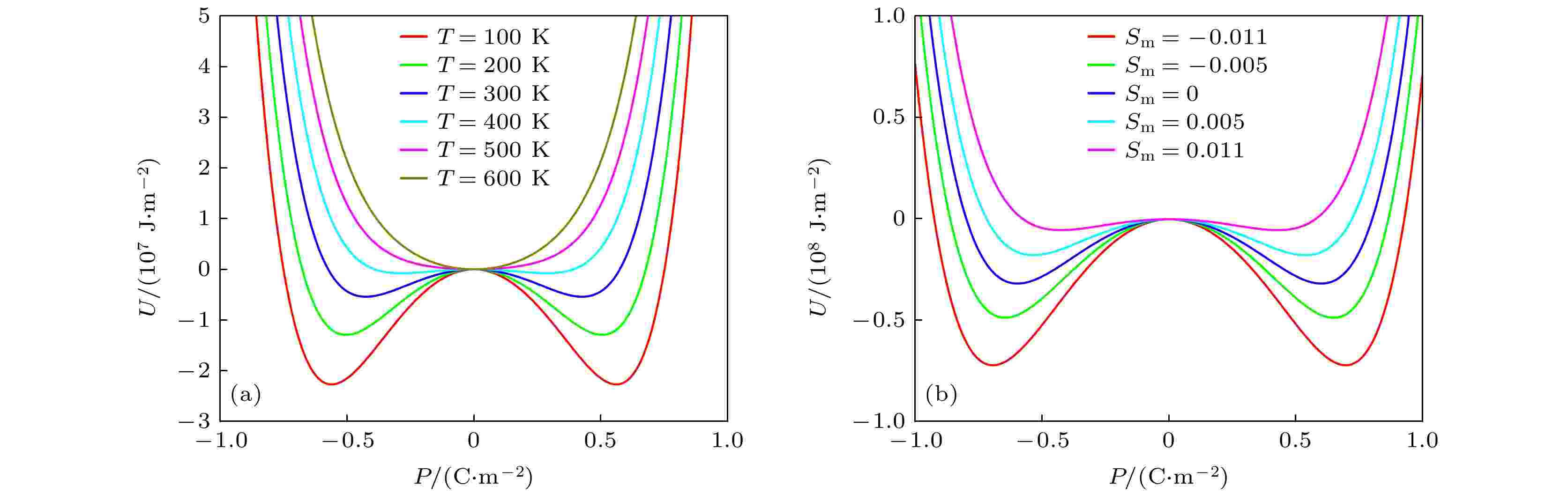图 5 自由能U与极化P的关系图 (a)恒定应变
