摘要:基于微扰理论研究了静电场Stark效应诱导的类氢离子2s_1/2-1s_1/2跃迁, 给出了Z = 1—92类氢离子的Stark混合系数和2s_1/2-1s_1/2跃迁几率, 讨论了Stark效应诱导的类氢离子2s_1/2-1s_1/2跃迁几率随原子序数的变化规律以及相对论效应对Stark混合系数和诱导跃迁几率的影响. 结果表明, 给定电场强度时, 类氢离子的Stark诱导跃迁几率随着原子序数Z的增大单调减小. 另外, 相对论效应使得类氢离子的Stark诱导跃迁几率减小, 甚至在Z = 92时会减小到非相对论近似的55%.
关键词: Stark诱导跃迁/
Stark效应/
类氢离子/
标度关系

English Abstract

全文HTML

--> --> -->

外电场会使原子能级发生分裂和位移, 这种效应被称为 Stark效应. 同时, 由于外电场会破坏原子体系的空间对称性, 进而导致具有不同宇称的原子态发生混合, 从而可能打开新的跃迁通道, 导致原子能级尤其是亚稳态能级的寿命显著减小, 这种由外电场诱发的跃迁称为Stark诱导跃迁(Stark-induced transition, SIT).
Stark诱导跃迁与其他跃迁通道之间产生的干涉效应是探测微弱原子跃迁振幅的一种强有力的手段, 通常被用于观测一些极其细微的原子物理过程. 例如, Bucksbaum等^[1]及Drell和Commins^[2]通过Stark诱导跃迁和弱相互作用跃迁之间的干涉观测了Tl原子6²P_1/2-7²P_1/2跃迁过程中的宇称不守恒效应. Gilbert等^[3]通过Stark诱导干涉法观测了Cs原子6S-7S跃迁过程中的宇称不守恒效应. Maul等^[4]对重原子中的宇称破坏效应进行了观测, 并得到了弱相互作用矩阵元. Hunter等^[5]及Lellouch和Hunter^[6]首次观察到Sr原子和Ca原子中Stark诱导跃迁振幅和电四极跃迁振幅之间的干涉, 先后测定了5s5p ¹P-5s4d ¹D的跃迁几率和4s4p ¹P-4s3d ¹D的跃迁几率. Wielandy等^[7]又使用相同的Stark诱导跃迁干涉技术研究了Ba原子6s5d ¹D的诱导取向.
实际上, 早期已通过Stark诱导跃迁对中低Z类氢离子的Lamb位移进行了精密的测量. Fan等^[8]在1967年首次通过测量类氢Li²⁺离子亚稳态2S_1/2在静电场中的Stark猝灭寿命确定了2S_1/2和2P_1/2的能量差即Lamb位移. 他们根据实验观测的电场强度和相应的2S_1/2能级寿命, 利用三能级系统的Bethe-Lamb含时理论反推出类氢Li²⁺离子的Lamb位移, 达到5位有效数字的精度. Leventhal和Murnick^[9]及Murnick等^[10]分别于1970年和1971年通过运动电场猝灭实验, 利用二能级含时理论公式对类氢C⁵⁺离子的Lamb位移实现了间接测量, 得到具有3位有效数字的Lamb位移. 1972年, Kugel等^[11]也通过运动电场的Stark猝灭研究了类氢C⁵⁺离子的Lamb位移, 他们使用二能级和三能级体系的含时理论对类氢C⁵⁺离子的Lamb位移进行了详细的分析和讨论, 得到的Lamb位移具有4位有效数字. 同年, Leventhal等^[12]和Lawrence等^[13]通过Stark猝灭技术又分别利用二能级和三能级含时理论公式分析了类氢O⁷⁺离子的Lamb位移, 均达到6位有效数字的精度. 1978年, Gould和Marrus^[14]通过运动电场猝灭实验, 利用比较简单的二能级含时理论公式分析得到了类氢Ar¹⁷⁺离子的Lamb位移, 其精度达到3位有效数字.
尽管在类氢离子Lamb位移的实验观测中存在大量涉及Stark诱导跃迁几率的工作, 但是Stark诱导跃迁几率的测量结果却鲜有提及, 也缺乏系统的理论研究. 本文基于微扰理论, 分别推导和计算了类氢离子的相对论Stark诱导跃迁几率及其非相对论近似, 并给出了非相对论和相对论Stark诱导跃迁几率随原子序数Z的标度关系.

如图1所示, 把原子置于沿z方向的外电场ε中, 电场和原子相互作用的哈密顿量算符可以表示为
图 1 外电场取向示意图
Figure1. Schematic diagram of an external electric field.

$ {H}^{\prime }_{\rm{elec}}=-{\boldsymbol{D}}\cdot \boldsymbol{\varepsilon } =e\varepsilon r{C}_{0}^{\left(1\right)},$

其中, ${\boldsymbol{D}} = - e{\boldsymbol{r}}$是原子的电偶极矩, ε是电场强度. 在外加电场与原子内部电场相比较弱的情况下, 电场与原子相互作用的哈密顿量可以被视为零场哈密顿量的微扰.
图2是Stark诱导跃迁示意图. 无静电场(此文中也称为零场)时, 亚稳态$| {\varPsi _i^{(0)}} \rangle $到基态$| {\varPsi _k^{(0)}} \rangle $是单光子电偶极禁戒跃迁, 激发态$| {\varPsi _j^{(0)}} \rangle $到基态$| {\varPsi _k^{(0)}} \rangle $之间存在强的E1跃迁. 双向箭头表示外电场作用下零场亚稳态$| {\varPsi _i^{(0)}} \rangle $和零场激发态$| {\varPsi _j^{(0)}} \rangle $之间的混合, 这导致了外电场中亚稳态$| {{\varPsi _i}} \rangle $到基态$| {{\varPsi _k}} \rangle $的Stark诱导跃迁. 在外电场的微扰作用下, 由于亚稳态和相反宇称态的混合, 亚稳态能级波函数变成如下形式^[15]:
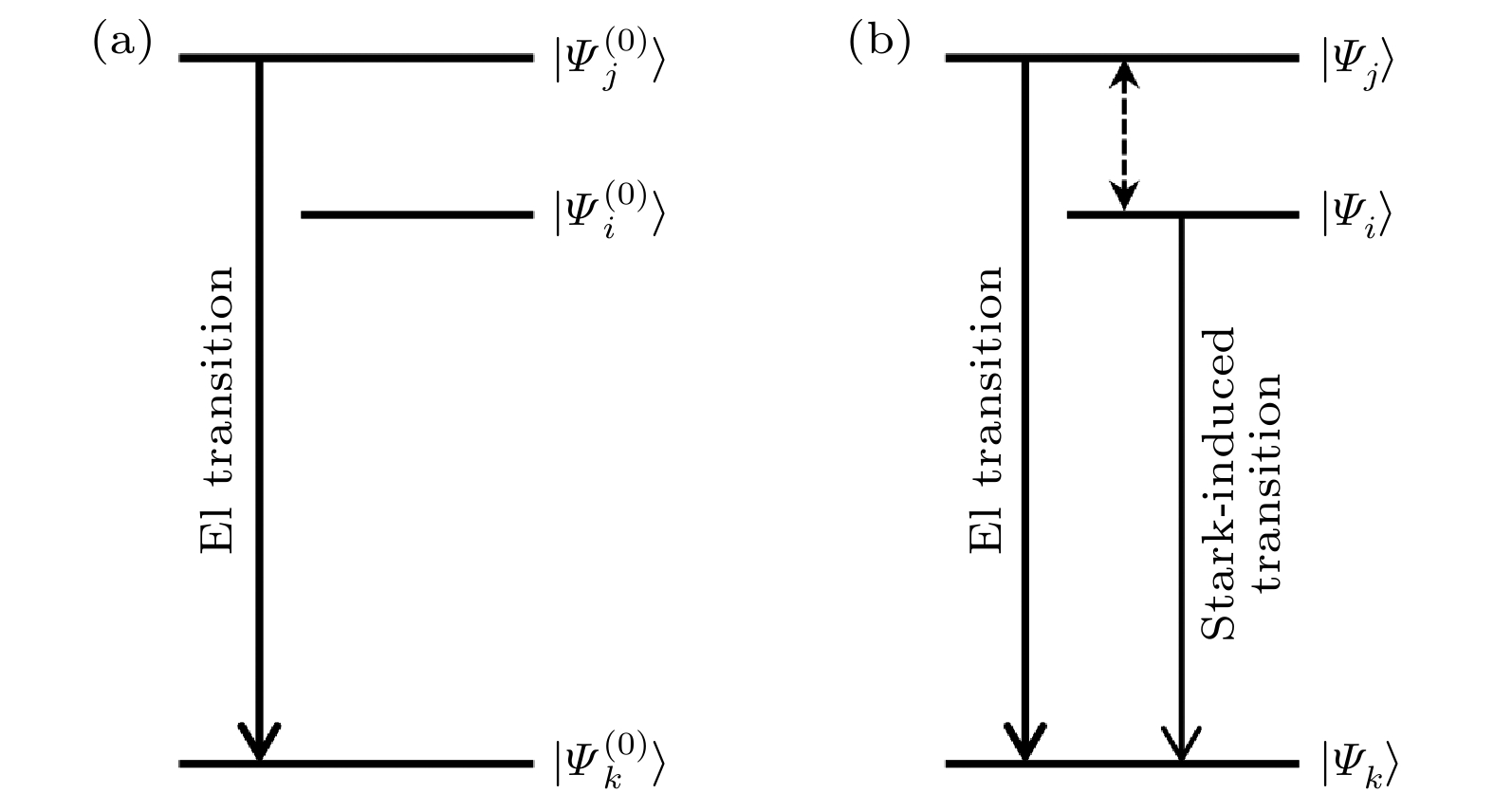图 2 Stark诱导跃迁示意图 (a) 无电场; (b) 外加电场
Figure2. Stark-induced transition diagram: (a) without electric field; (b) with electric fieled.

$\left| {{\varPsi _i}} \right\rangle = | {\varPsi _i^{(0)}} \rangle + {c_{ij}} | {\varPsi _j^{(0)}} \rangle, $

其中, ${c_{ij}}$表示亚稳态$| {\varPsi _i^{\left( 0 \right)}} \rangle$和相反宇称激发态$| {\varPsi _j^{\left( 0 \right)}} \rangle$之间的Stark混合系数, 在一阶微扰近似下

${c_{ij}} = \frac{{\langle {\varPsi _j^{(0)}} | {{{H'}_{{\rm{elec}}}}} | {\varPsi _i^{(0)}} \rangle }}{{E_i^{(0)} - E_j^{(0)}}},$

若外电场中基态依然用零场基态近似表示, 即

$ |{\varPsi }_{k}\rangle =|{\varPsi }_{k}^{(0)}\rangle ,$

从而, 外电场中亚稳态能级到基态能级的Stark诱导跃迁几率可以写成^[16]

$ \begin{split}{A}_{i\to k}^{\rm{SIT}}\; &=\frac{4}{3}{\alpha }^{3}{\omega }_{i\to k}^{\rm{3}}{\left|{\langle \varPsi }_{k}\left|{\boldsymbol{r}}\right|{\varPsi }_{i}\rangle \right|}^{2}\\ & =\frac{{\omega }_{i\to k}^{3}}{{\omega }_{j\to k}^{3}}{c}_{ij}^{2}{A}_{j\to k}^{\left(0\right)},\end{split}$

由于电偶极算符仅导致宇称相反的态发生混合, 因此, 对于类氢离子, 电场将使零场态2s_1/2和np_{1/2, 3/2}发生混合, 如图3所示.
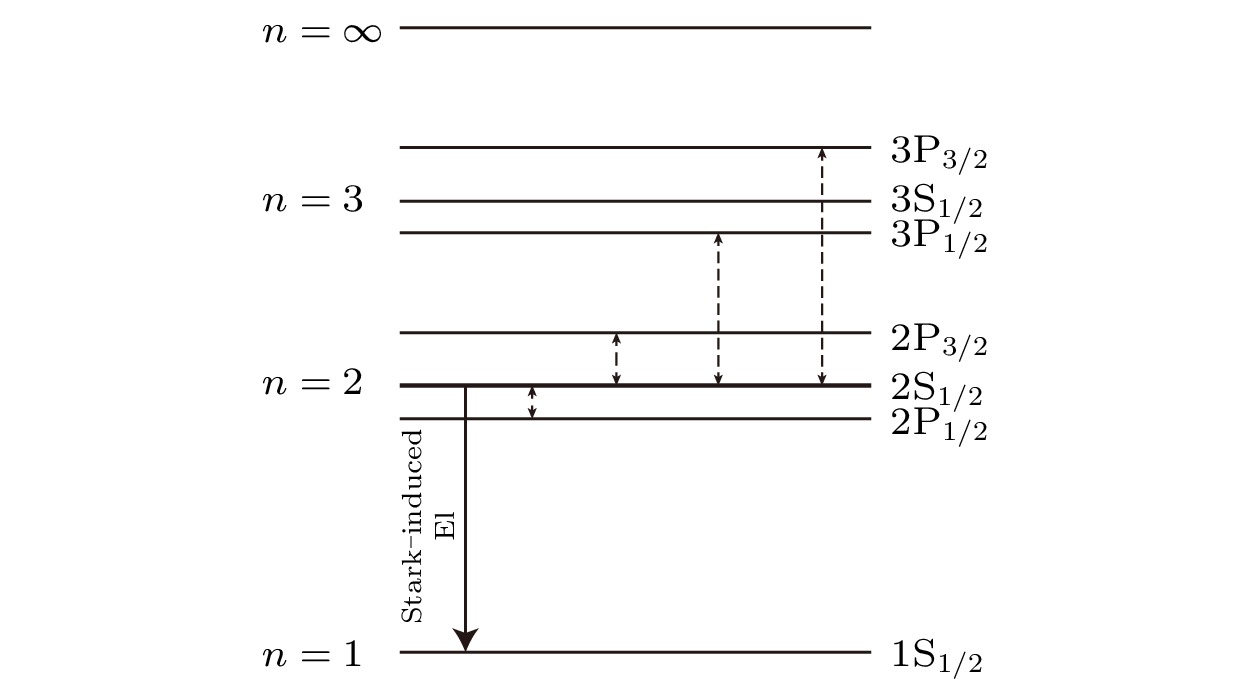图 3 类氢离子能级示意图
Figure3. Schematic diagram of hydrogen-like ion levels.

2

-->

2.1.相对论Stark诱导跃迁几率

在相对论框架下, 类氢离子的相对论波函数写成^[17]:

$ {\varPsi }_{n\kappa m}\left({\boldsymbol{r}}\right)=\frac{1}{r}\left(\begin{array}{c}{P}_{n\kappa }\left(r\right){\varOmega }_{\kappa m}\left(\theta ,\phi \right)\\ {\rm{i}}{Q}_{n\kappa }\left(r\right){\varOmega }_{-\kappa m}\left(\theta ,\phi \right)\end{array}\right),$

其中, n是主量子数, m表示总角动量j在z方向的分量, $\kappa $表示相对论角量子数, 当$l = j \pm 1/2$时对应的$\kappa = \pm \left( {j + 1/2} \right)$, 角向函数${\varOmega _{\kappa m}}\left( {\theta , \varphi } \right)$由自旋函数$\chi _{{m_s}}^{{1}/{2}}$和球谐函数${{\rm{Y}}_{l{m_l}}}$耦合而成, 即

$ {\varOmega }_{\kappa m}(\theta ,\phi ) \!=\!{\displaystyle \sum _{{m}_{l}}{\displaystyle \sum _{{m}_{s}}\langle l,{m}_{l},\frac{1}{2},{m}_{s}|j,m\rangle {{\rm{Y}}}_{l{m}_{l}}\left(\theta ,\phi \right){\chi }_{{m}_{s}}^{{\scriptscriptstyle \frac{1}{2}}}}},$

波函数的径向部分由大分量${P_{n\kappa }}\left( r \right)$和小分量${Q_{n\kappa }}\left( r \right)$组成, 具体形式如下^[17]:

$\left\{ \begin{aligned} {P_{n\kappa }}\left( r \right) =\; & {N_{n\kappa }}\sqrt {1 + {W_{n\kappa }}} r{\left( {2qr} \right)^{s - 1}}{{\rm{e}}^{ - qr}} \\ & \times \left[ { - n'{F_1} + \left( {\frac{{\alpha Z}}{{q{\lambda _{\rm{c}}}}} - \kappa } \right){F_2}} \right], \\[2mm] {Q_{n\kappa }}(r) = \; &- {N_{n\kappa }}\sqrt {1 - {W_{n\kappa }}} r{\left( {2qr} \right)^{s - 1}}{{\rm{e}}^{ - qr}}\\ & \times \left[ {n'{F_1} + \left( {\frac{{\alpha Z}}{{q{\lambda _{\rm{c}}}}} - \kappa } \right){F_2}} \right], \end{aligned} \right.$

其中,

$n' = n - \left| \kappa \right|,\quad s = \sqrt {{\kappa ^2} - {{\left( {\alpha Z} \right)}^2}},$

$q = \dfrac{Z}{{\sqrt {{{\left( {\alpha Z} \right)}^2} + \left( {n' + s} \right){}^2} }},$

${N_{n\kappa }} = \dfrac{{\sqrt 2 {q^{\frac{5}{2}}}{\lambda _{\rm{c}}}}}{{\Gamma \left( {2 s + 1} \right)}}{\left[ {\dfrac{{\Gamma \left( {2 s + n' + 1} \right)}}{{n'!\left( {\alpha Z} \right)\left( {\alpha Z - \kappa q{\lambda _{\rm{c}}}} \right)}}} \right]^{\frac{1}{2}}},$

${W_{n\kappa }} = {1}\bigg/{{{{\bigg[ {1 + {{\left( {\dfrac{{\alpha Z}}{{n' + s}}} \right)}^2}} \bigg]}^{\frac{1}{2}}}}}.$

另外,

${F_1} = F( - n' + 1,2s + 1;2qr),$

${F_2} = F( - n',2s + 1;2qr)$

是合流超几何函数. 一般而言^[18]:

$ \langle {\varPsi }_{n\kappa m}^{\left(0\right)}\left|{H}^{\prime }_{\rm{elec}}\right|{\varPsi }_{{n}^{\prime }{\kappa }^{\prime }{m}^{\prime }}^{\left(0\right)}\rangle =\langle n\kappa m\left|\varepsilon r{C}_{0}^{\left(1\right)}\right|{n}^{\prime }{\kappa }^{\prime }{m}^{\prime }\rangle ,$

根据Wigner-Eckart定理:

$ \begin{split}& \langle n\kappa m\left|\varepsilon r{C}_{0}^{\left(1\right)}\right|{n}^{\prime }{\kappa }^{\prime }{m}^{\prime }\rangle \\= \;&\varepsilon \langle n\kappa \Vert r{C}^{\left(1\right)}\Vert {n}^{\prime }{\kappa }^{\prime }\rangle {\left(-1\right)}^{j-m}\begin{pmatrix}j & 1 & {j}^{\prime } \\ -m & 0 & {m}^{\prime}\end{pmatrix}\\ =\; &\varepsilon \langle n\kappa \Vert r\Vert {n}^{\prime }{\kappa }^{\prime }\rangle \langle n\kappa \Vert {C}^{\left(1\right)}\Vert {n}^{\prime }{\kappa }^{\prime }\rangle {\left(-1\right)}^{j-m} \\ & \times\begin{pmatrix}\!\! j & 1 & {j}^{\prime } \\ -m & 0 & {m}^{\prime}\!\!\end{pmatrix}\!,\end{split}$

其中角向部分是:

$\begin{split} \left\langle {n\kappa } \big\| {{C^{\left( 1 \right)}}} \big\| {n'\kappa '} \right\rangle = {\left( { - 1} \right)^{j + 1/2}}{\left[ {j,j'} \right]^{\tfrac{1}{2}}}\begin{pmatrix} j & 1 & {j'} \\ \dfrac{1}{2} & 0 & - \dfrac{1}{2}\end{pmatrix},\\ \end{split} $

径向部分是:

$\begin{split} &\left\langle {n\kappa } \right.\left\| r \right\|\left. {n'\kappa '} \right\rangle \\ =\; & \int_0^\infty {\left[ {{P_{n\kappa }}\left( r \right){P_{n'\kappa '}}\left( r \right) + {Q_{n\kappa }}\left( r \right){Q_{n'\kappa '}}\left( r \right)} \right]r{\rm{d}}r}. \end{split}$

若微扰中只考虑邻近能级2p_1/2的影响(记作Model I), 波函数表示为

$\begin{split} & \left| {{\varPsi _{2{{\rm{s}}_{1/2}},m = \pm \tfrac{1}{2}}}} \right\rangle \\= \; &\left| {\varPsi _{2{{\rm{s}}_{1/2}},m = \pm \tfrac{1}{2}}^{\left( {\rm{0}} \right)}} \right\rangle + {c_{1,m = \pm \tfrac{1}{2}}}\left| {\varPsi _{2{{\rm{p}}_{1/2}},m = \pm \tfrac{1}{2}}^{\left( {\rm{0}} \right)}} \right\rangle; \end{split}$

若不仅考虑2p_1/2, 还考虑2p_3/2(记作Model II), 波函数表示为

$\begin{split} & \Big|{\varPsi }_{2{\rm{s}}_{1/2},m=\pm {\scriptscriptstyle \frac{1}{2}}}\Big\rangle \\=\;& \Big|{\varPsi }_{2{\rm{s}}_{1/2},m=\pm {\scriptscriptstyle \frac{1}{2}}}^{\left(\rm{0}\right)}\Big\rangle + {c}_{1,m=\pm {\scriptscriptstyle \frac{1}{2}}}\Big|{\varPsi }_{2{\rm{p}}_{1/2}, m=\pm {\scriptscriptstyle \frac{1}{2}}}^{\left(\rm{0}\right)} \Big\rangle \\ &+ {c}_{\rm{2},m=\pm {\scriptscriptstyle \frac{1}{2}}} \Big|{\varPsi }_{2{\rm{p}}_{3/2},m=\pm {\scriptscriptstyle \frac{1}{2}}}^{\left(\rm{0}\right)}\Big\rangle ,\end{split}$

根据类氢离子2s_1/2和2p_1/2之间的能级差由Lamb位移^[19]给出, 在原子单位下表示为

$ \Delta {E}_{\rm{1}}=\frac{{\alpha }^{\rm{3}}{Z}^{4}}{\rm{6\pi }}F\left(\alpha Z\right),$

其中, α是精细结构常数, F(αZ)是无量纲的缓变函数^[19]. 另外, 2s_1/2和2p_3/2之间的能级差可由能级公式给出, 即:

$\Delta {E_2} = - \frac{{{\alpha ^2}{Z^4}}}{{32}}.$

则2s_1/2和2p_1/2, _3/2的混合系数分别为

$ {c}_{1,m=\pm { \tfrac{\rm{1}}{\rm{2}}}}=\mp \dfrac{\rm{2\pi }}{{\alpha }^{\rm{3}}F\left(\alpha Z\right)}\langle {\rm{2p}}_{1/2}\Vert r\Vert {\rm{2s}}_{1/2}\rangle \frac{\varepsilon }{{Z}^{4}},$

${c_{2,m = \pm \tfrac{{\rm{1}}}{{\rm{2}}}}} = - \frac{{32\sqrt {\rm{2}} }}{{{\rm{3}}{\alpha ^2}}}\left\langle {{\rm{2}}{{\rm{p}}_{{\rm{3}}/2}}} \right.\left\| r \right\|\left. {{\rm{2}}{{\rm{s}}_{1/2}}} \right\rangle \frac{\varepsilon }{{{Z^4}}}{\rm{.}}$

在Model I中, 类氢离子2s_1/2-1s_1/2的相对论Stark诱导跃迁几率表达为

$\begin{split} & \qquad A_{{\rm{2}}{{\rm{s}}_{1/2}} \to 1{{\rm{s}}_{1/2}}}^{{\rm{SIT}}}\\ & = \frac{1}{2}\sum\limits_{m' = \pm \tfrac{{\rm{1}}}{{\rm{2}}}} {\sum\limits_{m = \pm \tfrac{{\rm{1}}}{{\rm{2}}}} {A_{{\rm{2}}{{\rm{s}}_{1/2}},m' \to 1{{\rm{s}}_{1/2}},m}^{{\rm{SIT}}}} } \\ & = \frac{{\omega _{{\rm{2}}{{\rm{s}}_{1/2}} \to 1{{\rm{s}}_{1/2}}}^3}}{{\omega _{{\rm{2}}{{\rm{p}}_{1/2}} \to 1{{\rm{p}}_{1/2}}}^3}}c_{1,m' = \pm \tfrac{{\rm{1}}}{{\rm{2}}}}^{\rm{2}}{A_{{\rm{2}}{{\rm{p}}_{1/2}} \to 1{{\rm{s}}_{1/2}}}}.\end{split} $

在Model II中, 类氢离子2s_1/2-1s_1/2的相对论Stark诱导跃迁几率表达为

$\begin{split} \; & A_{{\rm{2}}{{\rm{s}}_{1/2}} \to 1{{\rm{s}}_{1/2}}}^{{\rm{SIT}}} = \frac{1}{2}\sum\limits_{m' = \pm \tfrac{{\rm{1}}}{{\rm{2}}}} {\sum\limits_{m = \pm \tfrac{{\rm{1}}}{{\rm{2}}}} {A_{{\rm{2}}{{\rm{s}}_{1/2}},m' \to 1{{\rm{s}}_{1/2}},m}^{{\rm{SIT}}}} }= \\ & \frac{{\rm{2}}}{3}{\alpha ^3}\omega _{{\rm{2}}{{\rm{s}}_{1/2}} \to 1{{\rm{s}}_{1/2}}}^3 \!\!\sum\limits_{m' = \pm \tfrac{{\rm{1}}}{{\rm{2}}}} \sum\limits_{m = \pm \tfrac{{\rm{1}}}{{\rm{2}}}} \!\! \big| {c_{1,m'}} \langle {1{{\rm{s}}_{1/2}},m} | {\boldsymbol{r}} | {2{{\rm{p}}_{1/2}},m'} \rangle \\ & \!+\! {c_{2,m'}} \langle {1{{\rm{s}}_{1/2}},m} |{\boldsymbol{r}}| {2{{\rm{p}}_{3/2}},m'} \rangle \big|^2 .\end{split} $

2 -->

2.2.非相对论近似

为了研究相对论效应的影响, 进一步考虑了相对论径向轨道波函数的非相对论极限, 即在计算矩阵元时直接使用非相对论径向波函数, 则:

$\begin{split} {c}_{1,m=\pm {\tfrac{\rm{1}}{\rm{2}}}}=\,& \mp \frac{\rm{2\pi }}{{\alpha }^{\rm{3}}F\left(\alpha Z\right)}\langle \rm{2p}\Vert {\boldsymbol{r}}\Vert \rm{2s}\rangle \frac{\varepsilon }{{Z}^{4}} \\=\,& \mp \frac{\rm{6}\sqrt{3}\rm{\pi }}{{\alpha }^{\rm{3}}F\left(\alpha Z\right)}\frac{\varepsilon }{{Z}^{5}},\end{split}$

$\begin{split}c_{2,m = \pm \tfrac{1}{2}} =\,& - \frac{{32\sqrt{2}}} {3\alpha ^2} \langle {\rm 2p} \| {\boldsymbol r} \| {\rm 2s} \rangle \frac{\varepsilon}{Z^4} \\=\;& \frac{32\sqrt{6}}{\alpha ^2}\frac{\varepsilon}{Z^5},\end{split}$

在Model I中, 类氢离子2s_1/2-1s_1/2的非相对论Stark诱导跃迁几率表达为

$\begin{split} &~~~~ A_{{\rm{2}}{{\rm{s}}_{1/2}} \to 1{{\rm{s}}_{1/2}}}^{{\rm{SIT}}}\; \\ \,&= \frac{1}{2}\sum\limits_{m' = \pm \tfrac{{\rm{1}}}{{\rm{2}}}} {\sum\limits_{m = \pm \tfrac{{\rm{1}}}{{\rm{2}}}} {A_{{\rm{2}}{{\rm{s}}_{1/2}},m' \to 1{{\rm{s}}_{1/2}},m}^{{\rm{SIT}}}} } \\ &= \frac{{\omega _{{\rm{2}}{{\rm{s}}_{1/2}} \to 1{{\rm{s}}_{1/2}}}^3}}{{\omega _{{\rm{2}}{{\rm{p}}_{1/2}} \to 1{{\rm{p}}_{1/2}}}^3}}c_{1,m' = \pm \tfrac{{\rm{1}}}{{\rm{2}}}}^{\rm{2}}{A_{{\rm{2}}{{\rm{p}}_{1/2}} \to 1{{\rm{s}}_{1/2}}}} \\ & = \frac{{\lambda _{{\rm{2}}{{\rm{p}}_{1/2}} \to 1{{\rm{s}}_{1/2}}}^3}}{{\lambda _{{\rm{2}}{{\rm{s}}_{1/2}} \to 1{{\rm{s}}_{1/2}}}^3}}c_{1,m' = \pm \tfrac{{\rm{1}}}{{\rm{2}}}}^{\rm{2}}{A_{{\rm{2}}{{\rm{p}}_{1/2}} \to 1{{\rm{s}}_{1/2}}}} \\ & = \frac{{64{{\rm{\pi }}^4}{e^2}a_0^2}}{{3h\lambda _{{{\rm{H}}_{{\rm{2s}}}} \to {{\rm{H}}_{{\rm{1s}}}}}^3}}{\left[ {\frac{{{\rm{256}}}}{{{\rm{27}}}}\sqrt {\frac{{\rm{2}}}{{\rm{3}}}} \frac{{\rm{\pi }}}{{{\alpha ^{\rm{3}}}F(\alpha Z)}}} \right]^2}\!\! \times \!\frac{{{\varepsilon ^{\rm{2}}}}}{{{Z^{\rm{6}}}}} ,\end{split} $

为简单起见, (23)式中仅考虑非相对论波长

${\lambda _{{\rm{2s}} \to 1{\rm{s}}}} = \frac{{{\lambda _{{{\rm{H}}_{{\rm{2s}}}} \to {{\rm{H}}_{{\rm{1s}}}}}}}}{{{Z^2}}} = \frac{{{\rm{121}}{\rm{.503~ nm}}}}{{{Z^2}}}.$

可见, 非相对论近似的几率表达式能够呈现出更加明确的标度关系. 在Model II中, 类氢离子2s_1/2-1s_1/2的非相对论Stark诱导跃迁几率表达为

$\begin{split} & {A}_{{\rm{2}}{\rm{s}}_{1/2}\to {1}{\rm{s}}_{1/2}}^{\rm{SIT}} =\\ & \frac{1}{2}\displaystyle \sum _{{m}^{\prime }}\displaystyle \sum _{m}\frac{64{\rm{\pi }}^{4}{e}^{2}{a}_{0}^{2}}{3h{\lambda }_{{\rm{2}}{\rm{s}}_{1/2}\to {1}{\rm{s}}_{1/2}}^{3}} \big|{c}_{1,{m}^{\prime }}\langle {1}{\rm{s}}_{1/2},m\left|{\boldsymbol{r}}\right|{2}{\rm{p}}_{1/2},{m}^{\prime }\rangle \\& +{c}_{2,{m}^{\prime }}\langle {1}{\rm{s}}_{1/2},m\left|{\boldsymbol{r}}\right|{2}{\rm{p}}_{3/2},{m}^{\prime }\rangle \big|^{2}, \\[-12pt]\end{split}$

可以得出, 两种非相对论近似均包含相同的标度因子${\varepsilon ^2}{Z^{ - 6}}$.

本文对类氢离子2s_1/2-1s_1/2能级之间的Stark诱导跃迁几率进行了系统的计算. 表1给出2s和2p之间的能量差以及相对论和非相对论径向矩阵元的计算结果, 其中ΔE₁ = E(2s_1/2) – E(2p_1/2)取自文献[19], ΔE₂ = E(2s_1/2) – E(2p_3/2). 从表1可以看出, 2s_1/2和2p_1/2, _3/2之间能量差的绝对值随着原子序数Z的增大而急剧增大, 且2s_1/2-2p_3/2的间距总是大于2s_1/2-2p_1/2的间距. 这表明随着Z的增大, 相对论效应越来越显著, 使得2p_1/2, _3/2轨道的能级分裂越来越明显. 另一方面, 从径向矩阵元中也可以看出相对论效应的影响. 对于低Z离子, 相对论轨道径向矩阵元和非相对论轨道径向矩阵元均非常接近, 而对于高Z离子, 不仅相对论轨道径向矩阵元与非相对论轨道径向矩阵元均存在较大差别, 而且相对论矩阵元之间的差别也越来越明显. 例如Z = 1时, 相对论轨道径向矩阵元$\langle $2p_1/2, _3/2||r||2s_1/2$\rangle $, $\langle $1s_1/2||r||2p_1/2, _3/2$\rangle $和对应非相对论轨道径向矩阵元$\langle $2p||r||2s$\rangle $, $\langle $1s||r||2p$\rangle $的相对差别分别是0.002%, 0.0008%和0.002%, 0.002%, Z = 92时, 对应的相对差别分别达到了20.81%, 9.46%和18.76%, 19.22%. 对于相对论轨道径向矩阵元, $\langle $2p_1/2||r||2s_1/2$\rangle $的绝对值均小于$\langle $2p_3/2||r||2s_1/2$\rangle $的绝对值, 而$\langle $1s_1/2||r||2p_1/2$\rangle $ 的绝对值均大于$\langle $1s_1/2||r||2p_3/2$\rangle $的绝对值.

Z	Energy difference/cm–1			Matrix element
	ΔE1[19]	ΔE2		$\langle $2p1/2|r||2s1/2$\rangle $	$\langle $2p3/2||r||2s1/2$\rangle $	$\langle $2p||r||2s $\rangle $	$\langle $1s1/2||r||2p1/2$\rangle $	$\langle $1s1/2||r||2p3/2$\rangle $	$\langle $1s||r||2p$\rangle $
1	3.52868[-2]	–3.65221[-1]		–5.19604	–5.19611	–5.19615	1.29024	1.29024	1.29027
2	4.68400[-1]	–5.84353[0]		–2.59785	–2.59798	–2.59808	0.64509	0.64508	0.64513
3	2.09220[0]	–2.95829[1]		–1.73170	–1.73191	–1.73205	0.43002	0.43001	0.43009
4	5.99720[0]	–9.34965[1]		–1.29858	–1.29885	–1.29904	0.32247	0.32247	0.32257
6	2.60840[1]	–4.73326[2]		–0.86533	–0.86575	–0.86603	0.21490	0.21489	0.21504
8	7.32500[1]	–1.49594[3]		–0.64860	–0.64915	–0.64952	0.16109	0.16108	0.16128
10	1.62100[2]	–3.65221[3]		–0.51846	–0.51915	–0.51962	0.12879	0.12878	0.12903
12	3.08800[2]	–7.57322[3]		–0.43163	–0.43246	–0.43301	0.10724	0.10722	0.10752
14	5.30600[2]	–1.40303[4]		–0.36954	–0.37051	–0.37115	0.09183	0.09181	0.09216
16	8.46400[2]	–2.39351[4]		–0.32291	–0.32402	–0.32476	0.08026	0.08024	0.08064
18	1.27570[3]	–3.83394[4]		–0.28659	–0.28784	–0.28868	0.07125	0.07123	0.07168
20	1.83800[3]	–5.84353[4]		–0.25749	–0.25888	–0.25981	0.06403	0.06401	0.06451
24	3.45000[3]	–1.21171[5]		–0.21372	–0.21539	–0.21651	0.05318	0.05315	0.05376
28	5.86400[3]	–2.24485[5]		–0.18232	–0.18426	–0.18558	0.04540	0.04537	0.04608
32	9.28800[3]	–3.82962[5]		–0.15865	–0.16087	–0.16238	0.03954	0.03950	0.04032
36	1.39300[4]	–6.13430[5]		–0.14013	–0.14263	–0.14434	0.03496	0.03492	0.03584
40	2.00100[4]	–9.34965[5]		–0.12522	–0.12799	–0.12990	0.03127	0.03123	0.03226
44	2.78800[4]	–1.36888[6]		–0.11292	–0.11597	–0.11809	0.02823	0.02819	0.02932
48	3.78200[4]	–1.93874[6]		–0.10259	–0.10592	–0.10825	0.02568	0.02563	0.02688
52	5.03100[4]	–2.67035[6]		–0.09376	–0.09737	–0.09993	0.02351	0.02345	0.02481
56	6.56100[4]	–3.59176[6]		–0.08612	–0.09001	–0.09279	0.02162	0.02156	0.02304
60	8.45400[4]	–4.73326[6]		–0.07942	–0.08359	–0.08660	0.01997	0.01991	0.02150
64	1.08200[5]	–6.12739[6]		–0.07348	–0.07793	–0.08119	0.01850	0.01844	0.02016
68	1.37000[5]	–7.80892[6]		–0.06817	–0.07290	–0.07641	0.01720	0.01713	0.01897
72	1.73900[5]	–9.81489[6]		–0.06338	–0.06839	–0.07217	0.01601	0.01595	0.01792
76	2.20000[5]	–1.21846[7]		–0.05902	–0.06432	–0.06837	0.01494	0.01487	0.01698
80	2.79500[5]	–1.49594[7]		–0.05503	–0.06060	–0.06495	0.01395	0.01388	0.01613
84	3.56700[5]	–1.81833[7]		–0.05135	–0.05720	–0.06186	0.01304	0.01297	0.01536
88	4.62700[5]	–2.19021[7]		–0.04793	–0.05406	–0.05905	0.01219	0.01212	0.01466
92	6.07300[5]	–2.61642[7]		–0.04473	–0.05114	–0.05648	0.01139	0.01133	0.01402

表1类氢离子n = 2能级差及径向轨道矩阵元, 其中a[b]表示a × 10^b
Table1.Energy differences and radial orbital matrix elements for hydrogen-like ions, where a[b] stands for a × 10^b

图4给出不同电场强度下2s_1/2和2p_1/2, _3/2之间的非相对论和相对论Stark混合系数模方与原子序数Z的依赖关系. 可以看出, 在给定电场强度时, 类氢离子2s_1/2和2p_1/2, _3/2之间的混合系数模方均随着原子序数Z的增大而迅速减小而且前者比后者大1个数量级以上. 表明在给定的电场中2s_1/2和2p_1/2, _3/2之间的混合程度随着原子序数Z的增大会急剧降低且2p_1/2的混合占据主导地位. 另一方面, 对于给定的原子序数, 电场越强, 混合系数的模方就越大且与电场强度的平方成正比. 这说明只要电场足够强, 都可以使给定类氢离子2s_1/2和2p_1/2, _3/2之间产生足够强的混合而导致足够强的Stark诱导跃迁. 换句话说, 不论低Z离子还是高Z离子, 都可以通过调节电场对Stark诱导跃迁进行调控.
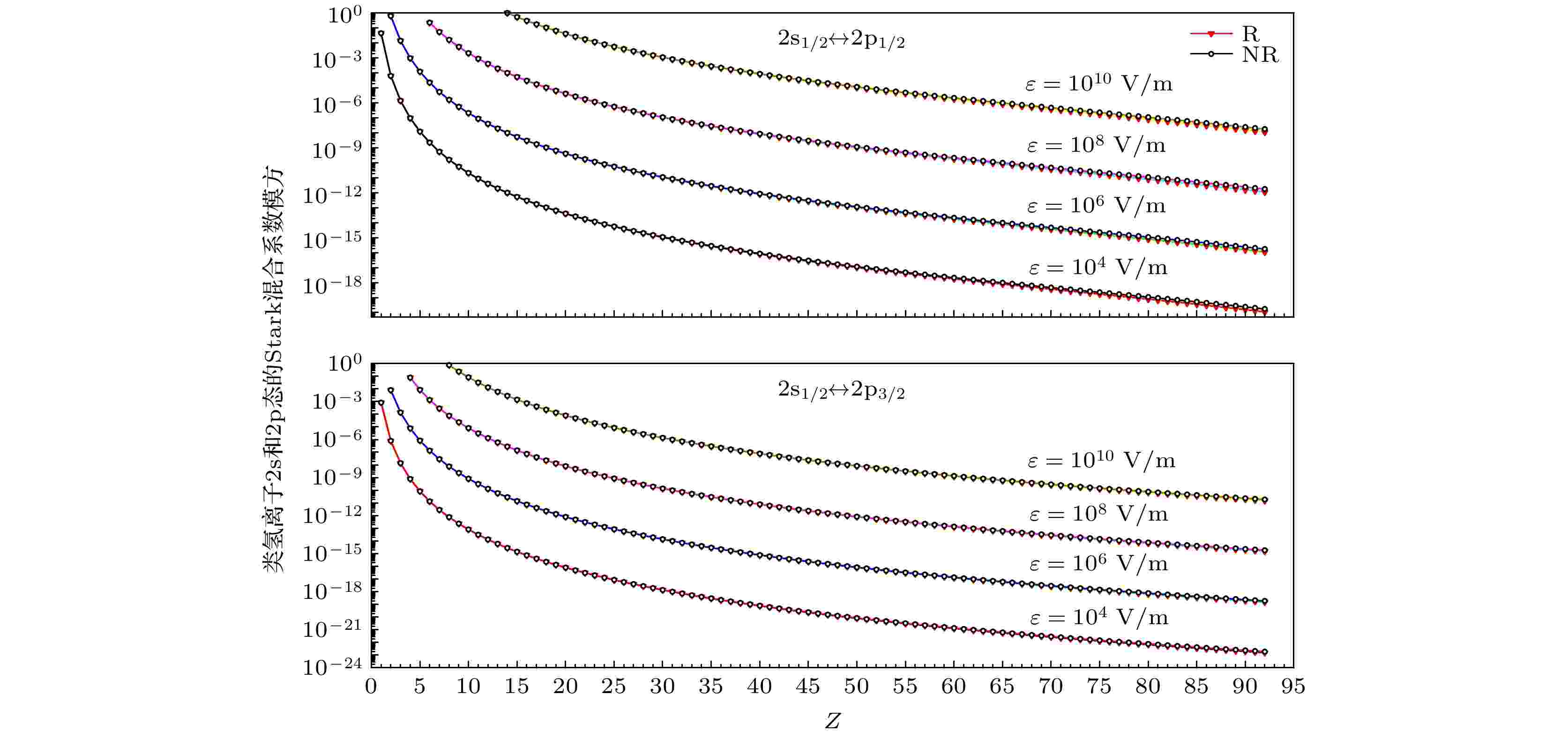图 4 类氢离子2s_1/2和2p_{1/2, 3/2}之间的Stark混合系数模方(NR和R分别表示非相对论和相对论结果)
Figure4. Module squares of Stark mixing coefficients between 2s_1/2 and 2p_{1/2, 3/2} states of hydrogen-like ions (NR and R stand for nonrelativistic and relativistic cases, respectively).

表2列出了2s_1/2-1s_1/2之间的非相对论跃迁波长和1 V/m的电场中使用两种计算模型得到的非相对论和相对论Stark诱导跃迁几率, 其中, Model I表示只考虑2p_1/2的Stark混合, Model II表示同时考虑2p_1/2, _3/2的Stark混合. 从表2可以看出, 类氢离子2s_1/2-1s_1/2之间的跃迁波长随Z的增大而急剧减小. 另一方面, 在Z = 1—92的范围内, 不论是非相对论还是相对论的模型, 1 V/m的电场中Model II的结果都是略大于Model I的结果, 具体地说, 2p_3/2的混合对2s_1/2-1s_1/2的Stark诱导跃迁几率的提高不超过2%, 这说明2p_3/2的Stark混合与2p_1/2的Stark混合相比依然是相当弱的. 同时, 本文的计算还发现, 类氢离子(Z = 1—92) 3p_1/2激发态的Stark混合对2s_1/2-1s_1/2, 电场诱导跃迁几率的提高不超过0.22%, 而3p_3/2激发态的Stark混合对2s_1/2-1s_1/2, 电场诱导跃迁几率的降低不超过0.01%, np_{1/2, 3/2} (n > 3)激发态的Stark混合对2s_1/2-1s_1/2电场诱导跃迁几率的贡献将会更小, 因此对2s_1/2只考虑2p_1/2和2p_3/2的Stark混合是合理的.

Z	λ/nm	Transition probability/s–1
		Model I			Model II
		ASIT (NR)	ASIT(R)		ASIT (NR)	ASIT (R)
1	121.50287	2.7510[–1]	2.7508[–1]		2.8023[–1]	2.8022[–1]
2	30.37572	6.2450[–3]	6.2439[–3]		6.3253[–3]	6.3242[–3]
3	13.50032	7.0428[–4]	7.0399[–4]		7.1133[–4]	7.1104[–4]
4	7.59393	1.5238[–4]	1.5227[–4]		1.5364[–4]	1.5353[–4]
6	3.37508	1.8124[–5]	1.8095[–5]		1.8234[–5]	1.8205[–5]
8	1.89848	4.0858[–6]	4.0740[–6]		4.1054[–6]	4.0936[–6]
10	1.21503	1.3036[–6]	1.2978[–6]		1.3087[–6]	1.3029[–6]
12	0.84377	5.1727[–7]	5.1392[–7]		5.1899[–7]	5.1564[–7]
14	0.61991	2.3847[–7]	2.3637[–7]		2.3915[–7]	2.3705[–7]
16	0.47462	1.2240[–7]	1.2099[–7]		1.2271[–7]	1.2130[–7]
18	0.37501	6.8196[–8]	6.7198[–8]		6.8347[–8]	6.7348[–8]
20	0.30376	4.0558[–8]	3.9825[–8]		4.0638[–8]	3.9904[–8]
24	0.21094	1.6577[–8]	1.6143[–8]		1.6603[–8]	1.6169[–8]
28	0.15498	7.8098[–9]	7.5301[–9]		7.8204[–9]	7.5406[–9]
32	0.11866	4.0660[–9]	3.8747[–9]		4.0708[–9]	3.8794[–9]
36	0.09375	2.2878[–9]	2.1507[–9]		2.2901[–9]	2.1530[–9]
40	0.07594	1.3688[–9]	1.2668[–9]		1.3700[–9]	1.2680[–9]
44	0.06276	8.5316[–10]	7.7563[–10]		8.5387[–10]	7.7630[–10]
48	0.05274	5.5176[–10]	4.9160[–10]		5.5218[–10]	4.9199[–10]
52	0.04493	3.6594[–10]	3.1869[–10]		3.6620[–10]	3.1894[–10]
56	0.03874	2.4954[–10]	2.1184[–10]		2.4971[–10]	2.1199[–10]
60	0.03375	1.7254[–10]	1.4233[–10]		1.7265[–10]	1.4243[–10]
64	0.02966	1.1984[–10]	9.5735[–11]		1.1992[–10]	9.5802[–11]
68	0.02628	8.4389[–11]	6.5035[–11]		8.4441[–11]	6.5081[–11]
72	0.02344	5.8719[–11]	4.3471[–11]		5.8755[–11]	4.3503[–11]
76	0.02104	4.0878[–11]	2.8934[–11]		4.0905[–11]	2.8956[–11]
80	0.01898	2.8062[–11]	1.8889[–11]		2.8082[–11]	1.8905[–11]
84	0.01722	1.8996[–11]	1.2085[–11]		1.9011[–11]	1.2096[–11]
88	0.01569	1.2390[–11]	7.3978[–12]		1.2401[–11]	7.4061[–12]
92	0.01436	7.8610[–12]	4.3696[–12]		7.8695[–12]	4.3757[–12]

表2类氢离子2s_1/2-1s_1/2之间的跃迁波长和1 V/m 电场中的Stark诱导跃迁几率, 其中a[b]表示a × 10^b
Table2.Transition wavelength and Stark-induced probability between 2s_1/2-1s_1/2 of hydrogen-like ions in electric field of 1 V/m, where a[b] stands for a × 10^b

根据计算得到的非相对论和相对论跃迁矩阵元, 可以进一步计算不同电场强度下类氢离子2s_1/2-1s_1/2能级之间的Stark诱导跃迁几率. 表3和图5给出类氢Li²⁺离子和Ar¹⁷⁺离子2s能级的相对论Stark诱导跃迁寿命的计算结果与实验结果^[8,14]的比较, 其差别最大不超过10%. 研究发现, Li²⁺离子跃迁寿命的计算结果偏低, 而Ar¹⁷⁺离子的计算结果略高于实验测量寿命^[14], 并且两者在电场强度较大时符合较好. 可推测Li²⁺离子跃迁寿命差异较大的原因或许是因为理论仅考虑了2p_1/2和2p_3/2的Stark混合的一阶微扰, 而对于其他更高轨道的一阶微扰和所有的高阶微扰都没有计及, 将在进一步的工作中继续深入研究该问题. 另一方面, 实验测量的Stark跃迁寿命需要扣除磁偶极(M1)和双光子(2E1, 2M1)等电偶极禁戒跃迁的贡献, 而这些实验使用的电偶极禁戒跃迁的几率基本都是根据其他理论工作提供的标度公式得到的, 因此可认为这也是实验观测误差的主要来源之一, 所以期望能出现更新的实验测量结果作以比较.

Z	ε/(V·m-1)	τSIT/ns
		Exp	Model I	Model II
3	7.425(2)[5]	2.629(21)[8]	2.58	2.55
	9.173(2)[5]	1.764(35) [8]	1.69	1.67
18	5.93[7]	3.86(3) [14]	4.23	4.22
	7.14[7]	2.80(6) [14]	2.92	2.91
	8.06[7]	2.28(2) [14]	2.29	2.29
	8.60[7]	2.00(2) [14]	2.01	2.01

表3类氢Li²⁺离子和Ar¹⁷⁺离子2s能级的相对论Stark诱导跃迁寿命, 其中a(b)[c]表示a(b) × 10^c, b是实验测量不确定度
Table3.Relativistic Stark-induced transition lifetime for 2s level of hydrogen-like Li²⁺ and Ar¹⁷⁺ ions, where a(b)[c] stands for a(b) × 10^c and b is the experimental uncertainty.

图 5 类氢Li²⁺离子和Ar¹⁷⁺离子2s_1/2能级的Stark诱导跃迁寿命
Figure5. Stark-induced lifetime of 2s_1/2 levels for hydrogen-like Li²⁺ and Ar¹⁷⁺ ions.

图6展示了电场强度分别为10⁴, 10⁶, 10⁸ 和10¹⁰ V/m时, 类氢离子2s_1/2-1s_1/2能级之间的Stark诱导跃迁几率以及相对论与非相对论诱导跃迁几率的比值随原子序数Z的变化趋势, 其中仅给出Model II的计算结果. 可以看出, 随着原子序数Z增大, 由于2p-1s跃迁径向矩阵元不断减小, 类氢离子2s_1/2-1s_1/2 能级之间的Stark诱导跃迁几率会不断减小. 给定原子序数Z, 由于Stark诱导跃迁几率与电场强度的平方成正比, 因此电场越强, 诱导跃迁几率也越大. 计算结果表明, 随着电场强度的增大, 对于原子序数较小的类氢离子体系, 其相互作用将强于电子和原子核之间的Coulomb相互作用, 微扰理论并不适用, 即本文推导的Stark诱导跃迁几率的公式不再适用. 由于相对论径向轨道矩阵元的绝对值均小于非相对论径向轨道矩阵元的绝对值, 因此相对论Stark诱导跃迁几率总是小于非相对论Stark诱导跃迁几率, 并且随着原子序数Z的增大这个差别将越来越大, 这也表明随着原子序数Z的增大, 相对论效应也逐渐变强. 例如, Z = 18时, $\langle $2p_1/2||r||2s_1/2$\rangle $ = 0.9928$\langle $2p||r||2s$\rangle $, 这与文献[14]的结果$\langle $2p_1/2||r||2s_1/2$\rangle $ = 0.992$\langle $2p||r||2s$\rangle $符合得很好. 当Z = 92时, 相对论Stark诱导跃迁几率仅仅是非相对论Stark诱导跃迁几率的55%左右. 另外, 由于电场的改变不会影响相对论Stark诱导跃迁几率与非相对论Stark跃迁几率的比值, 因此不同电场强度下类氢离子2s_1/2-1s_1/2之间相对论Stark诱导跃迁几率与非相对论Stark跃迁几率的比值是完全一致的.
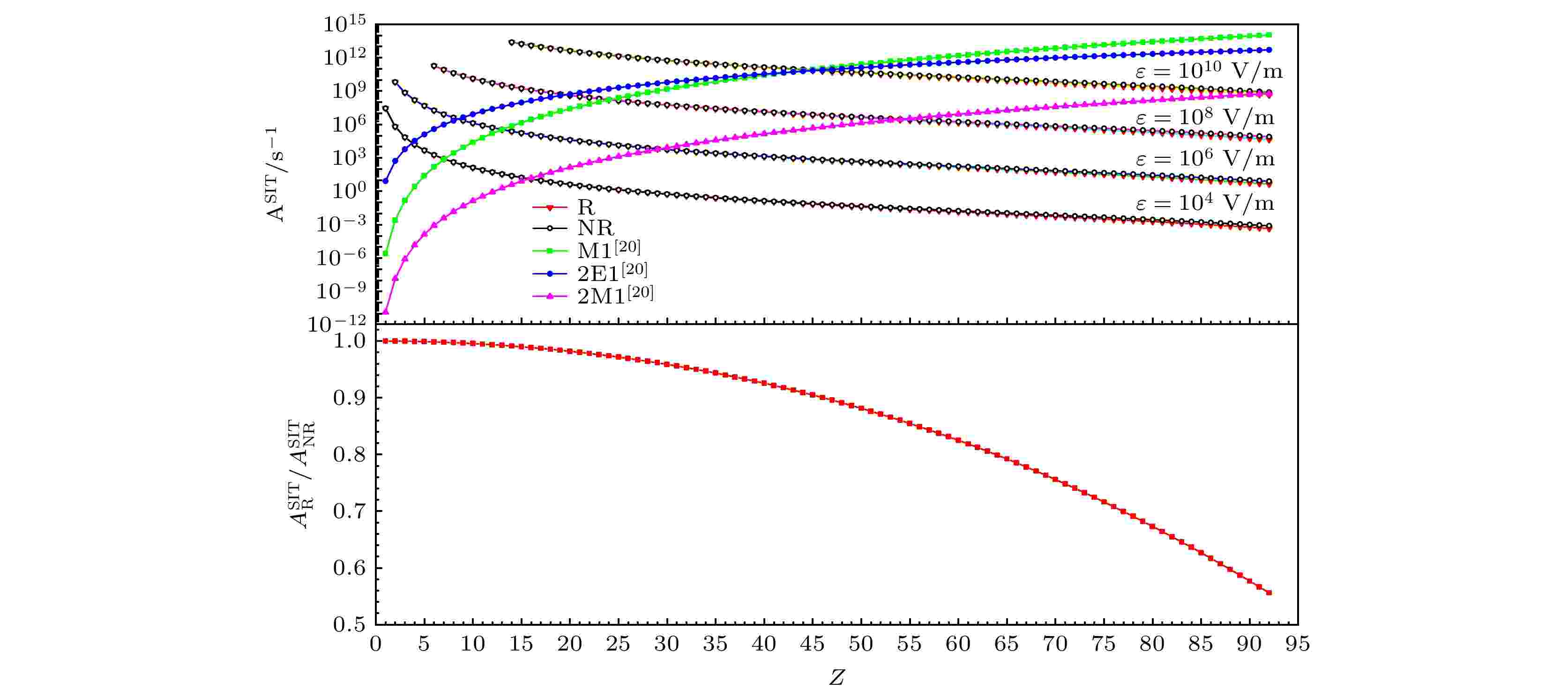图 6 类氢离子2s_1/2-1s_1/2能级之间的Stark诱导跃迁几率
Figure6. Stark-induced transition probability between 2s_1/2-1s_1/2 levels of hydrogen-like ions.

为了比较弱静电场对类氢离子中2s_1/2能级寿命的影响, 图6还给出了2s_1/2-1s_1/2磁偶极跃迁几率和双光子跃迁几率的标度曲线, 其中类氢离子2s_1/2-1s_1/2的磁偶极M1跃迁几率、双光子2E1跃迁几率和双光子2M1跃迁几率的标度关系分别是2.496 × 10^–6Z¹⁰ s^–1、8.2292Z⁶ s^–1和1.38 × 10^–11Z¹⁰ s^–1[20]. 可以看出, 磁偶极M1跃迁几率、双光子2E1跃迁几率和双光子2M1跃迁几率随着Z的增大均急剧增大且双光子2M1跃迁总是三者之中最弱的. 当Z = 1 — 42时, 2s_1/2-1s_1/2的自发辐射衰变的主要方式是双光子2E1跃迁. 当Z = 43— 92时, 磁偶极M1跃迁成为2s_1/2-1s_1/2自发辐射衰变的主要途径. 然而, 当电场强度为10⁴ V/m时, 类氢离子(Z = 1 — 3)的Stark诱导跃迁占主导地位. 当电场强度为10⁶ V/m时, 类氢离子(Z = 2—8)的Stark诱导跃迁占主导地位. 当电场强度为10⁸ V/m时, 类氢离子(Z = 6—19)的Stark诱导跃迁占主导地位. 当电场强度为10¹⁰ V/m时, 类氢离子(Z = 14—44)的Stark诱导跃迁占主导地位. 这说明当电场强度较弱时, 中低Z类氢离子2s_1/2-1s_1/2辐射衰变的主要途径以Stark诱导跃迁为主, 因此中低Z类氢离子可以作为研究Stark诱导跃迁较为理想的对象. 同时, 不同的电场强度下满足微扰适用条件的类氢离子范围不同. 通过微扰系数的计算将易于确定这个范围.

基于微扰理论, 本文研究了类氢离子的相对论Stark诱导跃迁及其非相对论近似, 解析推导并系统地计算了类氢离子(Z = 1—92)在电场诱导作用下的Stark混合系数和2s_1/2-1s_1/2能级之间的Stark诱导跃迁几率. 结果表明, 在给定电场的情况下, 随着原子序数Z的增大, 亚稳态和宇称相反态之间的混合程度急剧降低, Stark诱导跃迁几率沿等电子序列急剧减小. 而相对论效应使得Stark诱导跃迁几率整体下降, 并在Z = 92时减小到非相对论近似的55%.
另外, 类氢离子非相对论Stark诱导跃迁几率显示出明显的标度关系, 即在满足微扰适用条件时, 非相对论Stark诱导跃迁几率服从以下模型.

${\rm{Model\;I}}: \;\;\;\;\;\;\;\;\;\;\;\;{A}_{2\rm{s}\to 1\rm{s}}^{\rm{SIT}}={f}_{I}^{\left(\rm{NR}\right)}\left(Z\right)\times \frac{{\varepsilon }^{\rm{2}}}{{Z}^{\rm{6}}}{\rm{ s}}^{-1};$

${\rm{Model \;II}}: \;\;\;\;\;\;\;\;\;\;\;\;A_{2{\rm{s}} \to 1{\rm{s}}}^{{\rm{SIT}}} = f_{{\rm{II}}}^{\left( {{\rm{NR}}} \right)}\left( Z \right) \times \frac{{{\varepsilon ^{\rm{2}}}}}{{{Z^{\rm{6}}}}}{\rm{ }}{{\rm{s}}^{ - 1}}.$

由于系数中含有$F\left( {\alpha Z} \right)$, 对其系数直接进行多项式拟合给出定性趋势, 分别得到

$\begin{split} f_{\rm{I}}^{\left( {{\rm{NR}}} \right)}\left( Z \right) =\; & 0.1566 + 0.12496Z - 0.00317{Z^2} + 3.23122 \times {10^{ - 4}}{Z^3} \\ & - 1.38174 \times {10^{ - 5}}{Z^4} + 3.53579 \times {10^{ - 7}}{Z^5} - 5.66538 \times {10^{ - 9}}{Z^6} \\ & + 5.46049 \times {10^{ - 11}}{Z^7} - 2.93855 \times {10^{ - 13}}{Z^8} + 6.88431 \times {10^{ - 16}}{Z^9} , \end{split} $

$\begin{split} f_{{\rm{II}}}^{\left( {{\rm{NR}}} \right)}\left( Z \right) =\; & 0.1{\rm{6174}} + 0.12496Z - 0.00317{Z^2} + 3.23122 \times {10^{ - 4}}{Z^3} \\ & - 1.38174 \times {10^{ - 5}}{Z^4} + 3.53579 \times {10^{ - 7}}{Z^5} - 5.66538 \times {10^{ - 9}}{Z^6} \\ & + 5.46049 \times {10^{ - 11}}{Z^7} - 2.93855 \times {10^{ - 13}}{Z^8} + 6.88431 \times {10^{ - 16}}{Z^9}.\end{split} $

然而, 由于相对论轨道径向积分的复杂性, 本文只给出了数值结果, 并依据非相对论近似的标度关系拟合出了类氢离子2s_1/2-1s_1/2能级之间的相对论Stark诱导跃迁几率的标度关系, 即在满足微扰适用条件时, 相对论Stark诱导跃迁几率服从以下模型.

${\rm{Model\;I}}:\;\;\;\;\;\;\;\;\;\;\;\;\; A_{2{\rm{s}} \to 1{\rm{s}}}^{{\rm{SIT}}} = f_I^{\left( {\rm{R}} \right)}\left( Z \right) \times \frac{{{\varepsilon ^{\rm{2}}}}}{{{Z^{\rm{6}}}}}{\rm{ }}{{\rm{s}}^{ - 1}};$

${\rm{Model\;II}}:\;\;\;\;\;\;\;\;\;\;\;\;\; A_{2{\rm{s}} \to 1{\rm{s}}}^{{\rm{SIT}}} = f_{{\rm{II}}}^{\left( {\rm{R}} \right)}\left( Z \right) \times \frac{{{\varepsilon ^{\rm{2}}}}}{{{Z^{\rm{6}}}}}{\rm{ }}{{\rm{s}}^{ - 1}},$

其中:

$\begin{split} f_{\rm{I}}^{\left( {\rm{R}} \right)}\left( Z \right) =\; & 0.15{\rm{819}} + 0.12{\rm{364}}Z - 0.00{\rm{287}}{Z^2} + {\rm{2}}{\rm{.86138}} \times {10^{ - 4}}{Z^3} \\ & - 1.{\rm{20409}} \times {10^{ - 5}}{Z^4} + {\rm{2}}{\rm{.93685}} \times {10^{ - 7}}{Z^5} - {\rm{4}}{\rm{.48008}} \times {10^{ - 9}}{Z^6} \\ & + {\rm{4}}{\rm{.05953}} \times {10^{ - 11}}{Z^7} - 2.{\rm{00189}} \times {10^{ - 13}}{Z^8} + {\rm{4}}{\rm{.21183}} \times {10^{ - 16}}{Z^9} ,\end{split} $

$\begin{split} f_{{\rm{II}}}^{\left( {\rm{R}} \right)}\left( Z \right) =\; & 0.1{\rm{6332}} + 0.12{\rm{364}}Z - 0.00{\rm{287}}{Z^2} + {\rm{2}}{\rm{.86138}} \times {10^{ - 4}}{Z^3} \\ & - 1.{\rm{20409}} \times {10^{ - 5}}{Z^4} + {\rm{2}}{\rm{.93685}} \times {10^{ - 7}}{Z^5} - {\rm{4}}{\rm{.48008}} \times {10^{ - 9}}{Z^6} \\ & + {\rm{4}}{\rm{.05953}} \times {10^{ - 11}}{Z^7} - 2.{\rm{00189}} \times {10^{ - 13}}{Z^8} + {\rm{4}}{\rm{.21183}} \times {10^{ - 16}}{Z^9} . \end{split} $

可见, Z的低次幂和高次幂分别反映了低Z和高Z类氢离子Stark诱导跃迁几率的行为.