摘要: 相干布居振荡(coherent population oscillations, CPO)光谱是一种原子布居数调制光谱, 主要利用两束位相锁定、频率差小于原子自发辐射线宽的耦合光和探测光与原子相互作用, 激光强度调制会导致原子布居数相干振荡, 实现窄带宽的探测光透射. 本文基于Λ型原子能级结构, 在室温铯原子系综中实现了相干布居振荡光谱, 光谱典型线宽小于50 kHz, 远低于5.2 MHz的自发辐射线宽. Λ型能级结构的相干布居振荡光谱线宽依赖多个简并能级系统的布居数关联振荡, 其不要求原子态的相位关联, 有利于在长激发态寿命的Rydberg原子系统中基于相干布居振荡获得窄线宽光谱, 从而提高基于Rydberg原子光谱的精密测量的灵敏度.
关键词: 相干布居振荡 /
原子布居 /
铯原子气室 /
Rydberg原子 English Abstract Narrow-linewidth coherent population oscillation spectroscopy of room-temperature cesium atomic ensemble Liu Qiang 1 ,He Jun 1,2,3 ,Wang Jun-Min 1,2,3 1.State Key Laboratory of Quantum Optics and Quantum Optics Devices, and Institute of Opto-Electronics, Shanxi University, Taiyuan 030006, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 61875111, 11974226, 11774210), the National Basic Research Program of China (Grant No. 2017YFA0304502), and the 1331Project for Key Subject Construction of Shanxi Province, ChinaReceived Date: 03 March 2021Accepted Date: 07 April 2021Available Online: 07 June 2021Published Online: 20 August 2021Abstract: Coherent population oscillations spectroscopy, which is based on the interaction between atoms and the phase locked laser, is a kind of atomic population modulation spectroscopy. When the laser frequency difference is less than natural width of energy level, the coherent oscillation of atomic population will be induced by laser intensity modulation so that the probe laser transmission with narrow bandwidth can be realized. For a closed two-level system (TLS), the spectral line-width is limited mainly by the spontaneous emission lifetime of the upper atomic energy level. As for a three-level atomic system of Λ configuration, the two linearly polarized beams with both σ+ and σ- polarization component, the laser-atom interaction satisfies the selection rule. The spectral line-width mainly depends on the ground-state relaxation time, and the dependence on the line-width of spontaneous radiation is eliminated. In this paper, the laser from a external-cavity diode laser has its frequency locked to Cesium $6{{\rm{S}}_{1/2}}\left( {F = 3} \right) \to 6{{\rm{P}}_{3/2}}\left( {F' = 3} \right)$ transition. The frequencies of the two beams are shifted down by two independent double-passed acousto-optic modulators (AOM) to nearly resonate to Cesium $6{{\rm{S}}_{1/2}}\left( {F = 3} \right) \to 6{{\rm{P}}_{3/2}}\left( {F' = 2} \right)$ transition. The probe beam and the coupling beam are superposed at polarization beam splitter (PBS) cube and transmitted through the magnetically shielded cesium vapor cell in the same direction. The two beams have approximately the same Gaussian diameter of 6.6 mm. The beams are separated by another PBS behind the vapor cell, and the probe beam is detected by a photodiode. We realize the coherent population oscillation spectroscopy through the Cesium vapor cell at room temperature without buffer gas. The spectral linewidth is typically less than 50 kHz which is far below the spontaneous radiation linewidth(~5.2 MHz). The linewidth of coherent population oscillation spectroscopy of the Λ-type atomic energy level structure depends only on the population associated with the oscillation of multiple degenerate level systems except phase correlations of atomic states. Coherent population oscillation is beneficial to the obtaining of the narrow linewidth spectroscopy through the Rydberg atomic system with long excited state lifetime. Considering the importance of electric field measurement using Rydberg atoms, the method of coherent population oscillation can be used to improve the sensitivity of precise measurements based on Rydberg atoms.Keywords: coherent population oscillations /atomic population /cesium atomic vapor cell /Rydberg atom 全文HTML --> --> --> 1.引 言 高灵敏的光谱传感技术在基础物理研究、生物医学检测和通讯信号识别等领域都有重要的意义[1 -5 ] . 近年来, 基于量子理论的测量和传感方案, 已在光谱领域取得较大的进展. 基于量子态跃迁通道干涉的电磁感应透明光谱(electromagnetically induced transparency, EIT)可应用于光减速和光存储, 典型的存储寿命接近秒的量级[6 ,7 ] ; 基于原子相干叠加暗态的相干布居俘获光谱(coherent population trapping, CPT)广泛应用于磁场测量和时间频率标准[8 ,9 ] ; 基于原子自旋的噪声关联光谱已应用于半导体材料的自旋扩散等物理量测量[10 ] ; 基于室温Rydberg原子EIT光谱已实现高频微波强度测量和空间成像[11 -13 ] .[14 ,15 ] . 在上述技术的帮助下, 人们在室温气室中可以获得小于自发辐射线宽的光谱, 特别是铷原子的相干布居俘获光谱, 通过基态自旋弛豫时间的延长, 实验室已获得kHz的光谱线宽, 远低于激发态MHz的自发辐射线宽[16 ,17 ] . 上述抑制原子退相干的方案主要解决了原子态寿命相关的弛豫时间, 即纵向弛豫时间, 光谱分辨率依然受限于原子叠加态的相位退相干, 即横向弛豫时间. 更为重要的是, 对于广泛应用于微波测量的Rydberg原子光谱, 通常选用阶梯型的原子能级结构, 通过两步激发实现EIT, 由于级联激光波长差较大, 考虑室温原子的多普勒效应以及波长匹配等效应, 相关光谱线宽都较宽. 例如, 对于铯原子的Rydberg原子EIT光谱, 典型线宽在几十MHz, 远大于Rydberg原子kHz的自发辐射线宽[18 ,19 ] .[20 -22 ] . 通常的二能级CPO光谱可以获得接近原子自发辐射线宽的光谱; 基于两个或者多个二能级系统的相干耦合, 可以突破共用上能级自发辐射线宽的限制, 实现远小于上能态自发辐射线宽的窄线宽光谱[23 ] . CPO光谱线宽依赖简并二能级系统的布居数关联振荡, 其线宽极限主要依赖原子态自发辐射线宽, 不要求原子态的相位关联, 特别是Rydberg原子, 自发辐射寿命更长, 通过CPO方案可能获得窄线宽光谱.2.相干布居振荡光谱物理模型 铯原子能级如图1 所示, 基态为$ 6{\rm{S}}_{1/2}\left( {F}=3 \right) $ , 激发态为$6{\rm{P}}_{3/2}( F'=2 )$ , 考虑闭合二能级系统, 原子激发态和基态能级分别写为a和b, 三能级中的基态b和c可以是同一基态的Zeeman子能级, 能量差$ E_{\rm{ab}}=\hbar \omega _{\rm{ab}}$ . 耦合光频率共振ab能级, 探测光频率失谐$ \varDelta _{\rm{p}}=\omega _{\rm{ab}}-\omega _{\rm{p}}$ , $ \omega _{\rm{p}}$ 为探测光的频率, 失谐量Δ p 小于激发态自发辐射线宽γ ab . 耦合光和探测光相位锁定, 激光频率差$ \delta =\omega _{\rm{c}}-\omega _{\rm{p}}$ , $ \omega _{\rm{c}}$ 为耦合光的频率. 偏振相同条件下, 考虑探测光E 1 和耦合光E 2 的干涉效应, 总光强I 可以分解为$ I_{0}^{}$ 和$ I_{1}^{}$ 项:图 1 铯原子系综相干布居振荡光谱 (a)铯原子超精细跃迁及Zeeman能级结构; (b)二能级结构; (c)三能级结构Figure1. Schematic diagram of cesium atomic ensemble coherent population oscillations spectroscopy: (a) Hyperfine levels and Zeeman sublevels of the cesium D2 line; (b) two-level system and (c) three-level system associated with Zeeman sublevels of the ground and excited states.$ \varOmega _i$ 对应不同光强成分的Rabi频率, d 是电偶极跃迁偶极矩, $ \epsilon _0$ 是真空介电常数, c 是光速, $ \hbar $ 是约化普朗克常数. 采用文献[23 ]的方法处理光与原子的相互作用, 在偶极近似、旋波近似和绝热近似条件下, 探测光穿过原子介质后的光强为θ 是吸收色散系数, $\alpha =( \gamma _{\rm{ab}}+\gamma _{\rm{a}}+\gamma _{\rm{b}}+ \gamma _{\rm{t}}+ $ $ 2\gamma _{\rm{r}}) /2$ 是有效弛豫项, $ \gamma _{\rm{a}}$ ($ \gamma _{\rm{b}}$ )是激发态和基态的耗散项, $ \gamma _{\rm{ab}}$ 是a态到b态的自发辐射衰减项, $ \gamma _{\rm{r}}$ 是横向弛豫系数, $ \gamma _{\rm{t}}$ 是原子渡越或扩散相关的弛豫系数. 探测光强度依赖$ I_0$ 项光耦合导致的布居数差$ {\eta _0}$ 和$ I_1$ 项光耦合导致的布居数差$ {\eta _1}$ :$ \gamma _{\rm{ab}}$ , 饱和泵浦效应导致a, b能级布居数差接近零. 考虑较弱的耦合光和探测光条件, 整理(5b )式, 考虑一阶项布居数差对探测光的影响:$ \gamma _{\rm{a}}=\gamma _{\rm{b}}=\gamma =0$ , 原子能级为闭合二能级系统, 布居数差依赖(6 )式的$ 2\gamma _{\rm{ab}}$ 参数, 由(4 )式给出探测光透射光谱线宽为$ 2\gamma _{\rm{ab}}$ . 如果$\gamma _{\rm{a}}=\gamma _{\rm{b}}= $ $ \gamma \ne 0$ , 此时原子能级存在耗散, 不再是闭合二能级系统, 布居数差依赖(6 )式第一项, 给出探测光的透射光谱线宽为 $ 2\left( \gamma _{\rm{ab}}+\gamma \right) $ , 如图2(a) 所示. 当$ \gamma _{\rm{a}}>\gamma _{\rm{b}}$ , 激发态耗散项大于基态耗散项, (6 )式第二项给出Lorentz线型, 线宽依赖$ \gamma _{\rm{b}}$ , CPO光谱同时存在$ 2\left( \gamma _{\rm{ab}}+\gamma _{\rm{a}} \right) $ 和$ 2\gamma _{\rm{b}}$ 线型. 由于激发态的泄露, 原子需要更长时间返回基态, 相应的弛豫时间增加; 同时, 基态原子由于运动会进出光与原子相互作用区域. 因此, 接近共振处, 表现为透射背景下依赖基态弛豫线宽的窄透射线型. 如果$ \gamma _{\rm{a}}<\gamma _{\rm{b}}$ , 探测光透射光谱表现为较宽透射背景下的窄带宽吸收线型.图 2 (a)理论计算二能级模型与(b)三能级模型的透射线型Figure2. Calculated transmission lines of (a) the two-level model and (b) the three-level model.$ \eta _0$ , $ \eta _{{\rm{ba}}1}^{}$ , $ \eta _{{\rm{ca}}1}^{}$ 为相应能级的布居数差:γ 为原子能级耗散项, $\varGamma _0$ 为相应跃迁通道的自发辐射系数, 考虑b, c能级都为近简并的Zeeman态, $ \varGamma _0=\gamma _{\rm{ab}}=\gamma _{\rm{ac}}$ .$ \sigma ^+-\sigma ^+$ 和$ \sigma ^--\sigma ^-$ 跃迁的两套CPO系统. (8 )式所示的探测光强度I , 零阶光强不包含相位因子, 其相关的原子能态布居数差在稳态条件不随时间变化. 对于一阶项, 光强与布居数差都包含相位因子. 当耦合光和探测光偏振相同, 两臂Rabi振荡相位相同, (10b )式和(10c )式第二项为0, 相应的线宽因子是$ 2\left( \varGamma _0+\gamma \right) $ . 当耦合光和探测光偏振垂直, 共振条件下, ac跃迁通道中, E 1 分量相对于E 2 分量有π/2相位差; ab跃迁通道中, E 1 分量相对于E 2 分量有–π/2相位差. ac通道干涉相消, ab通道干涉增强, 共同作用下通过光泵浦实现原子由b态到c态的布居, 上述过程消除上能级自发辐射线宽$ \varGamma _{\rm{a}}$ 的依赖, 与b态对应的探测光吸收减弱, 透射线宽依赖于基态相干寿命, 如图2(b) 所示. 总的CPO效应, 光谱线宽主要依赖于原子基态弛豫时间, 典型线宽因子是2γ b . 对于简并的多能级系统, 上述CPO效应和EIT效应同时存在, 共振时EIT和CPO重合.3.实验过程和结果 实验选择铯原子超精细跃迁$6{\rm{S}}_{1/2}\left( F=3 \right) \rightarrow $ $ 6{\rm{P}}_{3/2}\left( F'=2 \right)$ 简并能级, 如图1(a) 所示. 耦合光和探测光由同一台激光器(Moglabs Cat-eye External Cavity Diode Laser: Model CEL002)提供, 典型输出功率100 mW, 线宽约百kHz. 输出激光一小部分用于搭建饱和吸收光谱, 目的是用来锁定激光频率于铯原子$ 6{\rm{S}}_{1/2}\left( F=3 \right) \rightarrow 6{\rm{P}}_{3/2} $ $ \left( F'=3 \right) $ 跃迁线. 输出激光另一部分经过$ \lambda /2$ 波片和偏振分束棱镜(PBS)分束, 较强的作为耦合光, 较弱的作为探测光. 典型耦合光功率为1 μW—10 mW, 探测光功率为0.1 μW—1 mW. 两束光分别利用声光调制器双次频移约–151 MHz, 频移后激光近共振于$6{\rm{S}}_{1/2}\left( F=3 \right) \rightarrow 6{\rm{P}}_{3/2} $ $ \left( F'=2 \right)$ 跃迁线. 频移后的泵浦光和探测光由PBS合束, 经望远镜系统扩束为高斯直径6.6 mm的光束, 光束穿过铯原子气室后由PBS分离, 探测光进入探测器(New Focus: Model 2051)进行光谱测量.图3 中铯原子气室前的$ \lambda /4$ 波片是为了将入射光变为圆偏振光, 铯原子气室后的$ \lambda /4$ 波片将耦合光与探测光分离. 实验所用铯原子气室长度约为10 cm, 室温下铯原子充气压强约$\sim 10^{-6} $ Torr (1 Torr ≈ 133.32 Pa), 原子热运动导致的多普勒展宽约$ \sim 400\;{\rm{MHz}}$ . 由于地磁等杂散磁场会使能级退简并, 导致CPO与EIT光谱同时存在, 不利于得到真实的CPO光谱的线宽, 所以原子气室放置在磁屏蔽桶中, 桶内剩余磁场约3 nT, 磁屏蔽桶内的线圈可以给原子提供z 方向磁场.图 3 铯原子系综相干布居振荡光谱测量的实验装置示意图. PBS, 偏振分束棱镜; AOM, 声光调制器; PD, 光电二极管Figure3. Schematic diagram of experimental setup for measuring cesium atomic ensemble coherent population oscillations spectrum. PBS, polarizing beam splitter; AOM, acousto-optic modulator; PD, photodiode.3.1.CPO光谱 3.1.CPO光谱 图4 为实验测得的典型CPO信号. 耦合光束和探测光束的高斯直径都是~6.6 mm. 耦合光功率150 μW, 探测光功率13 μW. 实验中, 耦合光频率共振于$ 6{\rm{S}}_{1/2}( F \!=\! 3 ) \rightarrow 6{\rm{P}}_{3/2}(F' \!=\! 2 ) $ 跃迁线, 探测光频率进行连续扫描, 获得典型光谱线宽49.3 kHz, 小于原子$ 6{\rm{P}}_{3/2}\left( F'=2 \right) $ 态自发辐射线宽5.2 MHz.图 4 典型的铯原子相干布居振荡光谱, 虚线为Lorentz拟合Figure4. Coherent population oscillations spectrum of cesium atoms.$ \lambda /2$ 波片和一个PBS后通过两个独立的声光调制器使其频率减小至近共振于$ 6{\rm{S}}_{1/2}\left( F=3 \right) \rightarrow 6{\rm{P}}_{3/2}\left( F'=2 \right) $ 跃迁, 这使我们能够独立地控制每个光束的振幅和频率. 为了避免频率扫描时光束的指向不稳定, 两路光都采用双次穿过声光调制器的方案. 为了最大程度地避免拍频产生, 两路光的偏振必须严格正交或两路光以一个小的夹角入射铯原子气室, 保证实验结果的可靠性.$ 6{\rm{S}}_{1/2}\left( F=3 \right) \rightarrow 6{\rm{P}}_{3/2}\left( F'=2 \right) $ 跃迁, 耦合光和探测光都是线偏振光, 二者偏振垂直, 可以独立分解为左、右旋圆偏振光. 近共振条件下, 考虑$ \varDelta m=+1$ 跃迁, 探测光$ \sigma ^+$ 分量相对于耦合光$ \sigma ^-$ 分量有π/2相位差; $ \varDelta m=-1$ 跃迁中, 探测光$ \sigma ^+$ 分量相对于耦合光$ \sigma ^-$ 分量有–π/2相位差. $ \varDelta m=\pm 1$ 跃迁中, 激光耦合原子的布居数反相位振荡, 共同作用下通过光泵浦实现基态原子的布居数泵浦, 消除上能级自发辐射线宽$ \varGamma _{a}$ 的依赖, 光谱线宽主要依赖基态相干时间.3.2.CPO和EIT光谱的磁场调谐 -->3.2.CPO和EIT光谱的磁场调谐 CPO光谱通过耦合光和探测光的光抽运过程实现原子布居数的调制, 考虑图5 所示的原子能级, 光谱依赖Zeeman态跃迁系数以及偏振相关的光泵浦. 考虑非简并Λ能级系统, 耦合光和探测光的传播方向、量子化轴磁场都沿z 方向. 有磁场时, 原子基态和激发态的Zeeman频移为$ \varDelta _F=g_F\mu _{\rm{B}}B$ 和$ \varDelta _{F'}=g_{F'}\mu _{\rm{B}}B$ , 其中, $ {\,\mu _{\rm{B}}}$ 为玻尔磁子, $g_{(F=3)}= $ $ -1/4$ 和$g_{(F'=2)}=-2/3$ 为基态和激发态的朗德g 因子, 基态和激发态有效Zeeman频移量为$\delta =\pm 2\times $ $ \left( \varDelta _{F^{'}}-\varDelta _F \right)$ . 探测光和耦合光都为线偏振, 偏振方向分别平行x 和y 方向. 在z 方向磁场中, 两束光偏振可以分解为$ {\sigma ^ + }$ 和$ {\sigma ^ - }$ 的偏振, 对于$ 6{\rm{S}}_{1/2}( F= $ $ 3) \rightarrow 6{\rm{P}}_{3/2}\left( F'=2 \right) $ 的能级系统, 原子激发满足$ \varDelta m_F=\pm 1$ 的选择定则, 分别形成$ {\sigma ^ + }$ 和$ {\sigma ^ - }$ 偏振的跃迁系统. 实验结果如图6(a) 所示, 磁场等于零时, δ = 0处为简并CPO透射谱, 磁场分别为14, 28和43 μT时, 光谱的频移分别为151 ± 9, 312 ± 11和460 ± 25 kHz, 给出与Zeeman子能级相关的EIT光谱.图 5 不同磁场方向, 光场k 方向, 不同原子能级构型的光偏振组合 (a) $ \sigma ^+-\sigma ^+$ 构型; (b) $ \sigma ^+-\sigma ^-$ 构型; (c) $ \pi -\pi $ 构型Figure5. Energy-level scheme for the interaction of the cesium D2 line with different laser polarization and magnetic fields: (a) $ \sigma ^+-\sigma ^+$ ; (b) $ \sigma ^+-\sigma ^-$ ; (c) $ \pi -\pi $ .图 6 探测光不同偏振状态时磁场环境中的CPO和EIT光谱 (a)线偏振光, (151 ± 9) kHz (红线), (312 ± 11) kHz (蓝线), (460 ± 25) kHz (绿线); (b)$ {\sigma ^ + }$ 圆偏振光, (153 ± 9) kHz (黑线), (314 ± 11) kHz (红线), (475 ± 25) kHz (蓝线); (c)$ {\sigma ^ - }$ 圆偏振光, (–155 ± 7) kHz (黑线), (–309 ± 15) kHz (红线), (–474 ± 22) kHz (蓝线)Figure6. Coherent population oscillations spectrum in magnetic field with different polarzaiton of probe beam: (a) linear polarization, (151 ± 9) kHz (red), (312 ± 11) kHz (blue), (460 ± 25) kHz (green); (b) $ {\sigma ^ + }$ circular polarization, (153 ± 9) kHz (black), (314 ± 11) kHz (red), (475 ± 25) kHz (blue); (c)$ {\sigma ^ - }$ circular polarization, (–155 ± 7) kHz (black), (–309 ± 15) kHz (red), (–474 ± 22) kHz (blue).$ \lambda /4$ 波片将入射的线偏光变为圆偏光, 探测器前再次利用$ \lambda /4$ 分离耦合光和探测光. 考虑$ \sigma ^+-\sigma ^+$ 和$ \sigma ^--\sigma ^-$ 耦合光和探测光偏振组合, 实验中弱磁场条件下, 观测到单个的EIT透射峰, 且透射峰的位置随磁场移动, 图6(b) 中磁场分别为14, 28和43 μT时, 光谱的频移分别为(153 ± 9), (314 ± 11) 和(475 ± 25) kHz, 图6(c) 中磁场分别为14, 28和43 μT时, 光谱的频移分别为(–155 ± 7), (–309 ± 15) 和(–474 ± 22) kHz.3.3.CPO信号与相关参数的依赖关系 -->3.3.CPO信号与相关参数的依赖关系 CPO是一种布居数调制光谱, 信号的强度依赖于耦合光和探测光强度, 线宽主要依赖于基态能级弛豫系数. 图7 给出了CPO光谱线宽与幅度分别随探测光功率和耦合光功率的变化, 可以看出, 其他条件相同, 探测光功率由10 μW增大至100 μW, CPO信号幅度随之增大; 耦合光功率由30 μW增大至250 μW, CPO信号的幅度增大, 但半高全宽变化不明显; 当探测光增加时, 光谱的线宽也相应展宽, 其主要来源是功率展宽; 实验中耦合光和探测光共同作用使原子的布居数振荡, 当原子布居数的振荡频率小于弛豫速率, 原子布居数形成时间上的光栅效应, 耦合光通过衍射补偿对探测光的吸收, 这两个过程的共同作用达到探测光在吸收背景下的窄带宽透射. 所以耦合光影响原子的布居数调制, 不影响光谱线宽. 光谱的线宽存在探测光的功率展宽、渡越展宽等.图 7 不同功率下铯原子相干布居振荡光谱的幅度与线宽Figure7. Amplitude and linewidth of coherent population oscillations spectroscopy of cesium atoms with different power.4.结论和展望 利用室温铯原子气室, 研究了相干布居振荡光谱. 实验中, 将相干布居振荡光谱的线宽和幅度对探测光和耦合光光强、激光频率等参数的依赖关系做了定量研究. 在室温铯原子气室获得约50 kHz的CPO光谱, 远低于原子上能级自发辐射线宽. 对于简并能级的铯原子系统, 通过偏振正交的耦合光和探测光实现了简并CPO系统的布居数调制, 获得探测光谱的干涉增强或者干涉相消. 该实验可扩展至Rydberg原子应用于精密测量, 提高电场测量的灵敏度, 为高信噪比、高灵敏度的电磁场测量与通信提供了可能的方向. 








 图 1 铯原子系综相干布居振荡光谱 (a)铯原子超精细跃迁及Zeeman能级结构; (b)二能级结构; (c)三能级结构
图 1 铯原子系综相干布居振荡光谱 (a)铯原子超精细跃迁及Zeeman能级结构; (b)二能级结构; (c)三能级结构



























 图 2 (a)理论计算二能级模型与(b)三能级模型的透射线型
图 2 (a)理论计算二能级模型与(b)三能级模型的透射线型





















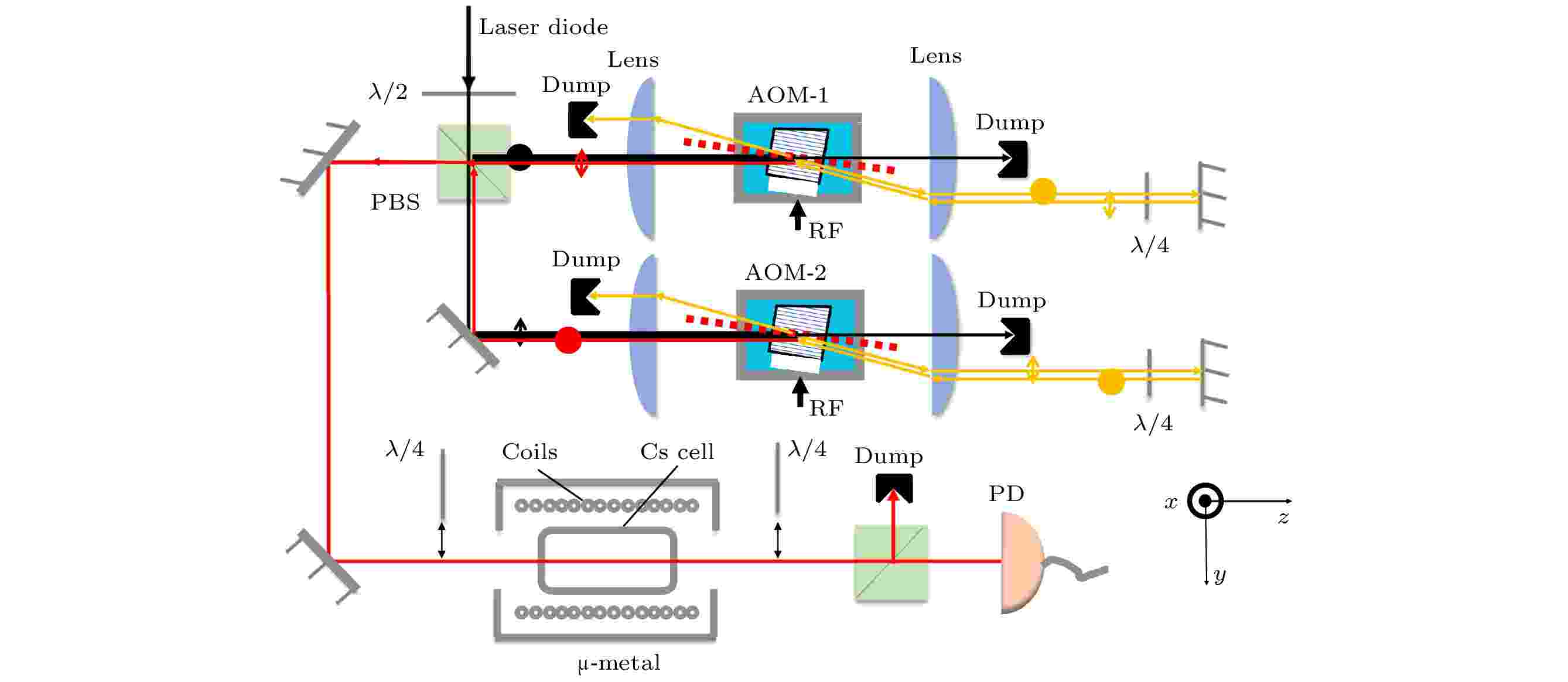 图 3 铯原子系综相干布居振荡光谱测量的实验装置示意图. PBS, 偏振分束棱镜; AOM, 声光调制器; PD, 光电二极管
图 3 铯原子系综相干布居振荡光谱测量的实验装置示意图. PBS, 偏振分束棱镜; AOM, 声光调制器; PD, 光电二极管

 图 4 典型的铯原子相干布居振荡光谱, 虚线为Lorentz拟合
图 4 典型的铯原子相干布居振荡光谱, 虚线为Lorentz拟合

































 图 5 不同磁场方向, 光场k方向, 不同原子能级构型的光偏振组合 (a)
图 5 不同磁场方向, 光场k方向, 不同原子能级构型的光偏振组合 (a) 





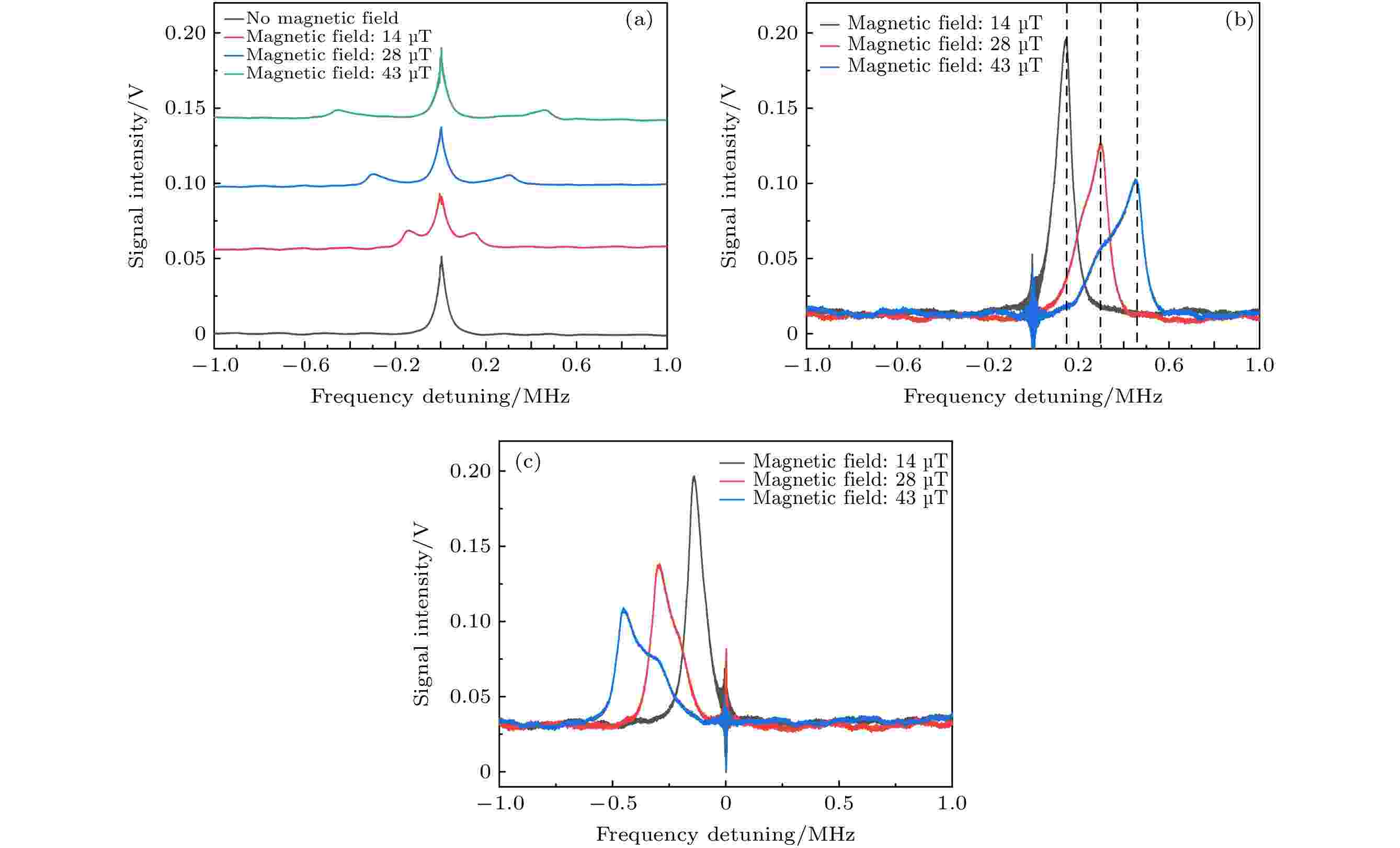 图 6 探测光不同偏振状态时磁场环境中的CPO和EIT光谱 (a)线偏振光, (151 ± 9) kHz (红线), (312 ± 11) kHz (蓝线), (460 ± 25) kHz (绿线); (b)
图 6 探测光不同偏振状态时磁场环境中的CPO和EIT光谱 (a)线偏振光, (151 ± 9) kHz (红线), (312 ± 11) kHz (蓝线), (460 ± 25) kHz (绿线); (b)









 图 7 不同功率下铯原子相干布居振荡光谱的幅度与线宽
图 7 不同功率下铯原子相干布居振荡光谱的幅度与线宽

