摘要:基于第一性原理的密度泛函理论计算了B在fcc-Fe的Σ3(112), Σ5(210), Σ5(310), Σ9(114), Σ9(221)和Σ11(113)六种对称倾斜晶界的偏析行为, 从原子和电子层次揭示了B的偏析机制. 结果表明: B更易偏析于Σ5(210), Σ5(310)和Σ9(114)晶界, 而在Σ9(221), Σ3(112) 和Σ11(113)晶界偏析的倾向较弱; B优先占据配位数最大、五面体或六面体构型的位置; 拉伸实验和Rice-Wang热力学模型计算表明, B在晶界的偏析可提高界面的结合能力; B在Σ9(114)晶界偏析后电子结构引起局部电荷密度增加导致的化学效应优于结构变化带来的不利影响, B-p电子与Fe-s电子间的强相互作用提高了界面的结合能力. 本研究结果对B优化奥氏体不锈钢界面结构具有一定指导作用.
关键词: 奥氏体钢/
硼/
第一性原理/
偏析/
界面结合能力

English Abstract

全文HTML

--> --> -->

B作为一种微合金化元素, 被称为钢中的维生素, 广泛应用于低合金高强钢、不锈钢和镍基合金等, 常被用来提高钢的淬透性^[1-3]、增强中子吸收能力^[4]、强化晶界、改善热塑性^[5-8]等. B在钢中溶解度极低, 故添加量很少, 其有益的作用归因于B在奥氏体晶界的偏析, 如Takahashi等^[9]利用原子探针层析成像技术(APT)分析了不同热处理状态下含Mo、B低碳钢中B在奥氏体晶界的偏析行为, 发现钢的淬透性主要由奥氏体晶界的B偏析总量决定. Li等^[10]利用APT分析认为低碳合金钢中奥氏体晶界B的偏析与空位相关联. 虽然APT技术具有很高的灵敏度、分辨率, 但过量添加B会形成硼化物, 导致B失效, 实际使用钢中由于硼含量很低, 且其分布区域极窄(小于1 nm), 往往难以检测到钢中B的晶界偏析量, 更难以解析偏析B所处的晶界结构类型. 第一性原理的密度泛函理论(DFT)为从原子层次解析元素在材料中存在方式、作用机制提供了便利. 近年来, 研究者们利用第一性原理对原子在Cu基^[11-15]、Fe基^[16,17]、Ni基^[18,19]等合金界面的偏析行为进行了研究, 如B, C, S和P等元素易在fcc-FeΣ5(210)晶界间隙偏析, S, P和C会降低界面的结合能力, 而B元素则可提高界面结合能力^[20]; Nb和V原子在bcc-FeΣ3(111)晶界处偏析所引起的化学和力学效应可改善钢的韧性^[21]; Cr可抑制H原子向fcc-FeΣ3(111)晶界的偏聚^[22]; B易偏析于fcc-FeΣ5(210)晶界, 并不同程度抑制Cr, Ni, Mn, Co和Mo元素在晶界的偏析^[23]. 利用Rice-Wang热力学模型^[24]可分析合金元素对界面结合能力的影响^{[14,17,25-27]}. 如, C在bcc-FeΣ3(112), Σ5(210), Σ5(310)晶界的偏析倾向是不同的, 均增强了界面的内聚力^[17]; 氢原子易偏析于W的Σ5(310)晶界, 却使界面结合减弱^[27].
总体看B在奥氏体不锈钢中主要分布于晶界, 通常多晶材料的力学性能、耐蚀性与晶界结构密切相关, 晶界是热力学不稳定的结构缺陷, 合金元素的添加是改变晶界局部结构、化学性质的有效方法之一, 处于晶界的B对于晶界临近区域的原子结构有很大的影响, 很有必要对B在不同晶界结构中的偏析行为及对界面特性的影响进行系统分析. 奥氏体不锈钢中, 具有低界面能Σ(Σ ≤ 29)的重合位置点阵具有较高稳定性, 尤以晶界占比最大的孪晶界面Σ3, Σ9具有更高的耐蚀性, 此外低能的Σ5, Σ11晶界尽管占比小, 也是不锈钢中常见的晶界结构^[28,29]. 因此研究B在这些晶界的占位及偏析倾向, 对于充分发挥B在奥氏体不锈钢中的作用至关重要. 本文结合奥氏体不锈钢中已有晶界研究成果, 构建出Σ3, Σ5, Σ9, Σ11等fcc-Fe对称倾斜晶界结构, 研究B原子在这些晶界的占位、偏析倾向及对fcc-Fe界面结合能力的影响, 以期为含B奥氏体不锈钢的成分优化设计提供理论指导.

2

-->

2.1.计算方法

计算采用基于DFT的Vienna Ab-initio Simulation Package (VASP)软件包^[30], 其中交换关联能采用广义梯度近似(GGA)^[31], 并结合缀加投影平面波(PAW)方法^[30], 平面波截断能为400 eV. 布里渊区则采用Monkhorst-Pack型K点网格进行划分, 具体的K点设置列于表1. 为验证参数设置的合理性, 先计算fcc-Fe的晶格常数, 结构优化后的晶格常数为3.43674 ?, 与其他计算结果相近^[23,32,33]. 本文选取fcc-Fe非磁性的奥氏体为模型, 故计算晶格常数与实验值3.648 ?存在一定偏差^[34]. fcc-Fe晶界结构的过剩体积(ΔV)反映界面原子体积相对于晶粒内部原子体积的增加量, 用于判定缺陷、元素偏析于晶界的程度, 根据文献[35], $\Delta V=\dfrac{{V}_{\mathrm{G}\mathrm{B}}-{n}_{\mathrm{G}\mathrm{B}}{V}_{\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}/\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{m}}}{S}$, 其中, V_GB是晶界超胞弛豫后的总体积, n_GB是晶界超胞中的原子数, V_bulk/atom是fcc-Fe块体结构中每个原子的体积, S是超胞结构对应的横截面积. 优化后结构模型用于体系晶界能、溶解能、偏析能、强化能等分析, 结构弛豫采用共轭梯度法, 固定晶胞体积和形状, 但完全放开所有原子位置. 能量收敛标准为1.0 × 10^–5 eV, 力收敛标准为每个原子的剩余力小于0.01 eV/?, 具体计算方法如下.

Grain boundaries	γGB/(J·m–2)	ΔV/(?3·?–2)	Angle/(°)	Numbers of atomes	Supercell dimensions/(? × ? × ?)	S/?2
∑3(112)[110]	0.341	0.207	109.47	48	4.86 × 5.955 × 17.037	28.94
∑5(210)[001]	1.661	0.762	53.13	76	6.873 × 7.685 × 15.37	52.82
∑5(310)[001]	1.925	0.543	36.87	78	5.434 × 6.873 × 21.736	37.35
∑9(114)[110]	1.546	0.771	141.06	68	4.86 × 10.31 × 14.58	52.54
∑9(221)[110]	1.716	1.143	38.94	68	4.86 × 7.29 × 20.62	35.43
∑11(113)[110]	0.559	0.499	129.52	88	4.86 × 8.06 × 23.296	39.17

表1fcc-Fe的CSL晶界的结构特性
Table1.Structural characteristics of calculated grain boundaries

晶界能为^[36]

${\gamma }_{\mathrm{G}\mathrm{B}}=\frac{{E}_{\mathrm{G}\mathrm{B}}^{\mathrm{F}\mathrm{e}}-{E}_{\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}/\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{m}}^{\mathrm{F}\mathrm{e}}\times {n}_{\mathrm{G}\mathrm{B}}}{2S}, $

式中, $ {E}_{\mathrm{G}\mathrm{B}}^{\mathrm{F}\mathrm{e}} $是晶界超胞经弛豫后的总能量, $ {E}_{\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}/\mathrm{a}\mathrm{t}\mathrm{o}\mathrm{m}}^{\mathrm{F}\mathrm{e}} $是fcc-Fe块体结构中每个原子的体能量.
溶解能为^[37]

${E}_{\mathrm{B}}^{\mathrm{s}\mathrm{o}\mathrm{l}}={E}_{\mathrm{G}\mathrm{B}}^{\mathrm{F}\mathrm{e}+\mathrm{B}}-{E}_{\mathrm{G}\mathrm{B}}^{\mathrm{F}\mathrm{e}}-{E}^{\mathrm{B}},$

式中, $ {E}_{\mathrm{G}\mathrm{B}}^{\mathrm{F}\mathrm{e}+\mathrm{B}} $为含B晶界超胞的总能量, $ {E}_{\mathrm{G}\mathrm{B}}^{\mathrm{F}\mathrm{e}} $为不含B晶界超胞的总能量, E^B为真空(10 ? × 10 ? × 10 ?立方晶格)中B原子的能量. 溶解能为负值且越小, 表明B原子越容易处于对应位点.
偏析能为^[38]

$E_{{\rm{seg}}}^{\rm{B}} = \left( {E_{{\rm{GB}}}^{{\rm{Fe}} + {\rm{B}}} - E_{{\rm{GB}}}^{{\rm{Fe}}}} \right) - \left( {E_{{\rm{bulk}}}^{{\rm{Fe}} + {\rm{B}}} - E_{{\rm{bulk}}}^{{\rm{Fe}}}} \right),$

式中, $ {E}_{\mathrm{G}\mathrm{B}/\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}}^{\mathrm{F}\mathrm{e}+\mathrm{B}} $是含B原子的晶界/块体结构的总能量, $ {E}_{\mathrm{G}\mathrm{B}/\mathrm{b}\mathrm{u}\mathrm{l}\mathrm{k}}^{\mathrm{F}\mathrm{e}} $是不含B的晶界/块体结构的总能量. 溶质负的偏析能会引起晶界能量的降低.
间隙原子与表面和晶界化学作用的强弱可由其相应束缚能表示, 计算方法如下:

$\Delta {E_{{\rm{GB}}}} = E_{{\rm{GB}}}^{{\rm{Fe}} + {\rm{B}}} - E_{{\rm{GB}}}^{{\rm{Fe}}} - {E^{{\rm{Fe}}}},$

$\Delta {E_{{\rm{FS}}}} = E_{{\rm{FS}}}^{{\rm{Fe}} + {\rm{B}}} - E_{{\rm{FS}}}^{{\rm{Fe}}} - {E^{{\rm{Fe}}}},$

式中, $ {E}_{\mathrm{F}\mathrm{S}}^{\mathrm{F}\mathrm{e}+\mathrm{B}} $和$ {E}_{\mathrm{F}\mathrm{S}}^{\mathrm{F}\mathrm{e}} $分别表示含B和不含B体系自由表面的总能量, $ {E}^{\mathrm{F}\mathrm{e}} $为真空(10 ? × 10 ? × 10 ?立方晶格)中Fe原子的能量. 自由表面模型中B原子位置的选择与晶界结构模型相同.
基于Rice-Wang理论, 由$ \Delta {E_{{\rm{GB}}}} - \Delta {E_{{\rm{FS}}}} $可得到强化能E_str, 用于分析B原子对界面结合强度的影响^[24,39]:

${E}_{\mathrm{s}\mathrm{t}\mathrm{r}}=\left({E}_{\mathrm{G}\mathrm{B}}^{\mathrm{F}\mathrm{e}+\mathrm{B}}-{E}_{\mathrm{G}\mathrm{B}}^{\mathrm{F}\mathrm{e}}\right)-\left({E}_{\mathrm{F}\mathrm{S}}^{\mathrm{F}\mathrm{e}+\mathrm{B}}-{E}_{\mathrm{F}\mathrm{S}}^{\mathrm{F}\mathrm{e}}\right).$

强化能负值代表B原子可提高界面强度.
为研究B原子对界面影响, 理论拉伸曲线先设定1个断裂平面, 并在该平面上引入预裂纹^[39-42], 对各种晶界的超胞进行单轴拉伸, 将超胞沿与晶界面平行的断裂平面分成2个晶块, 并将上下晶块沿z轴方向刚性隔开. 基于Rose^[43]关于金属材料界面断裂普遍存在的分离能与断裂距离($ {E}_{\mathrm{s}\mathrm{e}\mathrm{g}}^{x} - x $)关系理论, 拟合$ {E}_{\mathrm{s}\mathrm{e}\mathrm{g}}^{x} - x $关系曲线, 做$ {E}_{\mathrm{s}\mathrm{e}\mathrm{g}}^{x} $关于断裂距离x的一阶导数, 得到拉伸应力σ随断裂距离x的变化关系.
2 -->

2.2.晶界结构模型

重合位置点阵模型(CSL)晶界的原子排列有序度用重合阵点数占原阵点数比重的倒数Σ表示^[44-46], Σ值越小, 该CSL晶界中原子排列的有序度越高. 低Σ的CSL晶界的界面能较低. 基于弛豫后的fcc-Fe单胞构建出Σ3等六种晶界结构, 自由表面的计算使用与晶界模型相同大小的晶胞. 以Σ9(114) [110]对称倾转晶界模型为例加以说明, 是(114)面以[110]晶向为旋转轴, 将两部分晶体旋转141.06°所构成(见表1). 2个晶体的叠加导致2个晶格的子晶格的位置重合, 距离太近的位点将被合并^[47]. 其他晶界结构特性见表1.
图1为构建的Σ3(112), Σ5(210), Σ5(310), Σ9(114), Σ9(221)和Σ11(113)六种晶界及其多面体间隙的结构模型, 图中标出了B在晶界处可能的偏析位置. 间隙位依据结构区分为四大类型, 分别填充蓝、黄、绿、红色, 代表四面体、五面体、六面体和八面体, 五面体又分为两种, 图1(a)—(f)中的数字1—5分别对应不同类型的间隙位. 如Σ3(112)晶界的3个间隙位见图1(a), 均为五面体间隙, 其中1号间隙位对应图1(g)五面体的第一种结构, 2, 3号对应图1(g)五面体的第二种结构. 从图1(b)可看出, Σ5(210)晶界有5个间隙位, 其中1号间隙位是图1(g)五面体的第一种结构, 2, 3号是图1(g)五面体的第二种结构, 4, 5号是八面体间隙. 图1(c)—(f)以此类推. 图1(g)是六种晶界所涉及的四面体、五面体、六面体和八面体间隙位对应的结构模型.
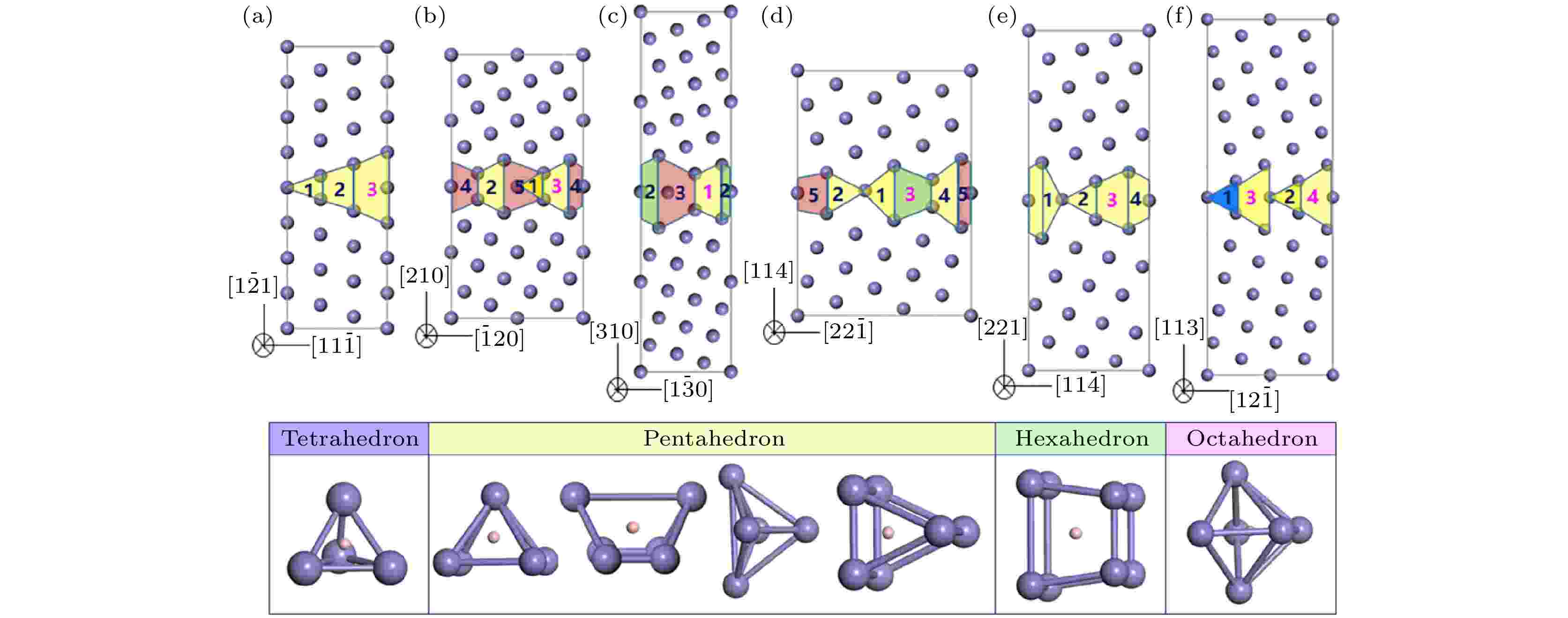图 1 fcc-Fe的　(a) Σ3(112), (b) Σ5(210), (c) Σ5(310), (d) Σ9(114), (e) Σ9(221), (f) Σ11(113)晶界和(g) B所处间隙位的模型图
Figure1. Schematic illustration showing (a) Σ3(112), (b) Σ5(210), (c) Σ5(310), (d) Σ9(114), (e) Σ9(221), (f) Σ11(113) grain boundaries and (g) polyhedron interstices where B located.

表1获得了六种晶界的晶界能γ_GB、过剩体积ΔV和相关的结构参数. 可看出Σ3(112)晶界的晶界能最低, 为0.341 J/m², 过剩体积最小, 为0.207 ?³/?², 说明该晶界的结构最紧凑、稳定. 其次是Σ11(113)晶界, 晶界能和过剩体积比Σ3(112)的值略大. Σ5(210)和Σ9(114)晶界的晶界能和过剩体积相近, 说明其紧凑性相近. 而Σ9(221)晶界有相对较大的晶界能和过剩体积, 具有最开放的晶界结构. Σ5(310)晶界虽具有较小的过剩体积, 但其晶界能最大.

2

-->

3.1.B在晶界的偏析倾向

图2为B原子在六种晶界不同间隙位的溶解能$ {E}_{\mathrm{B}}^{\mathrm{s}\mathrm{o}\mathrm{l}} $, 可以看出B原子在Σ3(112)晶界3种间隙位的溶解能差异较大, 在2, 3号间隙位溶解能为负值, 分别是–1.14和–6.63 eV, 即B原子在3号间隙位要比2号更为稳定. B原子在Σ5(210)晶界最佳的稳定间隙位是3号位, 次稳定偏析位置是2号位; B原子在Σ5(310)晶界最佳的稳定析出间隙位是1号位. 结合表1, Σ9(114)与Σ5(210)晶界有相近的晶界能和过剩体积, 它们对应的B原子的稳定存在间隙位的数量和溶解能数值很相近, 溶解能均为较小的负值. B原子在Σ9(114)晶界最佳的稳定析出间隙位是3号位, 溶解能为–8.02 eV. 对于Σ9(221)晶界, B原子只有1个间隙位的溶解能为负值, 即3号位, 溶解能为–7.32 eV. B原子在Σ11(113)晶界2—4号间隙位的溶解能均为负值, 其中3, 4号位的溶解能最小, 均为–6.27 eV, 所以B原子在Σ11(113)晶界有2个稳定析出间隙位. 后边所做的讨论, 均是针对B原子在这6个晶界的稳定析出间隙位(图1(a)—(f)晶界模型中以红色标注)进行的. 结合表1对比, B原子在各晶界溶解能的大小与晶界处可能的间隙位多面体的体积没有明显的相关性, 这与已有杂质偏析的研究结果类似^{[16,17,48,49]}.
图 2 B在6个晶界中不同间隙位置的溶解能
Figure2. The solution energies for B at different interstitial sites in the six studied grain boundaries.

由上述B在6个晶界的稳定间隙位, 分析其偏析能$ {E}_{\mathrm{s}\mathrm{e}\mathrm{g}}^{\mathrm{B}} $. 图3为B原子在6个晶界对应的偏析能, B原子在Σ5(210)、Σ5(310)和Σ9(114)晶界最佳的稳定偏析位的偏析能显著低于其在Σ3(112)、Σ9(221)和Σ11(113)晶界的偏析能, 表明这3个晶界捕获B原子的能力更强, 明显优于Σ3(112)等3个晶界. B原子在其他3个晶界偏析能分别为: Σ9(221)(–3.86 eV) < Σ3(112)(–3.17 eV) < Σ11(113)(–2.81 eV). 结合表1来看, 由于Σ3(112)和Σ11(113)晶界的晶界能和过剩体积都较小, 结构更紧凑, 所以奥氏体钢中晶界占比最大的Σ3(112)晶界相比于Σ5(210)、Σ5(310)和Σ9(114), 捕获B原子的能力较弱.
图 3 B原子在6个晶界中最稳定的偏析位点上的偏析能
Figure3. The segregation energies for B at the most stable segregation sites of the six studied grain boundaries.

图4给出了B原子在6个晶界相对稳定的偏析位的强化能$ {E}_{\mathrm{s}\mathrm{t}\mathrm{r}} $. 由于B原子在Σ5(210), Σ9(114)和Σ11(113)晶界有2个相对稳定的析出位, 所以本部分对B原子在Σ5(210)等3个晶界的2个稳定析出位均计算了强化能, 见图4. 可以看出, B原子在Σ5(210)、Σ9(114)和Σ11(113)晶界2个相对稳定析出位的强化能的数值接近. B原子在6个晶界稳定偏析位的强化能均为负值, 说明B原子处于这些析出位时都能增强晶界的内聚能力、强化晶界, 这与目前已知的实验结果一致^[50]. 对比发现, B原子在Σ9(114)晶界的强化能最低, 说明B原子对Σ9(114)晶界的强化程度最强, 对Σ9(221)晶界的强化效果次之, 强化程度依次为: Σ9(114) > Σ9(221) > Σ3(112) > Σ5(210) > Σ5(310) > Σ11(113). 结合图3, 对于奥氏体钢, B原子增强了易偏析Σ5(210), Σ5(310)和Σ9(114)晶界的结合能力, 同时也可改善晶界占比最大的Σ3(112)晶界的结合能力, 该结果为B原子偏析于奥氏体不锈钢晶界对界面结合能力的研究提供了理论依据.
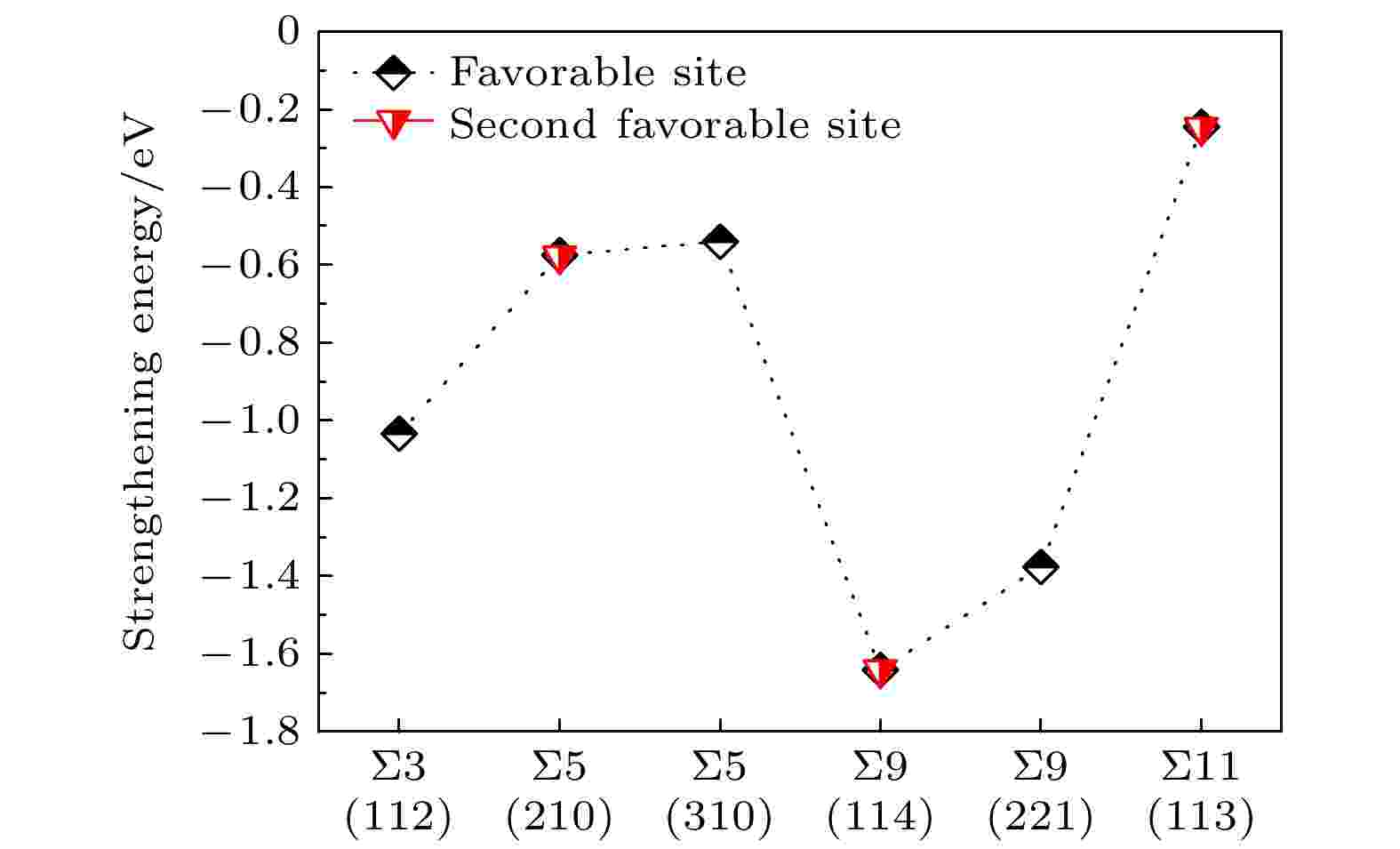图 4 B原子在6个晶界稳定偏析位的强化能
Figure4. The strengthening energies for B at the stable segregation sites of the six studied grain boundaries.

表2给出了B原子在各晶界最佳偏析位的多面体结构模型, 添加B原子前后的多面体的体积、B原子与近邻Fe原子的键长, 及添加B原子导致的多面体体积增量和晶界能的变化量. 可以看出, B原子稳定偏析位的局部区域原子构型涉及三种类型的多面体, 分别是一般五面体、六面体和三棱柱(特殊五面体). B原子在Σ3(112)、Σ5(210)、Σ5(310)和Σ9(221)晶界稳定偏析位的局部区域原子构型属于同一类型, 都是相对不规则的一般五面体结构; Σ11(113)晶界对应的也是五面体结构, 是规则的三棱柱结构. 而B原子在Σ9(114)晶界稳定偏析位的局部区域原子构型是六面体, 该构型所对应的初始体积最大. 结合图2, B原子在各晶界最稳定的偏析位具有最大配位数, 且是五面体或六面体的构型, 与常规块体结构中八面体构型的间隙不同. 对比添加B原子前后的偏析位多面体的体积, 发现当B原子处于最稳定的偏析位时, 晶界处都发生不同程度的晶格膨胀, 对应的晶界处的层间距均增大, 说明B原子的偏析所引起的结构弛豫作用(机械变形)削弱了晶界的内聚力. B原子偏析可提高体系晶界的结合强度, 即化学效应的贡献大于力学效应影响的结果.

		Σ3(112)	Σ5(210)	Σ5(310)	Σ9(221)	Σ9(114)	Σ11(113)
Polyhedron of favorable interstitial sites
Volume of polyhedron/?3	Vpure Fe	5.80	4.73	5.41	5.03	13.90	6.01
	Vwith B	7.67	4.91	5.75	5.16	15.09	6.06
	Vwith B-Vpure Fe	1.88	0.18	0.34	0.13	1.20	0.04
Bond length of Fe-B/?	Fe1-B	2.04	2.17	2.15	2.13	2.09	1.98
	Fe2-B	2.84	2.03	2.06	2.02	2.22	1.95
The change of grain boundary energy /(mJ·m–2)		–14.90	–8.72	–11.50	–31.10	–25.00	–5.02

表2B原子在各晶界最佳偏析位的多面体结构模型、添加B原子前后的多面体的体积和体积增量、B原子与近邻Fe原子的键长, 以及引起晶界能的变化量
Table2.The local atomic configurations of the stable segregation sites, the volume and volume increment of the polyhedron without and with B, the bond length between B and neighboring Fe atoms, and the change of grain boundary energy caused by B segregation when B at the stable segregation sites.

计算结果表明, B原子在稳定偏析位的析出位置接近多面体的重心, 与最近邻Fe原子的B—Fe键长保持在1.95—2.09 ?之间. B原子在Σ9(114)晶界的稳定偏析位对应的多面体具有更大空间, 并且配位数是8; 而在其他5个晶界的稳定偏析位具有相同的配位数为6. 与块体中B原子的配位原子数目6相比, 其在晶界偏析时的配位原子数目没有减少. 由表2加B原子引起的各种晶界能的变化量均为负值, 说明B原子的晶界偏析使所处晶界的晶界能降低, 提高了晶界结构的稳定性.
2 -->

3.2.B偏析对界面结合能力的影响

图5给出了晶界加B原子前后对各晶界拉伸获得的抗拉强度曲线, 曲线的峰值对应其理论抗拉强度σ_max. 可以看出, Σ5(310)晶界的理论抗拉强度最大, Σ11(113)和Σ9(114)晶界次之, 然后是Σ5(210)和Σ9(114)晶界, Σ3(112)晶界的理论抗拉强度最小. 添加B原子之后, 可以看出, 除Σ5(310)晶界外, 界面含B后均可提高晶界的理论抗拉强度值, B对Σ9(221)晶界强度的影响最明显, 理论抗拉强度增加了16%. 这应该与Σ9(221)晶界有最大的过剩体积相关, 而Σ3(112)和Σ11(113)晶界结构紧凑, 对比来看该晶界理论抗拉强度增量相对较少. 与其他5个晶界不同, B原子偏析对Σ5(310)晶界的拉伸强度有一定的减弱, 结合表1, Σ5(310)晶界具有最大的晶界能, 晶界失配度最大, 相对稳定性较弱, 以上因素造成B原子偏析使Σ5(310)晶界拉伸强度降低. 6个晶界的断裂能的变化规律与理论抗拉强度一致, 除Σ9(114)晶界的分离特征长度基本不变, B原子处于晶界后, 其他5个晶界的分离特征长度都减小, Σ3(112)晶界减少的最多.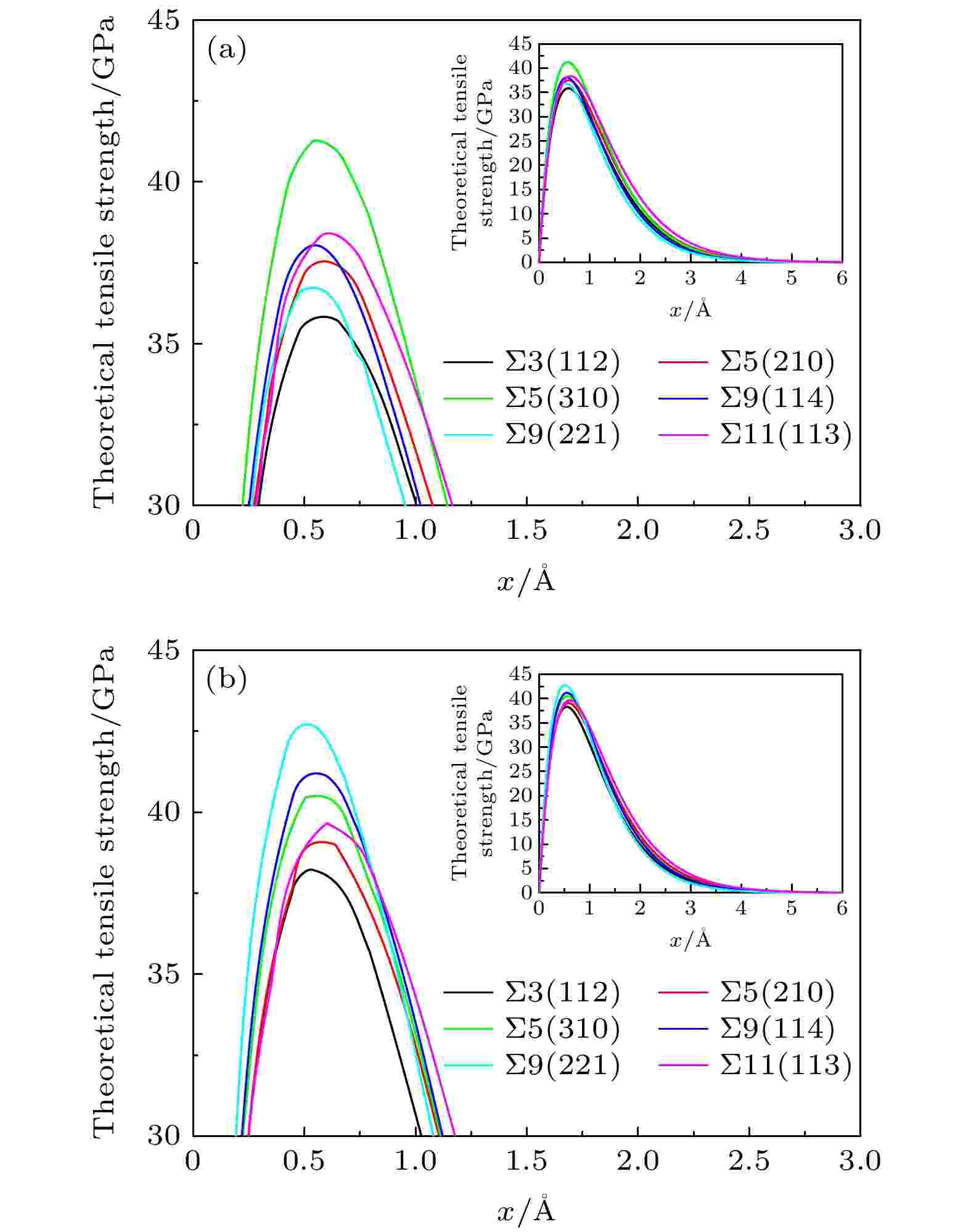
图 5 添加B原子前后6个晶界的抗拉强度曲线
Figure5. Tensile strength curves of the six studied grain boundaries without and with B.

Σ9晶界属于Σ3ⁿ (1 ≤ n ≤ 3)类型晶界, Σ3和Σ9晶界在奥氏体不锈钢中占比很高, 因为B原子在Σ9(114)晶界易偏析且强化晶界, 故本部分以Σ9(114)晶界为研究对象, 计算其电荷密度及态密度. 图6给出了添加B原子前、后Σ9(114)晶界的电荷密度图, 对比发现, 尽管B原子偏析使Σ9(114)晶界处上下层的Fe原子之间的距离由偏析前的2.57 ?增加到偏析后的3.04 ?, 但晶界处原子电荷得到补充, 晶界处原来的电荷低密度区域消失, 而晶胞内的电荷密度几乎没有变化.
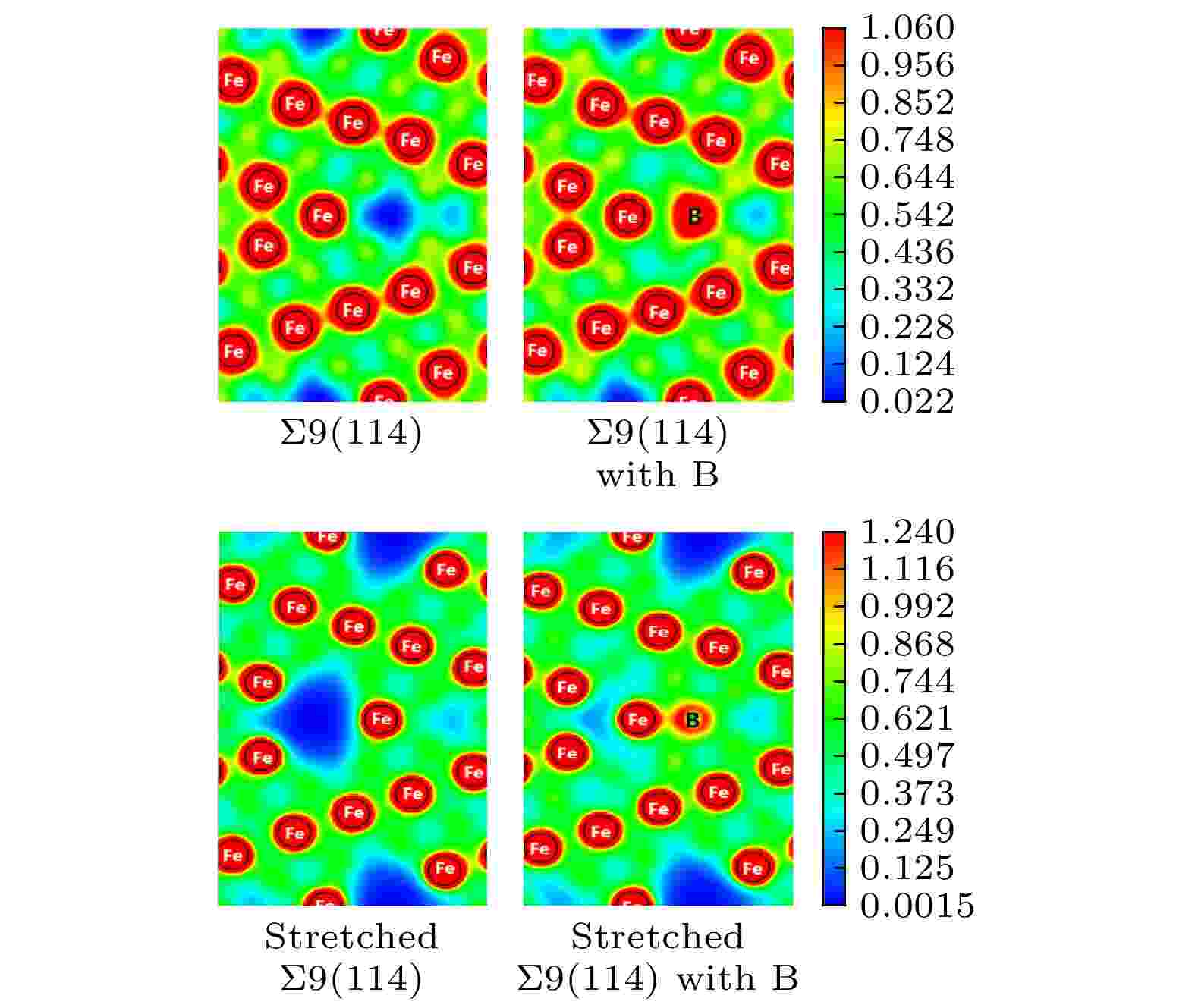图 6 添加B原子前后, Σ9(114)晶界体系(a)未形变及(b)均匀拉伸12%变形量后的电荷密度图
Figure6. The charge density of (a) undeformed and (b) 12% tensile deformed Σ9(114) grain boundary without and with B

图6给出了添加B原子前后, Σ9(114)晶界体系均匀拉伸12%变形量后晶界的电荷密度图. 可以发现, 经过12%的拉伸形变后, 无B晶界处原来的电荷低密度区域明显扩大, 说明晶界处是材料结构的最薄弱处, 随变形量的增加材料将在晶界界面处发生断裂. 而晶界含B后, B原子在晶界间隙位的偏析使得晶界处的电荷分布区域发生了变化, 尤其形变后的晶界结构仍保持完整, 且B原子使得周围的电荷密度增多、晶界的抗拉能力明显增强. 晶内的电荷密度变化不大, 晶界处较大空隙处开始出现电荷低密度区, 这说明B原子偏析前后的断裂面均通过晶界中心面. 基于Rice-Wang热力学模型, 计算出B原子偏析前后Σ9(114)晶界的断裂能, 由5.696 J/m²增大到6.032 J/m², 与拉伸曲线得到的断裂能数值(5.732 J/m²和6.047 J/m²)基本一致. 综上, 该结果为B偏析于晶界后对界面结合能力的影响给出了直观的认识.
图7给出了添加B原子前后Σ9(114)晶界的总态密度图, 以及B原子附近的Fe₁, Fe₂原子(标号与表2相同)和B原子的分波态密度图. 从添加B原子前后Σ9(114)晶界的总态密度图可以看出, 总态密度主要来源于Fe-d电子贡献, B偏析到晶界对总态密度无明显的影响, 但是使费米能级附近的峰值高度下降, 总态密度略向低能方向偏移, 使体系更加稳定. 从分波态密度来看, B-s电子的贡献主要来源于费米能级以下–9 eV至–8 eV区域, B-p电子主要来源于–7—1 eV区域, 使得紧邻的Fe-s、Fe-p电子态在–10 eV至–7 eV能量范围的态密度有所升高且区域明显变宽, Fe-d尤其是Fe₂-d电子态在费米能级附近的态密度明显升高. 这说明Fe电子的自由度更强, 离域性变大, 与B原子成键的程度增强. 另B-p电子与Fe-s特别是Fe₂-s电子的态密度峰形一致, 说明B-p和Fe-s电子之间存在轨道杂化. 综上, 偏析的B原子和Fe₁、Fe₂原子之间的电荷富集, 提高了B、Fe原子间的化学键合强度, 有利于B与邻近区域原子的结合.
图 7 (a)未添加B原子和(b)添加B原子Σ9(114)晶界的总态密度图, 以及B原子附近Fe₁, Fe₂和B原子的分波态密度图
Figure7. The total density of states (TDOS) of Σ9(114) grain boundary without and with B atom, correspond to (a) and (b) respectively, and the projected density of states (PDOS) of Fe atoms in the vicinity of B atom (Fe₁ and Fe₂)and B atom.

基于密度泛函理论研究了B在面心立方铁中Σ3(112), Σ5(210), Σ5(310), Σ9(114), Σ9(221)和Σ11(113)六种低能晶界的偏析及界面特性, 结论如下:
1)B更倾向偏析于Σ5(210), Σ5(310)和Σ9(114)晶界, 在Σ9(221), Σ3(112) 和Σ11(113)晶界偏析的倾向较弱, 结合晶界过剩体积来看, 过剩体积越小, 结构越紧凑, B偏析的倾向越小; 奥氏体钢中B不易在晶界占比最大的Σ3(112)偏析, 更倾向于在晶界相对宽松的Σ5(210), Σ5(310)和Σ9(114)晶界偏析, B在这些晶界的偏析均有利于提高界面的结合能力.
2)B易优先占据界面处配位数大的五面体或六面体构型位置, 对比加B原子前后的偏析位多面体体积, 晶界处均发生了不同程度的晶格膨胀、晶界处层间距增大, 削弱了晶界的内聚力. 从奥氏体钢中晶界占比次之的Σ9(114)晶界来看, B-p电子与Fe₂-s电子间的强相互作用使界面的结合能力得到提高, 抑制了结构变化带来的不利影响, 即B处于晶界后化学效应的贡献大于力学效应.
3)通过对不同晶界的拉伸变形, 发现B原子处于晶界后使得周围的电荷密度增加, 使晶界处原子间结合能力增强, 拉伸强度得到提高. 尤其奥氏体钢中占比最大的Σ3(112)、Σ9(114)晶界结合能力得到了提升.