摘要:当前, 对暴露于极端环境中的含能材料的相对安全性的关注日益增加. 理解含能材料在冲击加载下的初始分解机理是探索新型高能顿感材料的基础. 本文利用多尺度冲击技术(multi-scale shock technique, MSST)结合反应力场(ReaxFF)分子动力学的方法研究冲击加载下环三亚甲基三硝胺(RDX)的完美晶体和分子空位晶体的初始动态响应及反应机理, 计算了可能参与反应的原子间径向分布函数, 分析了不同冲击速度及分子空位缺陷对冲击加载过程的影响. 结果表明: 在冲击加载下, 完美RDX晶体和空位RDX晶体的初始分解方式均为首先发生N—NO₂键断裂, 随后是C—N键的断裂. 此外, 还可能会出现C—H键断裂, 并有氢转移到硝基中的氧原子上形成HONO. 随着冲击速度的增加, 两种RDX晶体的化学键断裂数目增多, 反应更强烈. 分子空位缺陷的存在增强了N—NO₂的反应活性, 使其更易发生断裂, 进而加速空位RDX晶体的初始反应.
关键词: 含能材料/
多尺度冲击/
分子动力学/
空位缺陷/
径向分布函数

English Abstract

全文HTML

--> --> -->

环三亚甲基三硝胺(RDX)是一种高性能的含能化合物, 广泛应用于多种聚合物键合炸药(PBXs)和推进剂配方中^[1]. 由于晶体生长过程中的各种不利条件, 通常会在晶体内部形成一些缺陷, 包括空位、杂质和位错等, 这对其初始反应性能有一定的影响^[2-4]. 当含能材料中含有大量缺陷时, 对外界热或冲击的感度将显著下降^[5]. Wang等^[6]和Kuklja等^[7]运用第一性原理的方法对含空位和位错缺陷的RDX晶体的电子结构性质进行了研究, 结果表明空位缺陷的存在会导致晶体光学带隙变窄, 并降低了其绝缘体相态向金属相态转变的临界压力. 我们先前的工作对含有分子空位的RDX晶体的几何结构、电子结构及振动特性进行了详细地分析, 表明了分子空位缺陷的存在使体系能带隙变小, 并使缺陷附近的分子结构松弛, 电荷分布增多, 反应活性增强^[8]. Chakraborty等^[9]利用密度泛函理论计算了HMX和RDX含能材料的分解途径, 表明了N—NO₂消去和氢转移形成HONO的能垒较低(约39 kcal/mol); Ge等^[10,11]利用多尺度冲击技术(MSST)对凝聚相β-HMX 和RDX进行分子动力学模拟, 给出N—NO₂键的解离和C—N键断裂是RDX的主要分解途径, 并指出单一RDX分子在11 km/s速度冲击下, 主要产物包括NO₂, NO, N₂O, CO和N₂. 郑朝阳和赵纪军^[12]利用第一性原理分子动力学方法研究了RDX的热解初始反应机制, 表明了分解方式主要包括质子转移、C—N键断裂和N—NO₂键断裂等方式, 并提出冲击加载可能带来C—H键断裂的反应机制. 然而, 在冲击加载下, 含空位的RDX晶体内部微观结构如何变化? 反应机理怎样? 还没有被澄清. 由于晶体内部微观现象较难通过实验分辨, 因此, 第一性原理和分子动力学方法被广泛地应用来研究含能材料的微观动态过程^[13-16].
本文主要利用基于ReaxFF (reactive force field)的分子动力学方法结合多尺度冲击技术(MSST)研究冲击加载下RDX的完美晶体和分子空位晶体的初始动态响应特性, 进而预测两种RDX晶体可能的初始反应机制, 为提高含能材料的安全性能提供必要的微观信息.

ReaxFF是一种以第一性原理为基础的反应力场^[17-22], 它能够较好地模拟含能材料在热或冲击作用下的化学反应过程. ReaxFF的参数是用量子力学计算或实验获得的, 具有量子力学的准确性^[19,20]. 因此, 对于较小的模拟尺度, ReaxFF分子动力学仍然能够给出较好的模拟结果^[22]. 使用Material Studio建立完美RDX超胞(2 × 1 × 1)和含有1个分子空位的超胞, 如图1(a)和图1(b)所示. A, B和C代表3个晶格方向. 采用了密度泛函理论中的广义梯度近似方法及Perdew-Burke-Ernzerhof泛函^[23], 对RDX完美超晶胞以及分子空位超晶胞进行几何结构优化. 由于RDX超晶胞的原子数较多, 计算量较大, 所以选取了Gamma-point, 即k = 1 × 1 × 1. 优化完美RDX超胞的晶格参数为a = 26.731756 ?, b = 11.500793 ?, c = 10.786047 ?, α = β = γ = 90°, 与文献[24]报道的数据基本相符. 在未加载冲击波情况下, 采用NVE系踪并结合Berendsen 控温方式模拟RDX平衡过程1 ps得到稳定的RDX晶体结构, 并以此作为冲击加载的初始结构, 初始温度为300 K, 初始压力设为1个大气压, 沿晶体A方向进行多尺度冲击压缩模拟. 时间步长为0.01 fs, 原子截断半径取1.5 ?. 分析了冲击速度为10, 11和13 km/s的冲击波作用下完美RDX晶体和空位晶体的微观动态过程, 计算可能参与反应的原子间的径向分布函数, 揭示两种晶体结构的可能的初始反应机制.
图 1 构建的完美RDX超胞(2 × 1 × 1)(a)和含1个分子空位的RDX超胞(b), 红、蓝、灰、白分别表示氧、氮、碳和氢原子
Figure1. Constructed perfect RDX supercell (2 × 1 × 1) (a) and RDX supercell with a molecular vacancy (b). Red, blue, gray and white represent oxygen, nitrogen, carbon, and hydrogen atom, respectively.

2

-->

3.1.晶体内部结构的动态变化

图2(a)和图2(b)分别为完美RDX晶胞和空位晶胞在冲击速度为11 km/s的冲击波作用下的动态变化过程. 可见, 随着冲击波作用时间的增加, 晶胞在A方向上逐渐被压缩, 尺寸减小. 晶体中的分子逐渐从有序排列到无序状态. 从图2(b)可见, 在冲击作用下, 空位附近的分子发生较大移动, 并逐渐填充到空位部分. 图3(a)和图3(b)分别为10 km/s和11 km/s冲击速度加载下RDX完美晶胞和空位晶胞的内能、体积比、压力和温度随时间的变化情况. 显然, 随着时间的增加, 两种情况下体系的热力学参数逐渐趋于稳定. 反应温度均稳定在5000 K左右, 压强大约维持在70 GPa左右, 冲击速度越大, 体积比减小的越快. 这些与文献[25,26]报道基本符合. 此外, 图4给出了冲击波加载条件下的冲击速度和粒子速度关系与先前实验和理论数据的比较^[27,28]. 可见, 完美晶体的冲击速度-粒子速度关系与目前实验和理论数据符合较好. 空位晶体的粒子速度比完美晶体的稍高, 但相差不多, 表明了计算结果的有效性.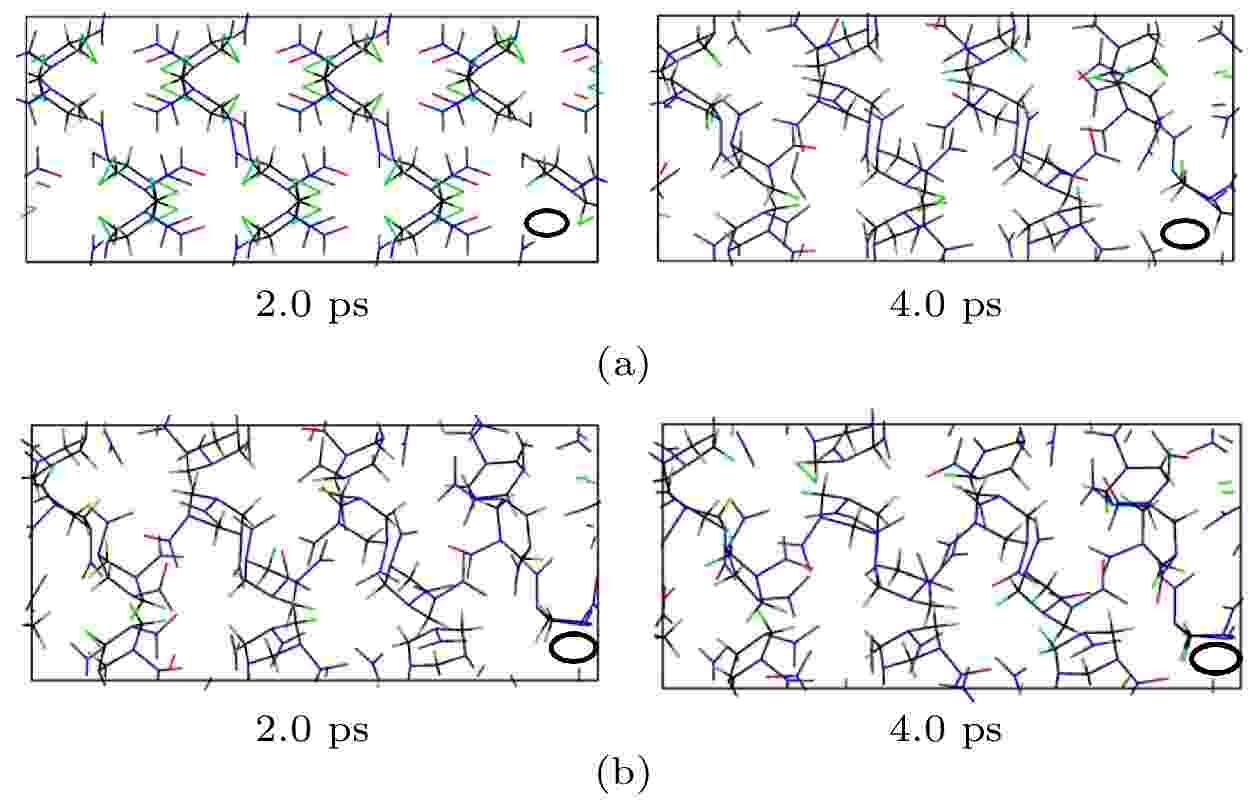
图 2 冲击速度为11 km/s加载下, 完美RDX超胞(a)和空位RDX超胞(b)在不同时刻的体系结构, 图中红色代表氧原子、黑色代表碳原子、蓝色代表氮原子、绿色代表氢原子
Figure2. System structure of perfect RDX supercell (a) and RDX supercell with a molecular vacancy (b) at different time under shock velocity of 11 km/s. The red for oxygen, the black for carbon, the blue for nitrogen and the green for hydrogen.

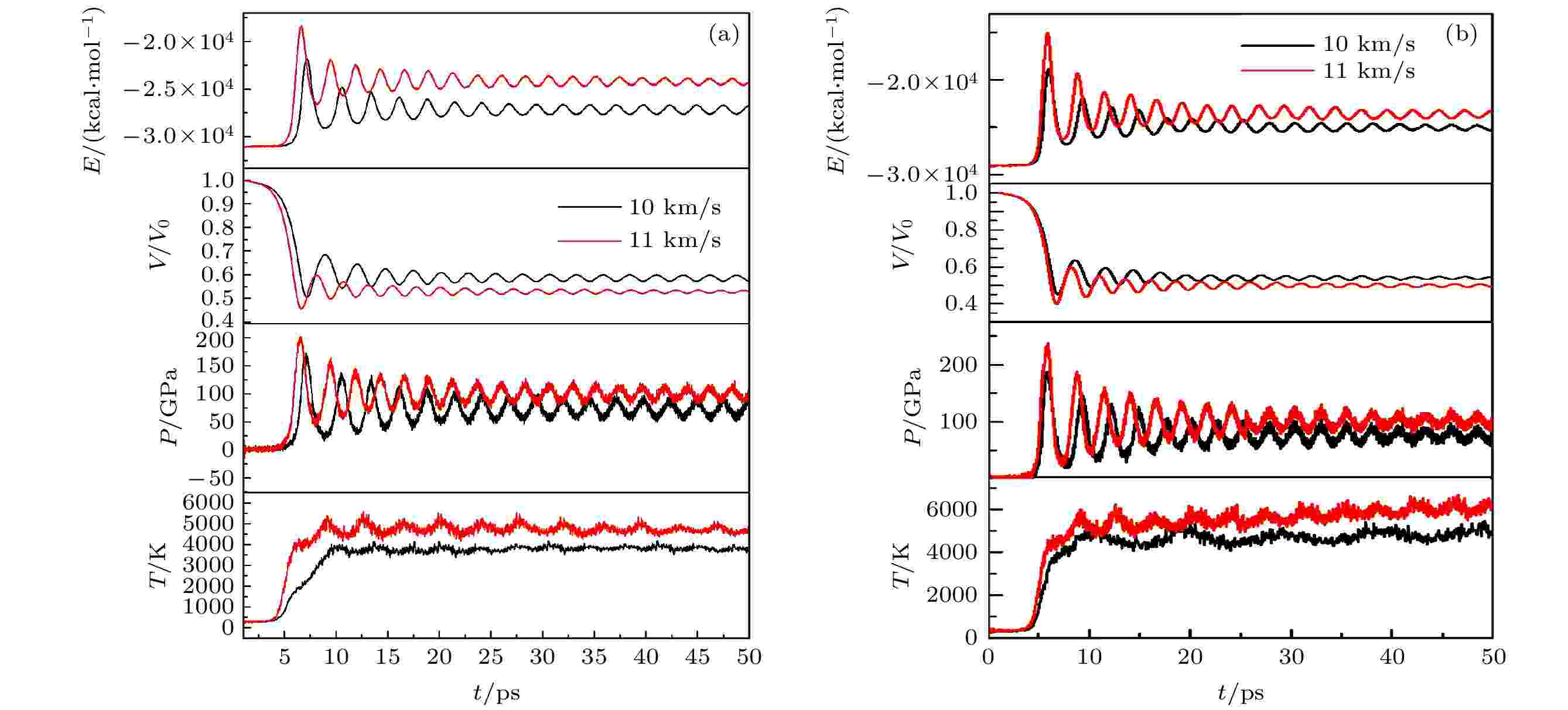图 3 冲击加载下, RDX完美超胞(a)和含1个分子空位超胞(b)的总能量、体积比、压强和温度随时间的变化
Figure3. Changes of total energy, volume ratio, pressure and temperature vs. time for RDX perfect supercell (a) and RDX supercell with a molecular vacancy (b) under shock loading.

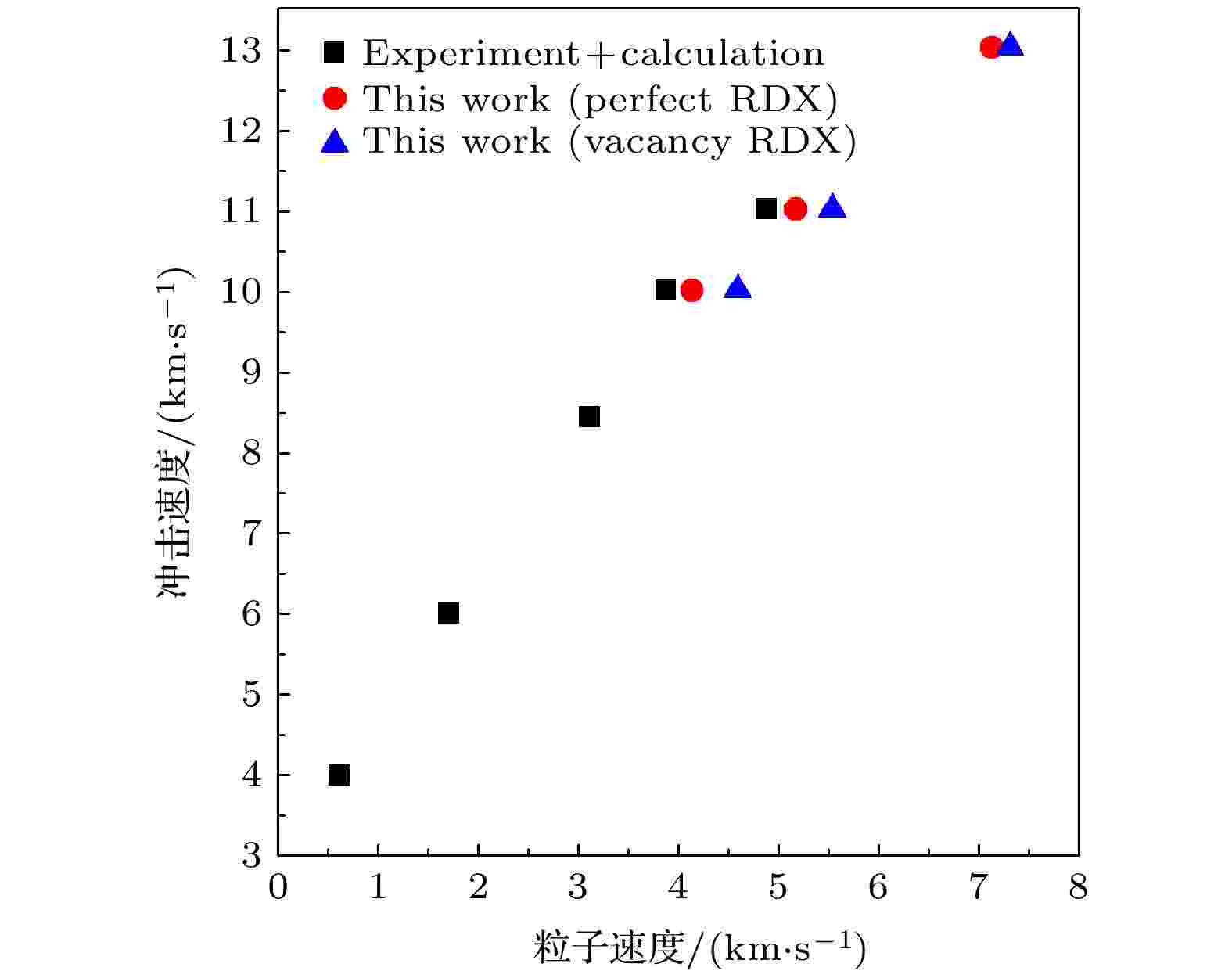图 4 RDX冲击速度与粒子速度对应关系, 其中, 黑色方形数据为起爆前(冲击速度低于8.6 km/s)实验数据和起爆后的理论计算数据^[27,28], 红色圆形和蓝色三角形数据为本计算的完美晶体和空位晶体的相应数据
Figure4. Shock velocity vs. particle velocity for RDX. Here, the black square data are the experimental data before detonation (below 8.6 km/s in shock velocity) and the theoretical calculation data after detonation^[27,28], and the red circle and blue triangle data are respectively that of the perfect crystal and the vacancy crystal in this calculation.

为了明确冲击过程中RDX分子结构的具体变化情况, 分别给出了冲击速度为11 km/s作用下完美晶胞和分子空位晶胞在不同时刻的分子结构的情况, 如图5和图6所示. 从图5(a)可见, 在1.015 ps时刻, 完美RDX晶体中的N—NO₂键发生了断裂, 而在1.125 ps时刻, C—N键发生了断裂(如图5(b)所示). 这表明, 在冲击加载下, 完美RDX晶体中N—NO₂键首先发生断裂, 随后C—N键发生断裂. 从图6(a)可以看出, 含分子空位缺陷的RDX晶体中N—NO₂键断裂时刻为1.010 ps, 而C—N键断裂时刻为1.043 ps (如图6(b)). 显然, 空位晶体中断键时间要比完美晶体中的断键稍早. 这表明了分子空位缺陷的存在使含能材料对冲击加载更敏感, 更容易发生化学反应. 这与目前文献[4, 5, 8]报道的结果是一致的.
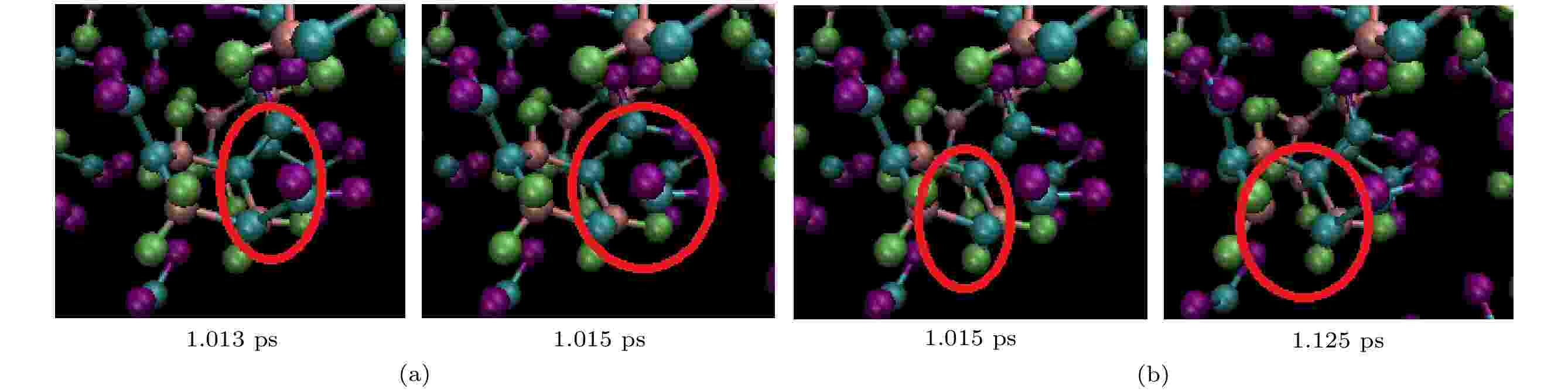图 5 在冲击速度为11 km/s作用下, RDX完美晶胞中N—NO₂键随时间演化情况(a)和C—N键随时间演化情况(b), 其中蓝绿色代表氮、紫色代表氧、绿色代表氢、橘红色代表碳
Figure5. Evolution of N—NO₂ bonds with time (a) and that of C—N bonds with time (b) in RDX perfect cell under shock velocity of 11 km/s. The blue-green represents nitrogen atom, the purple represents oxygen atom, the green represents hydrogen atom and the tangerine represents carbon atom.

图 6 在冲击速度为11 km/s作用下, 含分子空位的RDX晶胞中N—NO₂键随时间的演化情况(a)和C—N键随时间的演化情况(b), 其中蓝绿色代表氮、紫色代表氧、绿色代表氢、橘红色代表碳
Figure6. Evolution of N—NO₂ bonds with time (a) and that of C—N bonds with time (b) in RDX cell with a molecular vacancy under shock velocity of 11 km/s. The blue-green represents nitrogen atom, the purple represents oxygen atom, the green represents hydrogen atom and the tangerine represents carbon atom.

2 -->

3.2.冲击加载下完美RDX晶体的初始反应分析

从RDX分子本身结构和可能产生的产物碎片结构入手^{[11,15,16,29,30]}, 计算可能发生反应的原子间的径向分布函数, 如N—N, C—N, C—H, H—O等. 图7为计算获得的完美RDX晶胞在10, 11和13 km/s冲击速度作用下, 主要原子间径向分布函数情况. 为了分析原子间可能的成键概率情况, 考虑了径向分布函数相关峰的展宽效应, 即对几个主峰所包围的面积进行了计算, 结果见表1. 可见, 在不同冲击速度下, 由于径向分布函数的峰宽变化较小, 其所包围的面积基本由峰值决定, 峰值高的所包围的面积较大, 代表了该处原子成键数量较多. 从图7(a)可以看出, 对于氮氮原子, 当冲击速度为10 km/s时, 在径向半径为1.55 ?附近, 其径向分布函数g_N—N(r)出现最大峰值. 该径向长度符合RDX晶体中的N—NO₂键的成键范围, 表明该状态下, 氮-氮原子主要以N—NO₂形式存在. 随着冲击速度的增加, 1.55 ?附近径向分布函数的峰值逐渐降低, 而表征氮-氮三键的1.18 ?附近径向分布函数的峰值逐渐升高. 这表明在冲击加载下, RDX中的N—NO₂键将发生部分断裂, 形成产物氮气, 并随着冲击速度的增加而断裂程度增大, 最终形成氮气的量也增多; 从图7(b)可见, 在 1.45 ? 附近, 碳-氮原子间的径向分布函数g_C—N(r)出现峰值, 该距离属于RDX 环链中C—N 键的成键范围. 随着冲击速度的增加, g_C—N(r)峰值下降, 表明了C—N键将发生部分分解. 这些与对晶体中微观结构的观察结果是一致的. 从图7(c)可见, 在1.04 ?附近碳氢原子间的径向分布函数g_C—H(r)具有最高峰, 表明了C和H原子多数以环链上的C—H键存在. 随着冲击速度的增加, 该位置径向分布函数峰值降低, 表明了随着冲击速度的增大, C—H键可能会发生形变或断裂致使部分碳氢原子间距离改变. 从图7(d)可以看出, 当冲击速度为10 km/s时, 氢-氧原子的径向分布函数g_H—O(r)的峰值在2.45 ?附近, 该位置为RDX晶体中分子间的H和O原子距离范围. 而HONO和H₂O中H—O键的合理范围均为1.00 ?左右. 这表明该状态下RDX晶体中基本未发生C—H键断裂, 即未出现H原子转移到硝基中的氧原子上形成HONO的情况. 当冲击速度由10 km/s增大到13 km/s时, 2.45 ?附近的g_H—O(r)的峰值降低, 而1.52 ?附近的径向分布函数峰值明显增大, 这表明了随着冲击速度的增大, 分子间H和O形成了分子间氢键, 并可能会有较少部分C-H键断裂, 使H原子转移到硝基的O原子上形成HONO, 进而使H—ONO键的数量增多^{[22,25,31,32]}. 因此, 对于完美RDX晶体, 在冲击加载下, 随着冲击速度的增加, 表征N—NO₂键、C—N键和C—H键的原子间径向分布函数峰值均降低, 而分子间的H和O的距离先减小形成氢键, 之后在氢键作用下会有部分C—H键断裂形成H—ONO. 表明了RDX可能的初始分解反应为N—NO₂断裂或C—N键断裂. 当冲击速度增大到一定值时(如13 km/s), 会在H和O之间形成分子间氢键, 并有部分C—H键断裂, 进而H转移到硝基上形成HONO.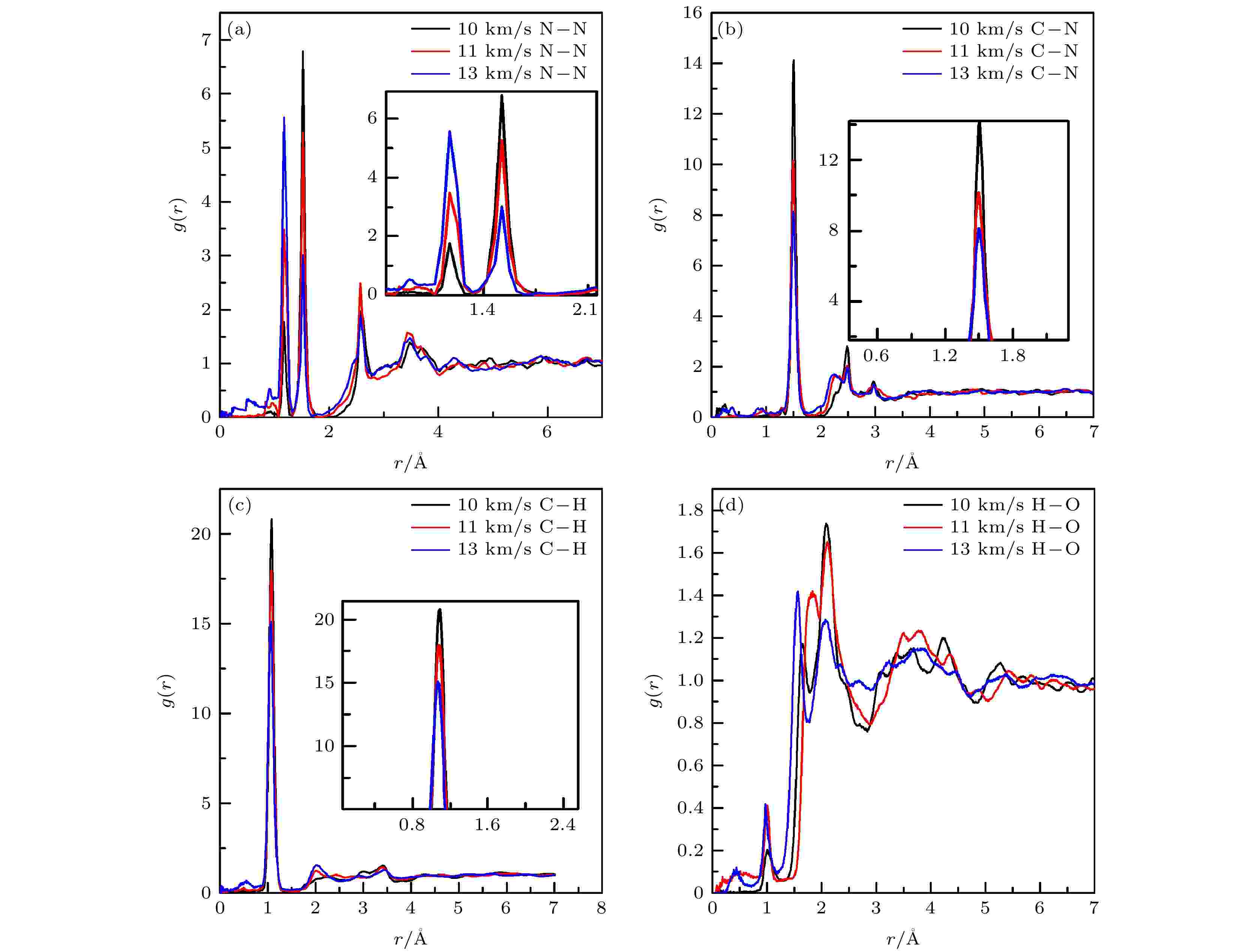
图 7 完美RDX晶体在冲击速度为10, 11和13 km/s作用下N—N (a), C—N (b), C—H (c)和H—O (d)原子间的径向分布函数
Figure7. Radial distribution function between atoms N—N (a), C—N bond (b), C—H bond (c), H—O bond (d) in the prefect RDX crystal at shock velocity of 10, 11 and 13 km/s.

Shock velocity/(km·s–1)	N—N			C—N		C—H		H—O
	r = 1.18 ?	r = 1.55 ?		r = 1.45 ?		r = 1.04 ?		r = 1.00 ?	r = 2.45 ?
10	0.1399	0.6488		1.3807		2.6913		0.0156	0.3824
11	0.3406	0.5048		1.2285		2.4445		0.0364	0.2695
13	0.5710	0.2831		1.1063		2.1975		0.0403	0.2616

表1完美晶体中原子间的径向分布函数相关峰所包围的面积
Table1.Area enclosed by a certain peak of inter-atoms radial distribution function in the perfect crystal

2 -->

3.3.冲击加载下含1个分子空位的RDX晶体的初始反应分析

图8(a)—(d)为含1个分子空位的RDX晶胞在冲击速度10, 11和13 km/s作用下的N—N, C—N, C—H和H—O原子间的径向分布函数. 表2为计算获得的主要径向分布函数峰所包围的面积. 显然, 对于主要位置的N—N, C—N, C—H和H—O原子之间成键数量基本还是受峰值影响较大, 但对13 km/s冲击速度情况, 在2.45 ?附近的H—O原子的径向分布函数面积比11 km/s的略大一些, 这可能是统计误差所致. 从图8(a)可见, N—N原子间的径向分布函数g_N—N(r)的最高峰仍然出现在1.55 ?附近, 随着冲击速度的增加, 该处峰值逐渐降低, 而1.55 ?附近峰值逐渐升高. 表明了冲击加载下, 空位RDX晶体中也将发生N—NO₂键断裂, 并且随着冲击速度的增加, N—NO₂断裂数量增加, 而最终形成的氮气数量也增多. 从图8(b)和图8(c)可看出, RDX中的C—N和C—H原子间的径向分布函数峰值也随着冲击速度的增加而逐渐降低, 表明了冲击加载下, 空位RDX也可能发生C—N键和C—H键断裂. 图8(d)表明, 随着冲击速度的增加, 2.45 ?附近的氢-氧原子间径向分布函数g_H—O(r)峰值同样也有所减小, 而在1.52 ?附近的峰值明显升高. 这说明随着冲击速度的增加, RDX空位晶体受压缩程度逐渐增大, 使分子间H和O更多地以分子间氢键形式存在, 并可能引发C—H键断裂, 使氢原子转移到NO₂的氧原子上形成HONO. 因此, 对于含1个分子空位的RDX晶体, 其初始分解方式基本与完美RDX分解方式相同, 即可能发生N—NO₂键断裂、C—N键断裂和C—H键断裂, 并且H会转移到硝基中的O原子上.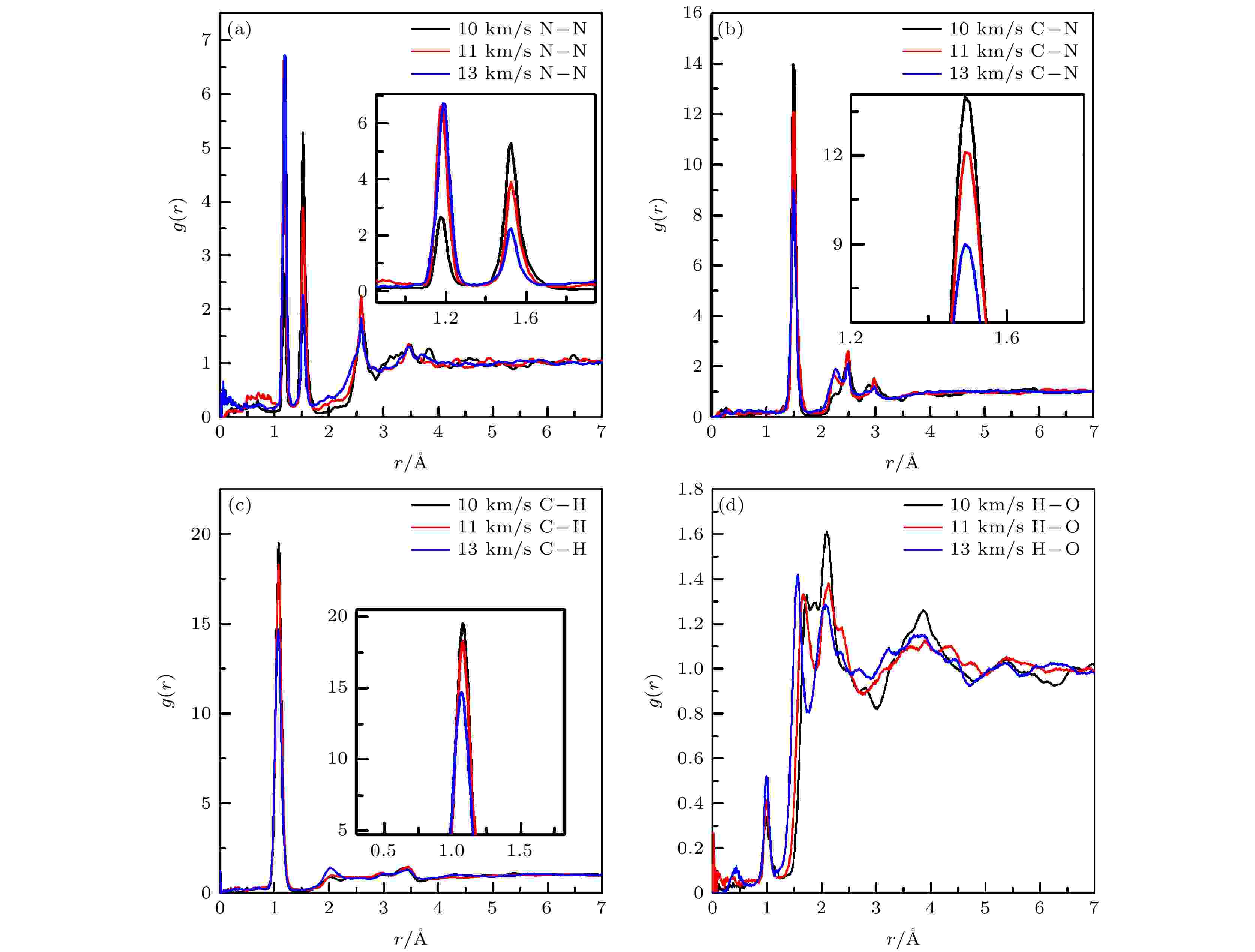
图 8 含1个分子空位RDX超胞在冲击速度为10, 11和13 km/s作用下原子间(N—N (a), C—N (b), C—H (c)和H—O (d))的径向分布函数
Figure8. Radial distribution between atoms (N—N (a), C—N (b), C—H (c), H—O (d)) of the vacancy RDX supercell at 10, 11 and 13 km/s.

Shock velocity/(km·s–1)	N—N			C—N		C—H		H—O
	r = 1.18 ?	r = 1.55 ?		r = 1.45 ?		r = 1.04 ?		r = 1.00 ?	r = 2.15 ?
10	0.1631	0.7238		1.3794		2.5649		0.0342	0.2328
11	0.4722	0.4398		1.3427		2.5349		0.0372	0.2268
13	0.5619	0.3095		1.0985		2.1741		0.0477	0.2316

表2空位晶体中原子间的径向分布函数峰所包围的面积
Table2.Area enclosed by a certain peak of inter-atoms radial distribution function in the vacancy crystal.

2 -->

3.4.冲击加载下分子空位缺陷对RDX初始反应的影响

为了明确分子空位缺陷对RDX晶体分解的影响, 图9(a)—(d)给出了完美RDX晶体和空位RDX晶体在11 km/s冲击速度下主要原子间的径向分布函数. 表3为计算的主峰所包围的面积. 可见, 此关系仍为峰值越高面积越大. 在相同冲击速度作用下, 空位晶体中表征N—NO₂键的氮-氮原子径向分布函数(1.55 ?)峰值减小, 而表征氮-氮三键的1.18 ?位置处的径向分布函数的峰值增大, 表明了N—NO₂键断裂程度增大, 而形成产物氮气的数量增多. 可见, 分子空位的存在增加了N—NO₂键的活性, 促进了其断键反应. C—N和C—H原子间的径向分布函数的峰值均与完美晶体的峰值相差不多. 对于氢氧原子, 空位晶体在2.15 ?和1.52 ?附近的径向分布函数峰值要比相应完美晶体的径向分布函数峰值低, 而在1.00 ?附近, 空位晶体比完美晶体的峰值稍高, 但不明显(面积差不到0.001). 这表明, 空位缺陷对HONO的形成影响较小. 因此, 在相同冲击速度加载下, 分子空位缺陷的存在, 主要增加了N—NO₂基团的反应活性, 使空位晶体更容易发生N—NO₂键断裂的化学反应, 这与目前文献[5]报道的缺陷的存在增加了含能化合物的反应活性的结果是一致的.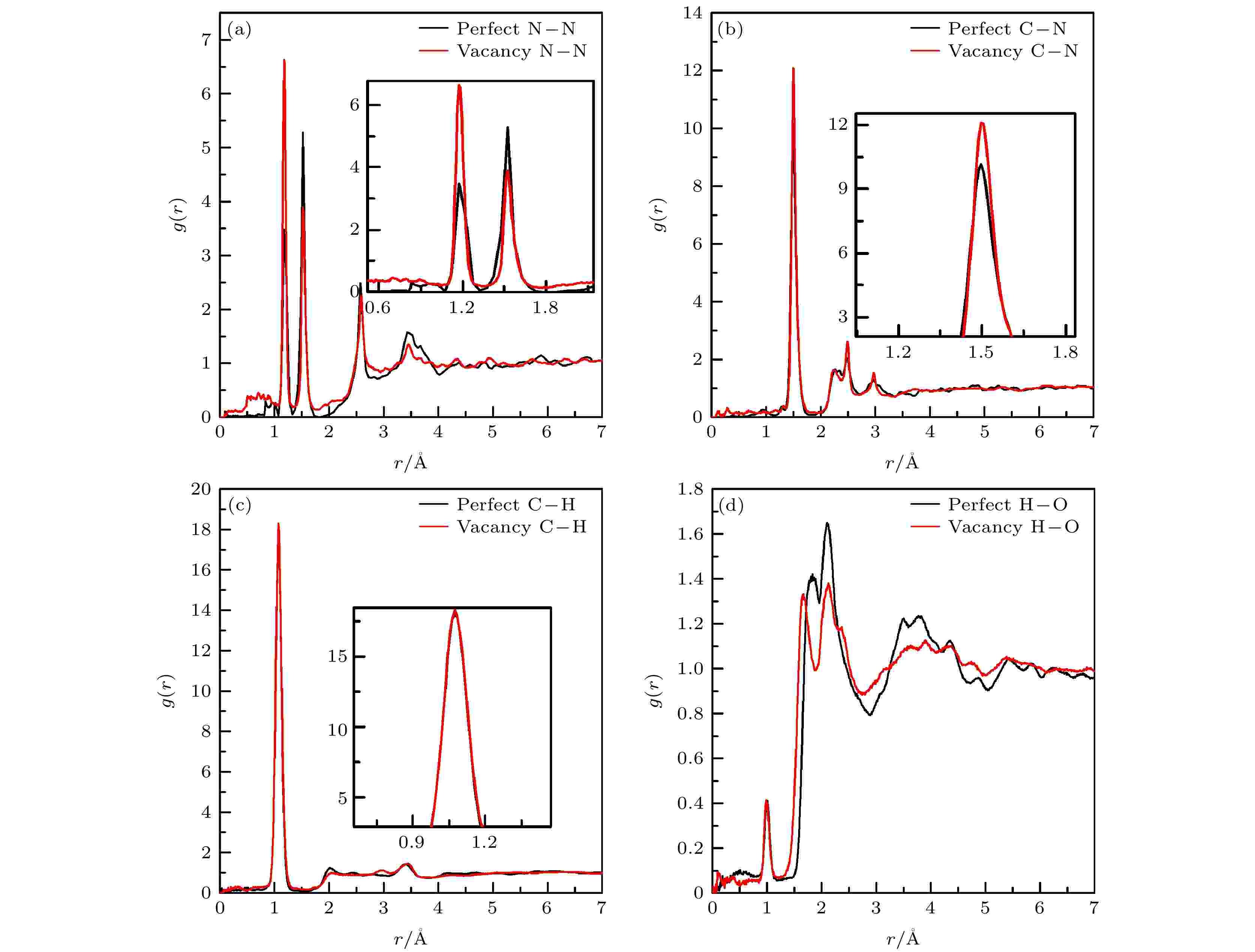
图 9 完美RDX晶体和空位RDX晶体在冲击速度11 km/s作用下原子间(N—N (a), C—N (b), C—H (c)和H—O (d))的径向分布函数
Figure9. Radial distribution function between atoms (N—N (a), C—N (b), C—H (c) and H—O (d)) of the perfect RDX crystal and molecular vacancy RDX crystal at shock velocity of 11 km/s.

RDX	N—N			C—N		C—H		H—O
	r = 1.18 ?	r = 1.55 ?		r = 1.45 ?		r = 1.04 ?		r = 1.00 ?	r = 1.52 ?	r = 2.15 ?
Perfect	0.3406	0.5048		1.2285		2.4445		0.0364	0.2226	0.2695
vacancy	0.4722	0.4398		1.3427		2.5349		0.0372	0.2027	0.2268

表311 km/s冲击速度加载下完美晶体和空位晶体中原子间的径向分布函数峰所包围的面积
Table3.Area enclosed by a certain peak of inter-atoms radial distribution function in the perfect and vacancy crystals at the shock velocity of 11 km/s.

本文运用ReaxFF分子动力学方法结合MSST研究了冲击加载完美RDX晶体和含有1个分子空位的RDX晶体的动态响应过程. 通过对两种微观结构的动力学分析, 表明了在冲击加载下, 两种RDX晶体的初始分解机理均为首先发生N—NO₂断裂, 然后是C—N断裂. 含有空位的晶体的初始反应时刻要早于完美晶体, 表明了空位晶体对冲击更敏感, 更容易发生分解反应. 此外, 本文计算了主要的可能参与反应的原子间的径向分布函数, 分析了不同冲击速度及分子空位缺陷对分解反应的影响. 结果表明, 随着冲击速度的增加, 两种RDX晶体中N—NO₂键及C—N键断裂数目增多, 还可能出现C—H键断裂, 并有氢转移到硝基中的氧原子上形成HONO. 在相同冲击速度作用下, 分子空位晶体中N—NO₂键的径向分布函数峰值比相应的完美晶体的径向分布函数峰值明显降低, 表明了空位缺陷的存在增加了N—NO₂的反应活性, 使其更易发生断裂, 形成产物氮气.