摘要: 为了进一步提高非线性自适应滤波算法在非高斯冲激噪声以及有色噪声环境下的鲁棒性, 提出了一种基于S型函数的变尺度核分式低次幂自适应滤波算法, 该算法利用S型函数的非线性饱和特性和低阶范数准则来克服训练数据被非高斯冲激噪声破坏时性能下降的问题, 并将S型函数与核分式低次幂算法的代价函数相结合后, 通过引入的变尺度因子来平衡和进一步提高算法的收敛速度与稳态误差性能. 仿真结果表明在不同噪声环境的系统识别中, 所提算法相比其他核自适应滤波算法的性能更优.
关键词: 核自适应滤波算法 /
变尺度因子 /
低阶范数准则 /
Sigmoid函数 English Abstract A variable-scale S-type kernel fractional low-power adaptive filtering algorithm Huo Yuan-Lian 1 ,Wang Dan-Feng 1 ,Long Xiao-Qiang 1 ,Lian Pei-Jun 1 ,Qi Yong-Feng 2 1.College of Physics and Electronic Engineering, Northwest Normal University, Lanzhou 730000, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 61561044)Received Date: 12 January 2021Accepted Date: 22 March 2021Available Online: 07 June 2021Published Online: 05 August 2021Abstract: The adaptive kernel algorithms usually achieve a good convergence performance and a tracking performance due to the universal approximator, offering an excellent solution to many problems with nonlinearities. However, as is well known, the convergence rate and steady-state error of adaptive filtering algorithm are a pair of inherent contradictions, and the kernel method is not exceptional. For this problem, a robust kernel adaptive filtering algorithm, called the variable-scaling factor kernel fractional lower power adaptive filtering algorithm based on the Sigmoid function, is developed by creating a new framework of cost function which combines the kernel fractional low power error criterion with the Sigmoid function for system identification of different noise environments. This new cost framework incorporates a scaling factor into the cost function of the Sigmoid kernel fractional lower power adaptive filtering algorithm (VS-SKFLP) in this paper. One of the main features in the new framework is its scaling factor. This scaling factor is used to control the steepness of the Sigmoid function, and the steepness can affect the convergence speed of filtering algorithm. The scaling factor provides a tradeoff between the convergence rate and the steady-state mean square error (MSE), which improves the convergence rate under the same steady-state mean square error. However, it is also an important problem to choose an appropriate scale factor. Therefore, a variable-scale factor SKFLP algorithm is also proposed to improve the convergence rate and steady-state MSE, simultaneously. The proposed variable-scale factor structure consists of a function of error, featuring the adaptive updates of their parameter estimated by making discerning use of the error. In this paper, the nonlinear saturation characteristic of the Sigmoid function and low order norm criterion are used to overcome the performance degradation of training data destroyed by non-Gaussian impulse noise and colored noise. Through the convergence analysis, the parameter estimation sequence of our proposed algorithm proves convergent. Simulation results show that the proposed algorithm (VS-SKFLP) outperforms other kernel adaptive filtering algorithms in system recognition with different noise environments.Keywords: kernel adaptive filtering algorithm /variable scaling factor /low order norm criterion /Sigmoid function 全文HTML --> --> --> 1.引 言 自适应滤波[1 ] 在自适应控制、回声消除、系统识别、信道均衡等领域有着重要作用, 也是近几十年大量研究的热点. 科学研究是为了更好地认识客观世界, 而客观世界中各种物理量变化的表达概念就是波、信号等, 例如: 混沌是在相对论和量子力学之后的第三次关于物理基础科学的革命, 其代表非线性动力学研究, 自适应滤波技术在混沌系统识别[2 ] 中应用而生. 柴金华和陈飞[3 ] 研究了一种准平行光干涉滤波型相控技术, 利用滤波相关知识来解决相位差矫正问题. 机器学习的发展也进一步推进了自适应滤波算法的研究, 其利用参数的自适应调整使得学习过程更加精确以及灵活. 事实上, 传统的自适应滤波算法通常被理解为一个线性结构, 例如广受欢迎的最小化均方误差[4 ] 算法和归一化最小均方误差[5 ] 算法. 然而实际应用中空间环境是不确定的, 这一定程度上限制了传统滤波算法的性能. 为了有效解决算法的适用性问题, 选择合适的代价函数也就成为自适应滤波算法设计的关键. 它可以发现受非高斯噪声以及有色噪声污染的数据系统的期望结构. 基于二阶统计量的均方误差(mean squared error, MSE)准则因其低计算复杂度和凸性被广泛用作代价函数, 然而这种准则下的自适应滤波算法仅仅适用于高斯噪声环境. 非高斯噪声背景下的信号检测, 通常的做法是先对接收信号进行非线性处理, 以抑制接收信号中的大幅值样本, 然后再进行匹配滤波处理[6 ] . 因此一旦环境发生改变, 基于MSE准则的自适应滤波算法性能将严重下降, 而且实际应用中大部分为非高斯环境, 其中包括冲激和有色噪声信号. 基于以上分析, 为解决基于均方误差准则算法存在的问题, 在过去的十几年里大量的鲁棒性估计模型被提出[7 -12 ] , 如基于梯度的最小平均四阶[11 ] 算法、递归最小p 范数[13 ] 算法和最小平均p 功率[14 ] 算法等. 然而到目前为止, 以上提及的鲁棒性自适应滤波算法仍为线性自适应滤波算法, 这些自适应滤波算法的应用仍然主要集中在线性参数滤波器上, 当面对像非线性系统识别[15 ] 和非线性时间序列预测[16 ] 等实际的非线性问题时此类线性自适应滤波算法性能出现严重下降.[17 ] , 例如像支持向量机、高斯过程以及正则化网络等[18 ] . 近年来核自适应滤波算法(kernel adaptive filtering, KAF)作为一种高效的在线学习算法被广泛研究, 简单来说KAF是线性滤波在希尔伯特空间的实现, 其将非线性问题在输入空间中作为空间变换的凸优化问题解决. 传统的自适应滤波算法可被直接内核化变为相应的KAF算法, 如核最小均方误差(kernel least mean square, KLMS) 算法[19 ] 、核仿射投影算法[20 ] 和核递归最小二乘算法[21 ] 等. 然而这些非线性自适应滤波算法也都是在假设高斯噪声环境下产生的, 同样不具备抗冲激性以及有色噪声环境下的鲁棒性. α 稳定分布是一种典型的非高斯分布噪声, 具有显著的尖峰脉冲特性, 其概率密度函数的衰减过程比高斯分布慢, 表现为较长的拖尾[22 ] , Dai等[23 ] 充分考虑了涉及α 稳定噪声分布的长尾分布噪声环境, 提出了核仿射投影p 范数(kernel affine projection p -norm, KAPP)算法, 该算法代价函数为误差绝对值的p 次幂, 当p = 2时算法变为KAP算法, 当p = 1时算法变为核最小平均p 功率(kernel least mean square p -power, KLMP)算法[24 ] . 文献[24 ]提出的KLMP算法, 主要研究在低概率大幅度的非高斯重尾冲激噪声环境中核自适应滤波算法的性能. 之后Dong等[25 ] 在KLMP算法的启发下, 提出了基于分数低阶统计误差准则的抗冲激噪声核分式低次幂自适应滤波(kernel fractional lower power, KFLP)算法, 然而低阶统计量最大的缺点是相比于KLMS算法, 其收敛速度严重下降.26 ]的启发下, 本文构造了一种新的代价函数框架. 将核分式低次幂算法的代价函数与Sigmoid函数框架相结合, 并且加入一个比例因子λ , 将该比例因子作为低次幂误差的调节量使算法能够兼顾收敛速度与稳态误差性能. 同时考虑到合适的比例因子对算法性能的影响, 提出了基于S型函数的变尺度核分式低次幂自适应滤波(variable scaling factor sigmoid kernel fractional lower power adaptive filtering algorithm, VS-SKFLP)算法来进一步提高了算法的收敛速度与稳态误差, 并讨论分析了算法的稳定性能. 由于S型函数的非线性饱和特性可以平滑掉脉冲干扰引起的扰动, 再结合含有比例因子的低阶统计量使所提算法具有良好的性能, 在非线性系统识别和不同有色噪声环境下的仿真结果表明, 本文算法比核最大相关熵算法(kernel maximum correntropy criterion, KMCC)、KLMS算法、和KFLP等其他核自适应算法的性能更优.2.VS-SKFLP算法原理 假定存在一非线性系统识别问题, 该未知系统必然存在被噪声干扰的数据, 其中噪声干扰包括非高斯冲激噪声和有色噪声. 在这种情况下利用误差信号高阶统计量的核自适应滤波算法会遭受性能下降, 因此本文提出一种新的鲁棒性代价函数框架. 首先定义一个Sigmoid函数模型:$J(e(i))$ 是一个核自适应滤波算法的代价函数, 它是关于误差的函数. 从(1 )式可以看出当算法的误差值接近于0时该代价函数${S_i}$ 的值达到最小值; 当算法遭遇非高斯冲激噪声干扰时, 误差突然剧增使代价函数${S_i}$ 的值接近于1, 这表明该函数模型与一般自适应滤波算法代价函数结构特性一致. 据此, 基于该函数模型框架再利用低阶误差准则来推导本文算法, 首先定义一个代价函数形式:2 )式可以看出, 接下来本文算法的关键是将$J(e(i))$ 的表达式推导出来. 给定一个以输入向量u [24 ] 核$ \kappa ({\boldsymbol{u}}, \cdot )$ 作为再生核, 通常使用的再生核包括多项式核和高斯核, 因为高斯核具有类似于径向基网络的无限逼近性, 所以本文算法采用高斯核作为再生核, 其定义为$\kappa ({\boldsymbol{u}}, {{\boldsymbol{u}}'}) = $ $ \exp ( - h{\left\| {{\boldsymbol{u}} - {{\boldsymbol{u}}'}} \right\|^2})$ . 利用核方法将输入信号通过再生核变换到高维空间, 并且根据Mercer定理任意再生核可以扩展为${\boldsymbol{u}} \!=\! [u(n), u(n-1), \cdots, u(n - L \!+\! 1) ]^{\rm T}$ 通过非线性映射φ 从输入空间U 变到希尔伯特空间, 得到映射后的信号$\varphi ({\boldsymbol{u}}) = [\varphi (u(n)), \varphi (u(n - 1)), $ $ \cdots, \varphi (u(n - L + 1))]^{\rm{T}}$ , 根据(3 )式得到$\varphi {(u(n))^{\rm{T}}} $ $ \varphi (u{(n)'}) = \kappa ({\boldsymbol{u}}, {{\boldsymbol{u}}'})$ , 为方便表达令$\varphi (u(n)) = \varphi (i)$ . 基于文献[25 ]的代价函数:$d(i)$ 为期望信号, $w(i)$ 为滤波器权重, p 为代价函数的幂次, 将(4 )式代入(2 )式, 就得到了本文算法的代价函数为w φ 是一个隐藏函数, 只在算法迭代中体现, μ 是算法的步长因子.5 )式中引入一个尺度因子$\lambda > 0$ , 该尺度因子用来控制${S_i}$ 的陡峭程度, 那么(5 )式变为${S}_{m}=\dfrac{1}{1+{\rm{e}}^{-\lambda {\left|e(i)\right|}^{p}}},$ 那么(8 )式将变为$\dfrac{1}{{1 + {{\rm{e}}^{ - {{(e(i))}^2}}}}}$ , $\dfrac{1}{{1 + {{\rm{e}}^{ - {{(e(i))}^4}}}}}$ 和$\dfrac{1}{{1 + {{\rm{e}}^{ - {{\left| {e(i)} \right|}^{}}}}}}$ 等几种不同的代价函数进行比较, 结果如图1 所示. 从图1 可以看到相比于其他代价函数, 本文算法代价函数曲线在误差接近于0时的收敛速度是最快的, 且在误差较大时也是比较平滑的, 这充分说明了该代价函数能够保证稳态平稳的前提下提高收敛速度.图 1 不同代价函数曲线Figure1. Different cost function curves.图2 给出了引入的尺度因子λ 对算法性能的影响. 从图2 可以看出λ 取值越大, 收敛速度越快. 但也不是越大越好. 因为从自适应滤波算法的调整原则出发, 希望在误差较大时取一个大的λ 值使梯度下降快从而提高收敛速度, 而当误差较小时取一个小的λ 值来使梯度平缓进而提高算法的稳定性. 因此考虑需要一个变化的尺度因子去自动调节算法的性能. 而误差的随机信息都直接受这一尺度因子的影响.图 2 不同λ 值对代价函数的影响Figure2. Effect of different λ values on the cost function.27 ]中变步长方法的变尺度因子策略, 来代替尺度因子的手动设置. 可得$0 < \beta < {\rm{1}}$ , $\gamma > 0$ , β 和γ 是共同调节$\lambda (i)$ 的常数. 将变尺度因子表达式代入(10 )式便得到了VS-SKFLP算法的权重更新公式:β 和γ 对算法性能的影响以及后续仿真中的取值原则, 图3(a) 和图3(b) 所示为在固定$\gamma = 0.001$ 、改变β 以及固定$\beta = 0.1$ 、改变γ 的情况下VS-SKFLP算法学习曲线. 从图3(a) 可以观察到以下情况: 当$\beta = 0.1$ 时, 相比于更小的β 取值具有较快的收敛速度, 而相比于更大的β 取值具有更低的稳态误差. 从图3(b) 可以看出, 并非所有取值都能达到好的学习效果, 当γ 取值太大时会使收敛速度过慢, 而取值太小时性能极其不稳定, 只有当$\gamma = 0.001$ 时算法性能达到最优. 所以在本文中取$\beta = 0.1$ , $\gamma = 0.001$ .图 3 不同参数β , γ 下VS-SKFLP算法的学习曲线 (a) β 取不同值; (b) γ 取不同值Figure3. Learning curves of VS-SKFLP algorithm with different parameters of β (a) and γ (b).3.VS-SKFLP算法的性能分析 利用能量守恒关系, 来分析评价算法的收敛性能. 假设存在一非线性系统模型:${w_{\rm{o}}}$ 表示该未知非线性系统的冲激响应, $v(i)$ 为干扰噪声. 那么算法的输出误差可以表示为13 )式代入(14 )式, 即:${e_{\rm{a}}}({{i}})$ 为先验误差, ${\tilde w (i-1)} = {w_{\rm{o}}} - w(i - 1)$ 为权重偏差. 将(10 )式两边同时减去${w_{\rm{o}}}$ 得到偏差的迭代表达式:${e_{\rm{p}}}(i) = {\tilde w} {(i)^{\rm{T}}}\varphi (i)$ , (16 )式证明过程之所以用λ 而不是用$\lambda (i)$ , 是因为对于权重的每一次迭代都对应一个特定的λ 值, 为了使证明过程表达式更为简单. 之后对(16 )式两边同乘以$\varphi (i)$ 得到后验误差迭代表达式:18 )式两边二范数平方求期望得到能量关系:20 )式, 若要使算法均方收敛, 则需满足$E\left[ {{{\left\| {\tilde w(i) } \right\|}^2}} \right] \leqslant E\left[ {{{\left\| {\tilde w (i-1)} \right\|}^2}} \right]$ , 即:μ > 0, 则存在22 )式确定. 但在实际应用中由于计算复杂, 一般以仿真值为准.4.模拟仿真与结果分析 为了验证本文所提VS-SKFLP算法的优良性能, 将其与KFLP, KLMS, KMCC算法等其他核自适应滤波算法在被非高斯噪声干扰的非线性系统识别环境下进行比较. 实验仿真条件为: 给定一个n 时刻随机输入序列$\{ u(1), \;u(2), \; \cdots ,\;u(N)\}$ , 该组数据经过由线性模型和非线性模型组合而成的非线性系统, 并被非线性信道噪声干扰, 其中线性模型为$H(z) = 1 + 0.2{z^{ - 1}}$ , 输出为$x(n) = u(n) + $ $ 0.2 u(n - 1)$ , 非线性模型为$g(n) = x(n) - 0.6 x{(n)^2}$ , 因此该非线性系统的期望输出模型为$d(n) = $ $ x(n) - 0.6 x{(n)^2} + v(n)$ , 其中$v(n)$ 为额外噪声. 本文采用非高斯噪声干扰和有色噪声干扰两种不同的额外噪声来对算法进行分析, 其中非高斯噪声采用高斯噪声与冲激噪声相结合的形式产生. 一般的冲激噪声可以被表示为伯努利-高斯过程[24 ] , 由$q(n) = a(n)c(n)$ 表示, $c(n)$ 是一个伯努利过程, ${{a}}(n)$ 是一个零均值的高斯白噪声过程, 且设定高斯核函数的核宽参数$h = 0.2$ . 归一化均方误差性能曲线被用来评价算法性能, 为了使各算法在最理想的情况下进行比较, 给出了不同算法的参数选择, 如表1 所列, 且各参数的选择都是经过交叉验证所得.SP-KFLP KFLP KMCC KLMS 本文算法 μ 0.5 0.1 0.5 0.1 0.1 P 0.9 0.9 0.9 β 0.1 γ 0.0001 h 0.2 0.2 0.2 0.2 0.2
表1 各算法参数设置Table1. Parameter setting of each algorithm.4.1.本文算法与其他核自适应滤波算法性能比较 4.1.本文算法与其他核自适应滤波算法性能比较 将本文算法VS-SKFLP与对比算法用于未知系统的追踪, 并就收敛性和抗冲激干扰性能进行如下比较.图4 所示. 从图4 可以看出, 在高斯噪声环境下, 除KMCC算法外本文算法与其他算法均可以达到良好的收敛效果, 但本文VS-SKFLP算法的收敛速度比其他几种算法快, 说明本文算法具有更优的收敛性能.图 4 高斯噪声环境下五种算法的性能比较Figure4. Performance comparison of five algorithms in Gaussian noise environment.${p_{\rm{q}}} = 0.03$ . 其他参数同上面实验的选择, 实验结果如图5 所示. 从图5 可以看出, KLMS算法的脉冲噪声抑制能力相对较差, 而本文算法和KFLP算法均具有很强的脉冲噪声抑制能力, 但本文VS-SKFLP算法的收敛速度比KFLP算法快.图 5 非高斯干扰下的KFLP, KLMS与VS-SKFLP算法性能比较Figure5. Performance comparison of KFLP, KLMS and VS-SKFLP algorithms under non-Gaussian interference.${p_{\rm{q}}} = 0$ )且在第600次迭代时产生一个冲激噪声的情况下, 本文的VS-SKFLP算法和其他两种算法SP-KFLP, KFLP的性能对比. 参数选择同上面实验, 结果如图6 所示. 从图6 不难看出, 收敛性能基本和图5 的结论一致, 另外当冲激噪声产生时, KLMS算法不具有抗冲激噪声的性能, 而本文算法相比于其他算法收敛速度最快, 并且能有效避免冲激噪声干扰.图 6 在第600次迭代过程中加入冲激噪声时各算法性能对比Figure6. Performance comparison of various algorithms when impulse noise is added during the 600th iteration.4.2.不同有色噪声环境下算法性能比较 -->4.2.不同有色噪声环境下算法性能比较 为进一步验证本文算法的鲁棒性, 给出了非线性系统被不同有色噪声干扰下的VS-SKFLP算法的追踪性能. 所谓有色噪声是指序列没有一个时刻是不相关的, 与高斯白噪声相比其幅度谱基本一致, 即幅度大小表现相同但频谱却相差较大. 如图7 为常见的几种有色噪声, 其中包括红噪声、蓝噪声、粉噪声和Violet噪声, 将这四种有色噪声作为系统的额外噪声$v(n)$ 对算法进行验证, 结果如图8 所示.图 7 几种常见的有色噪声Figure7. Several common colored noises.图 8 不同有色噪声环境下算法性能比较Figure8. Performance comparison of algorithms in different colored noise environments.图8 可以看出, 本文算法对红噪声和Violet噪声具有一定的鲁棒性, 这表明本文算法在一定程度上是可以抵制有色噪声的. 但是当噪声为蓝噪声和粉噪声时算法性能严重下降, 后续工作有待进一步的改进.5.结 论 基于低阶统计准则和Sigmoid函数的非线性饱和特性, 本文通过将核分式低次幂算法的代价函数嵌入S型函数来构造了一种新的代价函数框架, 并通过引入的变尺度因子, 进一步有效地提高了核自适应滤波算法在非高斯环境下的非线性系统追踪性能. 仿真结果表明, 与KLMS, KMCC, KFLP, SP-KFLP等其他核自适应算法相比, 本文算法不论是在非高斯冲激噪声下还是有色噪声干扰下都具有良好的收敛性能和低稳态误差, 并且在有色噪声环境下具有一定的鲁棒性. 当然对于算法在粉噪声和蓝噪声环境下性能下降的问题, 有待进一步的研究与改进. 






















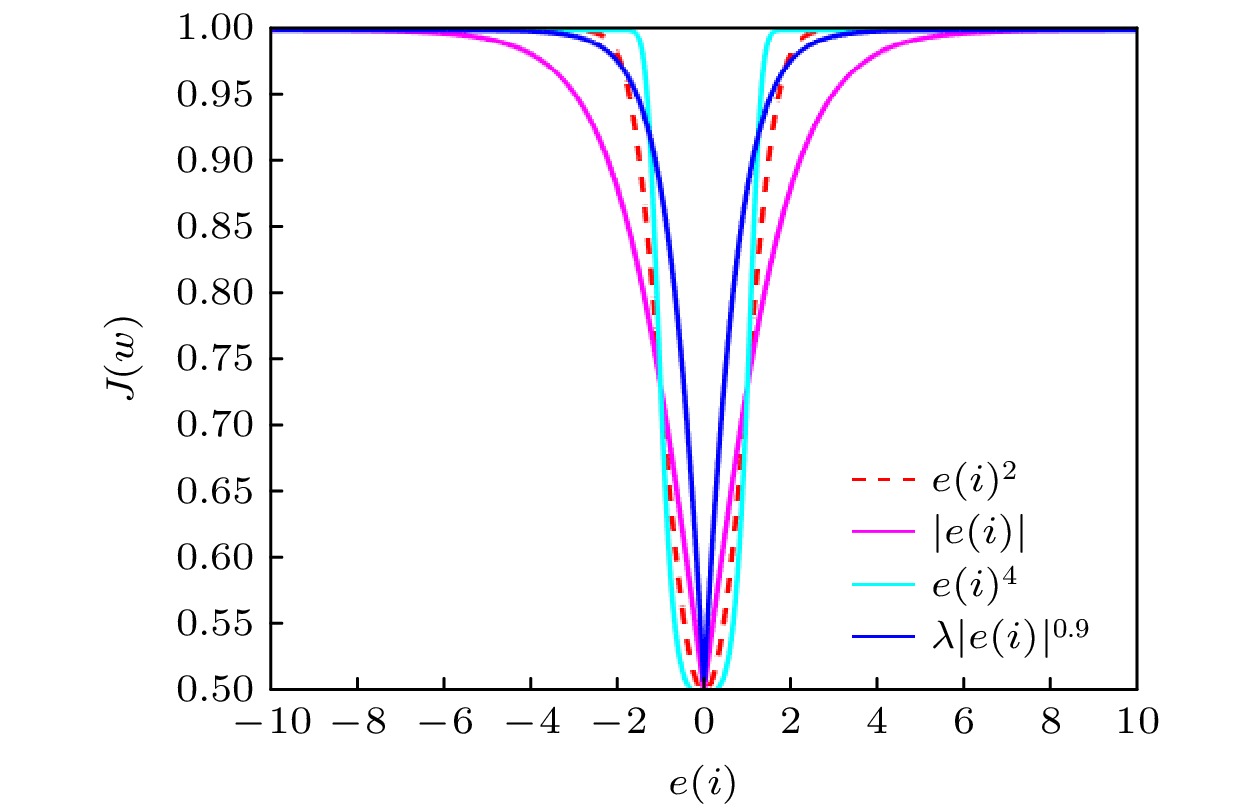 图 1 不同代价函数曲线
图 1 不同代价函数曲线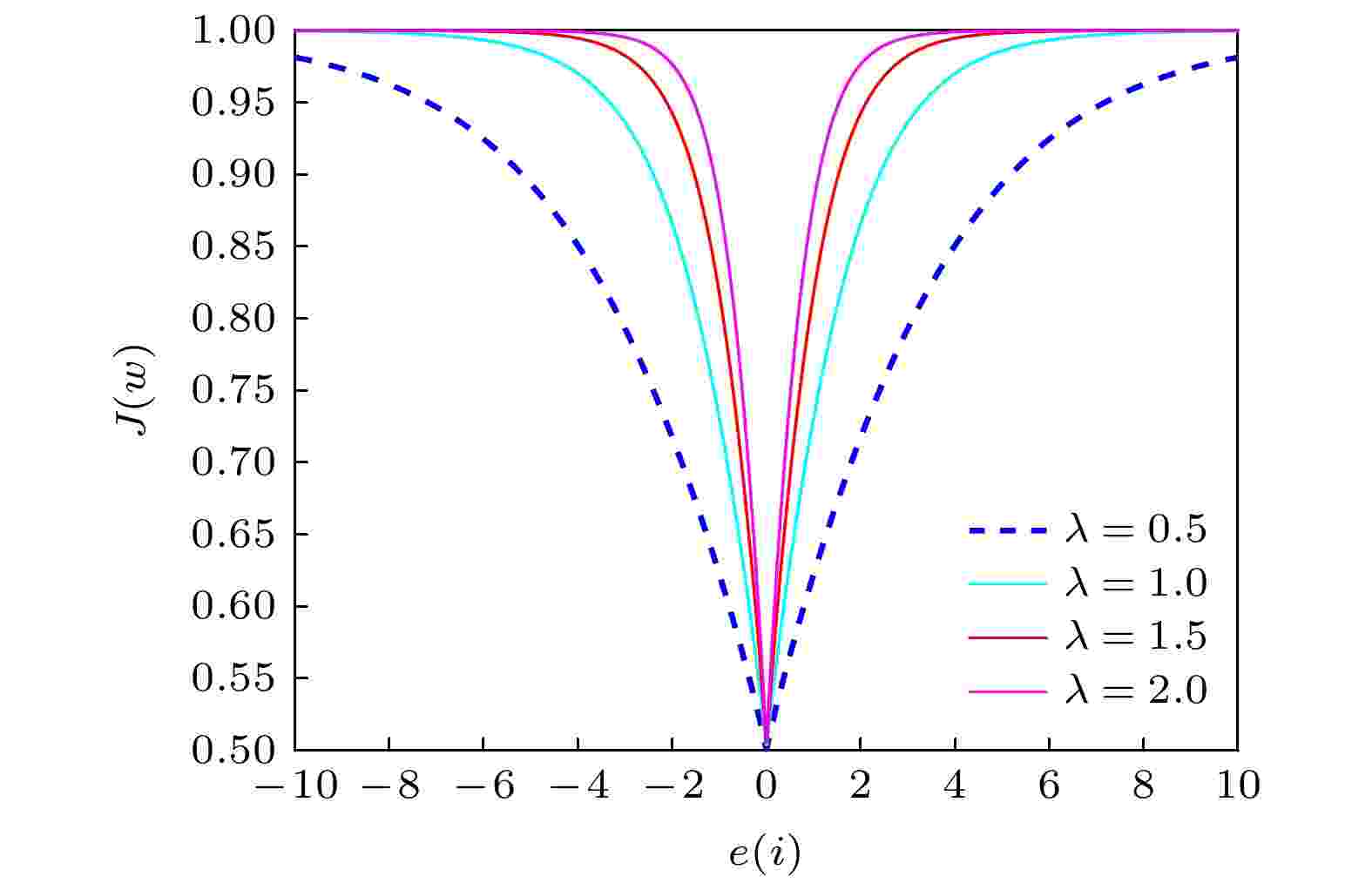 图 2 不同λ值对代价函数的影响
图 2 不同λ值对代价函数的影响




















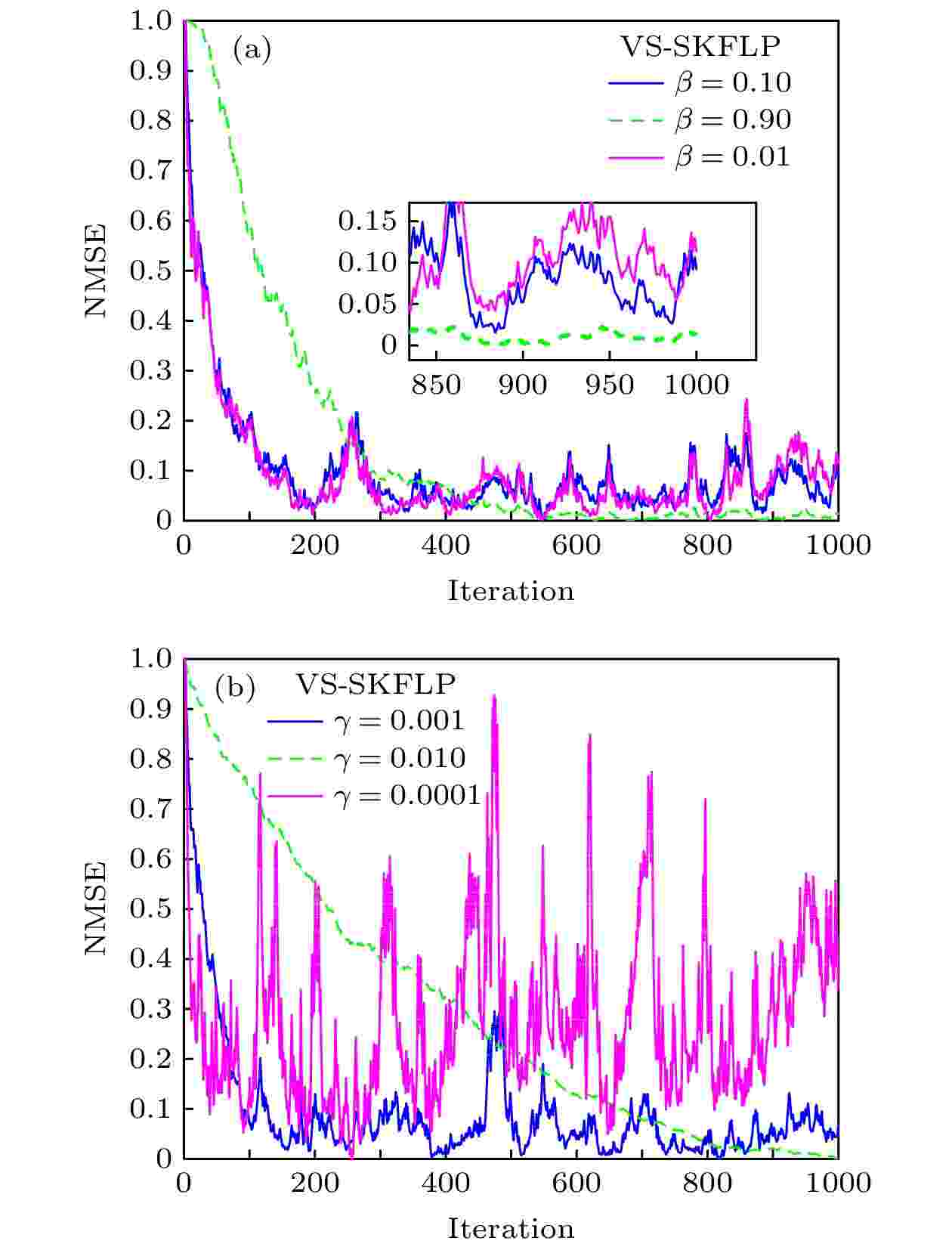 图 3 不同参数β, γ下VS-SKFLP算法的学习曲线 (a) β取不同值; (b) γ取不同值
图 3 不同参数β, γ下VS-SKFLP算法的学习曲线 (a) β取不同值; (b) γ取不同值




















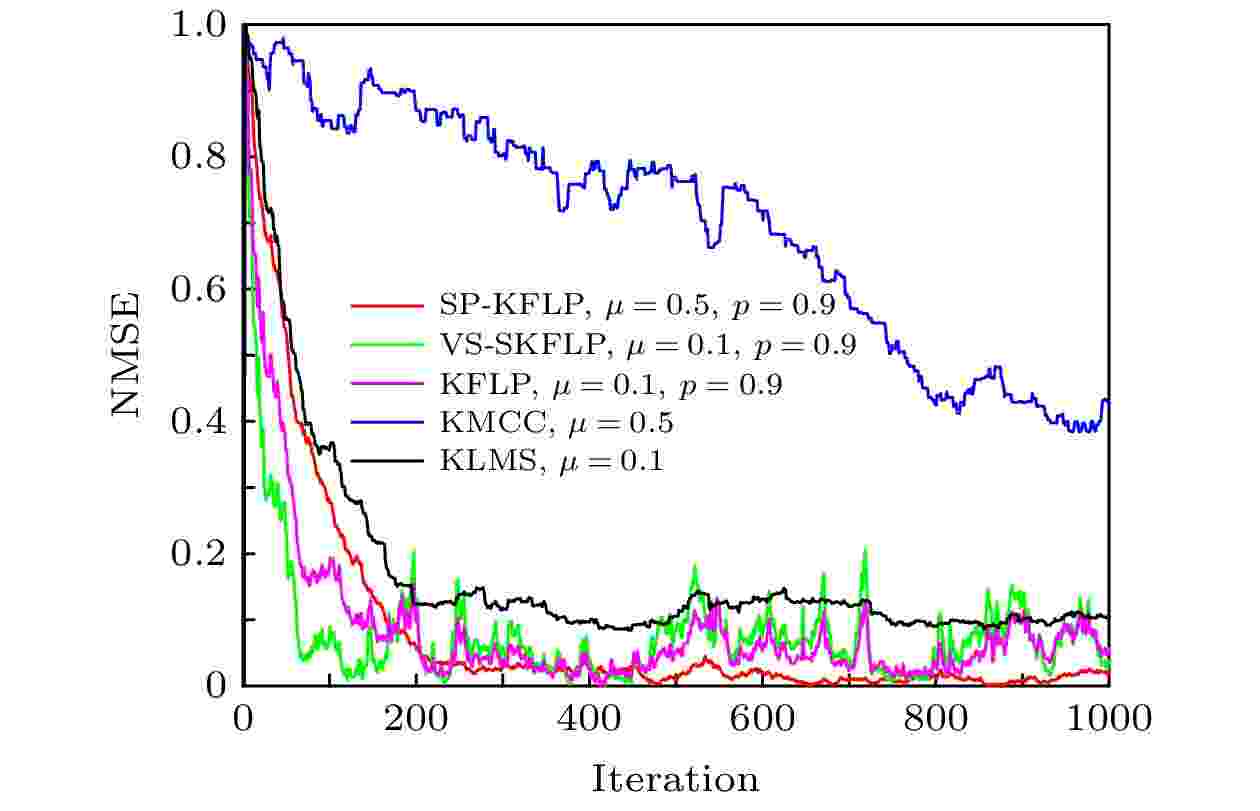 图 4 高斯噪声环境下五种算法的性能比较
图 4 高斯噪声环境下五种算法的性能比较
 图 5 非高斯干扰下的KFLP, KLMS与VS-SKFLP算法性能比较
图 5 非高斯干扰下的KFLP, KLMS与VS-SKFLP算法性能比较
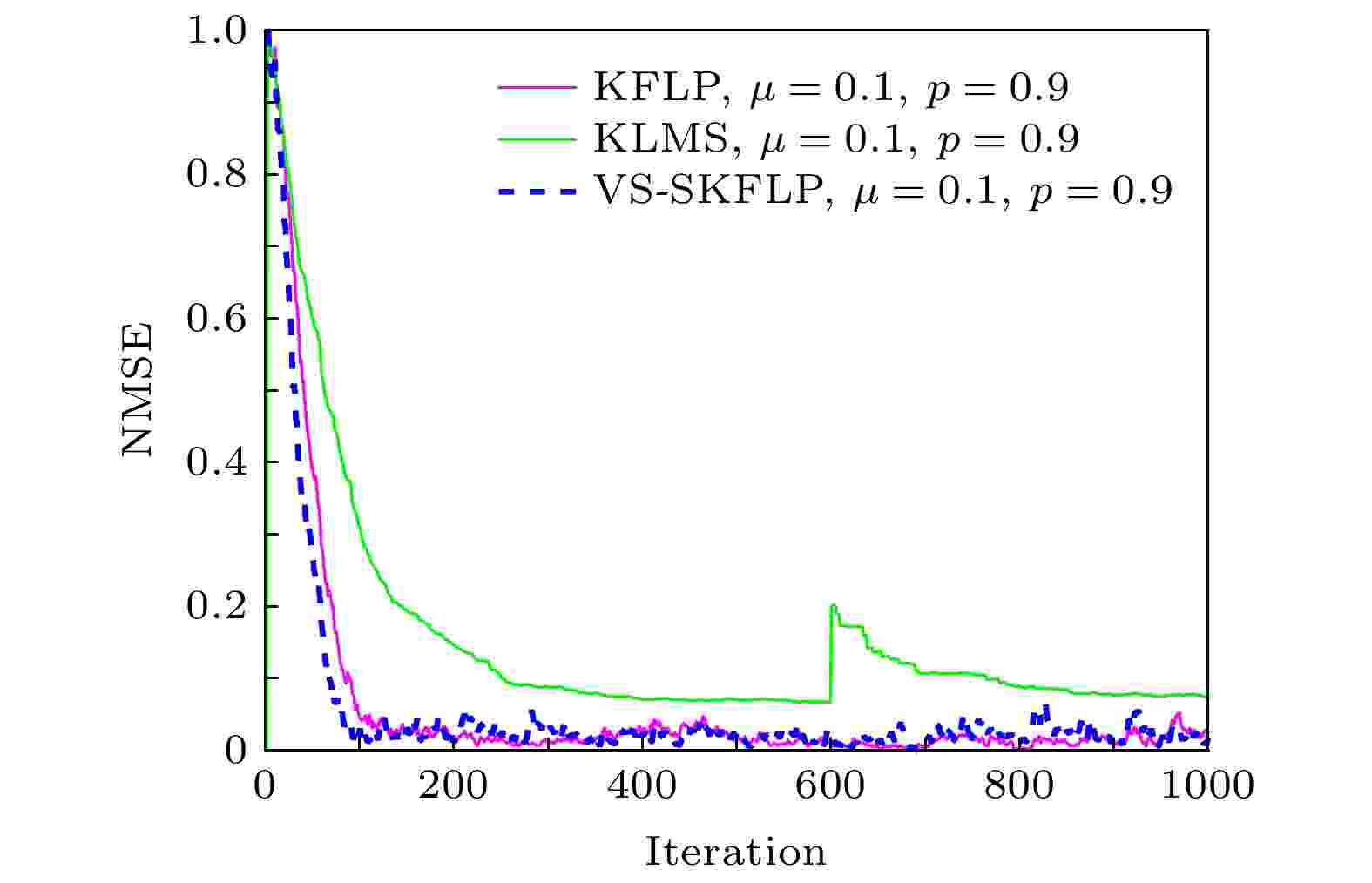 图 6 在第600次迭代过程中加入冲激噪声时各算法性能对比
图 6 在第600次迭代过程中加入冲激噪声时各算法性能对比
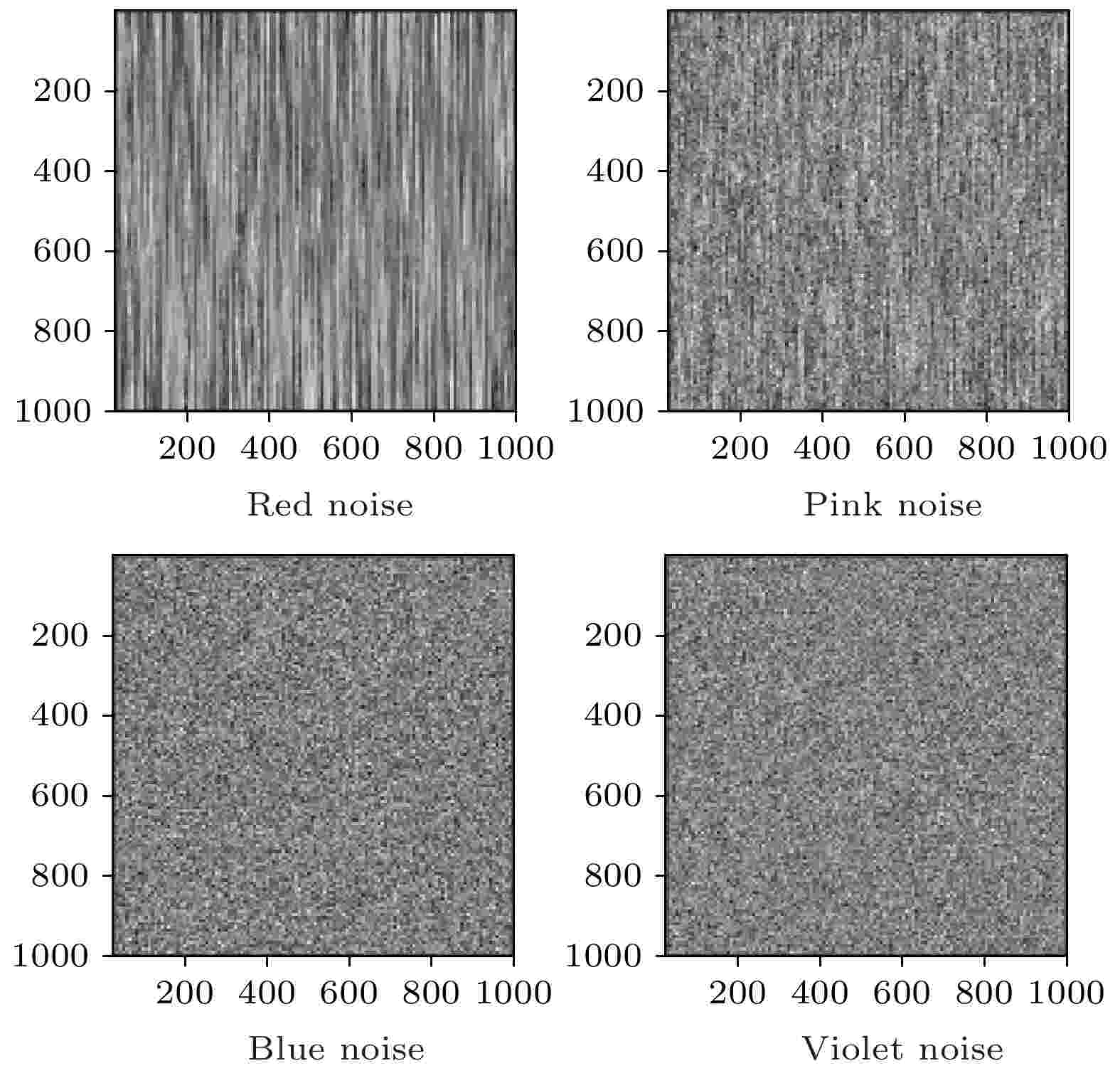 图 7 几种常见的有色噪声
图 7 几种常见的有色噪声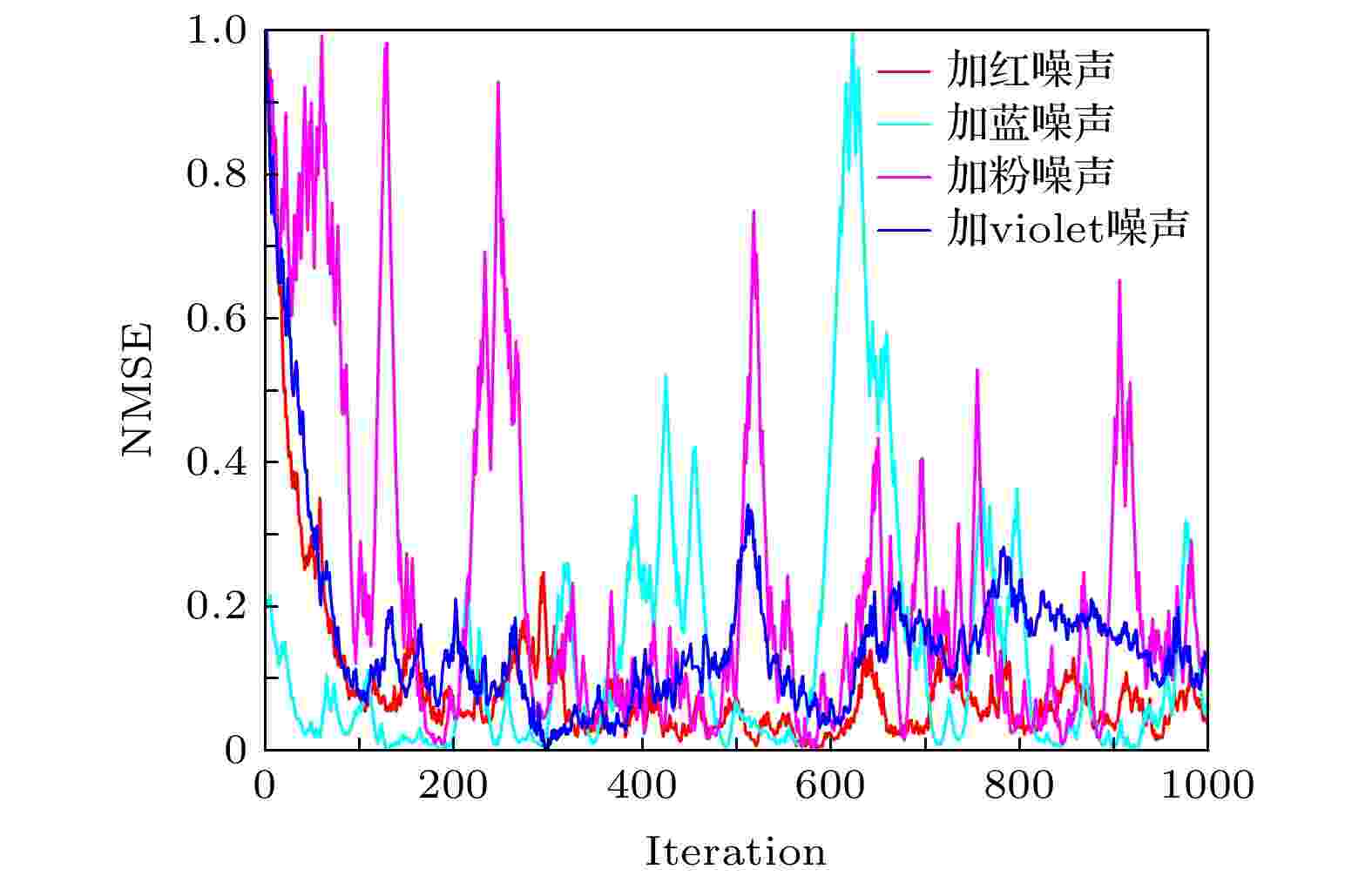 图 8 不同有色噪声环境下算法性能比较
图 8 不同有色噪声环境下算法性能比较