全文HTML
--> --> -->因为高光谱层析成像技术能显著地减少测量投影的数量, 及能同时重建温度和气体浓度分布、对噪声不敏感性等优势, 受到了科研人员的重视. 近年来涌现出大量运用HT技术测量燃烧流场分布的报道, 如克莱姆森大学Ma等[13]将TDLAS技术与HT技术结合, 测量了Hencken火焰炉的温度和H2O浓度. 牛津大学Paul等[14]数值仿真模拟了10 × 10网格的燃烧场分布, 通过在场分布上叠加5%的高斯噪声来模拟真实实验条件, 数值研究结果验证了HT技术在空间分辨火焰测温中的可行性和鲁棒性. 国内上海交通大学Cai和Ma[15]采用1.8 μm附近的10条H2O吸收谱线仿真重建了燃烧场的温度和气体浓度分布, 并与传统依赖于双波长的层析成像技术相比, 验证了高光谱层析成像在同时重建、层析反演的灵敏度和稳定性上的优越性. 东南大学李根[16]研究了HT技术在火焰二维场重建上的应用, 分别以光谱积分吸收率和谱线峰值吸收率为投影值进行重建, 研究表明以光谱积分吸收率为投影值的重建效率和精度较高, 而以谱线峰值吸收率为投影值因为加入了线型, 效率和精度略有下降, 但后者具有较强的环境适应性. 虽然已有的利用HT技术重建燃烧流场分布的研究很多, 但对于重建中如何选取谱线组合的研究较少, 且在重建中常用的模拟退火算法(simulated annealing algorithm, SA)收敛速度慢、运行效率低, 严重影响了HT技术在实际测量燃烧场中的应用.
本文研究了Ma等[17]提出的基于基本二区分布的最优谱线组合选取方法, 从12条预筛选谱线中分别选取出最优的5条谱线组合和8条谱线组合. 在重建算法的改进上, 通过对模型扰动方式以及退火策略上的改动, 进一步提高了算法运行效率和跳出局部最优解空间的机会. 数值仿真结果表明, 选取最优谱线组合能提升燃烧场分布重建的精度, 且光谱信息的增加有利于重建精度的提升, 经过改进后的SA算法重建燃烧场相较于传统SA算法在重建精度上保持一致, 但运行时间加快了近40倍. 实验室验证实验结果表明, 改进后的SA算法在重建实际燃烧场上, 能够较好地还原原始场分布, 重建分布与原始场分布燃烧特征基本一致. 通过本文研究最优谱线组合及对传统SA算法的改进, 对利用HT技术对燃烧流场在实际应用中的温度和浓度场分布反演研究工作具有重要意义.
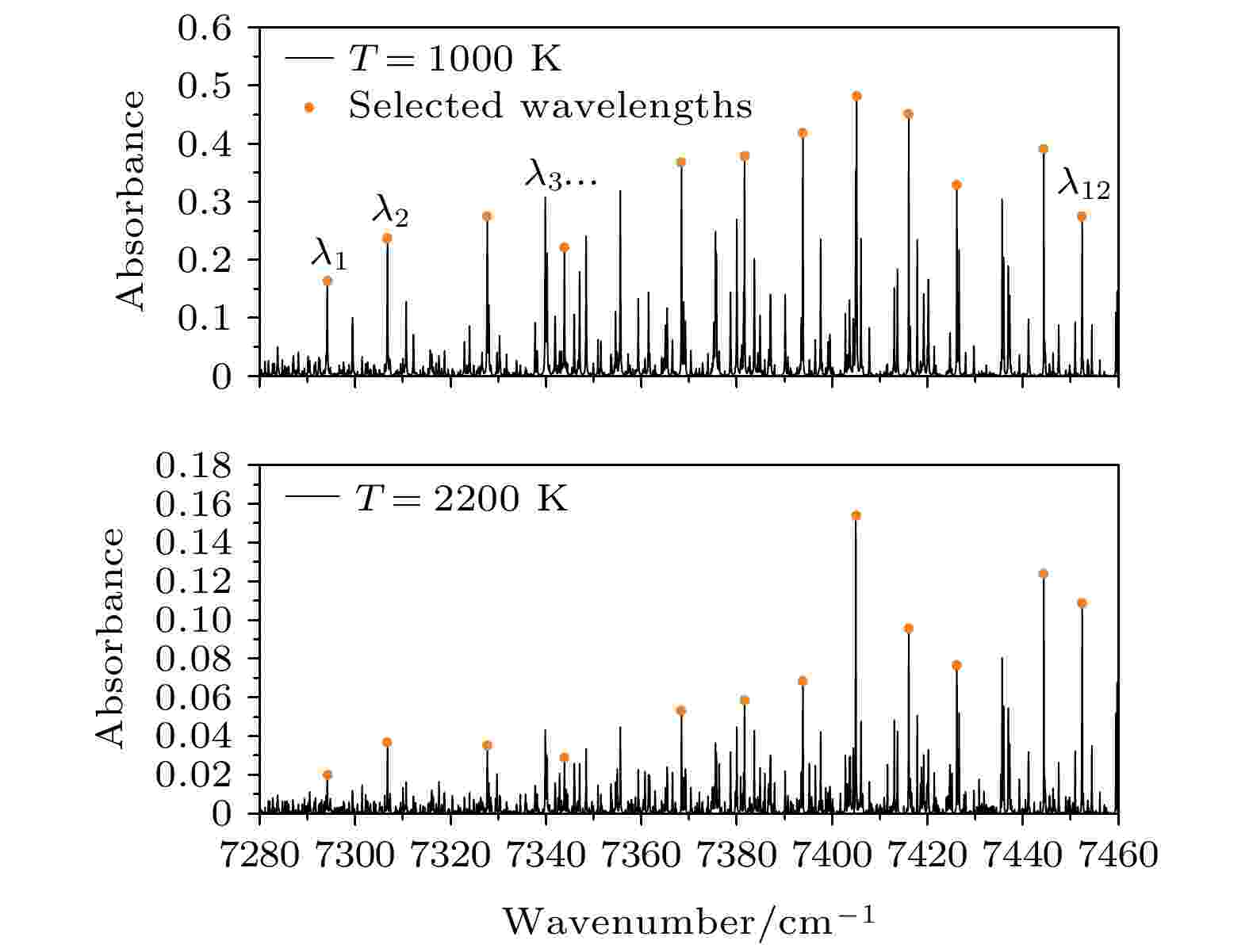 图 1 预先筛选出的12条吸收谱线
图 1 预先筛选出的12条吸收谱线Figure1. The 12 candidate absorption transition lines.
| ${\nu _0}/{\rm{c}}{{\rm{m}}^{ - 1}}$ | $S({T_0})/({\rm{c} }{ {\rm{m} }^{ - 2} } \!\cdot\! {\rm{at} }{ {\rm{m} }^{ - 1} })$ | $E''$ |
| 7294.12 | 0.4041 | 23.7944 |
| 7306.75 | 0.4463 | 79.4964 |
| 7327.68 | 0.4612 | 136.7617 |
| 7343.85 | 0.3298 | 173.3658 |
| 7368.41 | 0.1731 | 447.2523 |
| 7381.61 | 0.0999 | 586.2435 |
| 7393.85 | 0.0516 | 744.1626 |
| 7405.11 | 0.0247 | 920.1680 |
| 7416.05 | 0.0142 | 1114.4030 |
| 7426.14 | 0.0042 | 1327.1096 |
| 7444.35 | 0.0005 | 1774.7503 |
| 7452.41 | 0.0002 | 2073.5139 |
表112条H2O吸收谱线的光谱参数
Table1.Spectral parameters of 12 H2O absorption lines.
对于非均匀燃烧场, 根据文献[17]中分析, 存在一个假设: 如果对于任意的非均匀分布, 存在一组谱线组合是最优的, 那么这组谱线组合对于特定的二区分布也一定是最优的. 可以通过求解一系列基本二区分布来得到任意分布, 即首先将待测区域划分为两个区域, 每个区域内的温度






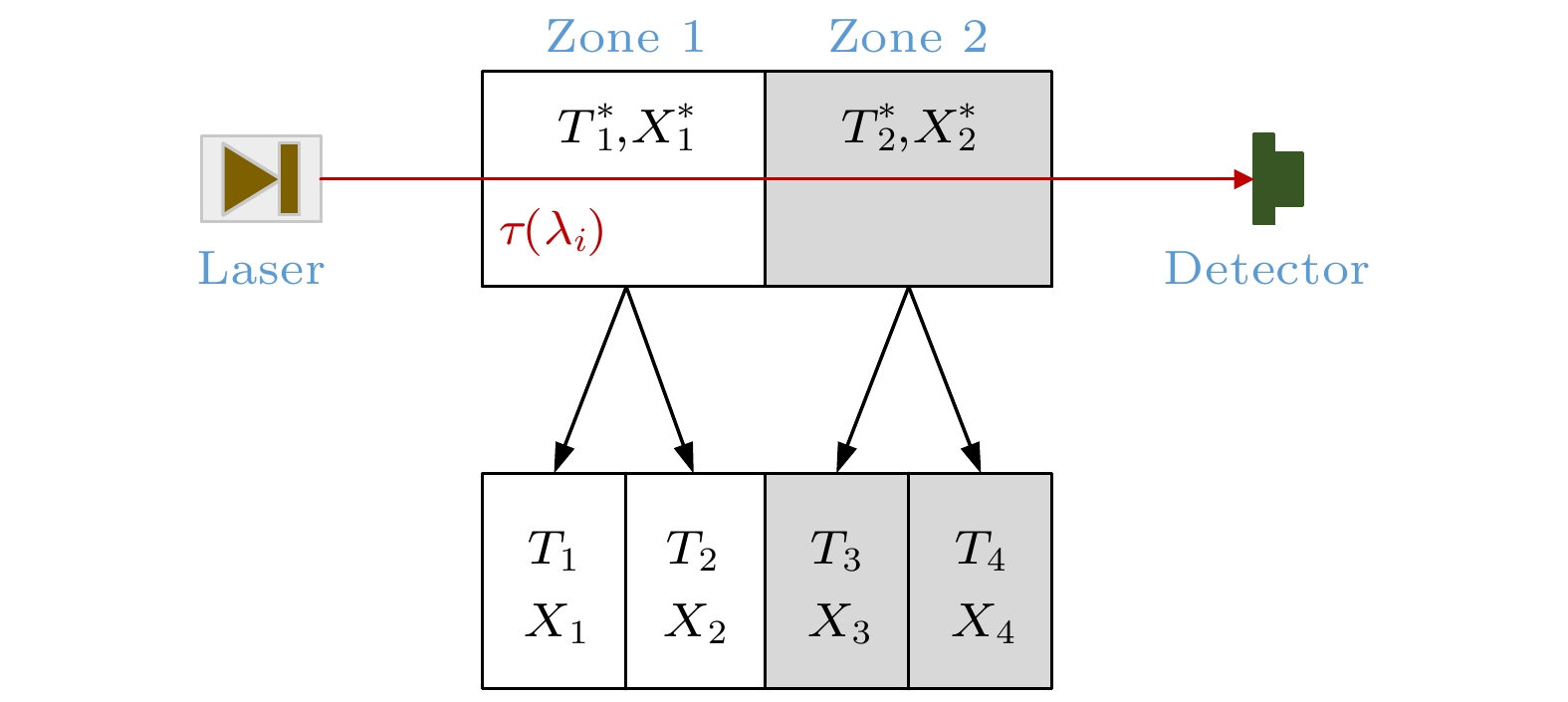 图 2 基本的二区分布及其进一步划分
图 2 基本的二区分布及其进一步划分Figure2. The basic simple two-zone distribution and its further division.
针对上述提到的选择最优谱线组合的方法, 需要一个量化标准来判断选取谱线组合的优劣, 文献[17]用式(1)来定义这个量化标准, 其表达式为
























在高光谱层析成像背景下, 进行非均匀分布的多个跃迁谱线的选择. 为更好地贴近真实燃烧流场情况, 通过在一个抛物面上叠加四个高斯峰来模拟实际燃烧装置中遇到的多模态和不对称温度分布, 场分布呈8 × 8网格离散分布, 如图3左侧所示, 图3右侧为模拟的浓度分布, 通过对待测区域形成8 × 8共16条光路呈正交分布的探测阵列, 得到光谱信号. 层析反演时可以通过模拟退火算法求解非线性最小化问题来进行, 算法及其改进将在下一小节中单独讨论.
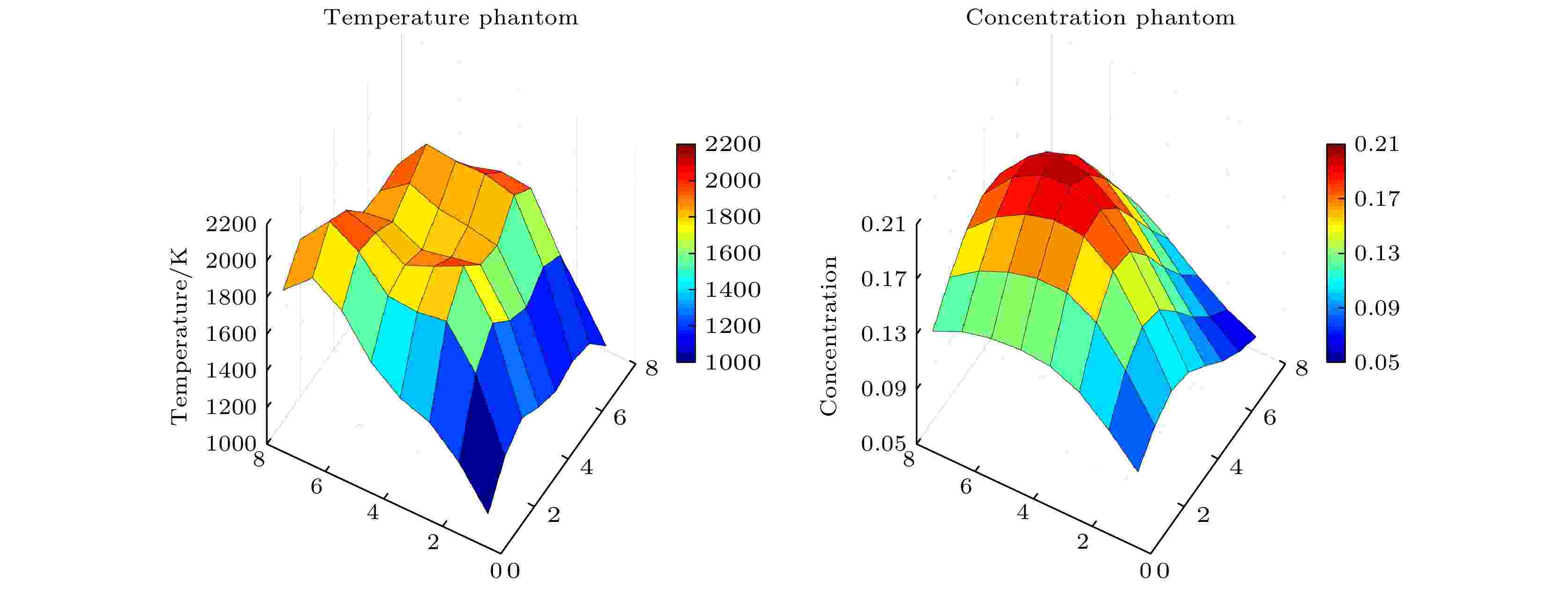 图 3 模拟的燃烧流场的温度和浓度分布
图 3 模拟的燃烧流场的温度和浓度分布Figure3. Temperature and concentration distribution of simulated combustion flow field.
为更好地定量重建场与模拟场之间的误差, 使用归一化平均绝对误差来定义, 其表达式为




为更好地说明










 图 4 所有5条谱线组合的重建误差
图 4 所有5条谱线组合的重建误差Figure4. Reconstruction error of all 5 spectral line combinations.
从图4中可以得知, 在实际应用中, 并不一定要完全得到精确的谱线组合排序, 当最佳谱线组合的重建精度没有特别差异性的时候, 只需要选取到最优的50组内的一组即可.
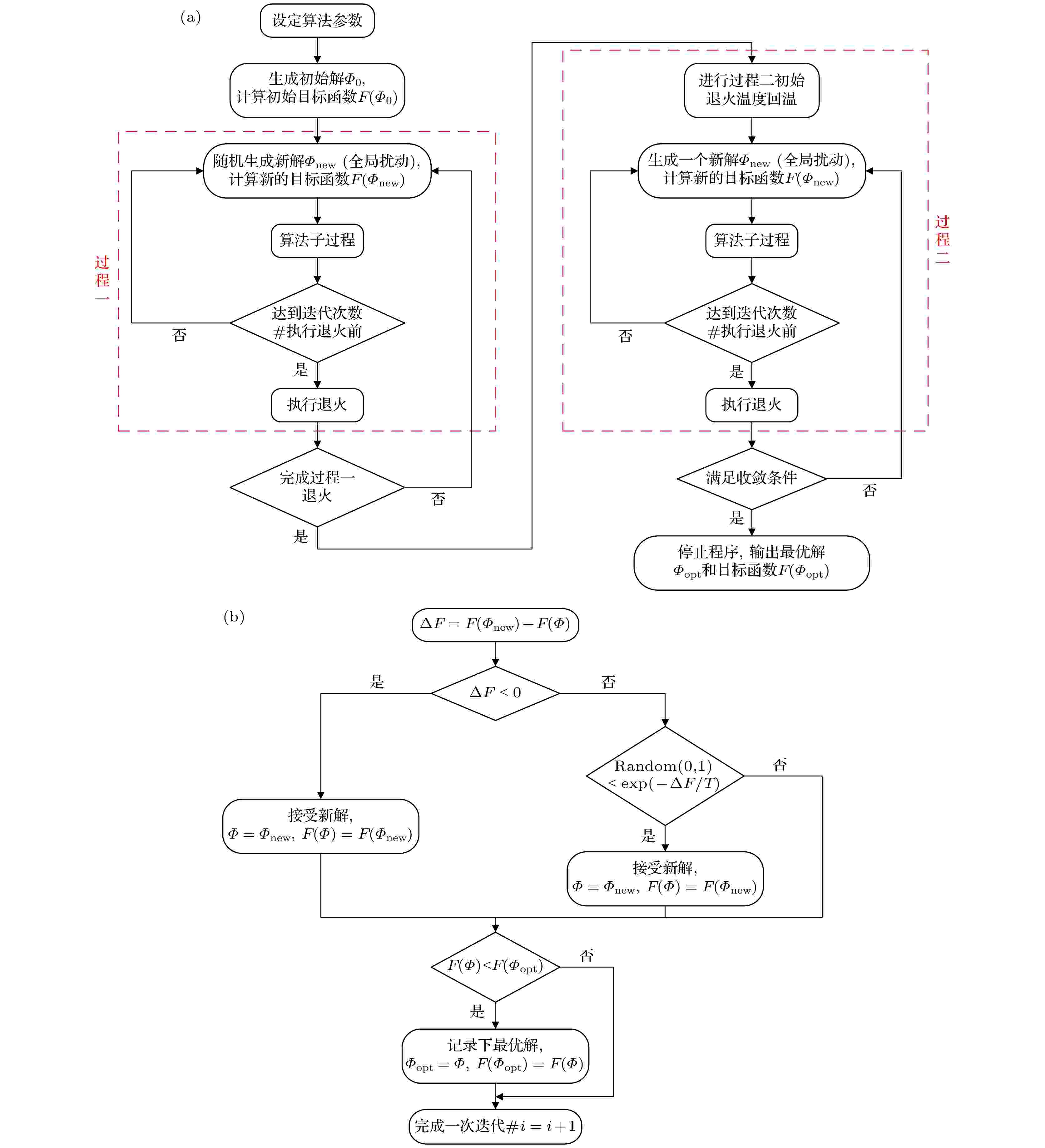 图 5 两段式模拟退火算法流程图 (a) 算法主流程; (b) 算法子过程
图 5 两段式模拟退火算法流程图 (a) 算法主流程; (b) 算法子过程Figure5. Flow chart of two-stage simulated annealing algorithm: (a) Main flow of algorithm; (b) subprocess of algorithm.
在本文中, 判断过程一是否完成退火准则为过程一退火迭代次数达50次. 下面给出过程一和二中具体改进后的模型扰动表达式.
过程一: 全局搜索, 以找到及锁定最优解区间, 模型扰动方式采用的是随机的全局扰动方式, 这与传统模拟退火算法中的固定步长的初始模型扰动方式不一致, 表达式如下式所示:




过程二: 回火升温, 局部搜索, 在被锁定的最优解空间内进行局部搜索, 每次搜索空间的步长根据模型扰动后接受解的概率进行调整, 相较于传统模拟退火算法, 模型扰动方式有了较大的改变, 表达式如下式所示:










除上述模型扰动方式以外, 还在退火策略上作出了改动, 不同于传统模拟退火算法中用到的三种温度衰减函数[20], 应用了包含快速冷却机制和再加热机制的温度衰减函数, 能更有效地控制退火温度, 并且使得模型拥有再次跳出局部最优解的机会.
在算法程序运行过程中, 计算出目标函数的变化率, 定义为







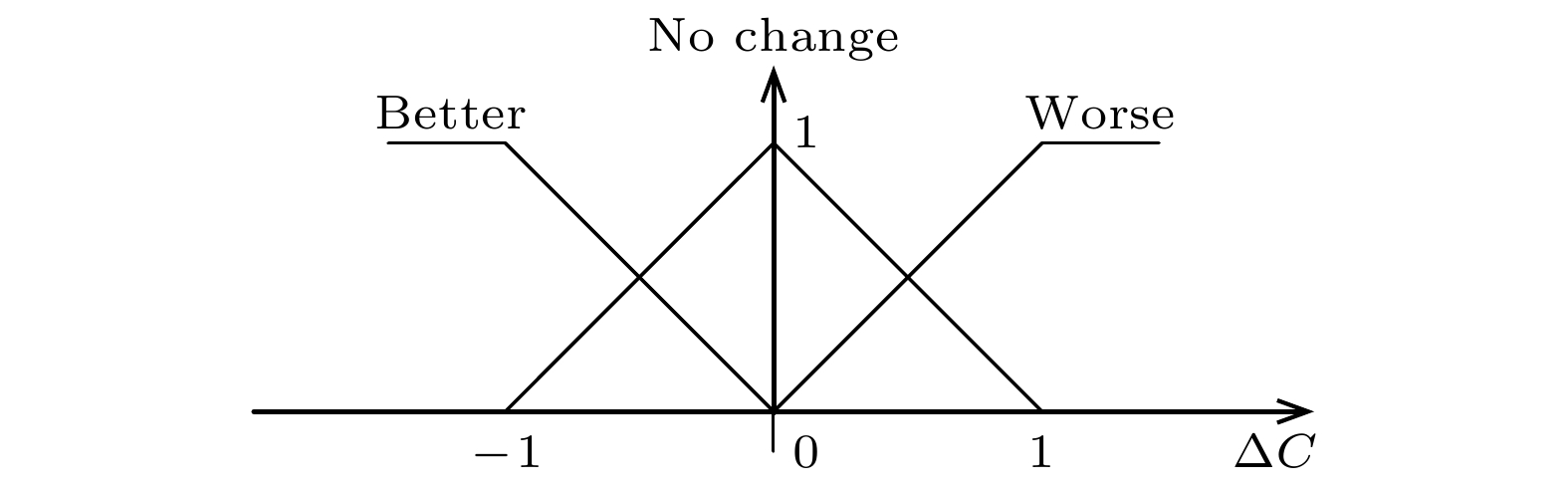 图 6
图 6 
Figure6. The three fuzzy sets of






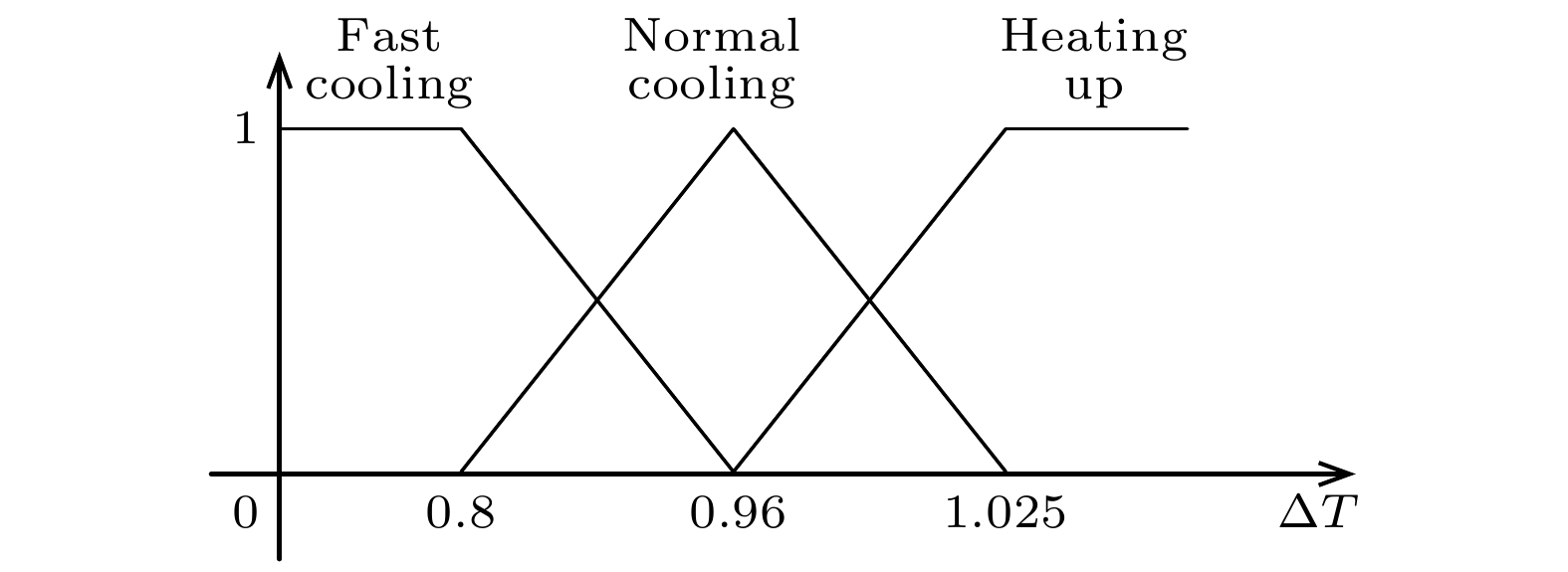 图 7
图 7 
Figure7. The three fuzzy sets of




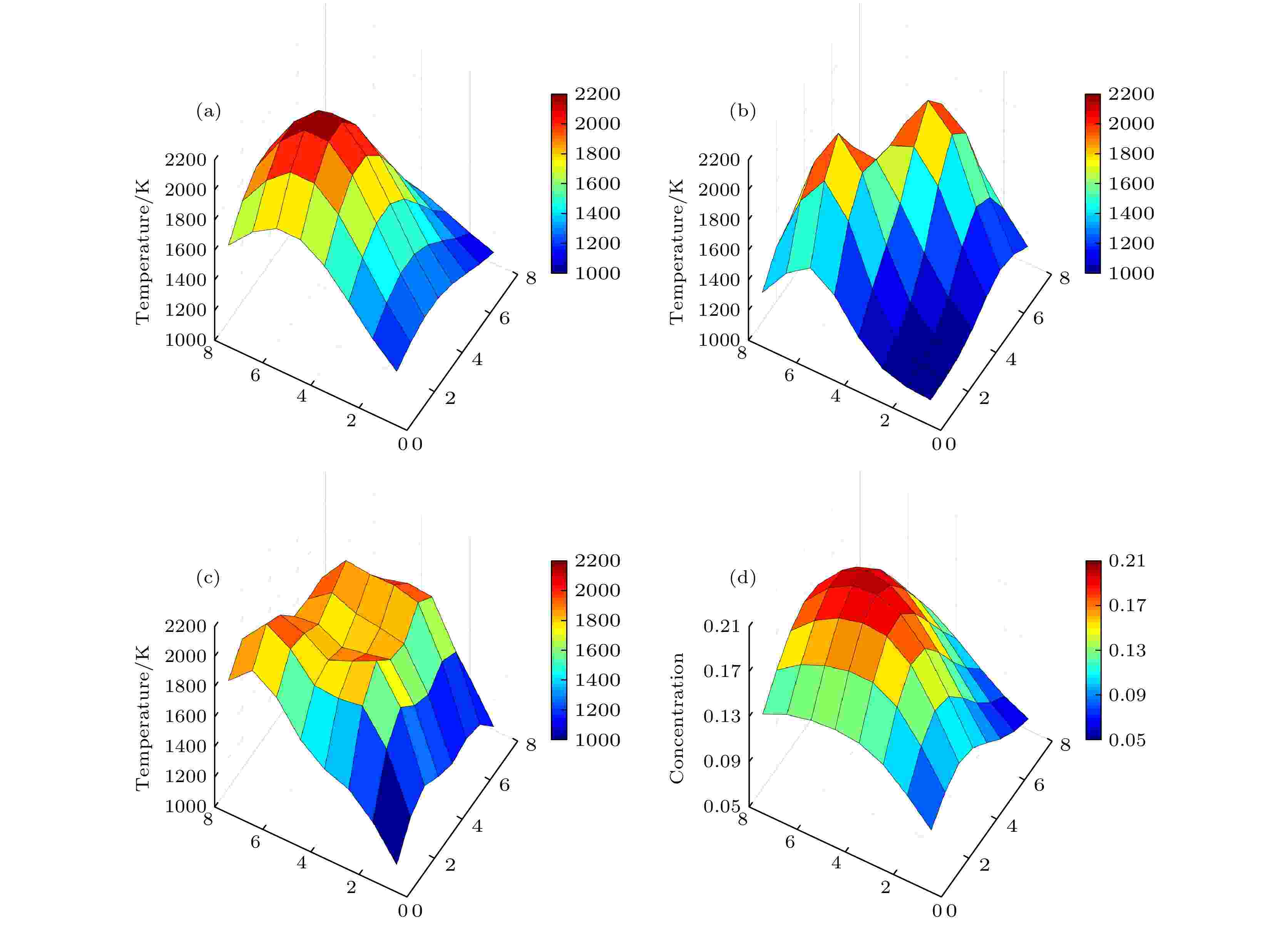 图 8 三种不同模态燃烧场分布 (a) 单高斯峰; (b) 双高斯峰; (c) 多高斯峰; (d) 浓度分布
图 8 三种不同模态燃烧场分布 (a) 单高斯峰; (b) 双高斯峰; (c) 多高斯峰; (d) 浓度分布Figure8. Three different modes of combustion field distribution: (a) Single Gaussian peak; (b) two Gaussian peaks; (c) multiple Gaussian peaks; (d) concentration distribution.
利用改进后的算法, 结合之前小节中所述选取的最优谱线组合(5条谱线, 对应于表1谱线中的2, 6, 9, 10和12), 对三种不同模态的燃烧流场进行了反演重建, 重建精度效果以(2)式评判. 为更好地验证其对噪声的敏感性, 在仿真模拟中, 添加了不同水平的高斯噪声(0%, 0.5%, 1%, 1.5%, 2%, 3%, 4%, 5%), 反演结果如图9所示.
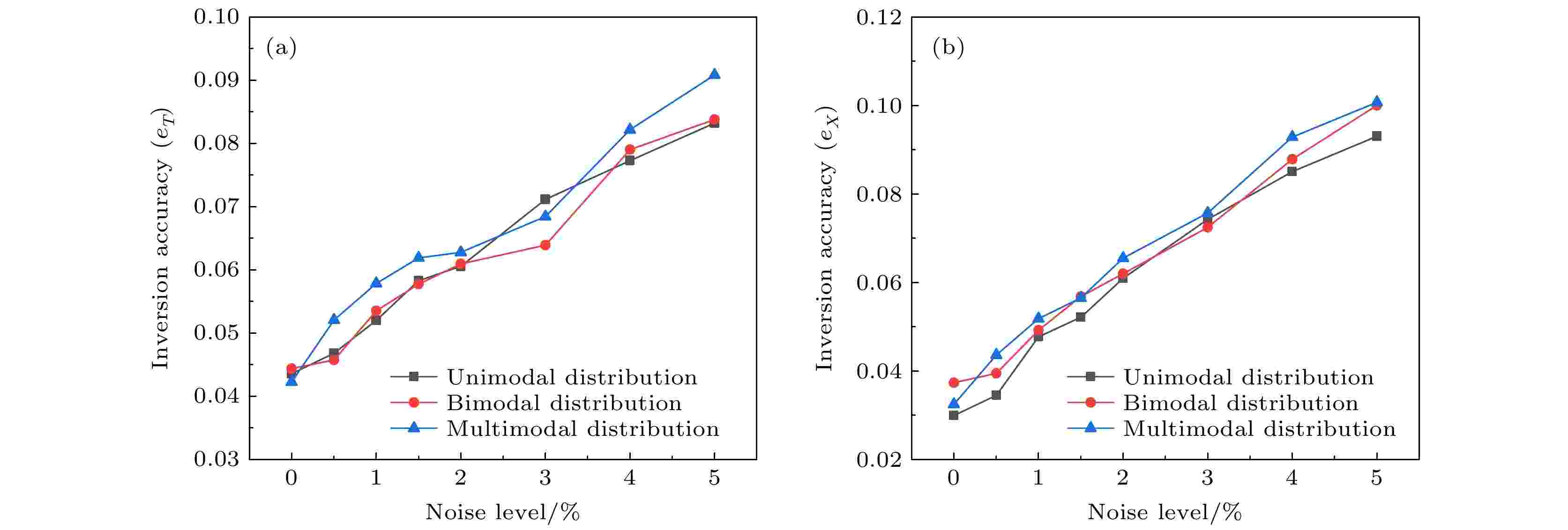 图 9 三种不同模态燃烧流场的温度浓度反演精度
图 9 三种不同模态燃烧流场的温度浓度反演精度Figure9. The inversion accuracy of three different modes of combustion field distribution.
从图9可以看出, 随着燃烧流场分布的复杂化, 温度及水汽浓度的反演精度也会随之略有下降.
为验证纳入多个光谱信息在反演燃烧流场分布时的作用, 采取改进后的算法, 对不同谱线组合反演重建温度浓度场分布的精度进行了对比, 其中最优5条谱线组合对应于表1谱线中的2, 6, 9, 10和12, 最优8条谱线组合对应于表1谱线中的2, 4, 6, 7, 8, 9, 10和12. 同样地, 在对比中添加了不同水平的高斯噪声. 对图8中的三种不同模态燃烧流场均进行了反演对比, 对比结论基本一致, 所以在接下来的内容以图8(c)的多峰分布作为例子进行说明, 对比结果如图10所示.
 图 10 最优5条、8条谱线组合和非最优5条、8条谱线组合以及所有12条谱线在不同噪声水平下温度浓度的反演精度
图 10 最优5条、8条谱线组合和非最优5条、8条谱线组合以及所有12条谱线在不同噪声水平下温度浓度的反演精度Figure10. The inversion accuracy of the optimal 5, 8 transition lines combinations, the non-optimal 5, 8 transition lines combinations and all 12 transition lines combinations under different noise levels.
从图10的对比结果来看, 纳入更多的光谱信息能提高测量精度和增强对测量噪声的免疫性, 原因在于更多的跃迁谱线提供了更广阔的温度范围. 同时, 对比结果突出了选择最优谱线组合的重要性, 比如, 最优5条谱线组合在测量精度和对噪声的免疫性上甚至优于非最优8条谱线组合.
为比较改进后的算法与传统模拟退火算法重建场分布的差异, 将两种算法得到的重建图像精度和算法运行时间进行对比, 依然以图8(c)中的燃烧场分布举例说明, 两种算法重建结果如图11所示(选取最优5条谱线组合, 零噪声水平下), 上面板为传统模拟退火算法重建, 下面板为本文改进后算法重建.
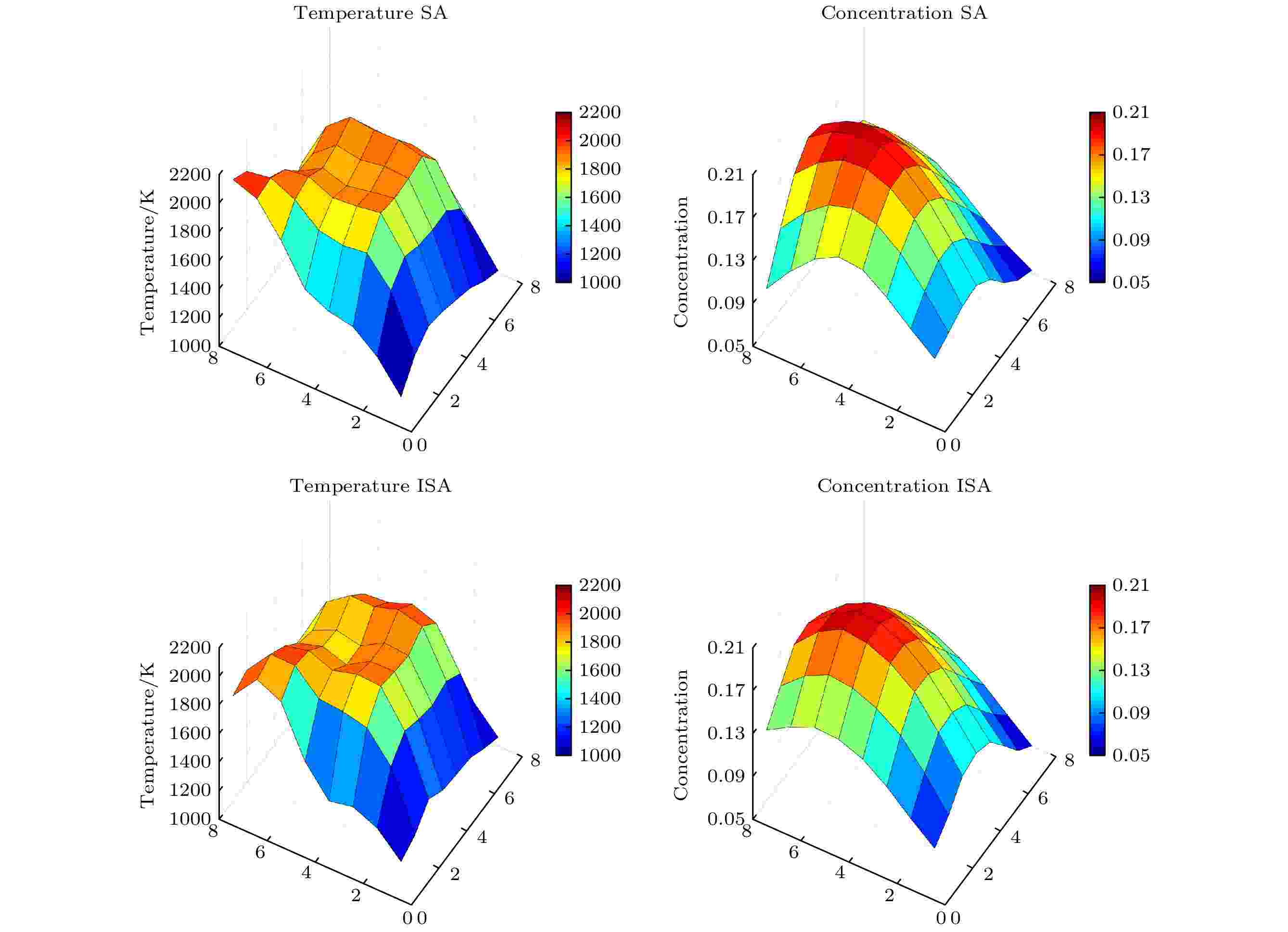 图 11 零噪声水平下两种算法重建结果对比, 上面板为传统模拟退火算法重建结果, 下面板为改进模拟退火算法重建结果
图 11 零噪声水平下两种算法重建结果对比, 上面板为传统模拟退火算法重建结果, 下面板为改进模拟退火算法重建结果Figure11. Under zero noise level, the reconstruction results of two algorithms. Top: SA algorithm reconstruction results, Bottom: ISA algorithm reconstruction results.
且为考证不同规模问题下, 两种算法的重建图像精度与算法运行效率是否会有差异, 分别利用前文所述的最优5条谱线组合和最优8条谱线组合去进行反演重建, 重建精度对比结果如图12所示, 改进前后算法运行时间对比如表2所示.
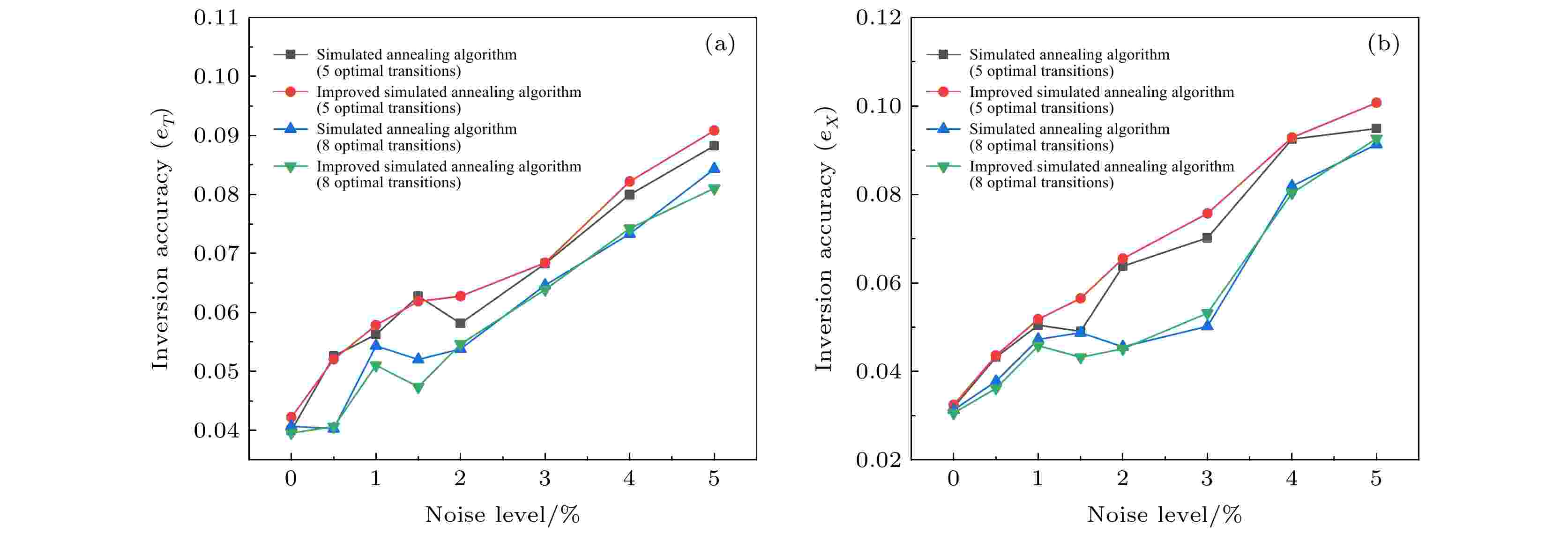 图 12 两种算法的重建精度对比
图 12 两种算法的重建精度对比Figure12. Comparison of reconstruction accuracy between the two algorithms.
| Noise level | Simulated annealing algorithm | Improved Simulated annealing algorithm | |||
| 5 optimal transitions | 8 optimal transitions | 5 optimal transitions | 8 optimal transitions | ||
| 0% | 8704 s | 12379 s | 231 s | 364 s | |
| 0.5% | 8346 s | 12265 s | 242 s | 372 s | |
| 1% | 9213 s | 12403 s | 237 s | 384 s | |
| 1.5% | 9001 s | 12608 s | 217 s | 379 s | |
| 2% | 8945 s | 12337 s | 230 s | 342 s | |
| 3% | 8573 s | 13151 s | 225 s | 356 s | |
| 4% | 8733 s | 12726 s | 240 s | 351 s | |
| 5% | 8667 s | 12516 s | 235 s | 347 s | |
表2两种算法应用于高光谱层析成像的运行时间对比
Table2.Comparison of running time of two algorithms applied to hyperspectral tomography.
从图11、图12和表2可以看出, 改进后的模拟退火算法相较于传统模拟退火算法, 在高光谱层析成像的重建精度上保持一致, 但在运行效率上得到了极大提高, 在不同规模的问题处理上, 运行效率提高基本一致, 均提升了近40倍, 节省了大量时间.
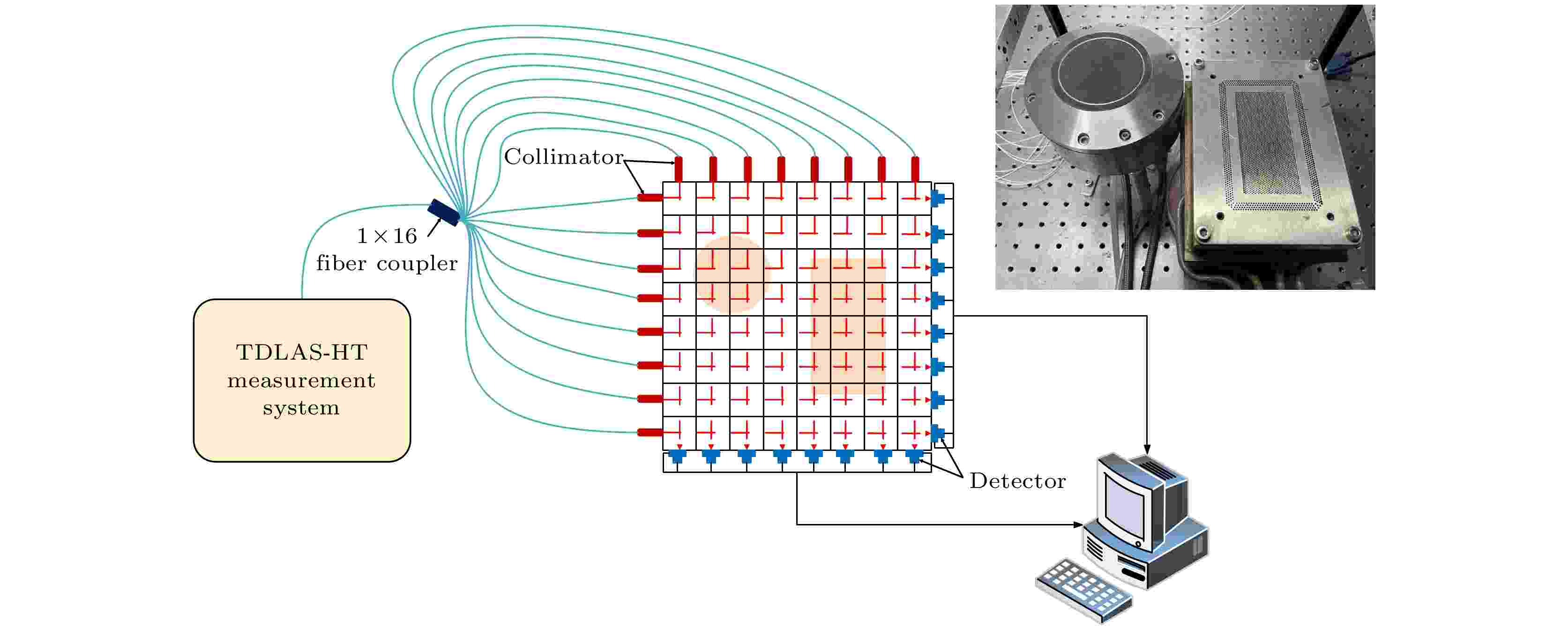 图 13 TDLAS-HT系统测量示意图
图 13 TDLAS-HT系统测量示意图Figure13. Schematic diagram of measurement of TDLAS-HT system.
根据前文所述谱线选取方法, 结合实验室TDLAS-HT测量系统, 本文选用如表3所示的5条谱线组合, 平焰炉设置在当量比为1的条件下燃烧. 系统光路呈8 × 8路正交分布, 空间分辨率为20 mm, 穿过待重建目标区域, 激光束位于炉面上方5 mm高度位置. 实验测量期间, 平焰炉始终保持连续燃烧状态, 直至完成所有信号采集. 为更好地分析改进后算法在不同燃烧情况下重建图像质量, 在实验中通过将一把钢尺横跨在两个平焰炉表面, 形成更复杂火焰分布, 如图14所示.
| ${\nu _0}/{\rm{c}}{{\rm{m}}^{ - 1}}$ | $S({T_0})/({\rm{c}}{{\rm{m}}^{ - 2}} \cdot {\rm{at}}{{\rm{m}}^{ - 1}})$ | $E''$ |
| 7467.77 | 1.093 E-5 | 2551.48 |
| 7444.36 | 1.100 E-3 | 1790.04 |
| 7185.60 | 1.905 E-2 | 1045.06 |
| 7179.75 | 5.814 E-3 | 1216.19 |
| 6807.83 | 6.032 E-7 | 3319.45 |
表3实验所用谱线及光谱参数
Table3.Spectral lines and spectral parameters used in the experiment.
 图 14 钢尺放置前后平焰炉燃烧分布
图 14 钢尺放置前后平焰炉燃烧分布Figure14. The combustion distribution of Mckenna flat flame furnace before and after placing the steel ruler.
重建过程中使用到的投影数据采用在线获取的方式, 并多次测量取平均值以消除偶然误差. 由于平焰炉面积较小, 实验室内实现的空间分辨率不高, 重建后的温度浓度原始二维分布图像不能很好地显示火焰燃烧状态, 所以对重建得到的低空间分辨率分布进行了插值处理, 可以更直观地观察到流场结构. 图15给出了经插值处理后获得的71 × 71网格下的高分辨率温度浓度二维分布图像.
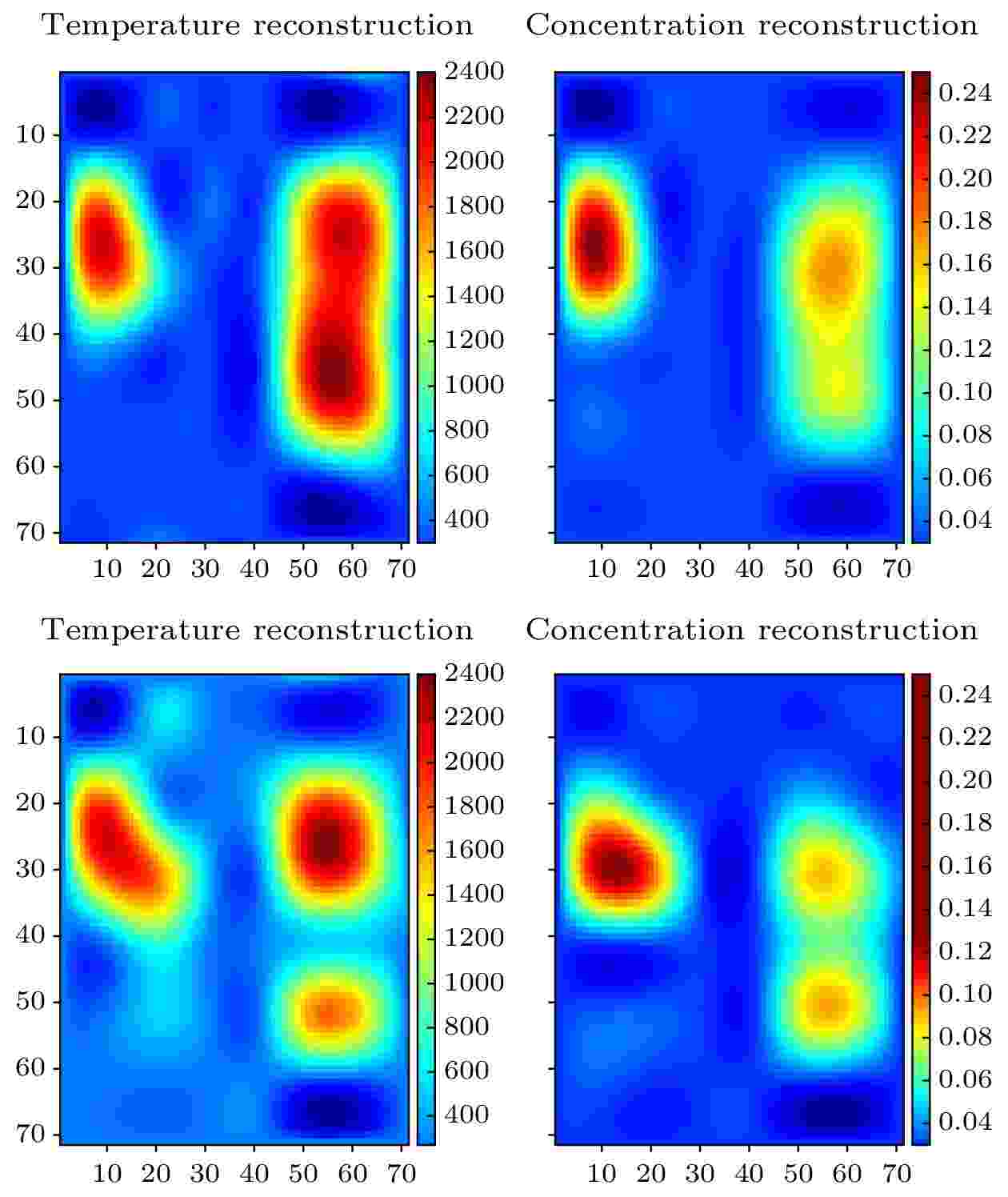 图 15 钢尺放置前后重建结果, 上面板为未放置钢尺前重建结果, 下面板为放置钢尺后重建结果
图 15 钢尺放置前后重建结果, 上面板为未放置钢尺前重建结果, 下面板为放置钢尺后重建结果Figure15. Reconstruction results before and after steel ruler placement. Top: Reconstruction results before placing the steel ruler; Bottom: Reconstruction results after placing the steel ruler.
从图15中可以看出, 经改进模拟退火算法重建的燃烧场分布较好地再现了原始场内部信息, 测量区域内两个平焰炉的重建结果符合真实燃烧状态特征, 程序运行时间约为270 s. 在这里需要说明的, 钢尺放置前的圆形平焰炉重建结果未呈现正圆形趋势的原因在于, 实验过程中测量区域内的激光束并未完全覆盖圆形平焰炉, 即最终只重建了在待测区域内的部分燃烧分布. 同时从图15中也可以看出, 在放置钢尺后, 破坏了平焰炉原有的氮气吹扫保护结构, 出现了一定的扩散, 而水汽浓度分布相较于温度分布受到的影响较小, 且由于长方形平焰炉被激光束完全覆盖, 所以在重建时受放置钢尺带来的影响更为明显.
