摘要:误差补偿是保证水下传感器网络时钟同步精度的一个重要保障, 现有研究方法主要采用线性拟合和最小二乘法对时钟同步参数进行误差补偿, 但该类方法并未考虑受海流影响时节点移动所导致的时钟同步精度问题. 针对此问题, 本文提出一种基于BP神经网络模型的时钟同步误差补偿算法. 首先采用深海拉格朗日洋流模型描述水下节点运动规律, 模拟水下节点运动速度, 进而建立时钟同步参数模型, 最后构建符合水下环境的BP神经网络时钟同步误差补偿模型, 通过定义激励函数, 引入正则项因子和补偿性因子避免模型过拟合, 建立误差反向传播的BP神经网络模型时钟同步误差补偿算法. 仿真实验表明, 本文提出的算法与TSHL算法、MU-sync算法、MM-sync算法相比, 在时钟同步精度(即时钟同步时间与标准时间的误差)上分别提升了37.42%, 17.29%和21.86%, 并且均方误差得到显著降低.
关键词: 误差补偿/
时钟同步/
BP神经网络/
水下传感器网络

English Abstract

全文HTML

--> --> -->

海洋是未来世界各国竞争的核心基地^[1-3], 拥有大量的资源, 对海洋资源的开发利用离不开水下无线传感器网络(underwater wireless sensor networks, UWSNs), UWSNs是由许多水下节点构成的无线网络, 该网络在人类获取海洋信息中扮演着不可忽视的角色. 同时时钟同步对水下传感器网络有着非常重要的意义, 时钟同步对传感器网络许多关键技术起着非常重要的作用, 如: 节点定位、数据融合等^[4-6], 但由于水下环境条件恶劣、声波通信受到较多不确定因素影响, 目前现有的时钟同步研究成果在误差补偿方面仍存在如下挑战: 1)水下节点会随着海洋或者潮汐的运动而发生移动, 故水下节点具有移动性; 2)单向同步数据报文算法交换少, 时钟频偏估算精度高, 但相偏估算误差大; 3)双向同步数据报文算法时钟相偏估计精度高, 但数据报文交换多次, 时钟频偏估算误差较大, 而且传输延迟不一致也降低了时钟相偏的估算精度; 4) UWSNs普通节点能源有限, 传输距离过长导致能耗高.
水下无线传感器网络节点具有移动性, 导致网络节点始终处于时变状态. 在同步转发过程中, 节点发送和接收数据报文的位置会发生变化, 从而产生相对移动距离, 导致动态时延增大. 如此随着转发次数增多, 时钟的误差(主要由传送时间、传播时间和接收时间组成)也逐渐增大, 造成水下传感器无线网络同步精度(节点估算的参考时间与实际参考时间的偏差)逐渐降低. 现存的水下无线传感器网络时钟同步算法, 并没有充分考虑到节点随洋流运动而产生的动态时延, 只是利用时间戳机制求解时钟同步参数, 然后利用传统的线性拟合对同步参数进行求精处理, 如TSHL^[7], MM-sync^[8]和MU-sync^[9]等算法. 对动态时延的精确求解是同步精度的一个关键因素. 利用传统的优化算法(如最小二乘法)对同步参数进行求精, 容易陷入局部最优, 进而使得同步精度不高. 因此现有传统的时钟同步算法研究不能很好地解决由于节点移动性导致的时钟同步精度问题.
因此, 在设计UWSNs时钟同步算法时, 时钟同步参数的精度是水下传感器网络时钟同步算法需要着重考虑的因素, 为了提高时钟同步的参数精度, 需要对同步误差进行补偿.
本文的篇章组织结构如下: 第1节介绍UWSNs时钟同步算法的研究意义及误差补偿的重要性; 第2节详细给出现有时钟同步算法及研究现状; 第3节给出了各种模型的搭建过程; 第4节详细介绍BP神经网络模型时钟同步误差补偿算法; 第5节通过仿真实验证明该误差补偿模型的实用性; 第6节对整篇文章进行分析总结.

目前, 国内外****对陆地无线传感器网络时钟同步算法的研究取得了一些成果, 由于水下传感器网络独特的传播特点, 使得现有的陆地传感器时钟同步算法(如: RBS算法, TPSN算法, DMTS算法)^[10-12]并不适用于水下复杂的环境.
针对水下无线传感器网络时延的随机性, 研究者们提出了一系列适用水下传感器网络的时钟同步算法. Eidenbenz等提出了高延迟时钟同步算法TSHL, 该算法首先利用信标节点发送数据报文, 然后待同步节点将收到报文的时间与本地时间组成元组, 再利用线性拟合计算频偏, 最后根据一次双向数据报文求解相偏, 该算法解决了高时延的问题, 但是因为需要多次发送数据报文, 所以存在能耗较高的问题, 同时该算法忽略了水下节点移动的特点, 因此算法的时钟精度不高. 与此同时, 该算法用的是线性拟合求解方法, 其误差较大. Sajjad等^[13]在分析时间间隔对时钟同步精度影响的基础上, 增大了TSHL 算法的同步信号的时间间隔, 减少了同步信号的发送次数, 这种改进版的TSHL 算法降低了算法复杂度和能量消耗. 文献[14]针对TSHL算法同步交互信号多, 能量消耗大的不足, 提出了一个Tri-Message 同步算法, 首先改用3次发送-接收交互计算频偏, 然后使用双向交换计算相偏, 这可以降低消息开销并保持一定同步精度, 进一步优化了TSHL算法的性能. 文献[15]提出TSMU算法, 利用卡尔曼滤波对多普勒计算的相对速度求其精度, 再用线性回归和校准来计算时钟同步的频偏和相偏. 文献[16]提出的Hybrid-Sync同步算法, 利用混合时钟交换数据报文的方式计算相偏和频偏, 最后利用计算得到的频偏来进一步校正相偏. 与TSHL算法相比, 降低了算法的通信费用, 但是Hybrid-Sync的计算费用较高且时钟同步精度不高.
上述算法虽然在一定程度上解决了时钟同步问题, 但都没有考虑节点移动性导致时钟同步精度不高的问题.
MM-sync 算法考虑传感器网络移动性对同步参数的影响, 推出时钟同步参数模型, 进而构建出一种适合浅水域的时间同步算法. 文献提出的一个分簇UWSNs时钟同步算法MU-Sync. 该算法先对网络节点进行分簇, 再利用簇首周期性地广播同步信号来进行簇内时钟同步, 利用簇首节点收集到的同步信息进行两次线性拟合估计往返传播时延, 以此来降低误差, 通过多次双向信息交换, 使MU-Sync 算法获得了较好的同步精度. Shi等^[17]首次将水下时钟同步问题分为授权、簇内同步和簇间同步三个阶段; 在授权阶段, 所有的节点相互授权, 并确认和删除恶意节点; 在簇内同步阶段, 簇首节点通过发送、接收模式和普通节点进行同步. 该算法为了提高同步精度, 利用CESVM (centered hyperellipsoidal support vector machine based anomaly detection) ^[18]过滤非正常的接收端到接收端的传播延迟, 同时假设随机传输延迟符合方差为0的高斯分布, 进行时钟同步求精.
文献[19]提出D-sync时钟同步算法, 是基于水下通信产生的多普勒效应, 利用该效应计算节点间的相对速度, 估计传播延迟完成时钟同步. 但由于水声环境影响因素过多, 该算法测量的误差会较大. 因此, NU-sync算法^[20]加入了更准确的多普勒测量的方法因素, 通过计算节点的相对速度解决延迟多变的问题, 利用潜水器作为信标节点对节点进行同步, 极大降低了误差.
综上所述, 现今水下无线传感器网络时钟同步算法的研究需要综合考虑节点移动对同步精度的影响, 同时也要避免传统时钟同步算法使用线性拟合思想造成误差较大的问题. 因此, 本文综合考虑节点的移动性、误差补偿等因素构建符合水下网络的BP神经网络时钟同步误差补偿算法, 从而设计出一个精度高、误差小的水下传感器网络时钟同步算法.

2

-->

3.1.洋流模型

本节首先分析洋流运动对节点运动的影响, 然后根据速度计算公式计算待同步节点的移动速率.
由于水下环境复杂多变, 水下物体运动并不是完全无规律的, 而是呈现出半周期的运动特性. 文献[21]中提出一种权威的洋流模型, 本文用此模型对节点的运动进行分析. 模型公式为

$\left\{ \begin{aligned} &\varphi (x,y,t) \!=\! \\ &\; - \tanh \left[ {\frac{{y - B(t)\sin (k(x - ct))}}{{\sqrt {1 \!+\! {k^2}B{{(t)}^2}{{\cos }^2}(k(x - ct))} }}} \right]\\ & \;+ ly, \\& B(t) = R + \varepsilon \cos (\omega t), \end{aligned} \right.$

其中, l表示位移率, $B(t)$表示曲线的宽度, $\omega $表示洋流场的频率, $\varepsilon $表示振幅. R = 1.2, l = 0.12, $\omega $=0.4, $\varepsilon $=0.3, $k= {2{\text{π}} }/{7.5}$^[22]. 一般情况下只考虑节点在x和y方向上的位移, 节点在水平方向的速率为

$\left\{ \begin{aligned} &u = - \frac{{\partial \varphi }}{{\partial y}} + \sigma u(t), \\& v = \frac{{\partial \varphi }}{{\partial x}} + \sigma v(t). \end{aligned} \right.$

节点在x和y方向的运动情况如图1、图2所示.
图 1 x方向的速率
Figure1. The velocity in the x direction.

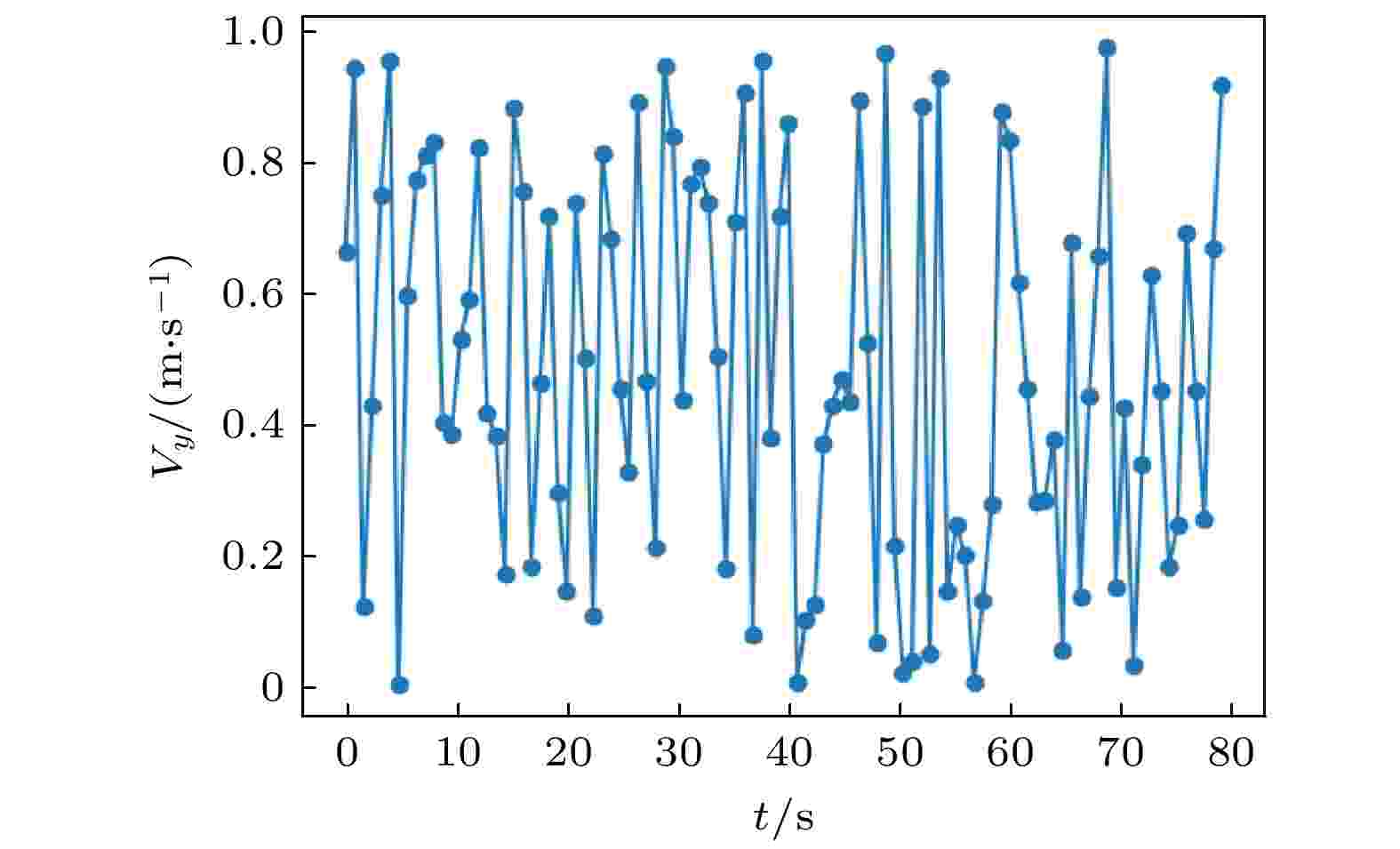图 2 y方向的速率
Figure2. The velocity in the y direction.

对普通节点来说, 难与浮标节点通信, 但利用自身的相关性, 可以获取移动速度. 假定节点i想要取得自身的速度$\left[ {{v_x}(i), {v_y}(i)} \right]$, 其中${v_x}(i), {v_y}(i)$分别是x轴和y轴上的速度分量. 如果节点i能够获取附近簇首节点的速度, 就可以使用(3)式计算得到自身速度:

$ \left\{ \begin{aligned}&{v}_{x}(i)={\displaystyle \sum _{j=1}^{m}{\xi }_{ij}{v}_{x}(j)}, \\ &{v}_{y}(i)={\displaystyle \sum _{j=1}^{m}{\xi }_{ij}{v}_{y}(j)}, \end{aligned} \right.$

其中, m为邻近簇首节点的数量, ${\xi _{ij}}$为差值系数, 可以用(4)式得到:

${\xi _{ij}} = \dfrac{{\dfrac{1}{{{r_{ij}}}}}}{{\displaystyle\sum\limits_{i = 1}^m {\dfrac{1}{{{r_{ij}}}}} }}, $

其中${r_{ij}}$为簇首节点与普通节点的距离, 可以使用欧几里得^[23]计算.
2 -->

3.2.时钟同步参数模型

本文传感器节点以线性模型为例, 根据文 献[24]节点的时钟t与标准时间T的关系为

$T = at + b, $

其中, a表示时钟漂移, b表示时钟偏移.
本文采用先分簇后对簇群进行时钟同步, 分为浮标节点、簇首节点、普通节点. 簇首节点可以直接获取浮标节点的标准时间, 故只需要考虑簇群的时钟同步. 报文交换过程如图3所示.
图 3 数据报文交换过程
Figure3. Data message exchange process.

普通节点分别向各个节点发送数据报文进行时间同步, 簇首节点收到后向普通节点发送多个数据分组. 信息交互过程如图3所示. C在${T_1}$时刻向簇首节点发起同步进程, Q在${T_2}$时刻收到该信息, 并随即向节点C发送多个数据包, 其时间戳用$t[i]$表示, C收到数据报文的时间戳用$T[i]$表示. 当节点Q第一次发送数据报文的发送时间是$t[1]$, 经过时间${d_1}$后, 到达节点C. 节点C记录下到达本地的时间$T[1]$. 过一段时间后, 节点C再向节点Q发送同步数据报文, 由于节点受到洋流的影响会发生移动, 故数据报文传播延迟不再是${t_1}$而是${t_2}$. 则可以得

$\begin{split} &{d_1} + t[1] = aT[1] + b, \\ &{d_2} + t[2] = aT[2] + b. \end{split} $

由于水下节点具有移动性, 故假设簇首Q的移动速率为${V_{{\rm{m}}i}}$, 待同步节点C的移动速率为${V_{{\rm{A}}i}}$, 水声传播速度为u, 则可得

$u{d_i} = u{d_{i - 1}} + {V_{{\rm{m}}i}}({d_{i - 1}} + {d_i}) + {V_{{\rm{A}}i}}({d_{i - 1}} + {d_i}),$

整理后可得:

${d_i} = \frac{{u{d_{i - 1}} + {v_{{\rm{m}}i}} + {v_{{\rm{A}}i}}{d_{i - 1}}}}{{u - {v_{{\rm{m}}i}} - {v_{{\rm{A}}i}}}},$

其中, ${V_{{\rm{m}}i}}$和${V_{{\rm{A}}i}}$可以由(3)式计算得到. 求出${d_i}$后, 漂移可由(8)式求得:

$\begin{split}{{a}} =\;& {[{a_1},{a_2},{a_3}, \cdots,{a_m}]^{\rm{T}}}\\=\;& \left[ \begin{array}{l} {a_1} = \dfrac{{t[1] - t[2] + {d_1} - {d_2}}}{{T[1] - T[2]}} \\ {a_2} = \dfrac{{t[2] - t[3] + {d_2} - {d_3}}}{{T[2] - T[3]}} \\ {a_3} = \dfrac{{t[3] - t[4] + {d_3} - {d_4}}}{{T[3] - T[4]}} \\ \quad \quad \quad \quad \quad \vdots \\ {a_i} = \dfrac{{t[i] - t[i + 1] + {d_i} - {d_{i + 1}}}}{{T[i] - T[i + 1]}} \end{array} \right]. \end{split}$

收集的时间戳为${T_a}, {T_b}, {T_c}, {T_d}$, 如图4所示, 并使用下式计算出频偏:
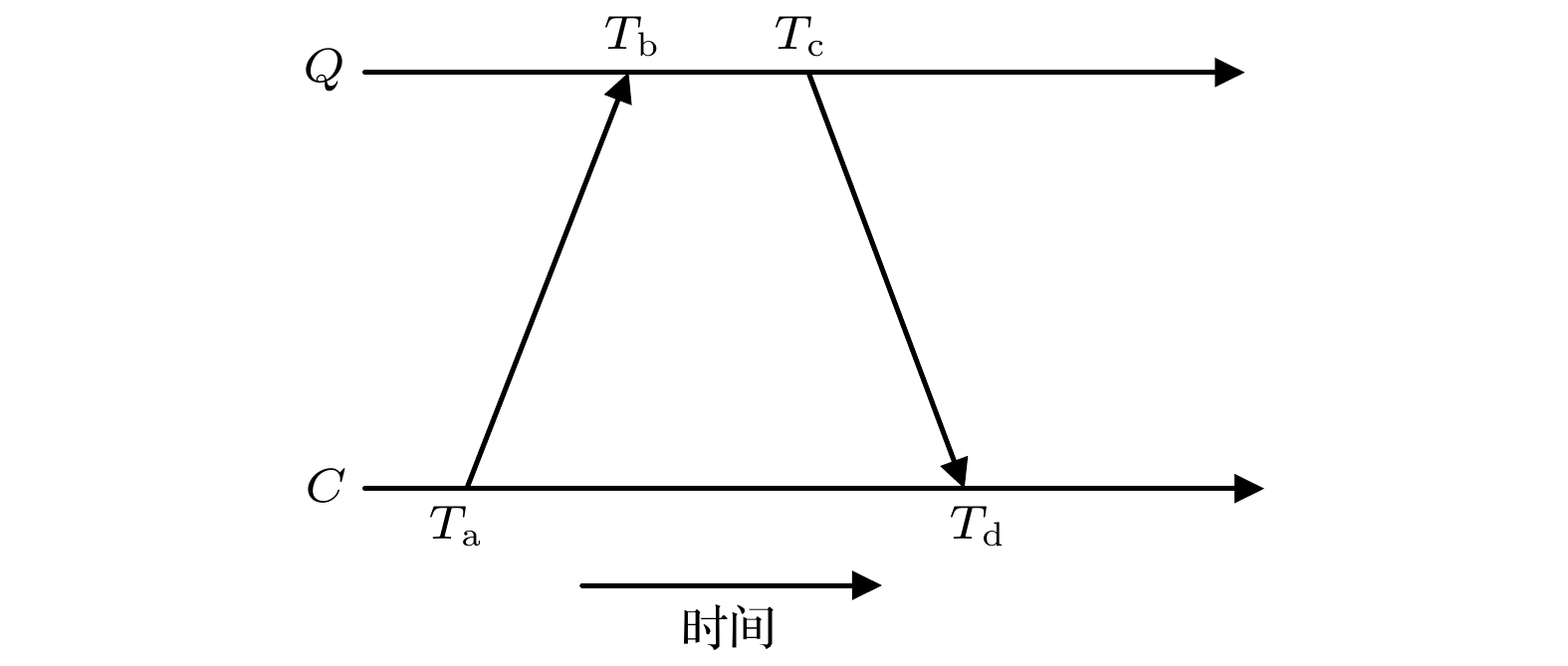图 4 数据报文交换过程
Figure4. Data message exchange process

$\left\{ \begin{aligned} &a{T_a} + {b_1} + {t_1} = {T_{b1}}, \\ &{T_c} + {t_2} = a{T_d} + b, \\ &{t_2} - {t_1} = a{T_d} + a{T_a} + 2{b_1} - {T_{b1}} - {T_c}, \\ &{t_2} - {t_1} = {{va({t_d} - {t_a})}}/{u}. \end{aligned} \right.$

其中a是(9)式中的列矩阵, 考虑到水下传感器网络时钟同步的时效性精准性, T_b1和b₁只有在计算频偏的时候才会使用. 由(10)式可推出:

$\begin{split}\;& {{b}} = {[{b_1},{b_2},{b_3}, \cdots,{b_m}]^{\rm{T}}}= \\\;& \!\!\!\left[ \!\! \begin{array}{l} {b_1} \!=\! \dfrac{{u({T_{a1}}\! +\! {T_{d1}}) \!-\! {a_1}[u({T_{b1}} \!+\! {T_c})\! +\! v({T_{d1}}\! -\! {T_{a1}})]}}{{2u}} \\ {b_2} \!=\! \dfrac{{u({T_{a2}}\! +\! {T_{d2}}) \!-\! {a_2}[u({T_{b2}} \!+\! {T_c})\! +\! v({T_{d2}} \!-\! {T_{a2}})]}}{{2u}} \\ {b_3}\! =\! \dfrac{{u({T_{a3}}\! +\! {T_{d3}}) \!-\! {a_3}[u({T_{b3}}\! +\! {T_c})\! +\! v({T_{d3}} \!-\! {T_{a3}})]}}{{2u}} \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \vdots \\ {b_i} \!=\!\dfrac{{u({T_{ai}} \!+ \!{T_{di}}) \!-\! {a_i}[u({T_{bi}} \!+ \!{T_c}) \!+\! v({T_{di}}\! -\! {T_{ai}})]}}{{2u}} \end{array}\! \! \right]\!,\end{split}$

其中T_bi 和T_ai是收集的一系列剪短时间戳, 主要是为了更精准地求出频偏. 本次时钟同步通过单向数据报文交换来减少双向交换的次数, 从而减少数据报文能耗, 但没有考虑时延带来的误差, 导致$\left\{ {a, b} \right\}$精度不高. 本文将针对该误差提出补偿模型.
2 -->

3.3.BP神经网络时钟同步误差补偿模型

基于BP神经网络的时钟同步误差补偿模型, 是将根据时钟同步参数模型中的(9)式和(11)式计算得到的m个同步参数估计值作为网络学习样本, 经过大量重复不断地学习, 沿着误差减小的方向, 不断调整各层神经元之间的权值和阈值, 目的是得到一个最佳预测补偿模型.
针对3.2节时钟同步参数模型精度不高提出的BP神经网络时钟同步误差补偿模型如图5所示.
图 5 BP神经网络时钟同步误差补偿结构图
Figure5. BP neural network clock synchronization error structure diagram.

3 -->

3.3.1.激活函数的设定

激活函数对本文算法网络尤为重要, 常用的sigmoid和tanx虽然易于实现, 但存在不可避免的缺陷. 基于此本文为避免陷入局部计算以及综合节点移动对水下传感器时钟同步产生的影响, 本文提出$f(x)$作为激活函数:

$f(x) = \left\{ {\begin{aligned}&{x,}\;\;\;\; {x \geqslant {\rm{0}},}\\&{\phi x,}\;\;{x < {\rm{0,}}}\end{aligned}} \right.$

其中, $\phi \in (0, 1)$通过先验知识赋值.
3 -->

3.3.2.代价函数、误差补偿模型和误差方向传播更新过程

1)代价函数
本文有m个输入样本$\{ {{t}} = [{t_1}, {t_2}, {t_3}, \cdots, {t_i}, \cdots, $$ {t_m}]\}$、$\{ {{a}} = [{a_1}, {a_2}, {a_3}, \cdots, {a_i}, \cdots, {a_m}]\} $、$\{ {{b}} = [{b_1}, {b_2}, $$ {b_3}, \cdots, {b_i}, \cdots, {b_m}]\}$, $d(i)$为期望输出, 输出向量${{g}} = \{ {g_1}, {g_2}, \cdots, {g_k}, \cdots, {g_m}\} $, 某层神经元输出: ${{{h}}^{(l)}} = $$ \{ h_1^{(l)}, h_2^{(l)}, \cdots, h_j^{(l)}, \cdots, h_{sl}^{(l)}\}$. 本文属于线性回归的问题, 故采用平方误差$E = \dfrac{1}{m}\displaystyle \sum\limits_{t = 1}^m {E(i)}$作为代价函数.
2)时钟同步误差补偿模型
为避免过拟合现象造成的误差无法达到极小值, 参数的更新过程采用随机梯度下降算法. 考虑到水下传感器节点资源有限并结合BP神经网络结构, 构造时钟同步误差补偿模型为:

$J = \frac{1}{m}\sum\limits_{t = 1}^m {E(i)} + P, $

其中

$\begin{split}P = \;&\frac{{\rlap-{\lambda}}}{2}{P_1} + \sigma {P_2} = \kappa \sum\limits_{l = 1}^{L - 1} {\sum\limits_{j = 1}^{{s_l}} {\sum\limits_{i = 1}^{{s_{l + 1}}} {w_{ij}^{(l)}} } } \\&+ \eta \sum\limits_{k = 1}^{{h_k}} {\sum\limits_{j = 1}^{{s_k}} {KL(\chi ||\hat \chi _j^k)} } , \end{split}$

其中, ${P_1}$表示正则化项惩罚因子, ${P_2}$表示补偿性因子, ||表示交叉熵运算.

$ E(i)=\frac{1}{2}{\displaystyle \sum _{k=1}^{n}{({d}_{k}(l)-{g}_{k}(i))}^{2}}, $

$P =\frac{{\rlap-{\lambda}}} {2}{P_1} + \sigma {P_2},$

${P_1}, {P_2}$计算方法如下:

${P_1} = \sum\limits_{l = 1}^{L - 1} {\sum\limits_{j = 1}^{{s_l}} {\sum\limits_{i = 1}^{{s_{l + 1}}} {{{(w_{ij}^{(l)})}^2}} } } ,$

$\begin{split}{P_2} =\;& \sum\limits_{k = 1}^{{h_k}} {\sum\limits_{j = 1}^{{s_k}} {KL(\chi ||\hat \chi _j^k)} } = \sum\limits_{k = 1}^{{h_k}} {\sum\limits_{j = 1}^{{s_k}} {\tau \log \frac{\tau }{{\hat \tau _j^{(k)}}}} }\\&+ (1 - \tau )\log \frac{{1 - \tau }}{{1 - \hat \tau _j^{(k)}}},\end{split}$

其中, ${h_k}$为隐藏层个数, $\tau $为稀疏性因子, 满足$\tau \in (0, 1)$,

$\hat \tau _j^{(k)} = \frac{1}{m}\sum\limits_{i = 1}^m {a_j^{(k)}({x_i})} . $

3)误差方向传播参数迭代更新过程

$w_{ij}^{(l)} = \frac{{\partial J}}{{\partial w_{ij}^{(l)}}} = w_{ij}^{(l)} - \alpha \frac{{\partial E}}{{\partial w_{ij}^{(l)}}} + \frac{{\partial P}}{{\partial w_{ij}^{(l)}}},$

$b_i^{(l)} = \frac{{\partial J}}{{\partial b_i^{(l)}}} = b_i^{(l)} - \alpha \frac{{\partial E}}{{\partial b_i^{(l)}}} + \frac{{\partial P}}{{\partial b_i^{(l)}}},$

其中$\alpha \in (0, 1)$是学习率. 为提高收敛速度, 从局部极小值中跳出来, 根据文献[25]提出优化学习率的变换公式:

$\alpha = G{{\rm{e}}^{ - \lambda r}}.$

式中, r是迭代次数, G和$\lambda $是常数, 根据本文的学习样本, 选取G = 20, $\lambda =0.002$.
另外,

$\begin{split} \frac{{\partial E(i)}}{{\partial w_{ji}^{(l)}}} =\;& \frac{\partial }{{\partial w_{kj}^{(L)}}}\left\{ {\frac{1}{2}\sum\limits_{k = 1}^n {{{\left[ {{d_k}(i) - {g_k}(i)} \right]}^2}} } \right\} \\ =\;& - \left[ {{d_k}(i) - {g_k}(i)} \right]\frac{{\partial {g_k}(i)}}{{\partial Z_k^{(L)}}}\frac{{\partial Z_k^{(L)}}}{{\partial w_{kj}^{(L)}}} \\ =\;& - \left[ {{d_k}(i) - {g_k}(i)} \right]f{(x)'}{|_{x = Z_k^{(L)}}}\frac{{\partial Z_k^{(L)}}}{{\partial w_{kj}^{(L)}}}h_j^{(L - 1)} \\ =\;& \sum\limits_{k = 1}^{{s_{l + 1}}} {w_{kj}^{(l + 1)}} \left[ {{d_k}(i) - {g_k}(i)} \right]f{(x)'}{|_{x = Z_k^{(l + 1)}}}\\ &\times f{(x)'}{|_{x = Z_j^{(i)}}}h_i^{(l - 1)}.\\[-15pt] \end{split} $

同理可得:

$\begin{split}\frac{{\partial E(i)}}{{\partial b_j^{(l)}}} =\;& \sum\limits_{k = 1}^{{s_{l + 1}}} {w_{kj}^{(l + 1)}} \left[ {{d_k}(i) - {g_k}(i)} \right]f{(x)'}{|_{x = Z_k^{(l + 1)}}}\\&\times f{(x)'}{|_{x = Z_j^{(i)}}},\\[-15pt]\end{split}$

$\frac{{\partial P}}{{\partial w_{ij}^{(l)}}} = \frac{1}{m}{\delta ^{(l)}}{a^{{{(l)}^{\rm{T}}}}} + \lambda {w^{(l)}},$

$\frac{{\partial P}}{{\partial {b^{(l)}}}} = \frac{1}{m}{\delta ^{(l)}}{a^{{{(l)}^{\rm{T}}}}}.$

本文构建的BP神经网络时钟同步误差补偿模型是一种正向传递和误差反向传播的网络^[26], 采用随机梯度下降原理对参数进行调节, 经过多次反复训练就可以得到满足补偿条件的BP神经网络. 具体过程为: 模型搭建阶段、模型学习阶段、模型预测阶段.
2

-->

4.1.模型搭建阶段

如表1所示, 输入层节点个数设置为2, 输出层节点的个数设置为1, 隐藏层的神经元个数使用了经验公式^[27]

算法: 基于BP神经网络模型时钟同步误差补偿算法
输入: $\begin{array}{l} {{a}} = [{a_1}, {a_2}, {a_3}, \cdots, {a_i}, \cdots, {a_m}], i = 1, 2, \cdots m \\ {{b}} = [{b_1}, {b_2}, {b_3}, \cdots, {b_i}, \cdots, {b_m}], i = 1, 2, \cdots m \\ {{t}} = [{t_1}, {t_2}, {t_3}, \cdots, {t_i}, \cdots, {t_m}], i = 1, 2, \cdots m \end{array} $
阶段1: BP模型搭建阶段
01:　算法
02:　　算法阶段一开始
03:　　数据收集
04:　　　$\begin{array}{l}m\leftarrow \big\{ {{a} }=[{a}_{1}, {a}_{2}, {a}_{3}, \cdots, {a}_{i}, \cdots, {a}_{m}], \;\\{{b} }=[{b}_{1}, {b}_{2}, {b}_{3}, \cdots, {b}_{i}, \cdots, {b}_{m}], \\{{t} }=[{t}_{1}, {t}_{2}, {t}_{3}, \cdots, {t}_{i}, \cdots, {t}_{m}]\big\}\end{array}$
05:　　 　数据归一化
06:　　 　　$\tilde m \leftarrow m$
07:　　 　for $c = {\rm{ 1}}$, $c \leqslant 10, {\rm{c}} + + $
08:　　 　根据$l \!=\! \sqrt{q \!+\! s} \!+\! c$计算隐藏层的神经元的个数
09:　　 　BP神经网络模型
10:　　end for
11:　end

表1模型搭建阶段
Table1.Model construction phase.

$l = \sqrt {q + s} + c,$

式中q是输入层神经元的个数, s是输出层神经元的个数, $c \in \left[ {1, 10} \right]$, 根据本文实际需求与经验公式(27)式可知, 隐藏层的层数设置为2, 神经元个数为6个. 收集学习样本, 利用时钟同步参数模型输出得到的${{m}} = \{ { a_i}, { b_i}\}$组学习样本作为数据集, 再对学习样本进行数据归一化.
2 -->

4.2.模型训练阶段

如表2所示, 分别对$w \in (0, 1), b \in (0, 1), \alpha \in $$ (0, 1)$, $\rlap-{\lambda} \in (0, 1)$, $\sigma \in (0, 1)$随机赋初值, 同时设迭代次数r = 3000, $\rho $=0.001. 使用随机分成的训练集对误差补偿网络模型进行训练, 然后再用测试集对网络模型进行预测检测. 结合水下传感器网络时钟同步的特点对激活函数重新定义, 最终设为(12)式. 设定时钟同步误差补偿模型J. 然后开始对误差补偿网络进行训练, 将训练集输入到输入层神经元, 然后逐层将信号正向传播并计算输出, 直到有输出层的结果并计算输出层的误差, 再利用误差反向传播并根据(20)式、(21)式更新各层神经元的权重和阈值. 反复进行该过程直到满足迭代终止条件才停止训练, 得到的误差补偿模型参数几乎不再发生变化. 此时得到一个满足误差补偿条件且精准度较高的BP神经网络时钟同步模型J.

阶段2: BP网络模型训练阶段
01:　　算法开始
02:　　　开始训练网络
03:　　　参数初始化
04:　　　随机设置$w \in (0, 1), b \in (0, 1),~ \alpha \in (0, 1), $ $ \rlap-{\lambda} \in (0, 1),~ \sigma \in (0, 1)$
05:　　　r =3000, $\rho $ = 0.001
06:　　　create $f(x)$, P
07:　　　　$\tilde m$ 分成训练集和测试集
08:　 　 start training
09:　　 for all $\left\{ {{t_i}, {a_i}, {b_i}} \right\} \in \tilde m$ do
10:　　　　if ($E > \rho $) do
11:　　　　$w, b$ 被更新 $w_{ij}^{(l)}, b_i^{(l)}$ according to Eq. (20) and Eq. (21)
12:　　　　end if
13:　　end for
14:　　输出J
15:　end

表2模型训练阶段
Table2.Model training stage.

2 -->

4.3.模型预测阶段

如表3所示, 模型预测阶段具体过程如下: 当网络达到迭代终止条件, 即E小于期望误差$\rho $时, 得到一个满足条件的补偿模型J. 使用测试集对J进行预测, 最后只需将从时钟同步参数模型得到的第$i + 1$个同步估计参数$[{a_{i + 1}}, {b_{i + 1}}]$输入J中, 通过输出得到时钟同步参数补偿值$[{\tilde a_{i + 1}}, {\tilde b_{i + 1}}]$.

阶段3: BP网络预测
01:　　开始
02:　　　算法预测
03:　　　当满足条件时, 执行以下
04:　　　　if ($E < $$\rho $) do
05:　　　　停止训练
06:　　　　得到J
07:　　　输入$[{a_{i + 1}}, {b_{i + 1}}]$ to J
08:　　　输出$[{\tilde a_{i + 1}}, {\tilde b_{i + 1}}]$
09:　　end if
10:　end

表3模型预测阶段
Table3.Model prediction stage.

本文使用python语言, pycharm集成开发环境, 做了算法时间复杂度分析和两种仿真实验描述. 实验一: 将本文提出的算法与传统线性拟合在误差控制和预测方面做对比, 分别计算均方误差并分析它们对水下传感器时钟同步误差补偿的效果. 实验二: 本文算法与TSHL^[7]算法、MM-sync^[8]算法、MU-sync^[9]算法在同步精度和数据报文能耗方面进行对比分析.
2

-->

5.1.算法时间复杂度分析

时间复杂度是衡量一个算法的度量指标, 本节主要分析基于BP神经网络模型时钟同步误差算法. 本文算法的核心是网络的前向传播和误差反向调整权重和阈值部分. 前向信号传播时间复杂度为$O(n)$, 误差反向传播的时间复杂度为$O(m)$. 故本文算法的时间复杂度为$O({n^2})$.
2 -->

5.2.实验设置

本文仿真实验的相关参数如表4所示.

仿真实验参数	符号表示	数值
浮标节点	N	2
节点布置区域/m3	O	$400 \times 400 \times 400$
普通传感器节点	m	200
迭代次数	r	3000
正则惩罚因子	$\rlap-{\lambda}$	0.01
稀疏性惩罚因子	$\sigma $	0.03
稀疏性因子	$\tau $	0.6
激活因子	$\zeta $	0.4

表4实验参数
Table4.Experimental parameter setting.

3 -->

5.2.1.本文算法和线性拟合作同步时间与标准时间的误差对比分析

为了比较BP神经网络时钟同步误差补偿的效果, 引入利用传统线性拟合对数据报文交换进行误差补偿^[28], 同时使用传统线性拟合对m组训练样本进行拟合.
由图6可知, 精度在0.001时几乎看不出变化, 因为使用BP神经网络模型的补偿效果几乎与标准时间一致, 为了更好地看出BP补偿效果与传统补偿效果的区别, 将其扩大${10^4}$倍. 开始时BP神经网络误差大于线性拟合, 是因为开始时网络参数设置是随机设定. 当节点个数达到5时, BP神经网络的补偿效果明显优于线性拟合. 当节点个数达到90时, BP神经网络的误差补偿效果相比于线性拟合更加具有优势.
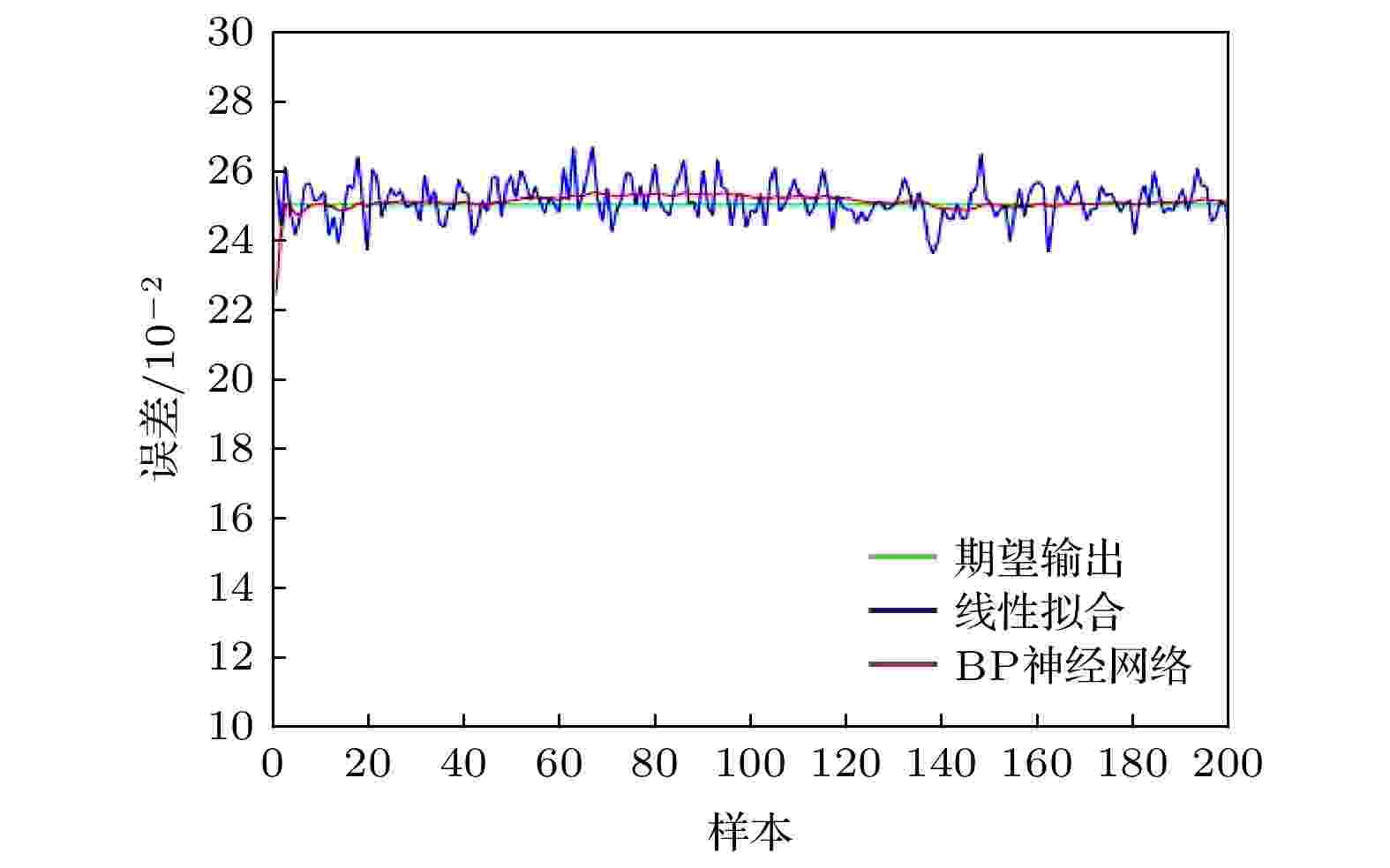图 6 误差对比分析
Figure6. Error comparison and analysis.

同时本文使用10个样本对已经训练好的补偿模型和线性拟合作对比预测, 对比它们之间的均方误差.
如图7和图8所示, 节点一开始是随机抛洒, 故需要将训练好的BP神经网络误差补偿模型和传统线性拟合去逼近节点真实值, 通过比较并计算可得图7的均方误差${R^2}=0.6972$, 图8的均方误差${R^2}=0.9116$. 比较可得, 使用BP神经网络时钟同步误差补偿模型的效果远高于线性拟合.
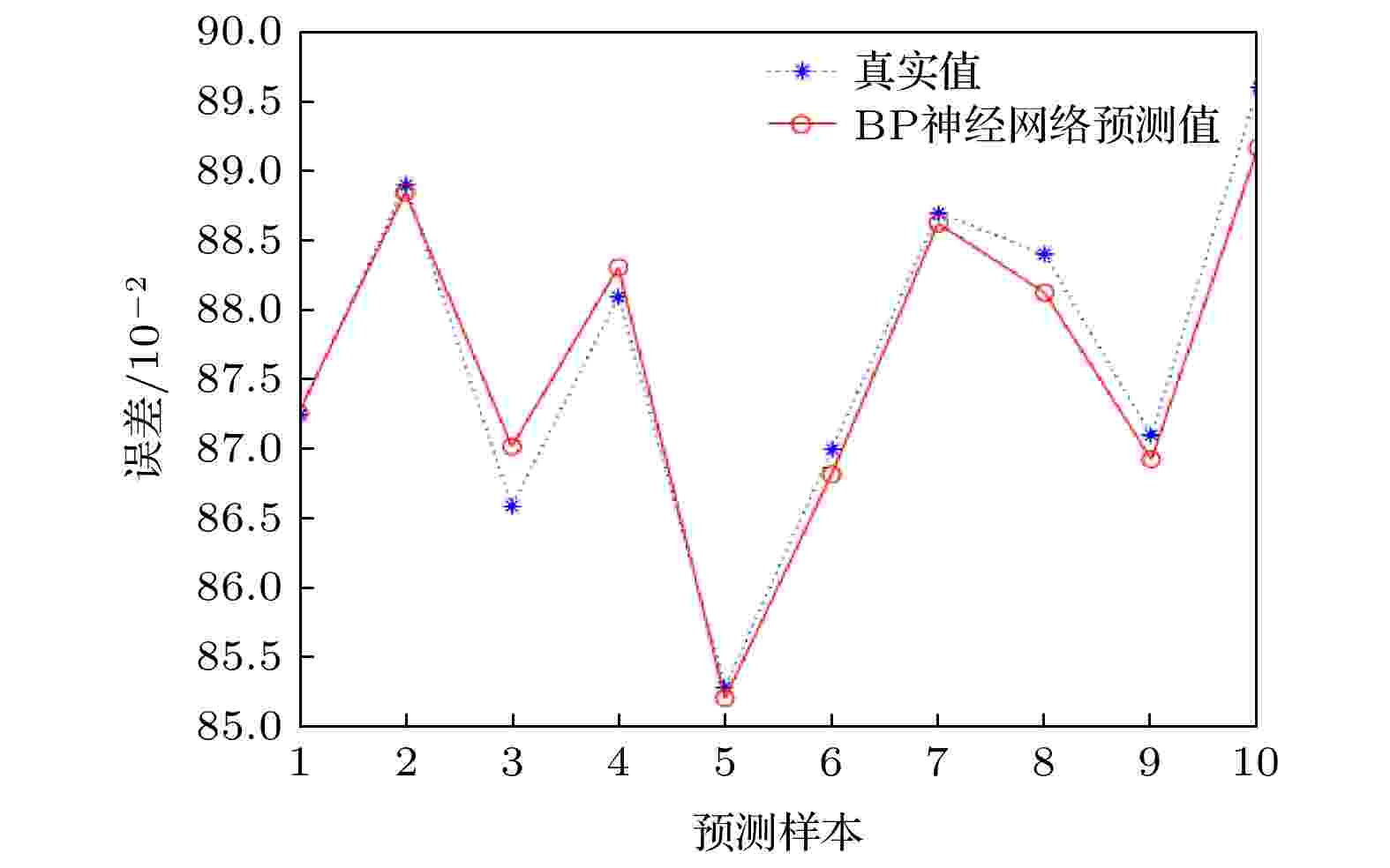图 7 BP神经网络预测
Figure7. BP neural network prediction.

图 8 线性拟合预测
Figure8. Linear fitting prediction.

3 -->

5.2.2.本文算法与其他时间同步算法的对比分析

本节针对时钟同步精度和数据报文能耗, 将本文算法与TSHL^[7]算法、MU-sync^[9]算法、MM-sync^[8]算法进行对比实验分析.
图9和图10分别表示时钟频偏a计算偏差随节点移动速度的变化情况和时钟漂移b计算偏差随节点移动速度的变化情况.
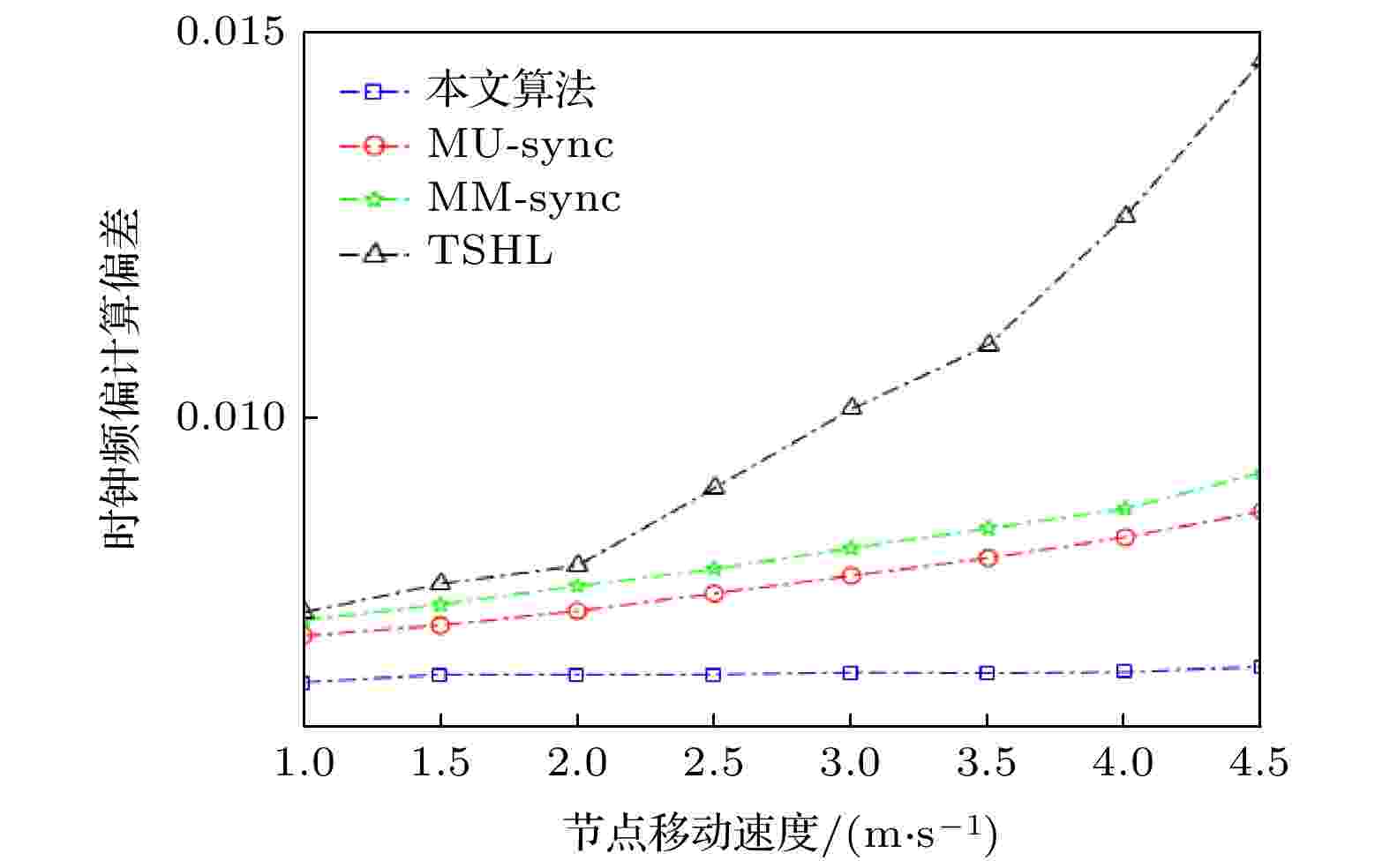图 9 时钟频偏计算偏差随节点移动的变化
Figure9. The variation of clock-frequency offset calculation deviation with node move.

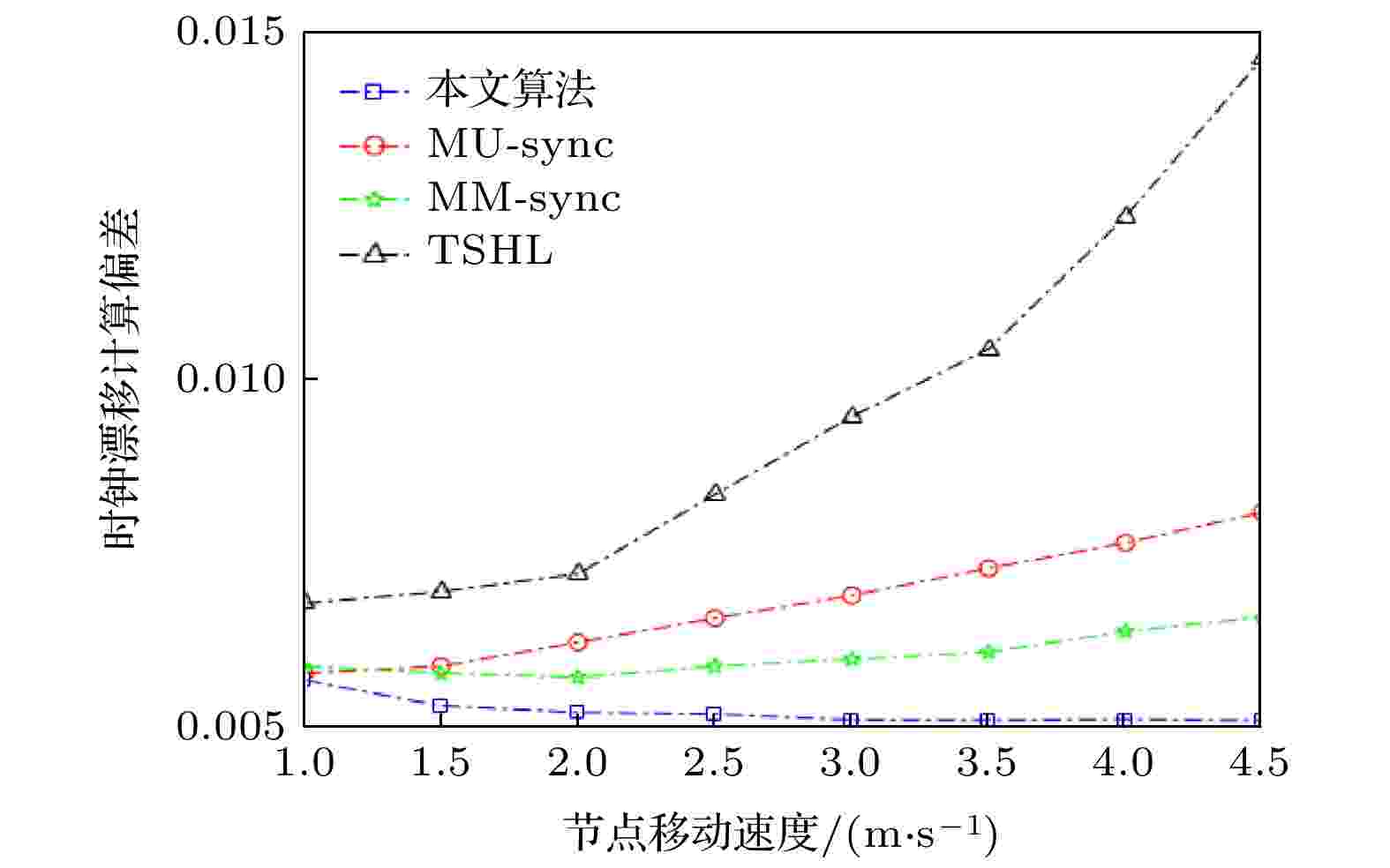图 10 时钟漂移计算偏差随节点移动变化情况
Figure10. The clock drift calculation deviation changes with the node movement.

由图9可知, 本文算法的误差明显小于其他算法, 分别比TSHL^[7]算法、MU-sync^[9]算法、MM-sync^[8]算法降低37.42%, 17.29%和21.86%. 因为随着节点速度增大, 而TSHL忽视了节点的移动性问题, 在时钟同步期间假定节点位置不变, 即传播过程时延没有发生变化, 导致速度增大时, TSHL的误差会异常明显. MU-sync是针对节点移动性提出的算法, 但忽视了传播时延, 采用不变的值去计算频偏, 再用线性拟合去除相应的传播时延, 从而求得时钟漂移, 当速度明显增大时, 算法表现就会减弱. MM-sync算法在误差补偿中, 假设节点做匀速运动, 当节点速度增大时, 误差补偿效果减弱. 本文算法基于BP神经网络的时钟同步误差补偿模型, 考虑了节点移动性带来的时延问题, 同时通过BP神经网络反复训练得到一个精度较高的误差补偿模型.
由图10可以看出, 本文算法明显优于其余三种算法, 当节点速度越大, 误差几乎不在发生变化, 其运动轨迹和移动模型更加符合实际, 并且时钟同步精度也更高, 因而计算偏差越小.
图11给出本文算法、MU-sync^[9]算法、MM-sync^[8]算法和TSHL^[7]算法在完成同步后, 本地时钟增长的误差趋势.
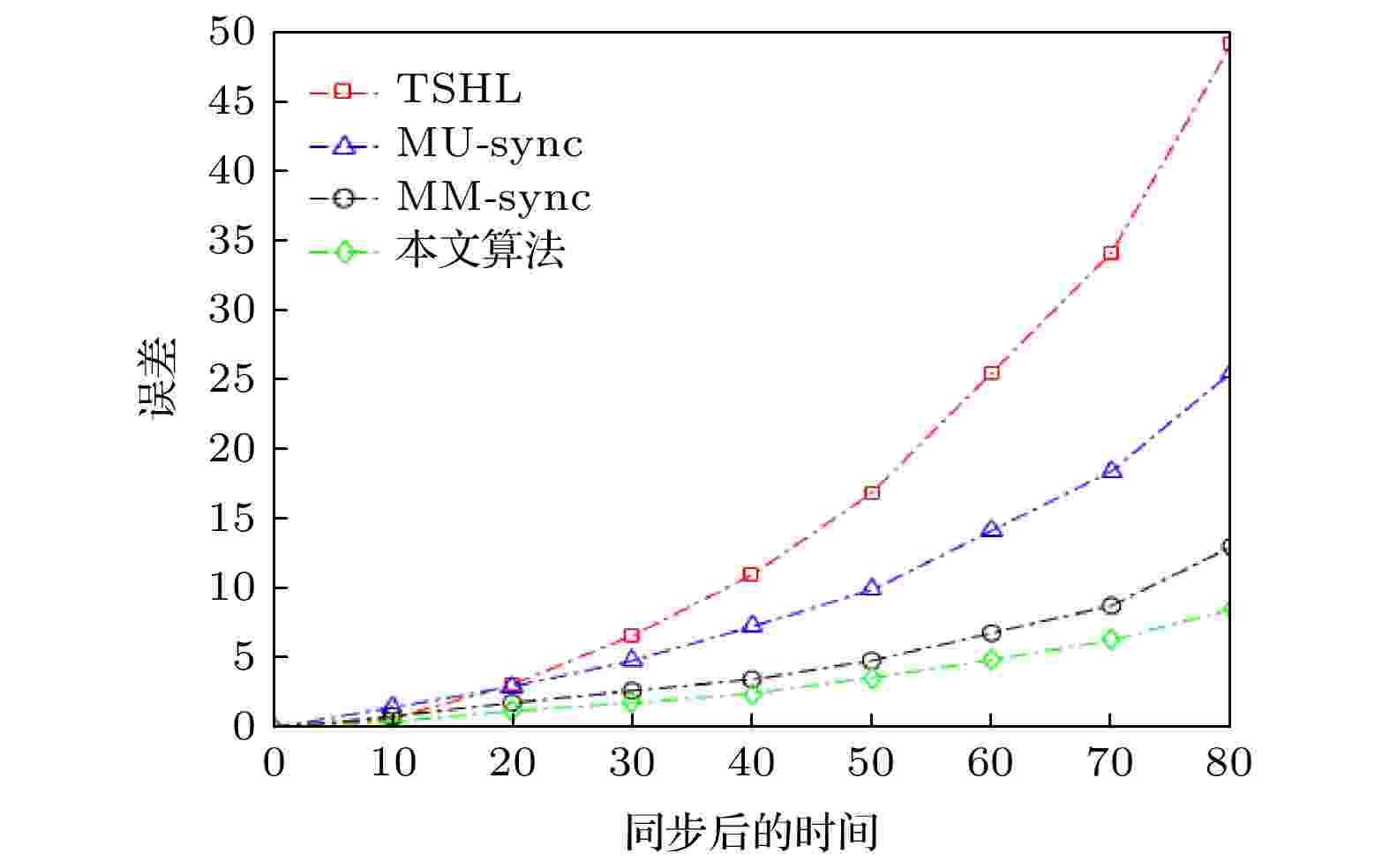图 11 时钟同步后本地时钟误差增长趋势变化
Figure11. The increasing trend of local clock error changes after clock synchronization.

由图11可知, 本文算法的误差明显小于其他算法, 分别降低47.12%, 31.37%和12.89%. 其他算法误差较大的主要是原因为: TSHL法假设网络为静态网络, 这势必会导致更大的同步误差; MU-sync使用两次线性回归来估计时钟频偏和相偏, 但该算法假设每一轮消息交换到的传播时延是一致的, 没有考虑往返时间不一致的传播时延, 这会导致更大的同步误差; MM-sync算法虽然考虑节点移动性, 但是在误差估计阶段, 将节点运动状态单一化的归结为匀速运动, 如此随着网络的动态变化, 该算法的性能也随之下降; 这三种算法并没过多考虑节点随洋流运动而产生的动态时延, 导致误差较大. 本文算法通过引入洋流模型估计待同步节点的速率, 提高了动态传播延时的精度, 且使用BP神经网络反复训练, 得到一个误差补偿精度很高的模型.
图12给出本文算法与其余三种算法在同步35次后产生的数据报文数, 以此来分析数据报文能耗的高低.
图 12 同步次数与数据报文的变化
Figure12. Changes in synchronization times and datagram.

由图12可知, 本文算法在能耗方面少于其他三种算法^[7-9]. 分别比其余三种算法降低了37.46%, 61.26%和18.75%. 本文算法只需要BP神经网络反复训练即可, 与其余三种算法的原理不同, 需要的数据报文较少. 随着同步次数的增加, TSHL算法在同步过程的第二阶段需要参考节点和普通节点进行一次双向数据报文交换, 用来计算时钟漂移. MU-sync算法为追求更高的精度, 通过增加了双向数据报文的交换次数, 导致当同步次数增加时, 数据报文量快速增加. MM-sync需要提高线性拟合的次数来提高精度, 导致数据报文的消耗大.

水下传感器网络具有移动性、能耗有限、高时延和随机动态时延的特点, 给设计水下传感器网络节点时钟同步带来巨大挑战. 本文创新性地提出利用BP神经网络对时钟同步误差进行补偿, 从而提高时钟同步精度. 本文算法首先考虑节点随洋流运动的影响, 采用深海拉格朗日洋流模型描述水下节点运动规律, 并算出待同步节点的运动速率, 进而建立时钟同步参数模型, 最后利用BP神经网络对时钟同步参数模型进行误差补偿. 与现有同步算法对比, 本文算法能高效补偿同步误差提高时钟同步精度, 且避免了节点的双向数据报文交换, 从而也降低了数据能耗. 与此同时, 由于本文算法考虑了节点受洋流运动的影响, 故节点在运动的情况下, 依然能有效进行误差补偿, 从而保持时钟一定的同步精度. 实验表明, 算法在水下复杂环境时候, 本文算法对水下传感器网络时钟同步具有很好地适用性, 同时也为时钟同步误差补偿的理论提供了新思路.