摘要: 在Nambu?Jona-Lasinio模型框架下, 研究温度和重子化学势对同位旋非对称量子色动力学物质状态方程和热力学性质的影响. 通过将零温和零重子化学势下的pion超流物质状态方程以及有限温下同位旋密度、压强与格点数据做比较, 发现两种方法给出的结果符合得较好. 进一步计算表明, 零温和零重子化学势下的平均同位旋能量随同位旋密度单调增加, 而非零重子化学势和有限温下却呈现具有极小值的非对称抛物线行为. 最后, 利用得到的状态方程探讨声速随同位旋化学势的变化行为, 结果显示有限温和(或)重子化学势下的声速在相变点不连续, 且超流相中的声速饱和值明显大于普通核物质及夸克物质中的值. 另外, 在超流相中重子化学势和温度具有软化状态方程以及降低声速的作用.
关键词: 同位旋化学势 /
玻色-爱因斯坦凝聚 /
二级相变 /
热力学 English Abstract Equation of state and thermodynamic properties of isospin imbalanced strongly interacting matter Lu Qi 1 ,Chen Wei-Jie 1 ,Lu Zhen-Yan 1 ,Xu Ying 1 ,Li Xiang-Qian 2 1.School of Physics and Electronic Science, Hunan University of Science and Technology, Xiangtan 411201, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11947135), the Natural Science Foundation of Hunan Province, China (Grant Nos. 2018JJ2111, 2020JJ4284), the Scientific Research Project of Hunan University of Science and Technology, China (Grant No. E52059), and the Natural Science Foundation for Young Scientists of Shanxi Province, China (Grant No. 201901D211110)Received Date: 20 January 2021Accepted Date: 15 February 2021Available Online: 07 July 2021Published Online: 20 July 2021Abstract: The effects of temperature and baryon chemical potential on equation of state and thermodynamics of isospin imbalanced QCD matter are investigated in the framework of two-flavor Nambu?Jona-Lasinio model. The equation of state at zero temperature and baryon chemical potential as well as the isospin density and normalized pressure at finite temperature are shown to be consistent with the lattice data. We also find that the energy per isospin increases monotonically with the increase of isospin density at vanishing temperature and baryon chemical potential, while it first decreases and then increases with the augment of isospin density, behaving as a non-symmetric parabolic curve. Finally, we compute the sound velocity and find that it is discontinuous at the phase transition point for finite temperature and/or baryon chemical potential. In particular, the sound velocity in the superfluid phase is distinctly larger than that in the ordinary nuclear matter and quark matter, while the temperature and baryon chemical potential included in the superfluid phase makes the equation of state softer and the sound velocity slower.Keywords: isospin chemical potential /Bose-Einstein condensation /second order phase transition /thermodynamics 全文HTML --> --> --> 1.引 言 随着标准模型预言的最后一个基本粒子, 即希格斯粒子, 于2013年在实验上第一次被发现, 并在2015年被另外一个合作组进一步证实后, 标准模型预言的61种基本粒子已经全部被找到. 在这61种粒子中, 包含三代夸克, 共计6种不同味道. 夸克间的强相互作用由量子色动力学(QCD)描述, QCD属于规范理论且是粒子物理学标准模型的一部分, 具有色禁闭和渐进自由性质. 在高能区, 强耦合常数较小, 可以对QCD作微扰展开, 对高密度的物质性质描述得很好[1 ] . 但是随着能标不断降低, 强耦合常数逐渐增大, 在低能区微扰QCD变得不可信赖, 且热力学自洽性问题会变得越来越突出[2 ,3 ] , 此时需要考虑QCD的非微扰效应. 另外, 基于第一性原理的格点QCD方法, 虽然在低重子化学势下可以通过泰勒展开获得有限重子数密度QCD物质性质[4 -6 ] , 但是费米子行列式的不正定性导致理论不可避免地碰到符号问题, 且所得结果的有效性只局限于低重子数密度情形.[7 ,8 ] 来研究QCD物质在低能区的行为以及真空的非微扰性质. 比较常见的模型有Nambu–Jona-Lasinio (NJL)模型[9 -11 ] 、夸克介子模型[12 -14 ] 、Dyson-Schwinger方程[15 -17 ] 、等效粒子模型[18 -22 ] 和准粒子模型[23 -25 ] 等. 由于有限同位旋化学势下费米子行列式是正定的, 格点QCD方法不会碰到符号问题. 所以, 原则上可以利用格点QCD方法计算非微扰区有限同位旋化学势下QCD物质状态方程以及相图等. 2001年, Son和Stephanov[26 ] 在手征微扰论框架下, 指出同位旋化学势等于pion介子质量处, 系统会发生一个二级相变, 即随着同位旋化学势的增加, 系统从正常相进入到带电pion介子组成的超流相, 反之, 则从超流相回到正常相. 随后, 格点QCD方法在数值上证实此论点[27 -29 ] . 何联毅等[30 ,31 ] 以及Warringa等[32 ] 在NJL模型框架下, 同样证实随着同位旋化学势的增加, 系统会在同位旋化学势等于pion介子质量时, 从正常相进入到超流相. 除此之外, Adhikari等[33 ,34 ] 将手征微扰论从领头阶推广到次领头阶水平, 并在此基础上再次验证从正常相到pion超流相的相变属于二级相变. 自Son和Stephanov[26 ] 的开创性工作之后, 同位旋化学势下相图及QCD物质性质获得了广泛的研究[35 -41 ] . 关于介子超流方面最新的一篇综述, 详见文献[42 ].[43 ] , 并将NJL模型零温结果与格点数据和领头阶手征微扰论结果作比较, 发现三者符合得很好, 尤其是在同位旋化学势小于两倍pion介子质量的区域. 另外, NJL模型给出的零温拓扑磁化率[44 ] 与格点QCD数值模拟[45 ] 和手征微扰论结果[46 ,47 ] 均定量相符, 而在有限温度下前者给出的结果比手征微扰论的预测更符合格点QCD数据[48 ] . 随后, 我们还将计算推广到有限温情形, 详细计算手征、pion和同位旋磁化率随同位旋化学势和温度的变化行为, 发现这些磁化率在临界同位旋化学势处不连续, 非常好地表征系统存在的二级相变. 但是文章并未包含重子化学势的影响, 而在现实世界中, 一般重子化学势并不为零, 比如致密星体环境[49 ] 等. 由于零温下NJL模型的研究结果与手征微扰论及格点结果符合得非常好, 我们自然而然地期待进一步考虑重子化学势的影响之后, NJL模型也能给出定性甚至是定量准确的物理结果. 本文将在两味NJL模型框架内, 研究重子化学势对同位旋非对称QCD物质状态方程和热力学性质的影响.2.理论框架 受到BCS超导理论的启发, NJL模型最初被提出为一个以核子为基本自由度的理论, 随后被发展为一个以夸克为基本自由度的QCD低能唯象模型. 在虚时有限温度场论中, NJL模型的配分函数为$ \beta = 1/T $ 表示温度的倒数, $ \mu_{\rm B} $ 和$ \mu_{\rm I} $ 分别表示重子化学势和同位旋化学势, $ {\cal{L}} $ 是NJL模型拉格朗日密度, 简称拉氏量密度, 其表达式如下:G 为四费米子相互作用常数, $ { q} = (u, d)^{\rm T} $ 表示夸克场矩阵, τ m . 作为外源引入的$ \hat{ {\mu}} = {\rm{diag}}\left\{\mu_{\rm u}, \mu_{\rm d}\right\} $ 表示夸克化学势的对角矩阵, 二者可以用重子化学势$ \mu_{\rm B} $ 和同位旋化学势$ \mu_{\rm I} $ 表示为2 )式中的NJL模型拉氏量具有$ U_{\rm B}(1) \otimes S U_{\rm I}(2) \otimes S U_{\rm A}(2) $ 对称性; 但同位旋化学势不为零时, 同位旋对称性$ S U_{\rm I}(2) $ 破坏到$ U_{\rm I}(1) $ 整体对称性, 并由此产生带电pion介子构成的玻色-爱因斯坦凝聚, 而手征对称性则同时破缺到$ U_{\rm {IA}}(1) $ 整体对称性, 对应于产生手征凝聚. 在有限重子化学势和同位旋化学势下, $ U_{\rm B}(1) $ 对称性没有发生破缺, 对应于系统重子数守恒.θ 是一个实数, 而$ \tau_\pm = \tau_1\pm {\rm i}\tau_2 $ . 由于θ 的取值不会改变系统的热力学势密度, 因此直接取$ \theta = 0 $ , 这时(7 )式正好表示处在$ \tau_1 $ 方向的pion凝聚, 即$ \varPi = \langle\bar{q}{\rm i}\gamma_5\tau_1{ q}\rangle $ . 经过一番计算, 最终得到平均场近似下系统热力学势密度表达式为$ M_{\rm q} = m-2 G\sigma $ 表示夸克有效质量, 其直接或通过凝聚间接依赖于温度、化学势和温度等系统参量. 对于唯象模型, 需要认真对待模型的热力学自洽性问题. 在准粒子模型中, 夸克有效质量也是化学势和(或)温度的函数, 模型的自洽性通过在系统热力学势密度添加一个也依赖于化学势和(或) 温度的有效袋常数来实现[50 -52 ] . 而在NJL模型中, 夸克有效质量对系统参量的依赖关系由能隙方程自洽地决定:10 )式的能隙方程可以明显地写成下面两个式子:$ n(x) = 1/[\exp(\beta x)+1] $ 表示费米分布函数. 这里需要说明的是, 如果能隙方程有多个不同解, 则只有满足热力学势密度取最小值的解才是我们想要的解, 也是系统基态所对应的解. 在热力学势密度给定之后, 由热力学基本关系式可以得到系统的同位旋密度、压强和能量密度分别为:14 )式中的$ \varOmega_0 $ 为系统温度、重子化学势和同位旋化学势都为零时的热力学势密度, 即$\varOmega_0 = \varOmega\; (\mu_{\rm B} = 0, $ $ \mu_{\rm I} = 0, T = 0)$ .3.数值结果和讨论 两味NJL模型有三个参数, 分别是夸克流质量m 、四费米子相互作用常数G 和为避免无穷大问题而引进的三维动量截断Λ . 在NJL模型框架下, 通过正确重复一些我们所熟知的物理参量经验值: pion介子质量$ m_{\pi} = 0.134 $ GeV, pion介子衰变常数$ f_{\pi} = 0.093 $ GeV 和真空中手征凝聚值$\sigma_0 = $ $ 2 \times (-0.25\; {\rm{GeV}})^3$ , 可以拟合得到NJL模型的三个参数取值[53 ] :$\Delta P\equiv $ $ \Delta P(T, \mu_{\rm B}, \mu_{\rm I})$ 概念, 其具体表达式为图1 给出温度$ T = 0.124 $ GeV时归一化同位旋密度$ n_{\rm I}/T^3 $ (上板面) 和归一化压强$ \Delta P/T^4 $ (下板面) 随同位旋化学势的变化关系. 黑色实线表示NJL模型结果, 而蓝色实心圆表示格点数据[54 ] . 在考虑的同位旋化学势范围内, 归一化同位旋密度和归一化压强与格点数据都符合得比较好, 尤其是在低化学势区域. 不久前, 我们[43 ] 和Avancini等[55 ] 都比较了零温下NJL模型、手征微扰论和格点QCD数值模拟结果, 发现三者在一定范围内定量上一致. 结合这里有限温的相符结果, 说明不论在零温还是有限温下, NJL模型在低能区的结果通常是可信赖的.图 1 温度$T=0.124$ GeV时, 归一化同位旋密度$n_{\rm I}/T^3$ (上板面) 和归一化压强$\Delta P/T^4$ (下板面) 随同位旋化学势的变化关系. 蓝色实心圆表示取自文献[54 ]的格点数据Figure1. Normalized isospin density $n_{\rm I}/T^3$ (upper panel) and normalized pressure $\Delta P/T^4$ (lower panel) as functions of $\mu_{\rm I}/m_\pi$ at fixed $T=0.124$ GeV. The blue circles are taken from Ref.[54 ] for comparison.[31 ] . 图2 给出手征凝聚σ 和pion凝聚Π 随同位旋化学势的变化关系. 当$ \mu_{\rm B} = T = 0 $ 且$ \mu_{\rm I} < m_{\pi} $ 时 (黑色实线), 手征凝聚保持为非零常数, 而pion凝聚始终为零. 此时, 由于同位旋化学势太小而不足以影响真空, 系统处于正常相; 在临界化学势$ \mu_{\rm I} = m_{\pi} $ 处, 系统发生一个二级相变: 同位旋对称性自发破缺, 带正电和带负电的pion介子成叠加态[38 ] , 形成一个无质量的哥德斯通态, 系统处于pion超流相中[26 ] ; 当$ \mu_{\rm I} > m_{\pi} $ 时, pion凝聚值随同位旋化学势的增加而迅速增加, 而手征凝聚则相应地随同位旋化学势的增加而减小. 为了探讨温度和重子化学势对凝聚的影响, 图2 中还展示了分别对应于$ \mu_{\rm B} = 0 $ 和$ T = $ $ 0.1 $ GeV (绿色点虚线), $ \mu_{\rm B} = 0.3 $ GeV和$T = $ $ 0.1$ GeV (红色点线) 以及$ \mu_{\rm B} = 0.6 $ GeV和$T = $ $ 0.1$ GeV (蓝色虚线) 情形的曲线. 可以看到, 温度以及重子化学势的存在均使二级相变点向更大同位旋化学势移动, 而且压低pion凝聚值. 另外, 与$ \mu_{\rm B} = T = 0 $ 的情形 (黑色实线) 相比, 温度和重子化学势在正常相中均压低手征凝聚值, 而在pion超流相中更慢趋于零.图 2 不同重子化学势和温度下手征凝聚σ 和pion凝聚Π 随同位旋化学势变化关系Figure2. Chiral and pion condensates as functions of $\mu_{\rm I}/m_\pi$ at different baryon chemical potentials and temperatures.[56 ] , 定义为$ E/n_{\rm B} $ 的平均重子能量是一个非常重要的物理量, 这里E 表示系统能量密度, 而$ n_{\rm B} $ 表示重子数密度. 仿照平均重子能量$ E/n_{\rm B} $ 的定义方式, 引入平均同位旋能量概念以研究同位旋非对称QCD物质性质, 其数学表达式为$ E/n_{\rm I} $ . 图3 给出平均同位旋能量随同位旋密度的变化关系. 图中曲线从下到上依次对应于$\mu_{\rm B} = $ $ T = 0$ (黑色实线), $ \mu_{\rm B} = 0 $ 和$ T = 0.1 $ GeV (绿色点虚线), $ \mu_{\rm B} = 0.3 $ GeV和$ T = 0.1 $ GeV (红色点线) 以及$ \mu_{\rm B} = 0.6 $ GeV和$ T = 0.1 $ GeV (蓝色虚线) 的情形. 对于表示$ \mu_{\rm B} = T = 0 $ 情形的黑色曲线, 其先是在靠近但小于临界同位旋化学势的区域快速上升, 并在相变点处向右上方有一个弯折之后, 平均同位旋能量开始随同位旋密度的增加而线性增加. 但当温度和(或)重子化学势不为零时, 平均同位旋能量不再随同位旋密度单调增加, 而是先随同位旋密度的增加而降低到极小值, 之后再随后者单调增加. 曲线的极小值位置随着温度和重子化学势的增大而向右上方移动. 除了表示$ \mu_{\rm B} = $ $ T = 0 $ 情形的黑色实线之外, 有限温和(或)重子化学势下的曲线行为与夸克物质平均重子能量随重子数密度的变化行为十分相似[57 ] .图 3 不同重子化学势和温度下平均同位旋能量随同位旋密度的变化关系. 曲线的标记方式与图2 相同Figure3. Energy per isospin as a function of the isospin density. Conventions for colors and symbols are the same used in Fig. 2 .图4 给出归一化同位旋密度$ n_{\rm I}/m_{\pi}^3 $ 随同位旋化学势$ \mu_{\rm I}/m_{\pi} $ 的变化关系. 对于$ \mu_{\rm B} = T = 0 $ 的情形 (黑色实线), 可以明显看到同位旋密度在$ \mu_{\rm I} < m_{\pi} $ 区域始终保持为零, 系统处于正常相, 而在$ \mu_{\rm I} > m_{\pi} $ 区域开始随着同位旋化学势的增加而单调递增, 表明pion凝聚的出现使系统的同位旋密度不再为零. 对于分别表示$ \mu_{\rm B}\! =\! 0 $ 和$ T \!=\! 0.1 $ GeV, $\mu_{\rm B}\! =\! 0.3$ GeV和$ T = 0.1 $ GeV, $ \mu_{\rm B} = 0.6 $ GeV和$ T = 0.1 $ GeV的绿色点虚线、红色点线和蓝色虚线, 三者有相似的变化行为: 在正常相和pion超流相中, 同位旋密度均随同位旋化学势的增加而近似线性增加, 且在临界化学势处各自有一个向左上方的弯折. 换句话说, 进入超流相后, 三条曲线所表示的同位旋密度随同位旋化学势的增长速度均(明显)大于正常相中的增长速度. 不管是在正常相还是pion超流相中, 重子化学势和温度均起到了抬升同位旋密度的作用.图 4 不同重子化学势和温度下归一化同位旋密度$n_{\rm I}/m_\pi^3$ 随同位旋化学势的变化关系. 曲线的标记方式与图2 相同Figure4. Normalized isospin density as a function of isospin chemical potential at various baryon chemical potentials and temperatures. Conventions for colors and lines are the same used in Fig. 2 .[39 ,40 ] . 图5 给出同位旋非对称QCD物质的状态方程, 其中图5(a) 是能量密度和压强随同位旋化学势变化得到的结果, 图5(b) 是随重子化学势变化得到的结果. 图5(a) 中曲线所对应的参数以及标记方式与图2 相同, 即黑色实线、绿色点虚线、红色点线和蓝色虚线分别对应于$ \mu_{\rm B} = T = 0 $ , $ \mu_{\rm B} = $ $ 0 $ 和$ T = 0.1 $ GeV, $ \mu_{\rm B} = 0.3 $ GeV和$ T = 0.1 $ GeV, $ \mu_{\rm B} = 0.6 $ GeV和$ T = 0.1 $ GeV的情形. 可以看到四条曲线的行为非常相似: 除了在各自起点处有一个向右上方弯曲的弧度之外, 曲线的其余部分均近似呈线性增加. 为了将NJL 模型结果与格点数据作比较, 还在图5(a) 中内插一个图, 黑色实线依旧表示$ \mu_{\rm B} = T = 0 $ 时得到的状态方程, 而橙色阴影区域表示取自文献[40 ]的格点数据. 可以看到零温和零重子化学势下的NJL模型结果与格点数据定量上相符. 有趣的是, 根据pion超流可以稳定存在的想法[38 ] , 一种主要由pion超流物质组成的玻色星(即pion 星)被提出. 依据是否满足电中性条件以及电中性条件所考虑的轻子类型, pion星最大质量可以达到十倍乃至几百倍太阳质量, 而其对应的半径可达到几十乃至上万千米[40 ] .图 5 同位旋非对称物质热力学量分别随(a)同位旋化学势和(b)重子化学势变化得到的状态方程. 图(a)内插图的橙色阴影区域表示取自文献[40 ]的格点数据Figure5. The equation of state obtained with the variation of (a) isospin and (b) baryon chemical potentials respectively, while the orange shaded area denotes the lattice data taken from Ref.[40 ].图5(b) 给出同位旋非对称QCD物质热力学量随重子化学势变化得到的状态方程, 其中黑色实线、绿色点虚线、红色点线和蓝色虚线分别对应于$ \mu_{\rm I} = T = 0 $ , $ \mu_{\rm I} = 0 $ 和$ T = 0.1 $ GeV, $ \mu_{\rm I} = $ $ 0.3 $ GeV和$ T = 0.1 $ GeV, $ \mu_{\rm I} = 0.6 $ GeV和$T = $ $ 0.1$ GeV的情形. 除了表示$ \mu_{\rm I} = T = 0 $ 的黑色曲线在起始点有一个近似竖直上升之外, 曲线的其他部分以及另外三条曲线均是随压强的增大而较为平缓地增加. 另外, 表示$\mu_{\rm I} \!=\! 0.3$ GeV和$T \!=\! 0.1$ GeV, $\mu_{\rm I} \!=\! 0.6$ GeV和$ T = 0.1 $ GeV的红色点线和蓝色虚线在上升过程中均有一个明显的弯折, 且前者比后者更明显. 这些弯折点对应于二级相变点.$V_{\rm s}$ 可以由下式计算:图6 给出不同重子化学势和温度下的声速平方随同位旋化学势的变化关系. 对于$ \mu_{\rm B} = T = 0 $ 的情形(黑色实线), 在$ \mu_{\rm I} < m_{\pi} $ 的区域(即正常相中), 由于同位旋化学势太小而不足以影响真空, 所以由(14 )式可知系统的压强为零, 这进一步使得声速平方随同位旋化学势的增加而保持为零; 而当$ \mu_{\rm I} > m_{\pi} $ (即超流相中)时, 声速平方开始随同位旋密度的增加而快速增加; 在同位旋化学势约大于两倍pion介子质量之后, 声速趋于饱和. 分别表示$\mu_{\rm B} \!=\! 0$ 和$T \!=\! 0.1$ GeV (绿色点虚线), $\mu_{\rm B} \!=\! 0.3$ GeV和$ T = 0.1 $ GeV (红色点线), $ \mu_{\rm B} = 0.6 $ GeV和$T = $ $ 0.1$ GeV (蓝色虚线)情形的三条曲线在正常相中的行为则与此略有不同: 虽然声速平方也是保持为常数, 但这个常数并不为零. 而在超流相中声速平方随同位旋化学势的变化行为与黑色实线相近, 均是在临界点附近随同位旋化学势的增加而迅速增大, 随后趋于饱和.图 6 不同重子化学势和温度下声速平方随同位旋化学势的变化关系. 曲线的标记方式与图2 相同Figure6. Sound velocity as a function of $\mu_{\rm I}/m_\pi$ at zero temperature at various baryon chemical potentials and temperatures. Conventions for colors and lines are the same used in Fig. 2 .$ \mu_{\rm B} = 0.6 $ GeV和$ T = 0.1 $ GeV情形的蓝色虚线在进入超流相之后, 则直接跳到某个更大值, 随后也开始随同位旋化学势的增加而增加. 声速在相变点处不连续的现象与文献[58 , 59 ]的描述相符. Pion凝聚的出现使状态方程变硬, 这导致pion超流中声速比普通核物质及夸克物质的都要大很多. 另外, 虽然pion超流中的声速比普通核物质中的更大, 但是并没有超过1, 因此满足因果律的要求, 而温度及重子化学势的存在均使声速减小, 但仍然大于普通物质中的声速. 近些年天文观测发现, 有几颗质量接近以及大于两倍太阳质量的致密星体[60 -63 ] , 对核物质和夸克物质状态方程给出了很强的限制: 一部分理论模型由于给出的状态方程太软, 不足以支撑最大质量达到约两倍太阳质量的星体而被排除掉. 对于这类具有约两倍太阳质量以及未来若可能观测到更大质量的致密星体[39 ] 或具有较大声速的星体[64 ] , 考虑内部具有不同程度强作用pion凝聚的状态方程将是一个自然且应该考虑在内的方案.4.结 论 有限同位旋化学势下pion超流的形成已经被多种理论方法证实. 本文将$ \mu_{\rm B} = T = 0 $ 时两味NJL模型的状态方程、温度$ T = 0.124 $ GeV时同位旋密度和压强随同位旋化学势的变化行为与格点数据作比较, 两种方法得到的结果在考虑的同位旋化学势范围内符合得较好, 尤其是在低密区. 随后, 进一步研究了重子化学势和温度对同位旋非对称QCD物质状态方程和热力学性质的影响. 得到如下主要结论.$ \mu_{\rm B} = T = 0 $ 时, 除了在相变点附近曲线上升过程中有一个向右上方弯折之外, 在超流相中平均同位旋能量随同位旋密度线性单调增加. 但进一步考虑温度和重子化学势的影响之后, 平均同位旋能量随同位旋化学势的变化行为与夸克物质平均重子能量随重子数密度的变化行为十分相似, 即呈现非对称的抛物线形状, 而且温度和(或)重子化学势越大, 曲线极小值点向更大同位旋密度和更高能量移动.图5(a) 所示, 给定的重子化学势越大, 曲线整体上越向右上方移动. 与此相反, 对于热力学量随重子化学势变化得到的状态方程, 如图5(b) 所示, 同位旋化学势越大, 曲线整体上越向右下方移动. 从声速的计算公式(18 )式来看, 这在一定程度上反映了超流相中重子化学势具有软化状态方程以及降低声速的作用, 而同位旋化学势的作用恰恰相反: 使状态方程变硬且升高声速.$ V_{\rm s}^2 = 1/3 $ .[65 ] . 同位旋化学势和奇异夸克化学势的存在会影响轻子衰变性质, 甚至给出一些新奇现象[38 ] . 目前文献中已有的手征微扰论结果只局限于密度较低的情形, 利用QCD有效模型研究介子超流相中轻子衰变性质具有重要意义. 






























 图 1 温度
图 1 温度






















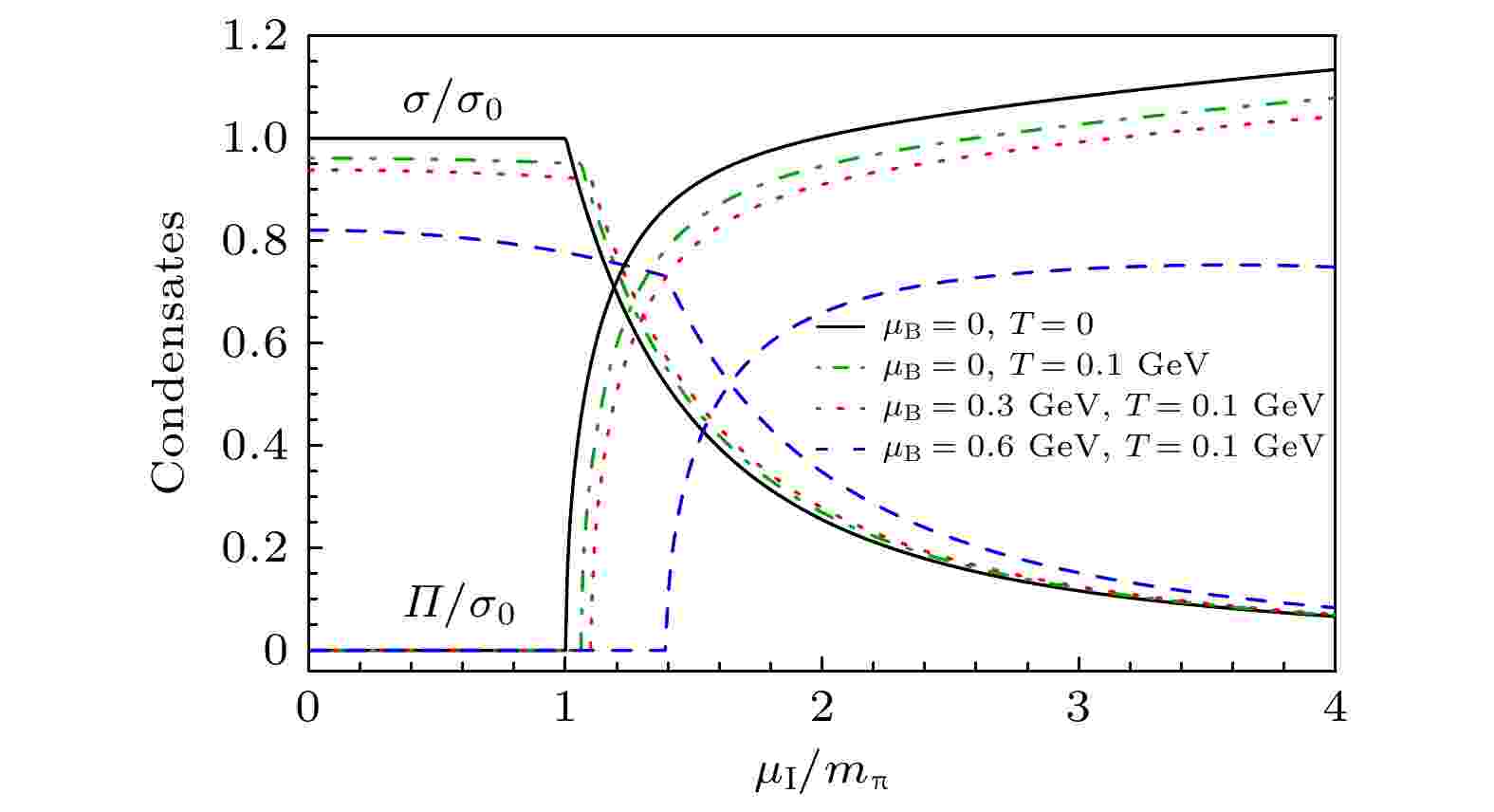 图 2 不同重子化学势和温度下手征凝聚σ和pion凝聚Π随同位旋化学势变化关系
图 2 不同重子化学势和温度下手征凝聚σ和pion凝聚Π随同位旋化学势变化关系























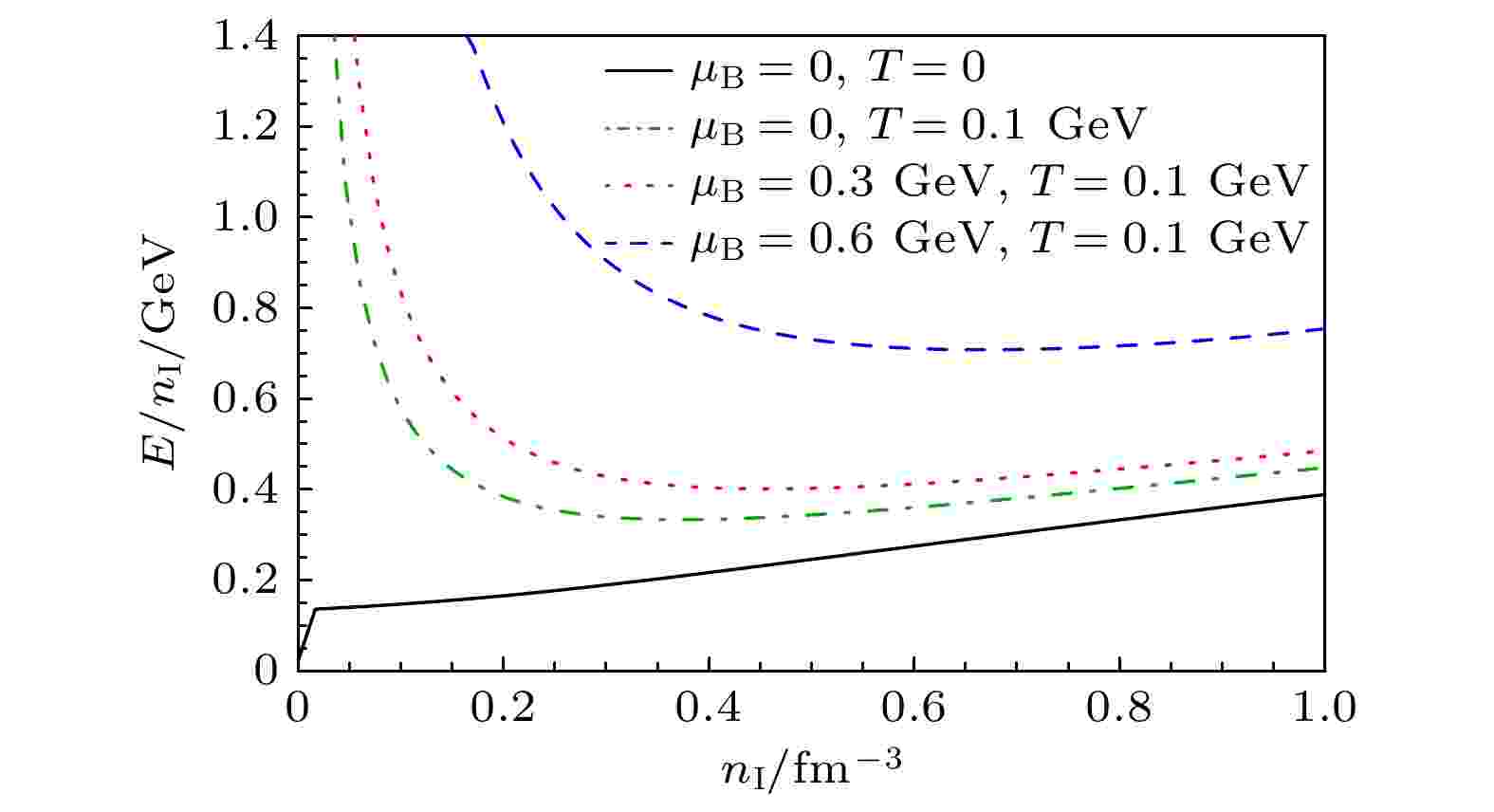 图 3 不同重子化学势和温度下平均同位旋能量随同位旋密度的变化关系. 曲线的标记方式与图2相同
图 3 不同重子化学势和温度下平均同位旋能量随同位旋密度的变化关系. 曲线的标记方式与图2相同












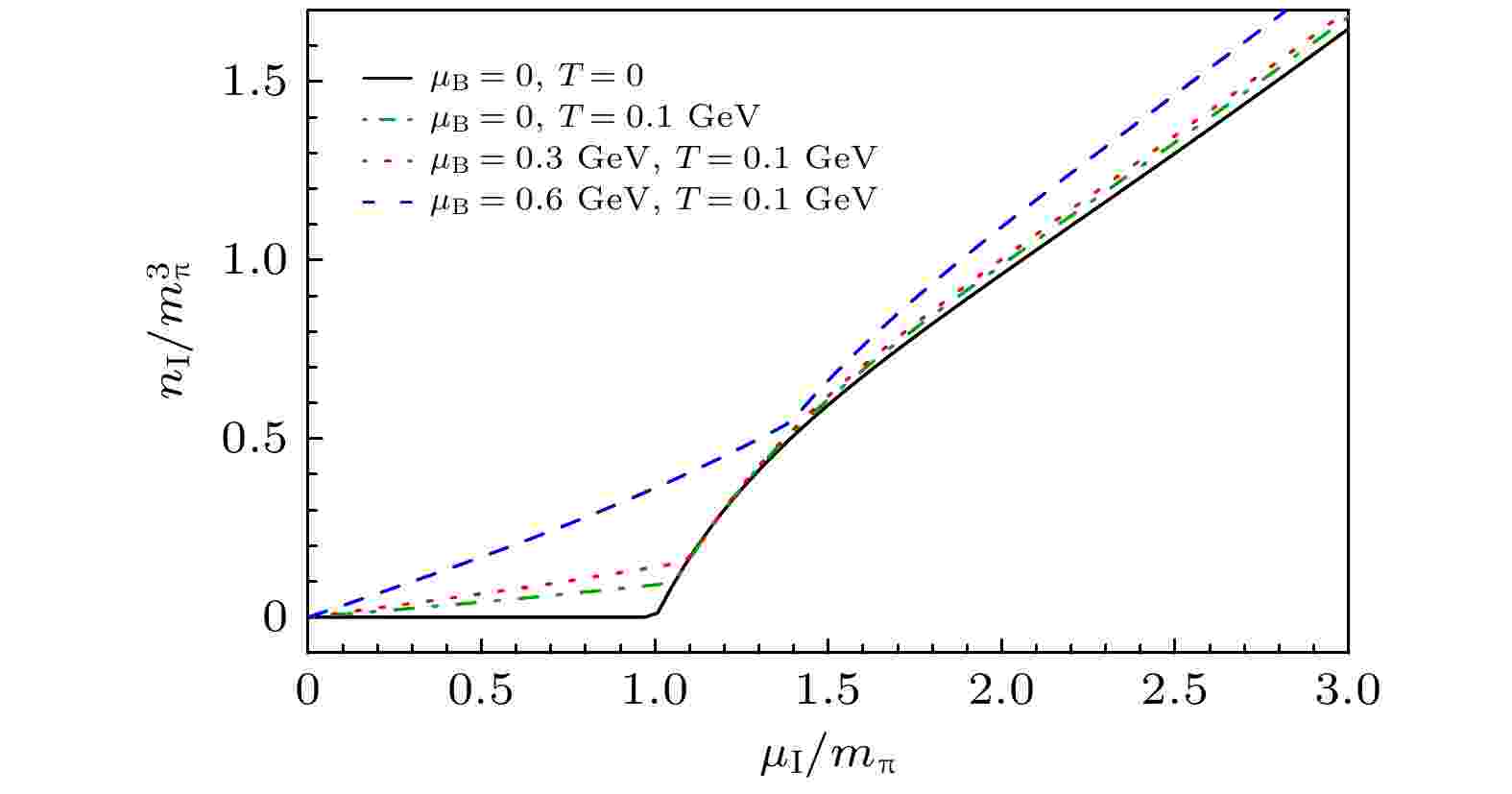 图 4 不同重子化学势和温度下归一化同位旋密度
图 4 不同重子化学势和温度下归一化同位旋密度

















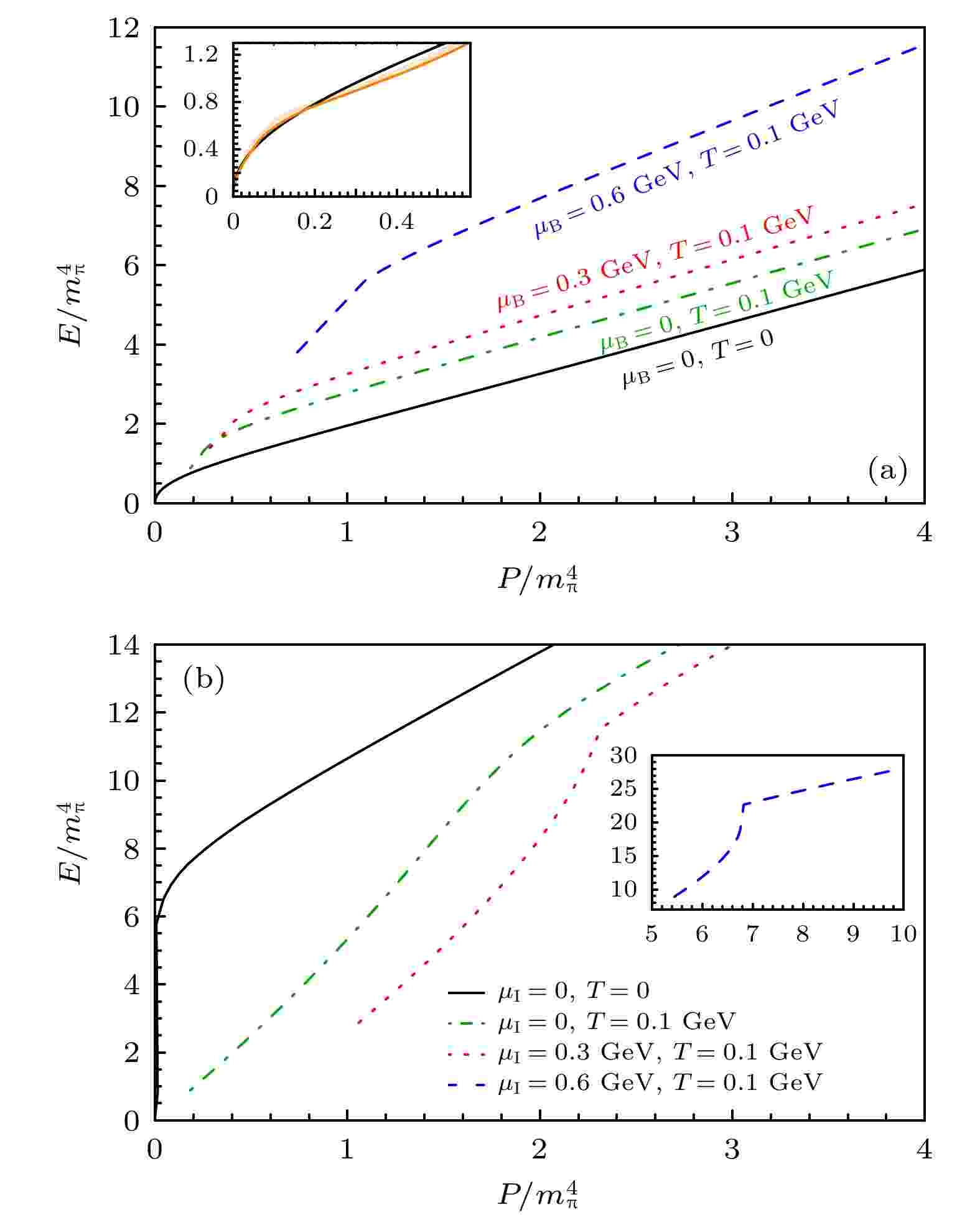 图 5 同位旋非对称物质热力学量分别随(a)同位旋化学势和(b)重子化学势变化得到的状态方程. 图(a)内插图的橙色阴影区域表示取自文献[40]的格点数据
图 5 同位旋非对称物质热力学量分别随(a)同位旋化学势和(b)重子化学势变化得到的状态方程. 图(a)内插图的橙色阴影区域表示取自文献[40]的格点数据
































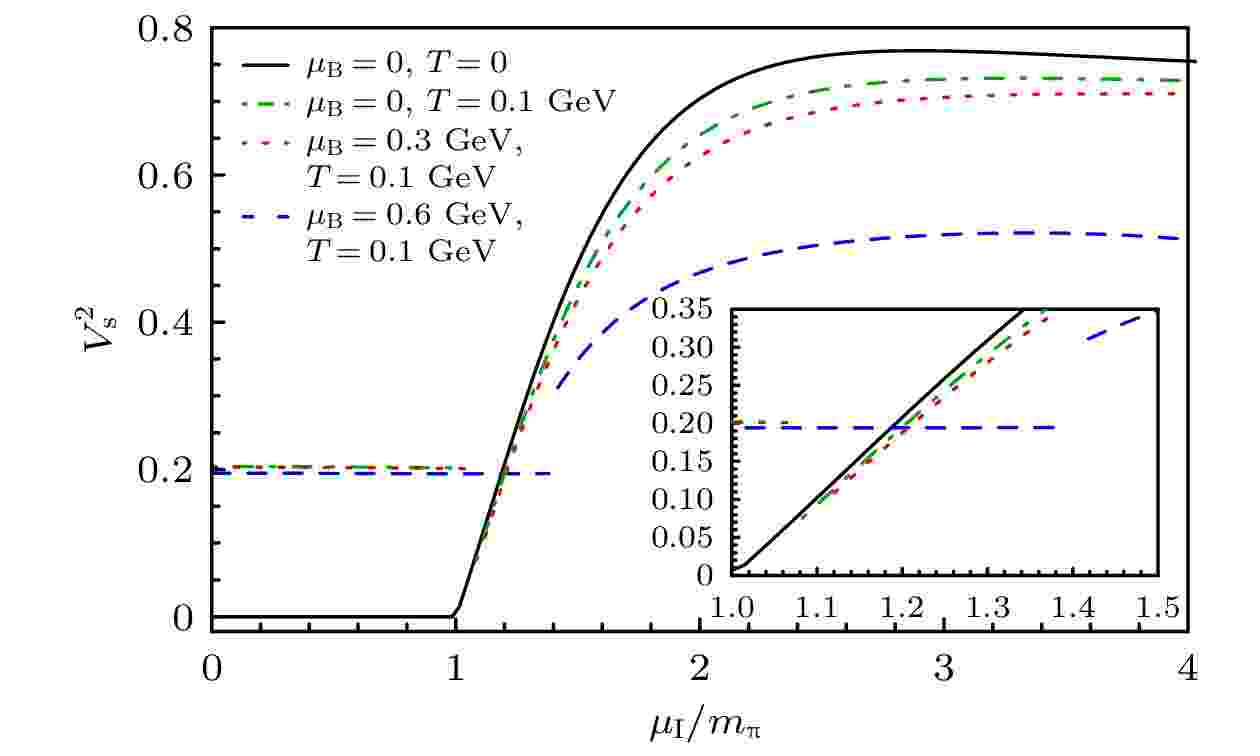 图 6 不同重子化学势和温度下声速平方随同位旋化学势的变化关系. 曲线的标记方式与图2相同
图 6 不同重子化学势和温度下声速平方随同位旋化学势的变化关系. 曲线的标记方式与图2相同






