全文HTML
--> --> -->目前, 锂离子电池的模型分为经验模型和机理模型两大类. 经验模型以等效电路模型(equivalent circuit model, ECM)为主, 主要包括内阻模型、戴维宁(Thevenin)模型和二阶阻容模型[1,2]. ECM对锂电池中各项参数进行集总处理, 利用集总的电阻、电容等元器件模拟锂离子电池内部的阻抗效应, 通过求解常微分方程来模拟锂离子电池的电压、电流等关系. 因此, ECM具有建模参数少、模型复杂度低、实时性好等优点, 在SOC估计、SOH预测等方面得到了广泛的研究, 并应用到BMS中[2,3]. 然而, ECM参数的物理意义并不明确, 难以真实反映电池的物理化学过程. 而且, 模型参数对SOC和温度的敏感性强、环境稳定性和工况适应性较差. 因此, 电池循环导致的容量退化、环境参数时变、温度变化都会影响ECM的准确性.
电化学模型通过偏微分方程描述电池内部锂离子的传输过程和电化学反应行为, 准二维模型(pseudo-two-dimensional, P2D)是一种常用的锂离子电池机理模型. P2D模型通过模拟锂电池内部的电化学行为, 能够描述锂电池的端电压、SOC、温度、循环寿命、容量衰减等宏观现象, 以及锂离子浓度分布、电势分布、局部生热、SEI (solid electrolyte interface)膜变化和电极极化等微观现象. P2D模型复杂而具有较高精确性, 适合锂电池设计等科学研究.
但是, 在实际工程应用中, P2D模型面临两个问题: 一方面, 电化学过程建模的参数量大, 均为电池材料级参数, 而且模型参数具有难测性或不可测性. 比如, 电极电势需要采用两电极或三电极的半电池结构进行测量, 测量成本较高且测量过程较为复杂. 锂离子扩散系数是表征电极动力学的一个指标, 扩散速率的快慢决定了电化学反应速率的快慢, 也反映了电池高倍率性能的好坏. 目前, 用于测量锂离子扩散系数的方法有循环伏安法、电化学阻抗谱、恒电流间歇滴定技术、电位弛豫技术等[4-6]. 各种测量方法之间存在不一致性问题, 如循环伏安法仅能测量锂离子扩散系数的平均值, 恒电流间歇滴定技术和电化学阻抗谱等方法必须依靠电极材料厚度上的电势梯度, 而电势梯度目前无法精确测量. 商用锂离子电池是全电池结构, 内部环境封闭, 其内部物理化学行为受到温度、倍率、时间等严重影响. P2D模型的液相扩散系数、固相扩散系数和迁移系数等在模型方程中强耦合, 具有现场不可测性. 另一方面, 严格的P2D模型不易实现在线计算, 计算资源消耗大导致其难以在BMS上得到应用. 因此, 面向工程应用的P2D模型需要进行降阶处理, 锂离子电池P2D模型的降阶主要有数学逼近和结构简化两种方法.
****们常采用多项式逼近等代数方法近似计算锂离子在固相和液相的扩散过程, 减少P2D模型中的偏微分方程个数, 从而简化模型并降低模型计算时间. 2005年, Subramanian等[7]基于球形粒子内部的锂离子浓度可以在空间方向上表示为多项式的假设, 根据球形粒子表面锂离子浓度、粒子平均锂离子浓度和平均锂离子通量参数, 采用双参数法和三参数法将菲克第二定律转化为常微分方程求解. 还可以利用固相粒子表面锂离子浓度和粒子内平均锂离子浓度计算每一点锂离子浓度, 采用体积平均法替代菲克第二定律, 降低模型计算的复杂程度[8]. 对于液相锂离子浓度的逼近, Dao等[8]将正负电极和隔膜中三个液相偏微分方程统一成一个, 采用正弦基函数与残差正交的Galerkin法将其转化为常微分方程进行求解. 基于稳态条件下, 锂离子浓度在电极和隔膜的液相分别呈现抛物线分布和线性分布的特点, Luo等[9]通过引入一个时变系数, 借助P2D模型电极液相偏微分方程和液相连续性条件, 求得时变系数的递归计算公式近似计算液相锂离子浓度变化. 在电池厚度方向上, 采用抛物线近似计算液相锂离子浓度, 运用多项式逼近方法直接求解降阶模型系数[10,11]. Cai和White[12]应用正交分解法将P2D模型离散成多个控制体积, 将锂离子浓度等状态变量的近似值代入P2D模型, 在子空间上投影计算结果, 获得降阶模型. Forman等[13]基于扩散过程明显慢于电化学动力学过程的假设, 通过拟线性化Bulter-Volmer方程和Pade近似固相扩散过程的方法降低了电化学模型的复杂性. 类似的处理方法还有Liapunov-Schmidt法和坐标变换法等[14,15].
基于P2D模型建模过程的多个粒子组成固液两相的多孔电极模型和浓溶液理论的思想, 研究人员通过模型结构简化对P2D模型进行降阶处理, 如单粒子模型(single particle model, SPM)[16]. SPM将正负多孔电极简化为单个球状粒子, 并且忽略电解液相锂离子浓度变化和电势变化, 从建模思想上对模型进行降阶处理. SPM可以快速模拟1C倍率下的电池充放电过程, 对于1C以上的高倍率下充放电行为, SPM的电压精度无法满足要求[17]. 在SPM的基础上, Di Domenico等[18]提出了一个与SPM类似的平均值模型, 该模型忽略了电极固体粒子浓度分布, 活性材料球状粒子内部的锂离子浓度等于整个电极材料中锂离子浓度的平均值, 且仅考虑液相电阻引起的电势差. Prada等[19]考虑液相中锂离子浓度分布对电势的影响, 进一步提高了平均值模型的精确性.
SPM和P2D模型都依赖半电池的电极电势, 电极电势受到温度等因素影响, 在工程应用中难以测量. 为此, Ekstr?m等[20]提出了集总粒子模型(lumped particle model, LPM), 采用一个球形粒子表征锂离子电池的全电池结构. LPM仅依靠电池开路电压、1C欧姆过电压、等效扩散系数和无量纲交换电流密度等参数, 建立锂电池模型. 并且, 针对不同材料和容量的锂电池单体, 通过恒温箱和充放电机等相对廉价的试验设备即可测量得到不同环境温度下的开路电压, 从而避免了SPM和P2D模型中通过半电池结构测量电极电势. 其他参数可以通过实验测量、参数优化等方式提取, LPM具有更好的工程应用前景.
目前, 已有****对比研究了P2D模型、SPM和ECM的性能[17], 但还没有对P2D, SPM和LPM开展对比研究, 对LPM的模型特点、适用范围等因素尚不明确. 为此, 本文通过相同的模型参数, 分别建立三种电化学机理模型, 并且仿真分析. 在均匀电流密度条件下, 由P2D模型的液相浓差过电压项补偿LPM对其进行性能优化, 以逼近P2D模型的电压. 而且, 通过恒流放电、动态电应力测试(dynamic stress test, DST)工况和脉冲放电工况对优化的LPM模型性能进行验证.
2.1.P2D模型
P2D模型是由Doyle等[21]和Fuller等[22]根据锂离子电池微观上负极-隔膜-正极的结构构建的电化学模型, 如图1所示. 正负电极分别由固相和液相混合而成, 固相为电极活性材料, 液相为电解液. 膈膜由带有微观通道的聚合物固相和液相电解质组成, 液相电解质具有传输锂离子的作用. 正负集流体为导电金属材质, 通常为正极集流体为铝, 负极集流体为铜, 正负集流体的电导率远高于电池电极材料, 不参与电化学反应过程, 因此不作为电化学反应的边界条件.
图 1 P2D模型示意图Figure1. Schematic diagram of P2D.
为了建立锂离子电池的P2D模型, 应作相关假设条件:
1)电池内部仅考虑固相和液相, 不考虑气相物质;
2)电极固相微观结构简化为多个半径相同的均匀球状粒子;
3)锂离子固相的扩散系数与锂离子浓度无关;
4)液相中离子的传输符合浓溶液理论, 并且仅考虑扩散和迁移过程, 不考虑对流和双层电容效应;
5)离子的传输仅考虑电池厚度方向, 即负极-隔膜-正极方向, 不考虑离子沿电极长度和宽度方向上的传输;
6)集流体电导率远高于电极材料;
7)在本文中, 不考虑SEI膜对电池性能的影响以及其他副反应的发生.
P2D模型主要模拟电池充放电过程的锂离子在电极和电解质中的迁移和扩散行为. 在离子传输过程中, 满足质量守恒、电荷守恒和电化学动力学平衡三大守恒条件, 采用极坐标系的菲克第二定律描述电极固相锂离子的扩散行为:
| 符号 | 物理量 | 单位 |
| $c_{\rm{s}}^i$ | 多孔电极固相锂离子浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| $c_{\rm{e}}^i$ | 多孔电极液相锂离子浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| $c_{\rm{e}}^{{\rm{sep}}}$ | 隔膜液相锂离子浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| $c_{{\rm{s, 0}}}^i$ | 多孔电极固相锂离子初始浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| ${c_{{\rm{e, 0}}}}$ | 液相锂离子初始浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| $c_{{\rm{s, max}}}^i$ | 多孔电极固相粒子最大 锂离子浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| $c_{{\rm{s, surf}}}^i$ | 多孔电极固相粒子表面 锂离子浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| $D_{\rm{s}}^i$ | 多孔电极固相锂离子扩散系数 | $ { {\rm{m} }^{2} } \cdot { {\rm{s} }^{ - 1} } $ |
| $D_{\rm{e}}^{}$ | 液相锂离子扩散系数 | $ { {\rm{m} }^{2} } \cdot { {\rm{s} }^{ - 1} } $ |
| $D_{{\rm{e, eff}}}^i$ | 多孔电极液相锂离子 有效扩散系数 | $ { {\rm{m} }^{2} } \cdot { {\rm{s} }^{ - 1} } $ |
| $D_{{\rm{e, eff}}}^{{\rm{sep}}}$ | 隔膜液相锂离子有效扩散系数 | $ { {\rm{m} }^{2} } \cdot { {\rm{s} }^{ - 1} } $ |
| $j_{\rm{n}}^i$ | 多孔电极锂离子孔壁通量 | ${\rm{mol}} \cdot {{\rm{s}}^{ - 1}} \cdot {{\rm{m}}^{ - 2}}$ |
| $j_{}^i$ | 多孔电极电流密度 | ${\rm{A}} \cdot {{\rm{m}}^{ - 3}}$ |
| ${R^i}$ | 多孔电极球形粒子半径 | m |
| $\varepsilon _{\rm{e}}^i$ | 多孔电极液相体积分数 | — |
| $\varepsilon _s^i$ | 多孔电极固相体积分数 | — |
| $\varepsilon _{\rm{e}}^{{\rm{sep}}}$ | 隔膜液相体积分数 | — |
| ${t_{ + }}$ | 锂离子迁移系数 | — |
| ${f_ \pm }$ | 液相平均摩尔活度系数 | — |
| $a_{\rm{s}}^i$ | 多孔电极球形粒子的比表面积 | ${{\rm{m}}^{ - 1}}$ |
| $\sigma _{\rm{s}}^i$ | 多孔电极固相电导率 | ${\rm{S}} \cdot {{\rm{m}}^{ - 1}}$ |
| $\sigma _{{\rm{s, eff}}}^i$ | 多孔电极固相有效电导率 | ${\rm{S}} \cdot {{\rm{m}}^{ - 1}}$ |
| $\kappa $ | 液相离子电导率 | ${\rm{S}} \cdot {{\rm{m}}^{ - 1}}$ |
| $\kappa _{{\rm{eff}}}^i$ | 液相有效离子电导率 | ${\rm{S}} \cdot {{\rm{m}}^{ - 1}}$ |
| ${\kappa _{{\rm{D}}, i}}$ | 有效液相离子扩散导电系数 | ${\rm{A}} \cdot {{\rm{m}}^2} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}$ |
| $\phi _{\rm{s}}^i$ | 多孔电极固相电势 | V |
| $\phi _{\rm{e}}^{}$ | 液相电势 | V |
| ${I_{\rm{b}}}$ | 电池电流 | A |
| $ j_0^i $ | 多孔电极参考交换电流密度 | ${\rm{A}} \cdot {{\rm{m}}^{ - 2}}$ |
| ${\eta ^i}$ | 电极过电势 | V |
| ${\alpha _{{\rm{a, i}}}}$/${\alpha _{{\rm{c, i}}}}$ | 电极氧化还原反应电荷传递系数, 为0.5 | — |
| ${k^i}$ | 电极反应常数 | ${{\rm{m}}^{2.5}} \cdot {\rm{mo}}{{\rm{l}}^{ - 0.5}} \cdot {{\rm{s}}^{ - 1}}$ |
| $U_{}^i$ | 电极平衡电势 | V |
| $R_{{\rm{SEI}}}^i$ | SEI膜电阻 | $\Omega \cdot {{\rm{m}}^{ - 2}}$ |
| ${V_{{\rm{P2 D}}}}$ | P2D模型端电压 | V |
| A | 电池横截面积 | ${{\rm{m}}^2}$ |
| Brug | Bruggman系数, 取值1.5 | — |
| F | 法拉第常数 | ${\rm{C}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}$ |
| R | 普适气体常数 | ${\rm{J}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}} \cdot {{\rm{K}}^{ - 1}}$ |
| T | 温度 | K |
表1P2D模型参数
Table1.Parameter symbols of P2D.
2
2.2.SPM
SPM忽略了电解液浓度随时间和空间的变化, 将每个电极等效为单个球状粒子. 由于假设液相锂离子浓度保持恒定, 从而不需要计算(5)式和(6)式, 简化了液相电势差的计算, 即(20)式中的
SPM对球状粒子内部的锂离子扩散过程仍采用菲克第二定律描述, 如(1)式所示, 满足边界条件(2)和(3)式, 满足初始条件(4)式. 在应用过程中, 通常采用二阶常微分方程化简菲克第二定律[9,15]:
| 符号 | 物理量 | 单位 |
| $c_{{\rm{s, avg}}}^i$ | 多孔电极粒子平均锂离子浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| $c_{{\rm{s, max}}}^i$ | 多孔电极最大粒子锂离子浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| ${c_{\rm{e}}}$ | 液相锂离子浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| ${\overline j ^i}$ | 平均交换电流密度 | ${\rm{A}} \cdot {{\rm{m}}^{ - 2}}$ |
| $\phi _{{\rm{SP}}}^i$ | 电池电极电势 | V |
| ${V_{{\rm{SP}}}}$ | 电池端电压 | V |
表2SPM参数
Table2.Parameter symbols of SPM.
2
2.3.LPM
LPM是在SPM的基础上, 将整个电池等效为一个球状粒子, 依靠单个粒子模拟整个电池的锂离子传递过程. 为提高LPM的普适性, 对相关变量作以下处理:1)归一化处理球状粒子半径, 归一化的半径采用X表述, 取值范围为0—1;
2)根据局部锂离子浓度和电池内部的锂离子浓度的比值计算SOC;
3)仅需测量不依赖于电极电势的电池开路电压.
定义球状粒子内部每一点处的SOC为球状粒子内部每一点处的锂离子浓度与电池最大锂离子浓度的比值:
3.1.模型差异分析
1)模型维度不同. 在P2D模型中, 锂离子宏观上沿电池厚度方向传输, 即负极-隔膜-正极方向; 微观上从电极球状粒子中心处沿球状粒子半径方向扩散至粒子表面, 脱嵌进入电解液后, 迁移和扩散至另一电极, 嵌入至另一电极表面后, 从该电极表面扩散至粒子中心. SPM相比于P2D模型, 仅考虑微观维度上锂离子从某电极粒子经过隔膜液相传输至另一电极粒子的过程. LPM(参数见表3)仅考虑锂离子在单个球形粒子中从粒子中心沿半径方向向粒子表面的扩散过程, 模型维度更低, 同时在建模过程中对粒子半径进行归一化处理, 从而不需要设置粒子半径.| 符号 | 物理量 | 单位 |
| c | LPM粒子内锂离子浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| ${c_{\max }}$ | LPM最大锂离子浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| ${\eta _{{\rm{ohm}}}}$ | 欧姆过电压 | V |
| ${\eta _{{\rm{act}}}}$ | 活化过电压 | V |
| ${\eta _{{\rm{conc}}}}$ | 浓度过电压 | V |
| ${c_{{\rm{surf}}}}$ | 粒子表面锂离子浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| ${c_{{\rm{avg}}}}$ | 粒子平均锂离子浓度 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| ${\eta _{{\rm{ohm, 1 C}}}}$ | 1 C欧姆过电压 | V |
| ${I_{{\rm{1 C}}}}$ | 1 C电流 | A |
| ${J_0}$ | 无量纲交换电流密度 | 1 |
| $\tau $ | 等效扩散系数 | s |
| ${Q_{{\rm{cell}}}}$ | 电池容量 | ${\rm{Ah} }$ |
| X | 归一化粒子半径 | — |
表3LPM参数
Table3.Parameter symbols of LPM.
2)球状粒子数目不同. P2D模型采用多孔电极模型来模拟正负电极, 多个球状粒子在电极固相中均匀分布, 而SPM采用单个球状粒子分别模拟正负电极, 共计两个球状粒子. LPM采用一个球状粒子模拟电池整体, 不区分正负电极, 因此不需要考虑电极中固相和液相占比和液相材料设置.
3)电解液浓度变化情况不同. P2D模型中液相电解质浓度存在梯度, 而SPM中忽略了电解液浓度梯度和电位的变化. 而LPM中不涉及液相电解质建模, 仅通过固相扩散的方法描述粒子内部的锂离子扩散过程.
4)模型参数数量和水平不同. P2D模型和SPM中涉及到的电池材料水平参数在33个左右, 需要单独对电极材料的相关参数进行测量或估计. 而LPM所需要的参数仅有3个, 且均为电池单体水平, 可以通过电池单体的测量实验直接获得, 实验数据提取成本降低.
综上所述, LPM在模型空间维度、电极微观结构的处理和电解液的数学描述等方面, 对P2D模型和SPM进行了不同程度上的简化. 因此, 使用相同的模型参数, 分别构建锂离子电池的P2D模型、SPM和LPM, 分析模型之间的差别, 并且优化LPM的降阶模型参数, 提高其适用性.
2
3.2.模型参数
本文建模对象为额定容量30Ah的健康锂离子电池, 相关电化学参数通过实测数据和文献整理获得, 并且所采用的P2D模型参数通过了实际电池单体的验证, 其具体电化学模型参数见表4[19,23]. 其中, 液相电导率与液相锂离子浓度的函数关系为| 中文参数名 | 负极 | 隔膜 | 正极 | 单位 |
| 厚度 | 10 | 25 | 100 | μm |
| 粒子半径 | 10 | — | 10 | μm |
| 锂离子扩散系数 | $3.9 \times 1{0^{ - 14}}$ | — | $1 \times 1{0^{ - 13}}$ | $ { {\rm{m} }^{2} } \cdot { {\rm{s} }^{ - 1} } $ |
| 初始固相浓度 | 19624 | — | 20046 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| 最大锂离子浓度 | 24983 | — | 51228 | ${\rm{mol}} \cdot {{\rm{m}}^{ - 3}}$ |
| 电导率 | 100 | $\kappa $ | 10 | S·m–1 |
| 初始电解液浓度 | 1000 | 1000 | 1000 | $ { {\rm{m} }^{2} } \cdot { {\rm{s} }^{ - 1} } $ |
| 电解液扩散系数 | $2.7877 \times 1{0^{ - 10}}$ | $2.7877 \times 1{0^{ - 10}}$ | $2.7877 \times 1{0^{ - 10}}$ | $ { {\rm{m} }^{2} } \cdot { {\rm{s} }^{ - 1} } $ |
| 传递数 | 0.4 | 0.4 | 0.4 | — |
| 电解液体积分数 | 0.3 | 1 | 0.3 | — |
| SEI膜电阻 | $0$ | — | $0$ | ${\rm{m}}\Omega $ |
| 反应速率常数 | $9.6487 \times 1{0^{ - 6}}$ | — | $2.89461 \times 1{0^{ - 6}}$ | ${\rm{mo}}{{\rm{l}}^{2.5}} \cdot {{\rm{m}}^{ - 0.5}} \cdot {{\rm{s}}^{ - 1}}$ |
| 活性材料体积分数 | 0.6 | — | 0.5 | — |
| 填料体积分数 | 0.1 | — | 0.2 | — |
| 电极横截面积 | 0.1 | — | — | ${{\rm{m}}^2}$ |
| 1 C电流 | 30 | — | — | A |
| 放电截止电压 | 3.4 | — | — | V |
| 充电截止电压 | 4.2 | — | V | |
| 容量 | 30 | — | — | Ah |
| 温度 | 298 | — | — | K |
| 普适气体常数 | 8.314 | — | — | ${\rm{J}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}} \cdot {{\rm{K}}^{ - 1}}$ |
| 法拉第常数 | 96487 | — | — | ${\rm{C}} \cdot {\rm{mo}}{{\rm{l}}^{ - 1}}$ |
表4电化学模型参数值
Table4.Parameter values of Electrochemical model.
2
3.3.结果分析
图2给出了在25 ℃条件下三种模型在各倍率下的放电曲线. 由于在文献[19]中已验证P2D模型能够很好地模拟锂离子电池的电性能, 说明模型参数具有可靠性和适用性. 因此, 本文以严格的P2D模型计算的电压曲线作为参考, 对比分析SPM和LPM的模型性能.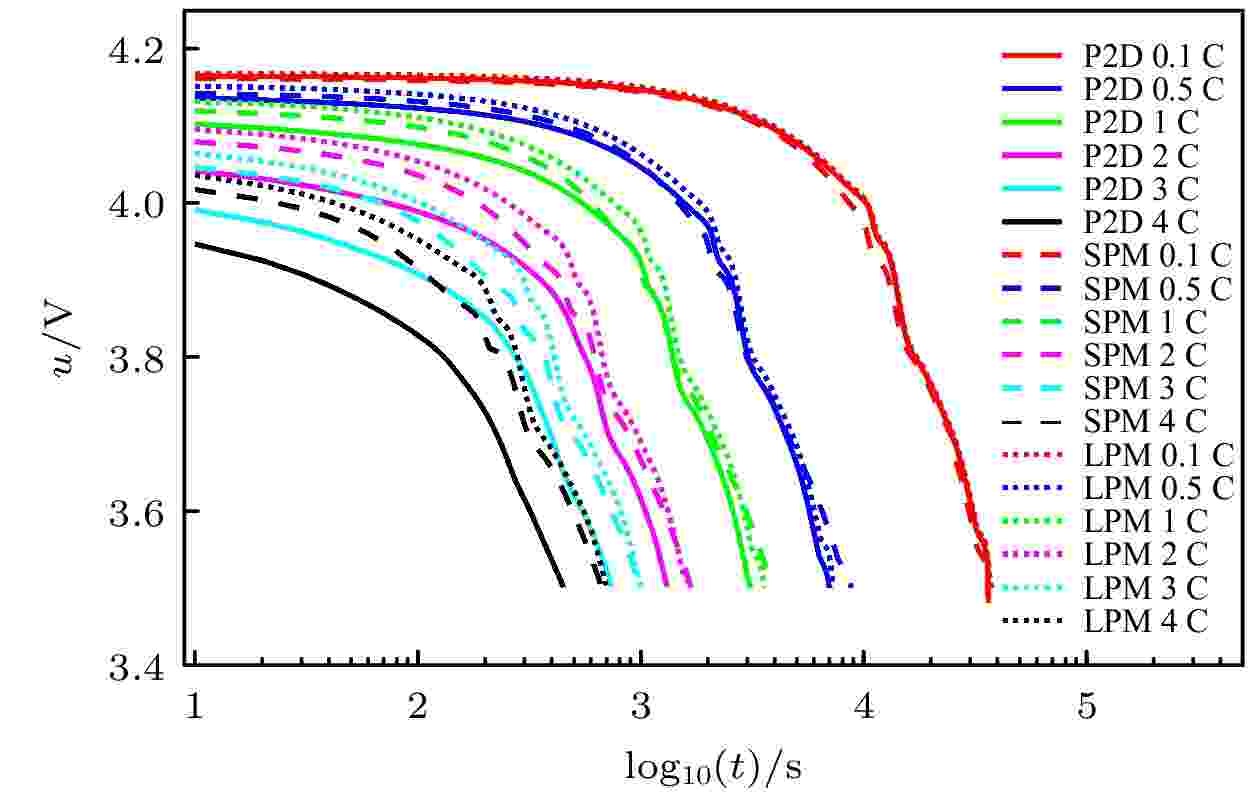
图 2 三种电化学模型电压曲线对比Figure2. Comparison of three electrochemical model voltage curves.
| 倍率/C | SPM绝对 误差/mV | SPM相对 误差/% | LPM绝对 误差/mV | LPM相对 误差/% |
| 0.1 | –44.50 | –1.28 | 30.03 | 0.87 |
| 0.5 | 74.20 | 2.12 | 42.30 | 1.21 |
| 1 | 83.70 | 2.39 | 60.70 | 1.72 |
| 2 | 88.00 | 2.51 | 103.40 | 2.95 |
| 3 | 98.50 | 2.81 | 129.30 | 3.66 |
| 4 | 125.50 | 3.58 | 173.20 | 4.75 |
表5测试集电压误差对比
Table5.Comparison of test set voltage errors.
相比于P2D模型电压, 在0.1, 0.5和1 C倍率放电下, 随着倍率的提高, SPM和LPM的电压误差增大了, SPM和LPM的模型电压误差绝对平均值分别为67.5和44.3 mV, 相对误差的均方根值分别为1.99%和1.31%; LPM比SPM更能逼近P2D模型电压, 精度提高了1/3. 但是, 在2, 3和4 C高倍率放电下, SPM和LPM电压均明显高于P2D模型电压, 电压误差随着倍率增加而增大; SPM和LPM的电压误差平均值分别为104.0和135.3 mV, 相对误差均方根值分别为3.00%和3.85%, LPM比SPM的电压误差精度降低了28.3%, 主要是由(39)式计算的过电压差异所引起的.
因此, 可通过补偿液相过电压, 提高LPM的电压模拟精度. 由于LPM仅考虑沿半径方向锂离子传输过程, 放电电流从粒子中心沿半径方向流动, 满足输入体电流密度均匀的前提条件. 假设正负电极区域电流体密度均匀, 且电极固相和电极液相的电流体密度也完全相同, 则电极固相和电极液相总电流体密度应该按照电极中固相和液相体积比进行分配, P2D模型的(20)式表达的液相体电流密度可简化为
| 倍率 | 参数a |
| 0.1 | –0.148 |
| 0.5 | –0.703 |
| 1 | –1.331 |
| 2 | –2.431 |
| 3 | –3.438 |
| 4 | –4.476 |
表6不同倍率下参数a取值
Table6.Parameter values of a in the different discharge rate.
在25 ℃条件下, 将0.1, 0.5, 1, 2, 3, 4 C倍率下的恒流放电记作测试集; 将0.25, 0.75, 1.5, 2.5, 3.5 C倍率下的恒流放电记作验证集. 测试集和验证集中的恒流放电工况用于表征模型在不同倍率放电时对电压曲线模拟的准确性, 其测试意义在于模拟纯电动汽车以低速、中速和高速匀速行驶时锂电池的放电状态. 图3和图4分别给出了优化LPM在测试集和验证集上的电压及其误差曲线, 表7给出了相应的误差统计数据, 可见模型电压误差的绝对值随着倍率升高总体呈现增大趋势. 在测试集中, 不大于1 C低倍率和大于1 C高倍率的优化LPM的模型电压误差绝对平均值分别为22.0和42.0 mV, 相对误差均方根值分别为0.63%和1.12%, 它们比未优化LPM至少提高了50%的模型电压精度. 在验证集中, 不大于1 C低倍率和大于1 C高倍率的优化LPM的模型电压误差绝对平均值分别为18.5和35.8 mV, 相对误差均方根值分别为0.54%和0.92%. LPM的误差主要来源于放电初始时刻的电压误差和电极电势波动所引起的误差, 这些误差是由于采用相同模型参数和电极电压测量过程中的波动所引起的.
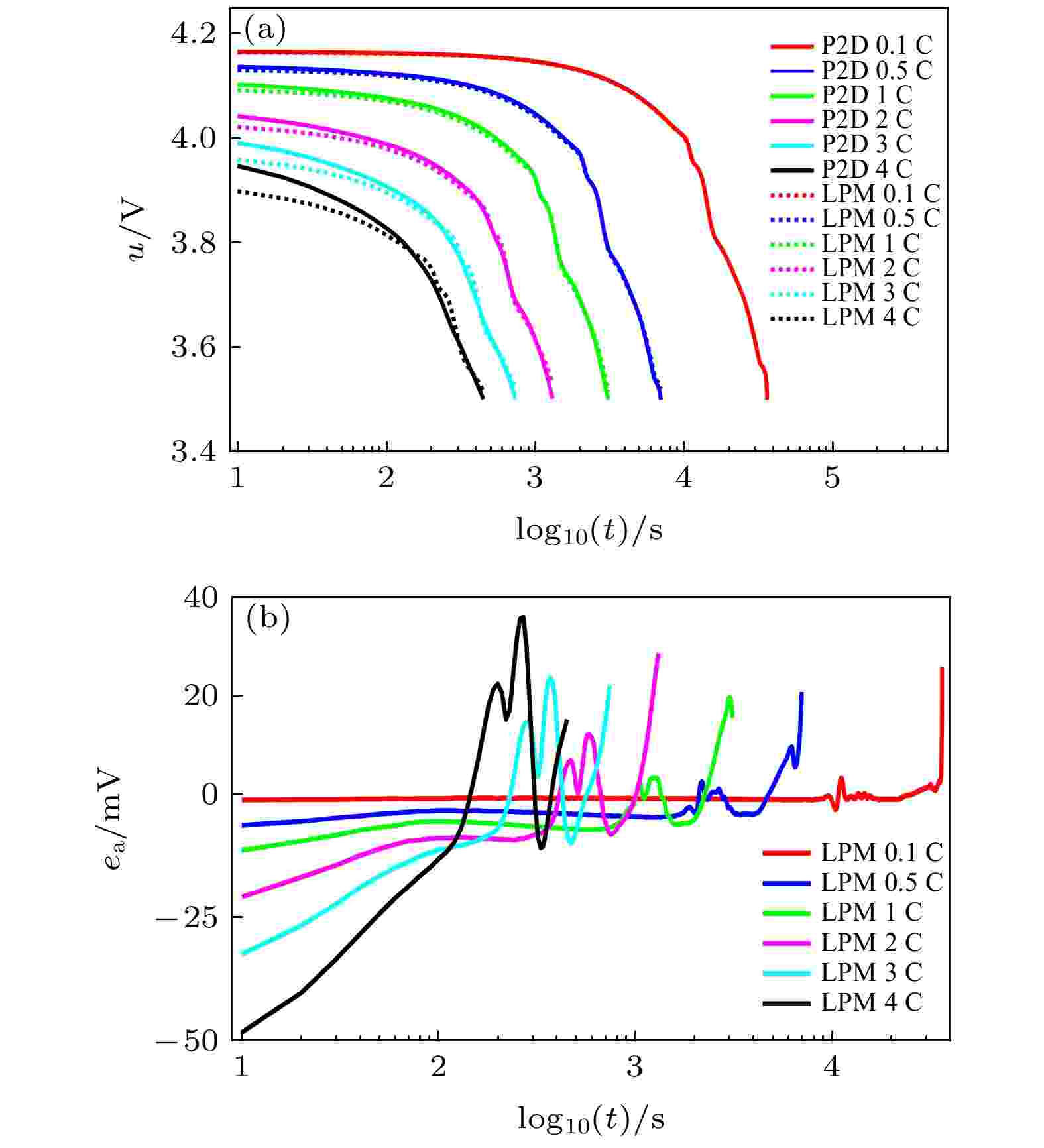图 3 测试集, 优化LPM电压及其误差 (a) 电压; (b) 电压误差Figure3. Voltage curves and voltage error curve of the optimized LPM under test set: (a) Voltage curves; (b) voltage error curves.
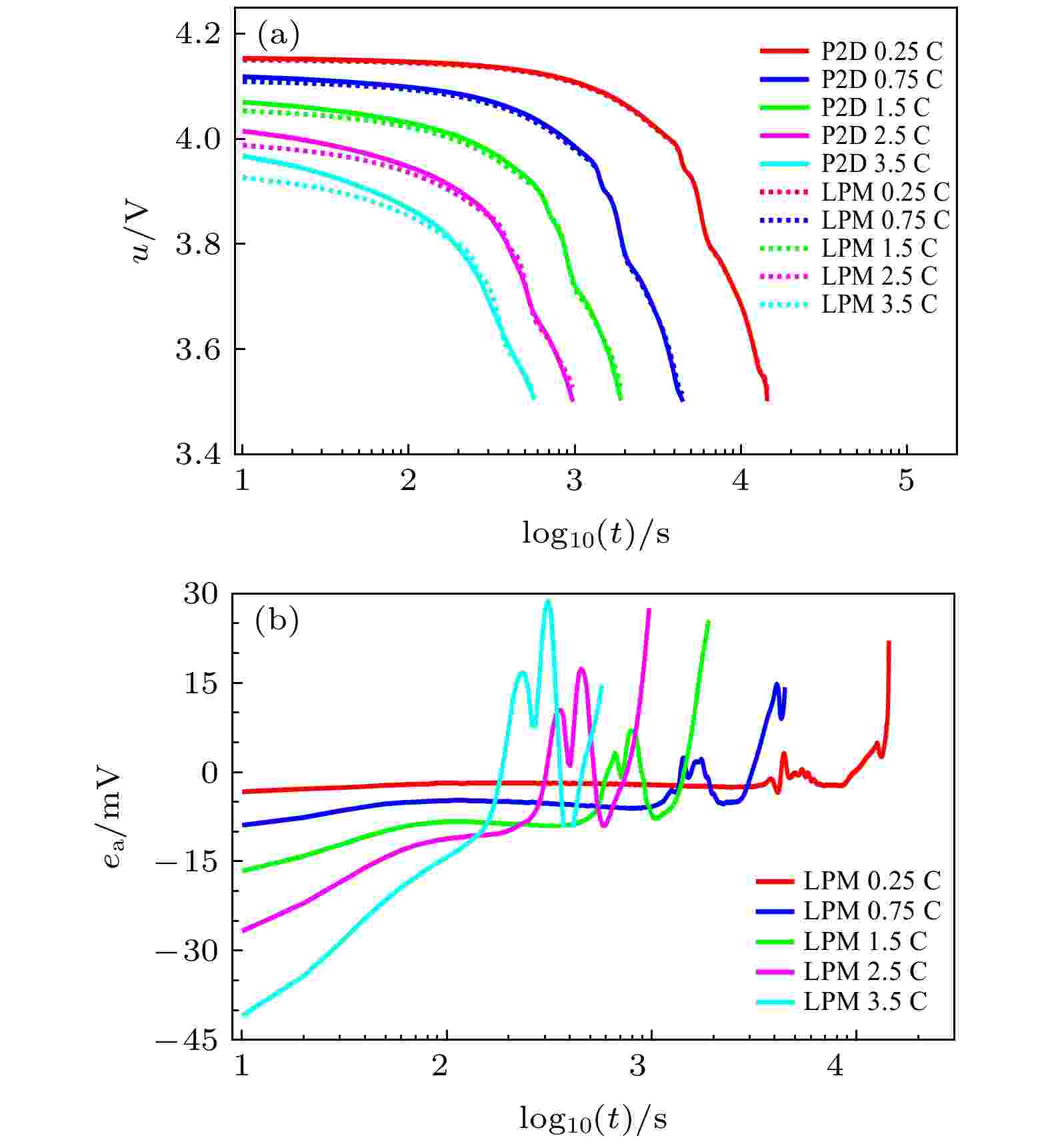图 4 验证集, 优化LPM电压及其误差 (a) 电压; (b) 电压误差Figure4. Voltage curves and voltage error curve of the optimized LPM under verification set: (a) Voltage curves; (b) voltage error curves.
| 倍率/C | 绝对误 差/mV | 相对误 差/% | 倍率/C | 绝对误 差/mV | 相对误 差/% |
| 0.1 | 25.7 | 0.73 | 0.25 | 22.1 | 0.63 |
| 0.5 | 20.7 | 0.59 | 0.75 | 14.8 | 0.42 |
| 1 | 19.7 | 0.56 | 1.5 | 25.5 | 0.73 |
| 2 | 28.5 | 0.81 | 2.5 | –32.7 | –0.81 |
| 3 | –39.9 | –0.99 | 3.5 | –49.2 | –1.23 |
| 4 | –57.6 | –1.45 | DST | –55.4 | –1.40 |
| 脉冲 放电 | 41.5 | 1.05 |
表7优化后LPM电压误差
Table7.Optimized LPM voltage errors.
在放电初始时刻, 欧姆过电压是LPM中电池端电压的主要影响因素, 由(40)式可知LPM中欧姆过电压随放电电流增加而线性增加, 而不同倍率条件下, P2D模型初始时刻电压差与放电电流并非正比关系, 因此导致初始时刻电压误差较大.
在恒流放电的情况下, P2D模型电池电压受正负电极平衡电势影响较大, 因此低倍率条件下电极电压波动有所表现. 在高倍率放电时, 正极粒子表面锂离子浓度变化较大, 正极电势波动所引起的电压波动没有得到体现, 因此高倍率放电的电压曲线较为平滑. 而LPM开路电压通过P2D电池模型0.01 C放电提取, 电极平衡电势引起的电池电压的波动无法通过过电压项抵消, 因此导致高倍率条件下, 优化LPM出现电压误差.
脉冲放电和DST工况是对实际工况进行简化和组合而成的, 用于验证LPM在脉冲放电和变电流工况下的模型准确性. 其测试意义在于模拟纯电动汽车在城市道路中变电流工况下锂电池的充放电状态, 放电脉冲用于模拟城市车速变化, 充电脉冲用于模拟车辆制动电流回馈, 表明LPM模型在简化的车辆运行工况下也具有良好的准确性, 说明优化后的LPM具有更好的适应性和模型泛化能力. 图5和图6给出了3 C脉冲放电和4 C DST工况的模型电压曲线及其误差曲线. 模型误差分别为–55.4和41.5 mV, 相对误差分别为–1.40%和1.05%. 在脉冲放电条件下, LPM在静止阶段电压能很好地跟随P2D模型, 电压误差主要存在于放电阶段, P2D模型电池电压下降更快. 在DST工况下, 电压误差主要体现在高倍率放电阶段和充电阶段, 是由于充放电扩散系数不同导致的, 其根源在于采用(52)式正负电极扩散系数平均值进行等价换算, 没有区分充放电过程的扩散系数. 在实际工程应用中, 针对等效扩散系数的选取应该根据充放电进行区别选取和优化, 以获得更好的模型计算精度.
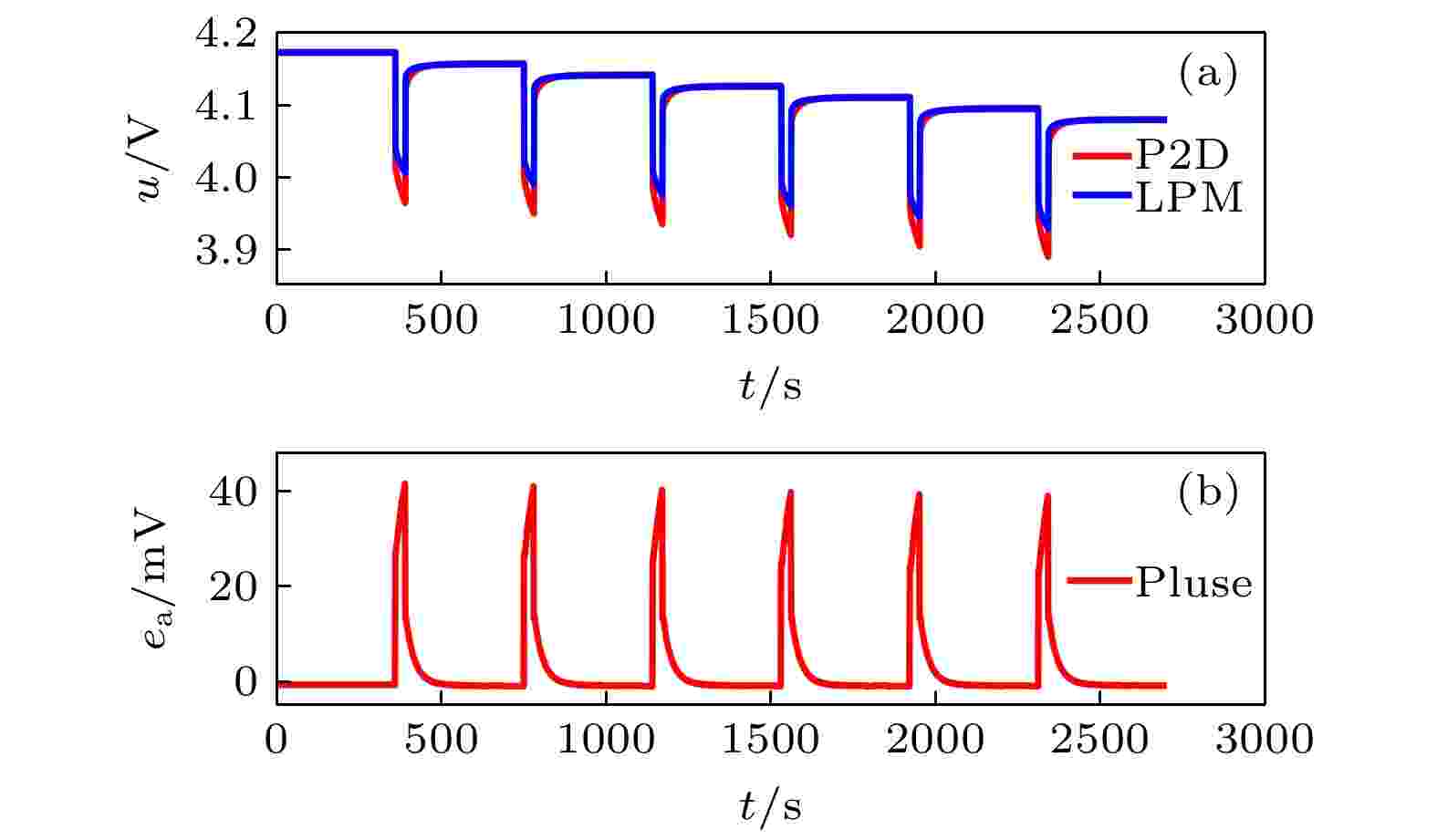图 5 脉冲放电条件下, 优化的LPM电压和电压误差曲线 (a) 电压; (b) 电压误差Figure5. Voltage and voltage error curve of the optimized LPM under pulse discharge condition: (a) Voltage curves; (b) voltage error curve.
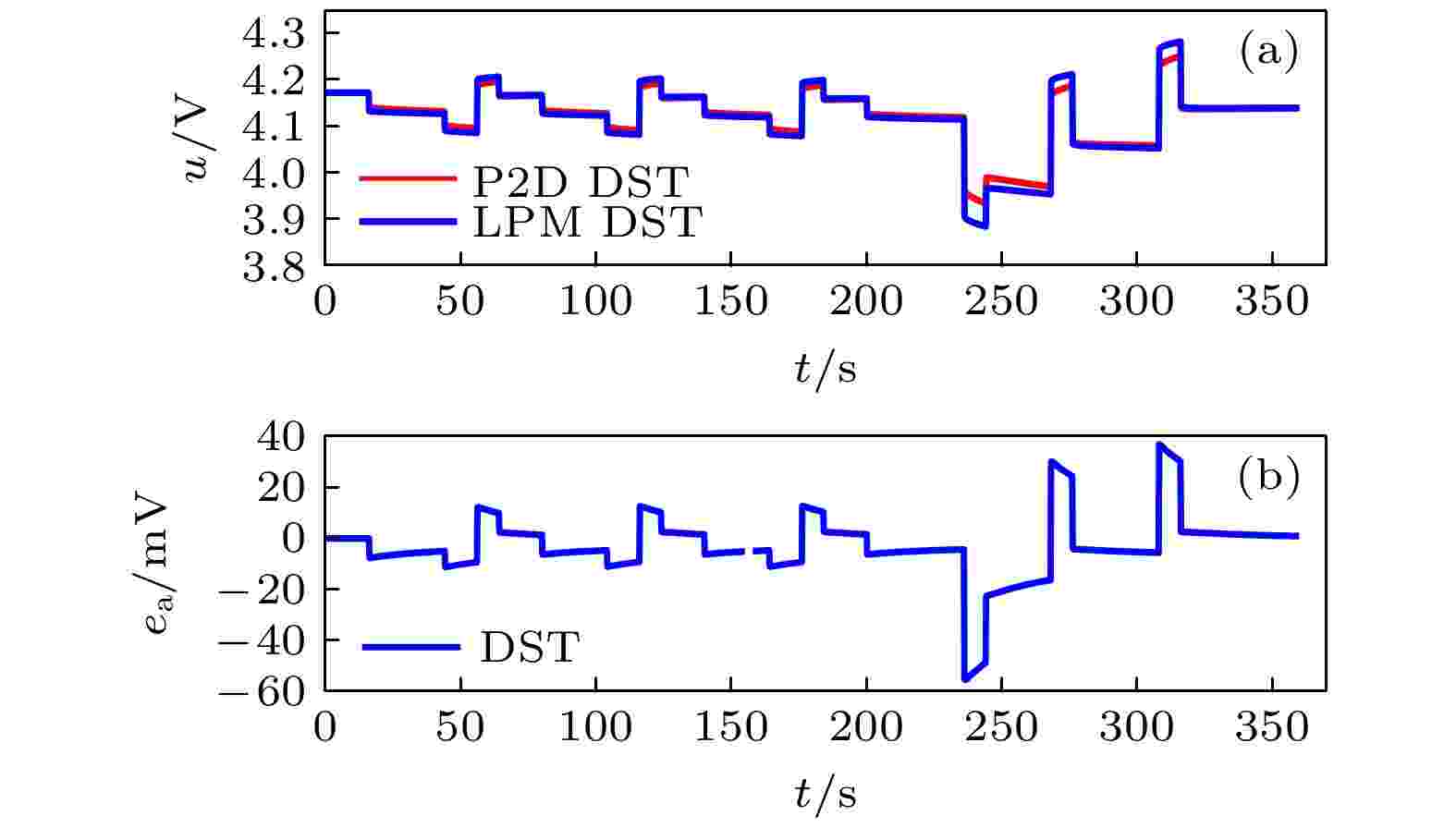图 6 DST工况下, 优化的LPM电压和电压误差曲线 (a) 电压; (b) 电压误差Figure6. Voltage and voltage error curve of the optimized LPM under DST condition: (a) Voltage curves; (b) voltage error curve.
模型计算采用基于Intel 9750H处理器和16G内存的笔记本电脑平台, 表8列出了三种锂离子电池机理模型的计算时间. 在0.5—4 C倍率的模型计算过程中, SPM计算耗时为67 s. 相比于P2D模型, LPM计算用时可缩减85%以上, 与SPM相比也能缩减约65%, 具有更高的计算效率.
| 测试集 用时/s | 验证集 用时/s | 脉冲放 电用时/s | DST工况 用时/s | |
| LPM | 24 | 14 | 8 | 11 |
| P2D | 169 | 92 | 85 | 108 |
| 占比 | 14.2% | 15.22% | 9.41% | 10.19% |
表8计算用时对比
Table8.Comparison of the calculation time.
综上所述, 基于锂离子电池均匀电流密度的前提条件, 结合抛物线近似电极液相锂离子浓度分布的方法, 通过P2D模型推导得到液相过电压和欧姆内阻, 引入LPM中对模型电压进行一定程度上的修正, 可以提高LPM电压精度, 使其很好地逼近P2D模型电压.
2)基于均匀电流密度假设, 结合LPM模型机理分析, 推导P2D模型中液相过电压项补偿LPM. 在不大于4 C的恒流放电倍率下, 优化的LPM能够提高模型电压精度50%以上. 在脉冲放电和4 C DST工况下, 优化的LPM能够准确预测锂电池端电压, 电压相对误差的绝对值控制在1.5%以内, 而且计算时间几乎未增加.
3)本文对比了P2D电化学模型及其降阶模型的电压精度和计算时间, LPM所选取参数由P2D模型等效换算得到. 将来将结合锂离子电池充放电实验, 研究LPM参数化问题以及对变温环境的适应性问题.
