摘要:本文采用数值求解多能带半导体布洛赫方程组的方法开展强激光与双层MoS₂材料相互作用产生高次谐波的理论研究. 模拟发现, T型堆栈双层MoS₂产生的高次谐波在高能区域的转换效率比AA型堆栈双层MoS₂高一个数量级. 理论分析表明, 由于原子级错位堆栈下晶体对称性被打破, 使原有的部分带间禁戒跃迁路径被打开, 带间跃迁激发通道增加, 大大增大了载流子跃迁概率, 从而增强了高次谐波转换效率. 此外, 对谐波产率的波长定标研究表明, 在较长波长的激光驱动下 (> 2000 nm), T型堆栈下所增强的高次谐波具有更高的波长依赖. 该工作为如何优化增强固体高次谐波的转换效率提供一种新思路.
关键词: 高次谐波/
双层MoS₂/
堆栈方式/
波长定标

English Abstract

全文HTML

--> --> -->

近十年来, 强激光与固体材料相互作用产生的高次谐波辐射逐渐成为国际强场激光物理研究领域重点研究的课题^[1-4]. 高次谐波研究的主要动力来源于其极有潜力的应用前景. 利用高次谐波辐射可以获得相干的、脉冲持续时间短的极紫外(XUV)光源和X射线源. 由于固体材料的介质密度远大于气体靶, 同等激光条件下固体产生的高次谐波转换效率高于气体. 在气体介质中, 高次谐波主要由电子电离、回碰产生, 而对于固体材料, 其高次谐波主要由带内电流和带间极化贡献. 最近, 实验上已经证明^[5-11], 强激光与固体材料相互作用能够提供一种全新的手段产生高效率的高次谐波, 将有希望实现一种新型阿秒光源.
2011年, Ghimire等^[5,6]首次在实验上成功应用中红外激光与ZnO晶体相互作用产生非微扰的高次谐波. 他们认为, 在激光驱动下, 晶体中的电子和空穴在布里渊区边界处反射产生布洛赫振荡, 从而导致高次谐波辐射. 随后, 采用不同的驱动激光, 科研人员陆续开展了固体高次谐波的实验研究^[7,8], 研究结果表明在太赫兹区域, 带内高次谐波占主要部分. Luu等^[9]利用脉宽在一个光周期量级的紫外与近红外光学叠加场和SiO₂相互作用, 实验发现光子能量大约为40电子伏特的相干极紫外光辐射. 在他们的工作中, 外场作用下电子在晶格中的失谐振荡运动被用来解释高频辐射, 并且观测到固体二氧化硅中产生的高能光子产率比稀有气体中产生的要高. 几乎同时, Vampa等^[10]通过加一束倍频激光来研究固体高次谐波的产生过程, 实验上证明了在中红外区域, 电子与空穴回碰产生的带间电流是ZnO晶体中高次谐波产生的主要机制, 随后他们建设性地提出了一种全光学技术用来重构晶体材料的能带带隙^[11]. 此外, You等^[12]测量了强激光与MgO晶体作用产生的高次谐波, 发现高次谐波随着激光偏振方向的各向异性, 预示着全光学方法可用来提取晶体结构、原子间势、价电子密度甚至波函数等信息.
为了理解固体高次谐波的产生机制, 理论研究工作者们提出了一系列模型和计算方法, 如Korbman等^[13,14]、Wu等^[15]以及Guan等^[16]通过数值求解一维含时薛定谔方程计算出晶格内电流变化, 得到谐波信号. 此外, Jin等^[17]、Li等^[18]和Li等^[19]通过数值求解二维含时薛定谔方程研究固体谐波的辐射特性. Vampa等^[20-22] 则提出求解密度矩阵方程组的方法来模拟固体谐波, 最终可以分别计算出带内电流和带间电流, 通过傅里叶变换带内和带间电流即可得到高次谐波谱, 他们应用此方法成功解释了带间谐波的产生机制. 此外, Golde等^[23-25]、F?ldi等^[26]和Tamaya等^[27]求解激光外场作用下的两能带半导体布洛赫方程来研究固体谐波辐射, 成功解释了一些实验现象. 2015年, Hohenleutner等^[28]完善了理论模型, 通过求解考虑多条能带的半导体布洛赫方程模拟强激光与晶体相互作用, 同时在时域上直接测量太赫兹场作用下的固体高次谐波. 他们的实验和理论模拟结果表明, 固体材料中电子从不同能带隧穿产生的量子相干能够有效控制超快高次谐波辐射. 最近, Yu等^[29]提出利用二维h-BN材料的双层或者多层纳米结构控制优化类原子的高次谐波辐射, 发现高次谐波截止能量随着层间距变化的依赖关系.
固体高次谐波可作为产生新型小型化阿秒光源的一种全新手段, 如何进一步增强其高次谐波的转换效率一直是研究工作者们关注的焦点. Li等^[30]通过双色叠加场技术, 理论优化增强了固体高次谐波的第二个平台效率, 选择合适的双色场激光参数可获得单个阿秒脉冲. 此外, Liu等^[31]结合纳米加工技术和超快强激光技术, 利用全介质超表面提高驱动激光的强度以及介质材料的损耗阈值, 从而有效地增强谐波效率约两个数量级. 最近, Franz等^[32]在半导体材料中发现利用纳米锥波导也能够有效增强固体谐波的转换效率.
本文针对固体高次谐波的转换效率问题, 以双层MoS₂为例, 研究其在不同堆栈方式下的高次谐波辐射特性, 理论模拟发现, 层间原子错位堆栈能够有效打破晶体对称性, 使得原有的部分带间禁戒跃迁被允许, 带间跃迁激发通道增加, 从而提升了载流子跃迁概率及高次谐波转换效率.

本文采用数值求解多能带半导体布洛赫方程组的方法(SBEs)开展强激光与双层MoS₂材料相互作用的理论研究^[33]. 模拟过程中, 晶体倒格矢坐标可在直角坐标系中表示为x||Γ – M, y||Γ – K, 和z||Γ – A (光轴), 线偏振激光的传播方向沿着光轴方向. 在单电子近似下, 多能带半导体布洛赫方程组可以写为

$\begin{split} {\rm{i}}\frac{\partial }{{\partial t}}p_k^{{{\rm{h}}_i}{{\rm{e}}_j}} =\;& \left( {\varepsilon _k^{{{\rm{e}}_j}} + \varepsilon _k^{{{\rm{h}}_i}} - {\rm{i}}\frac{1}{{{T_2}}}} \right)p_k^{{{\rm{h}}_i}{{\rm{e}}_j}} - \left( {1 - f_k^{{{\rm{e}}_j}} - f_k^{{{\rm{h}}_i}}} \right)d_k^{{{\rm{e}}_j}{{\rm{h}}_i}}E(t) + {\rm{i}}E(t){\nabla _k}p_k^{{{\rm{h}}_i}{{\rm{e}}_j}} \\ &+ E(t)\sum\limits_{\lambda \ne j} {\left( {d_k^{{{\rm{e}}_\lambda }{{\rm{h}}_i}}p_k^{{{\rm{e}}_\lambda }{{\rm{e}}_j}} - d_k^{{{\rm{e}}_j}{{\rm{e}}_\lambda }}p_k^{{{\rm{h}}_i}{{\rm{e}}_\lambda }}} \right)} + E(t)\sum\limits_{\lambda \ne i} {\left( {d_k^{{{\rm{h}}_\lambda }{{\rm{h}}_i}}p_k^{{{\rm{h}}_\lambda }{{\rm{e}}_j}} - d_k^{{{\rm{e}}_j}{{\rm{h}}_\lambda }}p_k^{{{\rm{h}}_i}{{\rm{h}}_\lambda }}} \right)},\qquad \end{split}$

$\begin{split} {\rm{i}}\frac{\partial }{{\partial t}}p_k^{{{\rm{e}}_i}{{\rm{e}}_j}} =\;& \left( {\varepsilon _k^{{{\rm{e}}_j}} - \varepsilon _k^{{{\rm{e}}_i}} - {\rm{i}}\frac{1}{{{T_2}}}} \right)p_k^{{{\rm{e}}_i}{{\rm{e}}_j}} + \left( {f_k^{{{\rm{e}}_j}} - f_k^{{{\rm{e}}_i}}} \right)d_k^{{{\rm{e}}_j}{{\rm{e}}_i}}E(t) + {\rm{i}}E(t){\nabla _k}p_k^{{{\rm{e}}_i}{{\rm{e}}_j}} \\ &+ E(t)\sum\limits_{\lambda \ne j} {d_k^{{{\rm{e}}_\lambda }{{\rm{e}}_i}}p_k^{{{\rm{e}}_\lambda }{{\rm{e}}_j}}} - E(t)\sum\limits_{\lambda \ne i} {d_k^{{{\rm{e}}_j}{{\rm{e}}_\lambda }}p_k^{{{\rm{e}}_i}{{\rm{e}}_\lambda }}} + E(t)\sum\limits_\lambda {\left( {d_k^{{{\rm{h}}_\lambda }{{\rm{e}}_i}}p_k^{{{\rm{h}}_\lambda }{{\rm{e}}_j}} - d_k^{{{\rm{e}}_j}{{\rm{h}}_\lambda }}{{(p_k^{{{\rm{h}}_\lambda }{{\rm{e}}_i}})}^ * }} \right)}, \end{split}$

$\begin{split} {\rm{i}}\frac{\partial }{{\partial t}}p_k^{{{\rm{h}}_i}{{\rm{h}}_j}} =\;& \left( {\varepsilon _k^{{{\rm{h}}_i}} - \varepsilon _k^{{{\rm{h}}_j}} - {\rm{i}}\frac{1}{{{T_2}}}} \right)p_k^{{{\rm{h}}_i}{{\rm{h}}_j}} + \left( {f_k^{{{\rm{h}}_i}} - f_k^{{{\rm{h}}_j}}} \right)d_k^{{{\rm{h}}_j}{{\rm{h}}_i}}E(t) + {\rm{i}}E(t){\nabla _k}p_k^{{{\rm{h}}_i}{{\rm{h}}_j}} \\ &+ E(t)\sum\limits_{\lambda \ne j} {d_k^{{{\rm{h}}_\lambda }{h_i}}p_k^{{{\rm{h}}_\lambda }{{\rm{h}}_j}}} - E(t)\sum\limits_{\lambda \ne i} {d_k^{{{\rm{h}}_j}{{\rm{h}}_\lambda }}p_k^{{{\rm{h}}_i}{{\rm{h}}_\lambda }}} + E(t)\sum\limits_\lambda {\left( {d_k^{{{\rm{e}}_\lambda }{{\rm{h}}_i}}{{(p_k^{{{\rm{h}}_j}{{\rm{e}}_\lambda }})}^ * } - d_k^{{{\rm{h}}_j}{{\rm{e}}_\lambda }}p_k^{{{\rm{h}}_i}{{\rm{e}}_\lambda }}} \right)}, \end{split} $

$\begin{split} \frac{\partial }{{\partial t}}f_k^{{{\rm{e}}_i}} = \;&- 2{\rm{Im}} \left[ {\sum\limits_{\lambda \ne i} {d_k^{{{\rm{e}}_i}{{\rm{e}}_\lambda }}E(t){{\left( {p_k^{{{\rm{e}}_\lambda }{{\rm{e}}_i}}} \right)}^ * }} + \sum\limits_\lambda {d_k^{{{\rm{e}}_i}{{\rm{h}}_\lambda }}E(t){{\left( {p_k^{{{\rm{h}}_\lambda }{{\rm{e}}_i}}} \right)}^ * }} } \right] + E(t){\nabla _k}f_k^{{{\rm{e}}_i}} - \frac{1}{{2{T_1}}}\left( {f_k^{{{\rm{e}}_i}} - f_{ - k}^{{{\rm{e}}_i}}} \right), \end{split} $

$\begin{split} \frac{\partial }{{\partial t}}f_k^{{{\rm{h}}_i}} =\;& - 2{\rm{Im}} \left[ {\sum\limits_{\lambda \ne i} {d_k^{{{\rm{h}}_\lambda }{{\rm{h}}_i}}E(t){{\left( {p_k^{{{\rm{h}}_i}{{\rm{h}}_\lambda }}} \right)}^ * }} + \sum\limits_\lambda {d_k^{{{\rm{e}}_\lambda }{{\rm{h}}_i}}E(t){{\left( {p_k^{{{\rm{h}}_i}{{\rm{e}}_\lambda }}} \right)}^ * }} } \right] + E(t){\nabla _k}f_k^{{{\rm{h}}_i}} - \frac{1}{{2{T_1}}}\left( {f_k^{{{\rm{h}}_i}} - f_{ - k}^{{{\rm{h}}_i}}} \right). \end{split} $

方程(1)—(3)表示电子、空穴在带间的跃迁过程, 而方程(4)和(5)描述电子、空穴在带内的运动过程. 其中, $p_k^{{{\rm{h}}_i}{{\rm{e}}_j}}$、$p_k^{{{\rm{e}}_i}{{\rm{e}}_j}}$和$p_k^{{{\rm{h}}_i}{{\rm{h}}_j}}$表示带间相干, $f_k^{{{\rm{e}}_i}}$和$f_k^{{{\rm{h}}_i}}$分别为电子和空穴的布居, e和h分别表示电子和空穴, E(t)为激光场, $\varepsilon _k^{{{\rm{e}}_j}}$和$\varepsilon _k^{{{\rm{h}}_i}}$为对应的载流子能带, T₁表示不对称载流子衰减时间, T₂为退相时间, d_k^nn′为带与带之间的跃迁偶极矩(n和n′代表e_i、e_j、e_λ、h_i、h_j、h_λ等指数对应的不同能带). 基于VASP软件, 应用高精度第一性原理计算得到固体材料的能带结构ε_k以及每条能带每个k点的波函数?_k. 通过公式

$d_k^{nn'} = \frac{{{\rm{i}}\left\langle {\phi _k^{n'}\left| {\hat p} \right|\phi _k^n} \right\rangle }}{{\left( {\varepsilon _k^{n'} - \varepsilon _k^n} \right)}},\;(n \ne n')$

计算出带与带之间的跃迁偶极矩. 带内电流密度与带间极化可以表示为

$J(t) = \sum\limits_{n,k} {\left[ { - 2\upsilon _k^nf_k^n(t)} \right]},$

$P(t) = \sum\limits_{n,n',k} {\left[ {d_k^{nn'}p_k^{nn'}(t) + \rm c.c.} \right]} .$

其中$\upsilon _k^n$为各能带的群速度. 高次谐波可以通过公式$S(\omega ) = {\left| {\omega P(\omega ) + {\rm{i}}J(\omega )} \right|^2}$得到.

通常, 双层MoS₂材料具有多种稳定的堆栈结构, 图1(a)和1(b)所示分别为双层MoS₂材料AA型(层间S原子顶对顶)和T型(层间S原子错位)堆栈下的结构. 通过结构优化, 计算得到的双层MoS₂材料在AA型和T型堆栈下的晶格参数都在3.19 ? (1 ? = 0.1 nm)左右. 然而优化所得的AA型堆栈双层MoS₂材料的层间距为3.69 ?, 较T型堆栈双层MoS₂材料的层间距3.09 ?大. 图1(c)中蓝色区域为双层MoS₂材料的第一布里渊区, 其中Γ–M和Γ–K分别为倒空间中的两个高对称性方向. 由于层状MoS₂材料在Γ–K方向的高次谐波转换效率要比Γ–M方向低很多^[34], 因此在本工作中只关注双层MoS₂材料在Γ–M方向的高次谐波辐射. 此外, 图1(d)和1(e)分别为AA型堆栈和T型堆栈双层MoS₂材料在Γ–M方向的能带结构, 图中所示共12条价带和8条导带. 对比双层MoS₂在两种不同堆栈方式下的能带结构, 发现不管是带隙还是能带的色散分布都几乎保持一致, 也就是说堆栈方式对其能带结构影响很小.
图 1 (a)和(b)分别为双层MoS₂材料AA型堆栈和T型堆栈结构的俯视图(上图)和侧视图(下图); (c) 双层MoS₂材料的第一布里渊区; (d)和(e) 分别为双层MoS₂材料AA型堆栈和T型堆栈在高对称性Γ–M方向的能带结构
Figure1. Top and side views of bilayer MoS₂ for (a) AA stacking and (b) T stacking; (c) the first brillouin zone of bilayer MoS₂; (d) energy bands of bilayer MoS₂ for (a) AA stacking and (b) T stacking in Γ–M direction.

图2(a)所示为模拟得到的双层MoS₂材料在AA型堆栈(蓝线)和T型堆栈(红线)下的高次谐波谱, 计算过程中共使用了12条价带和8条导带进行计算. 所用激光为波长为3200 nm的中红外激光场, 脉冲的半高全宽为2个光周期, 激光电场的峰值强度 I = 1.0 × 10¹¹ W/cm². 对比两种不同堆栈方式下产生的高次谐波谱, 惊奇地发现在谐波谱的高能区域, 双层MoS₂在原子错位的T型堆栈下产生高次谐波的转换效率比在AA型堆栈下的高次谐波效率高一个数量级. 通常, 固体高次谐波的高能区域主要来源于材料中更高的导带或更低的价带参与跃迁贡献. 如图2(b)所示, 若在模拟过程中只考虑2条价带(v₁, v₂)和4条导带(c₁, c₂, c₃, c₄), 则两种堆栈方式下产生的高次谐波谱基本没有区别, 同时高能区域高次谐波谱消失. 但在模拟中使用4条价带(v₁, v₂, v₃, v₄)和4条导带(c₁, c₂, c₃, c₄), 计算得到的高次谐波谱如图2(c)所示, 图2(a)出现的谐波高能区域增强现象又显现出来. 因此, 确定相比于图2(b)中使用的2条价带和4条导带, 在模拟图2(c)高次谐波中额外增加的价带v₃和v₄对高能高次谐波的产生起着重要作用, 同时也是影响两种不同堆栈方式下高次谐波谱区别的关键. 由于前面发现对于两种不同堆栈方式下的能带结构几无差别, 因此可认为带间跃迁偶极矩是T型堆栈谐波增强的主要因素.
图 2 模拟计算得到的双层MoS₂材料在高对称性Γ–M方向的高次谐波谱(红线为T型堆栈, 蓝线为AA型堆栈)　(a) 模拟过程中使用12条价带8条导带; (b) 模拟过程中使用2条价带4条导带; (c) 模拟过程中使用4条价带4条导带
Figure2. Calculated high harmonic spectra from bilayer MoS₂ in AA stacking (blue line) and T stacking(red line) with (a) twelve valence bands and eight conduction bands; (b) two valence bands and four conduction bands; (c) four valence bands and four conduction bands used in simulation.

为了阐明T型堆栈谐波增强背后的物理机制, 计算出双层MoS₂材料部分能带间的跃迁偶极矩. 图3(a)和3(b)分别为AA型堆栈的第三条价带v₃和第四条价带v₄与最低4条导带的带间跃迁偶极矩. 对于AA型堆栈, 双层MoS₂材料两层镜面对称, 层与层之间的相互作用非常弱, 电子很难从其中一层跃迁到另外一层, 价带v₃和v₄只与同一层内的导带c₃和c₄间有带间跃迁偶极矩, 因此相比于图2(b)只包含v₁和v₂价带, 图2(c) 中进一步考虑v₃和v₄价带贡献的谐波效率略有增强. 然而对于T型堆栈, 双层MoS₂镜面对称被打破, 电子有一定几率从其中一层跃迁到另外一层, 因此如3(c)和3(d)所示在T型堆栈中价带v₃和v₄与最低的4条导带间都有跃迁偶极矩. 分析认为, 正是由于在T型堆栈下材料对称性被打破, 使得原有的部分带间禁戒跃迁路径被打开, 带间跃迁激发通道增加, 大大增加了载流子跃迁概率, 使得高次谐波转换效率增强.
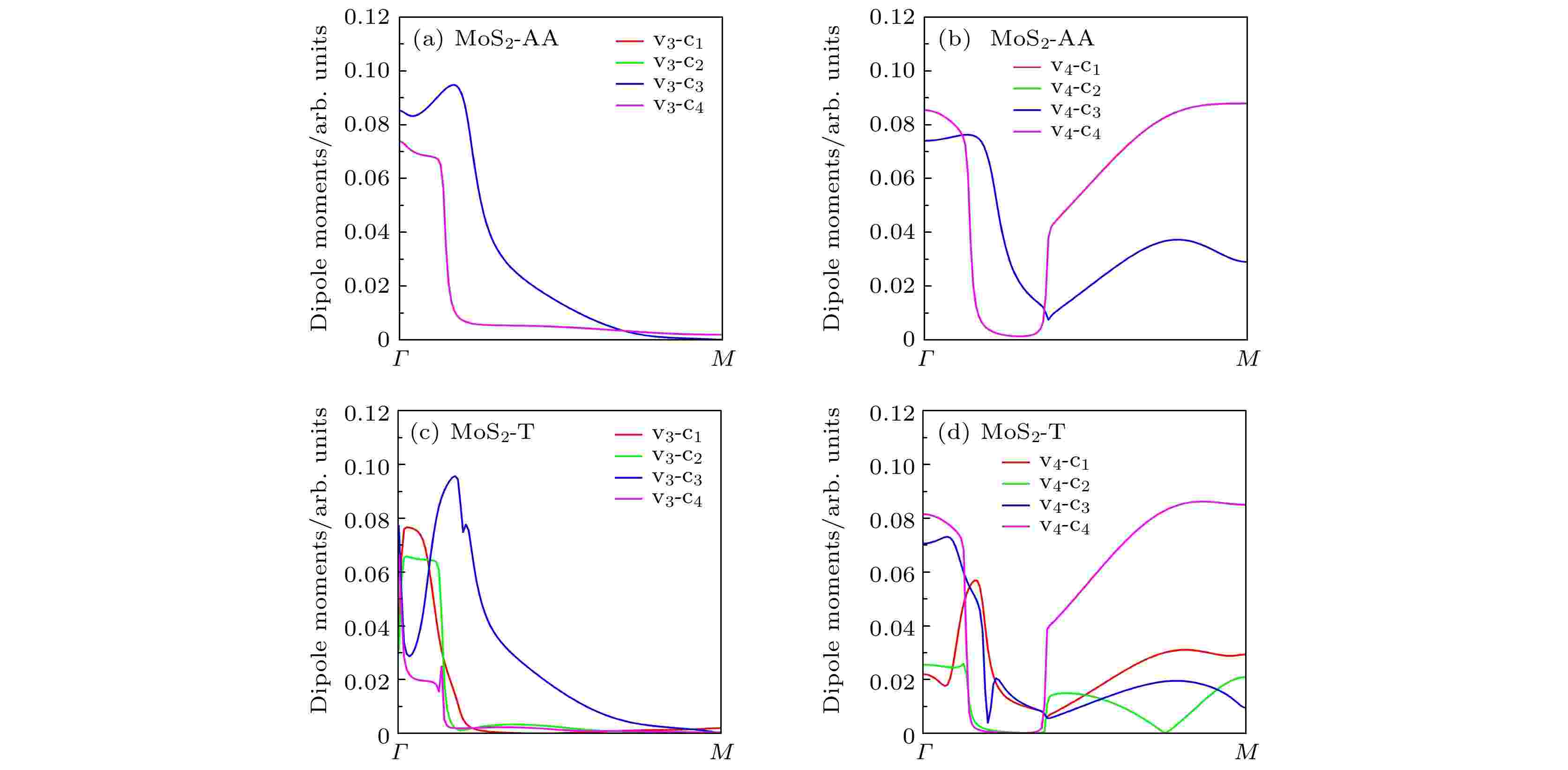图 3 双层MoS₂材料的部分带间跃迁偶极矩　(a)和(b)分别为AA型堆栈的双层MoS₂材料中第三条价带v₃和第四条价带v₄与最低4条导带的带间跃迁偶极矩; (c)和(d)分别为T型堆栈的双层MoS₂材料中第三条价带v₃和第四条价带v₄与最低4条导带的带间跃迁偶极矩
Figure3. The parts of transition dipole moments: (a) and (b) show the transition dipole moments among two valence bands (v₃ and v₄) and four lowest conduction bands in AA stacking, respectively; (c) and (d) how the transition dipole moments among two valence bands (v₃ and v₄) and four lowest conduction bands in T stacking, respectively.

此外, 本工作还研究了两种堆栈方式下双层MoS₂材料随驱动激光波长变化的高次谐波谱. 如图4(a)和4(b)所示, 高次谐波的转换效率随着激光波长的增加逐渐降低, 这主要是因为更长的激光波长对应更小的光子能量, 电子需要吸收更多的光子才能从价带跃迁到导带, 跃迁概率大为降低, 使得高次谐波效率逐渐衰减. 虽然谐波效率整体随着波长变大逐渐降低, 但发现相比于AA型堆栈, T型堆栈7—12 eV能量范围的高次谐波在1000—6000 nm波长范围内都增强1个数量级, 同时随着激光波长的增大该区域谐波相比AA型堆栈的增强越明显.
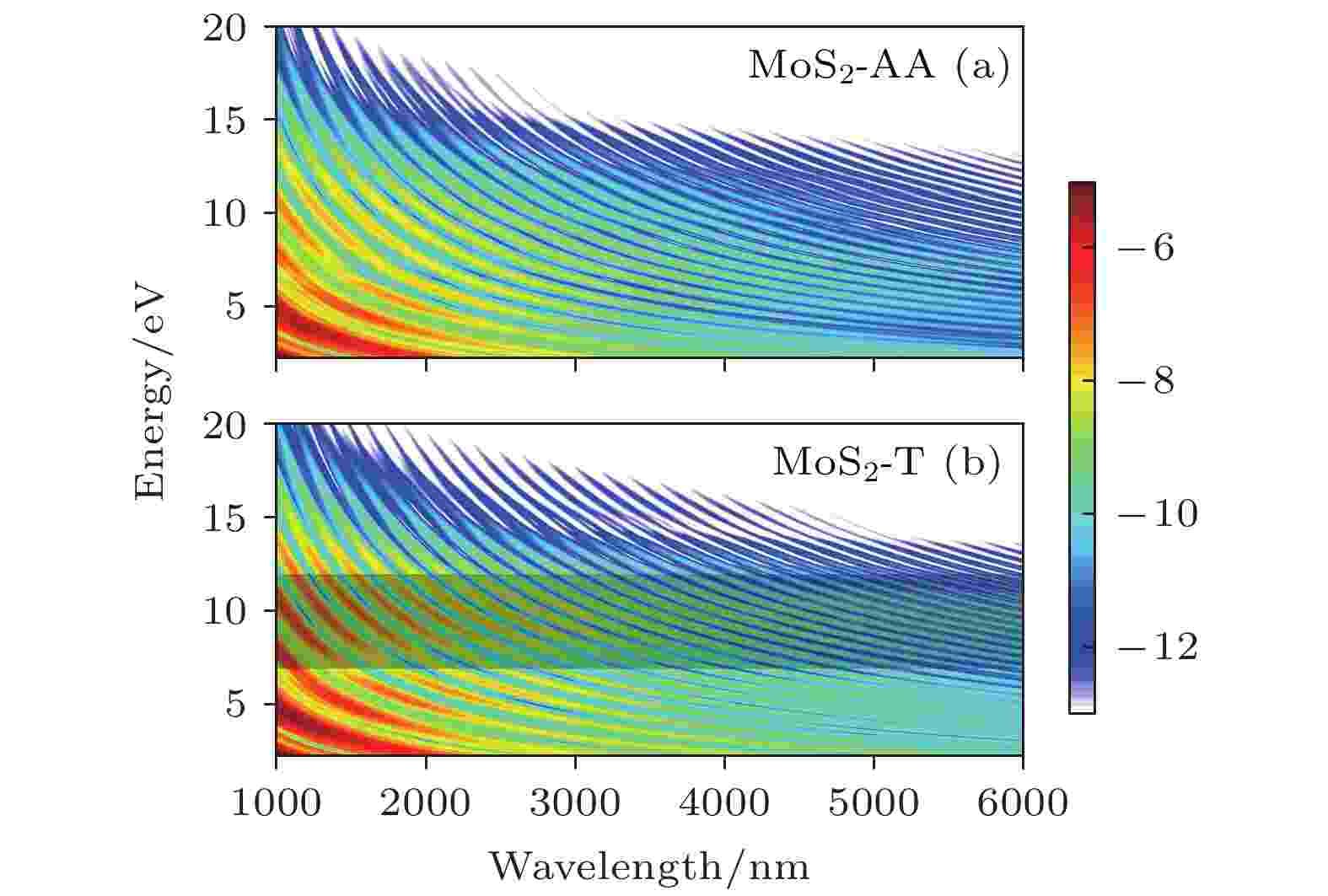图 4 模拟计算得到的双层MoS₂材料随驱动激光波长变化的高次谐波谱　(a) AA型堆栈; (b) T型堆栈
Figure4. Wavelength dependent high harmonic spectra from bilayer MoS₂ in (a) AA stacking and (b) T stacking.

为了定量比较不同堆栈方式下激光波长对双层MoS₂高次谐波效率的影响, 将固定能量范围内的高次谐波强度积分用于定标谐波的产率η(λ). 理论研究表明, 对于稀有气体产生的高次谐波产率遵循波长定标^[35,36]:

$ \eta (\lambda )\sim {\lambda }^{-x}{,}\;\;\;\;\;\;\;\;x\approx 5—6, $

而通过计算双层MoS₂高次谐波的波长定标发现, 波长范围不同, 高次谐波的波长定标也不同. 这里取T型堆栈相较AA型堆栈高次谐波显著增强的7—12 eV能量范围(图3(b)中灰色阴影区域)研究波长定标. 以AA型堆栈为例, 如图5(a)所示, 可发现激光波长在1000—2000 nm范围内, 高次谐波的波长定标遵循λ^{–1.44 ± 0.10}, 远高于气体高次谐波的波长定标. 随着激光波长的逐渐增大, 高次谐波的波长定标逐渐降低, 如在激光波长在2000—4000 nm范围时, 高次谐波的波长定标降为λ^{–3.78 ± 0.10}. 当激光波长达到4000—6000 nm时, AA型堆栈的双层MoS₂高次谐波波长定标则接近于气体高次谐波的波长定标. T型堆栈双层MoS₂高次谐波中具有类似的波长定标规律, 不同之处在于原子错位T型堆栈双层MoS₂的高次谐波波长定标随着波长的增大(2000—6000 nm)下降速度明显小于AA型堆栈, 这也预示着在波长较长的激光驱动下, T型堆栈相比AA堆栈所增强的高次谐波具有更优越的波长定标.
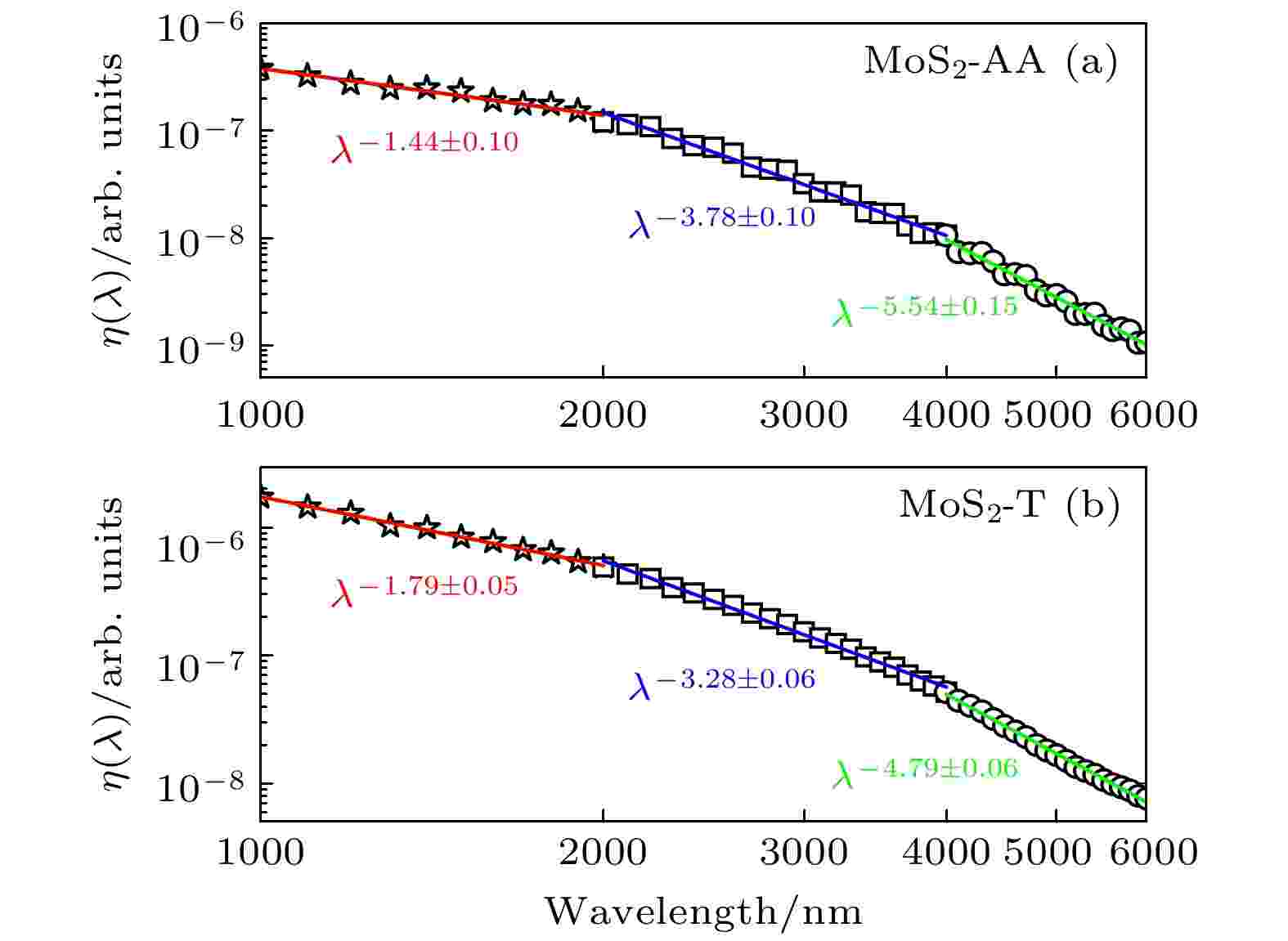图 5 模拟得到的双层MoS₂材料高次谐波产率的波长定标　(a) AA型堆栈; (b) T型堆栈; 图中直线由波长定标公式拟合得到
Figure5. Wavelength scaling of high harmonic yield from bilayer MoS₂ in (a) AA stacking and (b) T stacking. Lines are fits of the scaling law to the data.

本文理论研究了堆栈方式对双层MoS₂材料高次谐波效率的影响, 发现在谐波谱高能区域, 原子错位T型堆栈的双层MoS₂在强激光驱动下产生的高次谐波转换效率比AA型堆栈的双层MoS₂高一个数量级. 理论分析证明, 由于在T型堆栈下双层镜面对称性被打破, 部分带间禁戒跃迁被允许, 带间跃迁概率增加, 高次谐波强度从而提升. 进一步对谐波产率的波长定标研究表明, 在2000—6000 nm的中红外激光波长范围, 原子错位T型堆栈双层MoS₂材料的高次谐波具有更好的波长定标. 实际上本工作还研究了其他错位堆栈双层MoS₂材料的高次谐波辐射, 相应的谐波转化效率和波长定标介于AA堆栈与T型堆栈之间, 为免赘述, 未呈现在本文中. 该工作旨在对双层材料进行原子级调控, 探讨固体高次谐波辐射增强的潜在方案, 为实现极紫外阿秒光源提供理论新思路.