摘要:气-液-固三相流混合过程是一个复杂的多重流固耦合动力学问题, 颗粒参数与流道物理空间尺度之间的关系直接影响计算收敛性, 强剪切区域的流固双向耦合作用数值建模与网格处理具有较高难度. 针对上述问题, 提出了一种气-液-固三相流混合的建模与求解方法. 基于流体体积-离散单元耦合模型, 建立考虑颗粒运动的三相动力学模型, 通过求解动量方程, 实现两相流体与颗粒的双向耦合. 自主开发用户自定义函数(UDF)通信接口, 得到流体与颗粒间的相互作用力, 提出了一种多孔相间耦合解法来描述颗粒运动轨迹. 以带强剪切的三相流混合过程为例, 使用该方法研究了不同充气条件对流道物理空间内自由表面、速度分布和颗粒悬浮特性的影响规律. 结果表明, 强剪切和壁面作用可以将流体的切向速度转化为轴向和径向的速度; 选择合适的充气速度可以消除自由液面的不稳定性; 增加流体的流动速度, 对于部分区域颗粒的悬浮提升作用有限. 研究结果可为复杂多相流相间作用机理研究提供有益借鉴, 也可为气-液-固三相颗粒混合生产调控提供技术支持.
关键词: 三相流/
固体颗粒/
流体体积-离散单元耦合/
强剪切

English Abstract

全文HTML

--> --> -->

气-液-固三相流混合是高端化工、锂电生产的关键工艺环节, 混合执行构件和流道物理空间需要提供较高的传质和高湍流能力, 且伴随强剪切过程. 上述要求使得气-液-固三相流混合过程非常复杂, 且难于观察整体流场及关键区域的颗粒分布^[1-3]. 混合物理空间几何尺度相对于颗粒要高多个数量级, 其内部三维循环流动和湍流多相流的复杂性, 给混合执行机构优化设计、混合过程边界条件调控提出了重要技术挑战^[4,5].
当前计算流体力学(computational fluid dynamics, CFD)方法广泛应用于液-固混合过程的模拟计算, 一般基于欧拉-欧拉模型, 将颗粒固相视为连续相, 来描述相间相互渗透过程, 该模型占用计算资源比较少, 但模拟精度较低, 且无法获得颗粒运动状态^[6-10]. 基于欧拉-拉格朗日模型的离散单元法(discrete element method, DEM)可以获得颗粒的运动和相互作用, 可以与不同的流体动力学计算方法相结合, 来模拟流体-颗粒流^[11,12], 如格子-玻尔兹曼方法(lattice Boltzmann method, LBM). 该方法在离散的晶格网格上使用代表流体相的虚拟颗粒, 并通过求解离散的Boltzmann方程模拟流体的流动^[13]. 相关****已经对三维LBM-DEM耦合进行了尝试^[14], 但是由于要求流体尺寸要比固体颗粒尺寸小得多, 对计算能力要求非常高, 多数针对三维问题的LBM-DEM耦合解法仍在开发中. 将CFD与离散单元法(CFD-DEM)耦合使用, 可以预测颗粒尺度的变化, 颗粒-颗粒和颗粒-壁之间的相互作用都通过牛顿运动方程求解, 而颗粒-流体之间的相互作用则通过源相交换来实现. Bastien等^[15]使用CFD-DEM模型, 以非常好的可靠性再现了固-液混合系统中发生的各种现象, 研究证明, 在非惯性参考系下进行CFD-DEM模拟是可行的, 这为CFD-DEM的应用开辟了广阔的前景. Shao等^[16]利用CFD-DEM耦合的模型研究了三维混合过程中的固体悬浮行为, 与实验测量和基于欧拉-欧拉方案的CFD仿真相比, CFD-DEM仿真可以提供更多流场信息. Blais等^[17-19]开发了一种半解析CFD-DEM模型, 并利用该模型进行固-液混合操作的设计以及优化, 提高了颗粒悬浮比例, 改善了流型和颗粒分布, 但未考虑自由液体表面的分布及其稳定性.
对于自由液体表面流, 常用流体体积(volume of fluid, VOF)模型进行模拟, Xu等^[20]研究了表面涡流对混合物理空间中颗粒分散的影响, 研究发现表面涡流的产生降低了颗粒分布的均匀性, 混合挡流物理构件可使得表面涡流得到有效控制, 提高了颗粒分布的均匀性. Sun和Sakai^[21]开发了一种基于欧拉-拉格朗日方法的模型, 可以模拟复杂的三相流行为, 包括自由表面的变形和颗粒引起的液体位移. Wu等^[22]利用虚拟双重网格孔隙度模型改进了DEM-VOF模型, 新模型克服了计算过程中的不稳定性, 可用于固-液混合过程的流场模拟计算. Kang等^[23]利用DEM-VOF模型结合雷诺压力模型(RSM), 对具有自由表面的无挡流构件的混合物理空间中的颗粒悬浮动力学进行了模拟, 得到了混合流道的几何形状、叶轮转速、颗粒密度和直径等对自由表面涡流、流型和颗粒悬浮动力学的影响规律.
当前关于多相流的研究主要以两相为主, 考虑三相耦合过程的多集中于自由液面, 却鲜有考虑内部充气对液-固两相的影响, 尤其是视固相为离散颗粒相的情况. 因此, 建立流体和颗粒的动力学模型, 通过求解动量方程, 实现流体与颗粒的双向耦合, 进行气-液-固三相流混合的研究, 揭示三相耦合在复杂混合过程中的作用规律非常必要.
针对上述目标, 本文首先建立了气-液-固三相流动力学模型, 分别包括VOF模型、DEM模型以及两者的耦合模型; 然后进行了建模与网格划分以及边界条件和参数设置, 并进行了网格无关性验证, 进而选取最终使用的网格数量并开始不同案例的数值计算; 自主开发用户自定义函数(user defined function, UDF)通信接口, 得到流体与颗粒间的相互作用力, 提出了一种多孔相间耦合解法来描述颗粒运动轨迹; 最后通过计算结果讨论了充气对自由液面、流体速度以及颗粒悬浮的影响, 揭示了不同充气条件下混合物理空间内多相流的演变规律并得出了相应结论.

对于VOF-DEM模型耦合的多相流, 通过对体积平均的Navier-Stokes方程进行求解, 进而对连续相的流体进行描述, 针对VOF模型还存在自由液面的问题, 气-液两相存在明显交界面, 可通过2.1节模型求解气-液两相问题. 同时使用离散单元法对固体相颗粒进行建模, 可通过2.2节模型求解. 这两个模型以一定的时间步间隔进行双向耦合交换数据, 一般CFD的时间步长明显大于DEM时间步长, 以便正确获得接触作用, 颗粒通常不会在单个DEM时间步长中移动很远的距离. 因此, 不需要两者1∶1的时间步长比, 对于DEM, CFD的时间步长比一般从1∶10到1∶100不等, 两者耦合时选择合适的时间步长比, 不仅可以节省计算时间, 还可以避免计算的发散.
2

-->

2.1.VOF模型

混合过程中存在复杂的气-液两相耦合现象, 所以应该用多相流模型来描述. VOF模型是基于欧拉网格下的表面追踪模型, 通过求解单相或多相的体积分数来追踪和捕捉互不相融流体间的交界面. 通过计算各相的控制方程, 能够准确地模拟混合过程中多相组分的动态演化和瞬态特征的捕捉, 其中流体的连续性方程和动量方程表示如下^[21]:

$\frac{{\partial {\varepsilon _{\rm{f}}}}}{{\partial t}} + \nabla \cdot \left( {{\varepsilon _{\rm{f}}}{{u}}} \right) = 0, $

$\begin{split}&\frac{{\partial \left( {{\rho _{\rm{f}}}{\varepsilon _{\rm{f}}}{{u}}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\rho _{\rm{f}}}{\varepsilon _{\rm{f}}}{{uu}}} \right)= - {\varepsilon _{\rm{f}}}\nabla p \\&+ \nabla \cdot \left\{ {{\varepsilon _{\rm{f}}}\left[ {\mu \left( {\nabla {{u}} + \nabla {{{u}}^{\rm{T}}}} \right) + {\rho _{\rm{f}}}g + {F_{\rm{st}}}} \right]} \right\} + {F_{\rm{pf}}},\end{split}$

式中, ${\rho _{\rm{f}}}$是流体密度, ${\varepsilon _{\rm{f}}}$是空隙率, u是流体速度, p是压力, $\mu $是流体动力黏度, ${F_{\rm{pf}}}$是颗粒流体间的相互作用项的反作用力, ${F_{\rm{st}}}$是自由液面附近的表面张力. 为了提高模拟精度, 使计算更加接近实际情况, 本文采用连续表面张力(continuum surface force, CSF)模型处理表面张力, 其表达式如下:

${F_{\rm{st}}} = \sigma \cdot \kappa \cdot \nabla \phi , $

式中$\sigma $是流体的表面张力系数; 而$\kappa $是气-液相界面的曲率, 其表达式为

$\kappa = \frac{1}{{|{{n}}|}}\left[ {\left( {\frac{{{n}}}{{|{{n}}|}} \cdot \nabla } \right)|{{n}}|} \right] - (\nabla \cdot {{n}}), $

其中${{n}} = \nabla \cdot {\alpha _2}$是次相体积分数的法向量.
对于VOF模型气-液两相的交界面可通过界面传输方程求解:

$\frac{{\partial (\alpha )}}{{\partial t}} + \nabla \cdot (\alpha {{u}}) = 0, $

其中$\alpha $是液体的体积分数, 若$\alpha = 1$, 代表该计算单元全是液相, 不含气相; 若$0 < \alpha < 1$, 则说明该计算单元内同时包含气、液两相; 若$\alpha = 0$, 代表该相全部是气相. 因此, 基于VOF模型可以求解气-液交界面的相互作用过程, 尤其是在强剪切作用下的气相剥离过程.
此外, 多相流环境中尤其是强剪切区域处于湍流状态下, 为了能够得到精确的模拟结果, 流体控制方程选择标准的湍动能-耗散($k \text{-} \varepsilon $)模型, 该模型在剧烈变化的流场中有较好的计算性能, 其控制方程如下^[24]:

$\begin{split}&\frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] \\&+ {G_k} + {G_{\rm b}} - \rho \varepsilon - {Y_M} + {S_k}, \end{split}$

$\begin{split}&\frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] \\&+ {C_{1\varepsilon }}\frac{\varepsilon }{k}\left( {{G_k} + {C_{3\varepsilon }}{G_{\rm b}}} \right) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon },\end{split}$

式中, k是湍动能; $\varepsilon $是湍动能耗散率; ${G_k}$是由于平均速度梯度引起的湍动能产生项; ${G_{\rm{b}}}$是由于浮力影响引起的湍动能产生项; ${Y_{\rm{M}}}$为可压缩湍流脉动膨胀对总的耗散率的影响; ${C_{1\varepsilon }}$, ${C_{2\varepsilon }}$, ${C_{3\varepsilon }}$为经验常数, 张量下标$i, \;j$表示$x, \;y, \;z$三个方向分量; ${\sigma _k}$, ${\sigma _\varepsilon }$为湍动能和湍动耗散率对应的普朗特数.
2 -->

2.2.DEM模型

在考虑流体相时, 已经引入了颗粒与流体间的相互作用, 因此在该部分将分析颗粒模型. DEM是一种可以用于计算非连续颗粒的运动规律, 并且可以分析离散颗粒接触力以及运动的分析模型. 此模型中, 将颗粒相视为离散相, 相比于其他方法更加贴近实际, 更能还原颗粒的真实运动情况, 颗粒的运动是基于牛顿第二定律的计算得出的, 通过计算可以得到颗粒的平移、旋转的速度和位置随时间的变化关系, 颗粒的平移运动取决于作用在其上的力的总和, 而旋转运动则由接触的转矩控制, 其控制方程可表示为^[16,25]

${m_i} {{\ddot x_{{i}}}} = \sum\limits_j {{F_{{\rm{c}},ij}}} + {F_{{\rm{pf}},i}} + {m_i}g, $

${{{I}}_i}{{\ddot\theta _{{\rm{p}},i}}} = \sum\limits_j {\left( {{{{T}}_{{\rm{t}},ij}} + {{{T}}_{{\rm{r}},i{{j}}}}} \right)} .$

式中, ${m_i}$是颗粒i的质量; ${x_i}$是颗粒的位移; ${F_{{\rm{c, }}ij}}$是颗粒i和j之间的接触力; ${F_{{\rm{pf}}, i}}$是颗粒i与流体间的相互作用力; g是重力加速度; ${{{I}}_i}$是颗粒i的惯性力矩; ${\theta _{{\rm{p}}, i}}$是颗粒i的角位移; ${{{T}}_{{\rm{t}}, ij}}$和${{{T}}_{{\rm{r}}, ij}}$是作用在颗粒上的切向和滚动摩擦力矩, (8)式和(9)式中包含的一些力和扭矩的详细计算见如下公式.
接触力:

${F_{{\rm{c}},ij}} = {F_{{\rm{cn}},ij}} + {F_{{\rm{ct}},ij}}.$

法向接触力:

$\begin{split}{F_{{\rm{cn}},ij}} \!=\! \frac{4}{3}{Y^*}\sqrt {{R^*}} \delta _{{\rm{cn}},ij}^{3/2} \!+\! 2\sqrt {\frac{5}{6}} \frac{{\ln e}}{{\sqrt {{{\ln }^2}e \!+\! {{\rm{\pi }}^2}} }}\sqrt {{S_{{\rm{cn}},ij}}{m^*}} {v_{{\rm{cn}}}}.\end{split}$

切向接触力:

${F_{{\rm{ct}},ij}} = - {\delta _{{\rm{ct}},ij}}{S_{{\rm{ct}},ij}} + 2\sqrt {\frac{5}{6}} \frac{{\ln e}}{{\sqrt {{{\ln }^2}e + {\pi ^2}} }}\sqrt {{S_{{\rm{ct}},ij}}{m^*}} {v_{{\rm{ct}}}}.$

切向摩擦力矩:

${{{T}}_{{\rm{t}},ij}} = {L_{ij}}{{{n}}_{ij}} \times {F_{{\rm{ct}},ij}}.$

滚动摩擦力矩:

${{{T}}_{{\rm{r}},ij}} = - {\mu _r}{L_{ij}}\left| {{F_{{\rm{cn}},ij}}} \right|\frac{{{{{\omega }}_{ij}}}}{{\left| {{{{\omega }}_{ij}}} \right|}}.$

颗粒-流体作用力:

${F_{\rm{pf}}} = \frac{1}{{\Delta V}}\sum\limits_i^{{n_{\rm{p}}}} {{f_{{\rm{pf}},i}}} - {f_{\nabla p,i}} - {f_{\nabla \tau,i}} - {f_{{\rm{st}},i}}, $

$\begin{split}{f_{{\rm{pf}},i}} =\;& {f_{{\rm{d}},i}} + {f_{\nabla p,i}} + {f_{\nabla \tau,i}} + {f_{{\rm{st}},i}} \\&+ {f_{{\rm{vm}},i}} + {f_{{\rm{B}},i}} + {f_{{\rm{Saff}},i}} + {f_{{\rm{Mag}},i}}.\end{split}$

这里${Y^*}$表示接触颗粒间等效杨氏模量; ${R^*}$表示接触颗粒间等效半径; ${\delta _{{\rm{cn}}, ij}}$, ${\delta _{{\rm{ct}}, ij}}$分别表示接触颗粒间法向、切向重叠大小; ${S_{{\rm{cn}}, ij}}$, ${S_{{\rm{ct}}, ij}}$分别表示接触颗粒间法向、切向接触刚度; ${m^*}$表示接触颗粒间等效质量; ${v_{{\rm{cn}}}}$, ${v_{{\rm{ct}}}}$分别表示接触颗粒间的法向、切向相对速度; ${L_{ij}}$表示接触颗粒间中心距离; ${{{n}}_{ij}}$表示接触颗粒间单位矢量; ${\mu _r}$表示颗粒的滚动摩擦系数; ${{{\omega }}_{ij}}$表示颗粒接触平面上的角速度矢量; $\Delta {V}$是颗粒i所在的计算网格的体积; ${n_{\rm{p}}}$表示颗粒数量; ${f_{{\rm{pf}}, i}}$表示颗粒i受到的所有流体、固体对颗粒作用之和, 包括曳力${f_{{\rm{d}}, i}}$^[26,27]、压力梯度力${f_{\nabla p, i}}$、黏性力${f_{\nabla \tau, i}}$、表面张力${f_{{\rm{st}}, i}}$、虚拟质量力${f_{{\rm{vm}}, i}}$、Basset力${f_{{\rm{B}}, i}}$、Saffman升力${f_{{\rm{Saff}}, i}}$^[28]和Magnus升力${f_{{\rm{Mag}}, i}}$^[23]. 由于动量方程表达式已经直接包含了压力、黏性力和表面张力, 所以在${F_{\rm{pf}}}$中相应地把这些力减去了.
2 -->

2.3.耦合模型

为了获得流体与颗粒间准确的相互作用力, 提出了一种相间耦合解法—多孔模型来描述精确的颗粒运动轨迹, 其计算表达式如下:

${\varepsilon _{\rm{f}}} = 1 - \sum\limits_i {{\varepsilon _{{\rm{ps}},i}}} , $

式中, ${\varepsilon _{{\rm{ps}}, i}}$代表流体单元内第i个多孔球单位体积内的颗粒体积. 该模型克服了传统方法中当颗粒粒径接近网格尺寸时引起的计算不稳定性问题, 改善了颗粒-流体的相互作用, 并且在计算过程中, 把颗粒的体积考虑在内, 因此, 用该方法求解出的流场也更加精确.
将2.1节和2.2节两个模型以及多孔模型的控制方程写入接口程序, 进行编译, 最终通过动量方程中的动量源交换项实现双向耦合, 这样VOF-DEM耦合通过编好的用户自定义函数(UDF)进行数据通信, 实现欧拉双流体相和拉格朗日颗粒相的双向耦合.
整体模型的计算流程如上图1所示. 首先对流场和颗粒场进行初始化, 该过程通过CFD计算接口文件实现; 然后, 开始计算, 通过2.1节(1)式和(2)式迭代求解得到流场的速度和力等信息, 求解(5)式得到关于自由液面的变化信息, 通过(6)式和(7)式计算流体的湍动能-耗散; DEM通过利用2.2节的(8)式和(9)式迭代计算获得颗粒的速度和位置等信息, 并进行更新; 接着通过判断收敛与否, 进行选择, 如果不收敛通过求解2.3节(17)式得到流体单元的空隙率, 继续前述流场的计算, 如此循环实现双向耦合, 互相交换数据, 直到收敛停止计算, 完成模拟.
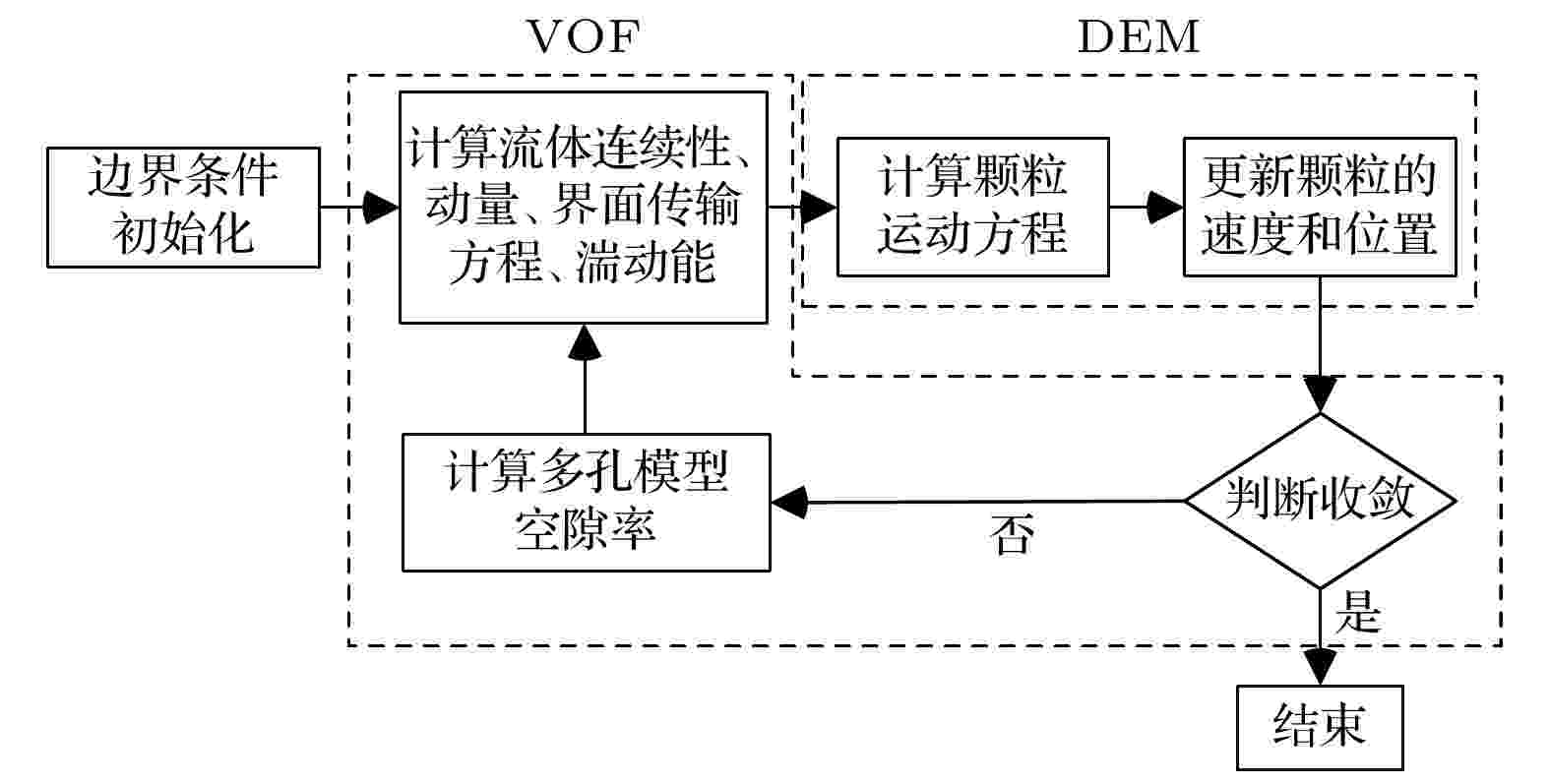图 1 VOF-DEM耦合计算流程图
Figure1. VOF-DEM coupling calculation flowchart.

2

-->

3.1.物理模型与网格划分

研究所选取的物理混合空间为带挡流板的半圆底容器, 混合执行构件为叶轮, 结构如图2所示, 具体物理参数如下: 直径T = 200 mm, 高度H = 3T/2, 液位高度h_l = T, 叶轮直径D = T/2, 桨叶长度L = 45 mm, 宽度W = T/10, 厚度t = 2 mm, 倾斜角为45°, 安装高度C = 93 mm, 搅拌轴直径d₁ = 14 mm, 底部进气口直径d₂ = 14 mm, 高度h_a = 4 mm, 挡流板高度h_b = 11 T/10, 宽度为T/10.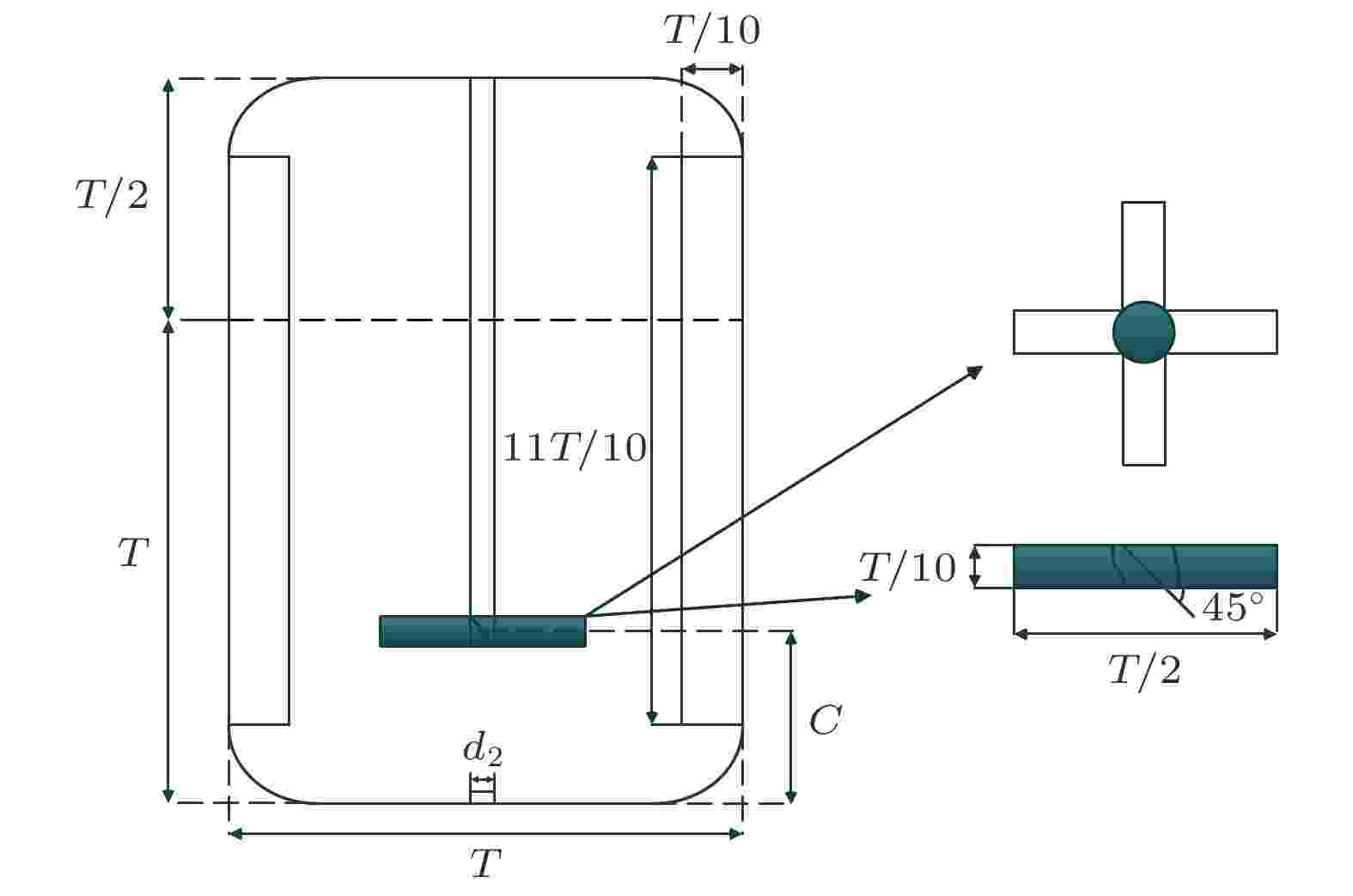
图 2 混合空间结构示意图
Figure2. Diagram of mixed space structure.

首先建立混合物理空间三维模型, 对流体域进行网格划分, 最终生成的网格如图3所示. 为了方便计算, 流体域被划分为包含混合叶轮的转子区域和除此以外的静子区域两部分. 然后对流体域进行离散化处理, 由于转子区域的变化梯度较大, 尤其是混合叶轮这种小尺寸, 强剪切区域变化梯度最大, 划分时要特别注意, 所以要进行局部网格的加密处理, 划分后的静子区域网格尺寸为7 mm, 转子区域网格尺寸为5 mm, 叶面网格尺寸进一步细化为3 mm, 进气口也进行适当的加密, 网格尺寸为3 mm, 划分网格后, 网格的正交质量保持在0.5以上, 最终用于计算的网格数目为31万.
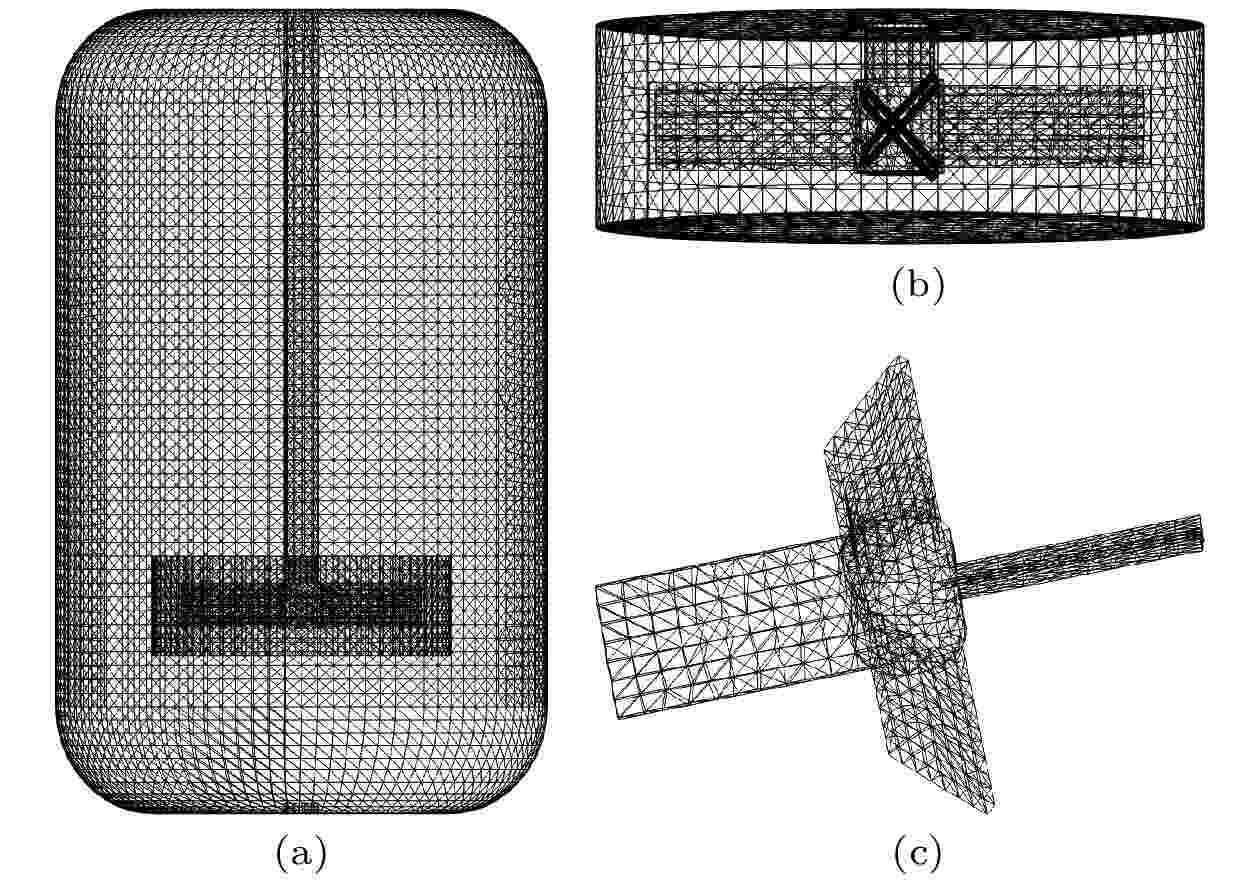图 3 网格划分　(a) 静子区域网格; (b) 转子区域网格; (c) 叶轮网格
Figure3. Grids division: (a) Grids of stator region; (b) grids of rotor region; (c) grids of impeller.

2 -->

3.2.边界条件及参数选择

混合过程模拟采用了瞬态的VOF模型计算, 选择显式的时间离散格式, 湍流模型使用标准的湍动能-耗散($k\text{-} \varepsilon $)模型, 该模型具有较高的物理可靠性, 可为混合湍流过程提供精确解, 近壁区域选择标准壁面函数. 混合容器顶部设置为压力出口边界条件, 容器壁面为无滑移壁面边界条件, 底部为充气管道, 并采用速度入口边界条件. 数值求解方法使用coupled方案, 该解法耦合了动量、能量及组分方程, 能比较快地得到收敛解, 动量离散格式、湍动能和湍动能耗散率离散格式均采用二阶迎风以获得精确的解^[29-31], 体积分数离散格式使用分段线性界面重构(piecewise linear interface construction, PLIC)算法, 这种方法是精度最高的一种^[24,29], 监视器收敛残差均为10^–6.
叶轮旋转模型常用到滑移网格(sliding-grid, SG)方法和多重参考系(multiple reference frames, MRF)方法. 其中, SG方法常用于瞬态模拟, 而MRF方法通常用于稳态模拟, 文献[32]采用两种方法对比得到的最终结果非常相似. MRF方法也能够用于瞬态仿真, 此种情况是以伪稳态方式进行计算, 与更准确、但更耗时的SG方法相比, 可节省大量计算机资源, 精度能满足多数场景的需要^[33-35]. 因此本次模拟采用瞬态MRF方法进行. 对于MRF方法, 需要将流体区域划分为内部动区域和外部静止区域两部分, 两部分通过交界面(interface)进行数据传递. 对于本研究所涉及的其他物理参数设置, 见表1.

参数	值
空气密度 ${\rho _{\rm{a}}}$/(${\rm{kg}} \cdot {{\rm{m}}^{{ - 3}}}$)	1
空气黏度 ${\mu _{\rm{a}}}$/(${\rm{Pa}} \cdot {\rm{s}}$)	1 × 10–5
水密度 ${\rho _{\rm{w}}}$/(${\rm{kg}} \cdot {{\rm{m}}^{{ - 3}}}$)	1000
水黏度 ${\mu _{\rm{w}}}$/(${\rm{Pa}} \cdot {\rm{s}}$)	0.001
颗粒密度 ${\rho _{\rm{p}}}$/(${\rm{kg}} \cdot {{\rm{m}}^{{ - 3}}}$)	1100
颗粒直径 ${d_{\rm{p}}}$/mm	1
颗粒数目 ${n_{\rm{p}}}$	10000
颗粒杨氏模量 ${Y_{\rm{P}}}$/${\rm{MPa}}$	1
颗粒泊松比 ${\nu _{\rm{P}}}$	0.25
壁面杨氏模量 ${Y_{\rm{w}}}$/${\rm{MPa}}$	70000
壁面泊松比 ${\nu _{\rm{w}}}$	0.3
滚动摩擦系数 ${\mu _{\rm{r}}}$	0.01
静摩擦系数 ${\mu _{\rm{s}}}$	0.5
恢复系数 ${e_{\rm{r}}}$	0.5
搅拌桨速度 $\omega $/(${\rm r} \cdot {\rm min }^{ - 1 }$)	400
CFD时间步 $\Delta {t_{\rm{CFD}}}$/${\rm{s}}$	$2 \times {10^{ - 4}}$
DEM时间步 $\Delta {t_{\rm{DEM}}}$/${\rm{s}}$	$2 \times {10^{ - 5}}$
耦合时间步 $\Delta {t_{{\rm{coupling}}}}$/${\rm{s}}$	$2 \times {10^{ - 4}}$

表1流体和颗粒特性设置
Table1.Characteristics settings of fluid and particle.

2 -->

3.3.网格无关性分析

网格的大小会直接影响数值模拟的结果, 一般情况下, 网格越小, 计算结果也越精确, 但是, 随之带来的是网格数量也越来越多, 需要更多的计算时间才能收敛, 给计算带来了很大的困难. 因此, 有必要进行网格独立性研究, 以确保计算误差在可接受的范围内, 得到准确的模拟结果. 本次以倾角45°的桨式叶轮进行网格无关性验证, 模拟转速为400 r/min时的混合流场, 使用了四种网格尺寸, 总网格数分别为219000, 311000, 425000, 661000, 考察网格数量对模拟结果的影响, 对5 s时槽内Z = 150 mm, Y = 0 mm, X从–100到100 mm的轴向速度场进行对比, 结果如图4所示.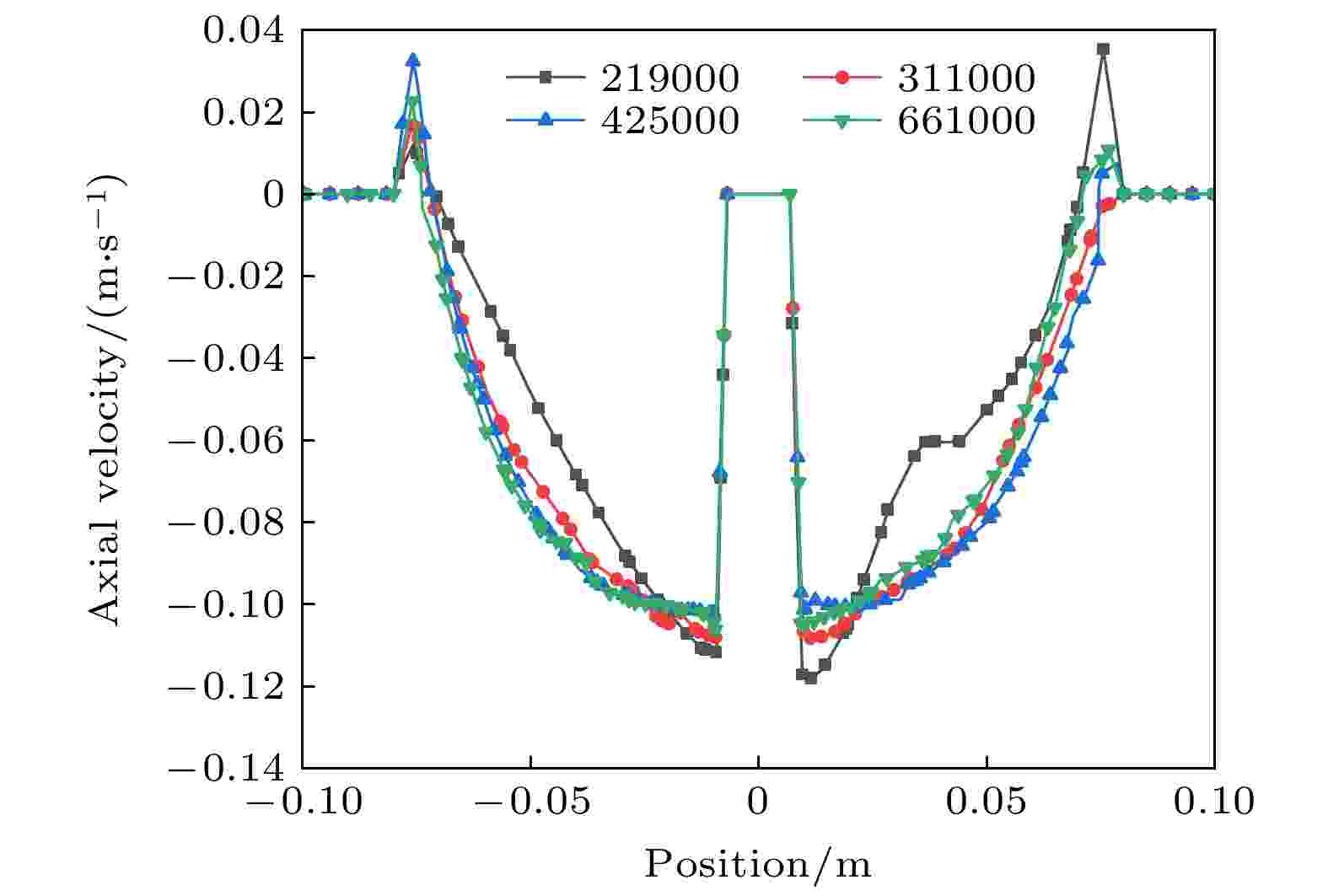
图 4 四种网格尺寸在t = 5 s时的轴向速度分布
Figure4. Axial velocity distribution of four grid sizes at t = 5 s

可以发现流场在不同位置的轴向速度具有相似的趋势, 但网格数量为219000时整体具有较大的误差, 而其他三种网格计算误差在5%以内, 满足网格独立性要求. 基于上述结果, 后面计算模型所采用的网格数量均为311000, 这样既减少了计算量, 又可以得到比较准确的结果.

如前所述, 气-液-固三相混合物理空间内部是一个复杂的湍流环境, 挡流构件的存在增加了搅拌速度下湍流场的无序性和非线性, 为了获得其中的流体-固体多相耦合和相间传质特性, 将深入研究对比不同充气条件下对混合空间内自由表面、流体流动和固体颗粒悬浮的影响. 在数值算例中, 颗粒直径均为1 mm, 颗粒数目均为10000, 且颗粒随机分布在混合容器的底部区域内, 在初始条件下仅受重力作用.
2

-->

4.1.对自由液面的影响

基于数值模拟的结果, 首先研究充气状态对自由液面的影响, 图5为t = 5 s时四种充气条件下混合空间内的实际自由液面图, 蓝色为自由液面的演化形态, 分别对应充气速度为0, 0.01, 0.05和1 m/s. 为了能够清晰地看出自由液面的变化, 隐藏了底部液体和颗粒, 只保留了自由液面.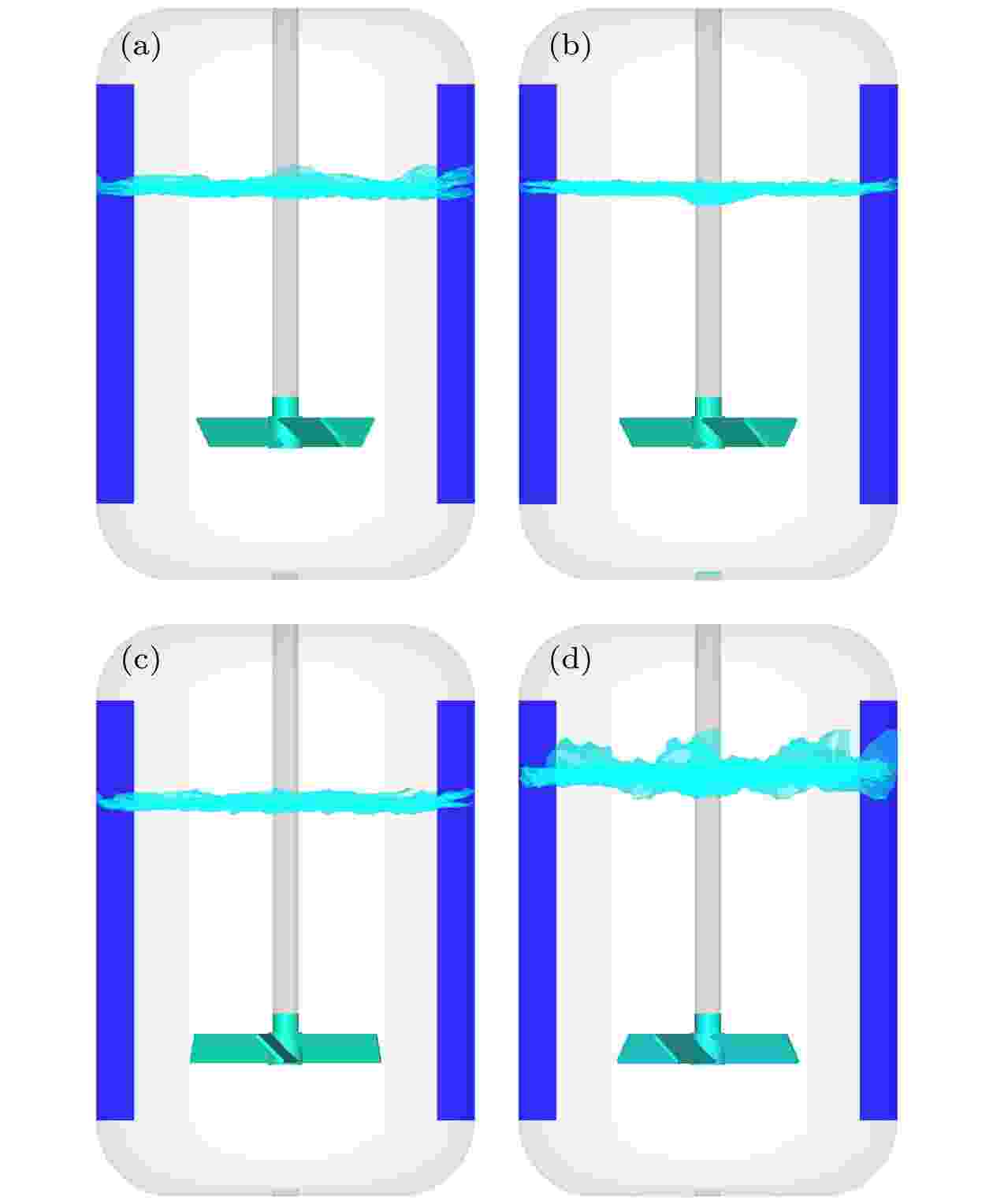
图 5 t = 5 s时四种充气条件下混合空间内的自由液面　(a) v = 0 m/s; (b) v = 0.01 m/s; (c) v = 0.05 m/s; (d) v = 1 m/s
Figure5. Free surface under four aeration conditions at t = 5 s: (a) v = 0 m/s; (b) v = 0.01 m/s; (c) v = 0.05 m/s; (d) v = 1 m/s.

通过图5(a)—(d)可以看出, 在图5(a)未充气的混合空间中液面存在小幅的波动, 因为底部搅拌对流场的扰动能量向上传输至自由液面时, 能量的衰减不足以对液面造成较大的扰动, 而这种轻微的波动主要是颗粒和液体的相互作用造成的; 对比之下, 充气速度v = 0.01和v = 0.05 m/s时, 如图5(b)和图5(c)时两者液面波动都很小, 显然传输的湍动能依然达不到自由液面的扰动阈值; 而当充气速度v = 1 m/s时, 其自由液面如图5(d)所示, 可以看出液面波动非常大, 尤其是挡流板之间的区域, 液面上升明显, 有漩涡的产生, 这主要是因为除了颗粒对液面的影响之外, 底部充气速度较大, 增加了湍流场的流体上冲动能, 对三相流系统造成了较大的扰动, 且气体上浮溢出造成了液面的不稳定, 进而有较大的振荡.
针对上述充气扰动液面的现象, 考虑与搅拌下流场的流动模式密切相关, 图6给出了不同充气条件下的切向速度矢量图. 从图6可以看出, 四种条件下挡流构件附近的切向速度都是该截面内最小的, 是因为挡流构件将流体的切向速度转换为了轴向速度. 而当高速旋转的流体与挡流构件接触时, 快速接触过程必然引起局部湍流涡团的耗散, 增加了流动模式的随机性, 故挡流构件附近的液面振荡相对明显. 同时, 通过对比可以发现, v = 1 m/s时的流体切向速度分布极不均匀并且最大, 较强的充气强度对底部分布的颗粒相起到扰动作用, 在搅拌速度和底吹作用下, 整个流场处于非线性湍流状态, 这也是引起自由液面漩涡和波动的主要原因; 而其他三种状态下的切向速度则相对较小, 其中 v = 0.05 m/s时的切向速度最均匀, 相对比较稳定, 其对应的自由液面也是最稳定的, 这也与文献[23]的结论相吻合.
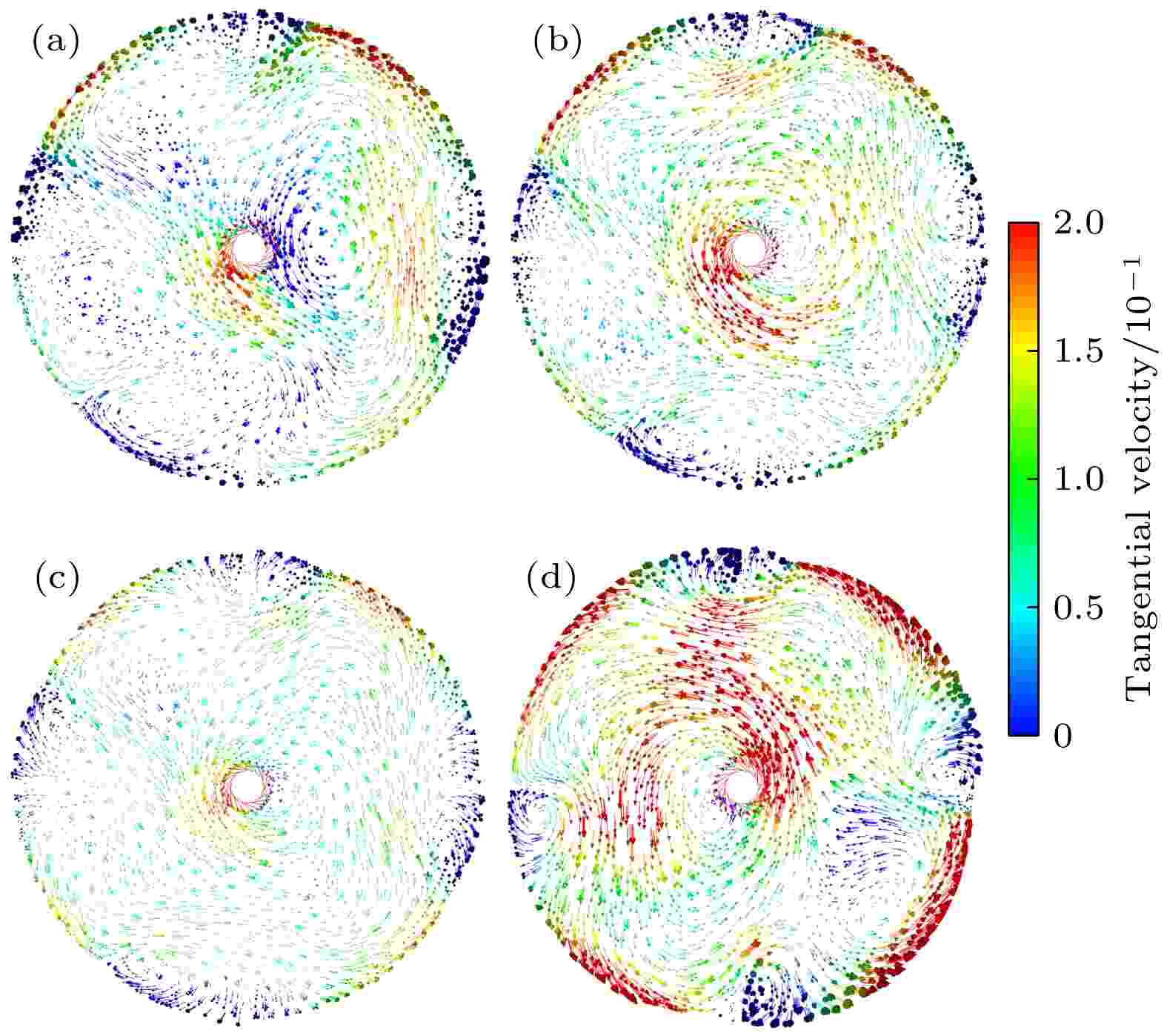图 6 t = 5 s时, 四种充气条件下混合空间内z = 0.15 m高度截面的切向速度矢量图　(a) v = 0 m/s; (b) v = 0.01 m/s; (c) v = 0.05 m/s; (d) v = 1 m/s
Figure6. Tangential velocity vector in height z = 0.15 m under four aeration conditions at t = 5 s: (a) v = 0 m/s; (b) v = 0.01 m/s; (c) v = 0.05 m/s; (d) v = 1 m/s.

通过与文献[22]关于自由液面的结果的对比可以发现, 本研究的混合容器虽然加装了挡流构件, 在不充气或者低充气速度时, 可以有效地消除混合过程中可能形成的漩涡的影响, 稳定混合空间内环境, 但是当充气速度过高时, 内部流场受到强烈扰动, 自由液面也会有大幅波动.
2 -->

4.2.对流体速度的影响

为了研究不同的充气状态对混合空间内流体速度的影响, 选取了t = 5 s时, 混合容器内径向位置r = 60 mm, 轴向高度从0到200 mm的速度分布情况, 如图7所示. 从图7可以看出, 最大速度出现在靠近叶轮的区域, 底部充气会使得出现最大速度的高度上移, 但并不是充气速度越大最大速度出现的位置越靠上, 四种流体速度分布出现最大速度的高度由低到高依次是充气速度为v = 0, v = 0.05, v = 0.01和v = 1 m/s时的混合空间. 上述现象主要原因为当轴向的充气速度介入流场时, 轴向动能和流场的切向动能发生了对冲能量耗散, 虽然流场的湍流随机性增加, 但流动的无序性对整个流场的总速度有所影响.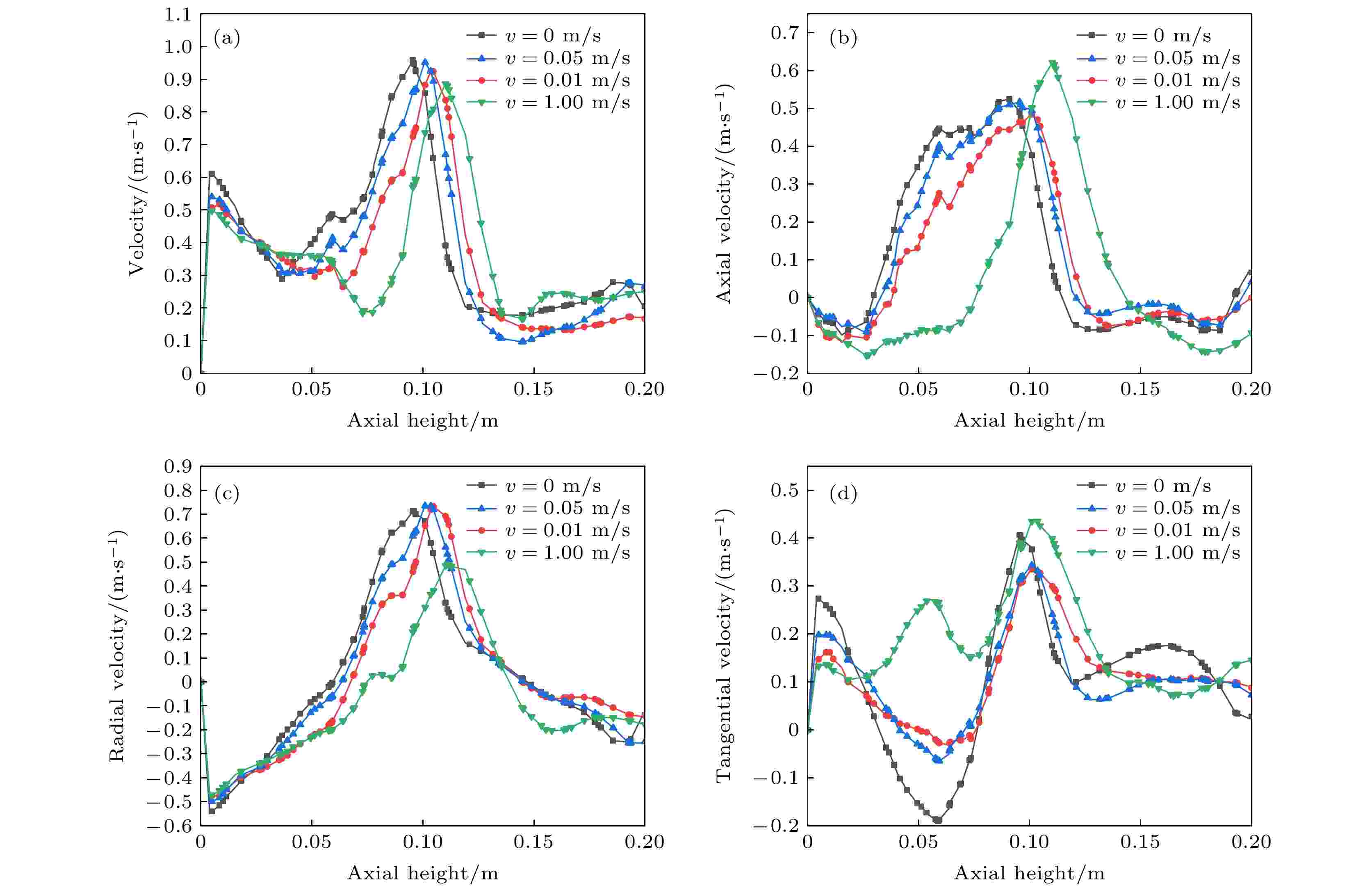
图 7 径向位置r = 60 mm处的轴向高度速度分布　(a) 总速度; (b) 轴向速度; (c) 径向速度; (d) 切向速度
Figure7. Axial velocity distribution at radial position r = 60 mm: (a) Total velocity; (b) axial velocity; (c) radial velocity; (d) tangential velocity.

从总速度、轴向速度和径向速度可以看出四种充气状态下的速度分布曲线趋势走向是相同的, 而对于切向速度, 在充气速度为v = 1 m/s的桨叶下方的流体切向速度方向和其他三种情况方向完全相反. 显然, 当充气速度足够大时, 气相对整个流场的流动模式造成较大的扰动, 剪切流动变得复杂, 增加了流场的湍流混沌特性. 此外还可以看出, 由于挡流构件的存在以及壁面的影响, 可以将切向速度转化为轴向速度和径向速度, 所以从图7可以看出切向速度的幅度要小于轴向速度和径向速度.
2 -->

4.3.对颗粒悬浮的影响

图8、图9、图10和图11是四种充气状态下混合空间内三相流的模拟计算结果, 截取了部分时刻的运动状态, 这些时刻基本包含了混合过程中的所有情形, 具有一定的代表性, 其中颗粒的颜色表示颗粒的速度大小. 可以很清楚地看到在t = 1 s时, 底部沉积的颗粒在桨叶旋转带动流体的作用下被卷吸起来. 初始状态时, 搅拌扰动流场, 增加了流场的切向流动和叶轮底部的轴向上升流运动, 颗粒以较小的速度向上升起.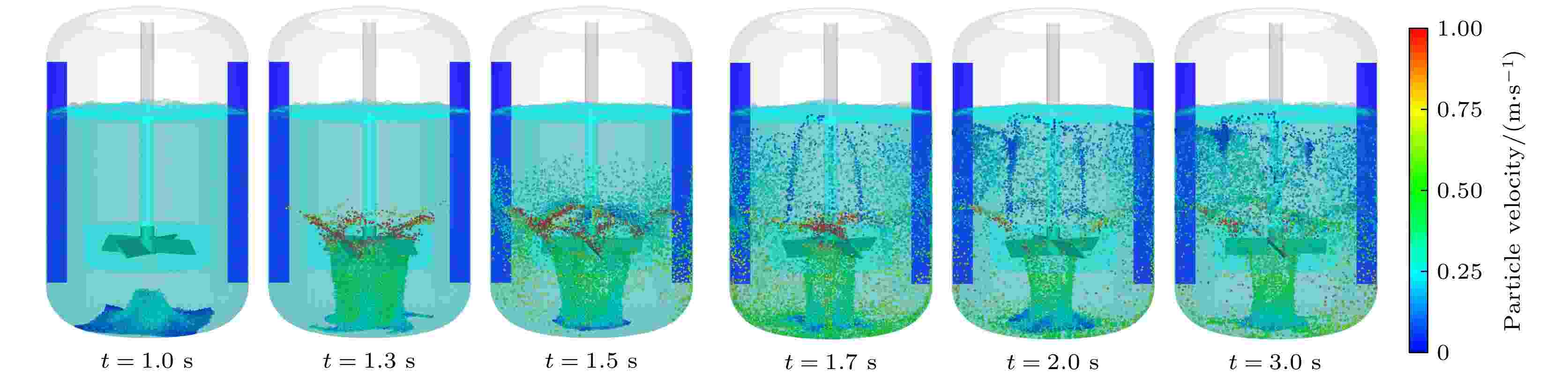
图 8 v = 0 m/s时不同时刻的三相混合系统模拟结果
Figure8. Simulation results of three-phase stirred system at different time when v = 0 m/s.

图 9 v = 0.01 m/s时不同时刻的三相混合系统模拟结果
Figure9. Simulation results of three-phase stirred system at different time when v = 0.01 m/s.

图 10 v = 0.05 m/s时不同时刻的三相混合系统模拟结果
Figure10. Simulation results of three-phase stirred system at different time when v = 0.05 m/s.

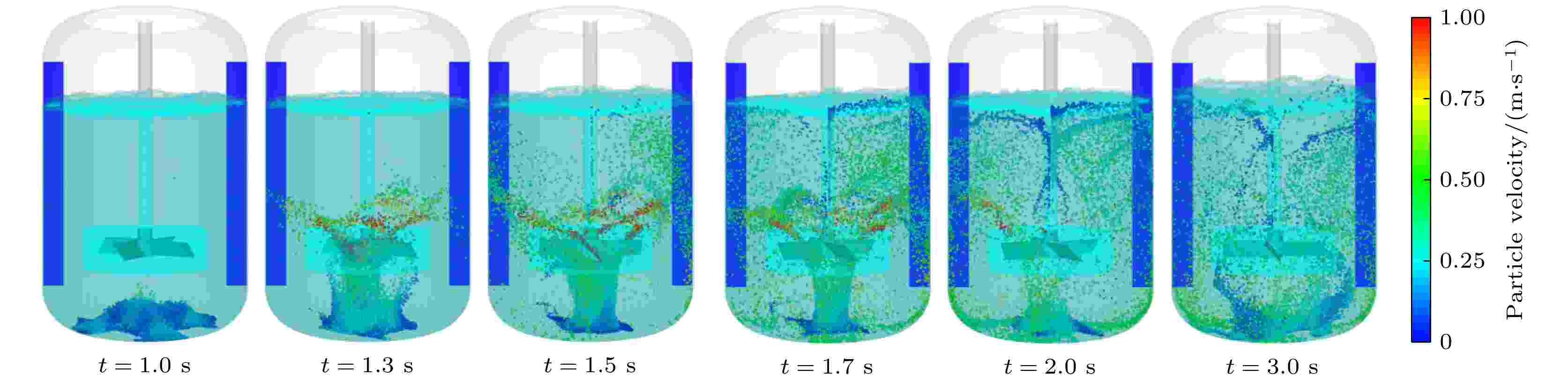图 11 v = 1 m/s时不同时刻的三相混合系统模拟结果
Figure11. Simulation results of three-phase stirred system at different time when v = 1 m/s.

在t = 1.3 s时, 颗粒群到达叶轮, 受到高速旋转的作用, 被桨叶打散高速向周围扩散, 同时可看出, 颗粒群在v = 0.01, 0.05和1 m/s要先于v = 0情况分散开. 这是因为底部吹气在初始状态就增大了流场的轴向剪切流动能量, 诱导流体的轴向速度增加, v = 1 m/s时最为明显, 如图7(b)所示. t = 1.5 s时, 颗粒受到流场离心力的作用下扩散到容器壁面和挡流构件, 在两者的作用下, 颗粒流动转变为上下两个方向的运动状态, 表明当旋转流场与挡流构件接触过程时, 流场以切向为主的流动模式遇阻, 切向速度流动转变为上下剪切流动模式. 剩余流场的湍动能推动部分颗粒作上升流运动, 另一部分颗粒在重力作用向下流动, 壁面附近的湍动能难以对这部分颗粒提供足够的驱动动能.
随着时间的推移, 在t = 1.7 s时, 颗粒到达自由液面附近, 受到液面振荡的作用, 分散至容器的各个位置; 随后的t = 2和3 s时, 除v = 1 m/s的混合空间外, 其他变化已经不明显, 趋于稳态, 可以看出, 速度最大的颗粒分布在叶轮附近, 具有较高速度的颗粒分布在容器的下部, 而越靠近液面处, 颗粒速度越低, 到达液面时速度几乎为0, 此区域的颗粒群对气-液交界面的冲击非常微小, 颗粒停止上升, 只有挡流构件附近的颗粒群受到局部流体漩涡的裹挟作用, 会继续上升, 形成局部的凸液面. 此外, 上下两股流动实现了循环, 对颗粒分散效果有良好的促进作用, 且除v = 1 m/s外, 其他都相对稳定, 颗粒分布都是对称的.
从整个时间段上三相流的模拟计算结果对比, 还可以看出底部充气使得下部伞状颗粒群伞柄处要比未充气状态的细, 而v = 1 m/s工况下, 随着混合的进行颗粒受到的作用不均匀, 底部伞状颗粒群会被破坏, 运动状态也更加复杂, 液面波动也会更加剧烈, 难以实现稳态.
为了更准确、更直观地描述颗粒分布的均匀性, 引入相对标准偏差(relative standard deviation, RSD)表征颗粒在液相中的分散效果^[36], 在这项工作中, 将液体覆盖的区域分为12个部分(3 × 1 × 4), 即12个等体积的采样空间. 通过多个样本空间内颗粒数目的相对标准偏差随时间的变化作为评价指标. 其评价公式如下:

$\sigma \!=\! \sqrt {\frac1{{n \!-\! 1}} {{\sum\limits_{i = 1}^n {{{\left( {{X_i} - {X_{\rm{avg}}}} \right)}^2}} }}},\;\;{\rm{RSD}} \!=\! \frac{\sigma }{{{X_{\rm{avg}}}}} \!\times\! 100{\text{%}} , $

其中${X_i}$是采样空间i中的颗粒数量, ${X_{\rm{avg}}}$是${X_i}$的平均值, n为划分的采样空间的数量. 从上面的相对标准偏差RSD评价公式可以看出, RSD越小代表颗粒在计算区域内的颗粒悬浮效果越好. 图12绘制了底部不同充气工作条件下的RSD随时间的变化曲线.
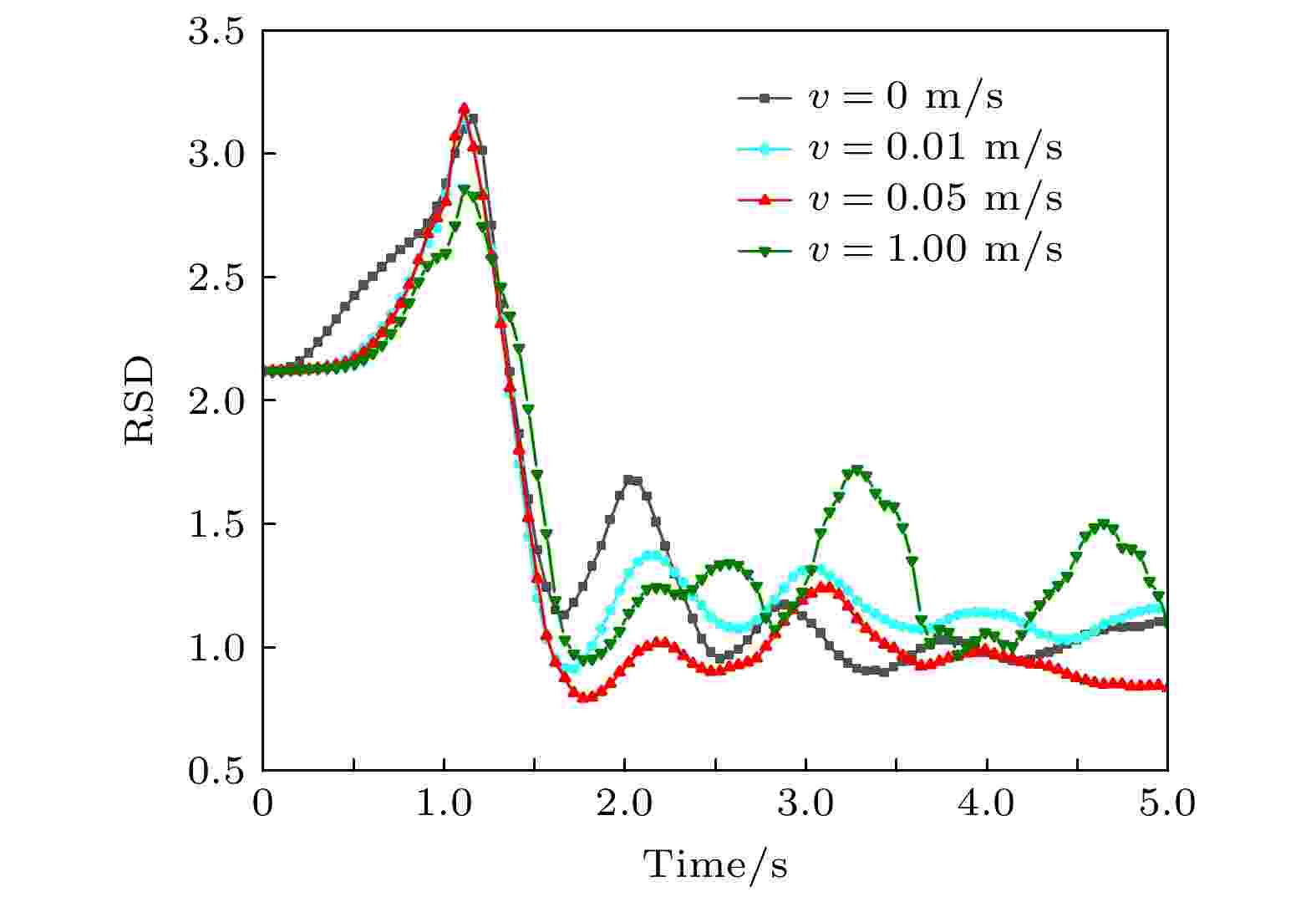图 12 不同充气工作条件下的RSD随时间的变化
Figure12. RSD changes with time under different aeration conditions.

从图12可以看出, 在混合容器刚开始工作的一段时间内由于颗粒沉积在底部, 随时间移动较缓慢, RSD的数值较大, 颗粒分布极不均匀, 所以RSD曲线有一段上升趋势, 这段时间里底部充气的混合空间由于气体的作用使得一部分颗粒上升较快, 相对未充气的颗粒率先上浮, 所以RSD值要低一些. 随着混合过程的持续进行, 颗粒到达叶轮高度, 在叶轮的作用下移动速度加快, 逐渐分散到混合空间的各个区域, RSD曲线呈现快速下降趋势, 然后趋于小范围的来回振荡达到准稳态状态. 从图12也可以发现, 充气速度为v = 0, 0.01和0.05 m/s的混合空间RSD曲线趋于平缓且处于较低的值, 代表了颗粒分布状态趋于稳定, 其中v = 0.05 m/s时, 颗粒分散效果最好, v = 0和0.01 m/s次之; 但是充气速度v = 1 m/s的混合空间的RSD曲线振荡幅度较大, 因为充气速度过大导致混合空间内局部的不稳定性增加, 一定程度上影响了颗粒的悬浮效果. 综上所述, 可以得出选择适当的充气速度可以提升容器内的颗粒悬浮效果, 提高颗粒分布的均匀性; 而如果充气速度过大则会导致混合系统的不稳定性, 不利于颗粒悬浮.

研究具有强剪切过程的气-液-固三相流混合过程机理与流场分布, 具有重要的科研价值和工程应用意义. 针对上述问题, 提出了一种研究气-液-固三相流混合建模与求解方法, 基于VOF-DEM模型建立了流体和颗粒的动力学模型, 进行求解, 并将其应用在了三相流的混合过程数值模拟中, 通过结果分析, 总结得到了以下结论:
1) 对自由液面的变化分析表明, 以较小的速度向带挡流构件的混合空间内部充气可以降低液面的波动幅度, 反之, 如果充气速度过大则会导致液面波动加剧;
2) 对流体的速度分析表明, 底部充气会使得轴向位置上出现最大速度的位置上移, 但并不是充气速度越大, 该位置就越高, 此外挡流构件和壁面的存在可以将流体的切向速度转化为轴向和径向的速度;
3) 就颗粒悬浮而言, 选择适当的充气速度可以提升混合空间内的颗粒悬浮效果, 有利于相间传质, 提高颗粒分布的均匀性, 本次模拟四种状态下, v = 0.05 m/s时颗粒悬浮效果最佳, 而如果充气速度过大则会导致混合系统的不稳定性, 不利于颗粒悬浮.
基于VOF-DEM模型的三相流混合系统具有高度的复杂性, 本文在此方面进行了有益的尝试. 在理论方面可为VOF-DEM模型的耦合、多相流系统的建模与求解方法等方面研究提供参考; 在技术方面, 可为工业混合过程等领域提供更多的技术解决方案, 具有较好的工程应用前景.