摘要:超疏水表面上液滴因聚并诱导而引起的自弹跳行为具有巨大的潜在应用价值, 因此有关问题引起了广泛关注. 目前液滴的物性参数对其自弹跳特性的影响却鲜有报道. 本文数值模拟了不同的液体物性参数下液滴的聚并自弹跳行为, 并利用灰色关联法研究了物性参数变化分别与液滴跳起时的真实弹跳速度及液滴和表面的真实接触时间的关联程度. 在无量纲的时间条件下, 液滴的聚并自弹跳的动力学特性仅受Oh数的影响. 在真实的时间条件下, 黏度变化与液滴聚并所需的真实时间无关, 而减小密度比会同时减少聚并过程和跳起过程中所需的真实时间. 无量纲的弹跳速度随着Oh数的增大而减小, 而减小黏度和密度都会增加液滴跳起时的真实弹跳速度. 根据灰色关联度的计算结果可知, 黏度的变化与真实弹跳速度的关联性更高, 密度的变化与真实接触时间关联性更高.
关键词: 物性参数/
液滴自弹跳/
灰色关联分析/
超疏水表面

English Abstract

全文HTML

--> --> -->

在滴状凝结过程中, 具有较低的固-液黏附力的超疏水表面上微尺度的液滴能因聚并诱导而发生自推进式的跳离表面行为^[1-5]. 液滴聚并后释放的过剩表面能可以转化为弹跳所需的动能, 促使聚并后的液滴在不借助外力(甚至可以忽略重力影响)的条件下能自发地跳离冷凝表面. 近年来的研究发现, 聚并后液滴自弹跳行为在强化滴状冷凝换热^[6-8]、自清洁^[9-11]、防冰^[12]和热点冷却^[13]等方面具有巨大的潜在应用前景, 因此相关问题受到了广泛的关注.
Boreyko和Chen^[1]在具有微纳米二级结构的超疏水表面上进行冷凝实验时, 首次发现微米尺度的两个液滴在聚并后可以跳离表面这一现象. 他们将这一过程分为初始成核、固定聚并和移动聚并这三个阶段, 并从能量守恒的角度解释了液滴聚并自弹跳这一行为: 聚并后释放的过剩表面能可以转化为弹跳所需的动能. 实验结果表明, 竖直的真实弹跳速度(有量纲的物理量)随着液滴半径的增大而先增大后减小, 而基于毛细-惯性尺度定律(capillary-inertial scaling law)下的无量纲弹跳速度的变化趋势则是先增大后保持稳定. 随后, Liu等^[14,15]利用莱登弗罗斯特表面, 实验测量了接触角为180°的液滴的聚并自弹跳行为, 确定了其基于毛细-惯性尺度定律下的无量纲弹跳速度约为0.2. 同时, 利用相场方法的数值模拟研究得到的弹跳速度结果与实验结果相符合. 他们依据质心处的弹跳速度的变化趋势而将整个过程细分为四个阶段, 并且解释了聚并后液滴能跳起的关键: 扩展的液桥必须撞击到超疏水表面上. 除了相场方法外, 格子玻尔兹曼方法^[16-19]和流体体积法(volume of fluid method, VOF)^[20-25]均可被应用于模拟液滴的聚并自弹跳行为. 另外, 许多****利用分子动力学方法^[26,27]证明纳米尺度的两个液滴在聚并后也能跳起.
相对于两个半径相等的液滴, 非等径的两个液滴的初始表面能更小^[21], 并且质量的非对称分布也会导致液滴在聚并后具有明显的旋转运动^[19,20-22], 因此半径比的存在会降低弹跳速度. 除了尺寸和半径比外, 其他因素如表面结构^[18,25,27]、液滴数量^[24,28]和接触角^[21-23,29]等也会对液滴的自弹跳速度有一定的影响.
由于液滴的自弹跳行为存在于气-液两相系统中, 因此流体的物性参数是不可忽视的. 空气物性参数的数值要远小于液滴物性参数的值, 所以空气的黏度和密度对液滴的弹跳速度的影响极小^[16]. 然而, 目前与液滴有关的物性参数的影响的研究仍鲜有报道, 没有引起重视, 甚至在一些文献中都无提及气液的相关物性值. 在考虑数值方法的有效性、广泛性及物性参数的值可大范围变化等因素后, 本文选用VOF方法数值模拟两个液滴之间的聚并自弹跳行为. 此项工作不仅揭示了液滴的不同物性参数对其聚并自弹跳特性的影响, 更利用灰色关联方法首次给出物性参数的变化分别与液滴跳离表面时的真实弹跳速度及液滴与表面之间的真实接触时间的远近关联程度, 为后续的相关研究提供思路和理论基础.

2

-->

2.1.模型介绍

两个半径r = 40 μm的液滴静止位于接触角为180°的超疏水表面上, 彼此相切. 计算域是一个长宽高分别为8r, 8r和6r的长方体, 底部的超疏水表面为无滑移壁面, 其他边界被指定为压力出口条件, 如图1所示. 为了减少收敛时间和节省计算资源, 在液滴内部和周围的核心区域采用细的结构化网格, 远离液滴的其余区域采用非均匀的结构化网格. 利用开源软件包OpenFOAM中的VOF方法^[21], 数值模拟了超疏水表面上液滴的聚并自弹跳行为.
图 1 计算域的边界条件与网格
Figure1. Boundary conditions and grids of computational domain.

在VOF方法中, 相分数α用于表示体积分数, 取值在0到1之间. 例如, α = 0时代表气体, α = 1时代表液体, 当α在0和1之间时, 表示气-液界面. 流体性质由下式给出:

$\rho =\alpha {\rho _{\rm{l}}} + (1 - \alpha ){\rho _{\rm{g}}}, $

$\mu =\alpha {\mu _{\rm{l}}} + (1 - \alpha ){\mu _{\rm{g}}}, $

其中ρ是密度, μ是动力黏度, 下标l和g分别是指液体和气体. 连续性和Navier-Stokes方程为

$\nabla \cdot {{U}}=0, $

$\begin{split}&\frac{{\partial \left( {\rho {{U}}} \right)}}{{\partial t}} + \nabla \cdot (\rho {{UU}}) \\=\;& \nabla \cdot \left[ {\mu \left( {\nabla {{U}} + {\nabla ^{\rm{T}}}{{U}}} \right)} \right] - \nabla p + \rho g + {{{F}}_{\rm{\sigma }}}, \end{split}$

其中U是速度矢量, p是压力场, g是重力加速度. 表面张力的计算如下所示:

${F_{\rm{\sigma }}}=\sigma k\nabla \alpha, $

其中σ是表面张力系数; k是自由表面的平均曲率, 其计算公式为

$k = - \nabla \cdot {{n}}. $

另外, 界面法向向量n可以近似为

${{n}} = \frac{{\nabla \alpha }}{{\left| {\nabla \alpha } \right|}}. $

在求解过程中, 加入了人工压缩项α(1－α), 使得两相的界面可以保持尖锐. 相方程为

$\frac{{\partial \alpha }}{{\partial t}} + \nabla \cdot (U\alpha ) + \nabla \cdot \left[ {{U_{\rm{r}}}\alpha (1 - \alpha )} \right] = 0, $

式中U_r是两相的相对速度,

${U_{\rm{r}}}={{n}}\min \left[ {{C_\alpha }\left| U \right|,\max \left( {\left| U \right|} \right)} \right], $

其中C_α是一个可调整的系数, 在我们的算例中默认值为1.
2 -->

2.2.无量纲分析

液滴的真实弹跳速度取质心处垂直于平面的法向速度的加权平均值:

${U_{\rm{j}}} = {{\displaystyle\int_\theta {\alpha \nu {\rm{d}}\theta } }}\bigg/{{\displaystyle\int_\theta {\alpha {\rm{d}}\theta } }}, $

其中v是垂直于平面的法向速度, θ为整个计算域. 定义的无量纲弹跳速度U ^*和无量纲时间t^*如下所示:

${U^{*}} = {{{U_{\rm{j}}}}}/{{{U_{{\rm{ci}}}}}}~{\text{和}}~{t^*} = {t}/{{{\tau _{{\rm{ci}}}}}},$

其中依据毛细-惯性尺度定律而定义的特征速度U_ci和特征时间尺度τ_ci分别为^[1]

${U_{{\rm{ci}}}} = \sqrt {\frac{\sigma }{{{\rho _{\rm{l}}}r}}}~ {\text{和}}~{\tau _{{\rm{ci}}}} = \sqrt {\frac{{{\rho _{\rm{l}}}{r^3}}}{\sigma }}.$

此外, 影响液滴动力学特性的参数有很多, 包括Bond数、Ohnesorge数、Weber数、气液黏度比和密度比, 分别为

$\begin{split}&Bo = \frac{{{\rho _{\rm{l}}}gr_{\rm{1}}^{\rm{2}}}}{\sigma },~\;Oh = \frac{{{\mu _{\rm{l}}}}}{{\sqrt {{\rho _{\rm{l}}}{r_1}\sigma } }},\;\\&We = \frac{{{\rho _{\rm{l}}}U_{{\rm{ic}}}^2r}}{\sigma },~\;\mu = \frac{{{\mu _{\rm{l}}}}}{{{\mu _{\rm{g}}}}}~{\text{和}}~\rho = \frac{{{\rho _{\rm{l}}}}}{{{\rho _{\rm{g}}}}}.\end{split}$

取温度为20 ℃时对应的液滴的物性参数^[21,25], 具体详见表1. 液滴的尺寸非常小^[16,22], 可以忽略重力的影响, 即Bo = 0. 在参考速度选取为特征速度后We = 1, 毛细效应和惯性效应的影响等同, 因此不必考虑表面张力变化带来的影响. 本文中所有算例的Oh值都很小(最大不超过0.04), 满足液滴跳起的要求^[14,22]. 最后, 重点考虑了黏性效应和惯性效应对液滴的聚并自弹跳行为的影响.

温度T/℃	表面张力系数σ/(N·m–1)	液体密度ρl/(kg·m–3)	液体黏度μl/(Pa·s)	气体密度ρg/(kg·m–3)	气体黏度μg/(Pa·s)
20	0.072	998	1.071 × 10–3	1.19	1.8 × 10–5

表1流体物性参数
Table1.Physical parameters of fluids.

由于液滴的质量分布对称, 故质心是在竖直方向上发生变化, 因此动能可由真实弹跳速度计算得到:

$\Delta {E_{\rm{k}}} \approx \frac{4}{3}{\rho _{\rm{l}}}{\rm{\pi}} {r^3}U_{\rm{j}}^2.$

聚并过程中释放的过剩表面能?E_s可由液滴的表面积计算得到:

$\Delta {E_{\rm{s}}} = {E_0} - {E_{\rm{s}}} = 8{\rm{\pi}} {r^2}\sigma - A\sigma, $

其中E₀为初始时刻两个液滴的表面能, E_s是跳起时刻的液滴表面能, A为跳起时刻的液滴表面积. 由于基底为超疏水表面且接触角为180°, 故黏附功的影响可忽略. 根据能量守恒定律, 黏性耗散能E_vis可近似等于过剩表面能?E_s与动能?E_k之差:

${E_{{\rm{vis}}}} = \int_0^t {\int_V {\phi {\rm{d}}V{\rm{d}}t} } \approx \Delta {E_{\rm{s}}} - \Delta {E_{\rm{k}}}, $

其中黏性耗散函数?为

$\begin{split}\phi =\;& \mu \left[ 2{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}^2} + 2{{\left( {\frac{{\partial v}}{{\partial y}}} \right)}^2} + 2{{\left( {\frac{{\partial w}}{{\partial z}}} \right)}^2} \right.\\&+ {{\!\left( {\frac{{\partial v}}{{\partial x}}\! + \!\frac{{\partial u}}{{\partial y}}} \right)}^2}\!+ \!{{\left( {\frac{{\partial w}}{{\partial y}} + \frac{{\partial v}}{{\partial z}}} \right)}^2} \!+\! {{\left( {\frac{{\partial u}}{{\partial z}}\! +\! \frac{{\partial w}}{{\partial x}}} \right)}^2} \\&\left.- \frac{2}{3}{{\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right)}^2} \right]. \\[-15pt]\end{split}$

最后对能量项进行无量纲化, 即:

${E^*} = \frac{{{\rm{Energy}}\;{\rm{term}}}}{{\sigma {r^2}}}. $

2 -->

2.3.结果验证

使用多套网格(核心区域的网格尺寸分别为1, 1.25, 1.5, 2, 2.5和3 μm)模拟了文献[25]中的相同算例(液滴半径为40 μm), 得到的最大弹跳速度的结果如图2所示. 当网格尺寸为1, 1.25和1.5 μm时, 最大真实弹跳速度分别为0.2648, 0.2661和0.2573 m/s (对应的最大无量纲弹跳速度U*分别为0.197, 0.198和0.192). 这3个结果全部与文献[25]的模拟结果0.2686 m/s非常吻合, 同时也均符合毛细-惯性尺度定律^[14,15]的相关结论(无量纲值约为0.2). 因此, 为了节省计算资源且具有良好的界面分辨率, 所有算例选取了核心区域尺寸为1.25 μm的这套网格(网格总数约为450万).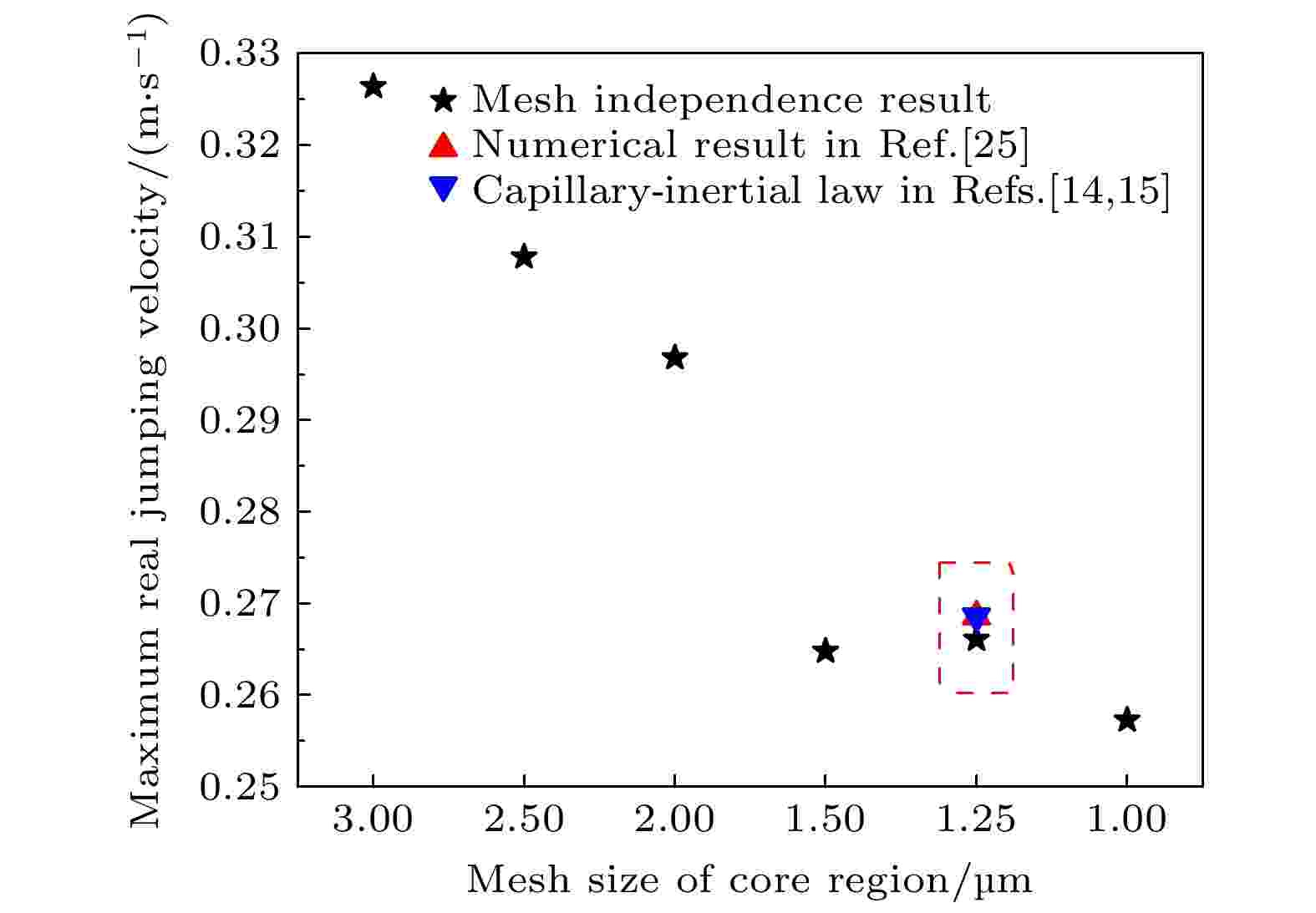
图 2 不同网格尺寸条件下的最大真实弹跳速度
Figure2. Maximum real jumping velocity with different mesh sizes of core region.

2

-->

3.1.黏性效应对聚并自弹跳行为的影响

在保持空气黏度和气-液密度比不变、只改变液滴的黏度的情况下, 不同黏度比时液滴的聚并自弹跳过程如图3所示. 在聚并开始阶段, 在表面张力的作用下两个液滴之间会形成液桥(见图3(a)、图3(f)和图3(k)), 之后液桥快速扩张(见图3(b)、图3(g)和图3(l)). 随后, 表面张力迫使两个液滴的外侧具有较大曲率的部分逐渐收缩(见图3(c)、图3(h)和图3(m)); 与此同时, 仍在快速扩张的液桥将会撞击下方的超疏水表面. 由于液桥的扩展会对表面进行撞击, 表面提供的反作用力迫使液滴向下运动的部分转而向上运动, 在此情况下液滴具有向上运动所需的动能(见图3(d)、图3(i)和图3(n)). 当液滴底部的三相接触线(在液桥撞击平面的过程中产生的)减小为0时, 才发生弹跳行为. 但是从图3(e)、图3(j)和图3(o)可以看出, 具有较小黏度的液滴更容易跳起. 跳起的液滴在空中振荡, 做减速运动. 在液滴界面的曲率变化程度较小时(如图3中t^* = 1.309之前), 改变液滴黏性对液滴界面的动力学演变影响较小. 但随着界面变化程度的增大, 黏性效应的影响也越来越强, 具有较大黏度的液滴的界面更为光滑.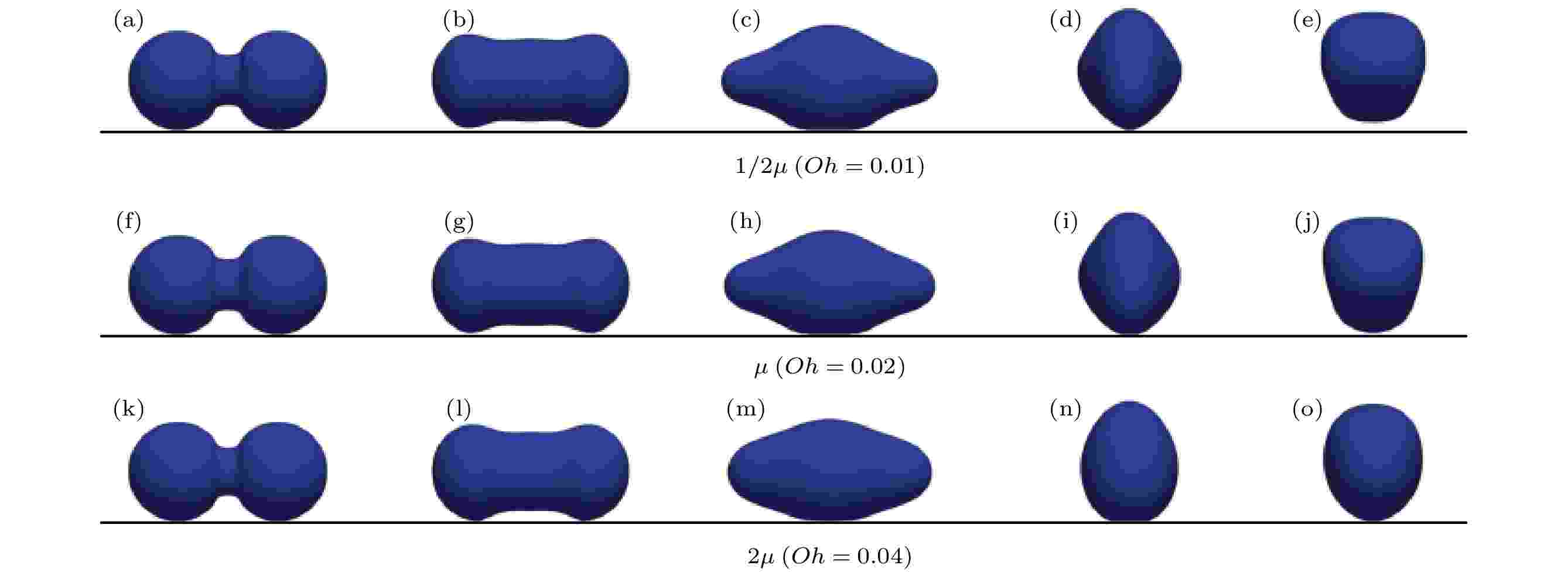
图 3 不同黏度比条件下液滴的聚并和自弹跳过程　(a), (f), (k) t^* = 0.168; (b), (g), (l) t^* = 0.604; (c), (h), (m) t^* = 1.309; (d), (i), (n) t^* = 2.686; (e), (j), (o) t^* = 3.257
Figure3. Coalescence and jumping process of droplets with different viscosity ratios: (a), (f), (k) t^* = 0.168; (b), (g), (l) t^* = 0.604; (c), (h), (m) t^* = 1.309; (d), (i), (n) t^* = 2.686; (e), (j), (o) t^* = 3.257.

依据液滴质心处的真实弹跳速度的变化趋势^[14], 整个弹跳过程可以分为4个阶段, 如图4(a)所示: 1) 弹跳速度从先下降后上升恢复至0; 2) 弹跳速度快速上升, 达到最大值; 3) 弹跳速度开始下降, 液滴跳离表面; 4) 跳起的液滴在空中做减速运动. 相邻两个阶段所间隔的时间在本文中被定义为这个阶段的持续时间. 例如, 第1个阶段的持续时间是指弹跳速度恢复至0的时刻与t^* = 0之差, 第2个阶段的持续时间是弹跳速度为最大值的时刻与前1个阶段(弹跳速度恢复至0)的时刻之差, 以此类推, 第3个阶段的持续时间为液滴跳起的时刻与前一个阶段(弹跳速度达到最大值)的时间节点之差. 由图4(b)可知, 黏性的变化基本不会改变两个液滴之间聚并所需的时间, 但增大液滴的黏度会显著增加第3个阶段(跳离表面阶段)所经历的持续时间. 图5中流场的矢量图也表明了这一点: 在图5(a)、图5(c)和图5(e)中, 随着黏度比的增大, 三相接触线收缩变缓慢了, 并且这也直接导致了黏度较小的液滴的三相接触线先收缩为0先跳起, 而黏度大的液滴三相接触线收缩慢后跳起, 如图5(b)、图5(d)和图5(f)所示.
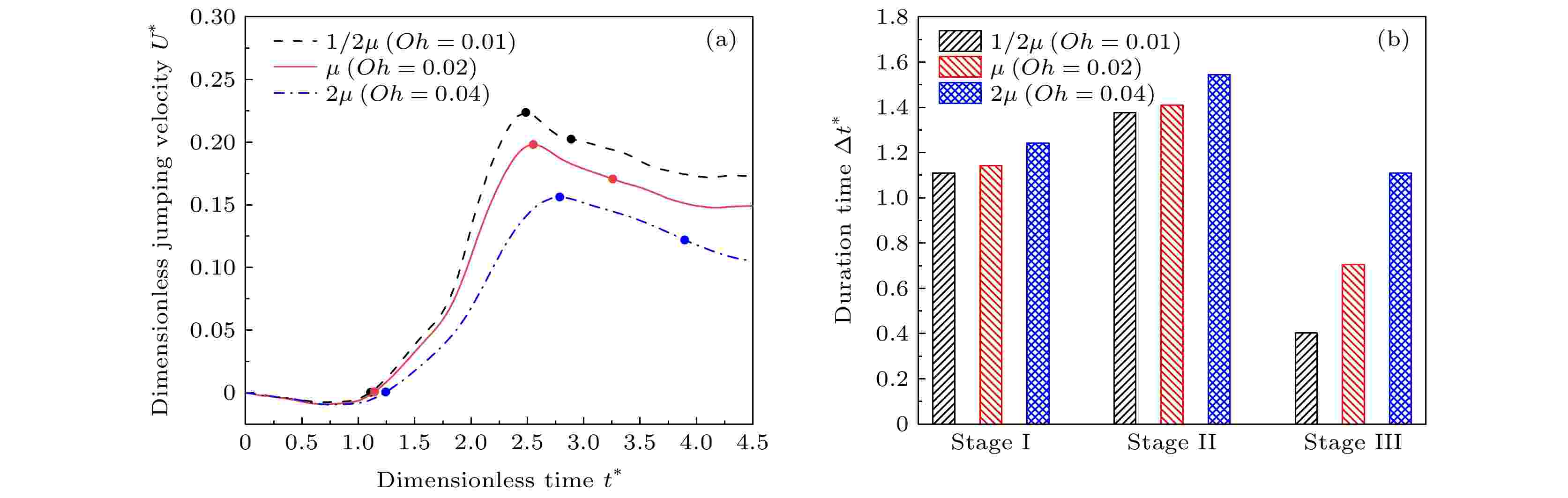图 4 (a) 不同黏度比时液滴质心处的无量纲弹跳速度; (b) 黏度变化对液滴跳离表面前所经历的各个阶段的无量纲持续时间的影响
Figure4. (a) Dimensionless jumping velocity of droplet with different viscosity ratios; (b) effects of the change of viscosity on the dimensionless duration of each stage prior to droplet jumping.

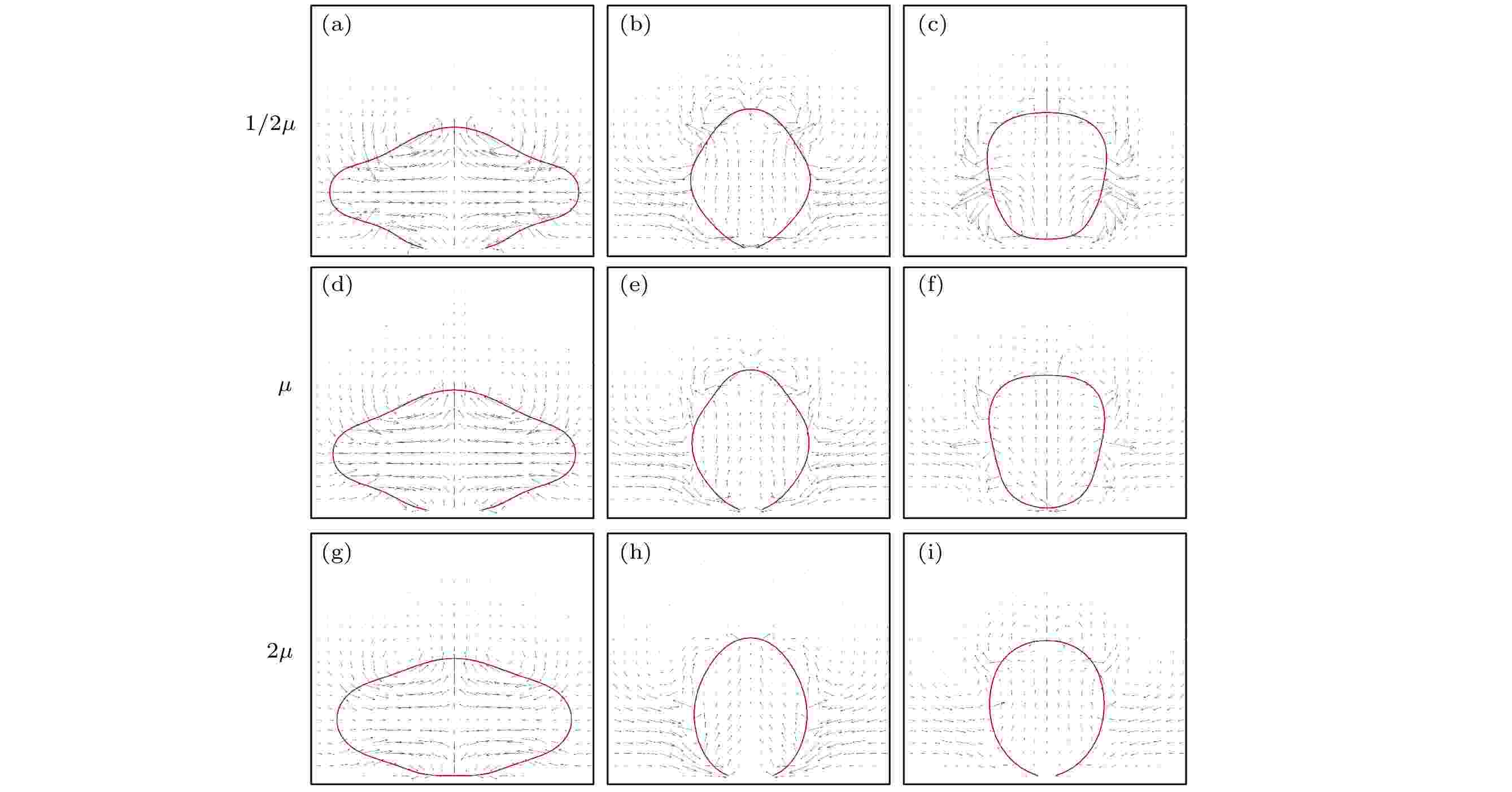图 5 不同黏度比条件下流场的速度矢量图　(a), (d), (g) t^* = 1.309; (b), (e), (h) t^* = 2.686; (c), (f), (i) t^* = 3.257
Figure5. Vectors of flow field with different viscosity ratios: (a), (d), (g) t^* = 1.309; (b), (e), (h) t^* = 2.686; (c), (f), (i) t^* = 3.257.

从图5可以看出, 黏度较小的液滴内部, 流动剧烈, 黏度的增大必然会带更大的内部流动阻力以及更多的能量损失. 由Oh数的定义可知, 其反映了黏性效应、惯性效应和毛细效应之间的影响程度. 增大黏度比会导致Oh数变大, 黏性效应越发明显, 不利于液滴的跳起, 甚至于当液滴的黏度过大时, 液滴完全可能因没有足够的动能而无法跳起.
无量纲弹跳速度随着液滴黏度的增大而逐渐减小. 从能量的角度来说, 虽然黏度的增大会让液滴的界面更为光滑, 从而有利于表面能的释放(图6(a)); 但这也会大大增加黏性耗散能(图6(b)). 由于总能量来源(过剩表面能)和能量损耗(黏性耗散能)同属一个数量级^[17], 最后支持液滴跳起的有效能量(动能)会随着黏性的增大而减少, 动能结果如图6(c)所示.
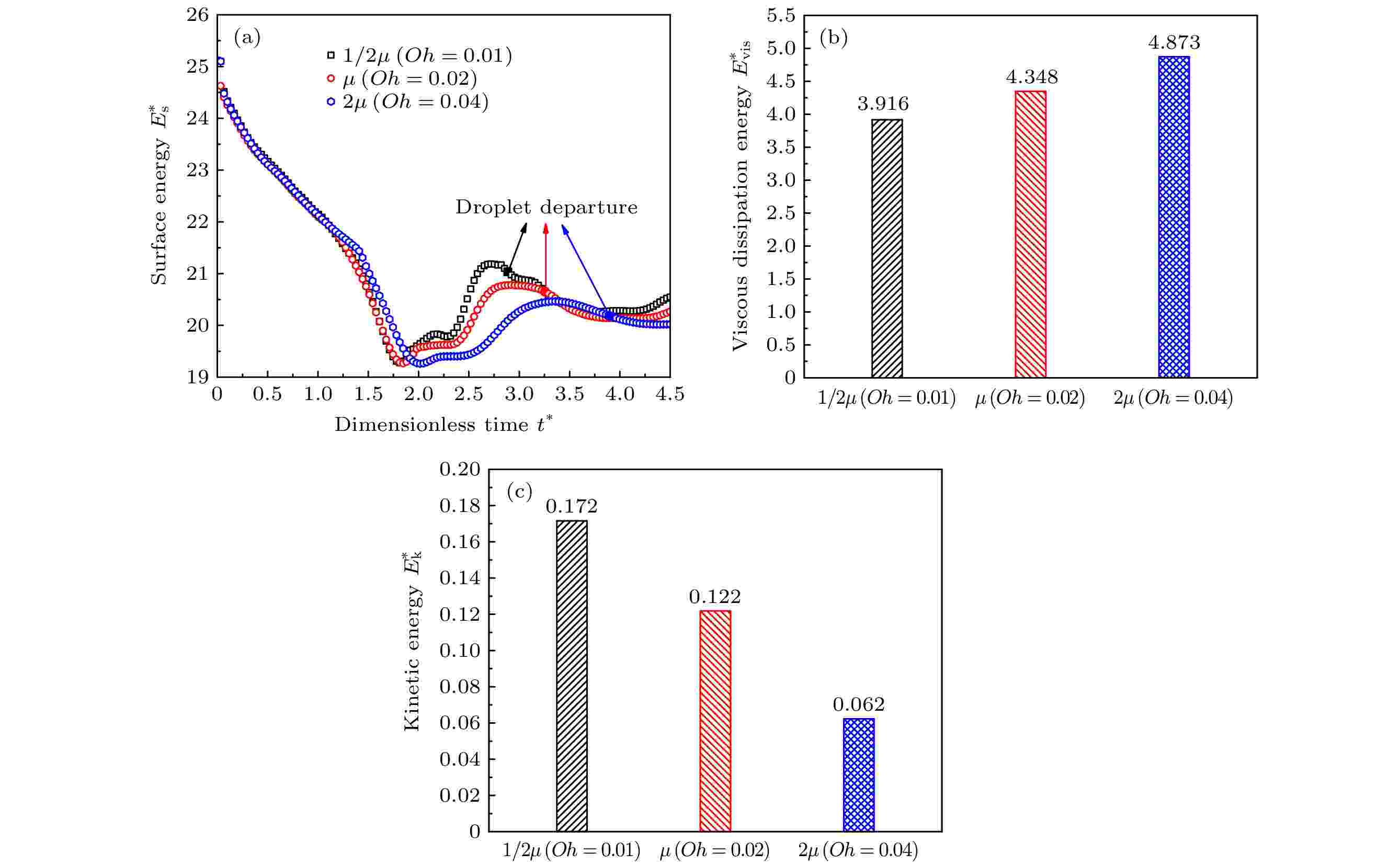图 6 (a) 不同黏度比时聚并自弹跳过程中表面能的变化; (b) 不同黏度比的液滴在跳起时具有的黏性耗散能; (c) 不同黏度比的液滴在跳起时刻具有的动能
Figure6. (a) Surface energy variation with different viscosity ratios during the coalescence and jumping process; (b) viscous dissipation energy of jumping droplets with different viscosity ratios at departure time; (c) kinetic energy of jumping droplets with different viscosity ratios at departure time.

2 -->

3.2.惯性效应对聚并自弹跳行为的影响

虽然图3和图7对应的分别是改变了黏性效应和惯性效应的结果, 但当Oh数保持相同时, 这意味着两者共同作用的综合效应也是不变的, 因此在相同的无量纲时间下液滴界面的动力学变化也相同, 这说明其变化特性由Oh数决定. 然而, 在有量纲的真实时间中, 惯性效应和黏性效应却有很大的不同之处, 主要体现为黏度对液滴的聚并时间无影响, 而密度却与聚并所需时间τ紧密相关^[30]: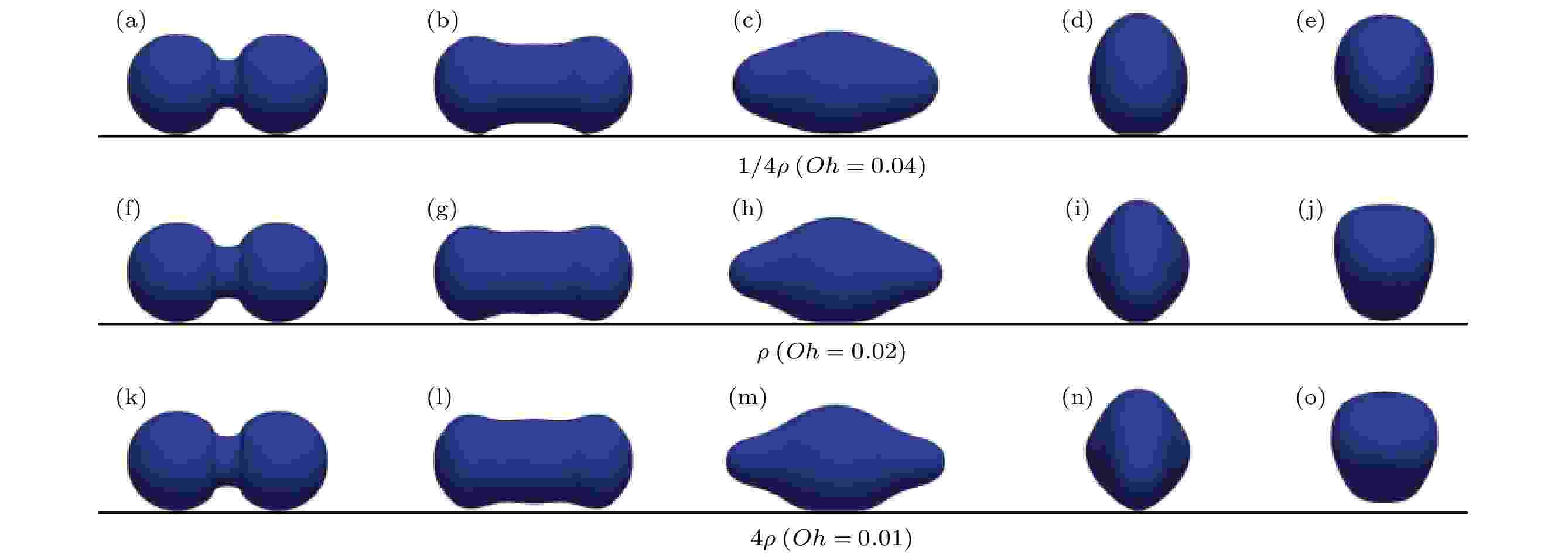
图 7 不同密度比条件下液滴的聚并和自弹跳过程　(a), (f), (k) t^* = 0.168; (b), (g), (l) t^* = 0.604; (c), (h), (m) t^* = 1.309; (d), (i), (n) t^* = 2.686; (e), (j), (o) t^* = 3.257
Figure7. Coalescence and jumping process of droplets with different density ratios: (a), (f), (k) t^* = 0.168; (b), (g), (l) t^* = 0.604; (c), (h), (m) t^* = 1.309; (d), (i), (n) t^* = 2.686; (e), (j), (o) t^* = 3.257.

$\tau =2{\tau _{{\rm{ci}}}} = 2\sqrt {{ {{\rho _{\rm{l}}}{r^3}} /\sigma }} . $

由于(19)式中聚并的真实时间τ与(12)式中时间尺度τ_ci是线性关系, 所以改变密度会改变聚并的真实时间, 但不会改变其所需的无量纲时间. 另外, 由此可知, 随着密度的减小, 事实上液滴聚并的真实时间会减小, 相应地也会更早地跳离表面. 在本节中, 虽然无量纲时间相同, 但是图7(k)—(o)过程中所需的真实时间却是图7(a)—(e)所需真实时间的4倍.
对于无量纲时间而言, 与黏性效应相同的是, 惯性效应也是仅改变液滴跳离表面的第3个阶段, 如图8(a)所示. 由于惯性的存在可以抵抗液滴的形变, 惯性较大的大液滴的“被动”抵抗变形的能力要大于小液滴, 因此从真实时间的角度来看, 改变密度会影响前3个阶段的真实持续时间, 随着密度的减小, 前3个阶段所需的真实时间也会减小, 如图8(b)所示.
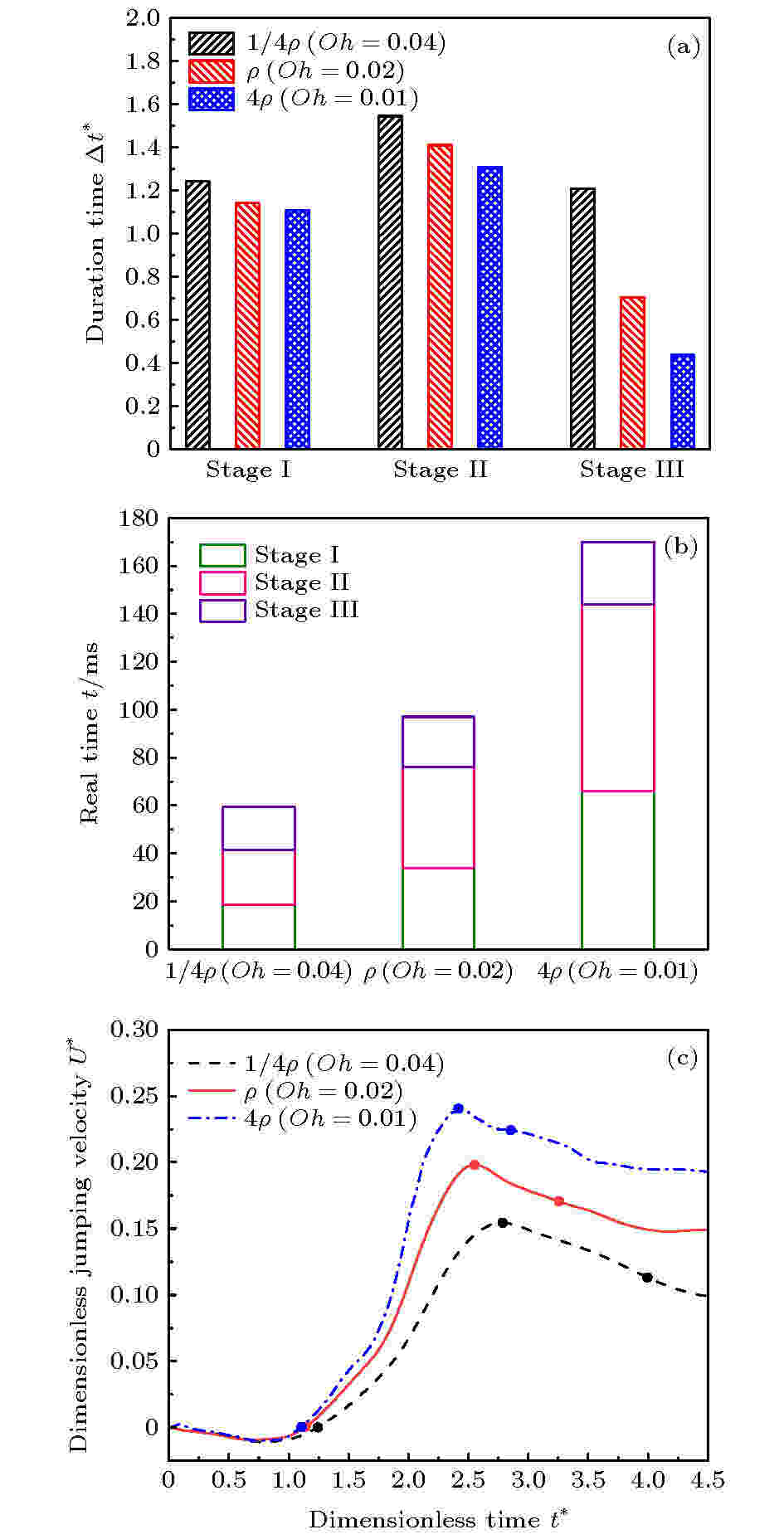图 8 (a) 密度变化对液滴跳离表面前所经历的各个阶段的无量纲持续时间的影响; (b) 密度变化对液滴跳离表面前所经历的各个阶段的真实持续时间的影响; (c)不同密度比时液滴质心处的无量纲弹跳速度
Figure8. (a) Effect of the change of density on the dimensionless duration of each stage prior to droplet jumping; (b) effect of the change of density on the real time of each stage prior to droplet jumping; (c) dimensionless jumping velocity of droplet with different density ratios.

从弹跳速度的变化曲线图8(c)可知, 密度较小的液滴的Oh数较大, 此时黏度效应占主导地位, 所以无量纲弹跳速度较小. 但是密度的改变也会改变(12)式中的特征速度, 由于本算例中密度比较小的液滴的特征速度要大于1, 而密度比较大的液滴的特征速度小于1, 因此实际上质量较小的液滴的真实弹跳速度要比质量大的液滴的真实弹跳速度更大一些, 这一变化趋势与其对应的无量纲速度的大小趋势正好相反.
当Oh相同时, 图6(a)和图9(a)的表面能的变化曲线是基本一样的, 这也证明了之前的结论: 液滴在聚并自弹跳过程中的动力学变化由Oh数决定. 密度较小的液滴的惯性效应小且黏性效应大, 在聚并后界面更光滑, 虽然可以释放较多的过剩表面能(图9(a)), 但其跳起时黏性耗散能更大(图9(b)), 过剩表面能的增量不能抵消黏性耗散能的增量所来带的负面影响, 因此质量大的液滴具有更大的动能(图9(c)). 从图10的流场速度矢量也可以看出, 密度比较大的液滴内部的流动剧烈. 这一结果也意味着即使密度小的液滴跳离表面所需的真实时间少并且真实弹跳速度大, 但减小密度比仍不利于液滴的自弹跳.
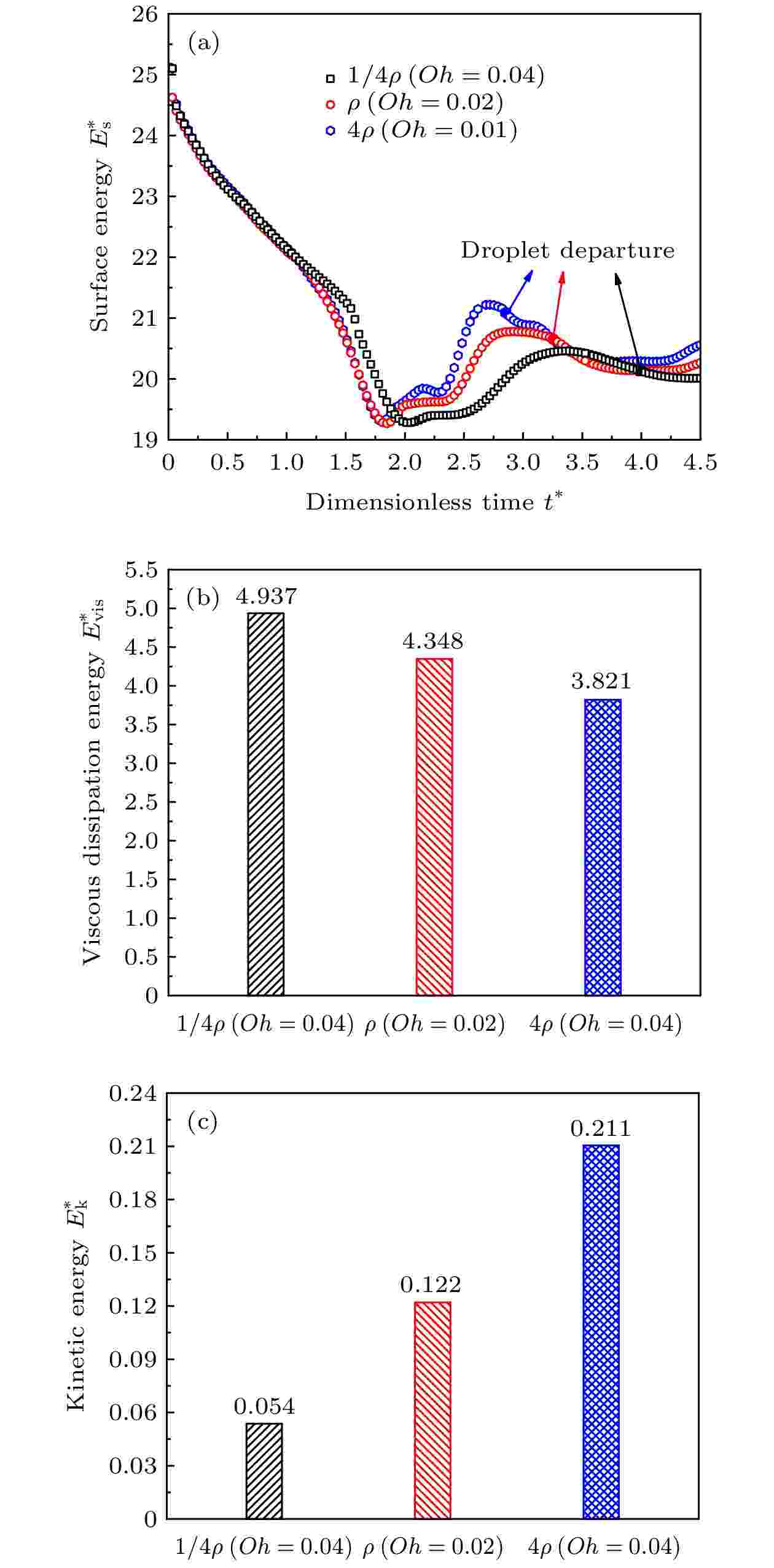图 9 (a) 不同密度比时聚并自弹跳过程中表面能的变化; (b) 不同密度比的液滴在跳起时具有的黏性耗散能; (c) 不同密度比的液滴在跳起时具有的动能
Figure9. (a) Surface energy variation with different density ratios during the coalescence and jumping process; (b) viscous dissipation energy of jumping droplets with different density ratios at departure time; (c) kinetic energy of jumping droplets with different density ratios at departure time.

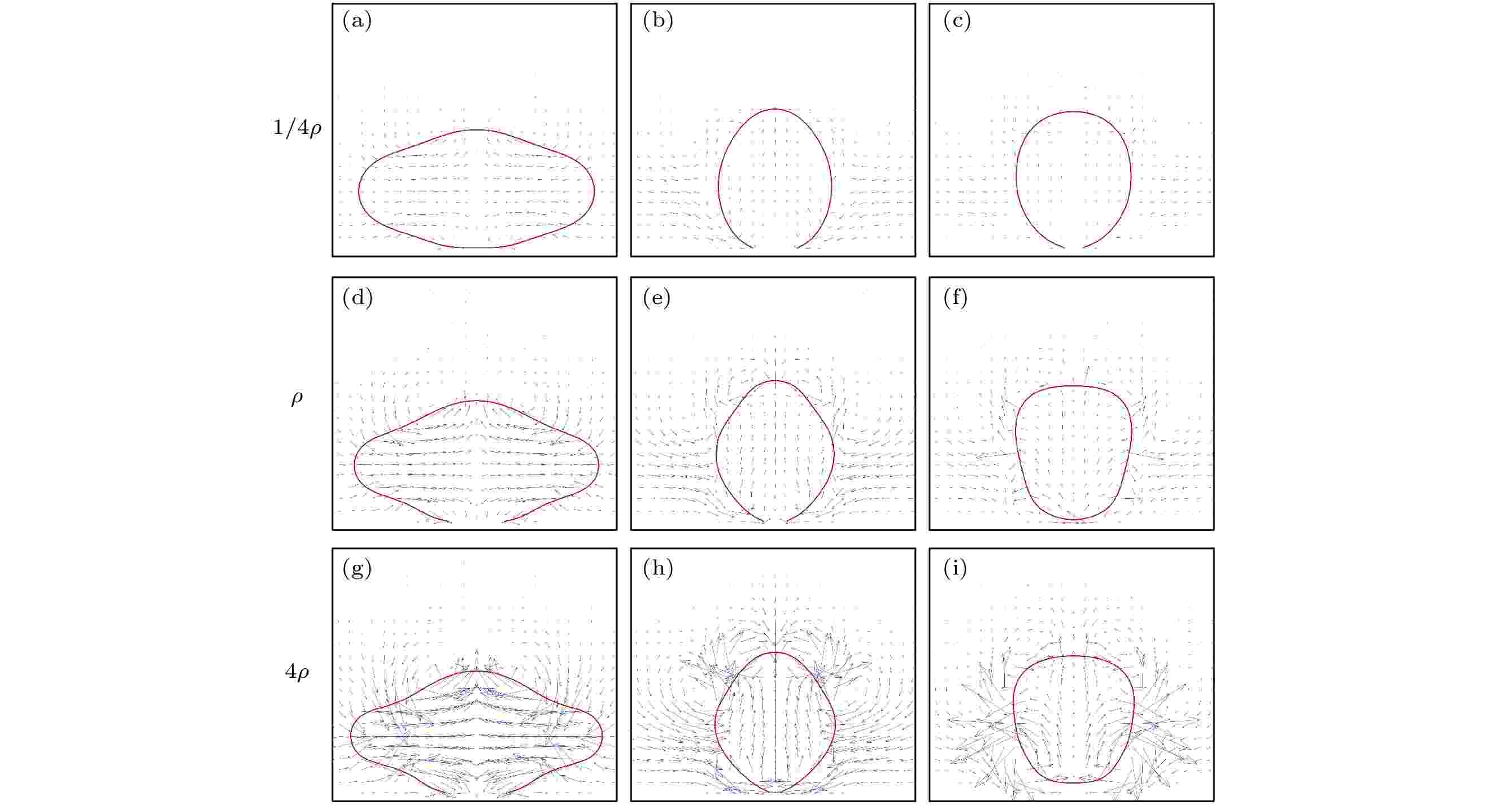图 10 不同密度比条件下流场的速度矢量图　(a), (d), (g) t^* = 1.309; (b), (e), (h) t^* = 2.686; (c), (f), (i) t^* = 3.257
Figure10. Vectors of flow field with different density ratios: (a), (d), (g) t^* = 1.309; (b), (e), (h) t^* = 2.686; (c), (f), (i) t^* = 3.257.

2

-->

4.1.灰色关联度的计算

液滴跳离表面时的弹跳速度和液滴与表面的接触时间这两个参数一直是评价液滴自弹跳及超疏水表面性能优劣的依据之一. 由前文的研究内容可知, 物性参数的改变对弹跳速度及接触时间均有影响, 但目前还无人给出这些物性参数与二者之间的远近程度. 因此本文应用灰色关联法^[31], 计算了物性参数(黏度和密度)变化分别与有量纲的真实弹跳速度和有量纲的真实接触时间之间的灰色关联度.
灰色关联法具有统计的样本少, 且样本无需具有经典分布等特点, 通过计算系统中的比较序列(物性参数)与参考序列(分别是真实弹跳速度和真实脱离时间)之间的关联度(即关联性大小)来度量数据之间的关联强度情况. 为了得到比较序列的更为精确的变化趋势, 本文中比较序列的结果取自于9组算例(1/2μ, 2μ, $ \sqrt{2} $/2μ, $ \sqrt{2} $μ, 1/4ρ, 4ρ, 1/2ρ, 2ρ和20 ℃对应的标准值), 考虑到参考序列有两列, 故分别做两次灰色关联度的计算. 灰色关联分析通常包括以下4步:
1)确定参考序列和比较序列: 设参考序列为$x_0' = \left\{ {x_0'(k)\left| {k = 1, 2, \cdot \cdot \cdot, n} \right.} \right\}$, 比较数列为$x_i' = $$ \left\{ {x_i'(k)\left| {k = 1, 2, \cdot \cdot \cdot, n} \right.} \right\}, i = 1, 2, \cdot \cdot \cdot, m$;
2)选用均值法对原始数据进行变换, 消除量级和量纲的影响: ${x}_{i}(k)=\dfrac{{x}_{i}'(k)}{\dfrac{1}{m}{\displaystyle \sum\nolimits _{k-1}^{m}{x}_{i}'(k)}}, \; i=0, $$ 1, \cdot \cdot \cdot, m$;
3)计算参考序列和比较序列之间的灰色关联系数: ${\xi _i}(k) = ({{a + \varepsilon b)} / {(\left| {{x_0}(k) - {x_i}(k)} \right| + }}\varepsilon b)$, 其中两级最小差a与两级最大差b分别为$a = $$ \mathop {\min }\limits_i \mathop {\min }\limits_k | {{x_0}(k) \!-\! {x_i}(k)} |$和$b = \mathop {\max }\limits_i \mathop {\max }\limits_k \left| {{x_0}(k) \!-\! {x_i}(k)} \right|$, 分辨率为$\varepsilon (0 < \varepsilon < 1)$, 通常取0.5;
4)计算关联度值: ${r_{{\rm{0 i}}}} = \dfrac{1}{N}\displaystyle \sum\nolimits_{i = 1}^N {{\xi _i}} (k)$, 排列灰色关联序列, 得到结果.
2 -->

4.2.关联度结果分析

物性参数变化(黏度和密度)分别与真实弹跳速度和真实接触时间的关联结果由表2给出. 当黏度和密度变化同等倍数时, 黏度引起的Oh数的变化范围更大; 另一方面, 黏度的改变直接地影响了黏性耗散能的多少, 而黏性耗散能在数值大小方面比跟密度相关的动能的数值高一个量级, 因此比较序列中黏度的变化与参考序列中的真实弹跳速度的关联性更高.

参考序列/比较序列	黏度μl	密度ρl
关联度r0i, velocity (弹跳速度)	0.758	0.684
关联度r0i, time (接触时间)	0.741	0.771

表2物性参数变化分别与真实弹跳速度和真实接触时间的关联度
Table2.Relational degree of the change of physical parameters to the real jumping velocity and the real contact time, respectively, at droplet departure time.

由于黏度变化对液滴聚并的真实时间基本无影响, 而密度的变化不仅会改变聚并的真实时间, 甚至于对前3个阶段的真实持续时间均有影响, 故密度的变化与参考序列中的真实接触时间关联性更高.

本文采用三维VOF方法对液滴的聚并自弹跳行为进行了数值模拟, 不仅关注了黏度效应和惯性效应对液滴的聚并自弹跳特性的影响, 同时对所有能量项进行了计算, 最后根据灰色关联法得到的结果, 给出了物性参数(黏度和密度)变化分别与液滴跳离表面时的真实弹跳速度和真实接触时间的关联程度.
根据弹跳速度的变化趋势, 液滴的聚并自弹跳运动可分为4个阶段, 即液桥扩张、液桥撞击表面、液滴跳离表面和空中减速振荡. 在无量纲的时间条件下, 液滴的聚并自弹跳的动力学特性仅受Oh数的影响, 与黏度比或密度比无关, 并且Oh数的改变只影响液滴跳离表面的第3个运动阶段. 在真实的时间条件下, 黏度的改变不会影响液滴聚并所需的真实时间, 只会改变跳离表面这一阶段所需的真实时间; 而各个运动阶段所需的真实时间都会随着密度比的增大而增加. 另外, 无量纲的弹跳速度随着Oh数的增大而减小, 增大黏度和密度都会减少液滴跳起时的真实弹跳速度. 根据灰色关联度的计算结果可知, 黏度的变化与真实弹跳速度的关联性更高, 而密度的变化与真实接触时间关联性更高.
感谢亚琛工业大学(RWTH Aachen University)传热传质研究所(WSA)的Wilko Rohlfs博士提供宝贵的意见和建议.