摘要:Cu_1.8S基热电材料因其丰富的原料储备、低毒性及优良的电学和热学性能而成为具有应用潜力的热电材料. 本文采用机械合金化(mechanical alloying, MA)结合放电等离子烧结(spark plasma sintering, SPS)工艺制备了一系列Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04)块体材料, 研究了不同Sb掺杂量对Cu_1.8–x Sb_x S相结构、微观形貌及热电性能的影响. 结果表明, 随着Sb含量的增加, Cu_1.8–x Sb_x S材料相结构由单相Cu_1.8S转变为多相共存, 其块体均呈p型导电特征. 样品Cu_1.77Sb_0.03S在723 K时取得最高ZT值约为0.37, 比未掺杂Cu_1.8S(0.33)提高了12%.
关键词: Cu_1.8S/
热电材料/
机械合金化/
放电等离子烧结

English Abstract

全文HTML

--> --> -->

热电材料是一类能够实现热能和电能直接相互转化的清洁能源材料, 利用热电材料制备的热电器件具有体积小、可靠性高、适用温度范围广以及环境友好等特点, 在工业废热回收和空间特殊电源等领域具有广阔的应用前景^[1-3]. 材料的热电性能可用无量纲热电优值ZT来衡量^[4-6], ZT = α²σT/κ, 其中α为Seebeck系数, σ为电导率, T为绝对温度, κ为热导率, α²σ称为材料的功率因子(PF ). 高性能热电材料需要具备高α, σ和低κ, 但由于构成ZT的物理量相互耦合, 如果单独追求其中一个参量的增大或减少往往会导致其他参量协同性的变化, 因此需要运用多种手段协同调控. 目前, 提高热电材料性能的手段主要有: 通过杂质掺杂和调控本征缺陷来优化载流子浓度, 提升PF ^[7]; 通过能带工程^[8], 包括使能带边缘平坦化, 引入共振能级和提高能带简并度的方法来提高态密度有效质量, 从而提升α; 通过引入多尺度缺陷^[9,10], 包含原子尺度点缺陷、纳米尺度第二相及位错、次微米级晶界等, 实现对全频率段声子的剧烈散射, 降低κ.
目前, 已经商业化应用的高性能热电材料体系如Bi₂Te₃, PbTe等因含有昂贵或有毒的重金属元素使其大规模化应用受到限制^[11,12]. 铜硫化物(Cu_2–x S)热电材料是一种新型热电材料, 因其组成元素丰度高、廉价易得、环境友好等特点, 成为极具发展潜力的绿色热电材料. Cu_2–x S (0 ≤ x ≤ 1)系列化合物中, Cu₂S, Cu_1.97S, Cu_1.9S及Cu_1.8S作为热电材料已得到广泛研究^[13-15]. 基于Cu/S比例的不同, Cu_2–x S (0 ≤ x ≤ 1)化合物具有不同的晶体结构、能带结构及热电传输特性. 由于晶格中存在本征铜空位, Cu_2–x S (0 ≤ x ≤ 1)均呈现p型半导体特性. 其中, Cu_1.8S因具有稳定的电学和热学性能而被认为是Cu_2–x S化合物中最具有潜力的热电材料^[16]. Cu_1.8S室温为六方相结构(R3-MH), 随着温度升高至360 K, 其转变为立方相结构(FM3-M), 相变后的Cu原子位置由有序态转变为无序态. 作为一种超离子导体^[17], Cu_1.8S因晶格中高的Cu离子迁移率及较多的本征Cu空位而具有高σ (～3000 S·cm^–1), 但其较低的α和高的κ限制了其热电性能. 因此, 提升Cu_1.8S热电材料性能的研究主要集中在提高α和降低κ方面, 如通过Na^[18], In^[19]和Ti等元素掺杂调整载流子浓度提升PF或通过复合SiO₂^[20], SiC^[21]和NH₄Cl^[22]等降低κ, 进而可有效提升其ZT值. Liang等^[23]通过在Cu位进行Bi元素掺杂, 有效地提升Bi_xCu_1.8–x S材料的PF、降低κ, 最终样品Bi_0.01Cu_1.79S在673 K时获得最大ZT值, 约0.61, 是未掺杂Cu_1.8S的两倍; Ge等^[24]在Cu_1.8S中直接引入质量分数为2%的LaCl₃, 有效地降低了载流子浓度、增强了α, 在773 K获得了超高的PF值(1600 μW·m^–1·K^–2), 同时析出纳米第二相, 有效地降低了κ, 最终将ZT值提升至约1.2. Tang等^[25]通过Sb, Sn共掺杂(Cu_1.8Sb_x Sn_yS), 在773 K时Cu_1.8Sb_0.02Sn_0.03S获得了最大ZT值约为1.2. 众多研究结果均表明, 调控掺杂剂的种类和含量能够显著地影响Cu_1.8S基材料的热电性能.
Sb元素作为一种有效的掺杂剂, 已在许多热电材料体系中得到了研究. Bayikadi等^[26]在GeTe中引入一定量的Sb元素, 在缺陷中心和畴结构的周围产生了多种形式的应变, 这种晶格应变可以散射较宽频率范围内的声子, 从而有效地降低了晶格热导率, Ge_0.9Sb_0.1Te在800 K时获得了较低的热导率约为1.1 W·m^–1·K^–1; Chen等^[27]在n型PbTe中掺杂微量的Sb元素, 所有样品均表现出单相微观结构以及微纳米级的不均匀晶粒尺寸. 高度不均匀的晶粒尺寸分布增强了晶界散射, 掺杂的Sb和Te空位导致点缺陷散射增强, 在723 K时Pb_0.988Sb_0.012Te获得了低的晶格热导率为0.68 W·m^–1·K^–1. 通常Sb元素呈现+3价或+5价, 在Cu_1.8S基热电材料中, 高价态的Sb可能进入间隙位或置换位取代低价Cu⁺离子, 提供电子从而实现对载流子(空穴)浓度的调控. 此外, Sb掺杂可以引入点缺陷, 降低热导率, 这对热电性能的提升是有利的.
本文采用机械合金化(mechanical alloying, MA)结合放电等离子烧结(spark plasma sintering, SPS)技术制备了一系列Cu_1.8–x Sb_x S块体材料, 系统研究了在化学计量比范围内Sb掺杂量对Cu_1.8S热电材料的相结构、微观形貌以及热电传输性能的影响. 与Cu₂Se, Bi₂Te₃, GeTe以及PbTe等其他体系热电材料常采用的制备方法如固相熔融^[28]、MA + 热压烧结(HP)^[29]、熔融 + HP^[30]、熔融 + SPS^[31]等相比, 本文采用的MA结合SPS技术制备工艺简单、大大地缩短了材料的制备周期、提高了热电材料的研发效率, 适于材料大规模生产应用.

采用单质Cu粉(99%)、S粉(99.5%)和Sb粉(99.7%)为原料, 按照化学式Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04)进行配料称量. 采用MA进行合成. 将称量好的原料粉末置于真空不锈钢球磨罐中, 球料比为20∶1. 密封后对球磨罐抽真空并充入保护气体(95%氩气和5%氢气), 此过程重复3次, 以防止在球磨过程中原料粉末被氧化. 将球磨罐置于行星式球磨机(QM-4F)以425 r/min转速球磨8 h. 球磨后的粉末置于Ф20 mm石墨模具中进行SPS (Sumitomo SPS1050, Japan), 烧结条件为40 MPa压力, 873 K下保温5 min, 最终获得厚度为3—4 mm的块体样品.
用X射线衍射仪(X-ray diffraction, XRD, Rigaku2000V, Japan)表征粉体和块体样品的相结构, 用场发射扫描电镜(field emission scanning electron microscope, FESEM, SUPRATM55, Japan)观察块体样品的断口形貌. 用Seebeck系数/电导率综合测试装置(ZEM-2Ulvac-Riko, Japan)在氦气中, 测试块体材料在323—773 K温度范围内的电输运性能. 用激光热导仪(NETZSCH, LFA427, Germany)测试样品的热扩散系数(D), 由阿基米德法测得样品的密度(ρ), 使用杜隆-珀替公式估算得到样品的比热(C_p), 并根据公式κ = DC_pρ计算样品的热导率(κ).

2

-->

3.1.相结构分析

图1为Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04)粉体样品的XRD图谱. 从图1(a)可以看出, 所有样品的衍射峰与标准卡片Cu_1.8S (PDF#47-1748)一致, 表明合成了单相Cu_1.8S; 图1(b)为不同Sb掺杂量粉体样品的(0 1 20)晶面衍射峰放大图, 可以看出, 随着Sb元素的掺杂, 衍射峰逐渐变宽, 表明引入Sb元素能够细化粉体样品的晶粒.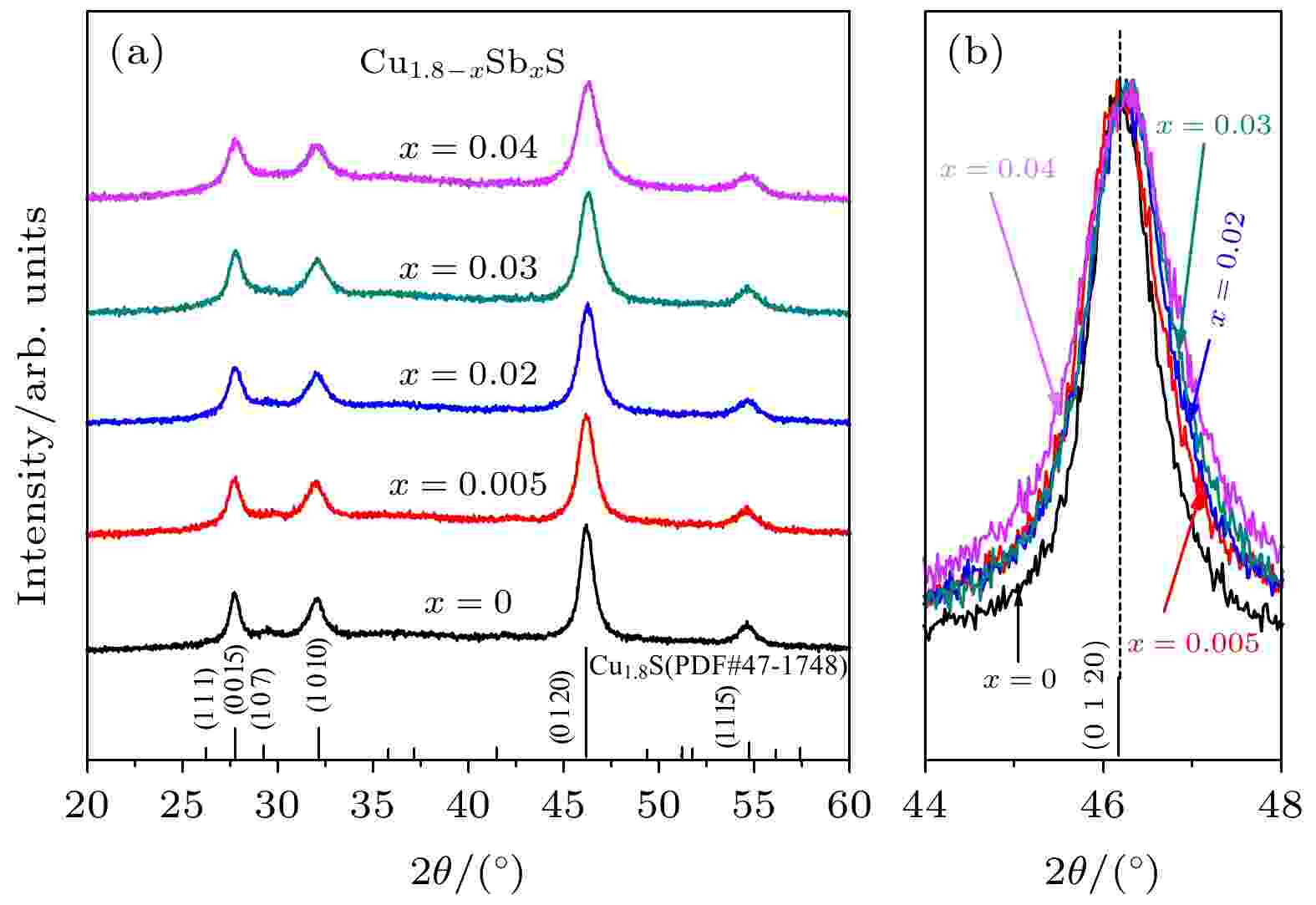
图 1 Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04)粉体样品的室温 XRD图谱(2θ = 20o?60o) (a)和(0 1 20)晶面放大峰(b)
Figure1. XRD patterns of the Cu_1.8–x Sb_x S powder samples (x = 0, 0.005, 0.02, 0.03, 0.04) at 2θ range of 20°?60° (a) and the enlarged (0 1 20) peaks (b).

图2为Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04)块体样品的XRD图谱. 与粉体样品相比(图1), 块体样品衍射峰的半峰宽变窄, 表明烧结后的块体样品具有更高的结晶度. 由图2(a)可以看出, 当0 ≤ x ≤ 0.02时, 样品的所有特征衍射峰与标准卡片Cu_1.8S (PDF#47-1748)一致, 表明合成了单相Cu_1.8S; 当0.03 ≤ x ≤ 0.04时, 出现了CuSbS₂ (PDF#44-1417)的特征衍射峰, 这是由于随着Sb掺杂量的增多, 超出了Sb在Cu_1.8S中的固溶极限, 因而产生了CuSbS₂第二相. 而CuSbS₂中Sb元素为+3价, 因此推测固溶在Cu_1.8S晶格中的Sb呈现+3价. 此外, 根据缺陷方程(2)—(5)可知, 无论Sb以何种价态(+3, +5)进入晶格, 其取代Cu⁺都将提供电子, 降低载流子浓度, 对于热电性能的影响机制本质是一致的.
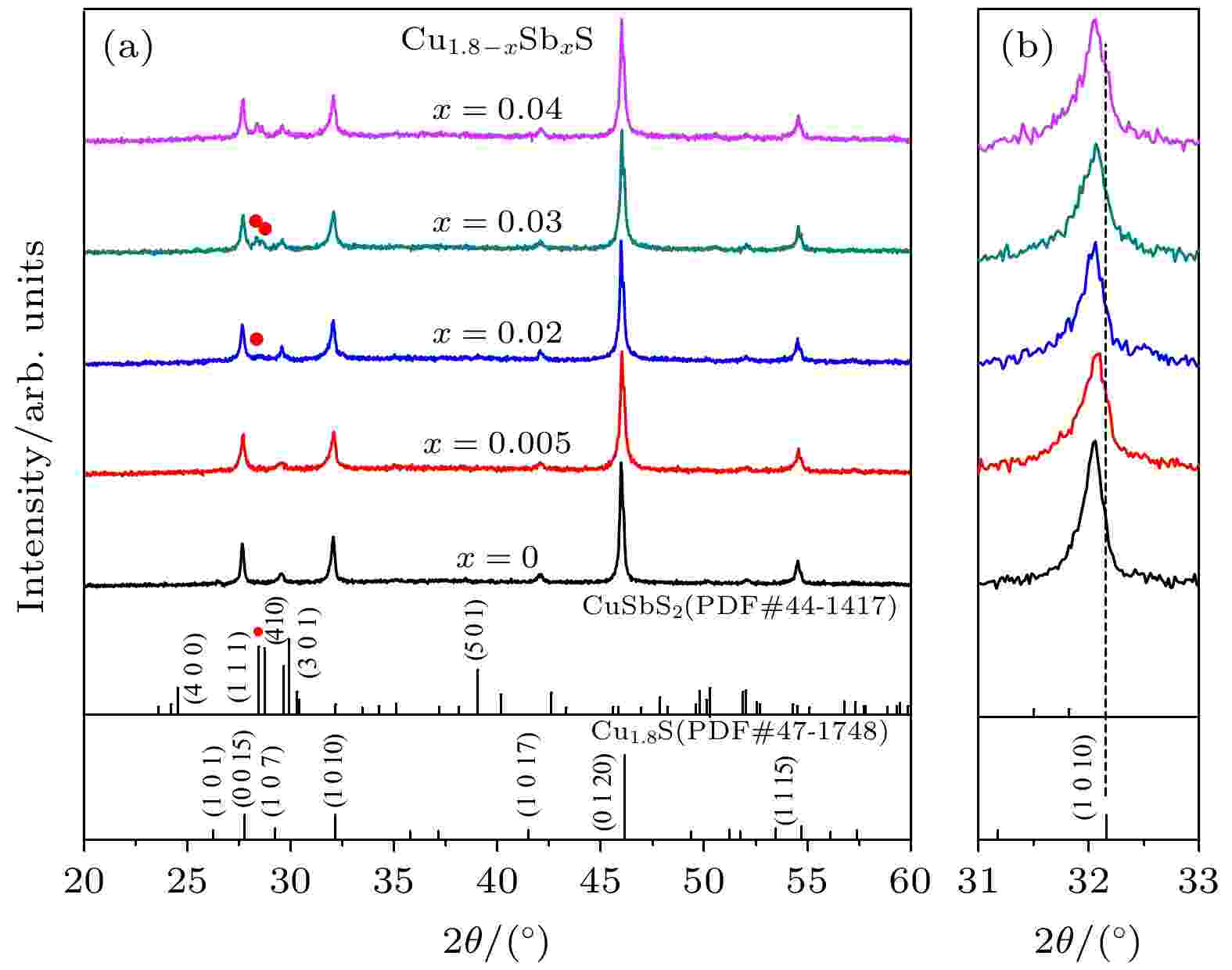图 2 Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04)块体样品的XRD图谱　(a) 2θ = 20o?60o; (b) 2θ = 31o?33o
Figure2. XRD patterns of the Cu_1.8–x Sb_x S bulk samples (x = 0.00, 0.005, 0.02, 0.03, 0.04) at 2θ range of 20o?60o (a) and 31o?33o (b).

由图2(b)晶面(1 0 10)对应的衍射峰放大图可以看出, 所有样品的衍射峰与标准卡片相比均向小角度偏移, 这是由于SPS烧结过程中, 部分S挥发引起了晶格膨胀, 如方程(1)所示, 这与其他文献报道一致^[1,18,23-25]. 与x = 0样品相比, x = 0.005样品衍射峰向大角度偏移, 这是由于具有较小离子半径的Sb³⁺(0.076 nm)替换了Cu⁺(0.096 nm), 使膨胀的晶格部分回复, 如方程(2)所示. 随着x的增加, 衍射峰又向小角度偏移, 这是由于析出了富S的第二相CuSbS₂, 消耗了Cu_1.8S基体中的部分S元素, 引起基体的晶格膨胀. 以上过程所涉及的方程如(1)—(5)式所示:

$ {\rm{C}}{{\rm{u}}}_{1.8}{\rm{S}}\xrightarrow{{\rm{SPS}}}{\rm{C}}{{\rm{u}}}_{1.8}{{\rm{S}}}_{1-y}+y{{\rm{V}}}_{{\rm{S}}}^{\centerdot \centerdot}+2y{\rm{e}}{'}+y{\rm{S}}\uparrow, $

$ \begin{split} &x{\rm{Sb}} \xrightarrow[0 < x\leqslant 0.02]{{\rm{C}}{{\rm{u}}}_{1.8}{\rm{S}}} x{\rm{S}}{{\rm{b}}}_{{\rm{Cu}}}^{\centerdot \centerdot}+{\rm{C}}{{\rm{u}}}_{1.8-x}{{\rm{S}}}_{1-y}\\ &+y{{\rm{V}}}_{{\rm{S}}}^{\centerdot \centerdot}+(2x+2y){\rm{e}}{'}+y{\rm{S}}\uparrow, \end{split} $

$\begin{split}&x{\rm{Sb}} \xrightarrow[{0.02 < x\leqslant 0.04}]{{{\rm{C}}{{\rm{u}}}_{1.8}{\rm{S}}} }\alpha {\rm{S}}{{\rm{b}}}_{{\rm{Cu}}}^{\centerdot \centerdot}+(x-\alpha ){\rm{Cu}}{\rm{Sb}}{{\rm{S}}}_{2}\\&+\beta {{\rm{Cu}}}_{1.8}{{\rm{S}}}_{1-y}+y{{\rm{V}}}_{{\rm{S}}}^{\centerdot \centerdot}+(2x+2y) {\rm{e}} ' +y{\rm{S}}\uparrow, \end{split}$

$ \begin{split}&x{\rm{Sb}} \xrightarrow[{0 < x\leqslant 0.02}]{{{\rm{C}}{{\rm{u}}}_{1.8}{\rm{S}}}}x{\rm{S}}{{\rm{b}}}_{{\rm{Cu}}}^{\centerdot \centerdot\centerdot \centerdot}+{\rm{C}}{{\rm{u}}}_{1.8-x}{{\rm{S}}}_{1-y}\\&+y{{\rm{V}}}_{\rm{S}}^{\centerdot \centerdot}+(4x+2y){\rm{e}}{'}+y{\rm{S}}\uparrow,\end{split}$

$ \begin{split}&x{\rm{Sb}}\xrightarrow[{0.02 < x\leqslant 0.04}]{{{\rm{C}}{{\rm{u}}}_{1.8}{\rm{S}}}}\alpha {\rm{S}}{{\rm{b}}}_{{\rm{Cu}}}^{\centerdot \centerdot\centerdot \centerdot}+(x-\alpha ){\rm{Cu}}{\rm{Sb}}{{\rm{S}}}_{2}\\&+\beta {{\rm{Cu}}}_{1.8}{{\rm{S}}}_{1-y}+y{{\rm{V}}}_{{\rm{S}}}^{\centerdot \centerdot}+(4x+2y) {\rm e} ' +y{\rm{S}}\uparrow. \end{split}$

2 -->

3.2.晶粒分布与SEM分析

图3(a)—(e)为Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04)块体样品的晶粒尺寸分布图, 内插图为对应的断口FESEM照片, 图3(f)为块体样品的密度和相对密度随Sb掺杂量的变化图. 由图3(a)可以看出, 未掺杂样品的平均晶粒尺寸为2.98 μm, 由于SPS烧结过程中S元素挥发导致晶粒内部和晶界处存在亚微米气孔. 随着Sb元素掺杂, 如图3(b)所示, x = 0.005样品平均晶粒尺寸减小至1.59 μm, 气孔含量增加, 相对密度从96.83%下降至82.14%. 这是由于Sb的掺杂会使粉体样品的晶粒尺寸减小, 提高了粉体活性, 加剧了烧结过程中S元素的挥发, 产生大量气孔, 因而抑制了晶粒长大, 获得了较小的晶粒尺寸^[1,17]. 当x增加至0.02时, 样品的平均晶粒尺寸增大至3.33 μm, 可能是由于析出了少量低熔点(551 ℃)第二相CuSbS₂, 促进了样品烧结使晶粒变大, 由于此时析出的CuSbS₂较少, 在XRD图谱中未能检测到其衍射峰. 随着x进一步增加, 如图3(d)和图3(e)所示, 样品的晶粒明显增大, 其平均晶粒尺寸分别达到了7.57和13.37 μm, 这是由于析出了更多的CuSbS₂, 进一步促进了样品烧结. 由图3(f)可以看出, Sb的掺杂使样品的密度从x = 0时的5.42 g/cm³降低至x = 0.005时的4.61 g/cm³, 随后保持在4.42 g/cm³附近, 相对密度则在x > 0.005后维持在79%左右.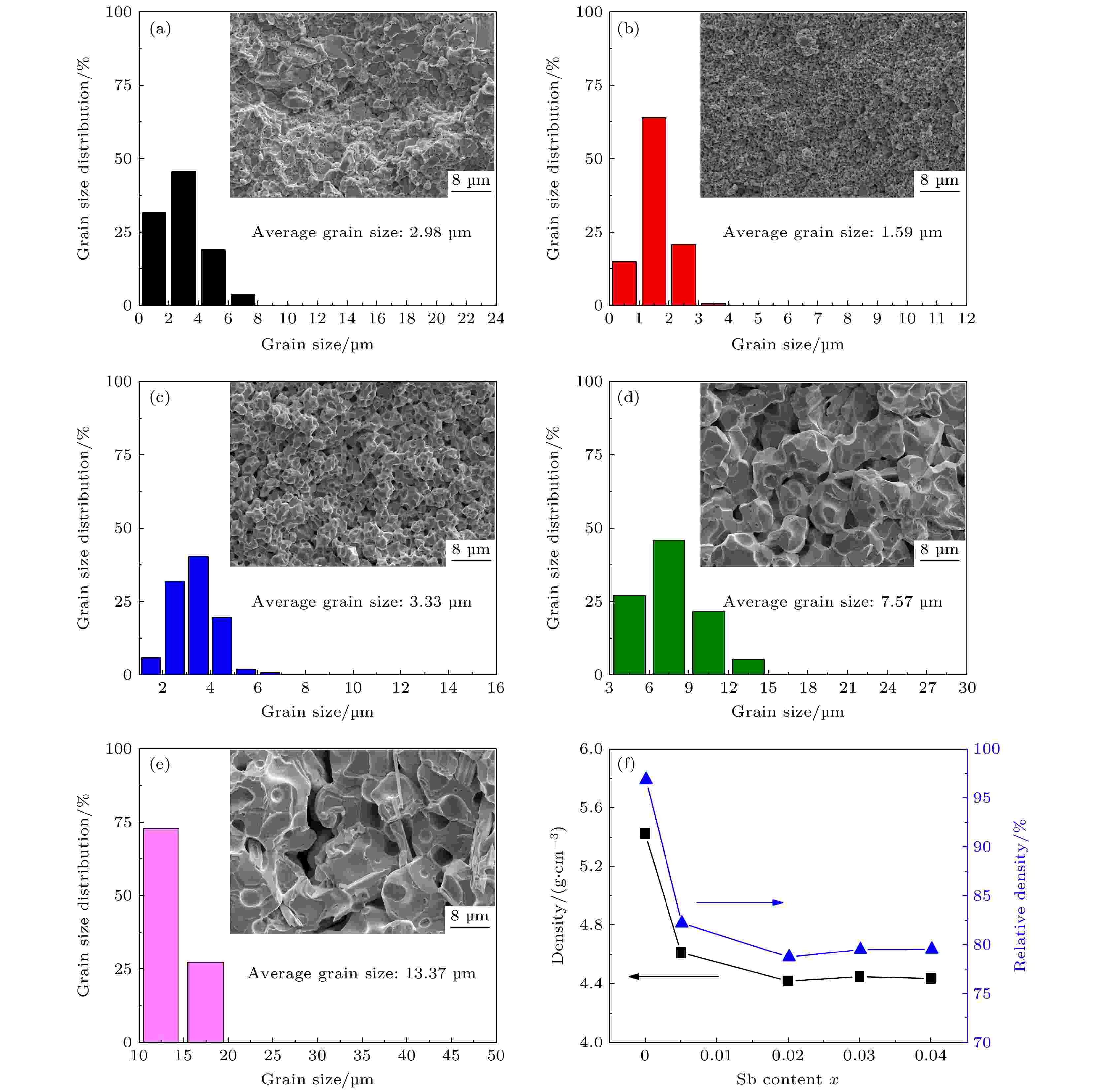
图 3 Cu_1.8–x Sb_x S块体样品的晶粒尺寸分布及断口FESEM照, 其中x取值分别为(a) x = 0, (b) x = 0.005, (c) x = 0.02, (d) x = 0.03, (e) x = 0.04; (f) 密度和相对密度随x变化图
Figure3. Grain size distributions of Cu_1.8–x Sb_x S bulks with FESEM images of the fractured surfaces in the inset at (a) x = 0.00, (b) x = 0.005, (c) x = 0.02, (d) x = 0.03, (e) x = 0.04; (f) density and relative density.

2 -->

3.3.电输运性能分析

图4(a)—(c)为Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04)块体的电导率(σ)、Seebeck系数(α)以及功率因子PF随温度的变化图. 由图4(a)可以看出, 所有样品的电导率σ在测量温度范围内先增大后减小, 在373 K左右出现转折点, 这归因于Cu_1.8S由六方相转变为立方相所致. 随着Sb掺杂量x的增多, σ呈下降趋势, 323 K时, 电导率由x = 0样品的2210 S·cm^–1降低至x = 0.04样品的1370 S·cm^–1. 根据缺陷方程(2)和(3), 由于Cu_1.8S为p型半导体, Sb³⁺的引入会产生额外电子, 降低载流子(空穴)浓度; 另一方面, CuSbS₂第二相的出现会增加相界面从而加强界面散射, 降低载流子迁移率(μ), 这两方面的原因导致了σ的下降. 其中, x = 0.03样品在低温段表现出比x = 0.02样品略高的σ, 这可能是因为x = 0.03样品的晶粒尺寸大于x = 0.02样品, 具有更大的μ所致. 而x = 0.04时σ进一步降低, 原因是析出了更多的CuSbS₂第二相, 加强了界面散射, 降低了μ. 另外, 由于CuSbS₂具有较低的σ, 因此进一步降低了体系的σ.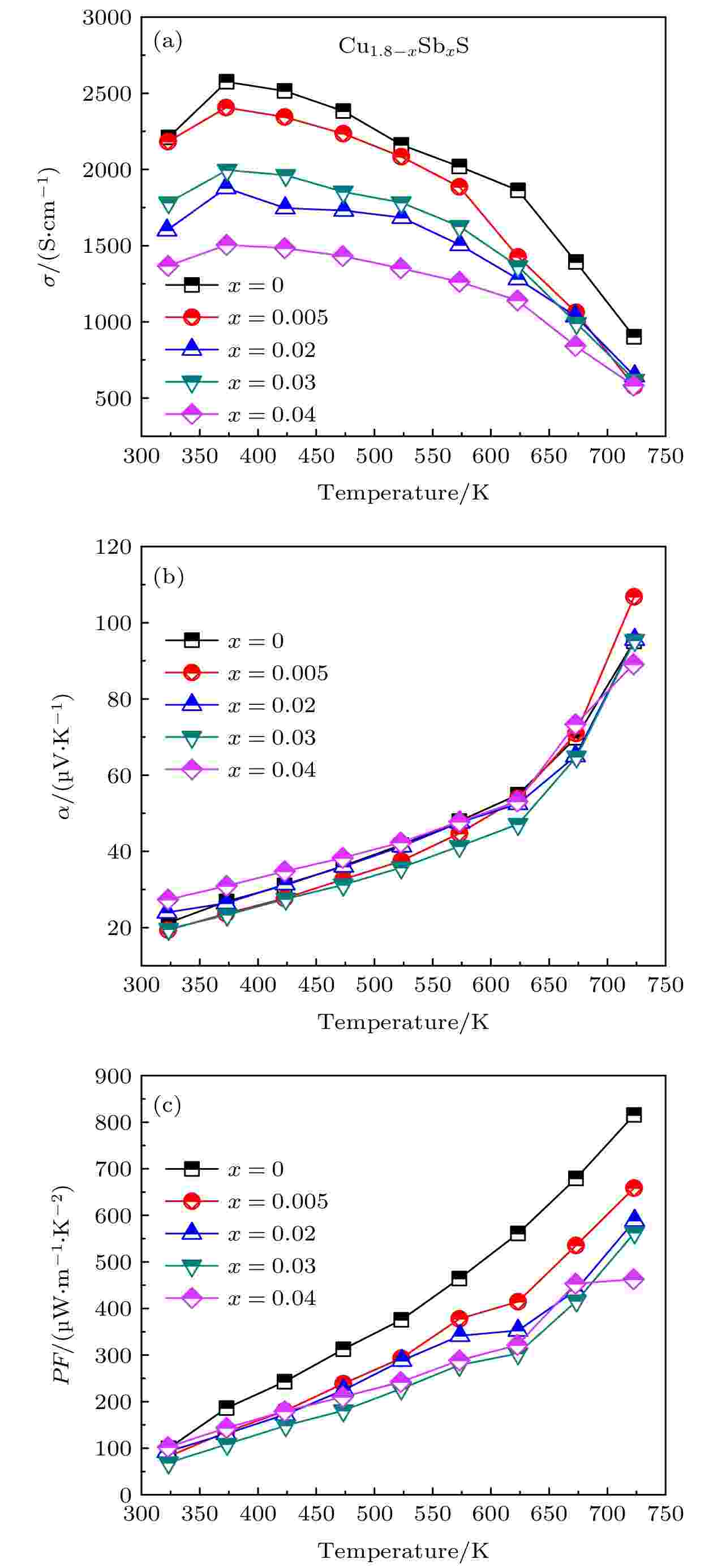
图 4 Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04)块体样品的电输运性能　(a) 电导率; (b) Seebeck系数; (c) 功率因子
Figure4. Temperature dependence of electrical transport properties for Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04) bulks: (a) Electrical conductivity σ; (b) Seebeck coefficient α; (c) power factor PF.

图4(b)中所有样品的Seebeck系数α均为正值, 表明Cu_1.8–x Sb_x S块体样品呈现p型半导体传导特征. 在整个测量温度范围内, x = 0样品的α随着温度的升高从21 μV·K^–1增加到95 μV·K^–1, 随着x的增加, 样品的α基本不变. 在723 K时, x = 0.005样品取得了最大α为107 μV·K^–1. 由于x = 0样品最大的σ (2580 S·cm^–1)以及所有样品接近的α值, 如图4(c)所示, Cu_1.8S在723 K时获得了最大PF为815 μW·m^–1·K^–2.
2 -->

3.4.热输运性能分析

图5(a)为Cu_1.8–x Sb_x S块体的热导率随温度的变化图. 所有样品的κ随测试温度的升高先增大后减小, x = 0样品的转折点为473 K, 这与Cu_1.8S由低温六方相到高温立方相的相转变温度^[18,32]一致. 随Sb掺杂量x的增加, κ的转折点向高温方向移动, 这是因为析出的富S第二相CuSbS₂消耗了基体中的S元素, 使Cu和S的比例偏离了Cu_1.8S的化学计量比, 这可以在Cu-S相图中得到证实^[33]. 同时由于Sb的掺杂引入了点缺陷、亚微米气孔以及CuSbS₂第二相, 增强了声子散射, κ随着Sb的增加逐渐降低. 最终Cu_1.76Sb_0.04S样品在723 K获得了最低的κ为0.99 W·m^–1·K^–1. 通常, 热导率(κ)由载流子热导率(κ_e)和晶格热导率(κ_l)组成, 即κ = κ_e + κ_l. 根据Wiedemann-Franz定律, κ_e可由公式κ_e = LσT计算得到, 其中L为洛伦兹常数, σ为电导率, T为绝对温度. 利用单抛物带模型计算得到L, 如(6)—(8)式^[23]: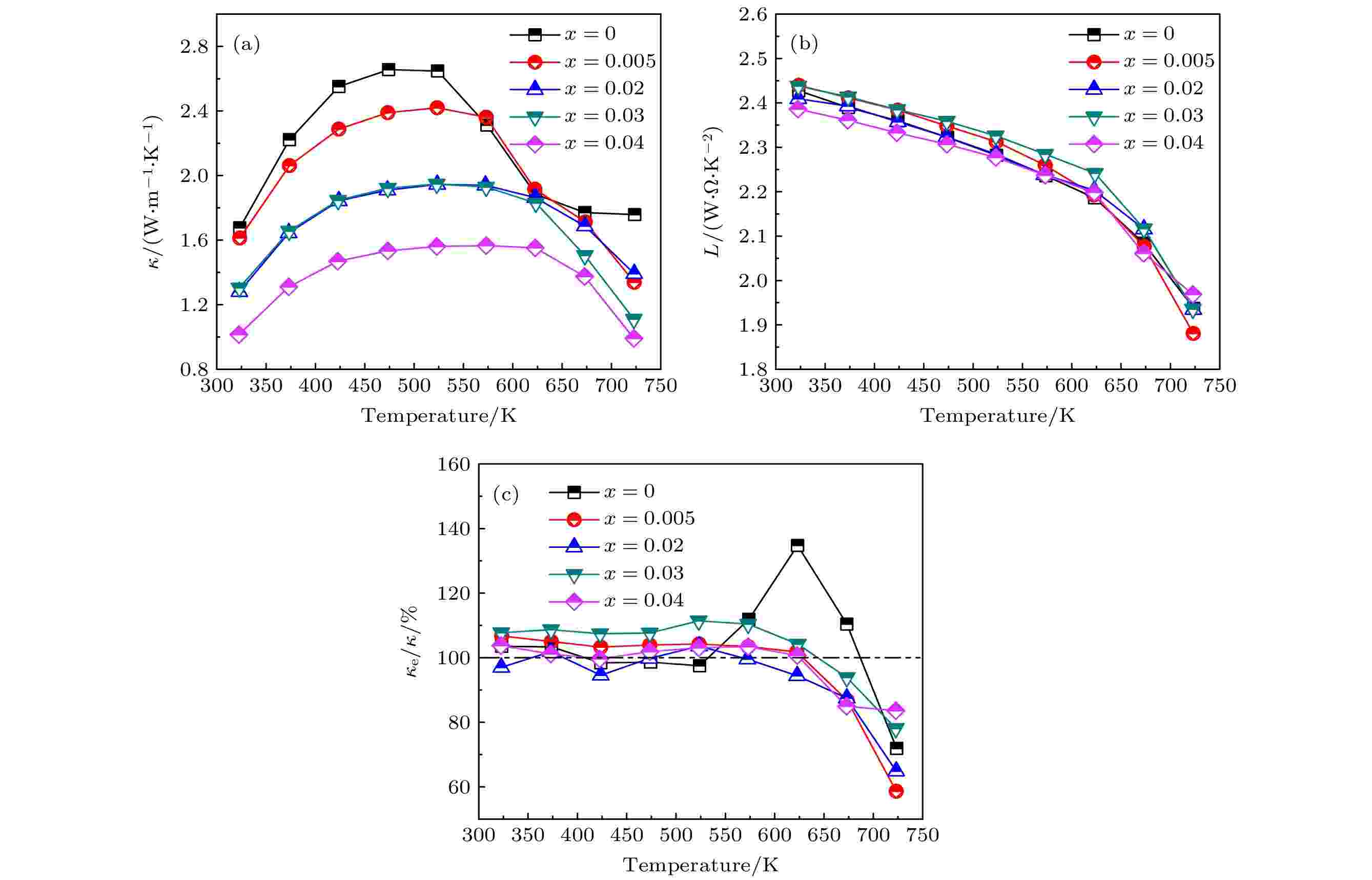
图 5 Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04)块体样品的热输运性能　(a) 总热导率κ; (b) 洛伦兹常数L; (c) 电子热导率与总热导率的比值κ_e /κ
Figure5. Temperature dependence of thermal transport properties for Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04) bulks: (a) Total thermal conductivity κ; (b) Lorenz number L; (c) the ratios of electronic thermal conductivity to total thermal conductivity (κ_e /κ).

$\begin{split}L =\;& {\left( {\dfrac{{{k_{\rm{B}}}}}{{{\rm{e}}}}} \right)^2}\left\{ \dfrac{{\left( {r + \dfrac{7}{2}} \right){F_{\left( {r + \tfrac{5}{2}} \right)}}\left( \eta \right)}}{{\left( {r + \dfrac{3}{2}} \right){F_{\left( {r + \tfrac{1}{2}} \right)}}\left( \eta \right)}} \right.\\&\left.- {{\left[ {\dfrac{{\left( {r + \dfrac{5}{2}} \right){F_{\left( {r + \tfrac{3}{2}} \right)}}\left( \eta \right)}}{{\left( {r + \dfrac{3}{2}} \right){F_{\left( {r + \tfrac{1}{2}} \right)}}\left( \eta \right)}}} \right]}^2} \right\},\end{split}$

$\alpha = \dfrac{{{k_{\rm{B}}}}}{{\rm{e}}}\left[ {\frac{{\left( {r + \dfrac{5}{2}} \right){F_{\left( {r + \tfrac{3}{2}} \right)}}(\eta )}}{{\left( {r + \dfrac{3}{2}} \right){F_{\left( {r + \tfrac{1}{2}} \right)}}(\eta )}} - \eta } \right],$

${F_n}\left( \eta \right) = \int\nolimits_0^\infty {\frac{{{x^n}}}{{1 + {{{\rm{e}}}^{x - n}}}}} {\rm{ d}}x,$

其中F_n(η)是n 阶费米积分, η是简约费米能级, r是散射因子, k_B是玻尔兹曼常数. 由于声学声子散射是大多数热电材料的主要散射机制, 因此r取值为–1/2, 计算得到的L如图5(c)所示, 可看出所有样品具有相近的L, 从323 K时的2.41 W·Ω·K^–2降低至723 K时的1.95 W·Ω·K^–2. 图5(d)为计算的载流子热导率κ_e与热导率κ的比值(κ_e/κ), 可以看出部分计算得到的κ_e超过了κ, 这归因于超离子导体Cu_1.8S存在大量可迁移的铜离子, 这些铜离子同时参与了电传导, 因此Wiedemann-Franz定律中的σ包含了Cu离子的离子电导率(σ_i), 实际的κ_e可以表示为: κ_e = L(σ－σ_i)T. 由于σ_i和离子热导率很难通过计算求得, 因此Wiedemann-Franz定律不适用于Cu_1.8S体系^[18].
2 -->

3.5.ZT值分析

图6(a)为Cu_1.8–x Sb_x S块体样品的ZT值随温度的变化. x = 0样品在723 K时获得了0.33的ZT值, 尽管Sb掺杂样品具有较低的κ, 但PF的降低不能被减小的κ所抵消, 因此ZT值没有得到明显的提升. 由于x = 0.03时低的κ (1.11 W·m^–1·K^–1)和合适的PF (563 μW·m^–1·K^–2), 最终Cu_1.77Sb _0.03S样品在723 K时获得了最大的ZT值0.37, 比未掺杂Cu_1.8S (0.33)提高了12%. 图6(b)为723 K时不同Cu_1.8S基材料的热电性能对比图. 从图6(b)可以看出, 与其他Cu_1.8S基热电材料相比, Sb掺杂Cu_1.8S热电性能没有明显提高. 虽然κ得到了有效降低, 但与其他高性能Cu_1.8S基热电材料相比仍然较高, 同时较低的PF值使Cu_1.8–x Sb_x S块体样品的热电性能未能明显提升. 因此Sb掺杂Cu_1.8S热电材料性能的提升仍存在较大的发展空间, 可以进一步通过纳米第二相复合、能带工程等手段^[8-10]进一步优化其热电性能.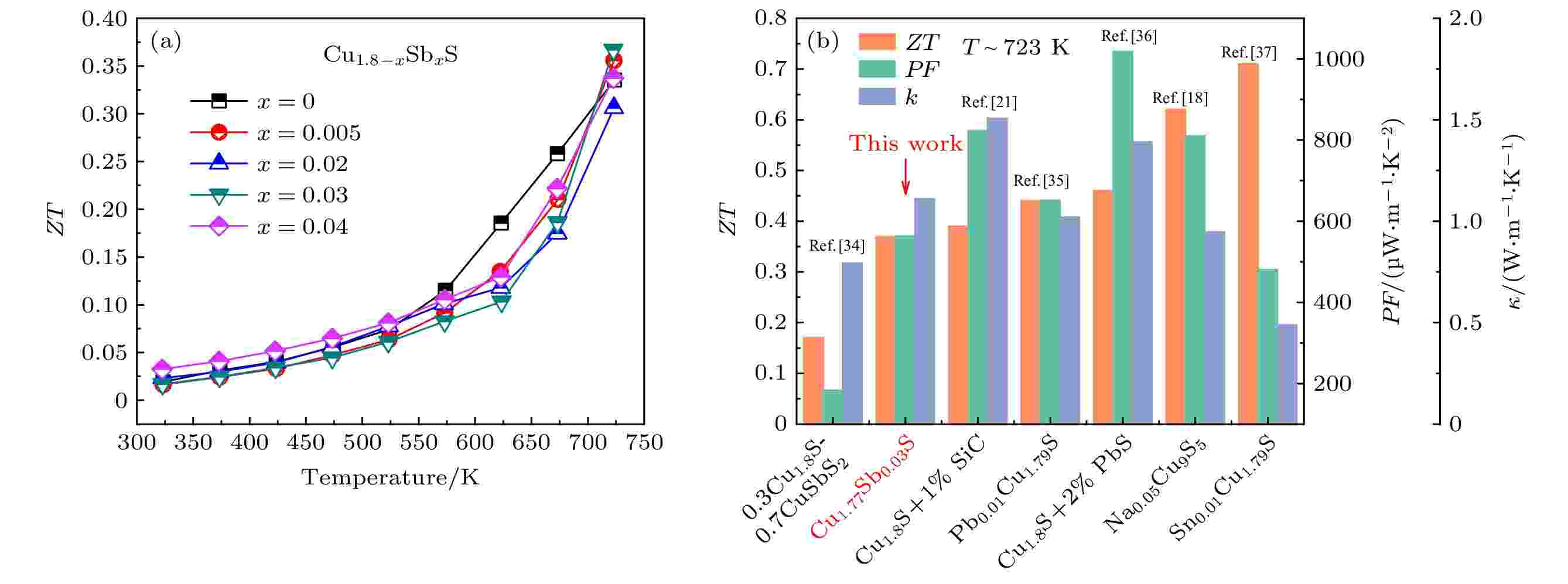
图 6 (a) Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04)块体的ZT值; (b) 723 K时不同Cu_1.8S基材料的热电性能对比^{[18,21,34-37]}
Figure6. (a) Temperature dependence of ZT for Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04) bulks; (b) comparisons of thermoelectric properties of different Cu_1.8S-based materials at 723 K^{[18,21,34-37]}.

通过MA结合SPS烧结技术制备了一系列p型Cu_1.8–x Sb_x S (x = 0, 0.005, 0.02, 0.03, 0.04)合金材料, 研究了Sb元素掺杂对Cu_1.8S的相结构、微观形貌以及热电性能的影响. 得到以下结论:
1)当0 ≤ x < 0.02时, 块体样品为单相Cu_1.8S, 随着Sb的掺杂量继续增加, 出现了第二相CuSbS₂;
2) Sb元素掺杂有效地引入了点缺陷, 与析出的第二相CuSbS₂共同作用增强了声子散射, 显著降低了热导率, 723 K时热导率由1.76 W·m^–1·K^–1(x = 0)降低至0.99 W·m^–1·K^–1 (x = 0.04);
3)块体样品Cu_1.8S在723 K时获得了最高的PF为815 μW·m^–1·K^–2. 在测试温度范围内, x = 0.04样品表现出了最低的热导率(0.99—1.57 W·m^–1·K^–1);
4)当x = 0.03时, 样品Cu_1.77 Sb_0.03S在723 K时获得了最高ZT值0.37, 较未掺杂Cu_1.8S(0.33)提高了12%.