全文HTML
--> --> -->虽然理论上摩尔超晶格系统的构建十分优美, 但是在实验上却是困难重重. 起初, 人们尝试在简单的晶格周期势中添加超晶格的周期势能, 形成子能带. 而传统人工超晶格体系的构建虽然很好地引入了超晶格的周期, 但同时也带来了样品的不均匀性和不够理想的输运性质[2]. 后来随着实验技术的进步, 通过范德瓦耳斯力相结合的二维材料很好地解决了这个问题, 它可以很干净地引入长周期的超晶格[3-9]. 早期最具代表性的是石墨烯/氮化硼(Gr/hBN)体系, 由于石墨烯和氮化硼的晶格匹配引入的长周期势, 使得实验上可以清晰地观测超晶格电阻峰[3-7]和Hofstadter 分形结构[4-6,10]. 但是, 在这个超晶格体系里面, 由于氮化硼与石墨烯的能带色散关系差异巨大, 两者之间无法耦合. 直到2018年, 科学家们在实验上获得了转角石墨烯体系, 这种超晶格体系中两层石墨烯的能带色散关系一致, 引入了层间电子耦合, 成功得到了摩尔超晶格体系中的强关联量子多体体系, 惊讶又毫不意外地发现了超导、铁电、铁磁等一系列凝聚态物理现象. 由此, 摩尔超晶格体系开始引起凝聚态物理学界的大范围关注, 大量优秀的理论和实验凝聚态****开始涉猎这个领域, 相互促进发展.
图 1 “魔角”石墨烯 (a) 摩尔超晶格和摩尔布里渊区示意图[12]; (b) 能带图[13]; (c) 半填充的莫特绝缘态和拱形的超导态[13]; (d) 3/4填充处的量子反常霍尔效应[36]Figure1. Magic angle twisted bilayer graphene: (a) Moiré pattern and the mini Brillouin zone[12]; (b) band energy E of TBG at
如何获得确定转角的石墨烯体系是这项任务的一个难点, 早期科学家们尝试用传统的转移方法, 将剥离的单层石墨烯样品通过直边对准的方式转移到另一个单层的石墨烯样品上. 然而, 这种方法一是很难确定直边的类型究竟是armchair还是zigzag, 二是在角度上很难精准地把控. 直到2016年德克萨斯大学奥斯汀分校的Emanuel Tutuc课题组[14]提出了“tear and stack”的制备方法, 突破了这个难题. 用剥离的氮化硼盖住一整片石墨烯的一半, 揭起氮化硼, 利用范德瓦耳斯力把这一半石墨烯提起, 而另一半留在硅片上, 从而将整片石墨烯一分为二, 再利用转移台旋转一定角度后将两片分离的石墨烯堆垛在一起. 由于上下两层都来自于同一片石墨烯, 因此角度能够得到很精准的把控. 除此之外, 为了尽量将样品做到干净, 可以利用机械力将气泡挤出石墨烯, 但这种方法同时也带来了让角度归零的风险[15,16].
两层石墨烯堆垛的时候, 由于Bernal堆垛(也称AB堆垛)是能量最低的堆垛方式, 因此转角会倾向于Bernal堆垛, 也就是0°转角. 而“魔角”是1.1°转角[11], 非常接近0°, 因此一旦有热、力或其他干扰因素, 会使得这个1.1°的小转角非常容易回到零转角[17-19]或转到大角度[20], 这也是为什么用力将气泡挤出转角石墨烯的时候会有转角变化的风险. 实际上, 早在魔角石墨烯出来之前, 马普所的Jurgen H. Smet课题组[21]、麻省理工的Pablo Jarillo-Herrero课题组[22]和德克萨斯大学奥斯汀分校的Emanuel Tutuc课题组[23]等多个研究小组制备了TBG样品并研究了其低温输运性质, 但是它们的转角要么偏大(约2°), 要么偏小(约0.8°); 罗格斯大学的Eva Y Andrei课题组[24]、北京师范大学的何林课题组[25]在转角石墨烯体系中利用扫描隧道显微镜(STM)测量也研究过TBG, 发现费米速度显著减小, 预示着转角石墨烯的角度接近1.1°的时候可能会有平带的出现.
直到2018年, 曹原和Pablo Jarillo-Herrero等[12]终于克服了这些困难, 成功制备出“魔角”石墨烯, 并证实了该体系中平带的存在. 其中“魔角”石墨烯中的费米速度只有单层石墨烯的1/25, 且在大于40 K时电中性点(CNP)处能够看到电导最小值随载流子浓度的变化是一条平直的线, 而不是像单层石墨烯一样具有CNP处的电阻峰. 同时, 在半填充处, 发现了电导骤降的绝缘态(图1(c)), 在温度达到4 K时绝缘态会相变成金属态, 在磁场逐渐变大的过程中绝缘态会被逐渐抑制, 且该现象与磁场方向无关, 说明绝缘态处的能隙来源于电子自旋劈裂而非轨道磁矩.
更有意思的是, 他们同时发现“魔角”石墨烯在半填充关联绝缘态附近出现了超导现象[13](图1(c)). 超导转变温度为1.7 K, 通过临界电流的测量, 证实了这是个BKT相变, 同时临界电流随磁场的响应图出现了类似于超导量子干涉仪(SQUID)测量中的干涉图样, 这些现象都表明魔角石墨烯是一个二维超导体系. 另外, 垂直临界磁场和水平临界磁场与温度的关系也满足Ginzburg-Landau理论, 但是零温下的临界水平磁场相比计算得到的BCS理论值要稍微大些, 这些现象意味着“魔角”石墨烯体系可能是非常规的超导体. 随后, Andrea F. Young和Cory R. Dean课题组[26]发现通过压力可以在1.27°非魔角转角石墨烯体系中诱导出超导态, 这是因为通过加压的方式可以使得两层石墨烯之间具有更强的耦合, 从而得到压力可调的超导态. 同时, 随着转角样品质量的提高, “魔角”石墨烯具有了更好的均匀性, 在1/4和3/4填充处隐约浮现出电阻峰的迹象. Dmitri K. Efetov课题组[16]通过机械力挤出气泡的方式进一步提高了样品的质量, 通过与Adrian Bachtold课题组[16]合作, 他们在价带和导带的填充数分别为1/4, 1/2, 3/4时都测到了关联绝缘态, 意味着所有的自旋和谷都发生了退简并. 更重要的是, 超导态不仅出现在半填充数处的绝缘态附近, 同时也存在于1/4或3/4填充数的绝缘态附近, 并且具有高达3 K的超导转变温度, 说明样品的质量得到了很大的提升.
以上的实验中, “魔角”石墨烯的超导态总是出现在有绝缘态的时候, 似乎都在指向TBG中超导态的本质来源类似于非常规超导. 然而, 后续实验的跟进渐渐出现了不同的声音, 一些****发现当在“魔角”石墨烯体系中叠上一层WSe2后, 由于WSe2会在TBG中引入强的自旋轨道耦合, 超导态不仅能与绝缘态相互独立存在, 且超导态相比于单纯的TBG体系能够在更小的角度下存在, 这意味着绝缘态和超导态的物理来源可能不一样[27]. 同时, ****们发现当使用更薄的氮化硼介电层时, 超导态能够在没有关联绝缘态的情况下出现, 这意味着库仑屏蔽效应可能会影响超导态和绝缘态产生[28,29]. 针对这个问题, J. I. A. Li课题组[30]利用原位过程系统地研究了库仑屏蔽效应对“魔角”石墨烯体系中超导态和绝缘态的的影响. 作者在TBG体系上设计了可调的Bernal双层石墨烯堆垛的调控层, 通过调控双层石墨烯中的载流子浓度来达到定量调控TBG中库仑屏蔽的目的. 实验发现由于屏蔽作用导致TBG中库仑相互作用变弱时, 绝缘态被削弱而超导态增强, 这种现象类似于常规超导体中弱的库仑相互作用会稳固超导, 其本质来源于电声耦合. 这进一步说明了TBG中随温度变化呈线性的电阻可能不一定来源于类似高温铜氧化物中的奇异金属[31,32], 也可能来源于常规超导体中的电声耦合[33,34]. 总的来说, “魔角”石墨烯体系中的超导是否是常规超导还不得而知, 后续还需要更多的实验来论证.
除了关联绝缘态和超导态之外, 斯坦福大学的David Goldhaber-Gordon课题组[35]在转角石墨烯体系导带填充数为3/4处发现了铁磁态, 测到了反常霍尔信号和磁滞回线, 他们认为这是由于封装的hBN和TBG对齐的结果. 之后, Andrea F. Young课题组[36]进一步的实验确认了在和hBN对齐的TBG样品中存在陈数为1的量子反常霍尔效应, 如图1(e)所示. 铁磁态往往来源于铁、钴、镍等带磁性的原子, 或者来源于重金属元素引入的自旋轨道耦合效应. 而转角石墨烯不满足以上任何一个条件, 因此****们推测是因为TBG与hBN对齐后打破C2对称性并引入带隙, 与TBG中强关联的摩尔平带共同作用形成陈绝缘体, 从而可以在实验上测得铁磁态和量子反常霍尔效应.
后来****发现不需要TBG和hBN对齐也可以观测到非平庸的拓扑物态. 此时C2对称性保持, 但是时间反演对称性(
总而言之, 自从“魔角”石墨烯出现以来, 超导、关联绝缘态、拓扑、磁性等现象引起了人们广泛的关注. 其中层出不穷的新现象还留有诸多疑问, 但不可否认的是, 转角石墨烯体系是凝聚态物理中一个崭新的体系分支, 它的出现可以为强关联体系提供一个新的研究思路, 推进凝聚态物理的发展.
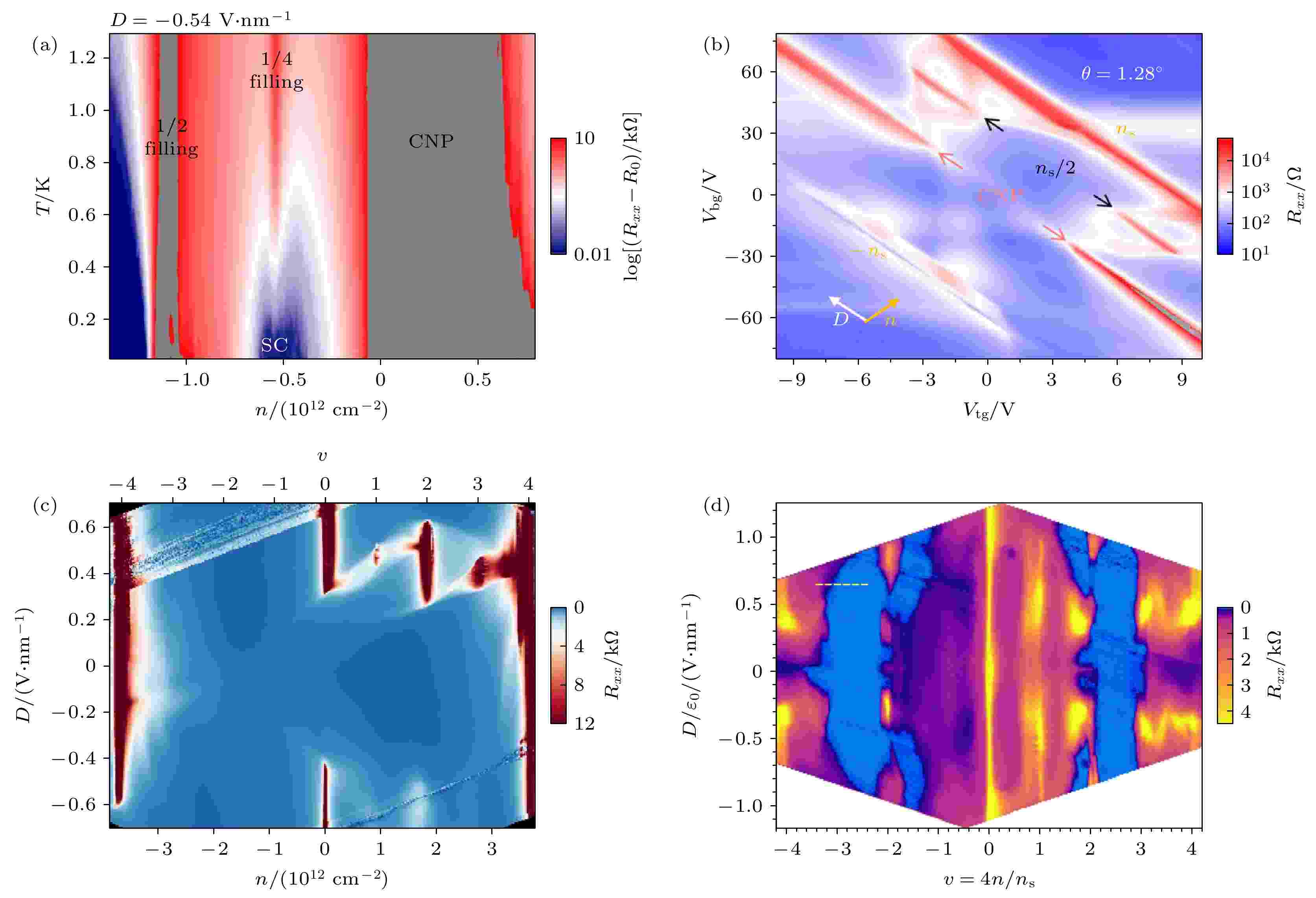图 2 电场可调的多层石墨烯转角体系 (a) ABC堆垛的三层石墨烯/氮化硼摩尔超晶格中关联绝缘态和超导态[43]; (b) 转角双层-双层石墨烯(TDBG, 2+2)中的关联绝缘态[45]; (c) 转角单层-双层石墨烯(TMBG, 1+2)中的关联绝缘态[54]; (d) 转角三层石墨烯体系(MATTG, 1+1+1)中的超导态[56]Figure2. Field tunable multilayer graphene twisted moiré superlattice systems: (a) Signatures of Mott insulator and the superconducting (SC) phase in ABC-trilayer graphene/hBN superlattice[43]; (b) correlated insulating states in twisted double bilayer graphene (TDBG)[45]; (c) correlated insulating states in twisted monolayer-bilayer graphene (TMBG)[54]; (d) MATTG phase diagrams, and the superconductivity is colored in blue[56].
除了对称的转角石墨烯体系, 在非对称的单层-双层转角石墨烯(TMBG)体系中, 也发现了非对称的关联绝缘态(图2(c)), 同时存在类似超导的迹象和铁磁态[53-55]. 最近, 麻省理工的Pablo Jarillo-Herrero课题组[56]、哈佛大学的Philip Kim课题组[57]在转角三层石墨烯体系中取得重要进展. 转角三层石墨烯样品, 即“1+1+1”体系, 第一层和第三层石墨烯相对于中间层石墨烯的转角分别为
此外, 在转角硒化钨(WSe2)中, 发现了大转角范围内的关联绝缘态[58]. 在转角硒化钨/硫化钨(WSe2/WS2)异质结中发现了莫特绝缘态和维纳尔晶格态[59,60]. 另外, 在WSe2/WS2[61], MoSe2/WS2[62]和MoSe2/WSe2[63,64]转角超晶格中都发现了摩尔激子.
德克萨斯大学奥斯汀分校的Allan H. MacDonald课题组[68]在研究二维TMD摩尔超晶格异质结体系时最早提出, 由于这个体系产生的平带可以被一个简单的三角格点Hubbard模型来描述, 相关的参数, 特别是体系动能与多体相互作用强度的比率, 可以较好地由转角来调控, 因此可以利用这个体系来研究三角格点Hubbard模型的物理. 这个理论预测后来得到了加州大学伯克利分校的Feng Wang课题组[59]和康奈尔大学的Jie Shan和Kin Fai Mak课题组[60]的实验验证. 他们分别通过光学与电输运的实验测量发现, 当价带顶的第一条超晶格能带被半填充时, WSe2/WS2 摩尔超晶格体系会出现一个具有Curie-Weiss行为的反铁磁莫特绝缘态(图3(a)). 这一现象与三角格点Hubbard模型在强电子关联效应下的预期一致. 此外, Jie Shan和Kin Fai Mak课题组[69]进一步的实验发现, 在这个WSe2/WS2摩尔超晶格体系中, 当价带顶能带处于一系列分数填充时, 即当填充数ν = 1/2, 2/5, 1/3, 1/4, 1/7等, 也会出现一些特殊的关联绝缘态(图3(b)). 这些关联绝缘态所处的分数填充值以及大部分关联绝缘态的转变温度, 都与包含长程电子关联相互作用的扩展Hubbard模型描述的结果符合. 因此支持了可以将摩尔超晶格作为研究Hubbard模型强关联体系的量子模拟器的想法.
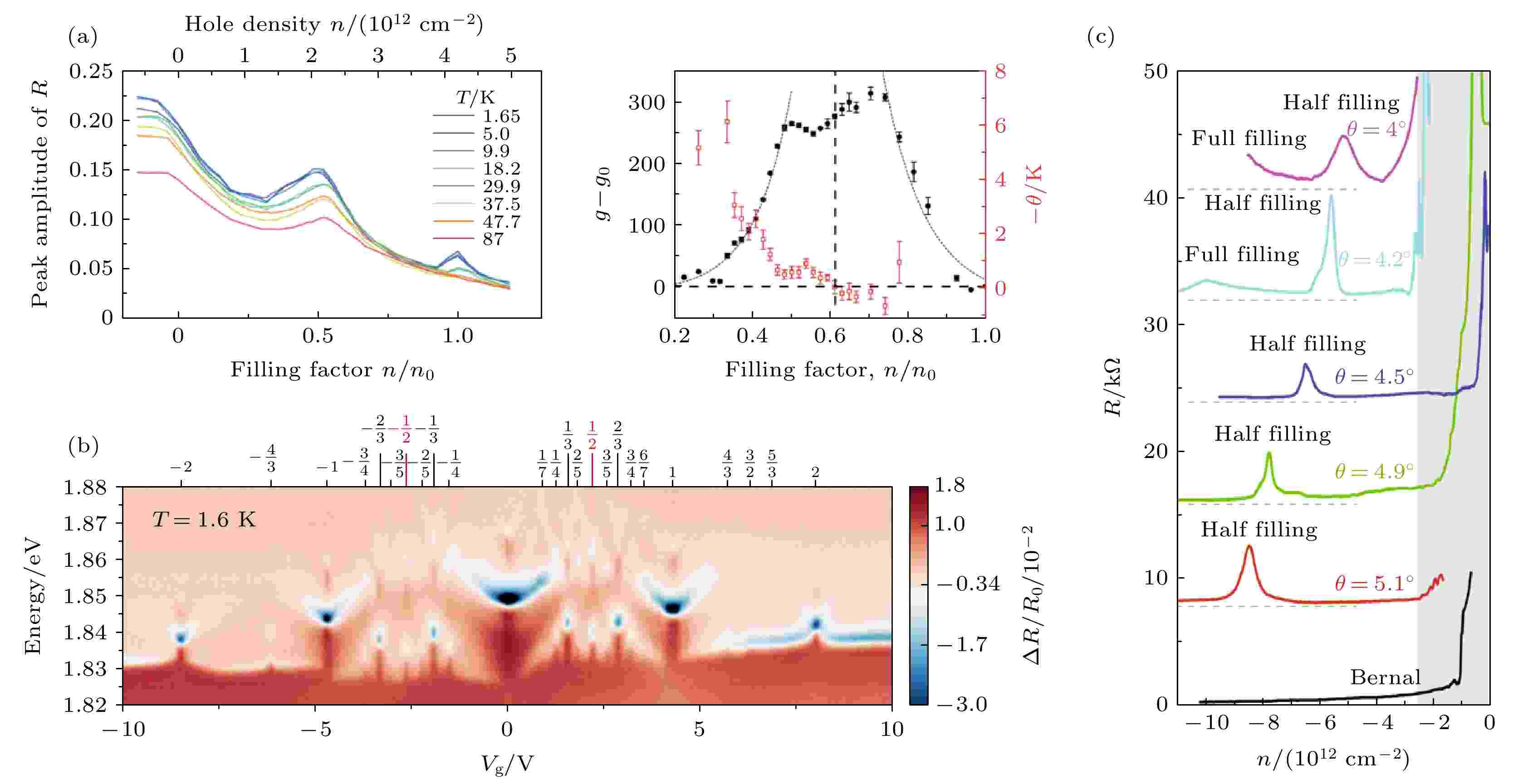图 3 转角过渡金属硫化物的关联效应 (a) WSe2/WS2异质摩尔超晶格半填充处的莫特绝缘态和不同填充处下的磁化率
Figure3. Correlated insulating states in twisted TMD superlattice: (a) Signature of correlated insulator at half filling in WSe2/WS2 moiré superlattice[60]; (b) fractional insulating states in WSe2/WS2 moiré superlattice[69]; (c) transport signature of half filling insulator in twisted WSe2/WSe2 moiré superlattice[58].
同一时期, 哥伦比亚大学的Cory R. Dean和Abhay N. Pasupathy课题组与马普所的Angel Rubio课题组[58]合作, 通过实验与理论结合的方法, 在双层转角WSe2体系中, 也发现了半填充关联绝缘态的存在, 见图3(c), 并且这些关联绝缘态的行为可以被三角格点Hubbard模型描述. 他们因此也提出可以通过研究这种摩尔超晶格体系来研究二维三角格点强关联体系. 理论研究上, 除了Allan H. MacDonald课题组的工作, 马普所的Angel Rubio课题组也通过一系列工作, 利用第一性原理计算和强关联计算方法, 预测了在双层转角hBN[70]、双层转角MoS2[71]以及双层转角GeSe[72]中, 在转角较小的情况下也能产生平带, 并且这些平带分别可以作为研究二维三角格点、六方蜂巢格点、准一维格点强关联体系的量子模拟平台, 并通过总结相关的理论和实验工作, 正式提出摩尔超晶格体系可以作为基于凝聚态体系的量子模拟器来研究各种量子关联体系, 并展望了摩尔量子模拟器未来的发展[73].
基于摩尔量子模拟器的成功, 理论上能更准确地预测实验体系和材料, 也为今后二维摩尔超晶格体系的研究指明方向.
