删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

无造影剂增强的超快超声脊髓微血管成像方法

本站小编 Free考研考试/2021-12-29
摘要:微小血管及其血流实时成像对监测生物体血氧代谢等具有重要意义. 在无微泡造影剂的情况下, 传统超声多普勒技术仍较难实现高信噪比的微小血管成像. 本研究提出了一种无造影剂增强的超快超声脊髓微血管成像方法. 本研究从基于多角度复合平面波的高帧频成像技术出发, 提出基于特征值分解的频率-幅值双阈值滤波法, 从而将脊髓组织信号和微血流信号分离, 可实现脊髓内微血流的动态成像. 在体成像实验结果表明, 无超声造影剂时, 超快超声多普勒成像技术仍可获得较为清晰的大鼠脊髓内微血流的实时图像, 并能够清晰地呈现脊髓受损所致的微血流缺失状况. 定量分析结果表明, 增大复合平面波角度数可有效提高图像的信噪比. 综上, 超快超声多普勒成像技术有潜力被应用于脊髓内微血管成像及功能实时监测与动态评价, 相关结果可为脊髓功能成像方法的研究提供借鉴.
关键词: 超快超声多普勒/
杂波滤除/
特征值分解/
脊髓微血管

English Abstract


全文HTML

--> --> -->
1.引　言
脊髓损伤往往会引起脊髓内血管网络受损和局部血流灌注量缺失, 进而引发继发性功能损伤[1-3], 如下肢功能障碍等, 这会给家庭和社会带来巨大负担[4]. 近年来, 针对脊髓损伤的血流成像与功能诊断方法已成为国内外学界的研究热点与重点[5-7].
目前对在体微小血管成像及分析血流动力学变化的方法包括电子计算机断层扫描血管造影(computed tomography angiography, CTA)[8,9]、磁共振血管造影(magnetic resonance angiography, MRA)[10]和超声多普勒成像技术[11,12]. CTA[13]和MRA[14]的血管成像分辨率可达到50和100 μm, 但以上两种技术存在扫描时间长、电离辐射和设备笨重等不足, 限制了其在实时血流成像领域的应用.
超声成像具有无辐射、便携与快速的特点, 当前超声多普勒成像技术已被广泛应用于人体血流成像以及包括血管内斑块与血栓等疾病的临床诊断与分析[15,16]. 近十年来, 基于平面波成像方法的超快超声多普勒成像技术得到了较快发展[17,18]. 相较于传统的波束聚焦成像方法, 平面波成像可大幅度提高成像帧频[19](由每秒几十帧提升至上万帧), 从而可用于观测血流量、流速和血管直径的瞬时微小变化并进行血流动力学分析. 顾名思义, 平面波方法所发射的是非聚焦声波; 因而, 与传统聚焦波束的成像方法相比, 单帧平面波成像存在信噪比(signal to noise ratio, SNR)低、对比度差的缺点. 就此, 2009年Montald等[20]提出了多角度平面波相干合成的方法, 实验结果表明该方法能够在保证高成像帧频的同时, 提高成像结果的SNR、对比度和分辨率. 2011年, Mace等[21]提出基于平面波发射的超声功能成像方法, 分别在刺激胡须和癫痫发作情况下对大鼠脑血流进行了高时空分辨率成像, 依据血流变化动态监测结果识别相关脑功能活动区. 2013年, Mace等[22]深入介绍了超快超声成像方法, 并与传统多普勒成像方法相对比, 通过大鼠脑的在体实验证明了该方法能有效提高微小血管血流变化的监测灵敏度. 2017年, Demene等[23]将超快超声多普勒成像技术应用于新生儿的脑血流成像, 在新生儿睡眠状态下观察了活跃态和安静态脑区的血流变化, 为脑功能超声成像技术的应用与发展开拓了前景.
相较于脑血流成像, 脊椎复杂的骨结构特征和呼吸运动的干扰给脊髓内微血流超声成像带来挑战[24], 2018年, Khaing等[7]应用超声微泡造影剂对椎板打开条件下的大鼠脊髓血流进行了对比度增强超声成像(contrast-enhanced ultrasound, CEUS), 成功观察到了脊髓中的微血管结构. 近期研究表明, 超快超声可在无造影剂条件下实现脑微血管成像[23], 但该技术在脊髓内的微血流成像仍待深入. 另外, 相关多角度成像方法、杂波滤除技术以及多普勒频偏分析等研究仍待探讨.
本文提出了一种无需注射超声造影剂的超快超声多普勒成像方法, 该方法基于超快超声平面波发射与接收序列, 利用基于爆炸反射器模型(exploding reflector model, ERM)的频率-波数域迁移(fk-migration)算法进行图像重建; 并利用基于特征值分解(eigenvalue decomposition, EVD)的频率-幅值双阈值滤波法进行动态血流信号与静态组织信号的分离, 最终实现了动态血流的功率多普勒成像. 本文进行了仿体实验和大鼠脊髓在体实验, 平面波成像帧频大于万帧每秒, 获得了脊髓内微血流的高时空分辨率的成像结果, 并探讨了超快多普勒血流成像中复合平面波角度数对成像质量的影响.
2.基本原理
方法流程示意如图1所示, 首先发射多角度平面波序列对感兴趣区域进行高帧频成像, 应用fk-migration算法进行波束合成并对多角度成像结果进行相干叠加. 随后, 对一段时间内得到的图像进行EVD处理, 采用频率-幅值双阈值滤波法进行杂波滤除, 从而提取动态血流信号. 最终, 对多帧血流图像进行叠加平均获得功率多普勒成像结果.
图 1 方法流程示意
Figure1. Flow chart of the proposed method.

2
2.1.超快超声成像
-->

2.1.超快超声成像

文中所用超快超声成像序列如图2所示. 该成像序列由若干个子序列构成, 每个子序列发射一组N角度的倾斜平面波并接收反射回波, 不断重复子序列从而进行连续成像. 为避免连续两次接收到的回波信号发生混叠, 脉冲发射时间间隔要大于超声波在成像区域往返一次所需的最长时间, 该时间所对应的最高极限帧频K, 其计算公式如下: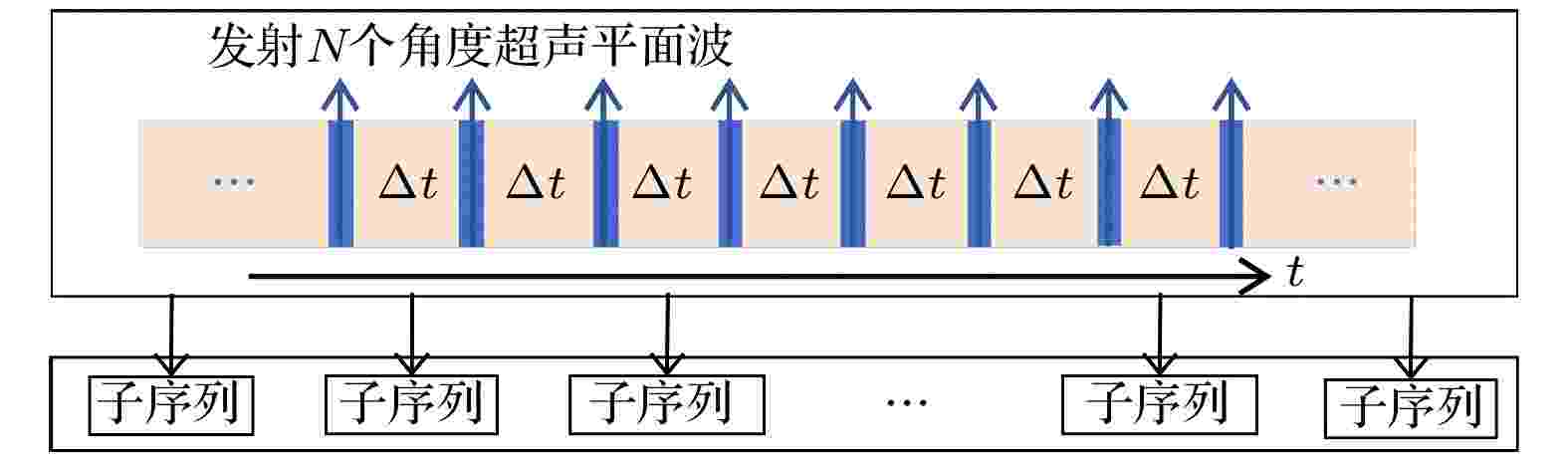
图 2 超快超声成像序列示意图
Figure2. Schematic diagram of ultrafast ultrasound imaging sequence.

$K={1}/({N \cdot \Delta t}),$
式中$ \Delta t $表示超声波在成像区域对角线长度上的往返走时,
$\Delta t=2 \cdot {\sqrt{{d}^{2}+{L}^{2}}}/{c},$
其中d表示成像区域的深度, L表示超声换能器阵列的总长度, c表示超声波的传播速度.
2
2.2.基于ERM模型的波束合成方法
-->

2.2.基于ERM模型的波束合成方法

2013年, Damien等[25]将Stolt提出的fk-migration算法应用于平面波成像, 并结合ERM模型进行波束合成, 从而实现图像重建. 相较于传统的延时叠加算法, fk-migration算法能够提高成像质量和计算效率, 计算过程中应用快速傅里叶变换算法可在保持图像高SNR和横向分辨率的前提下进一步提高计算速度[25].
3
2.2.1.ERM模型
-->
2.2.1.ERM模型
超声波在传播过程中遇到一系列散射子会发生散射, 反向散射回波会被超声换能器阵列接收. 超声波发射与回波接收模型如图3(a)所示, $ t=0 $时刻起, 某一阵元受到脉冲激励而发射超声波, 声波传播至($ {x}_{1} $, $ {z}_{1} $)处的散射子, 产生反向散射回波并最终由($ {x}_{0}, 0 $)处的阵元接收, 全过程时长为[25]
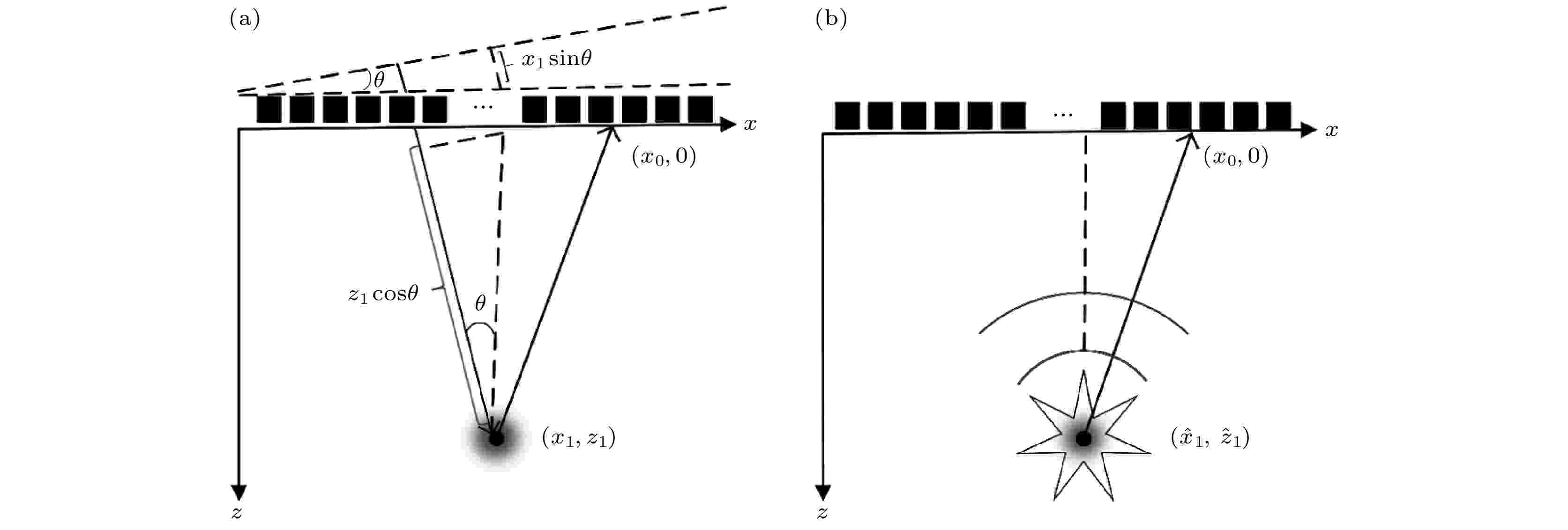图 3 超声波传播模型　(a) 超声波发射与回波接收模型; (b) ERM模型
Figure3. Ultrasonic propagation model: (a) Ultrasonic transmitting and echo receiving model; (b) exploding reflector model (ERM).

$\tau =\frac{{x}_{1}\mathrm{sin}\theta +{z}_{1}\mathrm{cos}\theta +\sqrt{{{z}_{1}}^{2}+{\left({x}_{1}-{x}_{0}\right)}^{2}}}{c},$
其中c表示超声波的传播速度, $ \theta $表示倾斜平面波的角度, 该角度可由控制换能器阵列的脉冲发射延时加以实现.
另外, 建立一个ERM模型, 如图3(b)所示, 该模型中假设(${\hat{x}}_{1}$, ${\hat{z}}_{1}$)处的散射子是$ t=0 $时刻产生反向散射回波的二次声源[26], 超声波传播的总时长为[25]
$\hat{\tau }=\frac1{\hat{c}} {\sqrt{{\hat{z}}_{1}^{2}+{\left({\hat{x}}_{1}-{x}_{0}\right)}^{2}}},$
其中$\hat{c}$表示ERM模型中超声波的传播速度.
为使ERM模型与上述超声波发射与回波接收模型等效, 令(4)式计算所得时长与(3)式及其一、二阶导数式相等, 通过解方程组可得如下参数变换[25]:
$\hat{c}=\frac{c}{\sqrt{1+\mathrm{cos}\theta +{\mathrm{sin}^2\theta }}},$
${\hat{z}}_{1}={z}_{1}\frac{{\left(1+\mathrm{cos}\theta \right)}^{\frac{3}{2}}}{1+\mathrm{cos}\theta +{\mathrm{sin}^2\theta }},$
${\hat{x}}_{1}={x}_{1}+{z}_{1}\frac{\mathrm{sin}\theta }{2-\mathrm{cos}\theta }.$

3
2.2.2.频率-波数域波束合成
-->
2.2.2.频率-波数域波束合成
首先, 对波动方程进行傅里叶变换可得亥姆霍兹方程[25]
$\left(\frac{{\partial }^{2}}{\partial {z}^{2}}+4{\mathrm{\pi }}^{2}{\hat{k}}_{z}^{2}\right)p\left(x, z, t\right)=0,$
其中$ p\left(x, z, t\right) $表示$\left(x, z\right)$处t时刻的声场, ${\hat{k}}_{z}$表示z轴方向上的波数分量, 由下式计算所得[25]:
${\hat{k}}_{z}^{2}= {{f}^{2}}/{{\hat{c}}^{2}}-{k}_{x}^{2},$
其中f表示超声波的频率, $\hat{c}$表示经(5)式参数变换后的声波传播速度, $ {k}_{x} $表示x轴方向上的波数分量. (8)式的解为[25]
$p\left(x, z, t\right)=P{\mathrm{e}}^{\mathrm{i}2\mathrm{\pi }\left({k}_{x}x+{\hat{k}}_{z}z-ft\right)}, $
其中P表示声场强度幅值.
由Stolt所提出的fk-migration算法中, 频域映射方式为[25]
$f\big({\hat{k}}_{z}\big)=\hat{c}\,\mathrm{s}\mathrm{g}\mathrm{n}\big({\hat{k}}_{z}\big)\sqrt{{k}_{x}^{2}+{\hat{k}}_{z}^{2}}, $
其中sgn函数为符号函数. 频率域傅里叶变换之后, 需对倾斜平面波的发射延时进行相位补偿, 其二维傅里叶变换的公式为[25]
$ \phi (x, z, f) \!=\!\int _{-\infty }^{+\infty }p\left(x, z, t\right){\mathrm{e}}^{-\mathrm{i}2\mathrm{\pi }ft}{\mathrm{e}}^{-\mathrm{i}2\mathrm{\pi }f\tfrac{x\mathrm{s}\mathrm{i}\mathrm{n}\theta }{c}}\mathrm{d}t,$
$ \mathrm{\varphi }\left({k}_{x}, z, f\right)=\int _{-\infty }^{+\infty }\phi \left(x, z, f\right){\mathrm{e}}^{\mathrm{i}2\mathrm{\pi }{k}_{x}x}\mathrm{d}x,$
其中$ \phi \left(x, z, f\right) $是对回波信号进行了时频域傅里叶变换以及相位补偿的结果, $ \varphi \left({k}_{x}, z, f\right) $是进行了频率-波数域二维傅里叶变换的结果, 二维傅里叶逆变换的公式为[25]
$\hat{p}(x, z, t)\!=\!{\left(\frac{1}{2\mathrm{\pi }}\right)}^{2}\!\!\!\!\iint _{-\infty }^{+\infty }\!\!\varphi \left({k}_{x}, z, f\right){\mathrm{e}}^{\mathrm{i}2\mathrm{\pi }\left({ft-k}_{x}x\right)}\mathrm{d}{k}_{x}\mathrm{d}f.$

2
2.3.基于EVD的频率-幅值双阈值滤波法
-->

2.3.基于EVD的频率-幅值双阈值滤波法

超声探头接收到的全部回波信号由组织、血流回波信号和噪声信号组成. 应用基于EVD的频率-幅值双阈值滤波法[27]进行血流信号的提取时, 首先对多帧图像进行特征值分解, 计算公式为[28]
$\mathrm{E}\left({{A}}^{\mathrm{T}}{{A}}\right)=\sum\limits_{k}{{\lambda }}_{k}{{e}}_{k}{{e}}_{k}^{\mathrm{T}},$
其中$ {{A}} $为$ ({n}_{x}\times {n}_{z}, {n}_{t}) $的二维矩阵, 由(14)式大小为$ ({n}_{x}, {n}_{z}, {n}_{t}) $三维时空矩阵$\hat{p}\left(x, z, t\right)$整合得到; $ {{{A}}}^{\mathrm{T}} $表示$ {{A}} $的转置矩阵, $ {{\lambda }}_{k} $表示第k个特征值, $ {{e}}_{k} $表示第k个特征向量. 每一个特征向量的多普勒频移$ {f}_{\mathrm{D}} $计算公式为[28]
${f}_{\mathrm{D}}=\frac{\mathrm{P}\mathrm{R}\mathrm{F} \cdot \mathrm{arg}\left(R\left(1\right)\right)}{2 \cdot \mathrm{\pi }}, $
其中$ \mathrm{P}\mathrm{R}\mathrm{F} $表示脉冲重复频率, $ R\left(1\right) $表示一个单位的延时自相关, 其计算公式为[28]
$R\left(1\right)=\frac1{{n}_{t}-1}{\sum\limits_{j=0}^{{n}_{t}-2}{{e}}_{k}^{*}\left(j\right)*{{e}}_{k}^{*}\left(j+1\right)}.$
因为静态组织信号对应特征值大、多普勒频移低的特征向量成分, 动态血流信号对应特征值小、多普勒频移高的特征向量成分[28], 所以可设定一个频率阈值和一个幅度阈值, 将多普勒频移小于频率阈值且特征值大于幅度阈值的特征向量加以滤除. 最后进行矩阵重构, 得到动态血流信号为${\hat{p}}_{\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w}}\left(x, z, t\right)$.
2
2.4.功率多普勒成像
-->

2.4.功率多普勒成像

当超声波通过血管时, 一部分能量被红细胞散射并由超声换能器阵列接收反向散射回波. 多普勒超声成像通过重复发射超声脉冲来监测血流中红细胞的运动从而得到血流变化的信息. 功率多普勒模式下平均强度的计算公式为[22]
${P}_{\mathrm{D}}\left(x, z\right)=\frac{1}{{n}_{t}}\sum\limits_{t=1}^{{n}_{t}}{\left|{\hat{p}}_{\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w}}\left(x, z, t\right)\right|}^{2}.$

3.实验设置
多通道超声数据发射与采集在可编程的Vantage 256相控超声实验平台(Verasonics Inc, WA, USA)上进行. 探头型号为L22-14vX, 包含128个阵元, 中心频率为15.625 MHz, 阵元间距为0.1 mm. 信号采样频率为62.5 MHz, 数据经由总线传输至计算机.
仿体采用长6 cm、宽5 cm、高5 cm的琼脂块, 在6—8 mm深处制备直径为2 mm的管路以模拟血管. 用注射泵以0.1 mL/s的速度将混有散射子的悬浊液注入中管道中模拟血流. 仿体测量中采用每秒3500次的超快超声脉冲发射序列, 该序列由500个子序列构成, 各子序列由–10°—10°之间等间隔分布的7个倾斜平面波组成, 复合成像帧频为每秒500帧. 成像区域为15.0 mm × 12.7 mm的矩形成像区域.
在体实验对象为Sprague-Dawley大鼠(雄性, 7周龄, 体重约350 g). 通过手术将T13-L2段椎弓板和棘突切除, 克服超声经过椎骨所致能量衰减. 用异氟烷麻醉大鼠(5%用于诱导麻醉, 2.5%—3.0%用于术中维持麻醉). 随后, 制作刺入型脊髓损伤模型. 实验结束时, 大鼠脱位处死. 实验中采用每秒14040次的超快超声平面波发射序列, 该序列由520个子序列构成, 每个子序列发射–10°—10°之间等间隔分布的27个倾斜角度平面波, 因此, 复合成像帧频为每秒520帧. 实际成像区域为14.0 mm × 12.7 mm的矩形成像区域(实验设定的成像深度为5.9 mm, 实际成像深度是设定成像区域的对角线长度). 实验装置示意如图4所示.
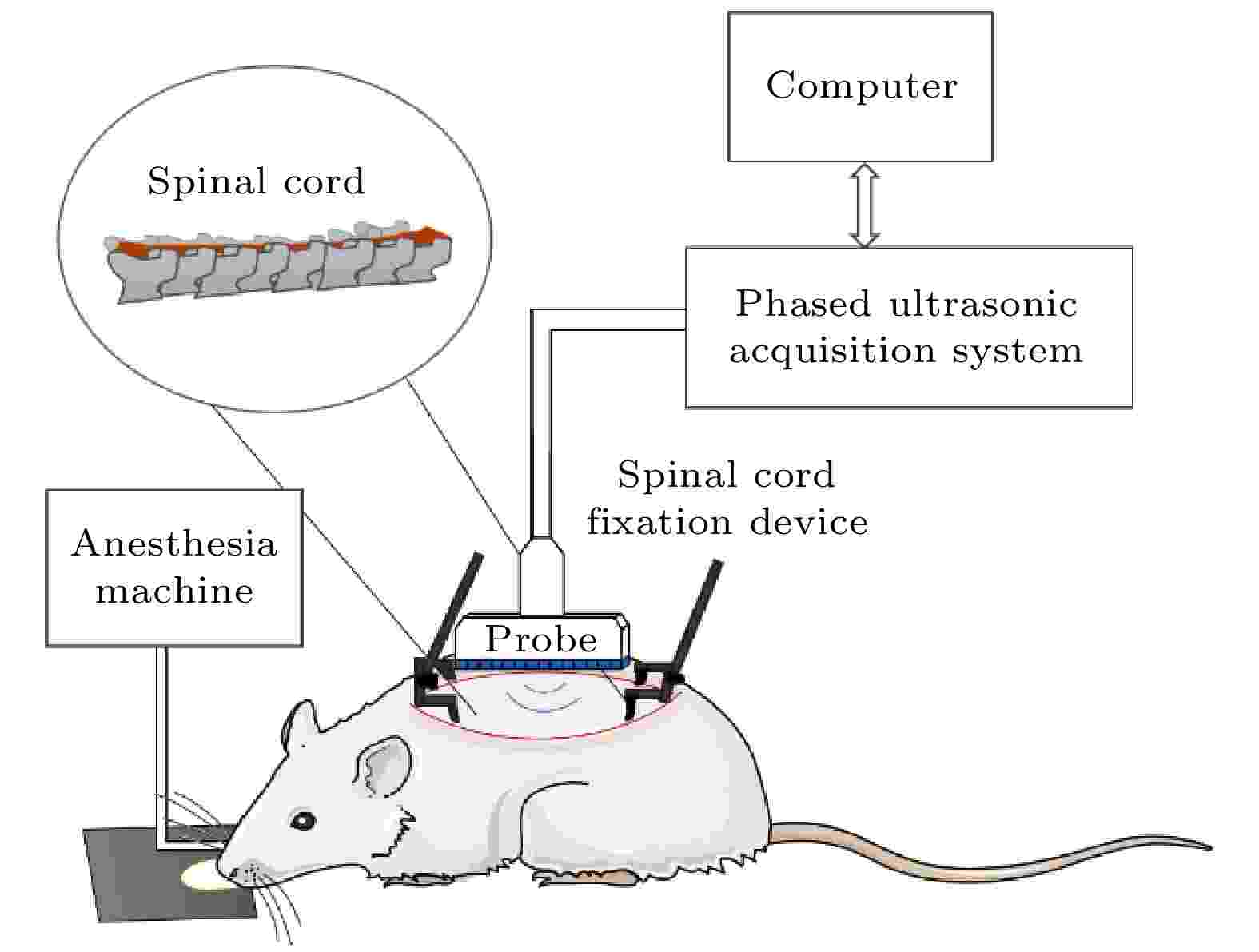图 4 大鼠脊髓血流超声成像实验装置示意
Figure4. Schematic diagram of experimental ultrasonic imaging set-up for blood flow of rat spinal cord.

4.实验结果
2
4.1.仿体实验结果
-->

4.1.仿体实验结果

对1 s内获得的回波数据进行波束合成与多角度平面波相干叠加, 共得到500帧复合B模式图像. 为提取仿体血流信号, 对500帧图像数据进行EVD处理和特征向量的多普勒频移分析. 特征值阈值选取会影响超快超声功率多谱勒成像结果的对比度和SNR, 相关选取标准仍有赖于经验性参数[28]. 通常, 动态血流信号对应多普勒频移高且特征值小的信号成分, 静态组织信号对应多普勒频移低且特征值大的信号成分. 图5(a)为归一化多普勒频移对应的特征向量个数的直方图, 纵坐标为特征向量个数. 由图可得, 低频分量集中分布在归一化多普勒频移小于0.1的区间, 因此将截止频率设为0.1以滤除低频组织信号. 在体实验中也采用了该阈值参数. 图5(b)为数据集的特征向量与特征值的对应关系, 图5(c)为特征向量与归一化多普勒频移的对应关系, 图5(d)为特征值与归一化多普勒频移的对应关系, 图中虚线为归一化多普勒频移为0.1的阈值线, 实线为幅值为–80 dB的阈值线. 将多普勒频移小于0.1且特征值大于–80 dB的特征向量滤除, 重建后的成像结果(第400帧)如图6所示. 图6(a)—(d)分别是滤波前的仿体成像结果、滤波后的仿体血流图、滤波后的仿体软组织图和仿体血流的功率多普勒成像结果. 如图6(d)所示, 通过上述杂波滤除方法可以得到6—8 mm深度处仿体血流的功率多普勒成像结果.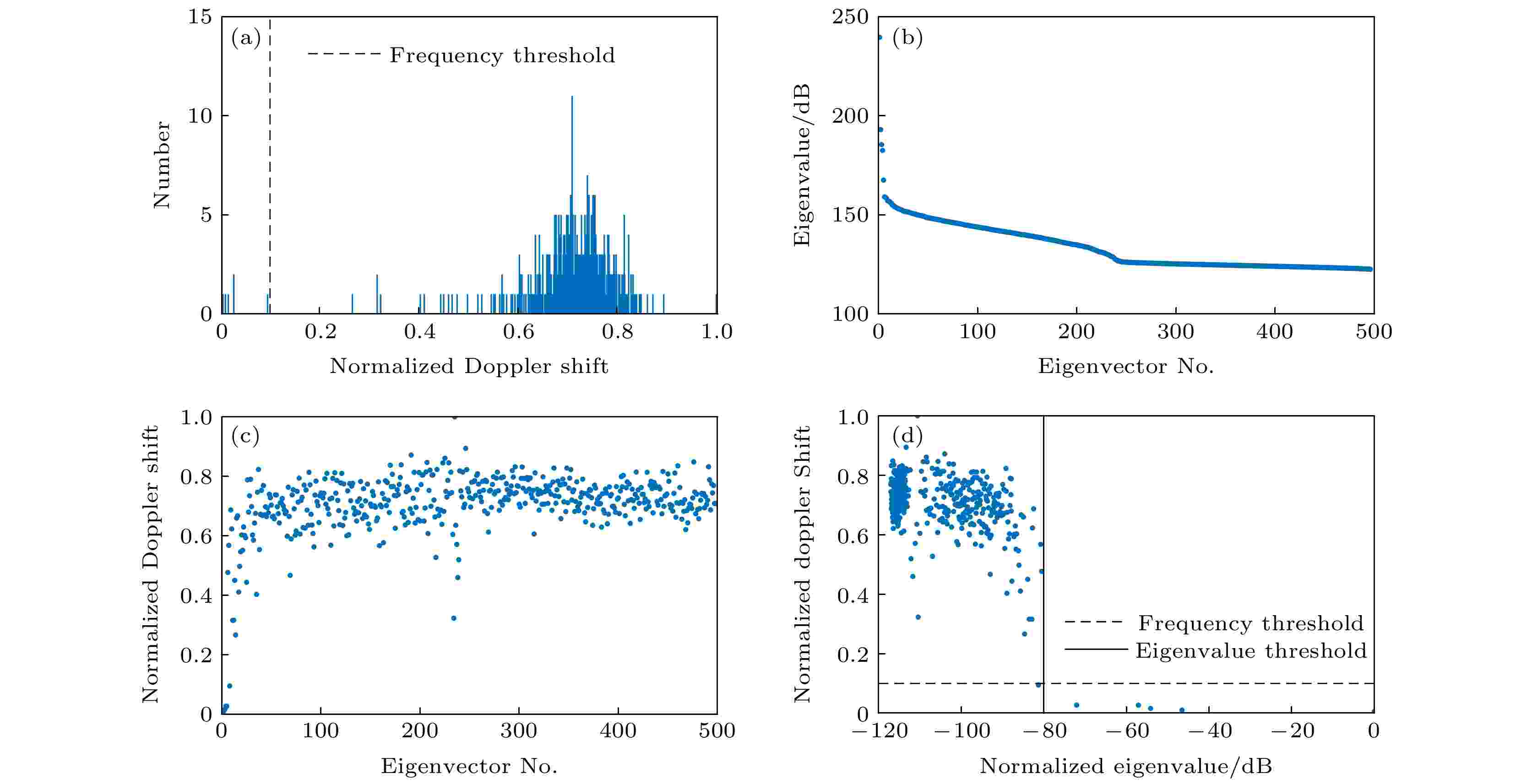
图 5 特征值分解与多普勒频移分析结果　(a) 归一化多普勒频移对应特征向量个数的直方图; (b)特征向量的特征值; (c) 特征向量的归一化多普勒频移; (d) 特征值对应的归一化多普勒频移
Figure5. Eigenvalue decomposition and Doppler shift analysis results: (a) Histogram of the number of eigenvectors corresponding to normalized Doppler shifts; (b) eigenvalues of eigenvectors; (c) normalized Doppler shifts of eigenvectors; (d) eigenvalues versus normalized Doppler shifts.

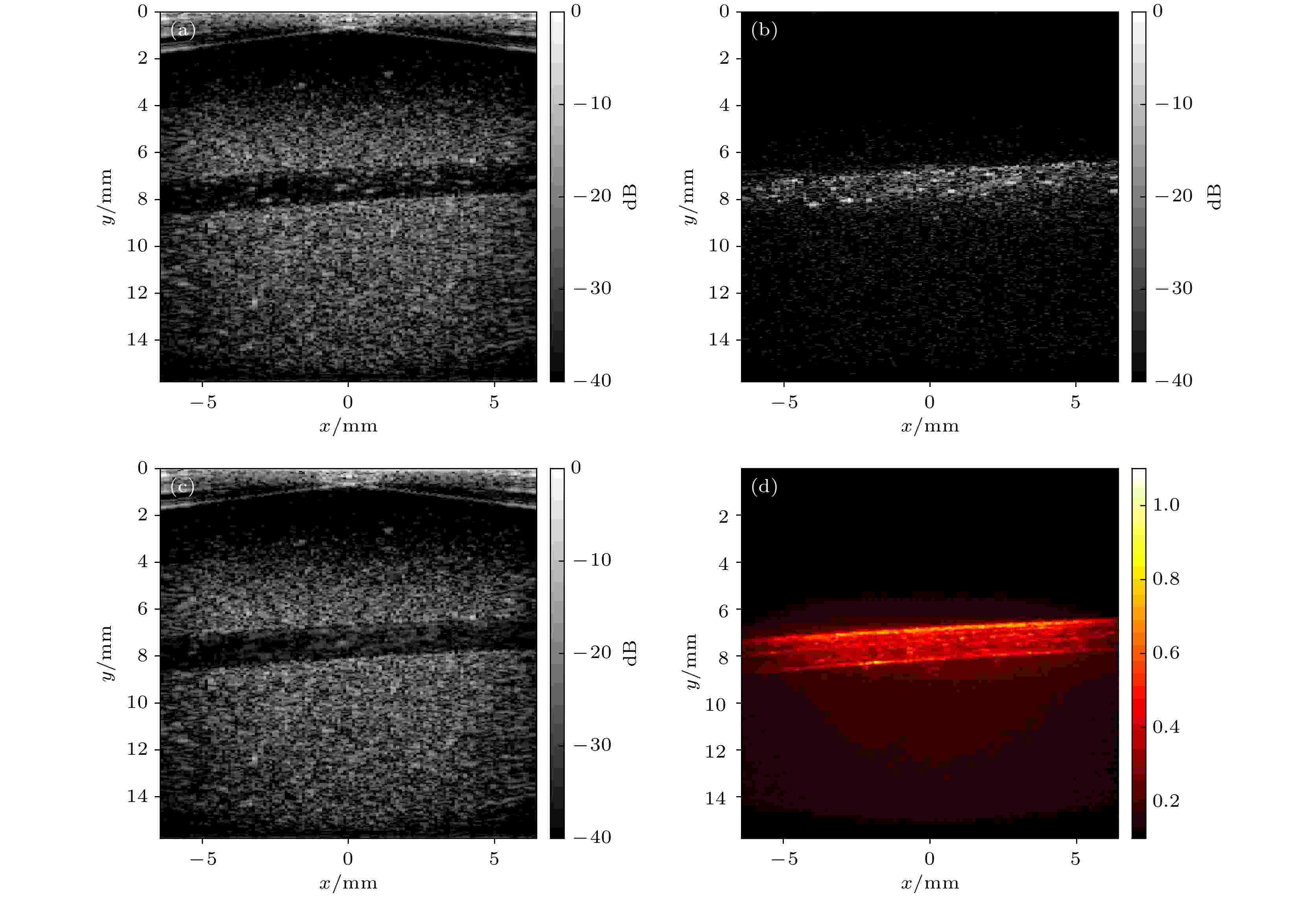图 6 仿体血流成像结果(第400帧)　(a) 滤波前的成像结果; (b) 滤波后的血流成像结果; (c) 滤波后的软组织成像结果; (d) 功率多普勒成像结果
Figure6. Imaging results of the 400th frame of the phantom blood flow: (a) Original image before clutter filtering; (b) blood flow image after clutter filtering; (c) soft tissue image after clutter filtering; (d) power Doppler imaging result.

2
4.2.大鼠在体实验结果
-->

4.2.大鼠在体实验结果

对1 s内得到的回波数据进行波束合成与多角度平面波相干叠加, 共得到520帧复合B模式图像. 对520帧图像数据进行EVD处理和特征向量的多普勒频移分析, 结果如图7所示. 图7(a)为归一化多普勒频移对应特征向量个数的直方图, 纵坐标为特征向量的个数, 相较于仿体血流, 实际血流有不同的流速, 因此其多普勒频移的分布区间更宽. 若频率阈值选取过高, 会损失低速血流信号成分, 导致有效信息缺失; 本实验采用与仿体实验一致的经验频率阈值, 即取归一化多普勒频移为0.1. 图7(b)为数据集的特征向量与特征值的对应关系, 图7(c)为特征向量与归一化多普勒频移的对应关系, 图7(d)为特征值与归一化多普勒频移的对应关系, 图中虚线为归一化多普勒频移为0.1的阈值线, 实线为幅值为–130 dB的阈值线. 将多普勒频移小于0.1且特征值幅值大于–130 dB的特征向量滤除. 图8为多角度平面复合和滤波前后的成像结果. 图8(a), (b)分别为发射单角度倾斜平面波得到的波束合成后的结果和发射27个倾斜角度平面波相干复合成像的结果, 图8(c)为滤波后的多帧脊髓血流图像, 从中可见微血流的变化情况.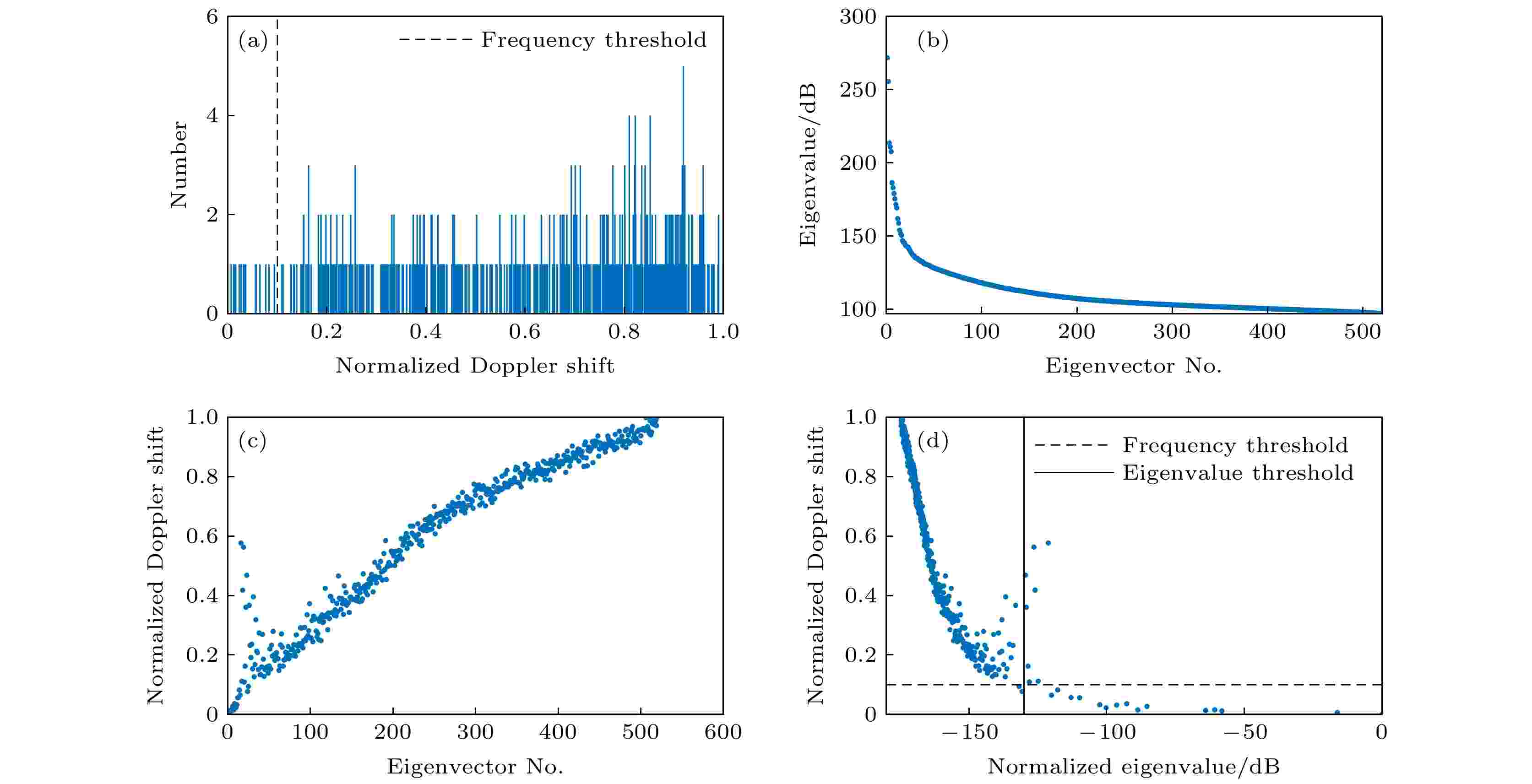
图 7 特征值分解与多普勒频移分析结果　(a) 归一化多普勒频移对应特征向量个数的直方图; (b)特征向量的特征值; (c) 特征向量的归一化多普勒频移; (d) 特征值对应的归一化多普勒频移
Figure7. Eigenvalue decomposition and Doppler shift analysis results: (a) Histogram of the number of eigenvectors corresponding to normalized Doppler shifts; (b) eigenvalues of eigenvectors; (c) normalized Doppler shifts of eigenvectors; (d) eigenvalues versus normalized Doppler shifts.

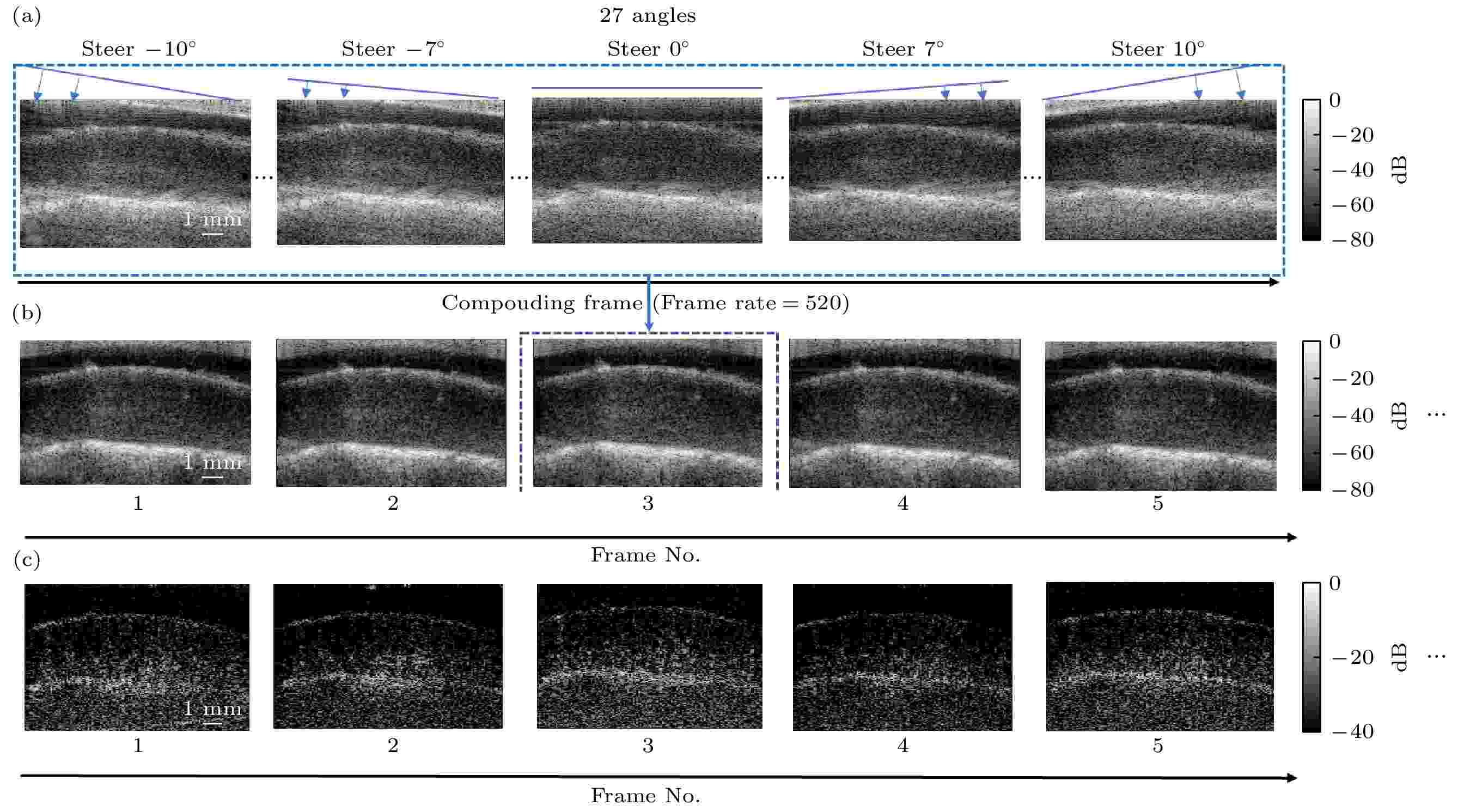图 8 基于多角度平面波复合成像的大鼠脊髓血流成像结果　(a) 单角度平面波发射成像; (b) 多角度平面波复合成像; (c) 杂波滤除结果. 每一次发射超声平面波的时间间隔为71.225 μs, 27次发射倾斜平面波与接收反射回波的总时长为1.923 ms, 对多角度信号经相干复合可获得单帧超声图像, 其所对应的成像帧率为每秒520帧
Figure8. Blood flow imaging results of rat spinal cord based on multi-angle compounding method: (a) Beamforming results after a single emission; (b) multi-angle compounding images; (c) images after clutter filtering. The time interval between each emission is 71.225 μs. Each compounded frame is obtained using 27 steering-angle plane-waves within a period of 1.923 ms. Consequently the frame rate is 520 frames per second.

为讨论复合平面波成像中倾斜平面波角度数在超快超声多普勒血流成像中的作用, 分别设定每个子序列中发射倾斜平面波的个数为N = 3 [–1°—1°], N = 9 [–3°—3°], N = 17 [–7°—7°], N = 27 [–10°—10°](倾斜平面波的角度在设定区间内均匀分布), 复合成像帧频均为520帧/s, 成像结果如图9所示. 图9(a)—9(d)的1—3图分别为上述4种情况滤波之前、滤波之后和功率多普勒成像结果. 当N = 3 [–1°—1°]时, 成像质量差, 无法辨别脊髓内部微血管分布(如图9(a)). 当N = 9 [–3°—3°]时, 多普勒成像方法能够对脊髓内部微血管结构进行成像, 但难以呈现完整的微血管结构(如图9(b)). 随着成像角度数的增大, 当成像角度N = 17 [–7°—7°]和N = 27[–10°—10°]时, 在多普勒成像结果中可以看到较为清晰的微血管结构(如图9(c),(d)), 其中微血管分布主要由靠近背侧和靠近腹腔的两部分血供构成, 该成像结果与组织病理学中脊髓血管的解剖结构形态相似[29]. 随着角度数的增大, 图像的对比度和SNR得到改善. 并能观察到水平方向–2.5 mm, 竖直方向1.5—2.0 mm处由细针刺入脊髓所致的局部微血流缺失现象.
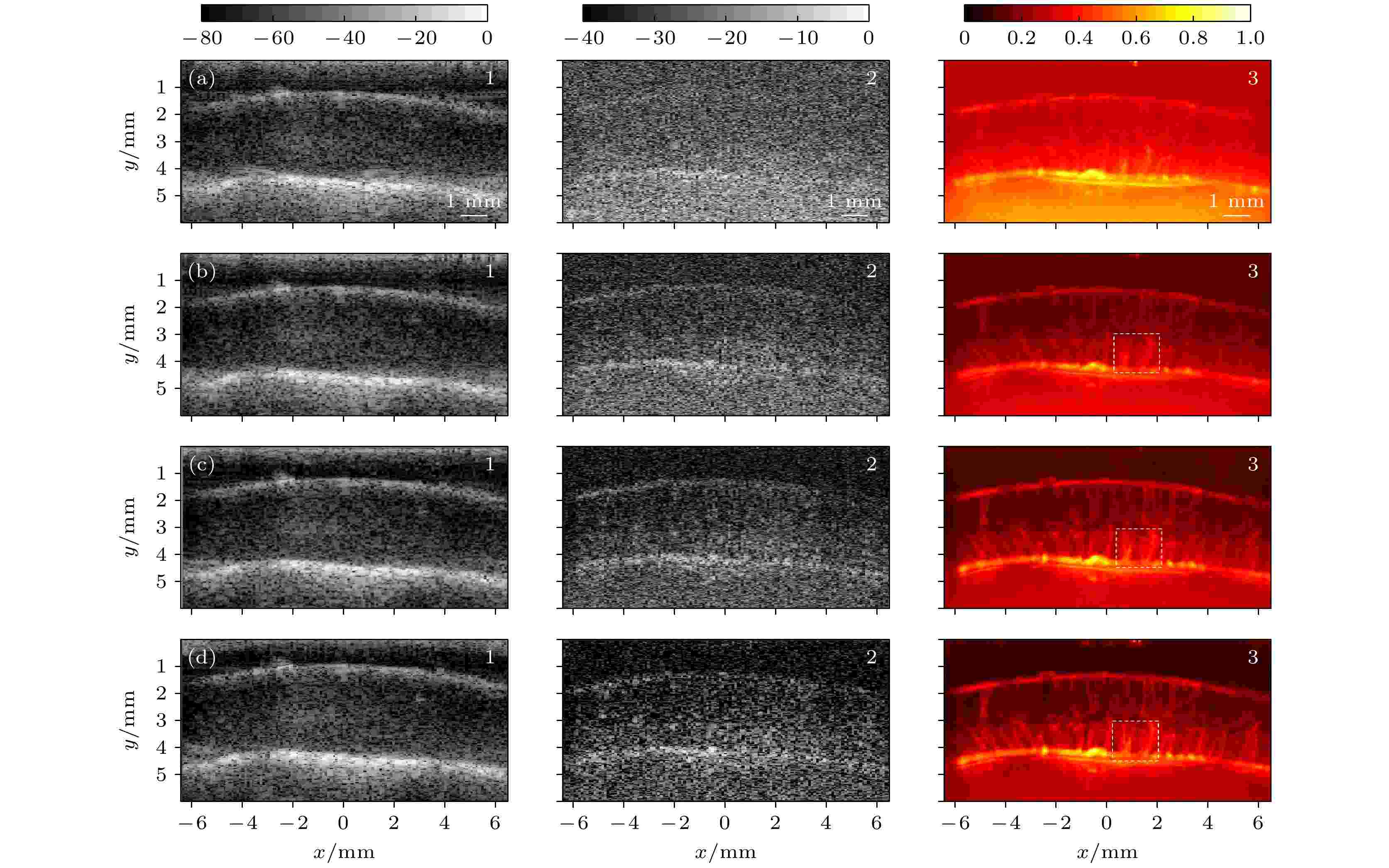图 9 不同角度复合平面波成像结果对比图(复合帧频均为每秒520帧)　(a) 3个角度[–1°—1°]倾斜平面波复合成像结果; (b) 9个角度[–3°—3°]倾斜平面波复合成像结果; (c) 17个角度[–7°—7°]倾斜平面波复合成像结果; (d) 27个角度[–10°—10°]倾斜平面波复合成像结果. 1为单帧原始B模式图像, 2为杂波滤除之后的成像结果, 其中可见微血流变化, 3为1 s内采集数据得到的功率多普勒血流图(1, 2色标单位为dB, 3为归一化数值的多普勒成像结果)
Figure9. Comparison of compounded images with different numbers of steering angles (composite frame rate is 520 frames per second): (a) Images compounded of data from emitting 3 [–1°—1°] steering plane-waves; (b) images compounded of data from emitting 9 [–3°—3°] steering plane-waves; (c) images compounded of data from emitting 17 [–7°—7°] steering plane-waves; (d) images compounded of data from emitting 27 [–10°—10°] steering plane-waves. Images labeled 1 are original B-mode images; images labeled 2 are imaging results after clutter filtering in which changes of blood flow can be observed; images labeled 3 are power Doppler images of micro-vessels (data was obtained within 1 s).

5.讨　论
在图9的功率多普勒血流图中选定一个感兴趣区域(如图9(b)—(d)编号3的图中矩形虚线框所示), 进而分析结果的对比分辨率. 如图10所示, 分别将角度数N = 9 [–3°—3°], N = 17 [–7°—7°], N = 27 [–10°—10°]的成像结果中该感兴趣区域放大. 图10(b)给出了图10(a)中虚线深度处的幅度曲线, 进而比较微血管成像分辨率. 由图可得, 当N = 27时, 可由箭头所指处的幅度峰值分辨两相邻微血管; 而当N = 9时, 因图像分辨率降低, 故无法分辨此处的两相邻微血管.
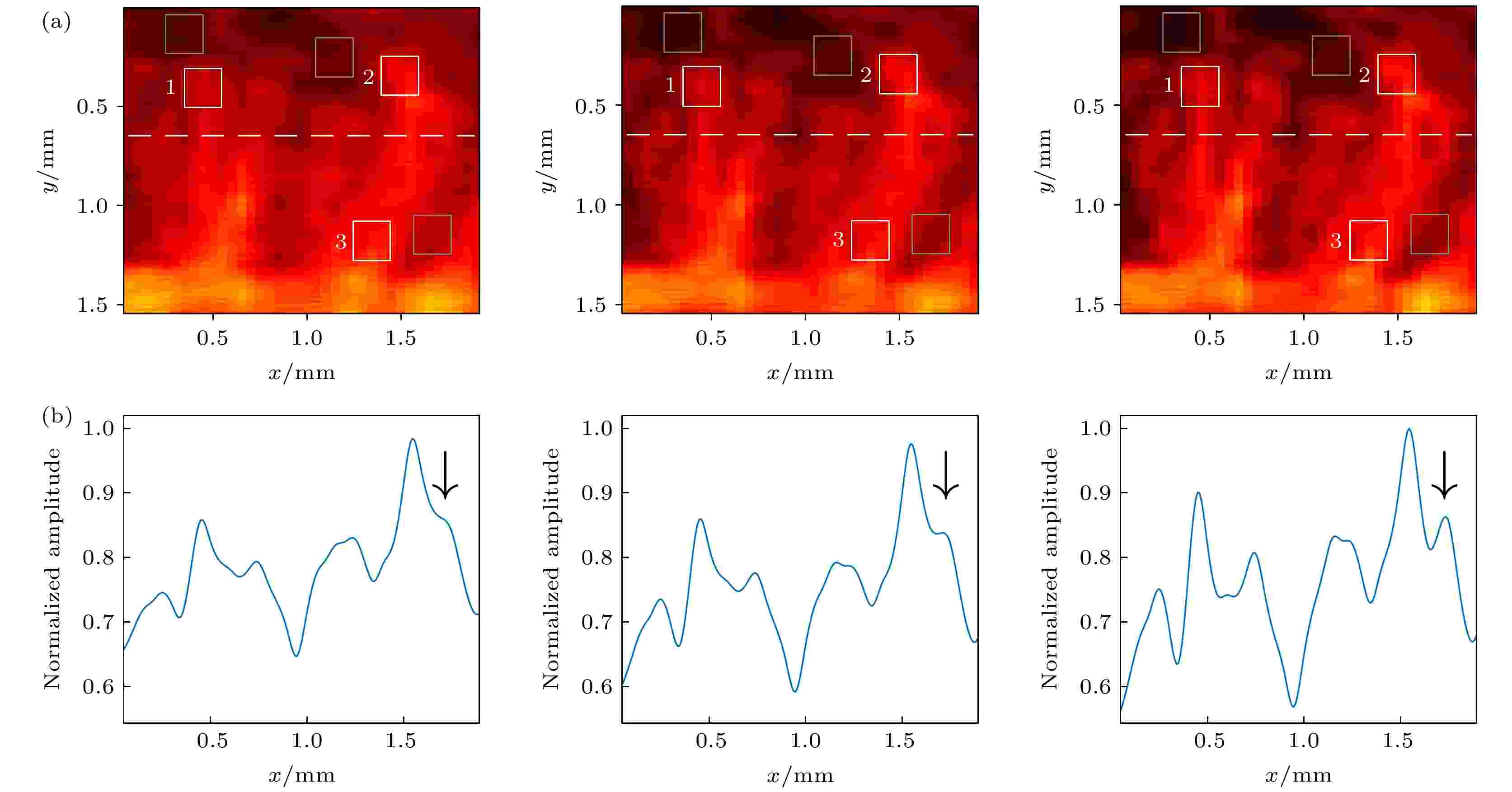图 10 对比分辨率随复合平面波角度数增加的变化情况　(a) 当角度数N = 9, 17, 27时, 图9(b)-(d)编号3的图中矩形虚线框中图块的放大结果; (b) 当角度数N = 9, 17, 27时, 图10(a)中虚线深度处的幅值曲线图
Figure10. Change of contrast resolution with the increase of the number of steering angles: (a) Enlarged image blocks in the rectangular dashed box in No.3 figure in Fig.9 (b)-(d) (angle numbers are 9, 17, 27, respectively); (b) amplitude curve of the dotted line position in Fig.10(a) (angle numbers are 9, 17, 27, respectively).

由图10可得, 随复合平面波角度数增大, 血流信号相较于背景噪声得到增强, 以下对图像的SNR加以量化分析. 当N = 27时最大的角度范围为–10°—10°, N = 9时的角度范围约为–3°—3°. 从图10(a)中选择3个尺寸为0.2 mm × 0.2 mm的感兴趣区域(编号为1, 2, 3), 白色方框为血流信号区域, 最临近的灰色方框为参考背景区域. SNR的计算公式如下[30]:
$\mathrm{S}\mathrm{N}\mathrm{R}=20{\mathrm{l}\mathrm{g}}\left(\dfrac{\sqrt{\dfrac{1}{{n}_{\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w}}}\displaystyle\sum\nolimits_{i=1}^{{n}_{\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w}}}{I}_{\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w}}^{2}\left(i\right)}}{\sqrt{\dfrac{1}{{n}_{\mathrm{b}\mathrm{k}\mathrm{g}\mathrm{d}}}\displaystyle\sum\nolimits_{i=1}^{{n}_{\mathrm{b}\mathrm{k}\mathrm{g}\mathrm{d}}}{I}_{\mathrm{b}\mathrm{k}\mathrm{g}\mathrm{d}}^{2}\left(i\right)}}\right),$
其中$ {I}_{\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w}}\left(i\right) $, $ {I}_{\mathrm{b}\mathrm{k}\mathrm{g}\mathrm{d}}\left(i\right) $分别为血流信号区域和参考背景信号区域中第i个像素点的幅值, $ {n}_{\mathrm{f}\mathrm{l}\mathrm{o}\mathrm{w}} $和$ {n}_{\mathrm{b}\mathrm{k}\mathrm{g}\mathrm{d}} $分别为血流信号区域和背景信号区域像素点的个数, SNR是所选区域血流信号幅度与背景噪声信号幅度均方根的比值. 不同角度倾斜平面波的情况下, 图10(a)中3个感兴趣区域的SNR变化曲线如图11所示.
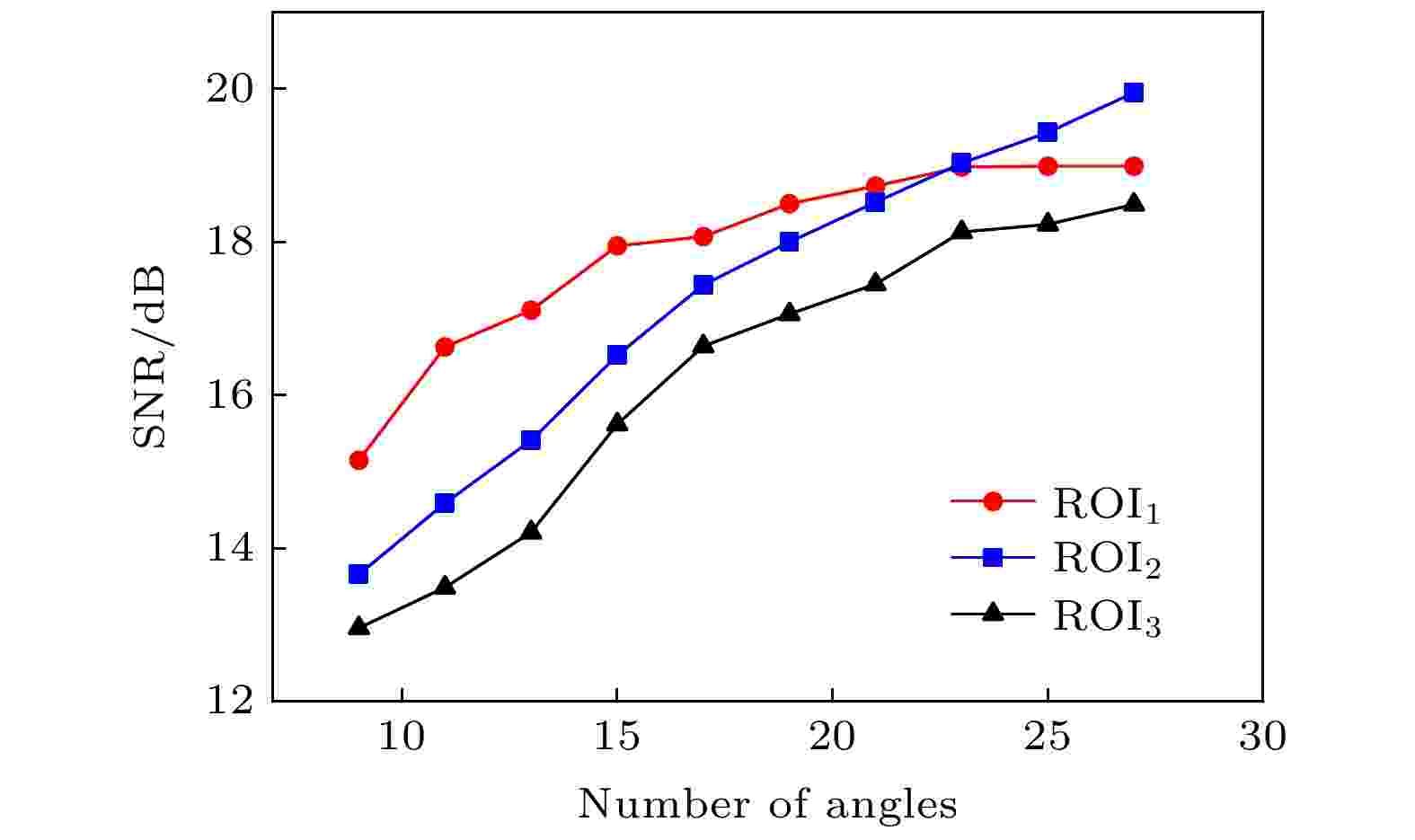图 11 SNR随复合平面波角度数增加的变化结果
Figure11. SNR versus number of steering angles.

如图11所示, 3个感兴趣区域的SNR都会随着平面波角度数的增加而增加. 对于1号感兴趣区域, 发射9个角度[–3°—3°]倾斜平面波时, SNR为15.15 dB; 发射27个角度[–10°—10°]的倾斜平面波时, SNR为18.99 dB. 类似地, 对于2号和3号感兴趣区域, 当发射9个角度[–3°—3°]倾斜平面波时, SNR较小, 分别为13.66 dB和12.96 dB; 当发射27个角度[–10°—10°]倾斜平面波时, SNR明显提高, 分别为19.95 dB和18.49 dB. 结果表明, 复合平面波角度数和角度范围的增大可显著改善多普勒成像结果的SNR.
在实际应用中, 骨衰减和相位畸变对经椎骨的超声成像影响不可忽略, 需要进行畸变校正与衰减补偿. 目前代表性的方法包括基于已知速度模型的相位畸变校正方法[31]和基于未知模型的全波反演技术[32]等, 相关技术已被用于经颅骨的脑组织超声成像. 后续研究可引入相关技术实现经椎骨的脊髓超声功能成像.
6.结　论
本文将超快多普勒技术应用于大鼠脊髓微血流实时成像, 通过发射高帧频、多角度平面波进行相干复合, 并采用fk-migration算法进行图像重建. 对高帧频复合图像进行EVD处理和多普勒频移分析, 并利用频率-幅值双阈值滤波法进行杂波滤除和动态血流信号的提取, 最终得到了可反映大鼠脊髓微血流的高质量功率多普勒图像. 实验中采用14040次/s的倾斜平面波发射频率, 通过基于EVD的频率-幅值双阈值滤波法, 得到了脊髓微血管的高质量图像. 结果表明, 增大复合平面波角度数可有效改善图像SNR, 与9个角度的倾斜平面波成像相比, 27个角度结果使得血流成像SNR值增强5 dB左右. 在大鼠脊髓微血管的多普勒成像结果中, 能够清晰地看到脊髓内部的微血管分布, 进而可由局部微血流缺失观察脊髓内微损伤区域. 本文采用的超快超声多普勒方法可在无需注射超声造影剂的情况下, 实现脊髓内微血流成像. 未来研究将围绕着脊髓超声功能成像展开, 特别是进行脊髓血流动力学分析和神经-血流耦合作用的研究.
相关话题/信号 图像 实验 序列 技术
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 氮化镓基高电子迁移率晶体管单粒子和总剂量效应的实验研究
    摘要:利用重离子加速器和60Coγ射线实验装置,开展了p型栅和共栅共源级联结构增强型氮化镓基高电子迁移率晶体管的单粒子效应和总剂量效应实验研究,给出了氮化镓器件单粒子效应安全工作区域、总剂量效应敏感参数以及辐射响应规律.实验发现,p型栅结构氮化镓器件具有较好的抗单粒子和总剂量辐射能力,其单粒子烧毁阈 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于晶向优化和Sn合金化技术的一种2.45 G弱能量微波无线输能用Ge基肖特基二极管
    摘要:肖特基二极管是2.45G弱能量密度无线能量收集系统的核心器件,其性能决定了系统整流效率的上限.从材料设计角度出发,利用晶向优化技术和Sn合金化技术,提出并设计了一种大有效质量、大亲和能和高电子迁移率的Ge基复合半导体.在此基础上,进一步利用器件仿真工具,设定合理的器件材料物理参数与几何结构参数 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 等离子气化技术用于固体废物处理的研究进展
    摘要:社会经济的快速发展致使固体废物的产量迅速增加,传统的处理工艺,如填埋、焚烧和堆肥等方法,不仅效率低下,而且存在着二次污染和资源浪费等诸多问题,因此,急需探索新的固体废物处理技术.等离子气化技术因具有高效、环保和能源转化率高等特点而被应用于固体废物的处理.本文介绍了等离子气化技术处理固体废物的背 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 多孔材料的低温刻蚀技术
    摘要:随着半导体芯片特征尺寸的持续减小,低介电常数的多孔材料在微电子领域得到广泛应用.然而,多孔材料在等离子体刻蚀工艺中面对严峻的挑战.等离子体中的活性自由基很容易在多孔材料内部扩散,并与材料发生不可逆的化学反应,在材料内部造成大面积损伤.本文介绍了业内比较前沿的低温刻蚀技术,通过降低基片台的温度, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 大功率热平衡感应耦合等离子体数值模拟及实验研究
    摘要:感应耦合等离子体发生器是“临近空间高速目标等离子体电磁科学实验研究装置”的核心部件之一,常用于模拟高焓高速等离子体鞘套环境,为了研究大功率射频中压下感应耦合等离子体发生器的放电特性,采用数值模拟和实验相结合的方法研究其内部的传热与流动特性.本文基于局域热力学平衡条件,通过湍流场-电磁场-温度场 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于高速相位型空间光调制器的双光子多焦点结构光显微技术
    摘要:多焦点结构光照明显微镜(multifocalstructuredilluminationmicroscopy,MSIM)能在50μm的成像深度内实现2倍于衍射极限分辨率的提升,但在对厚样品成像时,散射光和离焦光限制了其层析能力和图像衬度.双光子多焦点结构光照明显微镜(two-photonMSI ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 激光加速高能质子实验研究进展及新加速方案
    摘要:利用超强激光与等离子体相互作用来加速高能离子是激光等离子体物理及加速器物理领域的研究热点.经过了近20年的发展,激光离子加速已取得丰硕成果,催生了一批新的应用.本文概述了国内外激光离子加速所取得的标志性实验研究进展,围绕高能质子的产生这一关键问题进行了深入的探讨,介绍了近几年来发展的有潜力的新 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 飞秒超强激光驱动太赫兹辐射特性的实验研究
    摘要:强太赫兹源是太赫兹科学技术发展的关键,其中大能量强场太赫兹脉冲源在超快物态调控、新型电子加速器等领域具有重要的应用前景.超快超强激光与等离子体相互作用是近年来发展起来的一种新型的强场太赫兹辐射产生途径.本文报道了利用超强飞秒激光脉冲与金属薄膜靶作用产生太赫兹辐射的实验结果,研究了激光能量和离焦 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 态选择电荷交换实验测量以及对天体物理软X射线发射模型的检验
    摘要:在高温天体等离子体环境中,低能高电荷态离子与中性原子和分子之间的电荷交换是天体物理环境中软X射线发射的重要机制之一.电荷交换软X射线发射相关的天体物理建模需要大量的主量子数n和角量子数l分辨的态选择俘获截面数据,目前这类数据主要来自于经典或者半经典的原子碰撞理论模型.本文利用反应显微成像谱仪, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 非线性超声射频信号熵对乳腺结节良恶性的定征
    摘要:本文提出了一种基于非线性超声射频(radiofrequency,RF)信号熵对乳腺结节良恶性进行定征的方法.对306例乳腺结节样本(良性158例,恶性148例)提取了基于超声RF信号二次谐波的熵和加权熵,以及常规超声参数(图像灰度、纵横比、不规则度、乳腺结节大小、深度);采用t检验和线性分类器 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.