摘要:随着航空航天领域的飞速发展, 极端的环境要求超高温陶瓷材料具有更好的力学性能和超高熔点. 目前, 单金属碳化物的超高温陶瓷材料承受的压力日渐增大. 为了解决过渡金属单碳化物性能不足的问题, 我们基于密度泛函理论系统地研究了Ta_1–xHf_xC和Ta_1–xZr_xC (0 ≤ x ≤ 1)固溶体的物理性质. 通过调节Hf和Zr的浓度来研究它们的结构稳定性、晶格参数、力学性能、熔点和电子结构. 我们的计算结果表明碳化物固溶体的稳定性随Hf/Zr含量的增加而增加, 并且当Hf/Zr含量相同时, Ta_1–xZr_xC比Ta_1–xHf_xC的结构更稳定. 我们还发现随着Hf/Zr含量的增加, 固溶体的晶格常数和体积会膨胀. Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的体积模量随着Hf/Zr含量的增加而减小, 而固溶体的熔点、杨氏模量、剪切模量、维氏硬度和断裂韧性在掺杂含量x = 0.2处会出现峰值. 而且, 添加Hf和Zr可以提高TaC的耐磨性. 电子态密度结果显示随着Hf/Zr含量的增加, 固溶体费米能级处的态密度值逐渐降低, 这表明固溶体的结构稳定性逐渐增强.
关键词: 金属碳化物/
第一性原理/
力学性质/
电子结构

English Abstract

全文HTML

--> --> -->

过渡金属碳化物TaC, HfC和ZrC是应用于航空航天工业的最有前途的超高温陶瓷(UHTC)候选材料, 它们具有强的共价键和低的自扩散系数, 具有超高的熔融温度、高硬度、高模量, 高断裂韧性、高电导率、良好的耐腐蚀性和出色的化学稳定性^[1-7]. 然而, 随着社会日新月异的发展, 单碳化物承受着越来越大的压力, 要求它们在更苛刻的环境条件下使用, 应具有更好的抗氧化性、熔点、硬度和断裂韧性^[8]. 优异性能的结合很大程度上取决于化学成分和微观结构状态^[9]. 为了解决过渡金属单碳化物的性能不足, 研究者已经采用了各种技术. 除了纯金属碳化物外, 金属碳化物形成的固溶体具有潜在的应用价值, 因为可以通过改变二元或更多元体系中的成分和含量来优化其性能^[10].
最近, Ta_1–xHf_xC和Ta_1–xZr_xC固溶体引起了人们的关注, 因为它们的熔点超过TaC, HfC和ZrC, 并且固溶体的形成可以有效改善材料的性能^[11,12]. 但是, 研究主要集中在富Ta的TaC-HfC和TaC-ZrC固溶体上, 尤其是Ta_0.8Hf_0.2C和Ta_0.8Zr_0.2C固溶体^[4,13]. TaC-HfC和TaC-ZrC陶瓷具有超高的熔化温度, 分别约为4213 K和4170 K^[13]. Barraza等^[14]使用微米级碳化物粉末的混合物通过放电等离子烧结合成了TaC-HfC陶瓷. Smith等^[15]通过X射线衍射(XRD)和电子衍射证实Hf_xTa_1–xC化合物为岩盐构型B1结构, 研究了Ta含量对Hf_xTa_1–xC化合物硬度的影响并探究了其原因. Gladyshevsky等^[16]和Avgustinik等^[17]以及Rudy^[18]研究都表明, 在TaC和ZrC碳化物之间存在连续的固溶陶瓷. 最近, Yate等^[19]采用磁控溅射法制备了二元和三元Ta-Hf-C薄膜, 并研究了力学性能和磨损性能, 结果表明三元Ta-Hf-C具有更高的硬度和优异的磨损性能.
尽管已经合成了Ta_1–xHf_xC和Ta_1–xZr_xC固溶体, 并进行了大量的实验研究, 但仍缺乏相关的理论研究. 考虑到Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的许多优点吸引了研究者的广泛关注, 我们使用超胞(SC)方法和虚晶近似(VCA)方法对这些固溶体进行了第一性原理计算, 确定了固溶体的各种性能, 包括杂质形成能, 晶格常数、体积、弹性常数、弹性模量、维氏硬度、断裂韧性、耐磨性、熔点和电子态密度等.

2

-->

2.1.第一性原理计算

基于密度泛函理论(DFT)框架下的SC方法和VCA方法, 我们使用Cambridge Serial Total Energy Package (CASTEP)软件对Ta_1–xHf_xC和Ta_1–xZr_xC固溶体进行了第一性原理计算^[20,21]. 交换关联势采用了广义梯度近似(GGA)下的Perdew-Burke-Ernzerh(PBE)泛函来处理^[22-24]. 模守恒贋势用于描述核心电子与原子核之间的相互作用^[25]. 在波函数的平面波扩展中使用了660 eV的截止能量, 并使用Monkhorst-Pack 20 × 20 × 20 k点的超胞和虚晶近似模型对布里渊区进行了积分. 图1显示了Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的SC模型. 对于虚晶近似(VCA)方法, 立方Ta_1–xHf_xC和Ta_1–xZr_xC固溶体中的Ta原子和Hf或Zr原子占据相同的位置并且原子混合比例设置为1–x∶x^[26-33]. 这些模型使得可以在整个掺杂含量(0 ≤ x ≤ 1)范围内对Hf和Zr掺杂的TaC进行计算.
图 1 (a)纯TaC的晶体结构; 掺杂含量x为(b) 0.25, (c) 0.5, (d) 0.75, (e) 1的Ta_1–xHf_xC/Ta_1–xZr_xC的晶体结构
Figure1. (a) The crystal structure of pure TaC; and the crystal structure Ta_1–xHf_xC or Ta_1–xZr_xC with doping content x of (b) 0.25, (c) 0.5, (d) 0.75, (e) 1.

2 -->

2.2.形成能和混合能

为了分析立方Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的结构稳定性, 我们计算了形成能(E_form), 杂质形成能(E_imp)和混合能(?E_mix), 公式如下^[34-36]:

$ \begin{split}{E_{{\rm{form}}}} =\;& [ {E_{{\rm{tot}}}}\left( {{\rm{T}}{{\rm{a}}_m}{\rm{R}}{{\rm{M}}_n}{{\rm{C}}_p}} \right) - m{E_{{\rm{tot}}}}\left( {{\rm{Ta}}} \right) \\&- n{E_{{\rm{tot}}}}\left( {{\rm{RM}}} \right) - p{E_{{\rm{tot}}}}({\rm{C}}) ] / {\left( {m + n + p} \right)}, \end{split}$

$ \begin{split}{E_{{\rm{imp}}}} = \;&{E_{{\rm{tot}}}}\left( {{\rm{T}}{{\rm{a}}_{1 - x}}{\rm{R}}{{\rm{M}}_x}{C_{}}} \right) - {E_{{\rm{tot}}}}\left( {{\rm{TaC}}} \right) \\&+ x{E_{{\rm{tot}}}}\left( {{\rm{Ta}}} \right) - x{E_{{\rm{tot}}}}\left( {{\rm{RM}}} \right), \end{split}$

$ \begin{split}\Delta {E_{{\rm{mix}}}} =\;& {E_{{\rm{tot}}}}\left( {{\rm{T}}{{\rm{a}}_{1 - x}}{\rm{R}}{{\rm{M}}_x}{C_{}}} \right) \\&- (1 - x){E_{{\rm{tot}}}}\left( {{\rm{TaC}}} \right) - x{E_{{\rm{tot}}}}\left( {{\rm{RMC}}} \right), \end{split}$

其中RM代表固溶金属Hf和Zr; m, n和p分别是超胞中Ta, RM和C原子的数目; E_tot(Ta), E_tot(Hf), E_tot(Zr)和E_tot(C)分别是其固体状态下每个原子(Ta, Hf, Zr和C)的总能量; E_tot(Ta_1–xRM_xC)是掺杂Hf/Zr的TaC系统的总能量, E_tot(TaC)和E_tot(RMC)分别是TaC和RMC的总能量. 通常, 形成能越低固溶体越稳定. 杂质形成能越低越有助于掺杂工艺. 如果混合能为负(正), 则由单金属碳化物形成二元金属碳化物是放热(吸热)过程.
2 -->

2.3.力学性质

对于立方Ta_1–xHf_xC和Ta_1–xZr_xC固溶体, 通过CASTEP计算了三个独立的弹性刚度常数C₁₁, C₁₂和C₄₄. 然后, 通过弹性常数用Viogt-Reuss-Hill (VRH)近似计算了体积模量(B )和剪切模量(G ), 公式如下^[37-39]:

$B = \frac{{{C_{11}} + 2{C_{12}}}}{3},$

${G_{}} = \frac{{{G_{\rm{V}}} + {G_{\rm{R}}}}}{2},$

其中,

${G_{\rm{V}}} = \frac{{3{C_{44}} + {C_{11}} - {C_{12}}}}{5},$

${G_{\rm{R}}} = \frac{{5\left( {{C_{11}} - {C_{12}}} \right){C_{44}}}}{{4{C_{44}} + 3\left( {{C_{11}} - {C_{12}}} \right)}}.$

杨氏模量(E), 泊松比(υ), 维氏硬度(H_V)和断裂韧性(K_IC)可以根据体积模量和剪切模量确定, 计算公式如下^[40-42]:

$E = \frac{{9GB}}{{3B + G}},$

$\upsilon = \frac{{3B - 2G}}{{2\left( {3B + G} \right)}},$

${H_{\rm{V}}} = 0.92{k^{1.137}}{G^{0.708}},$

${K_{{\rm{IC}}}} = {V_0}^{1/6}G{(B/G)^{1/2}},$

其中, V₀是每个原子的体积, k是G/B比.
最后, 使用杨氏模量、泊松比和断裂韧性计算临界能量释放率(G_IC)^[43]:

${G_{{\rm{IC}}}} = K{_{{\rm{IC}}}^2}\left( {\frac{{1 - {\upsilon ^2}}}{E}} \right).$

2

-->

3.1.结构稳定性

图2(a)显示了Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的形成能和杂质形成能与Hf/Zr含量(x)的关系. 只要包含Hf/Zr掺杂剂(x > 0), 计算得出的Ta_1–xHf_xC和Ta_1–xZr_xC的形成能和杂质形成能始终为负值, 这表明固溶体的形成在能量上是有利的. 而且, 随着Hf/Zr浓度的增加, 固溶体的形成能和杂质形成能变小(更负), 使结构更加稳定. 因此, 掺杂增强了固溶体的稳定性. 此外, 当掺杂的Zr和Hf具有相同的浓度时, Ta_1–xZr_xC固溶体的形成能和杂质形成能低于Ta_1–xHf_xC固溶体, 这意味着Zr掺杂比Hf掺杂使结构更加稳定. 总体而言, 掺Zr的TaC (Ta_1–xZr_xC固溶体)比掺Hf的TaC (Ta_1–xHf_xC固溶体)更稳定. 如图2(b)所示, Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的混合能在整个浓度范围内均为负值, 表明由单一金属碳化物形成二元金属碳化物是放热过程. 混合能的负值还表明可以形成稳定的二元金属碳化物Ta_1–xHf_xC和Ta_1–xZr_xC固溶体.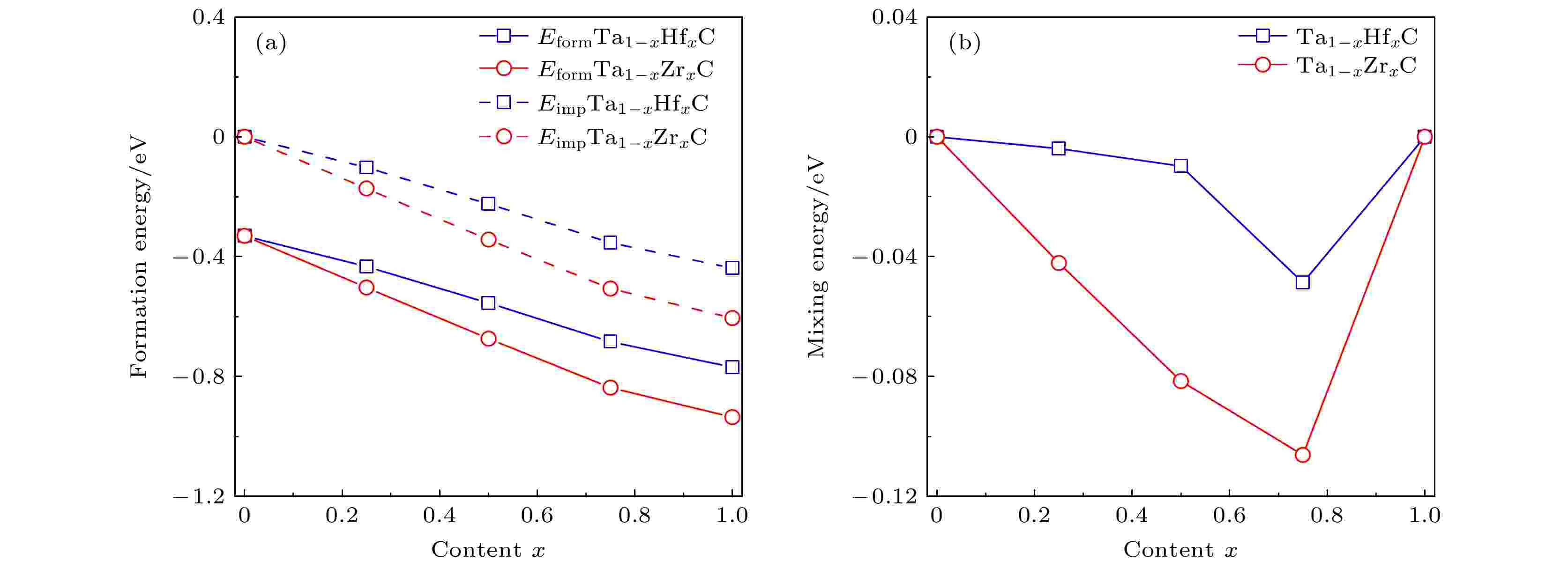
图 2 Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的(a)形成能(E_form)和杂质形成能(E_imp)及(b)混合能(?E_mix)随着Hf或Zr含量x的变化图
Figure2. (a) The formation energy (E_form) and impurity formation energy (E_imp), and (b) mixing energy (?E_mix) of Ta_1–xHf_xC and Ta_1–xZr_xC solid solutions as a function of Hf or Zr content x.

图3显示了通过SC和VCA方法得出的Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的晶格常数和体积与Hf/Zr含量的关系. 两种方法的计算结果几乎相同, 并且我们计算得到的晶格常数也与可用的实验和理论数据大体一致^[44,45], 这证实了SC和VCA方法均产生一致且可靠的结果. 我们观察到, 随着Hf/Zr含量的增加, 晶格常数和固溶体体积增加, 这主要归因于Hf (1.58 ?)和Zr (1.59 ?)的原子半径比Ta (1.45 ?)大^[46]. 另外, 如图3(a)所示, 固溶体的晶格常数随掺杂含量的变化比实验结果^[47,48]稍大, 误差在1.5%左右, 这归因于GGA-PBE交换相关泛函通常会稍微高估晶格常数.
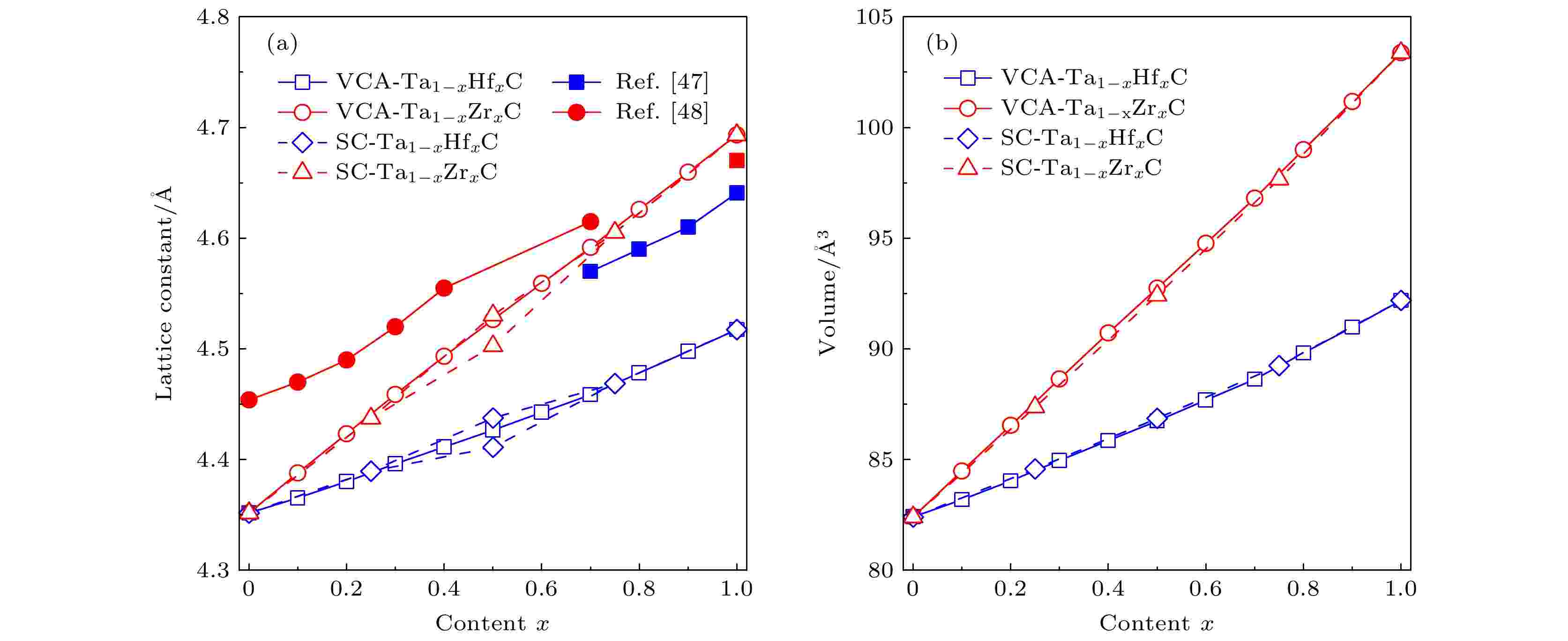图 3 通过超胞(SC)方法和虚晶近似(VCA)方法比较Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的(a)晶格常数和(b)体积随着Hf或Zr含量x的变化图
Figure3. Comparison of the (a) lattice constants and (b) volumes of the Ta_1–xHf_xC and Ta_1–xZr_xC solid solutions as a function of the Hf/Zr content by the supercell (SC) and virtual crystal approximation (VCA) methods.

2 -->

3.2.力学性质

对于立方晶体, 力学稳定性的标准为: C₁₁ > 0, C₄₄ > 0, C₁₁–C₁₂ > 0和C₁₁ + 2C₁₂ > 0^[49]. 图4(a)显示了Ta_1–xHf_xC和Ta_1–xZr_xC固溶体弹性常数. 由于所有弹性常数的值均为正, 并且C₁₁始终大于C₁₂, 显然满足上述标准, 因此固溶体具有力学稳定性. 对于Ta_1–xHf_xC和Ta_1–xZr_xC的端点一元碳化物(即TaC, HfC和ZrC), 发现计算出的弹性常数与实验数据和其他理论值趋势大体一致^[50-52]. 随着Hf/Zr掺杂含量的增加, Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的弹性常数C₁₁首先增大, 然后减小. 有趣的是, Ta_1–xHf_xC的C₁₁值在x = 0.2的掺杂含量处有一个峰值, 这表明Ta_0.8Hf_0.2C在单轴应力下沿x和z轴具有最高的抗压强度. 当掺杂含量变化时, 弹性常数C₁₂和C₄₄会在160 GPa附近波动. 此外, 当Hf和Zr掺杂含量相同时, Ta_1–xHf_xC的C₁₂和C₄₄值大于Ta_1–xZr_xC的相应值, 表明掺Hf的固溶体在单轴应力下沿x和z轴方向具有更大的抗压强度和剪切强度.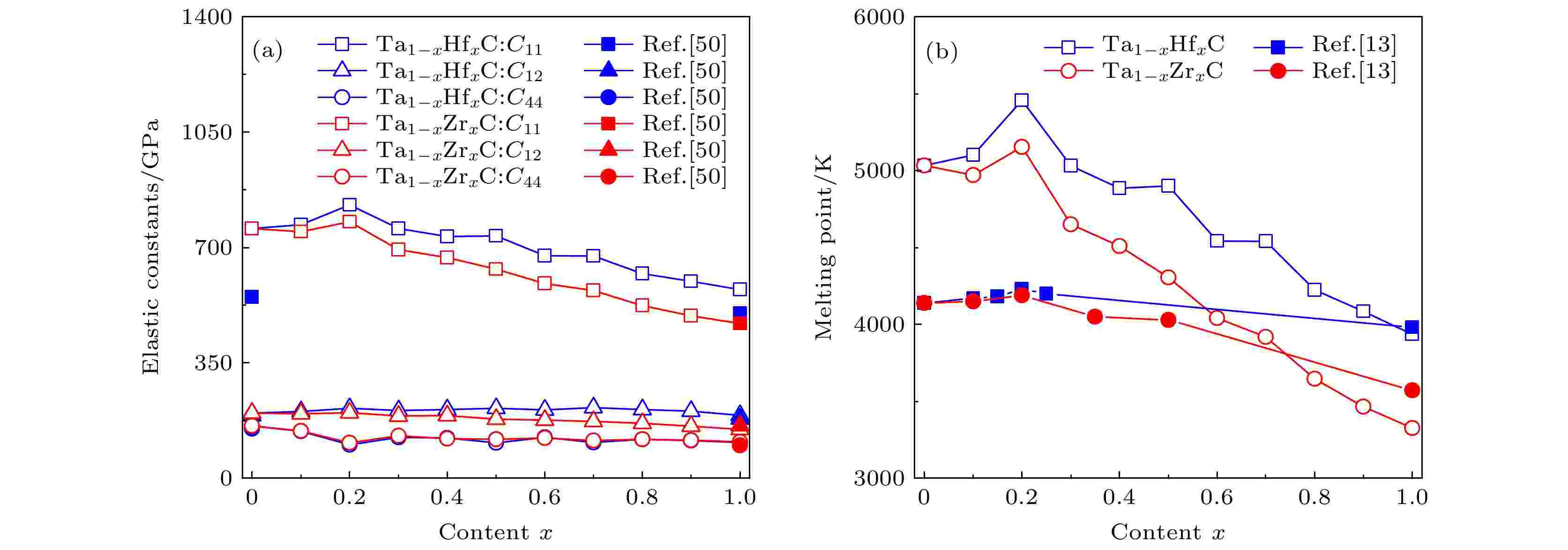
图 4 Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的(a)弹性常数和(b)熔点随着Hf或Zr含量x的变化图
Figure4. (a) The elastic constants and (b) melting points for the Ta_1–xHf_xC and Ta_1–xZr_xC solid solutions as functions of the Hf or Zr content.

熔点(T_m)是超高温陶瓷(UHTC)的重要参数. 在这项工作中, 根据弹性常数C₁₁计算了Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的熔点, 公式如下所示^[53,54]:

${T_{\rm{m}}} = 553\;{\rm{K}} + \left( {\frac{{{\rm{5}}.91\;{\rm{K}}}}{{{\rm{GPa}}}}} \right){C_{11}},$

其中, C₁₁以GPa为单位, 标准误差约为 ± 300 K. 图4(b)给出了我们计算的Ta_1–xHf_xC和Ta_1–xZr_xC端点单碳化物的熔点理论值和可用的实验值^[55,56]. 由于熔点T_m与弹性常数C₁₁成正比, Ta_0.8Hf_0.2C和Ta_0.8Zr_0.2C陶瓷具有最高的熔点(如预期的那样), 也与实验整体趋势基本一致^[13].
Pugh^[57]根据材料的B/G值确定其脆性和延展性, 即当B/G小于1.75时, 该材料为脆性; 否则, 材料是易延展的. 图5(a)显示了Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的B/G. 根据该准则, Ta_1–xHf_xC和Ta_1–xZr_xC固溶体都是脆性材料. 我们计算出端点一元碳化物的B/G值与前人的计算结果^[58]和实验测量结果^[59]基本一致. 此外, 当Hf和Zr的掺杂含量相同时, Ta_1–xHf_xC的B/G值始终低于Ta_1–xZr_xC的B/G值, 这表明Ta_1–xHf_xC更脆. 另外, 泊松比(υ)也可以作为延性和脆性的标准^[60], 也就是说, 如果υ小于0.26, 则材料是脆性的; 否则, 材料显示延展性. 如图5(b)所示, 端点单碳化物的泊松比计算值与实验值^[61]和先前的计算结果^[58]基本一致. 显然, 图5(b)中给出的泊松比值表明Ta_1–xHf_xC和Ta_1–xZr_xC固溶体都是脆性材料, 这与B/G值的分析结果是一致的.
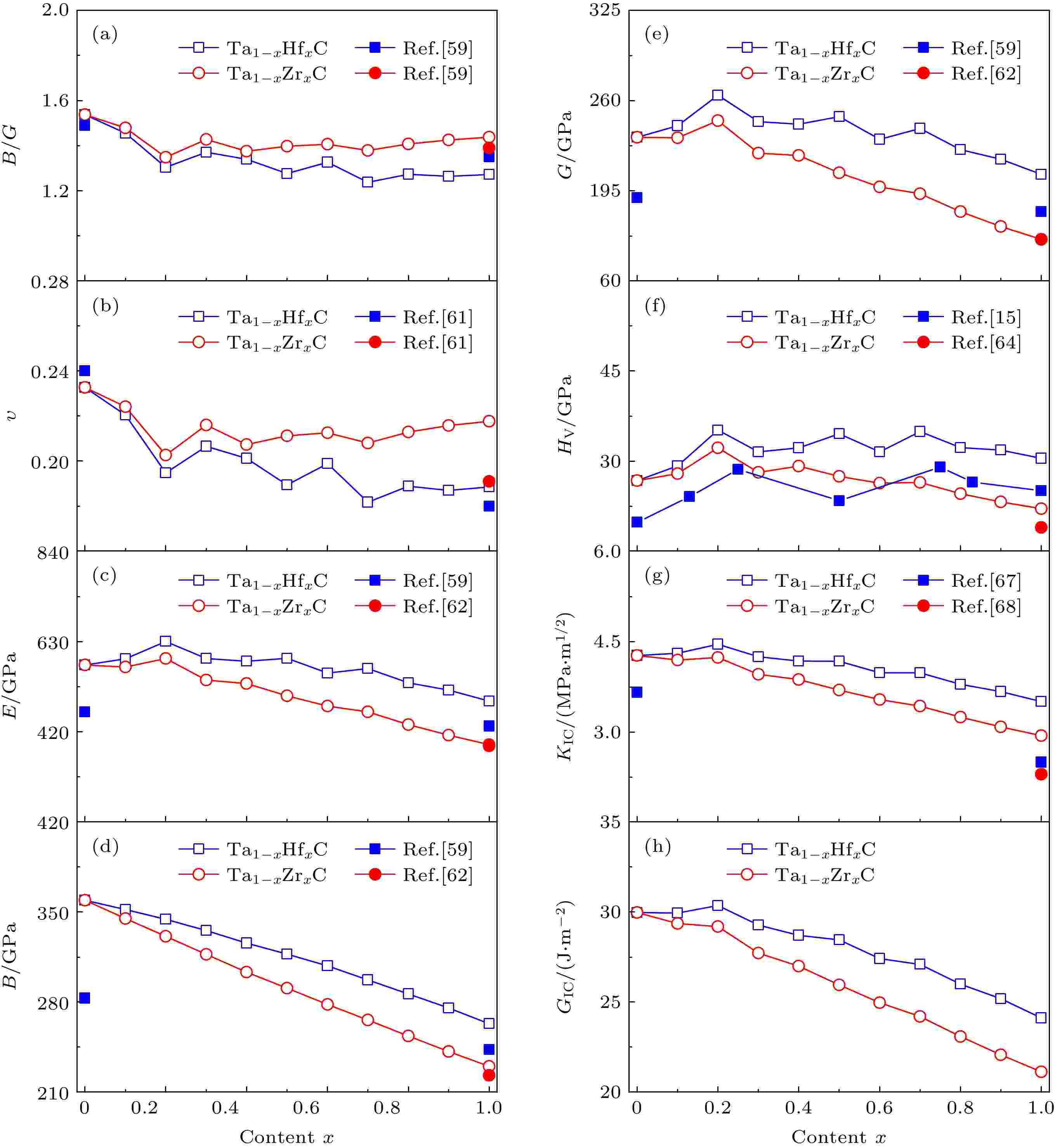图 5 Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的力学性质随Hf或Zr含量x的变化　(a) B/G比; (b)泊松比; (c) 杨氏模量; (d) 体积模量; (e) 剪切模量; (f) 维氏硬度; (g) 断裂韧性; (h) 临界能量释放率
Figure5. The mechanical properties of Ta_1–xHf_xC and Ta_1–xZr_xC solid solutions as a function of the Hf/Zr content: (a) B/G ratio; (b) Poisson’s ratio; (c) Young’s modulus; (d) bulk modulus; (e) shear modulus; (f) Vickers hardness; (g) fracture toughness; (h) critical energy release rate.

类似地, 图5(c)—(e)显示了两端的单金属碳化物的杨氏模量、体积模量和剪切模量的计算结果, 这与实验数据和先前的计算结果整体趋势大致相同^[59,62,63]. 杨氏模量主要反映材料的抗压强度. 从图5(c)中可以看出, Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的杨氏模量有一个峰值(最大值), 即Ta_0.8Hf_0.2C具有最大的抗压缩性. 图5(d)表明, 随着Hf/Zr含量的增加, 体积模量变小. 剪切模量可以衡量材料的剪切变形阻力. 图5(e)显示出Ta_0.8Hf_0.2C具有最大的剪切模量, 因此具有最强的剪切变形阻力. 图5(f)显示了Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的维氏硬度与Hf/Zr含量的关系. 同样, 端点单碳化物的计算值与实验和其他理论结果基本一致^[15,41,64]. 此外, 随着Hf含量的增加, Ta_1–xHf_xC固溶体的维氏硬度呈现出波峰和波谷的形状, 这也与现有的实验数据变化趋势基本一致^[15,19,65]. 特别地, Ta_0.8Hf_0.2C具有最高的维氏硬度.
断裂韧性(K_IC)用于描述材料对裂纹扩展的抵抗能力, 在超高温陶瓷材料的设计中起着重要作用^[43]. 图5(g)显示了我们计算的端点一元碳化物的断裂韧性理论值, 这与可用的实验数据基本一致^[64,66,67]. 再次发现, Ta_0.8Hf_0.2C具有最大的断裂韧性. 此外, 低浓度的Hf/Zr掺杂剂将增加陶瓷的断裂韧性, 而过量的掺杂剂浓度则显着降低断裂韧性. 与断裂韧性类似, 临界能量释放速率(G_IC)用于估算在材料中传播裂纹所需的能量^[42]. 从图5(h)可以看出, 陶瓷的临界能量释放率在x = 0.2处具有最大值, 这与断裂韧性具有相似的趋势.
耐磨性是极端环境下材料的重要指标. 根据Leyland和Matthews所提出的标准^[68], 我们通过计算弹性破坏应变H_V/E和塑性变形阻力$ H_{\rm V}^3/E^2 $来确定Ta_1–xHf_xC和Ta_1–xZr_xC陶瓷的耐磨性. 如图6所示, 我们计算出的端点一元碳化物的H_V/E和$ H_{\rm V}^3/E^2 $值与可用的实验数据基本一致^[15,64]. 此外, 随着Hf/Zr含量的增加, H_V/E和 $ H_{\rm V}^3 $/E²值的总体趋势将增加. 因此, 在固溶体中添加Hf/Zr提高了耐磨性.
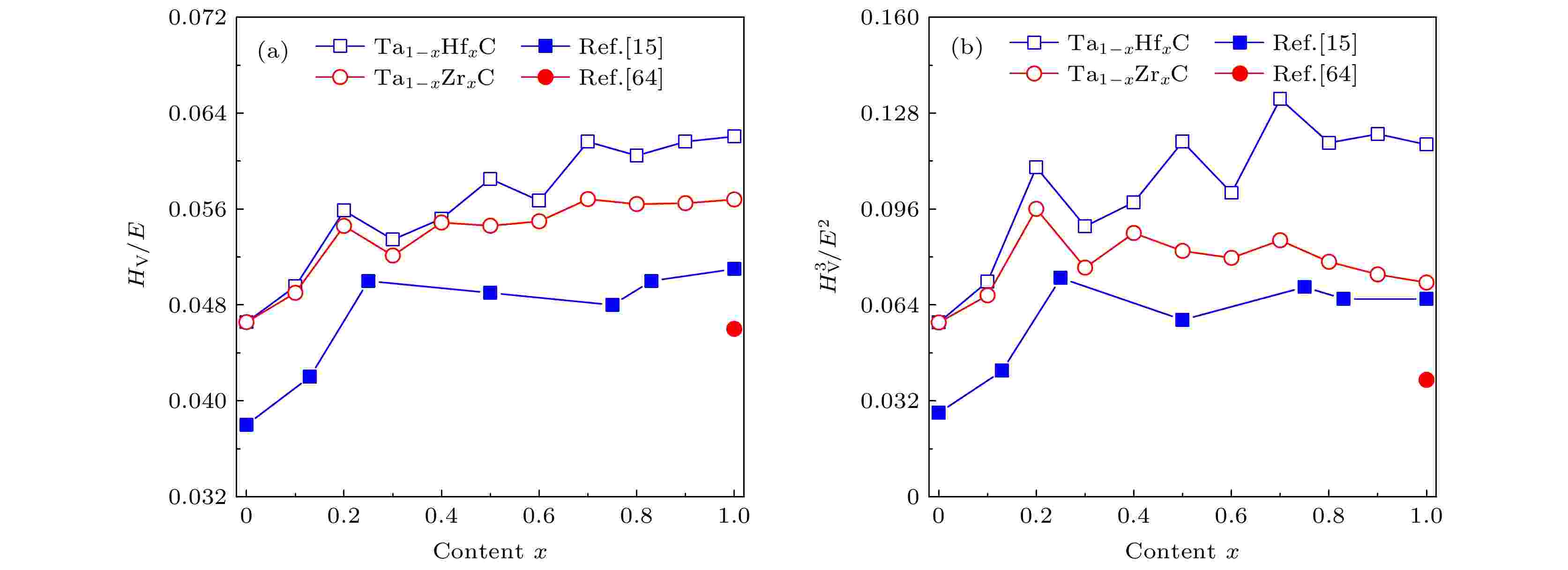图 6 Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的耐磨性随Hf或Zr含量x的变化图:　(a) H_V/E; (b) $ H_{\rm V}^3 $/E²
Figure6. The wear resistance of Ta_1–xHf_xC and Ta_1–xZr_xC solid solutions as a function of Hf or Zr content: (a) H_V/E; (b) $ H_{\rm V}^3 $/E².

2 -->

3.3.电子态密度

为了分析Hf和Zr掺杂TaC的结构稳定性, 我们计算了它们的总电子态密度(DOS), 结果如图7所示. 通常来说, 费米能级的位置和费米能级处电子态密度的数 N(E_F)决定着材料的结构稳定性, 对于金属体系而言, 费米能级处电子态密度的数 N(E_F)越低, 使得电子体系的能量有所降低, 因此材料结构越稳定^[69-71]. 从图7(a)可以看出, Ta_0.75Hf_0.25C在费米能级(E_F)的总DOS值低于纯TaC, 表明Ta_0.75Hf_0.25C比纯TaC的结构更稳定. 比较Ta_0.75Hf_0.25C, Ta_0.5Hf_0.5C, Ta_0.25Hf_0.75C和HfC的总态密度, 我们可以观察到, 随着Hf浓度的增加, Ta_1–xHf_xC固溶体的费米能级处的总态密度值变小, 这表明Ta_1–xHf_xC固溶体的结构稳定性随Hf浓度的增加而增加. 类似地, 如图7(b)所示, 在费米能级处Ta_0.75Zr_0.25C的DOS值低于纯TaC的DOS值, 这意味着Ta_0.75Zr_0.25C的结构稳定性比TaC高. 图7(b)还显示了随着Zr含量的增加, Ta_1–xZr_xC固溶体的DOS值逐渐降低, 这表明Ta_1–xZr_xC固溶体的结构稳定性随Zr浓度的增加而增加. 因此, Ta_1–xHf_xC和Ta_1–xZr_xC的稳定性都随着Hf/Zr含量的增加而增加, 这与形成能的结果一致. 另外, Ta_1–xHf_xC和Ta_1–xZr_xC固溶体的态密度与可用的实验测量值一致^[72].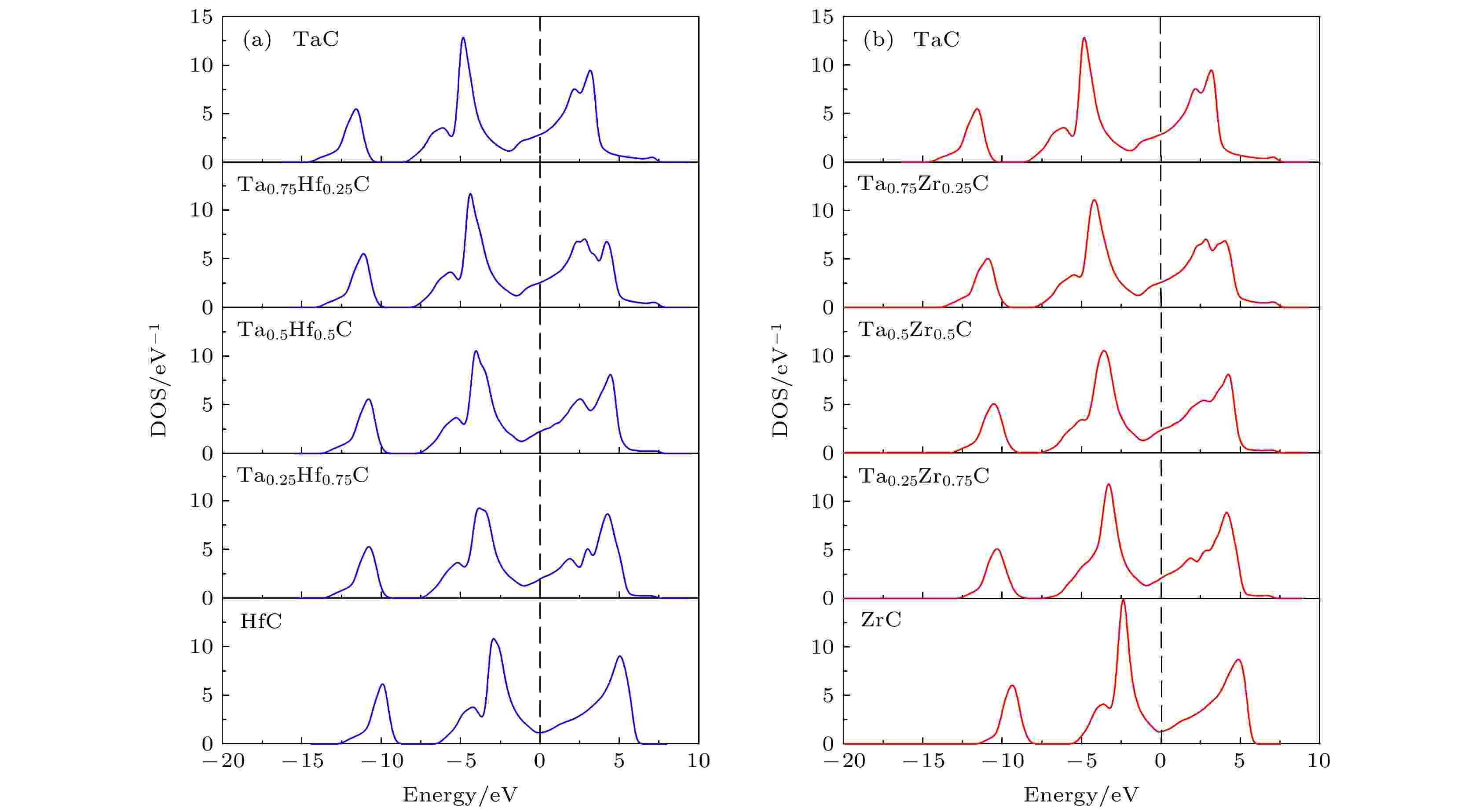
图 7 不同浓度的(a) Hf掺杂和(b) Zr掺杂TaC电子态密度(DOS)
Figure7. The electronic density of states (DOS) of (a) Hf-doped and (b) Zr-doped TaC with various doping contents.

总之, 本文通过第一性原理SC方法和VCA方法研究了Ta_1–xHf_xC和Ta_1–xZr_xC固溶体在整个掺杂浓度范围内的结构稳定性、力学性质、熔点和电子性质. 结果发现, 固溶体中的Hf/Zr浓度在结构稳定性、力学性质、熔点和电子性质中起着重要作用. 随着Hf/Zr浓度增加, Ta_1–xHf_xC和Ta_1–xZr_xC固溶体结构变得更稳定, 并且晶格常数和体积变大. 当Hf/Zr掺杂剂浓度相同时, 发现Ta_1–xZr_xC比Ta_1–xHf_xC更稳定. 我们的计算表明, Ta_1–xHf_xC和Ta_1–xZr_xC在整个Hf/Zr浓度范围内均具有力学稳定性和脆性. Hf和Zr掺杂可以增强TaC的耐磨性. 此外, Ta_0.8Hf_0.2C具有最高的硬度、最大的断裂韧性和最高的熔融温度. Ta_0.8Hf_0.2C具有最强的抗压缩性和抗剪切性. 最后, 这项工作可能为开发基于碳化物的超高温陶瓷提供有用的指导.