摘要:采用拉曼频移器在晶体介质中利用相干反斯托克斯散射效应可以获得超短脉冲(皮秒)反斯托克斯激光. 基于抽运-探测法的晶体拉曼频移器可以实现相干反斯托克斯散射的共线相互作用, 从而可以有效提高反斯托克斯光的转化效率. 本文在平面波近似下建立了基于抽运-探测法的皮秒反斯托克斯拉曼频移器的耦合波方程组, 引入归一化参量对方程组进行了归一化处理. 通过数值计算, 得到了描述皮秒反斯托克斯拉曼频移器运行的一组普适理论曲线, 分析了归一化拉曼增益系数G、归一化相位失配参数ΔK以及探测光脉冲能量占基频光总能量的比值r_probe三个变量对反斯托克斯拉曼频移器性能的影响, 确定了实现高效反斯托克斯转化时各归一化变量的合理取值. 采用实验数据对该理论模型的正确性进行了验证, 反斯托克斯转化效率的理论值与文献数据基本一致.
关键词: 相干反斯托克斯散射/
共线四波混频/
耦合波方程/
归一化理论

English Abstract

全文HTML

--> --> -->

随着晶体材料研究的不断深入, 基于受激斯托克斯拉曼散射(stimulated Stokes Raman scattering, SSRS)效应的晶体拉曼激光器作为扩展激光波长范围的重要手段之一, 已成为固体激光器领域研究的热点^[1-10]. 利用相干反斯托克斯拉曼散射(coherent anti-Stokes Raman scattering, CARS)效应, 可以在拉曼晶体中实现频率上转换, 从而获得反斯托克斯光^[11-19]. 它可以进一步扩大相干光谱范围, 产生具有重要应用价值的相干光. 例如, 晶体中的CARS效应能够将532 nm激光转化为在彩色全息、光学对抗、激光显示等方面有重要应用的蓝光输出. 另外, 皮秒激光以其超高的峰值功率在许多领域得到了广泛的应用. 因此, CARS效应与皮秒激光的结合为反斯托克斯激光的应用开辟了更多的可能性^[12,14].
拉曼频移器是产生超短脉冲反斯托克斯激光的有效方法. 2004年, Grasiuk等^[14]采用两级拉曼频移器在KGd(WO₄)₂晶体中实现了532 nm激光的频率上转换, 当第一级晶体产生的一阶斯托克斯种子光与抽运光在第二级晶体中的传播方向满足相位匹配条件时, 获得了转化效率为4%的511 nm反斯托克斯光输出. 然而, 第二级晶体中的非共线相位匹配导致抽运光、一阶斯托克斯光和反斯托克斯光的光束不能完全重合, 从而限制了反斯托克斯光的转化效率. 2017年, Smetanin等^[12]设计了一种新的实验方案, 采用抽运-探测法实现了CaCO₃晶体中共线相位匹配的皮秒反斯托克斯拉曼频移器, 由探测光向反斯托克斯光的转化效率高达30%. 基频光光源发出的基频光由分光装置分为不同偏振态的抽运光和探测光, 经光学延时系统进行时间和空间同步后入射到拉曼晶体中. 当抽运光和探测光束以一定的角度入射到拉曼晶体中时, 可以实现抽运光、探测光、一阶斯托克斯光和反斯托克斯光的共线相位匹配. 抽运光通过SSRS效应产生一阶斯托克斯光, 反斯托克斯光则由探测光经CARS效应产生.
理论模拟是研究激光运转的重要手段. Shen和Bloembergen^[20]采用耦合波方程解释了受激拉曼散射中高阶斯托克斯和反斯托克斯光的产生. 此后, 耦合波方程被广泛用来研究拉曼激光器^[8,9]和反斯托克斯激光器特性^[11-13]. Smetanin等^[12]采用物质方程和耦合波方程分析了探测光和抽运光光强三种占比情况下CaCO₃皮秒反斯托克斯拉曼频移器的转化效率. 然而, 以往报道的反斯托克斯拉曼频移器理论虽能反映频移器的运转规律, 但未有报道研究频移器的最优化问题, 也未有报道给出频移器参量对反斯托克斯激光输出特性的影响. 本文采用耦合波理论对基于抽运-探测法的皮秒反斯托克斯拉曼频移器进行了理论研究. 考虑探测通道中一阶斯托克斯光和抽运通道中二阶斯托克斯光的产生, 在平面波近似下, 建立了皮秒反斯托克斯拉曼频移器的耦合波方程. 对耦合波方程进行了归一化处理和数值求解, 得到了一组反映归一化参数对反斯托克斯拉曼频移器性能影响的曲线, 分析了归一化参量对反斯托克斯光转化效率的影响. 本文提出的归一化耦合波理论有助于了解皮秒反斯托克斯拉曼频移器的运转规律, 而且对频移器的设计具有指导意义.

2

-->

2.1.相互作用原理

考虑探测通道中一阶斯托克斯分量的产生和抽运通道中二阶斯托克斯分量的产生, 忽略高阶斯托克斯光和反斯托克斯光的产生, 各分量之间的相互作用原理如图1所示. 图1(a)为抽运通道SSRS过程的能级图. 频率为ω_pump的抽运光入射到拉曼晶体中, 与物质分子相互作用, 一个抽运光光子转化成一个频率为ω_1s的一阶斯托克斯光光子, 当一阶斯托克斯光强度大于二阶斯托克斯光阈值时, 作为抽运光产生频率为ω_2s的二阶斯托克斯光. 探测通道的CARS过程是抽运光、探测光、一阶斯托克斯光和反斯托克斯光的四波混频过程, 如图1(b)所示. 在这个过程中, 产生一个频率为ω_a的反斯托克斯光子的同时, 消耗一个一阶斯托克斯光子和一个频率为ω_probe的探测光光子, 产生一个抽运光光子. 当反斯托克斯光强度足够大时, 还可以作为抽运光通过SSRS向探测光转化, 如图1(c)所示.
图 1 抽运通道和探测通道中的拉曼散射能级图　(a) 抽运通道的SSRS能级图; (b) 探测通道的CARS能级图; (c) 探测通道的SSRS能级图
Figure1. Raman scattering energy levels in pump and probe channels: (a) SSRS in pump channel; (b) CARS in probe channel; (c) SSRS in probe channel.

2 -->

2.2.耦合波方程

在平面波近似下, 基于抽运-探测法的反斯托克斯拉曼频移器的耦合波方程为

$\begin{split}&\left( {\frac{\partial }{{\partial z}} + \frac{{{n_{\rm{a}}}}}{c}\frac{\partial }{{\partial t}}} \right){E_{\rm{a}}} \\=\;& - \frac{g}{2}\frac{{{\nu _{\rm{a}}}}}{{{\nu _{\rm{p}}}}}\left( {{{\left| {{E_{{\rm{probe}}}}} \right|}^2}{E_{\rm{a}}} + {E_{{\rm{probe}}}}{E_{{\rm{pump}}}}E_{1{\rm{s}}}^*{{\rm{e}}^{{\rm{i}}\Delta kz}}} \right),\end{split} \tag{1a}$

$\begin{split}&\left( {\frac{\partial }{{\partial z}} + \frac{{{n_{{\rm{pump}}}}}}{c}\frac{\partial }{{\partial t}}} \right){E_{{\rm{pump}}}} \\=\;& - \frac{g}{2}\left( {{{\left| {{E_{1{\rm{s}}}}} \right|}^2}{E_{{\rm{pump}}}} + {E_{1{\rm{s}}}}{E_{\rm{a}}}E_{{\rm{probe}}}^*{{\rm{e}}^{ - {\rm{i}}\Delta kz}}} \right), \end{split}\tag{1b}$

$\begin{split}&\left( {\frac{\partial }{{\partial z}} + \frac{{{n_{{\rm{probe}}}}}}{c}\frac{\partial }{{\partial t}}} \right){E_{{\rm{probe}}}}\\=\;& \frac{g}{2}\left( {{{\left| {{E_{\rm{a}}}} \right|}^2}{E_{{\rm{probe}}}} + {E_{1{\rm{s}}}}{E_{\rm{a}}}E_{{\rm{pump}}}^*{{\rm{e}}^{ - {\rm{i}}\Delta kz}}} \right), \end{split}\tag{1c}$

$\begin{split}\left( {\frac{\partial }{{\partial z}} + \frac{{{n_{{\rm{1s}}}}}}{c}\frac{\partial }{{\partial t}}} \right){E_{{\rm{1s}}}}=\;& \frac{g}{2}\frac{{{\nu _{{\rm{1s}}}}}}{{{\nu _{\rm{p}}}}}\Big[ \left( {{{\left| {{E_{{\rm{pump}}}}} \right|}^2} - {{\left| {{E_{{\rm{2s}}}}} \right|}^2}} \right){E_{{\rm{1s}}}} \\&+ {E_{{\rm{probe}}}}{E_{{\rm{pump}}}}E_{\rm{a}}^*{{\rm{e}}^{{\rm{i}}\Delta kz}} \Big],\\[-12pt] \end{split}\tag{1d}$

$\left( {\frac{\partial }{{\partial z}} + \frac{{{n_{2{\rm{s}}}}}}{c}\frac{\partial }{{\partial t}}} \right){E_{2{\rm{s}}}} = \frac{g}{2}\frac{{{\nu _{{\rm{2s}}}}}}{{{\nu _{\rm{p}}}}}{\left| {{E_{1{\rm{s}}}}} \right|^2}{E_{{\rm{2s}}}}, \tag{1e}$

式中, E_j (j = a, pump, probe, 1s, 2s)分别为沿z轴传播的反斯托克斯光、抽运光、探测光、一阶斯托克斯光和二阶斯托克斯光的缓变振幅, n_j为拉曼晶体中各辐射分量的折射率, c为真空中的光速, ν_m (m = p, a, 1s, 2s)分别为基频光、反斯托克斯光、一阶斯托克斯光和二阶斯托克斯光的频率, g为拉曼晶体对基频光的拉曼增益系数, Δk = k_1s – k_pump – k_probe + k_a为四波混频的相位失配参量. E_j为t和z的函数, 即E_j = E_j (t, z), 为方便起见, 这里采用简化形式.
抽运光和探测光单程通过拉曼晶体, (1)式的初始条件为

$\begin{split}&{E_{{\rm{probe}}}}\left( {t,0} \right) = \sqrt {{r_{{\rm{probe}}}}} {E_{\rm{p}}}\left( t \right),\;\\&{E_{{\rm{pump}}}}\left( {t,0} \right) = \sqrt {1 - {r_{{\rm{probe}}}}} {E_{\rm{p}}}\left( t \right),\end{split}$

式中, E_p(t)为从光源发出的基频光的缓变振幅, r_probe为探测光能量占基频光总能量的比例.
为使耦合波方程具有一般性, 引入归一化空间坐标ζ、归一化时间τ、归一化缓变振幅Φ_j、归一化拉曼增益系数G和归一化相位失配参量$ \Delta K $:

$\begin{split}&\zeta = \frac{z}{{{l_{\rm{R}}}}}, \;\tau = \frac{t}{{{t_{\rm{R}}}}},\; {\varPhi _j} = \frac{{{E_j}}}{{{E_{{\rm{pmax}}}}}},\\&G = \frac{g}{2}{\left| {{E_{{\rm{p}}\max }}} \right|^2}{l_{\rm{R}}},\; \Delta K = \Delta k{l_{\rm{R}}},\end{split}$

式中, l_R为拉曼晶体的长度, t_R为光在拉曼晶体中单程通过所需要的时间, E_pmax为光源产生的基频光的最大振幅.
假设基频光脉冲的强度在时间上为高斯分布, 脉冲宽度为w_p, 则基频光的归一化振幅Φ_p与归一化时间τ之间的关系可表示为

${\varPhi _{\rm{p}}}\left( \tau \right) = \exp \left( { - \frac{{\tau - {\tau _{{\rm{pm}}}}}}{{{W_{\rm{p}}}/2\sqrt {\ln (2)} }}} \right)\exp \left( {{\rm{i}}{\varphi _{\rm{p}}}} \right), $

式中, φ_p为随机相位, τ_pm为脉冲峰值对应的归一化时间, W_p = w_p/t_R为基频光的归一化脉冲宽度. 若基频光脉冲宽度w_p = 20 ps, 拉曼晶体长度l_R = 1.5 cm, 拉曼晶体折射率n = 2, 则估算出的W_p = 0.2.
将(3)式代入(1)式和(2)式中, 可以得到归一化耦合波方程组为

$\begin{split}&\left( {\frac{\partial }{{\partial \zeta }} + \frac{\partial }{{\partial \tau }}} \right){\varPhi _{\rm{a}}} \\=\;& - \frac{{{\nu _{\rm{a}}}}}{{{\nu _{\rm{p}}}}}G\left( {{{\left| {{\varPhi _{{\rm{probe}}}}} \right|}^2}{\varPhi _{\rm{a}}} + {\varPhi _{{\rm{probe}}}}{\varPhi _{{\rm{pump}}}}\varPhi _{1{\rm{s}}}^*{{\rm{e}}^{{\rm{i}}\Delta K\varsigma }}} \right), \end{split}\tag{5a}$

$\begin{split}&\left( {\frac{\partial }{{\partial \zeta }} + \frac{\partial }{{\partial \tau }}} \right){\varPhi _{{\rm{pump}}}} \\=\;& - G\left( {{{\left| {{\varPhi _{1{\rm{s}}}}} \right|}^2}{\varPhi _{{\rm{pump}}}} + {\varPhi _{1{\rm{s}}}}{\varPhi _{\rm{a}}}\varPhi _{{\rm{probe}}}^*{{\rm{e}}^{ - {\rm{i}}\Delta K\varsigma }}} \right),\end{split}\tag{5b}$

$\begin{split}&\left( {\frac{\partial }{{\partial \zeta }} + \frac{\partial }{{\partial \tau }}} \right){\varPhi _{{\rm{probe}}}} \\=\;& G\left( {{{\left| {{\varPhi _{\rm{a}}}} \right|}^2}{\varPhi _{{\rm{probe}}}} + {\varPhi _{1{\rm{s}}}}{\varPhi _{\rm{a}}}\varPhi _{{\rm{pump}}}^*{{\rm{e}}^{ - {\rm{i}}\Delta K\varsigma }}} \right),\quad \end{split}\tag{5c} $

$\begin{split}\left( {\frac{\partial }{{\partial \zeta }} + \frac{\partial }{{\partial \tau }}} \right){\varPhi _{{\rm{1s}}}} =\;& \frac{{{\nu _{1{\rm{s}}}}}}{{{\nu _{\rm{p}}}}}G\Big[ \left( {{{\left| {{\varPhi _{{\rm{pump}}}}} \right|}^2} - {{\left| {{\varPhi _{{\rm{2s}}}}} \right|}^2}} \right){\varPhi _{{\rm{1s}}}}\\&+ {\varPhi _{{\rm{probe}}}}{\varPhi _{{\rm{pump}}}}\varPhi _{\rm{a}}^{\rm{*}}{{\rm{e}}^{{\rm{i}}\Delta K\varsigma }} \Big],\\[-13pt]\end{split}\tag{5d}$

$\left( {\frac{\partial }{{\partial \zeta }} + \frac{\partial }{{\partial \tau }}} \right){\varPhi _{2{\rm{s}}}} = \frac{{{\nu _{2{\rm{s}}}}}}{{{\nu _{\rm{p}}}}}G{\left| {{\varPhi _{{\rm{1s}}}}} \right|^2}{\varPhi _{2{\rm{s}}}}. \tag{5e}$

归一化初始条件为

$\begin{split}&{\varPhi _{{\rm{probe}}}}\left( {0,\tau } \right) = \sqrt {{r_{{\rm{probe}}}}} {\varPhi _{\rm{p}}}\left( \tau \right),\;\\&{\varPhi _{{\rm{pump}}}}\left( {0,\tau } \right) = \sqrt {1 - {r_{{\rm{probe}}}}} {\varPhi _{\rm{p}}}\left( \tau \right).\end{split}$

运用初始条件(6)式对(5)式进行数值求解, 可以得到出射分量j的归一化振幅Φ_j(1, τ), 则各分量出射光的单脉冲能量为

$\begin{split}{e_j} =\;& {A_j}{\int {\left| {{E_j}\left( {{l_{\rm{R}}},t} \right)} \right|} ^2}{\rm{d}}t \\=\;& \frac{{{A_j}{l_{\rm{R}}}{n_j}}}{c}{\left| {{E_{{\rm{p}}\max }}} \right|^2}\int {{{\left| {{\varPhi _j}\left( {1,\tau } \right)} \right|}^2}} {\rm{d}}\tau ,\end{split} $

式中, A_j为分量j的光束面积.
各拉曼分量的转化效率定义为输出脉冲能量与入射基频光脉冲能量之比

$\frac{{{e_j}}}{{{e_{\rm{p}}}}} = \frac{{{A_j}\displaystyle\int {{{\left| {{\varPhi _j}\left( {1,\tau } \right)} \right|}^2}{\rm{d}}\tau } }}{{{A_{\rm{p}}}\displaystyle\int {{{\left| {{\varPhi _{\rm{p}}}\left( \tau \right)} \right|}^2}{\rm{d}}\tau } }}, $

式中, A_p为基频光的光束面积. 拉曼分量j的归一化转化效率定义为

${\eta _j} = \frac{{\displaystyle\int {{{\left| {{\varPhi _j}\left( {1,\tau } \right)} \right|}^2}{\rm{d}}\tau } }}{{\displaystyle\int {{{\left| {{\varPhi _{\rm{p}}}\left( \tau \right)} \right|}^2}{\rm{d}}\tau } }}. $

相位失配参量是影响四波混频强度的一个重要因素. 图2给出了不同r_probe时反斯托克斯光、一阶斯托克斯光和二阶斯托克斯光的归一化转化效率(η_a, η_1s和η_2s)随归一化相位失配参量ΔK的变化关系, 其中G = 90, W_p = 0.2. 当r_probe较小时(r_probe < 0.35), 抽运光的强度大于二阶斯托克斯光的阈值, 因此二阶斯托克斯光具有较大的转化效率. η_a在相位匹配(ΔK = 0)时有最大值, 且η_1s和η_2s随ΔK基本不变. 随着r_probe的增大, 二阶斯托克斯转化减弱, 反斯托克斯光的产生随一阶斯托克斯转化的增加而增加. 当r_probe约为0.35时, η_a和η_1s达到最大值, η_1s和η_2s的曲线中心出现凹陷. 抽运光强度低于二阶斯托克斯光阈值 (r_probe > 0.35) 时, 二阶斯托克斯光消失, η_a和η_1s随r_probe的增大而减小. 当r_probe > 0.37时, η_a的最大值偏离ΔK = 0处, 且ΔK = 0处的η_a和η_1s随r_probe的增加迅速减小.
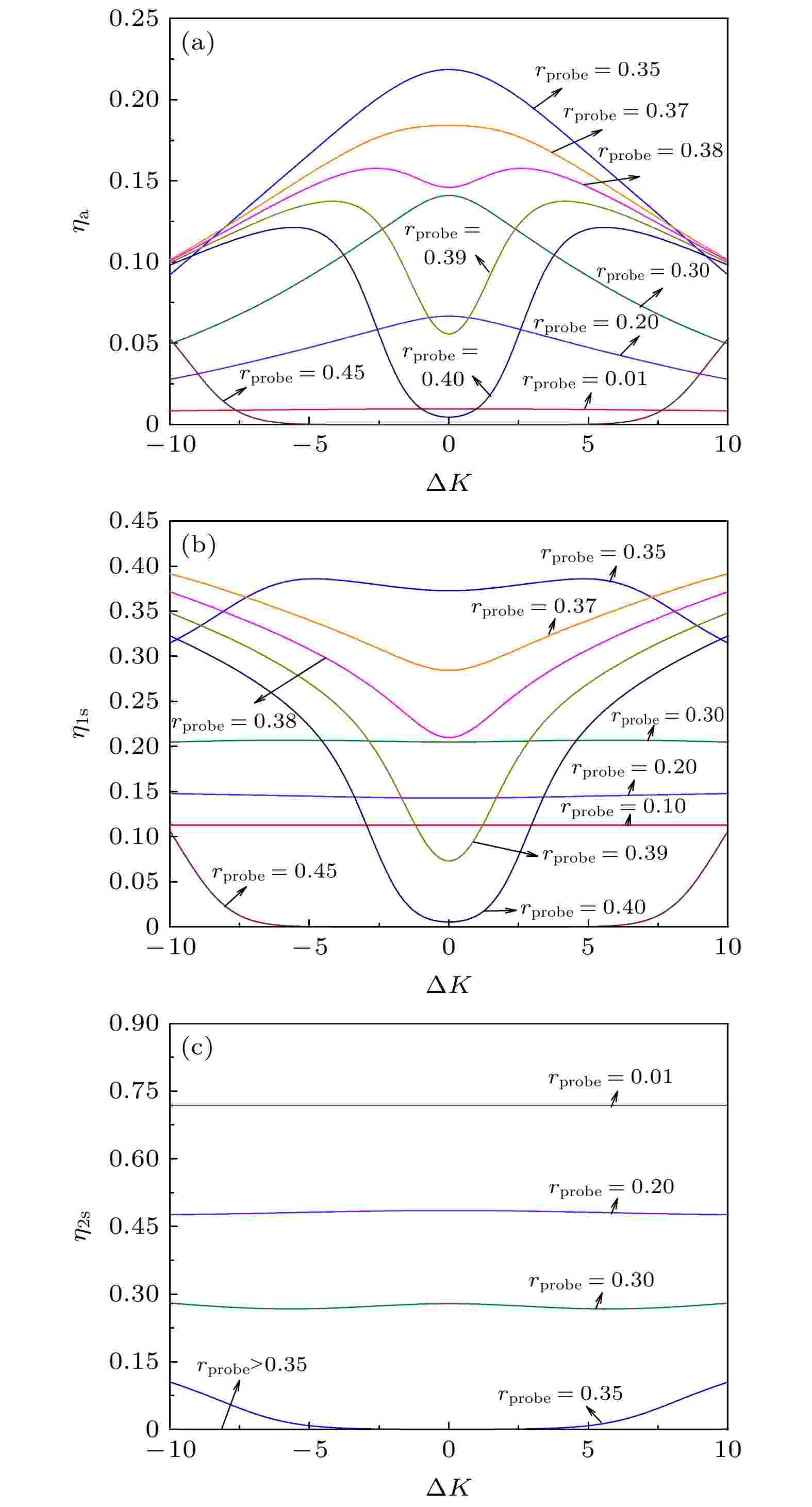图 2 G = 90, W_p = 0.2, r_probe取不同值时(a) η_a, (b) η_1s和(c) η_2s随ΔK的变化
Figure2. (a) η_a, (b) η_1s and (c) η_2s versus ΔK for different r_probe with G = 90 and W_p = 0.2.

图2中曲线的变化规律可以用图3和图4给出的抽运光、探测光、一阶斯托克斯光和反斯托克斯光的归一化强度在拉曼晶体中的空间演化进行解释, 其中图3中r_probe = 0.3, 图4中r_probe = 0.39. 对于每一组曲线, |ΔK| = 0, 4和8, G = 90, W_p = 0.2. 根据图5(a)所示的脉冲形状, 当r_probe = 0.3时, 二阶斯托克斯光的产生消耗了入射抽运光和探测光脉冲峰值附近大部分的一阶斯托克斯光, 这导致了峰值附近的反斯托克斯输出很弱. 因此, 将图3中基频光的归一化强度(|Φ_p|²)设为0.8, 从而偏离了二阶斯托克斯光产生的区域. 相反, 如图5(b)所示, 对于r_probe = 0.39, 没有二阶斯托克斯光产生, 一阶斯托克斯光和反斯托克斯光均产生于入射脉冲峰值附近. 因此图4中, 令|Φ_p|²等于基频光归一化强度的最大值, 即1.
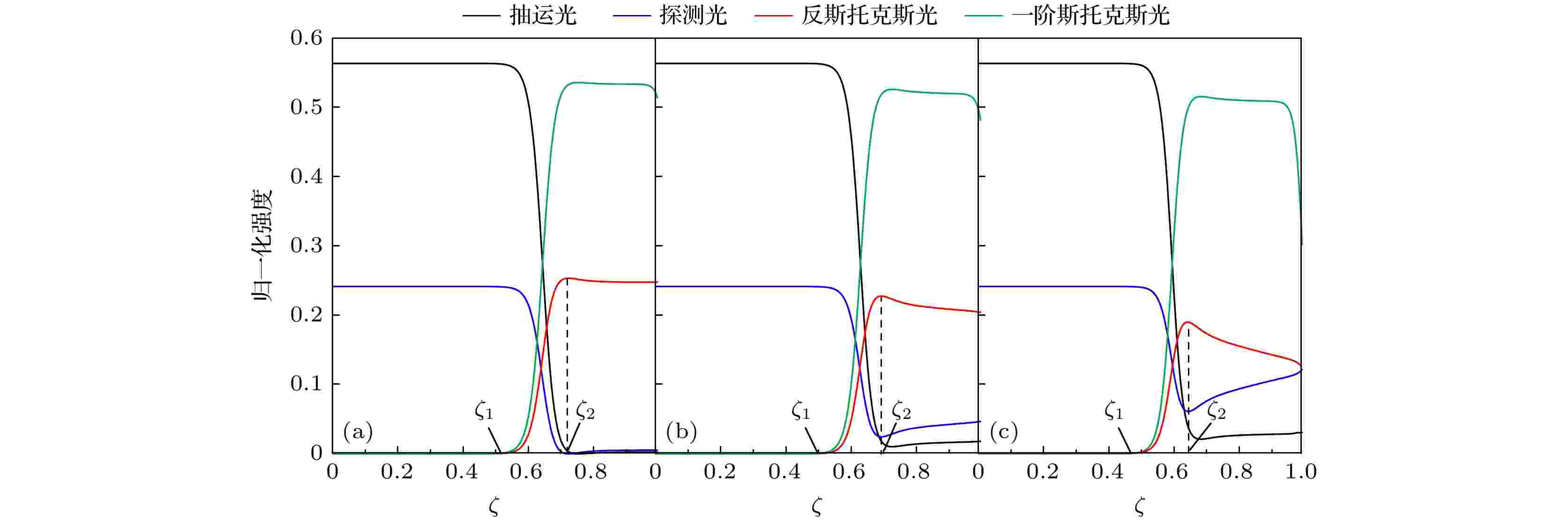图 3 r_probe = 0.3, G = 90, W_p = 0.2时, 抽运光、探测光、一阶斯托克斯光和反斯托克斯光归一化光强随ζ的空间演化　(a) |ΔK| = 0; (b) |ΔK| = 4; (c) |ΔK| = 8
Figure3. Plots of the spatial evolution of pump, probe, first Stokes, and anti-Stokes normalized intensities with r_probe = 0.3, G = 90 and W_p = 0.2: (a) |ΔK| = 0; (b) |ΔK| = 4; and (c) |ΔK| = 8.

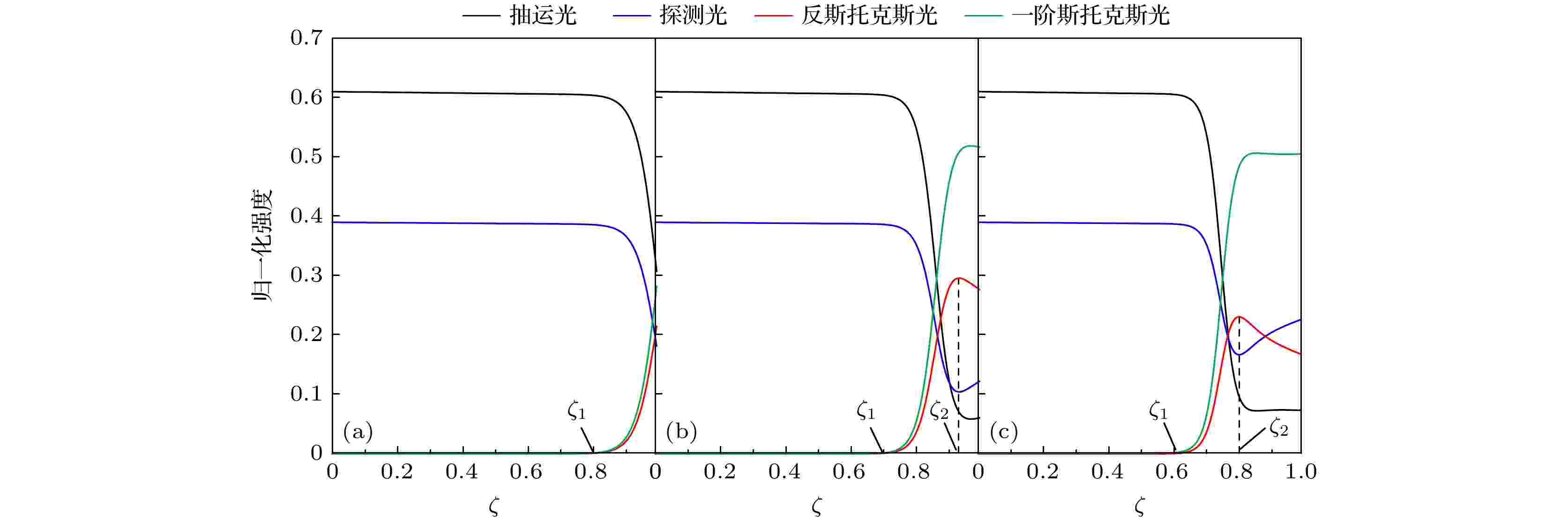图 4 r_probe = 0.39, G = 90, W_p = 0.2时, 抽运光、探测光、一阶斯托克斯光和反斯托克斯光归一化光强随ζ的空间演化　(a) |ΔK| = 0; (b) |ΔK| = 4; (c) |ΔK| = 8
Figure4. Plots of the spatial evolution of pump, probe, first Stokes, and anti-Stokes normalized intensities with r_probe = 0.39, G = 90 and W_p = 0.2: (a) |ΔK| = 0; (b) |ΔK| = 4; and (c) |ΔK| = 8.

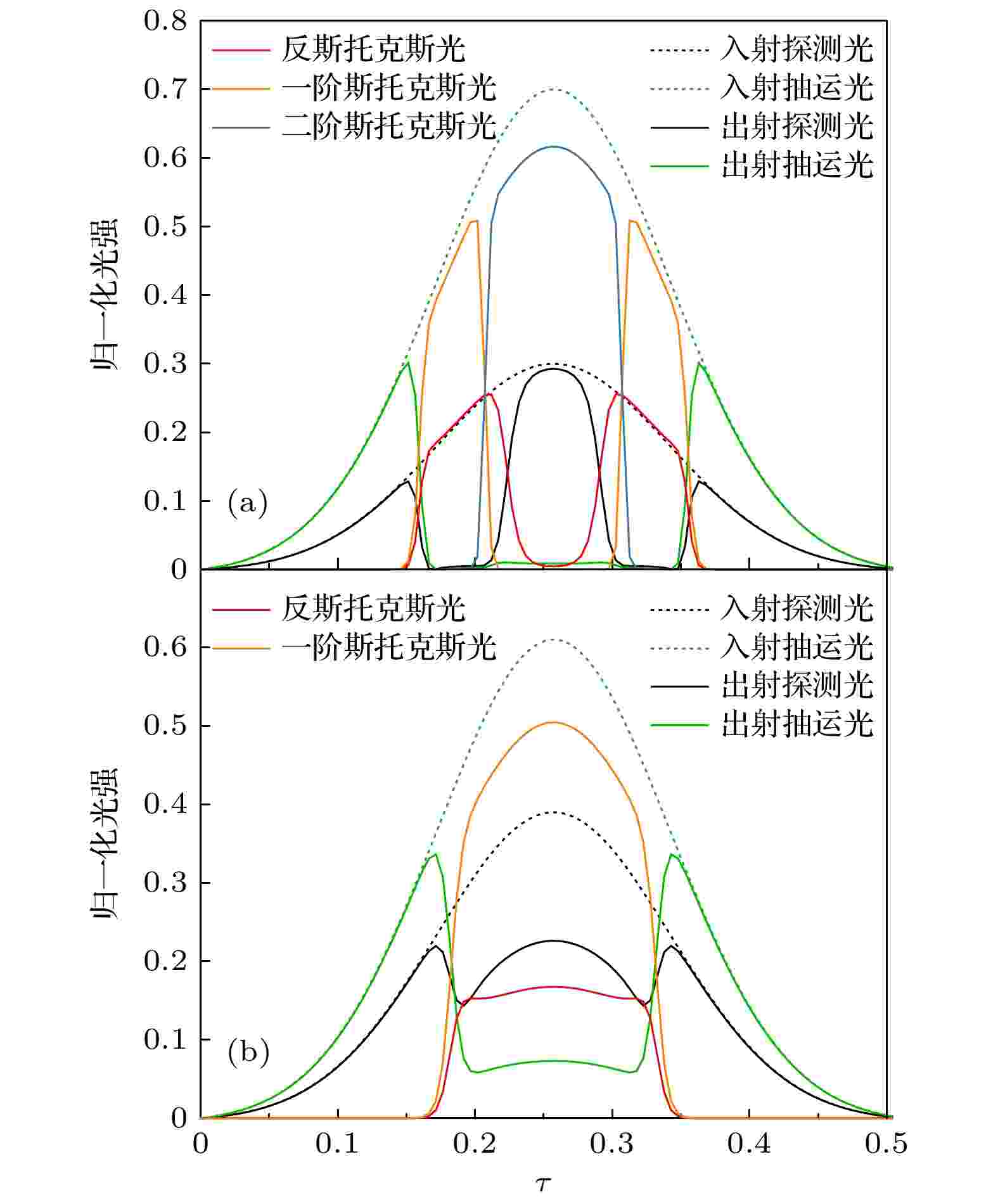图 5 G = 90, |ΔK| = 0, W_p = 0.2时抽运光、探测光、一阶斯托克斯光、二阶斯托克斯光和反斯托克斯光的脉冲形状　(a) r_probe = 0.3; (b) r_probe = 0.39
Figure5. Temporal profiles of the pump, probe, first Stokes, second Stokes and anti-Stokes pulses with G = 90, |ΔK| = 0 and W_p = 0.2: (a) r_probe = 0.3; (b) r_probe = 0.39.

在图3和图4中, 拉曼晶体中各分量归一化强度的空间演化分为以ζ₁和ζ₂为分界点的3个阶段. 第1个阶段(ζ < ζ₁)是受激拉曼散射的积累阶段, 散射光在ζ₁点达到一定强度时使抽运光迅速向一阶斯托克斯光转化. 与此同时, 产生的一阶斯托克斯光参与到CARS中, 反斯托克斯光强度在ζ₁点也快速增长. 在ζ₁点前, |ΔK|越小, CARS效应越强, 造成的斯托克斯散射损耗也就越大, 则ζ₁越大; 并且r_probe越大, 探测光越强, 反斯托克斯衰减越大, ζ₁也越大. 在第2个阶段(ζ₁ < ζ < ζ₂), 四波相互作用迅速增强, 抽运光通过SSRS转化为一阶斯托克斯光, 探测光通过CARS转化为反斯托克斯光, 一阶斯托克斯光和反斯托克斯光强在ζ₂处达到最大值. |ΔK|越小, 相互作用越强, 导致ζ₂处的一阶斯托克斯光和反斯托克斯光强度越大, 剩余抽运光和探测光强度越小. 在第3个阶段 (ζ > ζ₂), 反斯托克斯光的强度大于SSRS的阈值, 通过SSRS向探测光转化. 当|ΔK|较大时, 由于ζ₂处作为初始散射光的探测光强度大, 反斯托克斯光强度下降更快. 在图3所示的情况下, ζ₂均小于1, 因此, 输出的一阶斯托克斯光和反斯托克斯光的强度随|ΔK|的增大而减小. 然而, 当r_probe较大时, 在相位匹配时ζ₂大于1 (图4(a)), 因此输出的一阶斯托克斯光和反斯托克斯光的强度最低.
由以上分析可知, 在某些情况下, 相位匹配时反斯托克斯光的转化效率并不是最高的, 但只要r_probe在合理的范围内, |ΔK| = 0仍然是获得高反斯托克斯转化效率的必要条件. 因此, 在以下的计算中, 令|ΔK|的取值为零.
图6给出了不同r_probe时η_a, η_1s和η_2s随G的变化关系, 其中|ΔK| = 0, W_p = 0.2. 从图6(a)和图6(b)可看出, η_a和η_1s随G的变化规律几乎相同, 这是由于反斯托克斯光产生的前提是一阶斯托克斯光的存在, 如图1(b)所示. 定义G_ath, G_1sth和G_2sth分别为η_a, η_1s和η_2s的增益阈值, G_aopt和G_1sopt分别为η_a和η_1s最大值对应的最佳增益值, 则从图6可看出, G_ath ≈ G_1sth, G_aopt ≈ G_1sopt, G_1sopt ≈ G_2sth. 可以这样定性地解释: 开始阶段, G较小, 抽运光在拉曼晶体中受激拉曼散射增益很弱, ζ₁ > 1, 没有散射光输出. G > G_ath(G_1sth)时, 抽运光通过SSRS开始向一阶斯托克斯光转化, 与此同时探测光通过CARS开始向反斯托克斯光转化, η_a和η_1s迅速增长并分别在G_aopt和G_1sopt处达到最大值. 一阶斯托斯克光达到一定强度后进而向二阶斯托克斯光转化, η_a和η_1s随G的增大迅速减小, η_2s则随之单调增大, 如图6(c)所示. r_probe越小, 抽运光越强, 各阶散射分量的增益阈值和最佳增益值则越小.
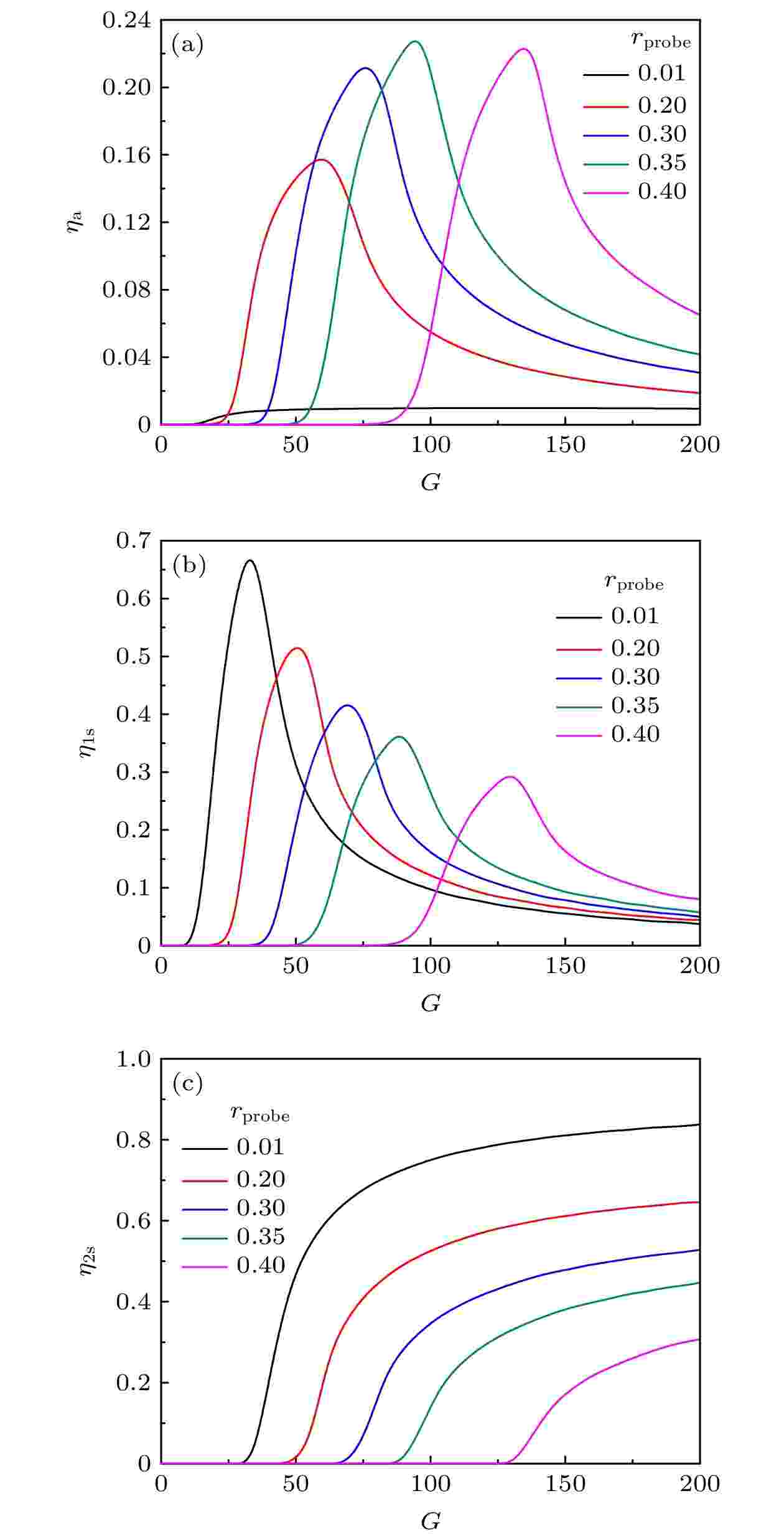图 6 |ΔK| = 0, W_p = 0.2, r_probe取不同值时(a) η_a, (b) η_{1 s}和(c) η_{2 s}随G的变化
Figure6. (a) η_a, (b) η_1s and (c) η_2s versus G for different r_probe with |ΔK| = 0 and W_p = 0.2.

由图2和图6可知, 当G一定时, 反斯托克斯光的转化效率在一个最佳的r_probe(r_opt)时有一最大值, 反之亦是如此. |ΔK| = 0, W_p = 0.2时, 反斯托克斯光最大归一化转化效率η_amax和对应的r_opt随G的变化见图7. r_opt随G的增大单调增长, 这与图6中得到的结果一致. G大于增益阈值后, η_amax随G的增大先迅速增长, 在G = 110, r_opt = 0.373时有最大值0.236, 随后缓慢下降. 这是由于反斯托克斯光是由探测光转化而来, 当G < 110时, 反斯托克斯光在低增益时几乎不向探测光转化, r_probe越大, 探测光越强, 则反斯托克斯光越强, 如图8(a)和图8(b)所示. 然而, 如图8(c)所示, 当G > 110时, G增大的同时r_opt也增大, G的增大使反斯托克斯光向探测光转化增强, r_opt的增大使探测光向反斯托克斯光转化增强, 但前者增量大于后者, 因此η_amax随G的增大有所下降.
图 7 |ΔK| = 0, W_p = 0.2时, r_opt和η_amax随G的变化
Figure7. r_opt and η_amax versus G with |ΔK| = 0 and W_p = 0.2

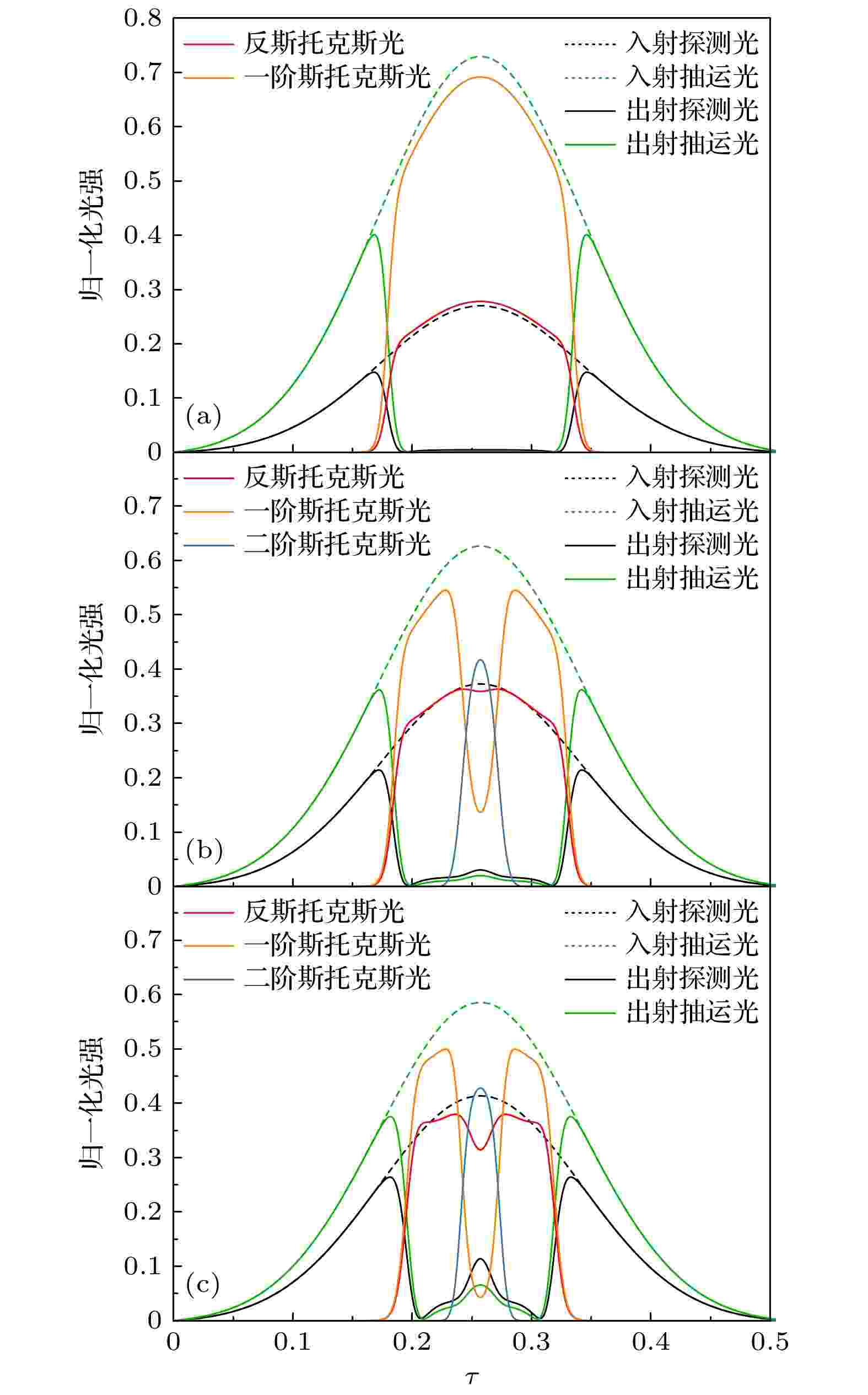图 8 |ΔK| = 0, W_p = 0.2时抽运光、探测光、一阶斯托克斯光、二阶斯托克斯光和反斯托克斯光的脉冲形状　(a) r_opt = 0.270, G = 60; (b) r_opt = 0.373, G = 110; (c) r_opt = 0.414, G = 160
Figure8. Temporal profiles of the pump, probe, first Stokes, second Stokes, and anti-Stokes pulses with |ΔK |= 0 and W_p = 0.2: (a) r_opt = 0.270, G = 60; (b) r_opt = 0.373, G = 110; (c) r_opt = 0.414, G = 160.

当r_probe一定时, 反斯托克斯光的转化效率在一个最佳的G(G_opt)时有一最大值. |ΔK| = 0, W_p = 0.2时, 反斯托克斯光的最大归一化转化效率η_amax和对应的G_opt随r_probe的变化曲线如图9所示. 与图7的分析和结论相同, 由于反斯托克斯光是由探测光转化而来, η_amax随r_probe的增大首先增长, 在G_opt = 110, r_probe = 0.373时达到最大值. 当r_probe > 0.373时, r_probe的增大使反斯托克斯光向探测光的转化多于探测光向反斯托克斯光的转化, 因此η_amax随r_probe的增大而下降.
图 9 |ΔK| = 0, W_p = 0.2时, G_opt和η_amax随r_probe的变化
Figure9. G_opt and η_amax versus r_probe with |ΔK| = 0 and W_p = 0.2

下面分析G_opt随r_probe的变化规律. 当r_probe < 0.05时, G_opt随r_probe的增大而减小, 这是因为当r_probe很小时, 抽运光很强, 大部分的抽运光通过SSRS效应转化成了二阶斯托克斯光, 参与CARS效应的一阶斯托克斯光很弱. G_opt的减小一方面减弱了抽运通道中的SSRS效应, 使得探测通道中的CARS效应增强, 另一方面减弱了探测通道中反斯托克斯光向探测光的转化. 当r_probe > 0.05时, 随着r_probe的增大, 抽运光强度逐渐减弱, G_opt随r_probe的增大而增大, 增强了抽运通道的SSRS效应以增大一阶斯托克斯光的强度, 使得CARS效应最强而获得最大的反斯托克斯转换效率.

已知基频光脉冲能量e_p、基频光脉冲宽度w_p、基频光光束面积A_p、拉曼增益系数g以及拉曼晶体的长度l_R, 可以估算出基频光脉冲的峰值振幅为${E_{{\rm{p}}\max }} = \sqrt {{e_{\rm{p}}}/\left( {{A_{\rm{p}}}{w_{\rm{p}}}} \right)} $、归一化拉曼增益系数为$G = $$ \dfrac{1}{2}g{\left| {{E_{{\rm{p}}\max }}} \right|^2}{l_{\rm{R}}}$以及归一化基频光脉冲宽度为W_p = w_p /t_R. 将归一化参量值和探测光所占的能量比r_probe代入归一化耦合波方程组中进行数值求解, 可以计算反斯托克斯光的转化效率.
如引言所述, 文献[12]采用抽运-探测法在CaCO₃晶体中实现了共线相位匹配的皮秒反斯托克斯拉曼频移器. 下面采用文献[12]中的实验结果对本文理论的正确性进行验证. 表1总结了文献[12]中的部分实验参数. 表2为反斯托克斯转化效率的理论值与实验数据的对比结果, 理论结果与实验结果基本一致. 误差产生的原因有: 1) 本文的耦合波理论基于平面波近似, 实际入射的抽运光和探测光的光强在横截面上近似为高斯分布, 且由于透镜的聚焦, 光束有一定的发散角, 在晶体不同位置处光束半径不同; 2) 理论上假设入射抽运光和探测光强度在时间上为高斯分布, 与实际光源产生的脉冲形状有所差异.

参数	值		参数	值
νa/νp	1.06		Ap/cm2	2.83 × 10–4
ν1s/νp	0.94		lR/cm	3.2
ν2s/νp	0.88		g/(cm·GW–1)	13
wp/ps	20		Δk	0

表1参考文献[12]中的参数
Table1.Parameters in Ref. [12].

抽运脉冲 能量/μJ	探测脉冲 能量/μJ	G	rprobe	实验 值/%	理论 值/%
30	25	206	0.45	2.80	2.54
30	2	118	0.063	1.88	1.86
26	12	140	0.32	3.50	4.13

表2不同情况下反斯托克斯转化效率的理论值与实验数据的对比结果
Table2.Comparisons of theoretical and experimental results of anti-Stokes conversion efficiency under different conditions.

为进一步验证本文理论的正确性, 下面考虑一种更接近实际的情况. 基频光光强在横截面上近似为高斯分布, 且在传播方向上各处的光束半径R均相等. 因此, 基频光的缓变振幅$ E _{\rm{p}}^{\rm{g}}$是径向坐标r和t的函数,

$E_{\rm{p}}^{\rm{g}}(r,t) = E_{\rm{p}}^{\rm{g}}(0,t)\exp\left( { - \frac{{{r^2}}}{{{R^2}}}} \right).$

为了与平面波近似时得到的结论有可比性, 即平面波近似和高斯近似时基频光具有相同的脉冲能量和光束面积, 高斯近似时基频光在光轴(r = 0)处的峰值振幅$ E _{\rm{pmax}}^{\rm{g}}$(0, t)为平面近似时基频光最大振幅E_pmax的$\sqrt 2 $倍^[8]. 因此, 高斯近似时基频光的归一化振幅$ \varPhi _{\rm{p}}^{\rm{g}}$(r, τ)表示为

$\begin{split}\varPhi _{\rm{p}}^{\rm{g}}\left( {r,\tau } \right) =\;& \sqrt 2 \exp\left( { - \frac{{{r^2}}}{{{R^2}}}} \right)\\&\times\exp \left( { - \frac{{\tau - {\tau _{{\rm{pm}}}}}}{{{W_{\rm{p}}}/2\sqrt {\ln (2)} }}} \right)\exp \left( {{\rm{i}}{\varphi _{\rm{p}}}} \right).\end{split} $

当考虑光强的横向分布时, 各拉曼分量的归一化振幅$ \varPhi _j^{\rm{g}}$为r, ζ和τ的函数, 则(5)式的归一化初始条件为

$\begin{split}&\varPhi _{{\rm{probe}}}^{\rm{g}}\left( {r,0,\tau } \right) = \sqrt {{r_{{\rm{probe}}}}} \varPhi _{\rm{p}}^{\rm{g}}\left( {r,\tau } \right),\;\\&\varPhi _{{\rm{pump}}}^{\rm{g}}\left( {r,0,\tau } \right) = \sqrt {1 - {r_{{\rm{probe}}}}} \varPhi _{\rm{p}}^{\rm{g}}\left( {r,\tau } \right).\end{split}$

由(3)式和(10)式可以看出高斯近似时归一化拉曼增益系数$G^{\rm g}(r) $与平面波近似时归一化拉曼增益系数G的关系为

$\begin{split}&{G^{\rm{g}}}\left( r \right) = \frac{g}{2}{\left| {E{{_{\rm{p}}^{\rm{g}}}_{\max }}\left( r \right)} \right|^2}{l_{\rm{R}}}\\=\;& \frac{g}{2}{\left| {E{{_{\rm{p}}^{\rm{g}}}_{\max }}\left( 0 \right)\exp \left( { - \frac{{{r^2}}}{{{R^2}}}} \right)} \right|^2}{l_{\rm{R}}} \\=\;& 2G\exp \left( { - \frac{{2{r^2}}}{{{R^2}}}} \right).\end{split} $

在时间上, 实际激光脉冲的上升沿比下降沿稍陡. 为使基频光脉冲形状更接近实际情况同时便于计算, 令$ \varPhi _{\rm{p}}^{\rm{g}}$(r, τ)的上升沿和下降沿均为高斯函数. 上升沿的宽度(由$ \varPhi _{\rm{p}}^{\rm{g}}$(r, τ_pm)/2到$ \varPhi _{\rm{p}}^{\rm{g}}$(r, τ_pm)的归一化时间)与下降沿的宽度(由$ \varPhi _{\rm{p}}^{\rm{g}}$(r, τ_pm)到$ \varPhi _{\rm{p}}^{\rm{g}}$(r, τ_pm) /2的归一化时间)的比值为0.8.
运用(12)式的初始条件对归一化耦合波方程组(5)进行数值求解, 可以得到出射分量j的归一化振幅$ \varPhi _j^{\rm{g}}$(r, 1, τ). 由(8)式, 高斯近似时反斯托克斯光的转化效率$ \eta _{\rm{a}}^{\rm{g}}$为

$\eta _{\rm{a}}^{\rm{g}} = \frac{{\displaystyle\iint {{{\left| {\varPhi _{\rm{a}}^{\rm{g}}\left( {r,1,\tau } \right)} \right|}^2}{\rm{2\pi }}r{\rm{d}}r{\rm{d}}\tau }}}{{\displaystyle\iint {{{\left| {\varPhi _{\rm{p}}^{\rm{g}}\left( {r,\tau } \right)} \right|}^2}{\rm{2\pi }}r{\rm{d}}r{\rm{d}}\tau }}}. $

在上述高斯近似条件下, 采用表1的实验参数进行计算得出的反斯托克斯转化效率的理论值如表3所列, 与表2中的结果相比可以发现, 两种近似条件下的理论值均与实验结果相符合, 同时也证明了平面波近似时耦合波理论可以正确地反映反斯托克斯拉曼频移器的运转特性.

抽运脉冲能量/μJ	探测脉冲能量/μJ	$ \eta _{\rm{a}}^{\rm{g}}$/%
30	25	2.63
30	2	1.91
26	12	4.09

表3高斯近似时反斯托克斯转化效率的理论值
Table3.Theoretical values of anti-Stokes conversion efficiency for Gaussian approximation.

本文在理论上研究了基于抽运-探测法的皮秒反斯托克斯拉曼频移器, 建立了平面波近似下的耦合波方程组. 为使方程组具有普适性, 引入4个无量纲综合参量对方程组进行了归一化. 对方程组数值求解显示该拉曼频移器的性能主要依赖于3个参量: 归一化相位失配参量ΔK、归一化拉曼增益系数G及探测光与基频光的能量比r_probe. 在以往的报道中, 相位匹配(|ΔK| = 0)是皮秒反斯托克斯拉曼频移器的搭建原则^[12,14]. 本文通过分析归一化相位失配参量对反斯托克斯转化效率的影响发现, 虽然在相位匹配条件下可以获得最大的反斯托克斯输出, 但前提是当G一定时r_probe在合理的范围之内. 在实际中, 较容易改变的参量为基频光的峰值光强(|E_pmax|²)和r_probe, 对于确定的拉曼晶体(g和l_R一定), |E_pmax|²决定了G的大小. 因此, 共线相位匹配时, 需选择合适的基频光能量和探测光比例才可以获得高效的反斯托克斯光输出. 需要说明的是, 由于理论上抽运光和探测光的脉冲宽度相同且同步单程通过拉曼晶体, 当其他条件一定时, 基频光的脉冲宽度对反斯托克斯光的转化效率几乎没有影响. 本文提出的归一化耦合波理论可以作为分析基于抽运-探测法的共线反斯托克斯拉曼频移器的理论工具, 辅助激光器的设计以实现超短脉冲(皮秒)反斯托克斯光的最大转化效率.