删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于超声波声压衰减效应的局部放电源定位与强度标定

本站小编 Free考研考试/2021-12-29
摘要:局部放电是导致电力设备绝缘劣化或击穿的重要原因之一. 为此, 结合即到达时差法定位原理, 在广义互相关法的基础上, 引入量子遗传算法对局部放电源进行精准定位. 而后以声波传播损耗、反射及折射现象导致的声压衰减效应为研究切入点, 首次建立局部放电源超声波信号标定的数学模型. 结果表明: 在针-板放电模型中, 利用量子遗传算法计算的局部放电源较为精准, 其最大偏差为(0.27 ± 0.13) cm, 与遗传算法、模拟退火算法、粒子群优化算法以及广义互相关法相比, 其定位精度分别提高了33.57%, 41.51%, 32.12%以及87.26%. 与此同时, 由于声压衰减效应, 当测量得到的超声信号电压幅值相同时, 随着测试距离增大, 放电源处的视在放电量逐渐增加. 若测试距离为37.80 cm时, 局部放电源的视在放电量为633.83 pC, 与7.00 cm相比, 放电强度增大了28.51%. 局部放电源的放电曲线与标定拟合曲线几乎完全重合, 验证了放电源放电程度标定模型的准确性.
关键词: 局部放电/
超声波定位/
放电强度/
数学模型

English Abstract


全文HTML

--> --> -->
1.引　言
在电力设备绝缘系统中, 短时的局部放电(partial discharge, PD)不会引起绝缘的穿透性击穿, 但长期的局部放电是导致介质局部损坏甚至击穿的重要原因之一[1]. 因此, 在电气绝缘系统的性能研究中, 局部放电得到研究****广泛关注[2-5].
关于电气绝缘材料局部放电的报道有很多[6-10]. 张若兵等[11]采用经验模态分解与Teager能量算子相结合的方法, 对放电脉冲进行有效分割, 并利用时域反射法对放电点进行精确定位. 经计算放电定位准确率高达81%, 验证了该方法可在允许误差范围内实现局部放电源的高准确定位, 这为电缆局部放电定位提供新的解决思路. Ahmed等[12]研究了中压交联聚乙烯电缆绝缘的诊断方法, 发现在局部放电发展过程中, 只有电树枝出现后放电强度急剧上升, 电缆绝缘性能的严重退化, 局部放电量才会出现激增现象. Iorkyase等[13]利用无线电指纹识别技术提取局部放电信号的强度, 进而利用k-近邻定位算法和前馈神经网络定位算法实现局部放电的精确定位. 结果发现, 神经网络算法在噪声环境下具有优异的稳定性, 平均定位误差均小于2 m.
将近年来研究****对局部放电定位的研究成果汇总, 如表1所列[14-22]. 大量相关文献报道发现[23-25], 局部放电定位研究主要集中在利用简单算法与传感器综合实现定位, 或复杂算法对放电信号进行图像化处理实现放电定位, 而关于不同算法的局部放电定位精度, 以及放电源真实放电量的相关研究至今未见报道.
使用算法研究对象综合距离误差ΔR/cm最大偏差Dmax/cm
广义互相关算法油箱体内3.94.4
时延法变压器绝缘0.80.6
基于高斯-牛顿迭代的等值声速修正算法1.71.6
粒子群优化算法2.21.9
遗传算法1.82.0
多平台测向与全局搜索的阵列定位的结合三电容放电管模型7.86.0
基于测向线公垂线中点的局部放电相控超声几何定位算法13.910.3
Chan算法电缆绝缘9.012.0


表1局部放电的超声定位精度比较
Table1.Comparison of ultrasonic location accuracy of PD.

本文采用声-声检测法结合不同算法对局部放电源的定位精度进行对比分析, 并结合声波传播损耗和声压衰减效应, 建立超声信号标定的数学模型, 揭示超声信号与放电量的定量关系, 为实现局部放电源放电强度的推算提供理论依据.
2.基于QGA局部放电源定位的理论基础
在局部放电超声波信号测试过程中, 以脉冲电流法测试系统为基础, 考虑到超声信号在金属内衰减小、速度快的传播特点, 特选用金属箱体作为试验箱, 并将压电传感器放置于样品附近, 从而得到局部放电的超声波信号[26]. 由于局部放电产生的声信息是很微弱的, 因此需将得到的超声信号经过前置放大, 而后利用数据采集器等器件输入计算机, 从而实现局部放电超声信号的检测, 试验系统电路图如图1所示.
图 1 超声波检测试验系统电路图(T1, 隔离变压器; T2, 调压器; C1, L1, 低压低通π型滤波器; T3, 高压实验变压器; C2, L2, 高压低通滤波器; CK, 耦合电容器; Zin, 检测阻抗; T, 油箱; S, 压电传感器; AMP, 前置放大器; DAQ, 数据采集卡)
Figure1. Test system schematic diagram of ultrasonic testing (T1, isolating transformer; T2, voltage regulator; C1, L1, low-voltage low-pass π filter; T3, high voltage test transformer; C2, L2, high-voltage low-pass filter; CK, coupling capacitor; Zin, detection impedance; T, Tank; S, piezoelectric sensor; AMP, preamplifier; DAQ, data acquisition card).

在试验系统中, 为了产生局部放电信号, 将针-板放电模型置于1 m × 0.5 m × 0.5 m箱体中, 其中直径为0.6 mm、曲率半径为3 μm的钨针为高压针电极, 直径为75 mm、厚度为10 mm的抛光黄铜板为地电极, 而4 mm针-板间放置不同厚度的电缆纸, 其结构示意图如图2所示. 值得注意的是, 为了避免外界空间中的电磁信号干扰, 需将整个实验系统置于良好的屏蔽室中, 以提高测量精度. 与此同时, 局部放电产生的声波在介质内以球面波的形式向外传播, 在电缆油与金属箱体介质的界面处会发生折射和反射, 因此, 箱壁处的传感器除了采集到正常声波外, 还存在界面处的反射波. 为了保证测量的准确性, 在不与传感器接触的其他三个箱壁和底部均铺设一层疏松多孔的聚酯纤维作为吸声材料.
图 2 针-板放电模型结构示意图(1, 高压引线; 2, 聚乙烯试验板; 3, 聚四氟乙烯支架; 4, 铜电极; 5, 电缆油)
Figure2. Schematic diagram of needle-plate discharge model (1, high voltage wire; 2, polyethylene sample; 3, support frame of polytetrafluoroethylene; 4, copper electrode; 5, cable oil).

本文以不同位置超声波传感器检测到的时间差为计算依据, 以确定局部放电源位置, 即到达时差法(time difference of arrival method, TDOAM)[27,28]. 由于TDOAM不用考虑声发射信号到达指定传感器的时间, 并且其定位精度满足要求, 因此, 利用TDOAM对油箱内局部放电源定位的基本原理进行分析. 为了研究方便, 选取油箱的一底角为坐标原点O(0, 0, 0), 并保证箱体处于第一象限, 建立空间笛卡尔坐标系. 在箱体内以针板模型的针尖为局部放电源, 其位置为P(x, y, z), 而箱体外表面安装n个传感器, 其位置坐标分别为: S1(x1, y1, z1), S2(x2, y2, z2), S3(x3, y3, z3), ···, Si(xi, yi, zi), ···, Sn(xn, yn, zn), 其示意图如图3所示. 以超声波传感器S1为参考传感器, 获取的信号为基准信号, 则传感器Si与传感器S1接收的声发射信号的时间差为${\tau _{i1}} = {t_i} - T$, 其中${t_i}$为局部放电信号到达传感器Si的时间, 而T为局部放电信号到达传感器S1的时间, 如图4所示.
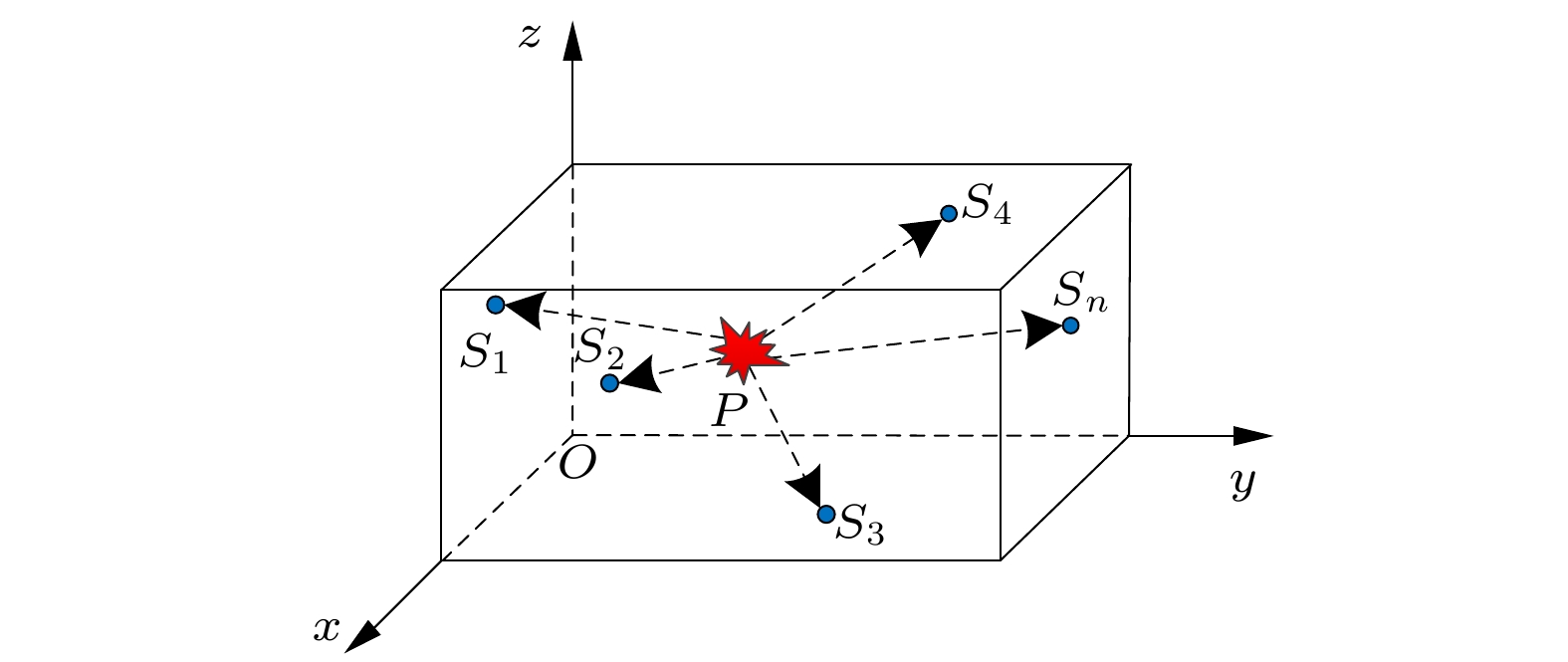图 3 油箱中放电源及超声波传感器的位置图
Figure3. Location illustration of PD source and ultrasonic sensors in the oil tank.

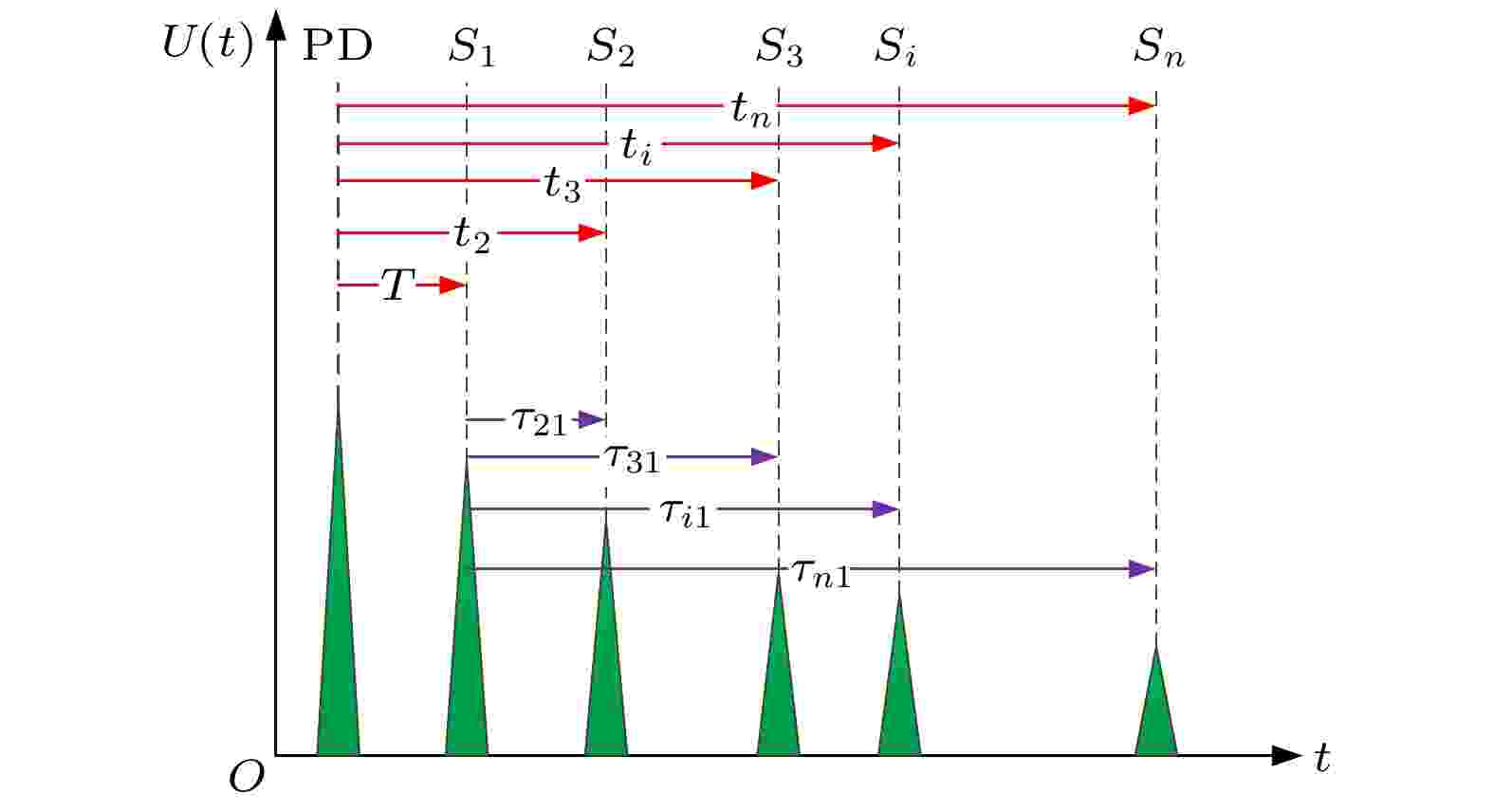图 4 TDOAM中的超声时差示意图
Figure4. Schematic diagram of ultrasonic time difference in TDOAM.

由于超声波在油箱内传播路径复杂, 等效声速ve受到温度、压力等因素的影响. 在实际应用中, 一般加入变量ve, 可以在一定程度上提高定位的精度. 此时, 局部放电源的定位方程应满足下式:
$\left\{ \begin{aligned}&{\left( {x - {x_1}} \right)^2} + {\left( {y - {y_1}} \right)^2} + {\left( {z - {z_1}} \right)^2} = {\left( {{v_{\rm{e}}}T} \right)^2}{{,}}\\&{( {x - {x_2}} )^2} \!+\! {( {y - {y_2}})^2} \!+\! {( {z - {z_2}} )^2} \!=\! {\left[ {{v_{\rm{e}}}\left( {T + {\tau _{21}}} \right)} \right]^2}{{,}}\\&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\&{\left( {x - {x_i}} \right)^2} + {\left( {y - {y_i}} \right)^2} + {\left( {z - {z_i}} \right)^2} = {\left[ {{v_{\rm{e}}}\left( {T + {\tau _{i1}}} \right)} \right]^2}{{,}}\\&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\&{( {x - {x_n}} )^2} \!+\! {( {y - {y_n}} )^2}\! +\! {( {z - {z_n}})^2} \!=\! {\left[ {{v_{\rm{e}}}\left( {T + {\tau _{n1}}} \right)} \right]^2}{{ }}{{.}}\end{aligned} \right.$
则此非线性方程可以简明地表示为
$\begin{split} {f_i}\left( {x, y, z, {v_{\rm{e}}}} \right) =\;& {\left[ {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2} + {{\left( {z - {z_i}} \right)}^2}} \right]^{\tfrac{1}{2}}} \\ & - {\left[ {{{\left( {x \!-\! {x_1}} \right)}^2} \!+\! {{\left( {y \!-\! {y_1}} \right)}^2} \!+\! {{\left( {z - {z_1}} \right)}^2}} \right]^{\tfrac{1}{2}}}\\ &- {v_{\rm{e}}}{\tau _{i1}} = 0 .\\[-13pt]\end{split}$
一般来说, (2)式为超定方程, 但求解其精确解比较困难, 因此要考虑x, y, z的约束条件并在约束条件中寻找最优解. 基于TDOAM的超声定位方法的数学模型可以归纳为一个约束优化问题:

$\begin{split}\; & \min\left\{ {{D_f}\left( {x, y, z, {v_{\rm{e}}}} \right)} \right\} =\sum\limits_{i = 2}^n \bigg\{ {{\left[ {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2} + {{\left( {z - {z_i}} \right)}^2}} \right]}^{\tfrac{1}{2}}} \\& \qquad \qquad - {{\left[ {{{\left( {x - {x_1}} \right)}^2} + {{\left( {y - {y_1}} \right)}^2} + {{\left( {z - {z_1}} \right)}^2}} \right]}^{\tfrac{1}{2}}} - {v_{\rm{e}}}{\tau _{i1}} \bigg\}^2 \begin{array}{*{20}{c}}{\left\{ \begin{aligned}&0 \leqslant x \leqslant {x_{\max}},\\&0 \leqslant y \leqslant {y_{\max}},\\&0 \leqslant z \leqslant {z_{\max}},\\&1200 \leqslant {v_{\rm{e}}} \leqslant 1500\;{\rm{m}}/{\rm{s}},\end{aligned} \right.}\end{array}\end{split}$
式中, xmax, ymax和zmax分别为油箱的等效长度、宽度和高度. 采用最小二乘法可以计算出传统意义上的最优解, 但该算法的初始值必须给定, 并且容易陷入局部收敛状态, 无法准确定位真实局部放电源的位置. 因此, 需要引入量子遗传算法(quantum genetic algorithm, QGA)改善其定位效果.
QGA是量子计算与遗传算法相结合的产物, 是一种基于量子比特(量子位)和量子力学状态叠加等计算原理的混合概率算法[29-31]. QGA的程序过程如表2所列, 其中N为种群大小, Q(t)为初始种群, Cmax为每一代的最大值, $\left| \psi \right\rangle $为量子位的状态($\left| \psi \right\rangle = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle $), α和β为振幅概率(${\left| {{\alpha _i}} \right|^2} + $$ {\left| {{\beta _i}} \right|^2} = 1$), Sk是字符串长度m(x1, x2, ···, xm)描述的第k个状态值(0或1), 得到的二进制解列为P(t); 而${P_i}$为轮盘选择中个体i被选中的概率, fi为个体i的适应度, fmax为种群的最大适应度, favg为每一代种群的平均适应度, $f' = {{\left( {{f_{\max}} + f_{{\rm{avg}}}^{}} \right)} / 2}$; f是交叉两个体中较大的适应度, $f''$为突变个体的适应度. 此外, 量子旋转门的调整策略如表3所列, 其中, xi和xbest,i分别为当前个体的第i个量子位和当前最优个体的第i个量子位, $ f(x) $和$ \Delta \theta_i $分别为适应度函数和旋转角度值, 而S(αi, βi)为旋转角度的方向. 至此, QGA通过采用量子比特编码和量子旋转门实现了个体的调整, 并引入了量子交叉变异可在很短的时间内寻找最优解, 进而可改善局部放电源的定位效果.
过程程序
种群初
始化		$Q\left( t \right) = \left| { {\psi _{q_j^0} } } \right\rangle = \displaystyle\sum\limits_{k = 1}^{ {2^m} } {\dfrac{1}{ {\sqrt { {2^m} } } }\left| { {S_k} } \right\rangle }$
预设进
化条件		Cmax, t, N, Pmax, Pc
算法
实现		For t = 1, 2, 3, ···, Cmax
　for i = 1, 2, ···, N
　${P_i} = {f_i}\Big/\sum\limits_{i = 1}^N { {f_i} }$
　$\quad P(t) = \left\{ {p_1^t, p_2^t, \cdots, p_n^t} \right\},$
　${P_c} \!=\! \left\{\!\!\!\! \begin{array}{l}\dfrac{ { { {P_{c\max} } + {P_{\min} } } } }{ {1 \!+\! \exp\left\{ {A\left[ {\dfrac{ {2(f-f')} }{ { {f_{\max} } - {f_{\rm{avg} } } } } } \right]} \right\} } } \!+\! {P_{c\min} }, ~{f \!\geqslant\! {f_{\rm{avg} } } } \\ {P_{c\max} }, \qquad\quad\qquad\qquad\quad\qquad\qquad{f \!\leqslant\! {f_{\rm{avg} } } } \end{array} \right.$
　${P_m} \!=\! \left\{\!\!\!\! \begin{array}{l} \dfrac{ { { {P_{m\max} } - {P_{\min} } } } }{ {1 \!+\! \exp\left\{ {A\left[ {\dfrac{ {2( {f'' - f'})} }{ { {f_{\max} } - {f_{\rm{avg} } } } } } \right]} \right\} } } \!+\! {P_{m\min} }, ~~{f'' \geqslant {f_{\rm{avg} } } } \\ {P_{m\max} },\;\;\; \qquad\quad\qquad\qquad\qquad\qquad\quad{f'' \leqslant {f_{\rm{avg} } } } \end{array} \right.$
　${F_{t + 1} }({U({x, y, z, {v_{\rm{e} } }})}) \!=\! {C_{t\max} } \!-\! {U_t}( {x, y, z, {v_{\rm{e} } }})$
　$X_i \;\& \; x_{ {\rm best}, i}\; \& \; f(x) > f(x_{ {\rm best}, i}) \; \& \; \Delta \theta_i$
　S(αi, βi);
　end
end
S(αi, βi); P(t); X;


表2QGA的程序过程
Table2.Procedures of QGA.

xixbest,if (x) > f (xbest,i)ΔθiS(αi, βi)
αi βi > 0αi βi < 0αi = 0βi = 0
00false00000
00true00000
01false0.01π+1–10 ± 1
01true0.01π–1+1 ± 10
10false0.01π–1+1 ± 10
10true0.01π+1–10 ± 1
11false00000
11true00000


表3量子旋转门的调整策略
Table3.Adjustment strategies of quantum rotation gates.

3.超声波放电信号标定的数学模型
一般认为, 局部放电剧烈时, 相应的超声波声强大, 视在放电量大; 而局部放电微弱时, 产生的超声波声强小, 视在放电量小; 由此可知, 局部放电超声信号的强弱与视在放电量的大小呈现正相关性[32-34].
以此为依据, 寻求局部放电过程中超声波信号的电压幅值与视在放电量间的关系, 并以相关系数作为表征二者相关性的特征参数. 为了描述两组不同变量的集合X与Y间的相关关系, 特引入统计学中的参数—相关系数. 设PXY为变量X与变量Y之间的相关系数, 则计算式如下式所示:
${P_{XY}} = {{{\rm COV}\left( {X,Y} \right)} / {\sqrt {D\left( X \right)D\left( Y \right)} }},$
式中, D表示变量的方差, 而COV(X, Y)为两组数据的协方差(${\rm COV}(X, Y) = E(XY) - E(Y)E(Y)$, E为数学期望). 当PXY = 1时, 变量X与变量Y的两组数据相关; 而当PXY = 0时, 变量X与变量Y的两组数据无关.
脉冲电流法测量局部放电时, 示波器仅显示放电的电压信号, 而不能直接显示放电量, 这需用脉冲电流法校正曲线来估算. 经脉冲电流法校正后, 脉冲电流电压U与视在放电量Q之间的关系如下式所示:
$Q = {K_0}U,$
式中, K0为局部放电的视在放电量Q与脉冲电流法的平均电压U的线性系数, 其大小等于校正脉冲发生器的注入电荷Q0与脉冲电压信号U0的比值. 相应的校正曲线如图5所示, 脉冲电流法的校正曲线Q = 5.01U – 0.26. 在示波器的灵敏度不变时, 均可依据此校正曲线推算出局部放电视在放电量.
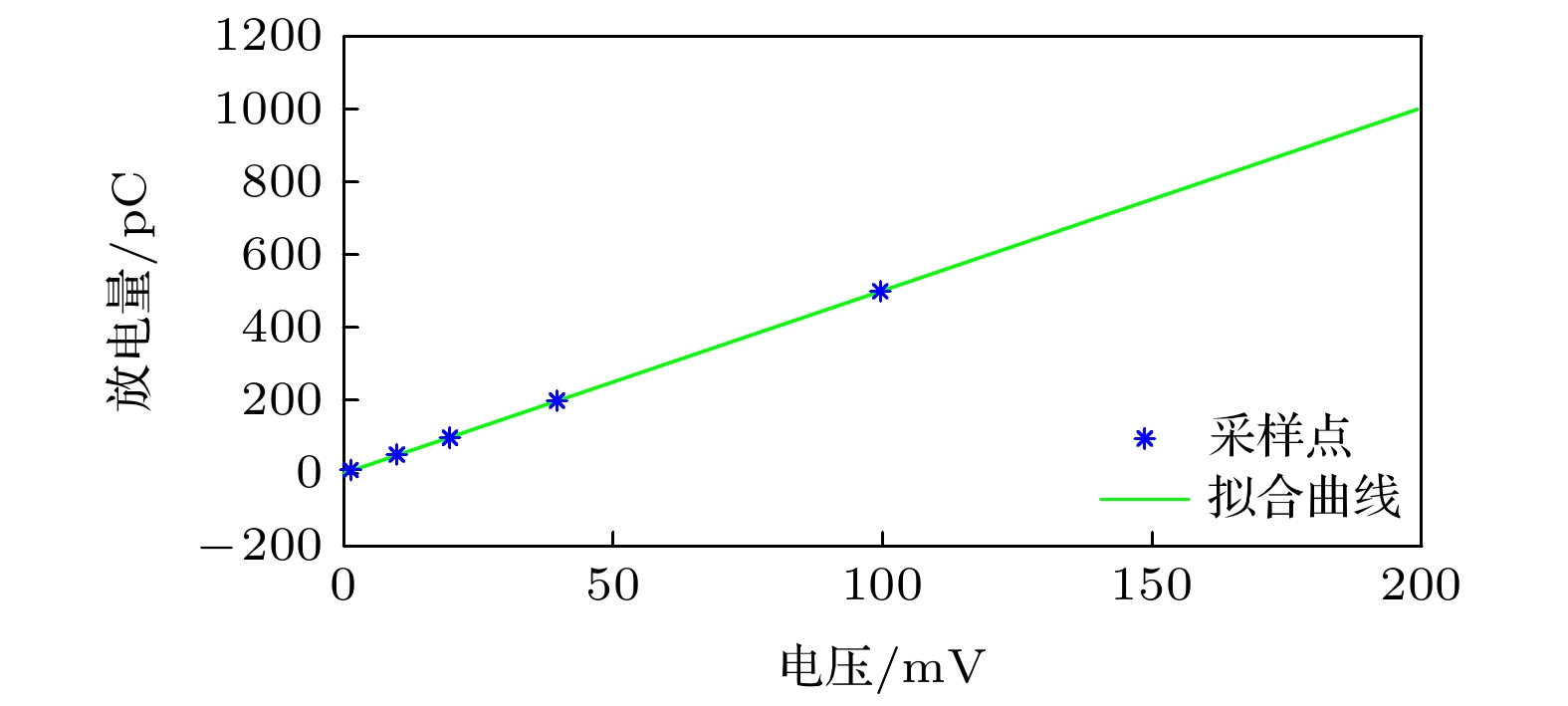图 5 脉冲电流法的校正曲线
Figure5. Calibration curve of pulse current method.

与此同时, 一段时间内局部放电的超声信号平均电压与脉冲电流平均电压呈线性关系, 则超声信号的平均电压$\bar U$与脉冲电流电压信号U关系为
$U = {K_1}\bar U,$
式中, K1为局部放电超声信号与脉冲电流法平均电压幅值的线性系数. 将(5)式代入(6)式得
$Q = {K_0}{K_1}\bar U.$
从而可以得到超声波信号的平均电压幅值与视在放电量间的关系.
利用4个不同位置超声波传感器进行局部放电试验. 设针-板模型中针电极的初始位置为(x0, y0, z0), 传感器1, 2, 3和4的位置分别为(x1, y1, z1), (x2, y2, z2), (x3, y3, z3)和(x4, y4, z4). 当局部放电位置和视在放电量均不确定时, 保持4个传感器位置不变, 利用(3)式即可通过传感器1, 2, 3和4的坐标位置, 计算出新的局部放电位置(x01, y01, z01). 此时, 以传感器1为例, 利用下面公式可计算出传感器1与初始标定放电点间距离为s10, 与新的放电点间距离为s11:
${s_{10}} = {\left[ {{{\left( {{x_0} - {x_1}} \right)}^2} + {{\left( {{y_0} - {y_1}} \right)}^2} + {{\left( {{z_0} - {z_1}} \right)}^2}} \right]^{\tfrac{1}{2}}},$
${s_{11}} = {\left[ {{{\left( {{x_{01}} - {x_1}} \right)}^2} + {{\left( {{y_{01}} - {y_1}} \right)}^2} + {{\left( {{z_{01}} - {z_1}} \right)}^2}} \right]^{\tfrac{1}{2}}}.$
当s10 ≠ s11时, 超声波信号在传输过程中由于多余的传播路径而造成更多的衰减, 使信号的声压Px改变, 如下式所示:
${P_x} = {P_0}{{\rm{e}}^{ - \alpha x}},$
式中, P0为放电点的初始声压, α为衰减系数. 由于此次标定过程中, 视在放电量未知, 则放电发生位置的初始声压设为Pnew. 将Pnew, s10以及s11分别代入公(10)式得
${P_{10}} = {P_0}{{\rm{e}}^{ - \alpha {s_{10}}}},$
${P_{11}} = {P_{\rm{new}}}{{\rm{e}}^{ - \alpha {s_{11}}}},$
式中, P10为传感器1在初始标定时的接触声压, 而P11为传感器1在新局部放电标定时的接触声压. (12)式与(11)式相减, 整理得
${P_{11}} - {P_{10}} = {P_0}{{\rm{e}}^{ - \alpha {s_{10}}}}\left[ {\frac{{{P_{\rm{new}}}}}{{{P_0}}}{{\rm{e}}^{ - \alpha \left( {{s_{11}} - {s_{10}}} \right)}} - 1} \right].$
与此同时, 超声波传感器在声电转换过程中, 必须考虑压电传感器的灵敏度和声压P的变化, 因此引入另一参数—压电系数W, 则不同放电位置激发超声波信号的电压幅值U10和U11可用下面公式表示:
${U_{10}} = W{P_{10}},$
${U_{11}} = W{P_{11}}.$
将两式相减, 并将(13)式代入可得
${U_{11}} - {U_{10}} = W{P_0}{{\rm{e}}^{ - \alpha {s_{10}}}}\left[ {\frac{{{P_{\rm{new}}}}}{{{P_0}}}{{\rm{e}}^{ - \alpha \left( {{s_{11}} - {s_{10}}} \right)}} - 1} \right].$
再将(14)式和(11)式代入(16)式可得
${U_{11}} = {U_{10}}\frac{{{P_{\rm{new}}}}}{{{P_0}}}{{\rm{e}}^{ - \alpha \left( {{s_{11}} - {s_{10}}} \right)}}.$
而后将(17)式代入(12)式可得
${Q_{11}} = {K_0}{K_1}{U_{10}}\frac{{{P_{\rm{new}}}}}{{{P_0}}}{{\rm{e}}^{ - \alpha \left( {{s_{11}} - {s_{10}}} \right)}}.$
此时, 只要初始声压比Pnew/P0已知, 通过(18)式即可得到初始标定值U10和当前视在放电量Q11的关系. 以目前的测试手段, 超声波的初始声压和初始声强并不易测量. 但当局部放电视在放电量较大时, 超声波信号的初始升压正比于相应的电压幅值, 可近似认为为线性关系, 则有[35]
$\frac{{{P_{\rm{new}}}}}{{{P_0}}} = \frac{{{U_{11}}}}{{{U_{10}}}}.$
将(19)式代入(18)式可得到
${Q_{11}} = {K_0}{K_1}{U_{11}}{{\rm{e}}^{ - \alpha \left( {{s_{11}} - {s_{10}}} \right)}}.$
采用类似的方法, 分别得到传感器2, 3和4的标定关系, 其如下式所示:
$\left\{ \begin{aligned}& {Q_{11}} = {K_0}{K_1}{U_{11}}{{\rm{e}}^{ - \alpha \left( {{s_{11}} - {s_{10}}} \right)}}, \\ &{Q_{21}} = {K_0}{K_2}{U_{21}}{{\rm{e}}^{ - \alpha \left( {{s_{21}} - {s_{20}}} \right)}}, \\ &{Q_{31}} = {K_0}{K_3}{U_{31}}{{\rm{e}}^{ - \alpha \left( {{s_{31}} - {s_{30}}} \right)}}, \\& {Q_{41}} = {K_0}{K_4}{U_{41}}{{\rm{e}}^{ - \alpha \left( {{s_{41}} - {s_{40}}} \right)}}, \end{aligned} \right.$
式中, Q11为新放电源的视在放电量, Q11 = Q21 = Q31 = Q41; K0为局部放电的视在放电量Q与脉冲电流平均电压幅值U的线性系数; K1, K2, K3和K4分别为传感器1, 2, 3和4测得的超声平均电压幅值与脉冲电流平均电压幅值的线性系数; U11, U21, U31和U41分别为传感器1, 2, 3和4测量的超声平均电压幅值; s11, s21, s31和s41分别为传感器1, 2, 3和4与新放电源间的距离; s10, s20, s30和s40分别为传感器1, 2, 3和4与初始标定时放电源间的距离.
4.结果与讨论
2
4.1.局部放电源的定位精度分析
-->

4.1.局部放电源的定位精度分析

若针-板放电模型的针尖为放电源, 则放电源的位置坐标为P(x, y, z), 而油箱外表面4个超声波传感器的位置坐标为Si(xi, yi, zi) (i = 1, 2, 3, 4). 此时以第1个传感器接收超声波信号的时刻T为时间基准, 而ti (i = 2, 3, 4)为其他传感器接收信号的时刻, 则时延${\tau _{i1}} = {t_i} - T$. 设介质超声波等值波速ve为(1380—1450) m/s, 根据(2)式可以计算出局部放电的位置. 在局部放电定位过程中, QGA、遗传算法(genetic algorithm, GA)、模拟退火算法(simulated annealing algorithm, SAA)以及粒子群优化(particle swarm optimization, PSO)算法的参数如表4所列.
算法参数数值
QGA群体数量40
最大遗传次数200
GA群体数量40
最大遗传次数200
重组概率0.9
变异概率0.01
SAA初始温度10
最终温度0.0001
衰减系数0.8
冷却新状态迭代次数1000
PSO种群大小40
学习因子2
初始惯性权值0.9
原始粒子群1
迭代次数100


表4局部放电定位的算法参数
Table4.Algorithm parameters of PD localization.

利用QGA, GA, SAA, PSO算法以及广义互相关法(generalized cross correlation method, GCC)等算法计算局部放电的位置和平均绝对误差如表5和图6所示. 此五种算法均可实现不同放电源的定位, 但其定位精度各有不同, 其中QGA的定位较为精准, 其平均绝对误差低至(0.17 ± 0.04) cm, 而GCC定位最为粗糙, 平均绝对误差高达(1.32 ± 0.14) cm.
算法位置
实验组1 (12, 14, 6) cm实验组2 (14, 10, 6) cm实验组3 (15, 11, 6) cm实验组4 (16, 12, 6) cm
QGA(11.79, 13.61, 5.78)(13.78, 9.88, 6.06)(14.88, 10.86, 5.90)(15.82, 11.84, 5.88)
GA(12.33, 14.24, 5.73)(13.62, 10.22, 6.16)(14.65, 11.24, 6.22)(16.34, 12.30, 6.24)
SAA(11.58, 13.41, 5.78)(13.66, 10.32, 6.24)(15.34, 11.22, 6.20)(16.32, 12.28, 6.26)
PSO(12.12, 14.21, 6.15)(14.32, 9.72, 5.84)(15.42, 11.28, 6.30)(16.42, 12.34, 6.32)
GCC(13.38, 15.06, 7.42)(15.51, 9.62, 6.94)(15.71, 8.32, 7.24)(14.76, 10.31, 7.13)


表5不同算法的局部放电定位
Table5.The PD location of different algorithms.

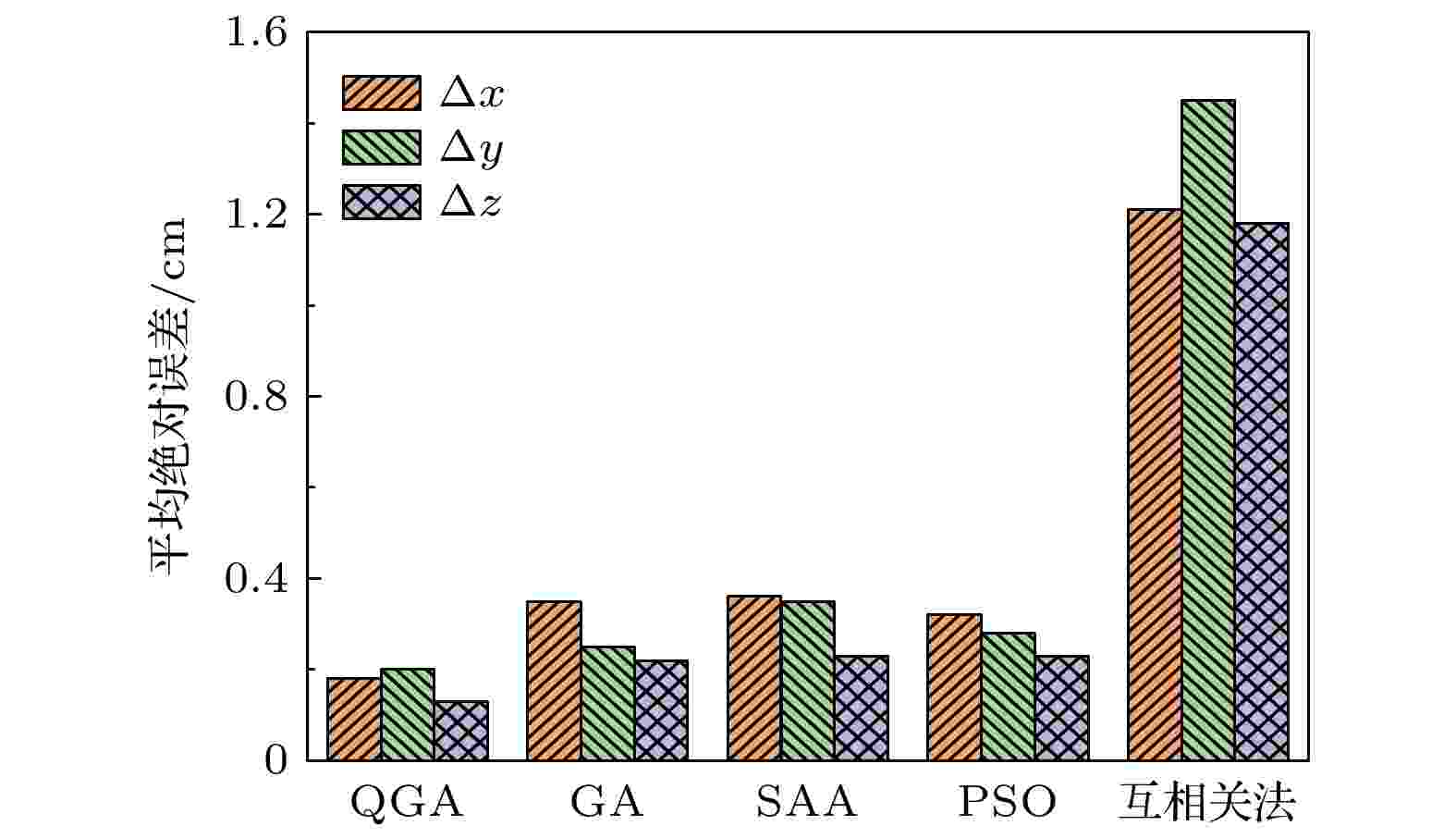图 6 不同算法下局部放电定位的平均绝对误差变化
Figure6. Average absolute errors of PD location under different algorithms.

但仅用绝对误差说明其定位精度是并不准确的, 特采用相对误差εr, 最大偏差Dmax以及综合距离误差ΔR等误差在各个角度进行分析, 其计算式分别如下面公式所示:
${\varepsilon _{\rm{r}}} = \left| {\frac{{{L_{\rm{act}}} - {L_{\rm{cal}}}}}{{{L_{\rm{act}}}}}} \right| \times 100{\text{%}},$
${D_{\max}} = \max\left\{ \begin{array}{l} \left| {{x_{\rm{act}}} - {x_{\rm{cal}}}} \right| \\ \left| {{y_{\rm{act}}} - {y_{\rm{cal}}}} \right| \\ \left| {{z_{\rm{act}}} - {z_{\rm{cal}}}} \right| \end{array} \right\},$
$\Delta R = {\left[ {{{\left( {x - {x_c}} \right)}^2} + {{\left( {y - {y_c}} \right)}^2} + {{\left( {z - {z_c}} \right)}^2}} \right]^{\tfrac{1}{2}}},$
式中, P(x, y, z)和Pc(xc, yc, zc)分别为实际和计算的放电源位置坐标, 而Lact和Lcal分别为实际和计算坐标. 基于不同算法的局部放电定位误差εr, Dmax和ΔR的平均误差如图7所示.
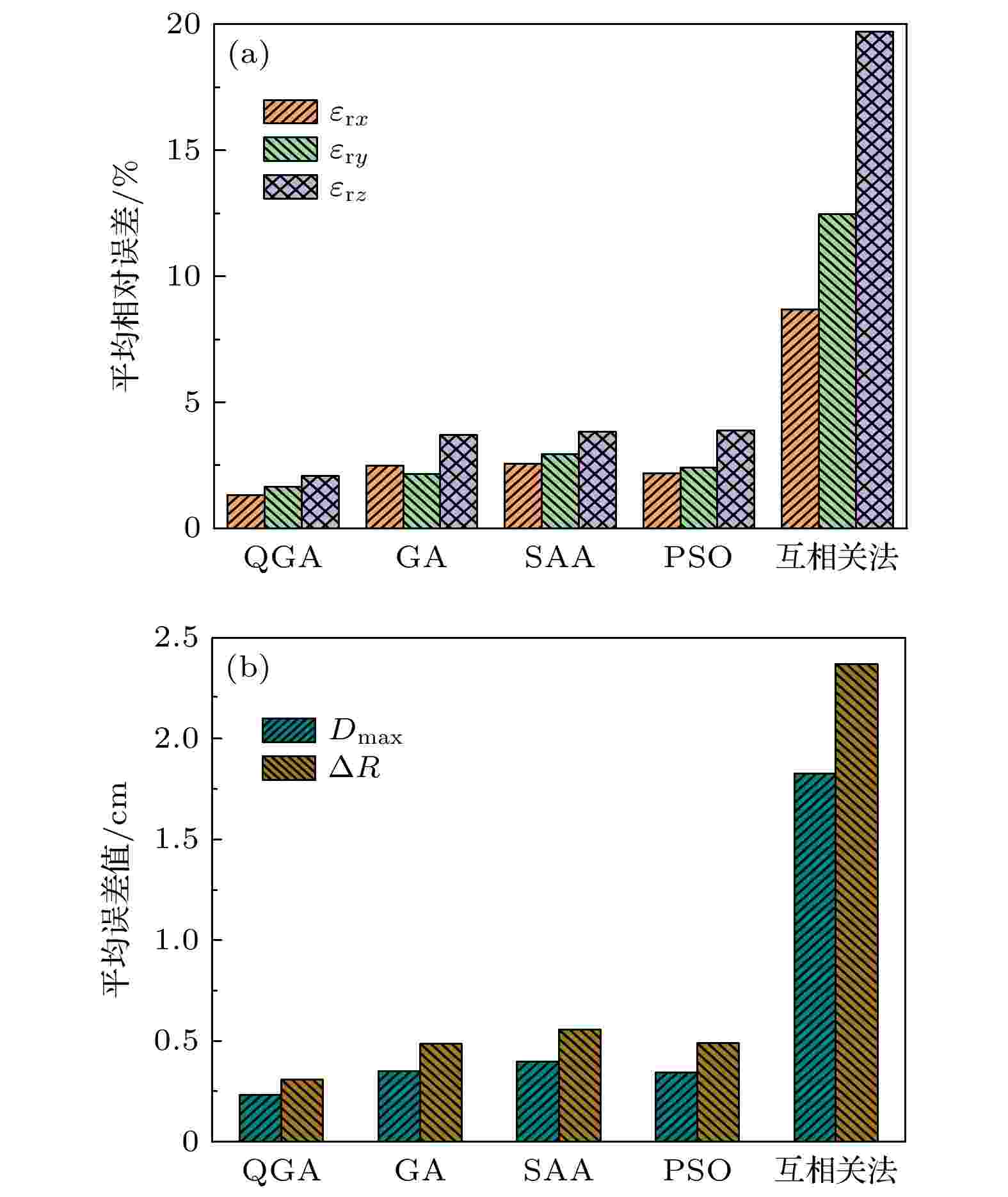图 7 不同算法下局部放电定位的平均误差变化　(a) 平均绝对误差; (b) 平均最大偏差和综合误差
Figure7. Average errors of PD location under different algorithms: (a) εrx, εry and εrz; (b) Dmax and ΔR.

在图7中, 无论是绝对误差、最大偏差还是综合误差, GCC的误差值均明显高于其他四种误差, 以综合误差为例, GCC的误差为2.37 cm, 约QGA的7.65倍, 定位精度最为粗糙. 而在其他四种误差中, QGA的误差量明显较小, 最大平均相对误差仅为2.08%, 相比传统的GA, SAA和PSO最高可提高86.54%, 占有绝对的定位优势, 这与绝对误差的计算结果相一致.
2
4.2.超声波信号标定精度分析
-->

4.2.超声波信号标定精度分析

为了保证测试数据的一致性, 采用脉冲电流法与超声波法同时测量局部放电信号, 可认为脉冲电流信号的放电量即为超声波信号对应的放电量. 为了减小误差, 在数据处理过程中, 每组试验均取150个数据进行曲线拟合, 并取400 μs内平均值作为超声信号电压$\overline U $与脉冲电流电压信号U.
利用超声波传感器分别在针-板电极间放入2, 3和4 mm的电缆纸进行局部放电试验. 针板间隙内不同电缆纸厚度的超声信号电压幅值与放电量的关系如图8所示, 其系统灵敏度和相关系数如表6所列. 由图8和表6可知, 超声波信号的平均电压幅值与视在放电量间呈现一定的正相关性, 且基本属于线性关系. 但随着传感器测量位置的不同, 放电信号测试距离的改变, 超声信号会由于衰减出现一定的误差, 这需要对局部放电超声波信号进行进一步的标定.
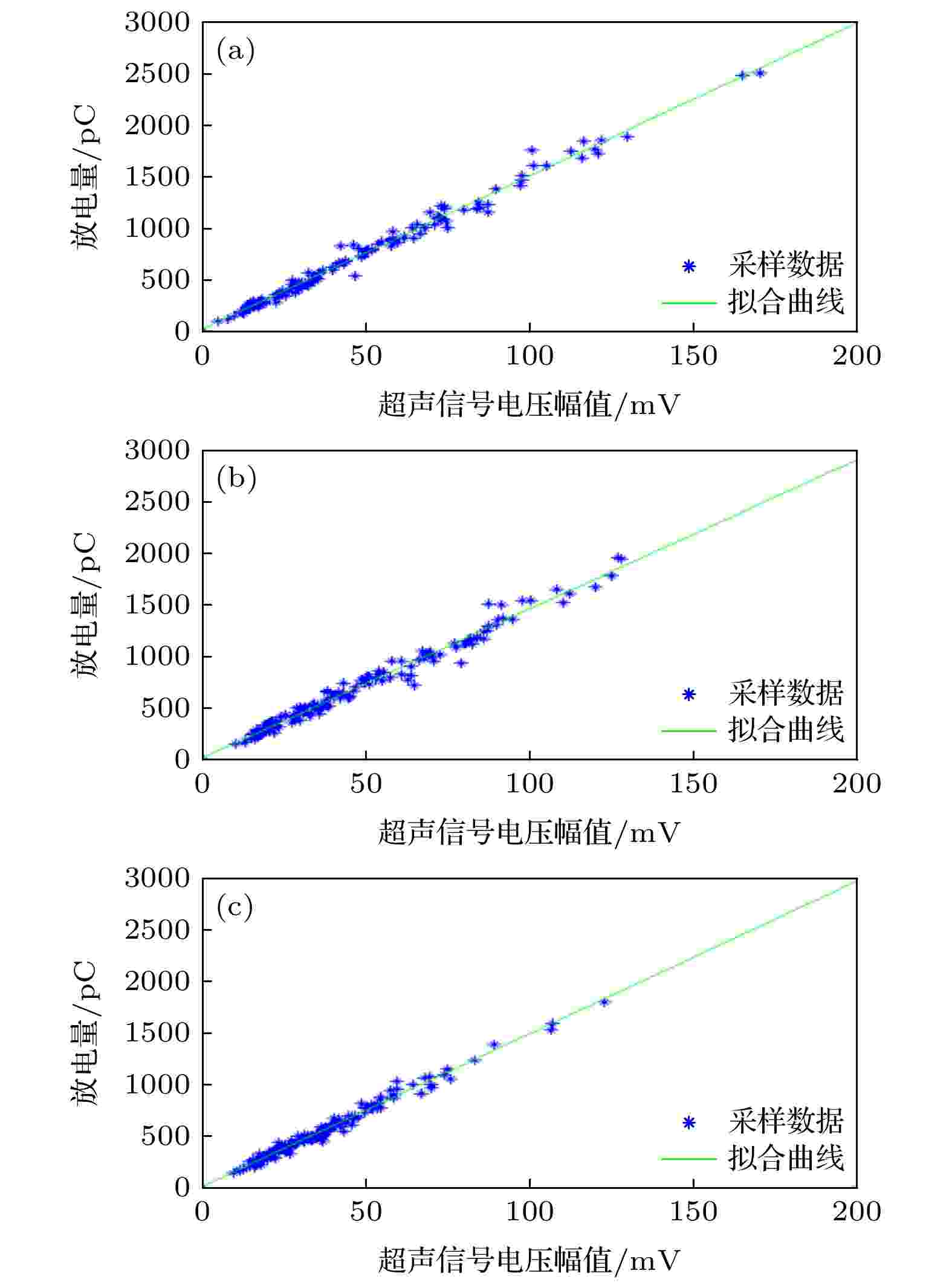图 8 不同绝缘纸厚度的电压幅值与放电量拟合曲线　(a) 2 mm; (b) 3 mm; (c) 4 mm
Figure8. Fitting curves of voltage amplitude and discharge amplitudes at different thickness of insulating papers: (a) 2 mm; (b) 3 mm; (c) 4 mm.

电缆纸厚度/mm系统灵敏度相关系数
214.910.99
314.370.99
414.840.99


表6系统灵敏度和相关系数的变化
Table6.Change of system sensitivity and correlation coefficients.

为了观察放电源与传感器间测量距离s对测量结果的影响, 在油箱外表面放置4个超声波传感器, 其位置分别(0, 7, 6), (17, 10, 6), (25, 7, 6)和(17, 23, 6), 经过大量实验数据计算可获取其标定参数, 如表7所列.
线性系数K0K1K2K3K4
数值5.012.982.932.862.95


表7局部放电的线性系数
Table7.Linear coefficients of PD.

在超声频率100 kHz下进行放电源视在放电量的计算, 其结果如图9所示, 其中sy为放电位置确定的放电曲线, 而sw为标定拟合, 即放电位置和视在放电量未知时计算的放电曲线. 当s为7.00 cm时, sy和sw的曲线完全重合, 这说明标定拟合是完全准确的.
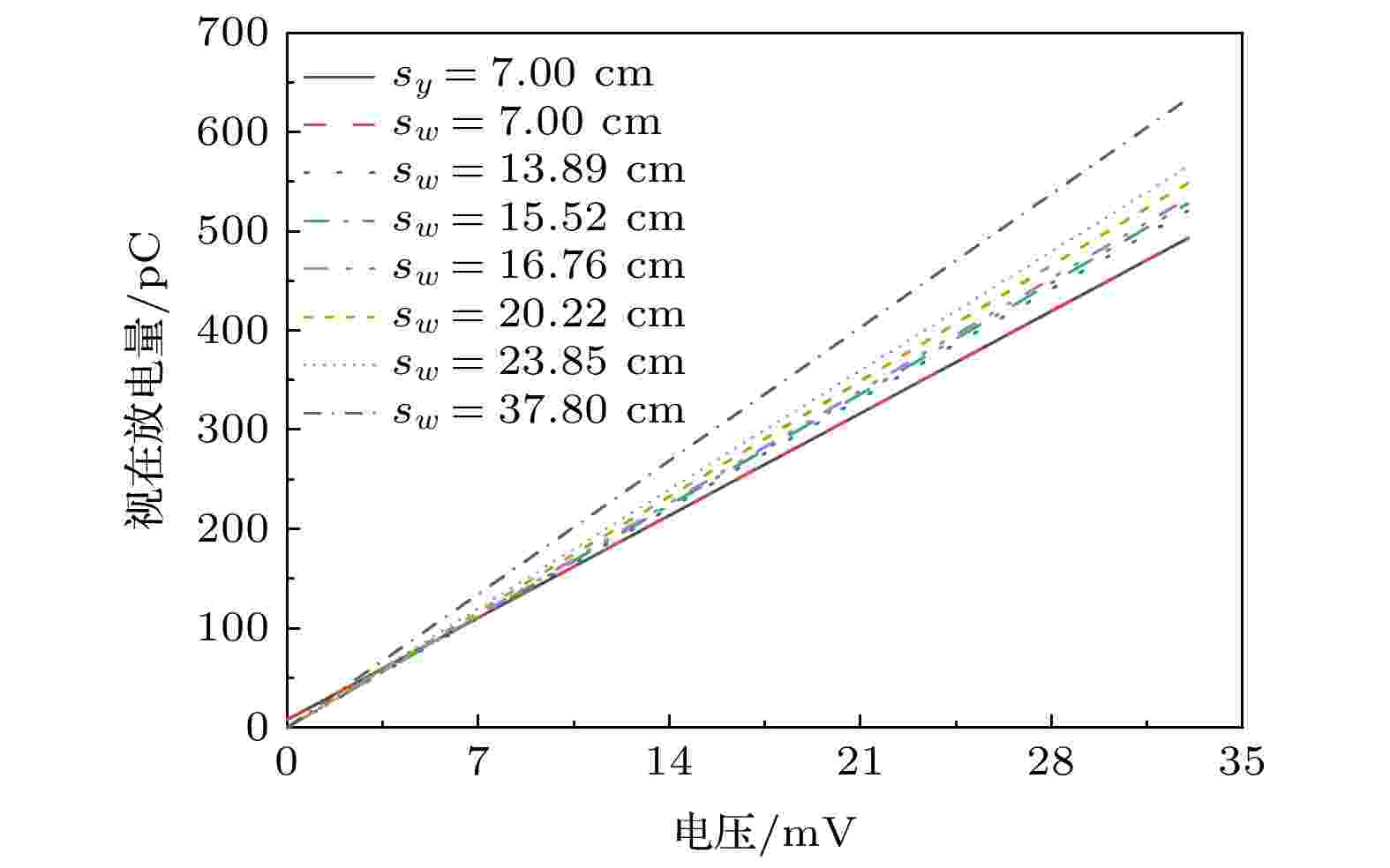图 9 不同测量距离下视在放电量与电压的关系
Figure9. Relationship between apparent charge and voltage at different measuring distances.

由图9可知, 当超声信号电压相同时, 随着测量距离s逐渐增加, 由于超声信号的衰减, 放电声源的视在放电量亦逐渐增大, 以超声波信号电压幅值33 mV为例, 当测量距离s为37.80 cm时, 经推算其对应的视在放电量为633.83 pC, 与测量距离7.00 cm相比, 视在放电量增大了28.51%. 并且, 随着测量距离增加, 单位测量距离的放电增长量ΔQ也在逐渐增大. 当s为13.89 cm时, 与测量距离7.00 cm相比, 放电增长量ΔQ为4.03 pC/cm, 而当s为37.80 cm时, 与测量距离7.00 cm相比, 放电增长量ΔQ为4.57 pC/cm, ΔQ的增长速率提高了13.40%. 通过视在放电量和放电增长量的分析可知, 放电源的定位计算对局部放电的视在放电量, 乃至放电强度的推算具有重要意义.
5.结　论
以TDOAM定位原理为基础, 对局部放电源实现智能定位, 并对局部放电超声信号的放电强度标定方程进行修正及验证, 得到以下结论.
1)局部放电源定位结果表明, 利用QGA计算局部放电源的定位较为精准, 其最大平均相对误差仅为2.08%, 与传统的GA, SAA和PSO相比最高可提高86.54%.
2)局部放电超声波信号电压幅值与视在放电量间的相关系数高达0.99, 从而揭示其线性正相关性.
3)利用局部放电的视在放电量与超声信号电压的线性关系, 结合声波传播损耗和反射及折射导致的声压衰减效应, 建立了局部放电源放电强度标定的定量计算模型. 在针-板放电模型中, 当超声信号电压为33 mV, 测试距离为7.00 cm时, 局部放电源的放电曲线与标定拟合曲线几乎完全重合, 说明了标定定量模型的准确性;
4)当超声信号电压幅值相同时, 由于声压衰减效应, 随着测试距离增大, 放电源处的视在放电量逐渐增加. 当测试距离为37.80 cm时, 局部放电源的视在放电量为633.83 pC, 与7.00 cm相比, 放电强度增大了28.51%.
相关话题/信号 电压 传感器 测量 计算
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于光谱法的发光二极管稳态热阻测量方法
    摘要:根据白光发光二极管(LED)发光光谱特点,通过分析蓝光光谱和由蓝光激发黄色荧光粉产生的黄光光谱的交点(即整个光谱的波谷点)特性,利用常规可见光光谱仪设计了一套基于光谱法的LED稳态热阻测量系统,采用正常的驱动电流通过一定的函数算法进行拟合,得到整体光谱波谷处归一化光谱强度与结温间敏感系数K和定 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于数字全息干涉术的云微物理参数同步测量方法
    摘要:云微物理参数对气候变化、天气预测、人工影响天气、飞行安全等领域具有重要的影响.目前,基于光散射、碰撞和成像理论的云微物理参数测量方法存在反演过程需要对云滴谱和粒子特性进行假设、撞击过程会破坏粒子特征、无法获得云粒子三维特征等瓶颈问题.本文提出了基于干涉理论,结合光信息处理、景深压缩与融合全息图 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 态选择电荷交换实验测量以及对天体物理软X射线发射模型的检验
    摘要:在高温天体等离子体环境中,低能高电荷态离子与中性原子和分子之间的电荷交换是天体物理环境中软X射线发射的重要机制之一.电荷交换软X射线发射相关的天体物理建模需要大量的主量子数n和角量子数l分辨的态选择俘获截面数据,目前这类数据主要来自于经典或者半经典的原子碰撞理论模型.本文利用反应显微成像谱仪, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Na||Sb-Pb-Sn液态金属电池电极的价电子结构与热-电性能计算
    摘要:应用固体与分子经验电子理论系统地研究液态金属池Na||Sb-Pb-Sn电极的价电子结构与热、电性能.研究结果表明:电极合金的价电子结构与其性能密切关联.阴极合金Na1–xIAx(IA=K,Rb,Cs)的晶格电子随着掺杂量的增加而减少,诱发合金的熔点、结合能随掺杂量的增加而降低.Na离子输运到阳 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 频域反射法光纤延时精密测量
    摘要:本文提出了一种应用于光纤延时系统中实现光纤延时精密测量的新方法,用以提高光纤延时测量的精度和准确性.该方法以1064nm激光调制信号作为光源,通过测量回波信号的幅值和相位信息得到被测通道的频率响应,采用快速傅里叶逆变换得到被测目标的延时信息,实现光纤延时测量.本文通过理论分析和延时测量实验对频 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于L型延迟阵列调制宽带转换器的信号载频和二维到达角联合估计
    摘要:针对现有的基于欠采样的频率和二维到达角的联合估计存在结构复杂问题,本文提出了一种基于调制宽带转换器技术的L型延迟阵列接收结构.利用延迟通道与未延迟通道采样值之间的相位差可直接估计载频,进而计算二维到达角,无需额外的参数配对操作,避免了配对步骤引入的误差和复杂度的提升.并结合所提L型延迟阵列结构 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 非线性超声射频信号熵对乳腺结节良恶性的定征
    摘要:本文提出了一种基于非线性超声射频(radiofrequency,RF)信号熵对乳腺结节良恶性进行定征的方法.对306例乳腺结节样本(良性158例,恶性148例)提取了基于超声RF信号二次谐波的熵和加权熵,以及常规超声参数(图像灰度、纵横比、不规则度、乳腺结节大小、深度);采用t检验和线性分类器 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 双温度氩-氮等离子体热力学和输运性质计算
    摘要:获得覆盖较宽温度和压力范围内的等离子体热力学和输运性质是开展等离子体传热和流动过程数值模拟的必要条件.本文通过联立Saha方程、道尔顿分压定律以及电荷准中性条件求解等离子体组分;采用理想气体动力学理论计算等离子体热力学性质;基于Chapman-Enskog方法求解等离子体输运性质.利用上述方法 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于忆容器件的神经形态计算研究进展
    摘要:人工智能的快速发展需要人工智能专用硬件的快速发展,受人脑存算一体、并行处理启发而构建的包含突触与神经元的神经形态计算架构,可以有效地降低人工智能中计算工作的能耗.记忆元件在神经形态计算的硬件实现中展现出巨大的应用价值;相比传统器件,用忆阻器构建突触、神经元能极大地降低计算能耗,然而在基于忆阻器 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于径向剪切干涉仪的三维位移测量技术
    摘要:本文提出一种基于双圆光栅径向剪切干涉仪的三维位移测量方法,其测量原理是径向剪切干涉仪所形成的莫尔条纹不仅由二维平面内位移决定,轴向位移会在+1和–1级莫尔条纹之间产生一个特定的相移.首先,基于标量衍射理论对双圆光栅径向剪切干涉仪的+1和–1级莫尔条纹强度分布进行推导,建立了三维位移量与莫尔条纹 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.