全文HTML
--> --> -->康普顿散射作为电动力学最基本的过程之一, 在学术界引起了广泛关注, 并在基础物理研究中得到了成功应用. 例如, 康普顿散射成功解释了许多天体物理过程[14-17], 如宇宙背景辐射中的散射光子能谱、宇宙中的超强伽马暴和太阳能冠电子产生的K型日冕等; 在惯性约束聚变(inertial confinement fusion, ICF)中, X射线汤姆孙散射是测量高温等离子体重要的诊断手段; 此外, 逆康普顿散射可以向外辐射出高能光源, 具有广泛的应用前景和重要的应用价值.
在2018年, 杰哈·莫罗(Gérard Mourou)和唐娜·斯特里克兰(Donna Strickland)共同分享了部分诺贝尔物理学奖, 表彰他们在超强激光技术方面的突破性贡献, 即利用啁啾脉冲放大(chirped pulse amplification, CPA)技术获得高功率超短激光脉冲[18]. 如今, 随着该技术的进一步发展, 超短飞秒脉冲太瓦(TW, 1012 W)甚至拍瓦(PW, 1015 W)激光装置已经商业化, 将这种高功率激光聚焦后可产生相对论强度的光场(I
当场强和粒子能量变得更高时, 甚至需要引入量子电动力学(quantum electro dynamics, QED)理论来解决其动理学过程[19,20]. 近期, 全球多台数拍瓦激光装置逐渐投入使用, 激光等离子体相互作用中的此类效应会变得极其显著. 因此, 系统地研究多光子汤姆孙散射过程是本领域未来十年极其重要的研究方向. 随着激光尾波场的电子加速 (laser wake field acceleration, LWFA)[21-26]和数拍瓦激光装置的建成[27-33], 基于激光加速的全光汤姆孙散射将是研究多光子汤姆孙散射可行性最高的实验方案. 可以预见, 在不久的将来, 极端光场散射过程[27,34], 如汤姆孙散射多光子吸收过程[35]、辐射阻尼效应[36-44]、正负电子对的产生[45-51]、Compton-Cherenkov辐射[52]、真空双折射[29,41]等前沿的基础理论, 将会被实验一一验证.
本文第2节介绍基于激光的全光散射实验在不同条件下的物理过程, 并讨论其独特性; 第3节概述全光散射的两种不同实验方案及研究进展; 第4节讨论全光散射实验的挑战及应用前景; 最后讨论未来全光实验面临的挑战.
2.1.理论模型
康普顿散射过程可以看作是光子与电子的弹性碰撞过程, 光子的能量发生改变, 一部分光子能量转移到电子上. 通常康普顿散射在汤姆孙极限[53-55]和克莱因-西那(Klein-Nishina, K-N)极限条件[56-58]下有不同表述方式, 取决于相互作用的光子对电子的反冲效应是否可以忽略. 其中在汤姆孙极限, 康普顿散射就是汤姆孙散射, 是弹性散射. 而在K-N极限下, 汤姆孙散射不再适用, 电子与光子之间会有明显的能量传递, 因此是非弹性散射.本文提到的大部分实验是可以在汤姆孙极限的框架内解释的, 在这个条件下, 整个动理学过程严格地依赖于激光场强度a0. 在a0 < 1时, 是线性散射, 电子主要受到电场作用做非相对论简谐振荡, 因此为偶极辐射模式, 辐射频率与入射光ω0相同. 线性汤姆孙散射截面为σr = 8π
当a0
无论电子静止还是相对运动, 都可以运用上述理论来处理该相互作用过程. 若电子在运动, 则取电子的平均静止坐标系(下简称“静止系”). 假设电子最初处于相对论运动中, 若在实验室坐标系(下简称“实验室系”)中观察, 则会观测到高能电子将能量传递给光子, 这与最初康普顿散射实验的能量传递过程“相反”, 因此该过程通常被称为逆康普顿散射. 而在静止系中, 逆康普顿散射就是汤姆孙散射, 因此这两个名称通常是可以互换使用的. 从静止系变换到实验室系时, 光子频率会经历两次多普勒蓝移过程, 因此实验室系中观测到的辐射光子能量由ω" ≈ 4γ2
2
2.2.从加速器布局到全光布局的汤姆孙散射
在20世纪60年代早期激光发明之后, 就在基于存储环的加速器上进行了汤姆孙散射早期的研究[62-65]. 而随着超快超强激光技术的发展, 科学家成功实现了激光驱动的尾波场电子加速, 尤其是在2004年, 通过LWFA获得了单能电子, 并在接下来的十多年里取得了快速发展, 相对稳定的[66,67]、大电荷量[68,69]、高能量[25,70-73]、能散度小于1%的电子源[74]相继被报道, 目前已报道准单能电子的最高能量达到了8 GeV[71]. 由于该种方案的电子源是超强激光驱动的, 而多光子汤姆孙散射本身是基于电子源与超强激光的相互作用, 因此基于LWFA的多光子汤姆孙散射可以使用同源的两束超强激光, 具有天然同步的优势, 通常将这类全激光驱动的散射实验称为全光汤姆孙散射. 图1概括了国际上全光汤姆孙散射的主要实验进展.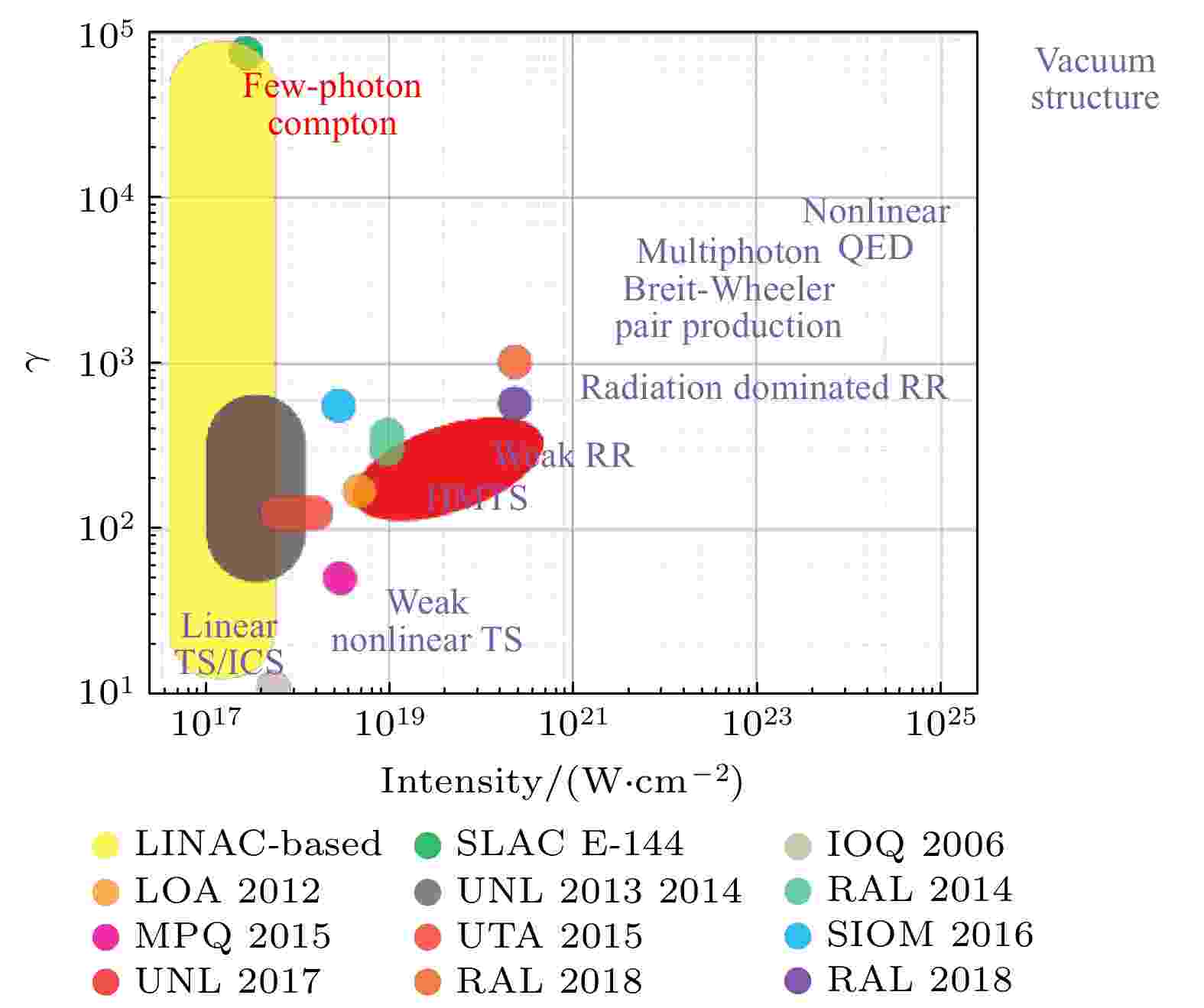
图 1 近期国际上全光汤姆孙散射的主要实验进展及发展方向Figure1. Recent progress and road map of the Thomson scattering.
随着LWFA的快速发展, 全光汤姆孙散射实验的条件逐渐成熟, 世界上多个实验小组相继报道了全光汤姆孙散射的实验结果. 目前主要有两种实验方案(如图2所示), 一种是单束激光束的等离子体镜方案, 激光束首先驱动LWFA加速得到电子束, 然后驱动激光中的剩余部分被等离子体反射镜(PM)反射到电子上, 实现散射; 第二种方案是两束激光方案, 一束驱动LWFA产生电子束, 另一束作为散射激光. 方案一不需要事先将激光与电子对准, 因而操作简单, 但相互作用参数可调谐性差, 而方案二需电子与散射激光精确对准, 因此操作复杂, 但参数可调谐性强.
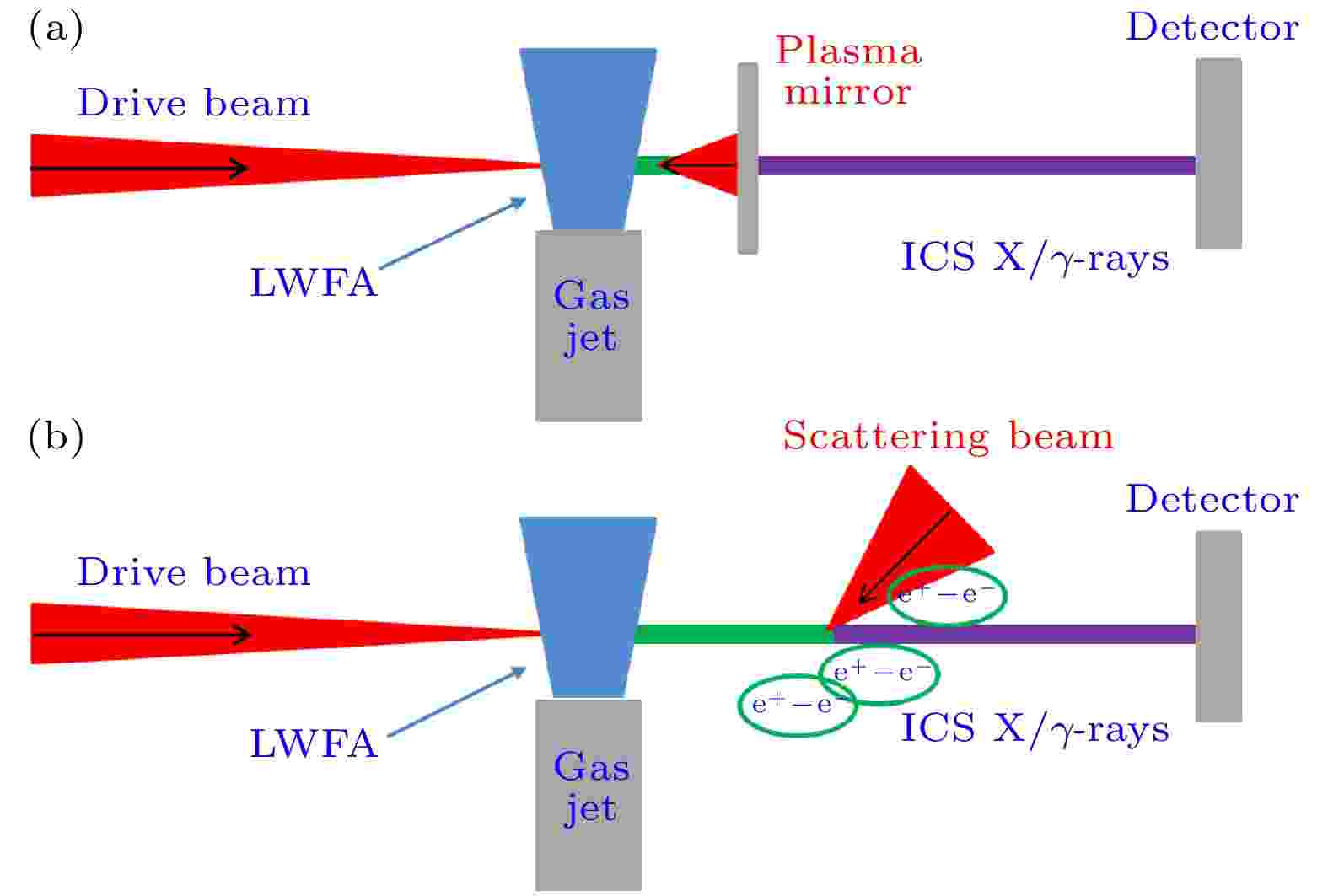图 2 两种不同的实验方案 (a)单束激光-等离子体镜方案; (b)双光束方案Figure2. Two different experimental geometries for all-optical scattering: (a) Single beam plasma mirror regime; (b) dual beam regime.
2
3.1.单束激光-等离子体镜方案
为实现全光汤姆孙散射, 需要将电子与激光在fs-μm3的尺度上精确对准, 实验技术非常具有挑战性. 为克服这一困难, 法国应用光学研究所(Laboratoire d'Optique Appliquée, LOA)的研究团队[76]提出了一种单束激光外加等离子体镜的实验方案, 克服了该技术挑战. 在这个过程中, 用来驱动LWFA的主激光脉冲的剩余部分撞击在固体箔上形成等离子体镜, 并被等离子体镜反射(如图3所示). 由于加速的电子束在驱动激光脉冲后面的几微米, 因此被反射的主激光正好可以与其发射碰撞, 从而实现全光汤姆孙散射.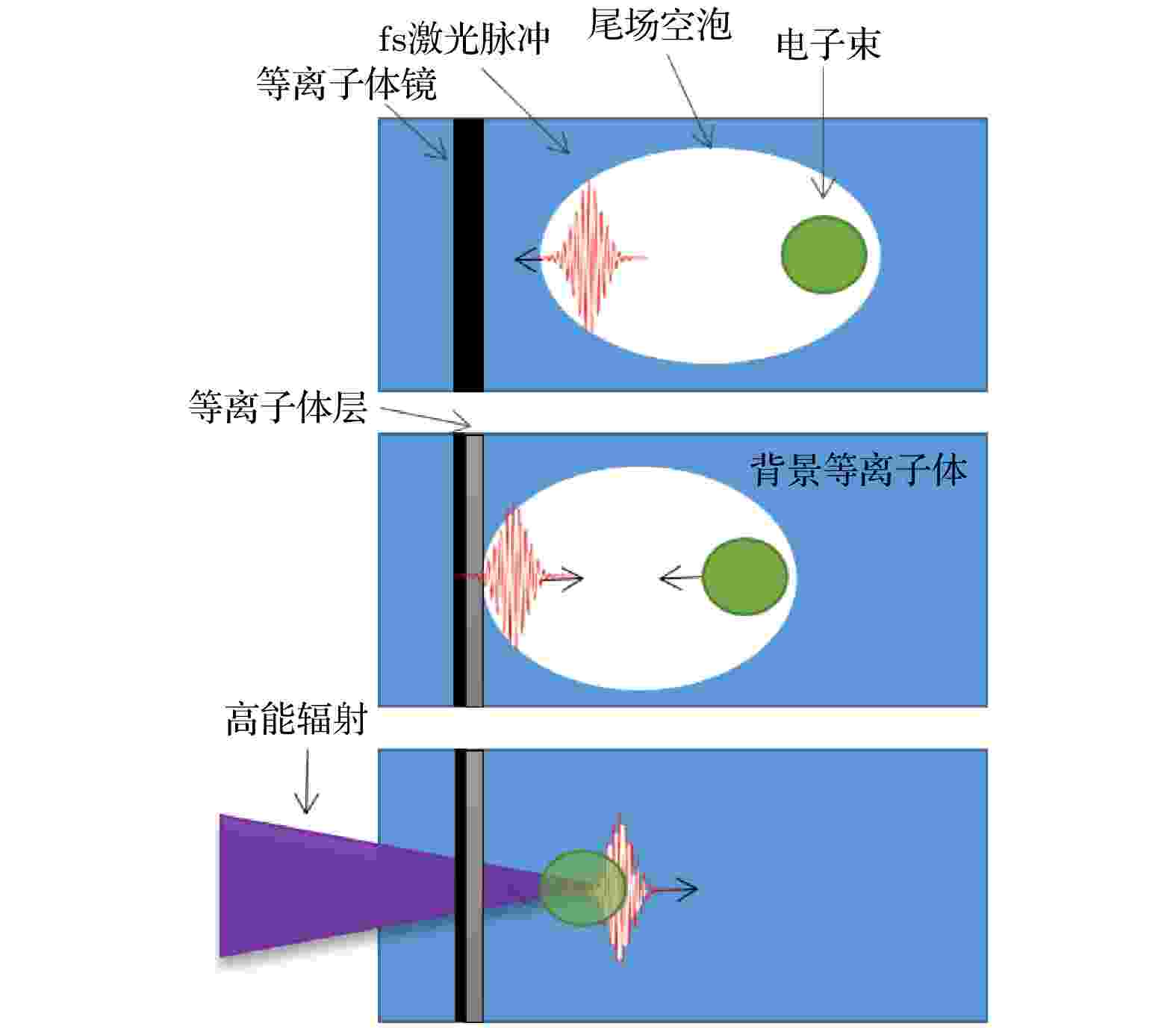
图 3 等离子体镜方案产生X射线的示意图Figure3. Illustration of the X-ray generation via plasma mirror regime.
由于实验的简单性和可行性, 该方案引起了世界范围的关注, 许多研究小组采用了类似的实验方案并进行了改进. 美国德克萨斯大学奥斯汀分校的研究团队[77,78]通过控制电子能量获得了能量在75—200 keV可调的准单能逆康普顿散射X射线. 德国慕尼黑大学的研究团队[79]生成了500 keV逆康普顿散射X射线, 并获得了放置在源后面1 m处的cm大小样品的单发成像. 我国科学家也进行了一系列研究. 中国科学院上海光学精密机械研究所的刘建胜团队[74]改进了电子加速, 获得了超高的六维电子亮度, 从而获得了很好的单能逆康普顿散射[80]. 中国科学院物理研究所的陈黎明团队[81]报道了使用凹面PM, 使激光重新聚焦, 显著增强了逆康普顿散射. 另外该团队还利用纯氮气靶的LWFA进行了实验, 由于气体密度比纯氦气低, 剩余能量仍然较高, 还将激光聚焦在喷嘴后沿，防止了返回光的发散, 提高了电子与激光的散射截面, 因此增强了逆康普顿散射通量[82]. 清华大学的鲁巍团队[83]使用磁带等离子体镜开展该实验, 大大提高了实验的重复频率, 并成功实现了对物体的CT成像. 目前, 单束激光等离子体镜的实验方案已经成为全光逆康普顿源的常规方法[84,85], 并有望在医疗、材料、基础科学等领域开展更多的应用.
2
3.2.双束激光对撞方案
单束激光-等离子体镜方案的巧妙之处在于驱动LWFA的激光与电子之间有飞秒量级的时间差, 剩余的主激光被反射后正好可以与电子发生碰撞, 因此实验的难度被大大降低, 对于全光逆康普顿源的实现具有重要意义. 但是由于对撞激光是主激光的剩余部分, 不具有可调控性, 因此若想进一步系统地研究全光汤姆孙散射, 必须采用双束激光的实验方案.双束激光的实验方案需要从驱动激光中分束获得一路相对独立的散射激光, 再实现与LWFA电子的精确对撞. 因此, 对撞激光有多项可以独立调控的参数, 如波长、脉冲宽度、总能量、激光场强度, 甚至激光模式等. 其中激光场强度a0决定了电子的运动状态, 与电子的相对论因子γ一起决定了相互作用的物理规律, 通常使用χ0=Epeak/(γmc2)≈ 2a0γElaser/(mc2)来表示. 当χ0
3
3.2.1.单光子吸收
在单光子吸收的条件下, 电子在激光场中做线性运动. 在保持散射激光条件不变的情况下, 可以通过调整电子的能量来实现对X射线能量的调谐.美国内布拉斯加大学林肯分校乌姆斯达特(Umstadter)团队[86]报道了第一个基于LWFA的双光束汤姆孙散射实验. 实验中, 实验人员从主激光脉冲能量中分出一部分激光单独进行聚焦, 聚焦峰值强度a0 ≈ 0.4, 散射激光与电子碰撞角度约为170°. 实验成功探测到了逆康普顿散射X射线, 最高能量达4 MeV. 使用相同的实验平台, Powers等[87]进一步研究了逆康普顿散射X射线能量的可调谐性, 并获得了准单能, 能量可调(范围从约70 keV到超过1 MeV)的X射线, 如图3所示. 该实验的LWFA中采用了双气体喷嘴, 实现了电子束能量的大范围调谐, 因此进一步实现了X射线能量的大范围调控[88].
在单光子吸收的条件下, 使用不同波长的激光, 获得逆康普顿X射线的光子能量也不同, 如图4所示. Liu等[89]报道了利用二次谐波(second harmonic generation, SHG)激光(400 nm, 约3 eV)作为散射激光产生逆康普顿散射X射线的实验结果. 实验中, 散射激光经过独立的压缩器, 然后通过非线性晶体(磷酸二氢钾晶体, 简称KDP晶体)转化为400 nm. 然后用SHG与LWFA电子发生碰撞. 获得了能量大于9 MeV的X射线光子. 该实验的物理过程依然是服从公式
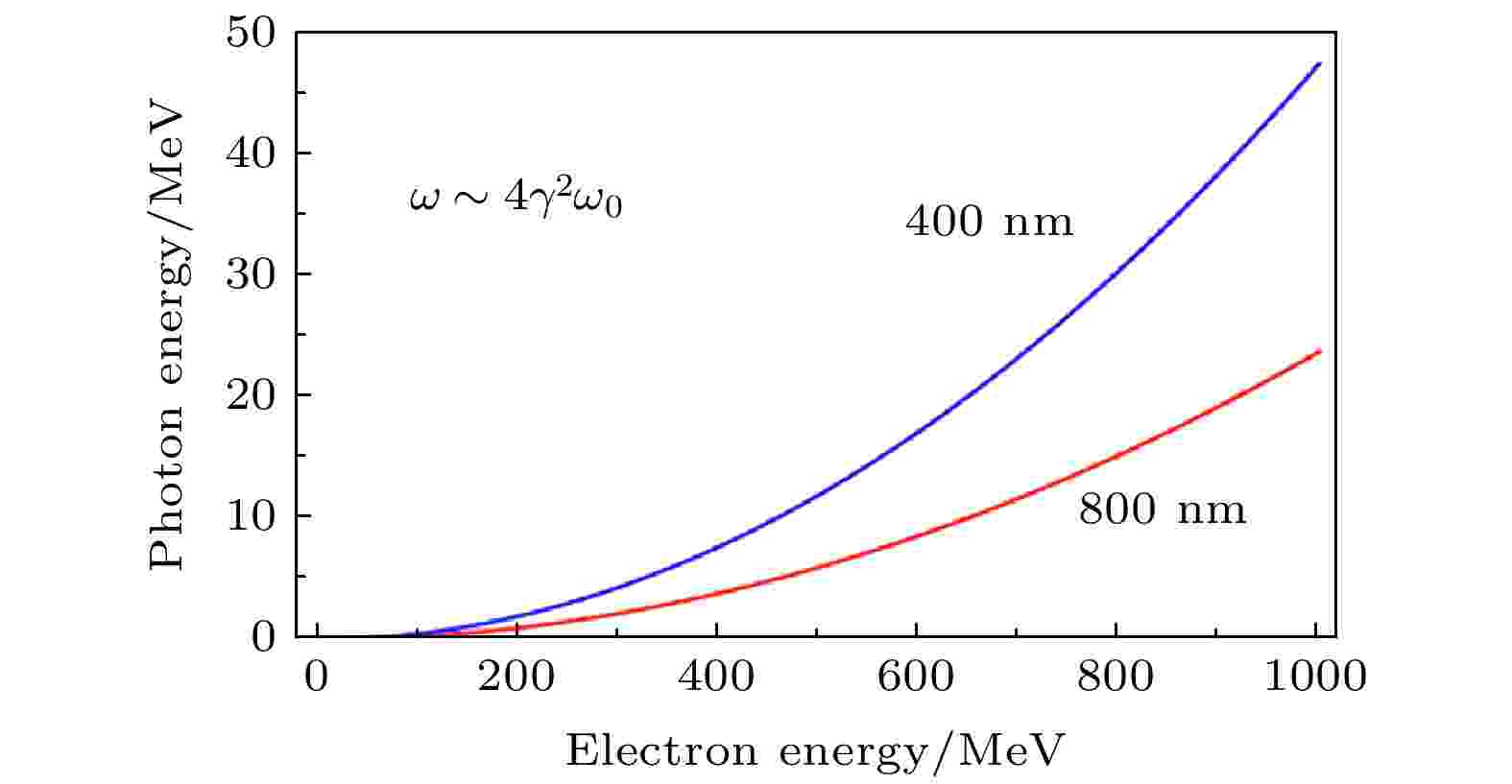图 4 全光逆康普顿散射X射线随电子能量的定标率, 红色代表使用800 nm散射激光, 蓝色代表使用400 nm散射激光Figure4. Scaling law of inverse Compton scattering X-ray energy by fundamental and second-order harmonics of Ti: Sapphire scattering laser.
3
3.2.2.低阶多光子散射
汤姆孙散射的非线性理论表明, 在更强的激光场中, 由于光子密度高, 单电子一次散射事件将吸收并散射超过一个以上的光子, 即多光子散射. LOA团队[76]报道的等离子体镜方案中, 已经获得了a0 > 1的散射激光, 但由于反射激光条件几乎无法被准确估计, 因此作者并没有强调相互作用的非线性效应.贝尔法斯特女王大学的研究团队[90]首次明确报道了汤姆孙的非线性效应, 该团队在实验中使用了a0 > 2的散射激光与电子相互作用, 实现了电子非线性运动的多光子散射过程, 辐射出的X射线光子能量明显大于线性汤姆孙散射. 但是X射线能谱并没有很好地符合非线性散射的理论公式. 主要原因可能是作者在实验中并没有很好地优化散射激光的焦斑, 其焦斑并非为高斯型, 另外电子的尺寸没有与激光焦斑尺寸很好地吻合, 因此相互作用的结果并不能由理想模型简单解释. 此外, 该实验的数据量较少, 很难获得理想的实验结果.
来自德国马普量子光学所(Max-Planck-Institut für Quantenoptik, MPQ)的团队[91]开展了一轮相对精细的实验, 他们从主激光中取了一小部分作为散射光, 并单独聚焦, 获得激光强度a0 ≈ 0.9的焦斑. 通过采集大量的X射线数据, 该团队明确地报道了汤姆孙散射过程中的非线性效应, 如图5所示, X射线的辐射能量明显偏离了线性条件下的光子能量, 这组实验数据非常好地符合了理论计算.
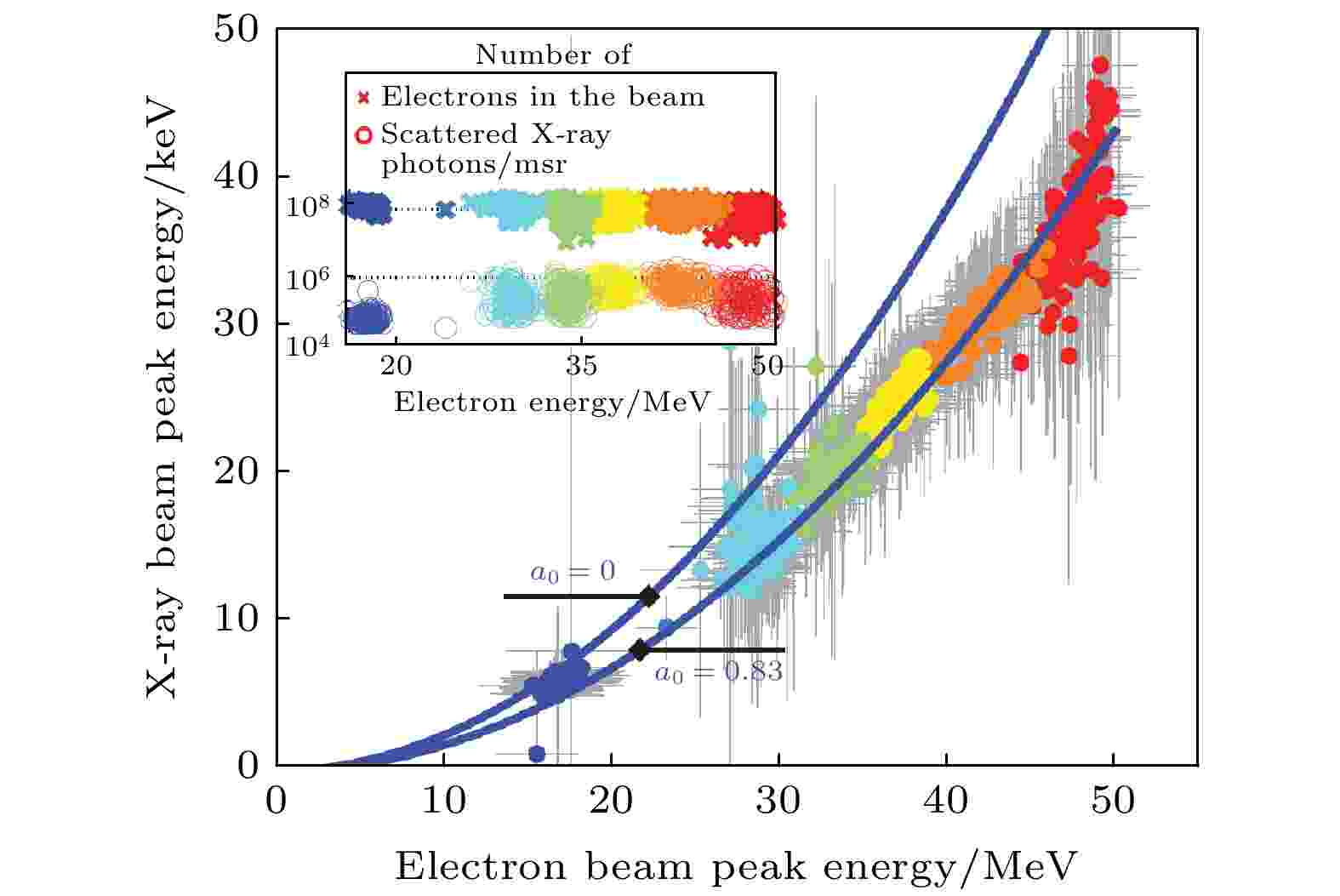图 5 文献[91]报道的全光汤姆孙散射的非线性效应, a0明显影响了X射线能量的定标率Figure5. Scaling shift in the few-photon scattering experiment. Reprinted with permission from Ref. [91].
总的来说, 这两组实验都引起了世界范围内本领域的广泛关注, 不仅因为它们都产生了明亮的准直高能高质量X射线源, 而且也证实了汤姆孙散射中电子的非线性运动引起的多光子效应. 当然, 这两组实验研究的范畴还处在低阶多光子效应阶段.
3
3.2.3.高阶多光子散射
当散射激光的强度进一步提升, 即a0
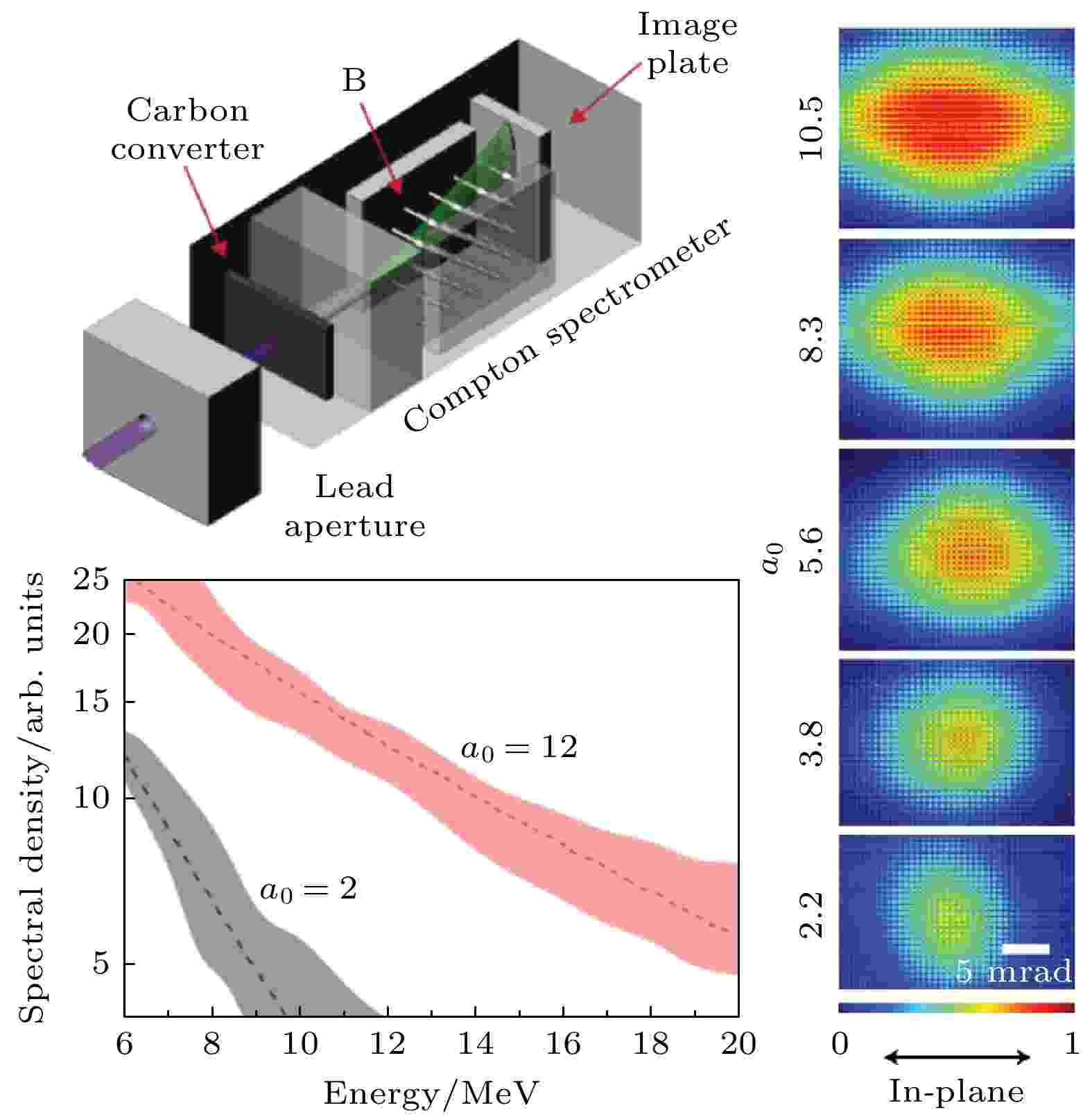图 6 文献[35]报道的高阶多光子效应Figure6. Effect of high-order multi-photon scattering reported in Ref. [35].
该工作最主要的意义在于, 实验明确证实了非线性汤姆孙散射中高阶的多光子效应. 在保持电子参数相同, 散射激光分别为a0 = 2和a0 = 12的情况下, 使用康普顿伽马射线能谱仪测量了逆康普顿散射X射线的能量分布[94-97], 可以观察到能谱的明显差异, 且与理论计算符合得很好, 从而验证了几十年前汤姆孙散射的高阶多光子散射理论的正确性.
实验还观测到, 随着a0的增大, X射线的空间分布沿散射激光偏振轴方向也会增大, 而在正交方向上的角宽几乎保持不变; 然而, 这与理想的单电子理论相距甚远, 这是由LWFA电子的发散角引起的. 当考虑电子本身的发散角时, 计算结果与实验数据符合得较好, 这证实了相互作用中的非线性效应, 同时也可确定激光峰值强度a0 ≈ 10, 如图7所示.
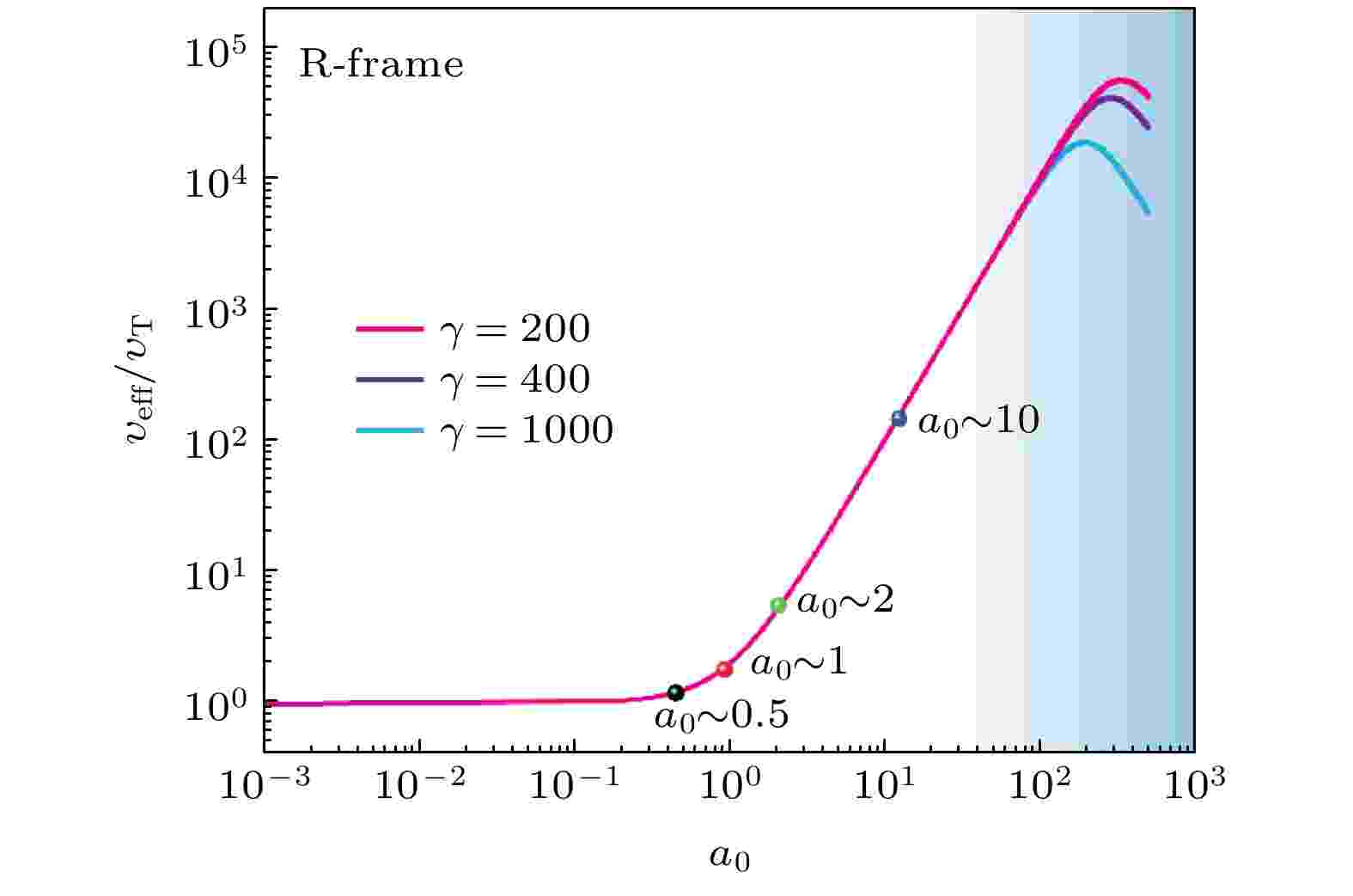图 7 汤姆孙散射截面随a0变化的定标率, 该变化曲线由文献[60]的理论计算得出Figure7. Scaling law of the Thomson scattering cross section vs. a0 in the rest frame. The blue range means where the RR effect matters. The curves were plotted based on Ref. [60]
当然, 该实验中还有一些值得继续深入探讨的问题, 例如, 实验观测到的光子-光子相干合成是如何发生的. 在这个过程中, 甚至可以把电子作为一种特殊的“催化剂”, 使光子-光子相互作用的实现条件远远小于真空中的光子-光子直接相互作用. 再如, 非线性汤姆孙散射中高阶光子吸收效应对汤姆孙散射截面的修正, 我们都知道经典汤姆孙散射截面是与电子经典半径相关的常数, 而理论表明, 在高阶多光子效应的影响下, 散射截面不再是常数, 而是与a0相关的变量. 从图7可以看出汤姆孙散射截面随a0的增加而成平方关系增加, 直到辐射阻尼效应出现之后会再次降低(渐变的蓝色区域). 该理论目前还没有得到实验的验证.
3
3.2.4.辐射阻尼
在高阶多光子汤姆孙散射过程中, 如果辐射光子集体对电子的反冲力足够大而不可忽略, 则电子将会失去大量的能量, 称为辐射阻尼效应(radiation reaction, RR). 它是QED中最古老和最基本的问题之一, 且对QED中的重整化问题有着重要的意义. 最初的Lorentz-Abraham-Dirac (LAD)方程的解是发散的, 违反了因果关系, 后来有多种理论尝试去解决此问题, 其中Landau-Lifshitz (LL)方程的解释最为自洽. 而这些理论一直没有被实验验证. 近期, 国际上两个研究小组相继报道了RR效应的验证[98,99]. 这两个实验都提到电子与超强激光相互作用后的能量损失. 然而, 由于实验技术上的困难[100], 两个团队都仅仅成功地进行了少量的实验, 且两组结果也有一定的分歧. 未来需要更多更优化的实验结果来更清楚地解释高阶多光子汤姆孙散射中的辐射阻尼效应.以上总结了目前全光汤姆孙散射的实验成果. 除了已经报道的实验结果, 还有更多的可调控参数对全光汤姆孙散射过程的影响值得进一步研究, 如散射激光的脉冲宽度[86]、拓扑性质[101,102]等.
| 参数 | 数值 |
| 源尺寸/μm | ～5 (root mean square) |
| 发散角/ mrad | ～5 (FWHM) |
| 峰值能量 | keV—20 MeV |
| 单能性 | 准单能(线性)/连续谱(非线性)* |
| 单发光子数 | 107—1010 |
| 峰值亮度/ ph·(s·mm2·mrad2·0.1%BW)–1 | 1017—1022 |
表1常见全光逆康普顿X射线源参数
Table1.Parameter of all-optical inverse Compton scattering X-ray source.
相干性是高亮度光源的重要特性之一[106-113]. 迄今为止, 还没有基于光子散射过程的完全相干X射线源的实验报道, 但是已经有人提出了利用全光汤姆孙散射获得全相干光源的研究方案, 未来如能实现全相干的全光汤姆孙散射X/伽马射线源, 将是重大突破.
全光汤姆孙散射还可作为诊断用来研究LWFA的性质[114,115]. 例如, 进行电子发射度测量. LWFA电子束离开加速器在自由空间传播过程中, 受到空间电荷效应, 发射度会增大. 而散射过程中辐射出光子束的空间分布可以携带最初的电子发射度信息. 因此可以将散射激光看作一种探针脉冲, 通过对X射线进行空间谱学分析, 从而可以测量电子的归一化横向发射度.
另外, 全光汤姆孙散射可以作为极端光场物理的重要研究平台. 极端光场中的QED效应还没有得到系统的实验验证, 而高能电子与超强激光相互作用过程是研究该理论最直观的方案. 当参量χ0 ≈ 1时, 辐射阻尼的量子效应不再可以忽略, 称为量子辐射主导区. 在这种情况下, 量子效应和RR效应都极大地改变了电子动力学行为. 在此条件下, 可以对RR进行充分测试, 并实现电子-正电子对的产生. 此外, 电子在全光散射过程中的自旋极化特性也是非常值得研究的问题. 另外, 使用等离子体镜方案也可以研究QED效应, 顾彦珺等[46,116]提出了在激光功率分别为1022和1024 W/cm2的条件下产生GeV光子和电子-正电子对的实验方案.
全光多光子散射实验将在未来的强场物理研究中占据重要的地位, 但与此同时也面临诸多的挑战. Samarin等[100]总结了人们在实验中可能面临的困难, 包括如何提升激光和电子的品质、稳定性、可重复性及克服相互作用中的技术难度等. 虽然实现激光与电子在fs时间尺度上的同步已经被许多实验小组证实, 但他们大多数是通过两束激光对准, 并假设LWFA电子完全跟随驱动激光来实现激光与电子的时空同步, 但实际上LWFA电子与驱动激光存在空间上的误差, 将导致激光与电子有效对撞截面下降, 最终会影响汤姆孙X射线源的产生. 因此, 如何让LWFA电子与散射激光直接对准就成为了一个世界级的技术难题.
此外, 电子和X射线的诊断技术都需要改进. 例如, 在辐射阻尼实验中, 考虑到阻尼水平和其他的一些不确定性, 需要非常精确地测量电子的能谱. 无论是电子指向还是磁体的不均匀分布都会导致阻尼百分比的误差比预期的要大. 在未来正负电子对的产生实验中, 对正负电子的精确的诊断也是非常重要的. 如何进一步提升X射线能谱仪的分辨率仍然是一个很大的问题, 常用的康普顿高能射线能谱仪由于转换体中正负电子对的产生等因素的影响, 极大地限制了其分辨率和能量分辨的范围. 因此, 研制高分辨率、大能量范围的能谱仪是诊断方面面临的挑战之一. 在未来的同类强场物理实验中, 装置运行的重复频率也对实验结果有着重要的影响, 短时间内采集大量数据会降低不确定度和扩大误差范围. 因此, 高重频实验诊断技术将为在高重频(> 10 Hz)的拍瓦级激光器和等离子体发生装置上开展前沿的强场物理实验提供重要的支撑.
