摘要: 通过测量含气泡水的声衰减反演气泡群参数是获取水中气泡分布的重要方法, 但是经典方法忽略了较高浓度气泡水中的强频散特性和气泡振动参数的改变, 导致反演较高浓度气泡群分布时会产生巨大误差. 为解决这个问题, 本文基于等效媒质理论建立起了声衰减和相速度的联系, 并考虑了含气泡水平均量对气泡阻尼系数和共振频率的影响. 在此基础上, 通过将反演气泡分布和修正相速度及气泡振动参数交替迭代的方法, 有效地消除了高浓度气泡水中由频散和气泡振动特性改变引起的误差. 与实验数据对比发现, 气泡群孔隙率达到10
–5 时, 考虑含气泡水的频散特性会显著降低反演误差; 而当气泡群孔隙率达到10
–3 时, 气泡阻尼系数和共振频率的修正会对反演结果变得重要. 本文方法在反演孔隙率为10
–3 —10
–2 的高浓度气泡群时, 仍有较好效果, 这可为获取水下较高浓度气泡群分布提供方法借鉴.
关键词: 气泡分布 /
声衰减 /
高浓度气泡群 /
迭代方法 English Abstract Inversion method for bubble size distribution with sound attenuation Hou Sen 1,2 ,Hu Chang-Qing 1 ,Zhao Mei 1 1.Shanghai Acoustic Laboratory, Institute of Acoustics, Chinese Academy of Sciences, Shanghai 201815, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11674353)Received Date: 24 August 2020Accepted Date: 05 October 2020Available Online: 04 February 2021Published Online: 20 February 2021Abstract: Measurement of the bubble size distribution (BSD) and the void fraction in bubbly liquids is very important for many areas, such as ocean science, cavitation inception studies, and military applications. The methods of using acoustical attenuation caused by bubbly liquid to estimate the BSD can date back to Medwin’s research in which the resonant bubble approximation (RBA) was proposed [Medwin H 1970 J.Geophys.Res . 75 599]. In the traditional theory, the methods used to invert the acoustical attenuation for obtaining the BSD are well developed and useful for the low void fraction. However, the comparison between the results from the conventional methods and the experimental results is not satisfactory when the void fraction is higher than 10–5 . In fact, the frequency dispersion and the bubble interaction in bubbly liquid should be considered in the process of inverting the BSD for the high-density bubble group. In this paper, the relationship between the attenuation and the phase velocity of bubbly liquid is analyzed based on the effective medium theory, and the bubbles’ interaction is considered by calculating the change of vibration parameters of bubbles. On this basis, we propose an iterative method to accurately determine the BSD of the high-density bubble group. In this iterative method, the errors of the inversion results are reduced by estimating the phase velocity and the vibration parameters of bubbles from sound attenuation. This iterative method is numerically tested for the bubble distributions of log-normal and power-law functions. The simulation results are in good agreement with the given bubble distributions for the void fractions higher than 10–3 . Further, the influence of the frequency dispersion and the bubble interaction on inversion results are discussed. Compared with the experimental data, the inversion results calculated by the iterative method show that considering the dispersion can significantly reduce the errors, when the void fraction of bubbly liquid increases up to 10–5 . And the correction to bubble damping coefficient and resonance frequency have an important effect on the inversion result when the void fraction of bubbly liquid is higher than 10–3 , indicating that the iterative method proposed by this paper can be a useful tool for inverting the BSD of the high-density bubble group in the liquid.Keywords: bubble distribution /sound attenuation /high-density bubble group /iterative method 全文HTML --> --> --> 1.引 言 获取水下气泡群分布在军事领域[1 ] 、工业领域[2 ] 以及科研领域[3 ] 都有巨大的应用价值, 其中通过声衰减或声散射反演气泡群分布是探测水下气泡群参数的重要方法[4 -7 ] . 上世纪七十年代, Medwin[5 ] 提出了共振估计方法(resonant bubble approximation, RBA), 在求解气泡群声衰减过程中只保留共振态气泡的贡献, 简化了计算过程, 得出了简明的由声衰减系数反演气泡分布的公式, 成为了经典的气泡参数反演理论. 此后很多****在RBA模型的基础上做了更深入研究. Commander和Moritz[8 ,9 ] 指出忽略非共振态气泡的影响会造成反演误差, 并通过数值方法将非共振气泡的贡献引入到反演过程中. Caruthers和Elmore[10 ] 通过采用声衰减数据和假定气泡分布交替计算校正的方法, 在孔隙率低于10–6 的条件下获得了良好的反演结果. Choi等[11 ,12 ] 则通过引入声速修正结合奇异值分解的数值反演方法, 实现了对孔隙率为10–4 气泡群的反演. 此外, 还有很多****研究了基于声衰减反演气泡群分布的方法, 但这些方法都只适用于反演孔隙率低于10–4 的气泡群[13 -16 ] .[17 ] 提出了通过声衰减和相速度联合反演气泡群参数的方法. Wu 和Chahine[18 ] , Chahine[19 ] 进一步发展了该方法, 并通过实验验证了可以对孔隙率高于10–3 的气泡群进行较为精确的反演. 但Leighton等[20 ] 指出, Duraiswami方法同样存在问题, 在一些情况下得到的反演值可能会偏离真实值. 原因有两方面, 一方面精确测量高浓度气泡水中的相速度技术难度大[20 -22 ] , 并且相速度在气泡共振频段附近测量误差远大于声衰减的测量误差[22 ] ; 另一方面, 随着气泡孔隙率的增加, 含气泡水中平均量对气泡振动参数的影响变得明显[23 ,24 ] , Duraiswami的方法由于没有考虑气泡本身振动参数的变化, 会在反演高浓度气泡群时产生误差.[25 ,26 ] , 在考虑了气泡孔隙率增高对气泡阻尼系数和共振频率影响的基础上, 推导了声衰减-气泡分布和声衰减-相速度的关系. 通过利用声衰减反演气泡分布和利用气泡分布修正声速及气泡振动参数交替迭代校正的方法, 将气泡群频散特性和气泡参数修正量引入到反演计算中. 通过实验数据的比对发现, 本文方法在反演孔隙率达到10–3 —10–2 量级的气泡群时, 依然有较好的效果. 拓宽了利用声衰减难以反演较高浓度气泡群的限制条件.2.气泡群分布的反演方法 22.1.气泡振动模型与线性化求解 2.1.气泡振动模型与线性化求解 假设气泡群在水中分布均匀, 且仅考虑气泡在小振幅波下做线性振动, 则基于等效媒质理论, 可以给出声波在含气泡水中传播时的等效波数[23 -26 ] :${k_{\rm{l}}}$ 为纯水中的波数; $r$ 为气泡半径; $n(r)$ 为气泡概率密度函数; $\omega $ 为入射声角频率; $\omega _{0{\rm{m}}}^{}$ 和${b_{\rm{m}}}$ 分别为气泡的共振角频率和阻尼系数, 通常可以由线性化Keller方程获得, 同时考虑气泡浓度较高时含气泡水平均量对气泡的作用, 则含气泡水中的气泡振动特性如(2 )式所示[23 ,26 ] :${p_{\rm{B}}}$ 为气液界面处液体侧压强, 可以表示为如下公式:$R$ 为任意时刻下的气泡半径; $r$ 为气泡平衡半径, 与(1 )式中表达相一致; ${p_0}$ 为环境压强; $\delta $ 为张力系数; $\mu $ 黏滞系数; ${c_{\rm{m}}}$ 为含气泡水中的复声速; $\gamma $ 为多方指数; ${\rho _{\rm{m}}}$ 为含气泡水的密度, 易得${\rho _{\rm{m}}} \approx (1 - \beta ){\rho _l}$ , ${\rho _l}$ 为液体密度; $\beta $ 为气泡群孔隙率, 物理含义为单位体积内气泡的体积, 可由下面公式表示:$R = r(1 + X{{\rm{e}}^{{\rm{i}}\omega t}})$ , 且$X \ll 1$ . 则通过线性化(2 )式, 可以得到阻尼系数和气泡共振角频率分别如下公式所示:$\varPhi $ 为一复数函数, 其主要由热扩散系数$D$ 决定, 如下式所示:$x$ 轴在含气泡水中传播, 可以写成如下式:$a$ 为复波数${k_{\rm{m}}}$ 的虚部, 表征声衰减; $\omega /{c_{{\rm{re}}}}$ 为${k_{\rm{m}}}$ 的实部, 其中${c_{{\rm{re}}}}$ 为含气泡水中的声速, 令$u = {c_{\rm{l}}}/{c_{{\rm{re}}}}$ , ${c_{\rm{l}}}$ 为纯水声速, 则复波数${k_{\rm{m}}}$ 可以展开为1 )式做同样展开处理, 则可以得到:10 )式和(11 )式联立并化简, 可以得到$a$ 和$u$ 的表达式如下:12 )式和(13 )式分别为考虑含气泡水平均量影响时的声衰减和频散特性的表达式, 对(12 )式逆求解即可以通过声衰减反演得到气泡概率密度函数$n(r)$ . 从(12 )式中可以看出, 相速度${c_{{\rm{re}}}}$ 取值对声衰减产生了直接的影响. 此外, 结合(5 )式和(6 )式, 含气泡水平均量通过改变气泡阻尼系数${b_{\rm{m}}}$ 和共振角频率$\omega _{0{\rm{m}}}^{}$ 间接影响了声衰减. 为了在下文更清晰地讨论这两种影响, 不妨在忽略含气泡水平均量影响下重写(12 )式和(13 )式. 即将${k_{\rm{m}}} \to {k_{\rm{l}}}$ , ${\rho _{\rm{m}}} \to {\rho _{\rm{l}}}$ 代入到(5 )式和(6 )式中, 则可得${\omega _0} = {\omega _{0{\rm{m}}}}$ , $b = {\rm{Re}} ({b_{\rm{m}}})$ , ${\rm{Im}} ({b_{\rm{m}}}) = 0$ , 其中${\omega _0}$ 和$b$ 分别为气泡在纯水中的共振角频率和阻尼系数, 则(12 )式和(13 )式可以得到化简:14 )式和(15 )式分别为不考虑含气泡水平均量影响时声衰减和频散特性的表达式. 将在第4 节通过与实验数据的比对, 具体探讨声速频散和气泡振动特性改变对反演结果的影响.2.2.正则化方法与迭代算法 -->2.2.正则化方法与迭代算法 反演的核心问题在于对(12 )式进行逆求解运算, 由于未知量${c_{{\rm{re}}}}$ , $\omega _{0{\rm{m}}}^{}$ 和${b_{\rm{m}}}$ 的取值并不影响反演过程, 我们不妨先假设它们已知. 首先做离散化处理, 将气泡半径区间$[{r_{{\rm{l}}o}}, {r_{{\rm{h}}i}}]$ 划分为$m$ 个子区间, 则(12 )式可以写成为$a({\omega _j})$ 为角频率为${\omega _j}$ 时的气泡群声衰减系数. ${N_i} = n(r) \times {\rm{d}}r$ , 为气泡分布函数, 表示单位体积内第$i$ 个半径区间内气泡数, ${\rm{d}}r$ 为区间宽度; ${A_{j, i}}$ 表示半径为${r_i}$ 的单个气泡在角频率为${\omega _j}$ 时的声衰减系数, ${A_{j, i}}$ 可以表示为16 )式和(17 )式具有一般性, 对任意角频率${\omega _j}$ 均满足, 设有$J$ 个发射角频率, 则合并结果可得${{AN}} = {{a}}$ , 展开如下式所示:18 )式中的方程组存在不适定问题, 数据微小变化会引起解集巨大波动. 这里运用Tikhonov正则化方法, 将方程组的求解转化为最优化问题, 如下式所示:$\lambda $ 为正则化参数, 经测试发现采用GCV(Generalized Cross-Validation)准则作为$\lambda $ 的选取策略有较好的稳定性, 如下面公式所示[27 ] . 其中$\lambda $ 为${\phi _{GCV}}(\lambda )$ 最小时的取值.16 )式—(20 )式离散化和正则化求解过程记为算子TIK. 为了获取准确的相速度、气泡阻尼系数和气泡共振角频率, 利用迭代方法对真实值进行逼近. 首先以纯水中的参数作为初始值代入到第一次反演过程中, 即${c_{{\rm{re}}}} = {c_{\rm{l}}}$ , ${b_{{\rm{m}}, 1}} = b$ , ${\omega _{0{\rm{m}}, 1}} = {\omega _0}$ , 则对气泡分布第一次求取过程可以写成:$n{(r)_1}$ 为气泡真实分布, 对各迭代参数进行更新. 联立(1 )式、(4 )式和(5 )式可以求得${b_{\rm{m}}}$ ; 联立(1 )式、(4 )式和(6 )式可得${\omega _{0{\rm{m}}}}$ ; 将${b_{\rm{m}}}$ , ${\omega _{0{\rm{m}}}}$ 代入(13 )式可以得到${c_{{\rm{re}}}}$ . 同样为了简化表达, 将上述参数的求解过程记为算子PAR, 可以写成为$n{(r)_1}$ 代入到(12 )式可以求得声衰减${a_1}$ , 并以相对误差$\partial = {{| {{a_1} - a} |}}/{a}$ 检验反演值是否收敛到真实值, 将上述过程记为算子ERR, 可以写成为21 )式—(23 )式步骤, 直到满足迭代次数为止, 反演过程的流程图如图1 所示.图 1 迭代方法反演气泡分布流程图Figure1. Flow diagram of the iterative inverse method.3.数值仿真 上一节给出了利用声衰减反演气泡群分布的方法, 本节通过数值模拟对该方法有效性进行验证, 并具体展示迭代反演的过程. 在本节算例中, 选取具有典型性的幂律分布和对数正态分布作为气泡群假定分布. 其中幂律分布代表以小气泡为主的分布情况, 算例中设概率密度函数$n{(r)_{{\text{Power-law}}}}$ 正比于${r^{ - 4}}$ . 对数正态分布代表气泡集中于平均半径的分布情况, 概率密度函数如下式所示.24 )式中, 设气泡平均半径${r_0} = 0.1\;{\rm{ mm}}$ , 并设对数标准差$\varepsilon = 0.1$ . 在给出气泡分布的基础上, 设气泡群孔隙率$\beta = {10^{ - 3}}$ , 纯水声速${c_{\rm{l}}} = 1500\;{\rm{ m/s}}$ , 分别对半径分布于$3 \times {10^{ - 4}}$ —$8 \times {{10}^{ - 4}}$ 和$0.5 \times {10^{ - 4}}{\rm{ }}$ —$1.5 \times {10^{ - 4}}\;{\rm{ m}} $ 的气泡群做参数反演, 结果如图2 .图 2 迭代算法反演结果 (a) 对数正态分布, $r \in \left[ {3 \times {{10}^{ - 4}}\;{\rm{ m}}, 8 \times {{10}^{ - 4}}\;{\rm{ m}}} \right]$ ; (b) 幂律分布, $r \in \left[ {3 \times {{10}^{ - 4}}\;{\rm{ m}}, 8 \times {{10}^{ - 4}}\;{\rm{ m}}} \right]$ ; (c) 对数正态分布, $r \in \left[ {0.5 \times {{10}^{ - 4}}\;{\rm{ m}}, 1.5 \times {{10}^{ - 4}}\;{\rm{ m}}} \right]$ ; (d) 幂律分布, $r \in \left[ {0.5 \times {{10}^{ - 4}}\;{\rm{ m}}, 1.5 \times {{10}^{ - 4}}\;{\rm{ m}}} \right]$ Figure2. The inversion results: (a) Log-normal, $r \in \left[ {3 \times {{10}^{ - 4}}\;{\rm{ m}}, 8 \times {{10}^{ - 4}}\;{\rm{ m}}} \right]$ ; (b) Power-law, $r \in \left[ {3 \times {{10}^{ - 4}}\;{\rm{ m}}, 8 \times {{10}^{ - 4}}\;{\rm{ m}}} \right]$ ; (c) Log-normal, $r \in \left[ {0.5 \times {{10}^{ - 4}}\;{\rm{ m}}, 1.5 \times {{10}^{ - 4}}\;{\rm{ m}}} \right]$ ; (d) Power-law, $r \in \left[ {0.5 \times {{10}^{ - 4}}\;{\rm{ m}}, 1.5 \times {{10}^{ - 4}}\;{\rm{ m}}} \right]$ .图2 中, 每个子图中的首张图对应TIK算子反演气泡分布的过程, 第二张图对应了通过PAR算子校正声速的过程, 第三张图对应了通过ERR算子计算声衰减的过程. 图2(a) 中, 第一次迭代反演结果与假定分布差距巨大, 这对应了含气泡水中声速等参数与纯水的巨大差异. 随着迭代次数增加, 误差迅速减小, 且最终反演值与假定分布吻合较好. 图2(b) 所示为幂律分布, 从图中可以看出除了最终结果符合假定分布外, 前几次迭代结果的误差明显要比图2(a) 更小, 主要原因是没有充分考虑含气泡水频散特性时, 反演结果往往会出现小气泡占多数而大气泡数较少的分布特征[11 ,15 ] , 正如四个子图中气泡分布反演图所示. 这使得相较于图2(a) 和图2(b) 的第1次反演结果与假定分布更接近, 即分布不同对收敛速度有一定影响. 图2(c) 和图2(d) 为气泡群半径在$0.5 \times {10^{ - 4}}{\rm{ }}$ —$1.5 \times {10^{ - 4}}\;{\rm{ m}} $ 范围内的反演结果, 对比图2(a) 和图2(b) 可以看出, 不同半径范围内的气泡群反演结果相似, 说明半径区间不同对迭代算法的影响较小. 计算四个算例输出的孔隙率误差分别为: ${\partial _{\rm{a}}} = + 2.7$ %, ${\partial _{\rm{b}}} = - 0.9$ %, ${\partial _{\rm{c}}} = + 3.6$ %, ${\partial _{\rm{d}}} = + 0.7$ %, 可以看出虽然算例间的误差存在微小差别, 但均在5%以内, 可以认为在以上四个算例中, 气泡分布和气泡半径区间的不同没有明显影响反演结果的准确性. 通过本节仿真可以看出, 本文方法在反演较高浓度气泡群分布时能得到较为稳定准确的解集.4.实验数据比对 为了进一步验证本文方法的实用性, 并比对不同方法的反演结果. 采用四份实验数据中的声衰减反演气泡分布, 其中实验中获得的气泡分布参数如表1 所列. Wilson[28 ] 于2005年测量了孔隙率为$6.2 \times {10^{{\rm{ - }}5}}$ 含气泡水的声衰减和相速度, 并通过拍照获得了气泡分布, 数据如表1 中例1所列. 本文在4.1节中用例1数据对比不同方法反演低孔隙率气泡群的结果. Leroy[22 ] 于2008年采用向胶质注射气泡的方法获取了半径单一稳定地高浓度气泡群, 并在此基础上测量了声衰减、相速度和气泡分布, 数据如表1 中例2和例3所列. 本文在4.2节中用以对比不同方法反演高孔隙率气泡群的结果. Silberman[21 ] 于1957年测量了声衰减数据, 并给出了大致的气泡分布范围, 如表1 中例4所列. 本文在4.3节中说明当声衰减测量数据稀疏时遇到的问题并讨论相关解决方法. 实验算例 例1(图3 ) 例2(图4 ) 例3(图5 ) 例4(图7 ) 分布 正态分布 对数正态 对数正态 — 平均半径(m ) 6.36 × 10–4 8.2 × 10–5 8.4 × 10–5 2.2 × 10–3 标准差(m ) 5 × 10–6 — — — 对数标准差 — 0.04 0.06 — 孔隙率 6.2 × 10–5 1.5 × 10–3 9.4 × 10–3 5.3 × 10–3
表1 各实验算例中的气泡分布Table1. Bubble distribution of 4 experimental examples4.1.低孔隙率气泡群的反演 4.1.低孔隙率气泡群的反演 RBA模型及其改进方法是利用声衰减反演气泡群参数最常用的方法, 但通常认为RBA模型在反演孔隙率为10–5 以上的气泡群时, 误差会急剧增大. 为了比较本文方法和RBA理论模型的反演结果, 对例1中的数据做反演, 结果如图3 所示.图 3 例1数据的反演结果图, 气泡群孔隙率$\beta = 6.2 \times {10^{ - 5}}$ , 平均半径$\overline r = 6.36 \times {10^{ - 4}}\;{\rm{ m}}$ (a) 气泡分布反演结果; (b) 相速度计算结果; (c) 声衰减计算结果Figure3. Inversion results of Example 1, void fraction$\beta = 6.2 \times {10^{ - 5}}$ , mean radius $\overline r = 6.36 \times {10^{ - 4}}\;{\rm{ m}}$ : (a) Bubble distributions; (b) phase speed; (c) sound attenuation.图3 中, 图例中RBA所示虚线代表RBA模型的反演结果, 方法一代表未考虑含气泡水平均量影响的反演结果, 即以(14 )式和(15 )式代入迭代算法得到的反演结果. 方法二代表考虑含气泡水平均量影响后的反演结果, 即以(12 )和(13 )式代入迭代算法得到的反演结果. 没有特殊说明, 后文图例标注和图3一 致.图3(a) 所示, 方法一与方法二均与测量值较为吻合, 两者间差别不大. 而RBA模型的反演值与实际分布误差巨大. 在实验测得的气泡分布区间, 即0.62—0.65 mm范围内, 反演值远低于实测值; 而在偏离实际气泡分布的大气泡区间和小气泡区间, 均有明显的高估现象. 其误差来源主要有两方面: 一方面为忽略了气泡非共振衰减的影响; 另一方面为将声速假设为常数忽略了声速频散. 而方法一和方法二在TIK算子计算中没有做与RBA模型中类似的近似求解, 保留了非共振衰减项. 并通过引入迭代方法, 在反演气泡分布的过程中校正了声速, 使得反演结果相较于RBA模型有了明显的改善.图3(b) 所示, 方法一和方法二计算得到的声速值差别不大, 与测量值相比在5200—5800 Hz段吻合较好, 而在高声速段存在一定偏差但可以大致反映相速度变化趋势. 相比于RBA模型中将声速假定为纯水声速, 由迭代方法校正的声速改善效果明显. 由反演得到的气泡分布计算出的声衰减如图3(c) 所示, 方法一和方法二均与实验值符合较好, 表明了迭代算法的输出结果较好地收敛到真值附近. 而基于RBA模型反演分布计算得到的声衰减结果与实测值偏离较大, 对应了RBA得到的气泡分布严重偏离真实值.–5 量级时, 声速频散和非共振衰减是影响反演结果准确性的主要因素.4.2.高孔隙率气泡群反演 -->4.2.高孔隙率气泡群反演 为了验证对孔隙率达到10–3 以上气泡群的反演能力. 本节对例2和例3的数据做了反演, 分别如图4 和图5 所示. 通过比较不同方法获得的反演结果, 着重讨论影响反演高浓度气泡群准确度的因素.图 4 例2数据的反演结果图, 气泡群孔隙率$\beta = 1.5 \times {10^{ - 3}}$ , 平均半径$\overline r = 8.2 \times {10^{ - 5}}\;{\rm{ m}}$ (a) 气泡分布反演结果; (b) 相速度计算结果; (c) 声衰减计算结果Figure4. Inversion results of example 2, void fraction$\beta = 1.5 \times {10^{ - 3}}$ , mean radius $\overline r = 8.2 \times {10^{ - 5}}\;{\rm{ m}}$ : (a) Bubble distributions; (b) phase speed; (c) sound attenuation.图 5 例3数据的反演结果图, 气泡群孔隙率$\beta {\rm{ = 9}}{\rm{.4}} \times {10^{{\rm{ - 3}}}}$ , 平均半径$\overline r = 8.6 \times {10^{ - 5}}\;{\rm{ m}}$ (a) 气泡分布反演结果; (b) 相速度计算结果; (c) 声衰减计算结果Figure5. Inversion results of example 3, void fraction$\beta = 9{\rm{.4}} \times {10^{{\rm{ - 3}}}}$ , mean radius $\overline r = 8.6 \times {10^{ - 5}}\;{\rm{ m}}$ : (a) Bubble distributions; (b) phase speed; (c) sound attenuation.图4(a) 所示, 除了RBA模型反演结果严重失真外, 方法一也存在较大偏差. 方法一高估了85—100 μm的大气泡数量, 低估了77 μm以下的小气泡数量, 同时反演得到的气泡峰值位置与实测值相比向小气泡区间偏离. 方法二较好地估计了气泡平均半径, 但反演得到的气泡分布相比于实测值更加集中, 即峰值更高分布区间更窄. 考虑到气泡分布标准差存在一定波动范围, 可以认为方法二反演值与实测值符合较好, 相比于方法一有明显的改善. 计算得到的孔隙率上, 方法一为1.42 × 10–3 , 方法二为1.47 × 10–3 , 两者都与测量值1.5 × 10–3 较为一致, 其中方法二符合更好.图4(b) 所示, 两种方法反演值在声速上升和下降的频段吻合较好, 而在高声速区间均存在一定偏差, 但方法二更好地符合了声速在峰值处的变化趋势. 计算得到的声衰减数据如图4(c) 所示, 可以看出, 方法一和方法二的结果均与实验值较为吻合, 说明迭代算法输出结果较好地收敛至输入实测值附近.图5(a) 所示, 相比于图4(a) , 可以发现随着气泡孔隙率升高, 方法一误差增大. 方法一反演得到的气泡分布峰值明显向小半径区间偏移, 同时高估了95 μm以上的大气泡数. 而方法二的反演值更符合实测值, 较好地估计了气泡分布平均半径和分布趋势. 方法一得到的孔隙率为8.6 × 10–3 , 方法二为8.8 × 10–3 , 两种方法结果相近且方法二更符合实验值. 声速值的反演如图5(b) 所示, 两种方法反演值在声速上升频段与实验值吻合较好, 而在高声速频段存在一定偏差, 但方法二在声速峰值频段及高频频段与实测值符合更好, 总体看方法二更能代表相速度变化趋势. 图5(c) 中, 两种方法声衰减计算结果均与实验值较为符合, 说明输出结果收敛至实测值附近.图4 和图5 的结果具有一致性, 除了RBA模型严重失真外, 方法一结果误差也较大, 且随着气泡群孔隙率增大误差有变大趋势. 而方法二反演结果相比于方法一有较为明显的改善, 可以较为准确地反演得到气泡的峰值位置和分布趋势. 相比于低空隙率气泡群反演结果, 可以看出当气泡群孔隙率较高时, 考虑含气泡水平均量对气泡的作用对反演结果具有不可忽略的影响因素.4.3.数据稀疏时的气泡分布反演 -->4.3.数据稀疏时的气泡分布反演 在研究气泡分布反演过程中发现, 当实验数据稀疏, 尤其是气泡共振频段处数据稀疏时, 会出现反演解集不稳定的问题, 对此做了进一步探讨分析.图6 所示为三组孔隙率$\beta {\rm{ = 1}} \times {10^{{\rm{ - 6}}}}$ , 半径单一的气泡群声衰减. 从图6 中可以看出, 气泡共振频段处声衰减对频率变化敏感, 而偏离共振频段后敏感性降低. 为了分析半径相近气泡的衰减峰位置, 假定气泡振动为绝热过程, 可以化简(6 )式得出气泡共振频率公式:图 6 不同半径气泡群衰减峰位置Figure6. Attenuation peak positions of bubble groups with different radius.${f_2}$ , ${f_1}$ 为两个间隔$\Delta f$ 的入射声频率; $\Delta r$ 为对应的气泡半径间隔, 则由(25 )式, 易得$\Delta f$ 与$\Delta r$ 的关系如下:${\rm{d}}r < \Delta r$ , 则容易出现解集不稳定的现象. Chahine[19 ] 也提到过类似问题, 为了解集稳定, 反演时划分的气泡半径区间数应当小于声衰减测量数据数. 但值得注意的是, 由图6 分析可知, 共振频段处声衰减(即强声衰减区)测量间隔对反演结果的影响更大. 且当测量值在强衰减频段数据点稀疏时, 往往会丢失衰减峰值信息, 易出现解集不稳定和解集偏离真实值的问题. 而插值等数据处理方法难以准确描述共振频段附近衰减的剧烈波动, 易引入较大误差. 为了在数据稀疏信息量较少的情况下, 保证反演结果中气泡群主要参数的准确度. 将反演气泡分布的问题简化为对气泡群平均半径$\overline r $ 和气泡数目$N$ 的反演, 则气泡概率密度函数可以写成为27 )式代入(12 )式中可以对声衰减公式进行化简, 后续迭代流程与方法一和方法二类似. 为了方便表述, 在数据稀疏情况下, 只针对平均半径和气泡数的反演记为方法三. 通过对例4数据的反演, 来对比方法二和方法三在数据稀疏时反演的结果.图7(a) 所示. 通过图7(a) 可以看出, 方法三得到的气泡平均半径与实测值较为吻合. 而方法二得到的结果与实测值偏差较大, 并没有反映出气泡群集中在2.2 mm这一趋势. 同时一般认为气泡分布在一定范围内是连续函数, 方法二的反演结果有明显的不稳定现象, 相比之下方法三的结果与Silberman给出的2.07—2.31 mm的气泡分布区间十分吻合. 图7(b) 为相速度的反演值, 由于实验只测量了低频段的声速值, 两种方法虽然在大于1000 Hz的频段处有明显差别, 但在低频段与实验值均符合较好. 图7(c) 为声衰减的计算值, 从图中可以看出, 虽然两种方法声衰减在峰值处差距明显, 但由于测量数据稀疏且没有明显峰值信息, 使得两种方法都与反演结果相近, 其中半径区间划分精细的方法二与实验值符合更好. 结合气泡分布反演结果中方法二结果偏离真实值. 这说明了由于气泡群共振频段处数据的稀疏以及共振峰数据的缺失, 很容易使反演结果收敛至偏离实际分布的错误解. 而方法三通过简化气泡概率密度函数有效改善了这个问题.图 7 例4数据的反演结果图, 气泡群孔隙率$\beta = 5.3 \times {10^{ - 3}}$ , 平均半径$\overline r = 2.2\;{\rm{ mm}}$ (a) 气泡分布反演结果; (b)相速度计算结果; (c)声衰减计算结果Figure7. Inversion results of example 4, void fraction$\beta = 5.3 \times {10^{ - 3}}$ , mean radius $\overline r = 2.2\;{\rm{ mm}}$ : (a) Bubble distributions; (b) phase speed; (c) sound attenuation.5.结 论 本文通过迭代方法, 将相速度和气泡振动参数修正通过迭代方法代入了反演计算过程中. 通过实验数据对比发现, 在孔隙率为10–5 的情况下, 含气泡水平均量对反演结果影响较小, 而声速频散的影响显著. 通过保留非共振衰减和考虑声速频散, 本文方法相比于经典的RBA模型有显著改善; 当气泡群浓度到达10–3 时, 含气泡水平均量的引入对反演结果的改善效果变得明显, 并随着孔隙率进一步增加而影响变大. 最后本文针对数据稀疏时遇到的问题给出了简化反演方法, 结果表明简化方法能够较为准确地给出气泡群分布的主要参数.–3 以上的气泡群进行反演. 拓展了利用声衰减反演气泡群的限制条件. 在反演气泡群分布的同时可以得到近似的气泡群相速度曲线, 本文方法将为利用声衰减反演气泡群参数的发展提供有益思考. 
































































































 图 1 迭代方法反演气泡分布流程图
图 1 迭代方法反演气泡分布流程图









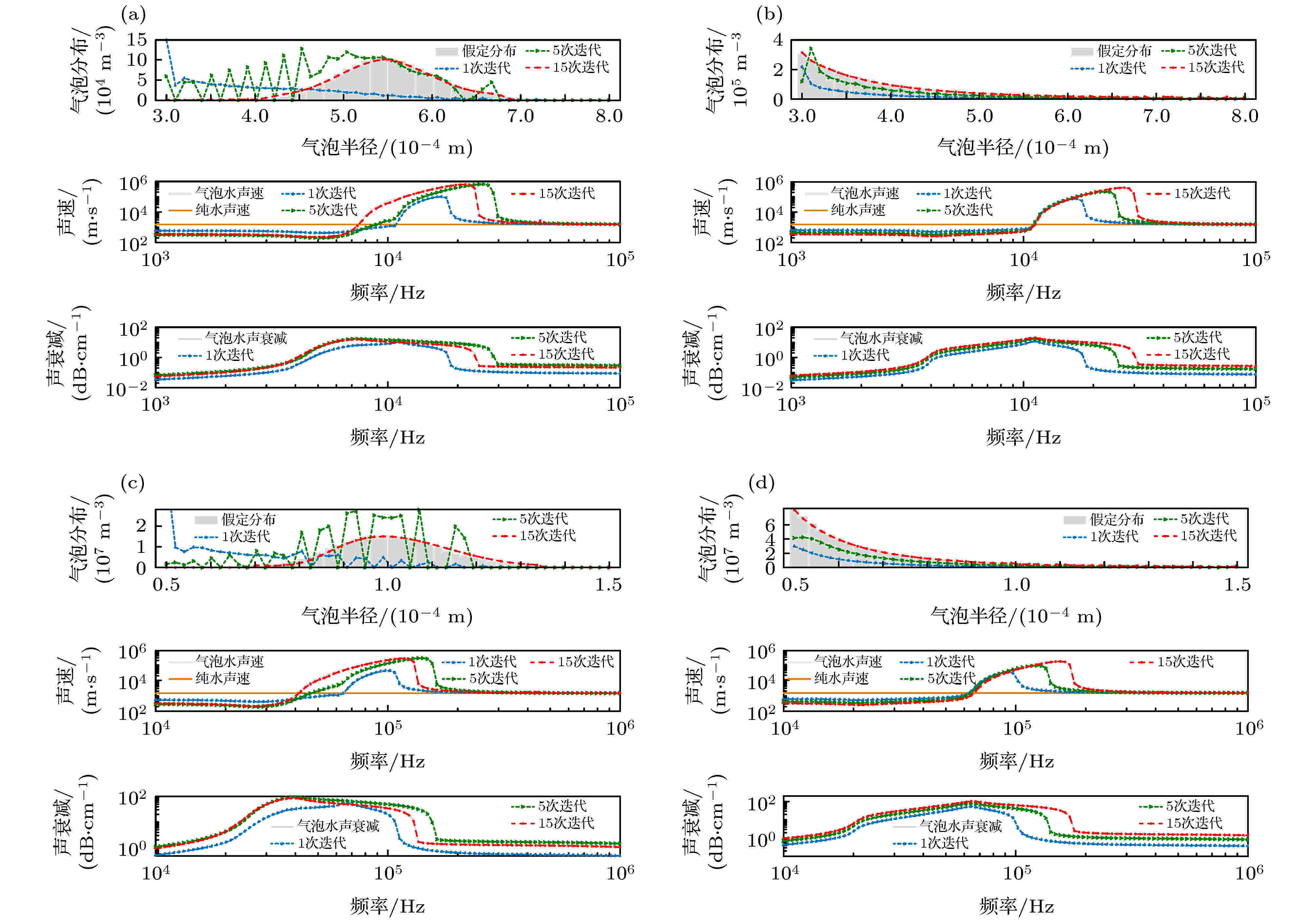 图 2 迭代算法反演结果 (a) 对数正态分布,
图 2 迭代算法反演结果 (a) 对数正态分布, 






















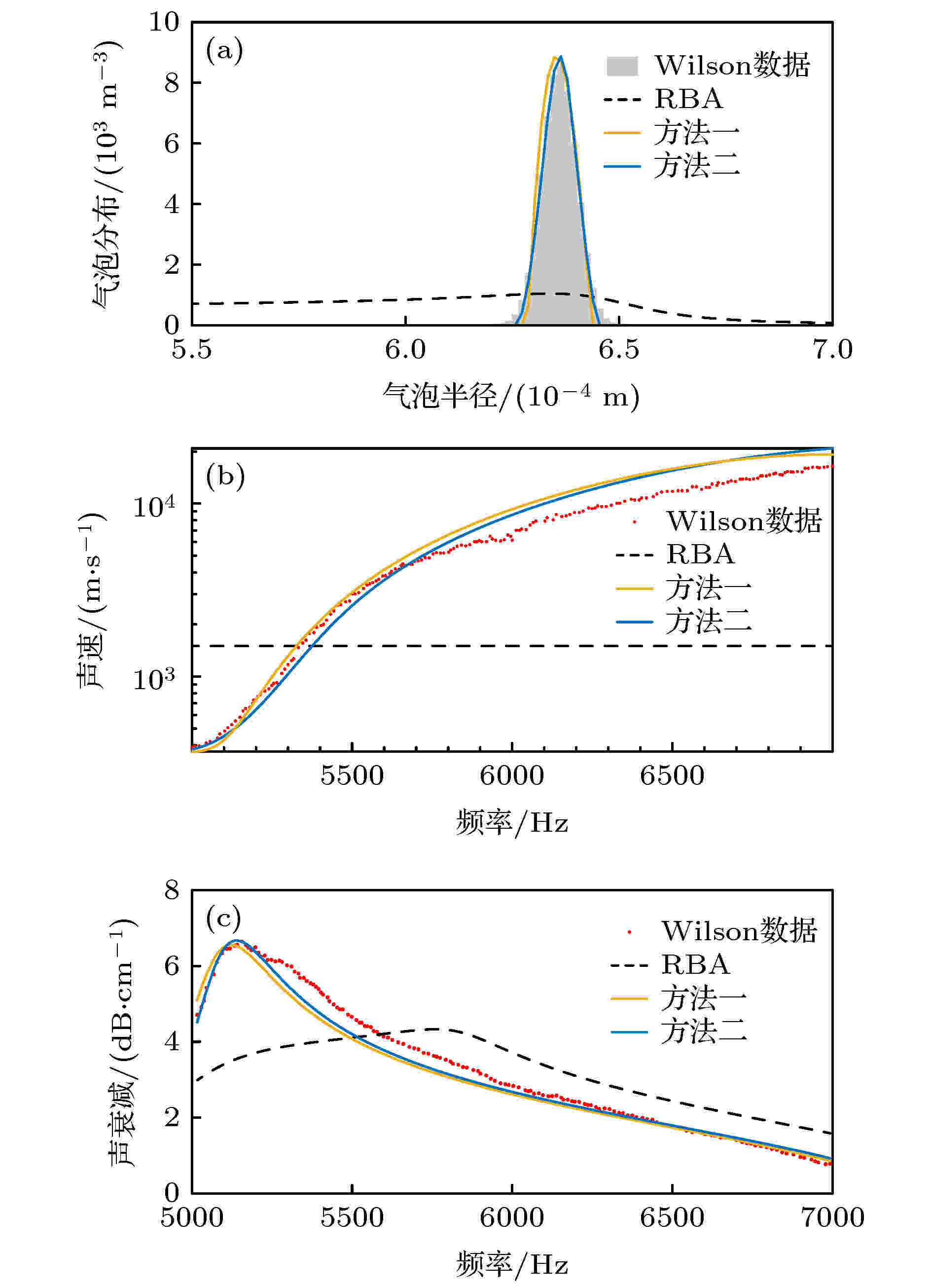 图 3 例1数据的反演结果图, 气泡群孔隙率
图 3 例1数据的反演结果图, 气泡群孔隙率



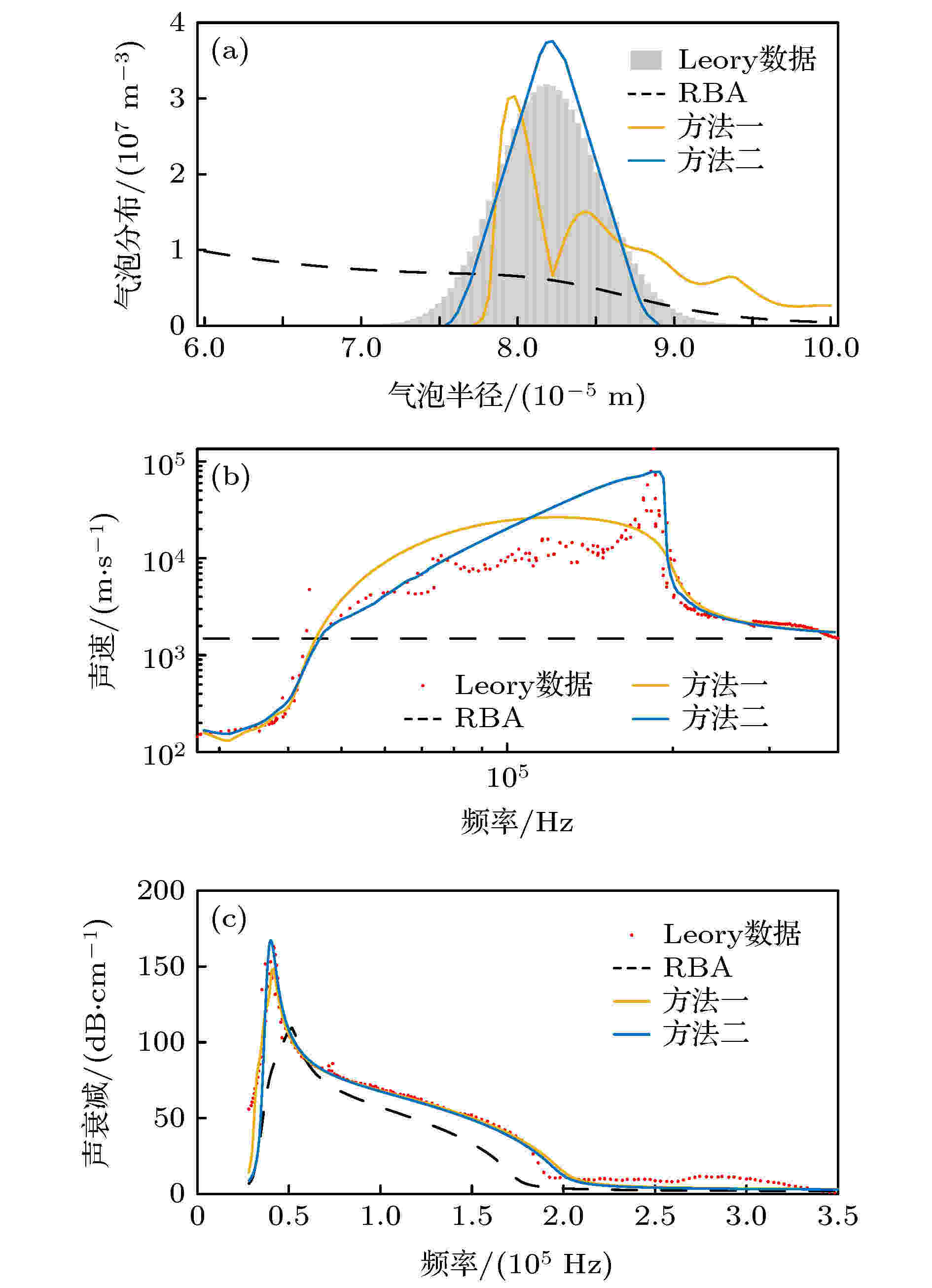 图 4 例2数据的反演结果图, 气泡群孔隙率
图 4 例2数据的反演结果图, 气泡群孔隙率



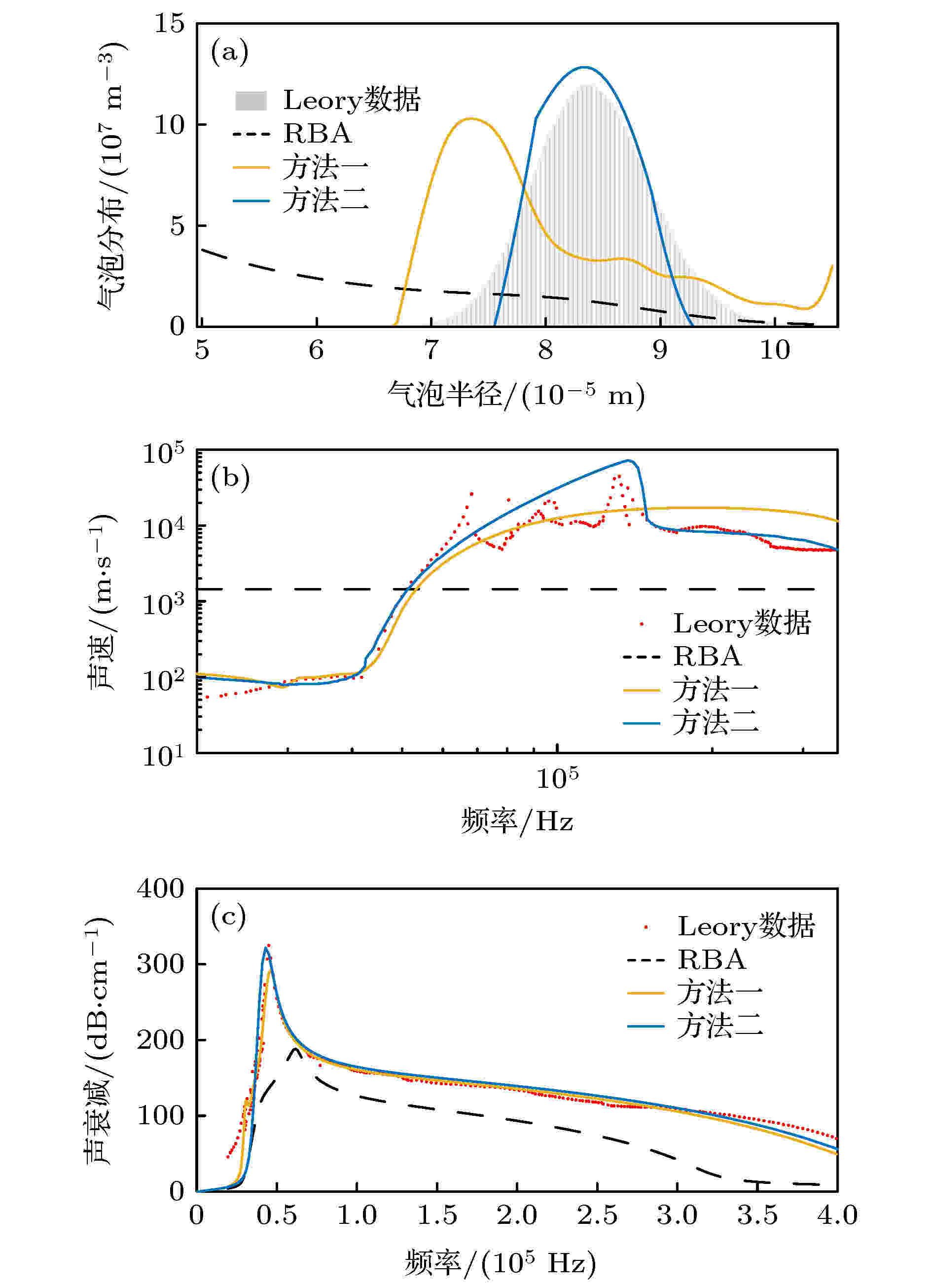 图 5 例3数据的反演结果图, 气泡群孔隙率
图 5 例3数据的反演结果图, 气泡群孔隙率




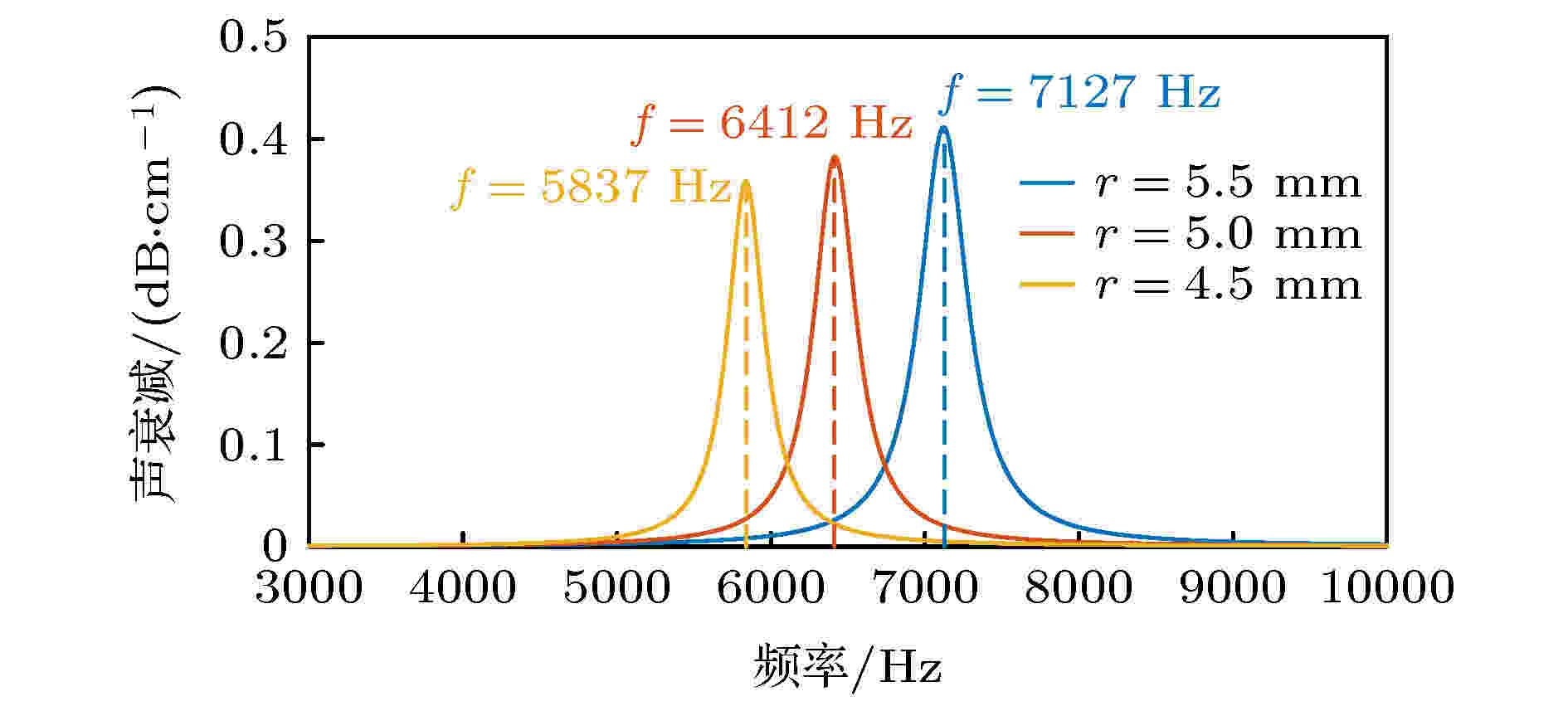 图 6 不同半径气泡群衰减峰位置
图 6 不同半径气泡群衰减峰位置












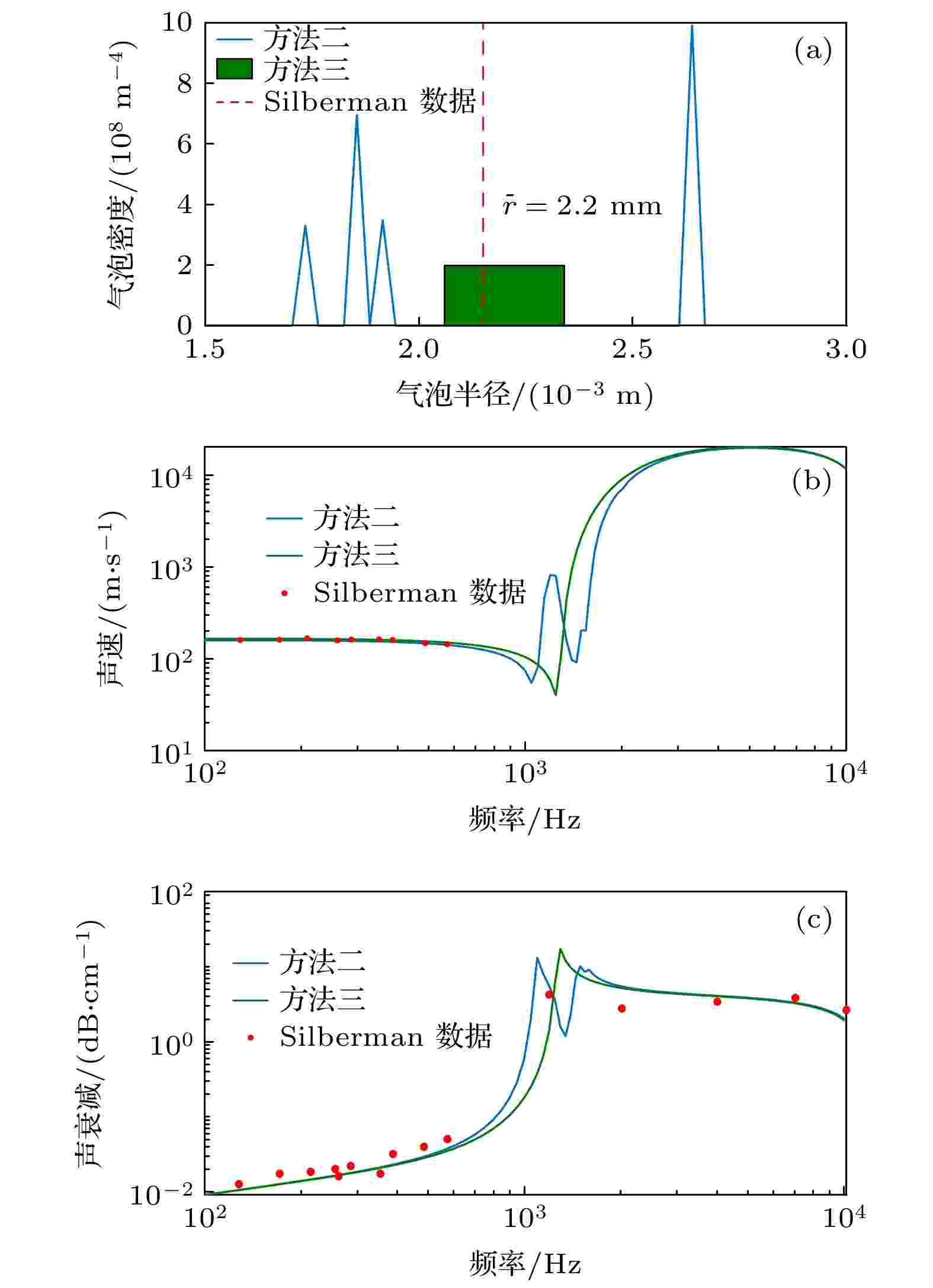 图 7 例4数据的反演结果图, 气泡群孔隙率
图 7 例4数据的反演结果图, 气泡群孔隙率



