摘要:基于高功率脉冲磁控溅射(HiPIMS)技术开发的筒形溅射阴极, 配合电磁系统可有效地提升等离子体的输运效率. 然而电磁系统的引入反作用于筒内放电特性, 从而使靶面放电面积和放电强度无法同时维持. 鉴于此, 本文通过调整磁场布局, 研究了靶面切向(横向)磁场和法向(纵向)磁场对靶面放电的作用规律, 优化后靶面切向磁场分布更加均匀, 磁场强度高于40 mT的靶面区域占比由51%增至67%, 同时法向峰值强度外移, 强度由73 mT增至96 mT. 采用Ar/Cr体系放电发现：相同工艺条件下, 优化后的溅射阴极辉光变亮, 靶电流增大, 放电面积变宽, 放电特性得到显著提升. 利用等离子体整体模型仿真和发射光谱仪检测发现优化后离子电流和光谱强度得到明显提升, Cr粒子密度提高一倍, 增至2.6 × 10²⁰ m^–3, 且离化率上升至92.1%, 同时输出离子通量提高近一倍, 实现了靶面放电与离子输出的双促进.
关键词: 高功率脉冲磁控溅射/
磁电协同/
增强放电/
输出效率

English Abstract

全文HTML

--> --> -->

高功率脉冲磁控溅射(HiPIMS)技术^[1]的等离子体离化率高^[2], 制备的薄膜组织致密^[3]、结合强度高^[4]、力学性能优异^[5], 但受困于放电不稳定^[6]和沉积速率低^[7]的问题. 基于HiPIMS技术开发的筒形溅射阴极能够将放电限制在筒形结构内部, 从而避免由于放电不稳定产生的“金属液滴”沉积影响薄膜质量^[8], 同时配合电磁系统引导等离子体向基片输运, 提高了薄膜沉积速率^[9]. 然而, 电磁系统的引入与阴极原有磁场产生相互作用, 使放电面积或强度产生大幅度减弱, 进而削弱沉积效率^[10].
一般来说, 磁场可对放电等离子体中远离靶面的电子起到约束作用, 从而增加靶前等离子体密度, 增强放电^[11], 但若其磁场强度过大, 也会抑制离子向工件输运, 从而影响沉积效率^[12]. 故对于磁控溅射来说, 通过磁场调控辉光放电来实现放电与输出的协调, 就需要一方面优化磁场强度, 实现磁场对放电的有效控制, 另一方面尽可能增加磁场均匀性, 提高放电面积^[13], 从而实现稳定的放电和高效的输出. 随着HiPIMS放电峰值功率的提高, 放电等离子体中电子能量成倍增加, 电子逃逸加快, 从而破坏了原有的磁电耦合, 故进一步提高靶面的磁场强度成为必然^[12,14]. ?apek等^[15]研究了磁场强度对不同靶材料放电波形的影响, 发现通过调整磁场大小可以有效地实现稳定的HiPIMS放电. Ganesan等^[16]研究了磁场分布对靶面放电的影响, 发现通过扩宽磁场的分布可以有效地提高HiPIMS的放电面积. 在筒形结构阴极中放电, 类空心阴极效应使得放电更加稳定, 不同脉冲内的放电重复性提高, 但电磁系统的增加, 反作用于原阴极磁场, 进而影响放电和输运^[17].
鉴于此, 本文以筒形溅射系统为研究对象, 研究筒形源与电磁系统在HiPIMS放电过程中的相互作用, 并通过新型磁铁布局作用于筒形源磁场与电磁系统磁场, 实现放电与输出的双促进. 结果表明: 通过磁场优化, 筒形阴极内壁仍能保持较大的放电面积和放电强度, 大量等离子体在离开放电区后聚集, 并形成较大束流向外输运, 等离子体密度、离化率以及沉积效率同时大幅度提高.

2

-->

2.1.磁场仿真

筒形溅射阴极的结构如图1所示, 主要包含筒形阴极和电磁系统两个部分. 其中筒形阴极包含一组磁极相反的永磁铁, 电磁系统置于筒形阴极两侧, 由直径为5 mm的铜导线缠绕而成. 仿真采用柱坐标体系, 图中z轴表示筒形溅射阴极的中心轴线^[12]. 仿真区域的总磁场强度B(T)为电磁场强度B_coil和永磁场强度B_magnet的矢量和, 如下式所示, 其中B_coil和B_magnet可分别通过方程组(2)和方程组(3)求得
图 1 筒形溅射阴极结构示意图
Figure1. Schematic diagram of the cylindrical cathode.

${B} = {{B}_{{\rm magnet}}} + {{B}_{{\rm coil}}},$

$ \left\{ \begin{aligned}&\nabla \times {{H}}_{{\rm coil}}=J, \\ &J=\frac{{N}_{{\rm coil}}}{{A}_{{\rm coil}}}{I}_{{\rm coil}}e, \\ &{{B}}_{{\rm coil}}={\mu }_{0}{\mu }_{{\rm r}}{{H}}_{{\rm coil }}, \end{aligned} \right.$

$ \left\{ \begin{aligned}&{{H}}_{{\rm magnet}}=-\nabla {V}_{{\rm magnet}}, \\&{{B}}_{{\rm magnet}}={\mu }_{0}{\mu }_{{\rm r}}{{H}}_{{\rm magnet}}, \end{aligned} \right.$

其中H_coil (A/m)为电磁线圈的磁场强度; J (A/m²)为电流密度; N_coil, A_coil (m²)和I_coil (A)分别为电磁线圈的匝数、截面积和电流; H_magnet (A/m)为永磁铁的磁场强度; V_magnet (A)为永磁铁的磁标势; μ₀ = 4π × 10^–7 N/A²为真空磁导率; μ_r为相对磁导率; e = 1.6 × 10^–19 C为单位电荷^[18].
2 -->

2.2.放电仿真

利用粒子网格/蒙特卡罗法(particle in cell/Monte Carlo collision, PIC/MCC)对优化前后的筒形溅射阴极进行等离子体放电仿真^[19,20]. 计算过程中, 屏蔽罩为阳极并设置为接地, 靶材为阴极, 电压为–800 V, 背景放电气体为Ar气, 温度为300 K, 气压为1.0 Pa. 初始电子和Ar⁺的密度设置为1 × 10¹⁴ m^–3, 仿真过程中仿真区域中分别随机取3600个仿真Ar⁺离子和仿真电子, 能量满足Maxwell分布, 每个粒子代表2 × 10⁶ 个实际粒子. 由于仿真区域为规则的矩形, 初始时刻将仿真区域划分成多个尺寸为1 mm × 1 mm 的正方形网格. 模型考虑简单的Ar气放电过程, 具体反应如表1所列, 其二次电子发射系数由Trim软件计算获得. 此外, 仿真过程中考虑仿真粒子的三维速度, 模拟计算时间步长为1 × 10^–12 s, 并且于每个步长之后都通过泊松方程计算等离子体的自洽电势^[10].

反应方程式	反应能量/eV	反应类型
${{{\rm e}}} + {{\rm Ar}} \to {{\rm Ar}} + {{{\rm e}}}$	—	弹性
${{{\rm e}}} + {{\rm Ar}} \to {{\rm A}}{{{\rm r}}^ + } + 2{{{\rm e}}}$	15.76	电离
${{{\rm e}}} + {{\rm Ar}} \to {{\rm A}}{{{\rm r}}^m} + {{{\rm e}}}$	11.56	激发
${{{\rm e}}} + {\operatorname{Ar} ^m} \to {{\rm Ar}} + {{{\rm e}}}$	–11.56	退激发
${{{\rm e}}} + {{\rm A}}{{{\rm r}}^m} \to {{\rm A}}{{{\rm r}}^ + } + 2{{{\rm e}}}$	4.2	电离
${{\rm A}}{{{\rm r}}^ + } + {{\rm Ar}} \to {{\rm A}}{{{\rm r}}^ + } + {{\rm Ar}}$	—	弹性
${{\rm A}}{{{\rm r}}^ + } + {{\rm Ar}} \to {{\rm Ar}} + {{\rm A}}{{{\rm r}}^ + }$	—	电荷交换

表1Ar气放电的主要反应表
Table1.The main reactions of simple Ar gas discharge.

2 -->

2.3.放电测试

放电测试在尺寸为600 mm × 600 mm × 500 mm的真空腔内进行, 所用电源为Melec GmbH复合高功率脉冲磁控溅射电源, 输出电压为: 600—1000 V, 脉冲频率: 50 Hz, 脉冲宽度: 300 μs. 溅射靶为Cr靶(99.5%), 靶内径: 120 mm, 外径: 132 mm, 高: 46 mm. 本底真空: 1.0 × 10^–3 Pa, 放电气压: 1.0 Pa, 溅射气体为Ar(99.99%).
使用Tektronix TDS1012 BSC示波器采集靶电压及靶电流曲线, 为优化测试信号, 测试时将测试电压及电流缩小100倍, 同时进行64倍平滑. 采用自主设计的等离子体发射光谱仪检测阴极轴心处等离子体的光谱强度, 自主搭建的等离子体电流测试装置测量离子电流, 具体的通过在真空腔室内放置厚度为0.5 mm, 直径为40 mm的不锈钢片, 一端串联一个1 Ω, 100 W的电阻, 并对不锈钢施加–100 V的偏压, 通过示波器测试电阻两端的电压差获得离子电流^[8].

2

-->

3.1.耦合磁场优化

图2(a)和图2(b)分别展示了电磁系统线圈电流对筒形阴极靶面切向磁场强度B_z和法向磁场强度B_r的作用. 为方便描述, 将电磁场方向与筒形阴极中永磁场方向相同时的线圈电流定义为正电流, 方向相反时的电流定义为负电流. 以前的研究表明, 靶面切向磁场强度B_z大于等于40 mT的区域更容易发生等离子体放电, 本文将此区域定义为有效磁场区域. 图2(a)中红色虚线表示切向磁场强度B_z等于40 mT, 红色虚线与每条曲线形成两个交点, 交点间的距离表示有效磁场区域的宽度. 如图2所示, 当线圈电流由0 A变为15 A时, 电磁场对阴极磁场产生压缩, 靶面切向磁场强度B_z增大, 导致靶面有效面积变宽, 筒内放电加强, 但靶面两侧法向磁场强度B_r强度减小, 对电子约束作用减弱, 导致大量电子从两侧逃逸, 等离子体难以形成积累, 此时虽阴极的放电面积增大, 但等离子体密度产生大量衰减^[12]. 当线圈电流由0 A变为–15 A时, 电磁场对阴极磁场产生拉伸, 靶面切向磁场强度B_z减小, 导致有效磁场区域变窄, 此时靶面放电面积减小, 放电强度稍微减弱. 但靶面两侧法向磁场强度B_r增大, 阻止了电子向两侧的扩散损失, 有助于电子密度向筒内中心区积累, 弥补切向磁场下降造成的放电损失, 形成仍然较强的放电, 但B_r的增大也严重阻止了等离子体向两侧的输运, 离子束流面积减小, 沉积效率无法进一步增强.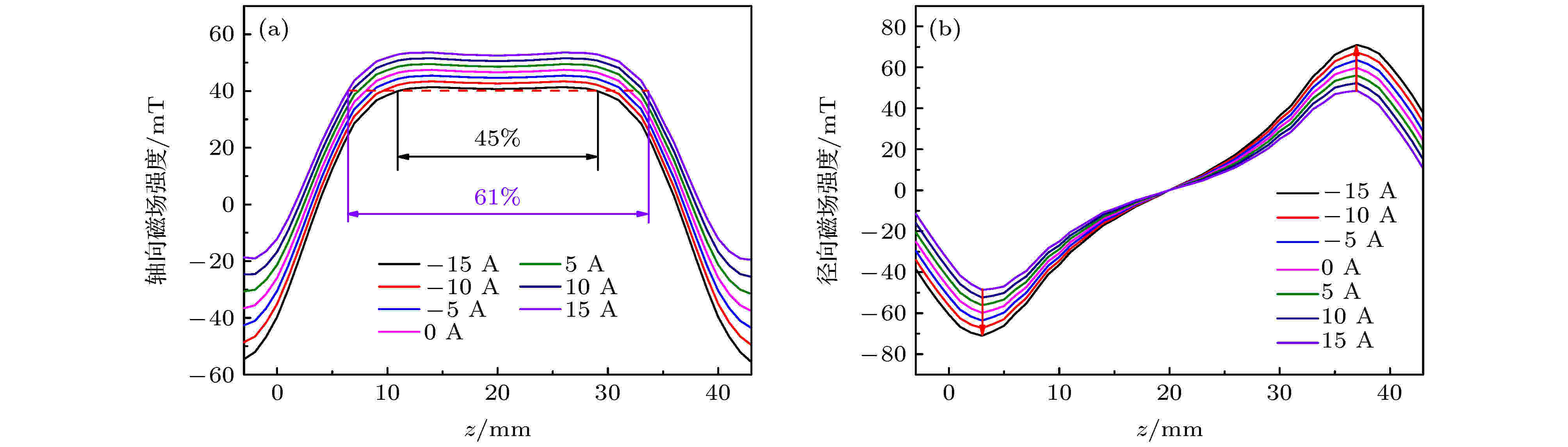
图 2 线圈电流对靶面磁场的作用规律　(a) 对切向磁场强度B_z的影响; (b)对法向磁场强度B_r的影响
Figure2. Effects of coil current on the target magnetic field: (a) Tangential magnetic field strength B_z; (b) longitudinal magnetic field strength B_r.

考虑到线圈电流–15 A时放电的强化效果, 选择在此条件下对阴极磁场进一步的设计, 在保证放电强度的同时, 进一步增大放电面积, 进而提高沉积束流强度, 提高沉积效率. 初始筒形阴极的磁场结构如图3(a)所示, 在线圈电流为–15 A的条件下, 筒内磁感线分布情况如图3(d)所示. 由于电磁场的磁极方向与相邻的永磁铁磁极方向相反, 二者之间形成磁感线回路, 因此两组永磁铁之间形成的磁感线密度减小, 导致切向磁场强度B_z的减小. 为补偿靶面切向磁场强度B_z, 在两组永磁铁中间增加一组横向磁铁, 如图3(b)所示, 为方便描述, 将其定义为中央磁铁. 图3(e)为仿真得到的磁感线分布, 可见中央磁铁N极和S极之间形成的磁场对永磁铁之间形成的磁场向上挤压, 使得靶面的磁感线密度得到提升, 从而使放电强度得到保证. 同时, 在电磁系统与阴极磁铁之间增加一组与相邻永磁铁磁极相同的小磁铁, 如图3(c)所示, 为方便描述, 将其定义为同极小磁铁. 可以看出同极小磁铁与电磁场之间形成了磁感线回路, 使电磁场对阴极磁场的影响大幅减弱, 如图3(f)所示.
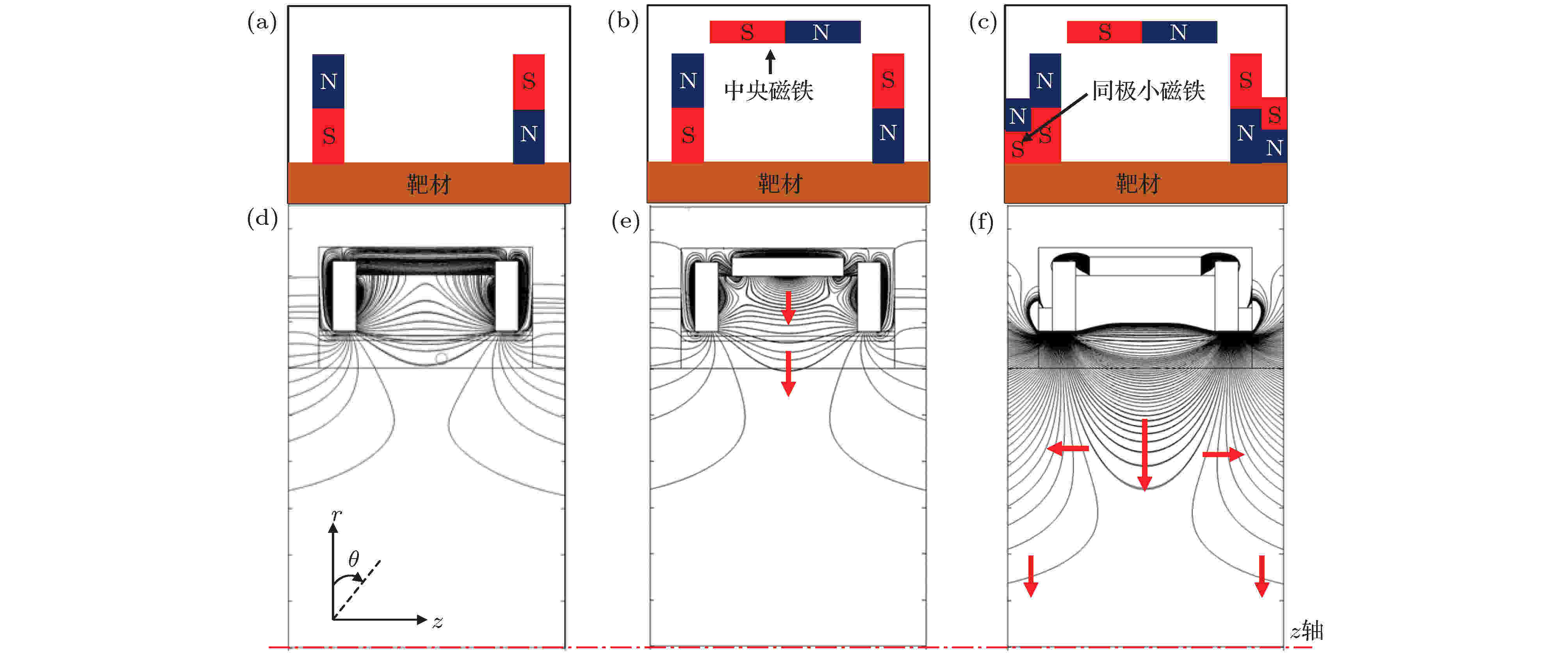图 3 –15 A条件下筒形溅射阴极磁铁排布示意图及其内部磁感线分布　(a), (d)优化前; (b), (e) 增加中央磁铁; (c), (f)含有中央磁场和同极小磁铁
Figure3. Magnet arrangement and magnetic induction lines distributions in the cylindrical cathode under –15 A: (a), (d) Before improvement; (b), (e) with the central magnets; (c), (f) with the central magnets and dipole magnets.

为获得最优的放电特性, 分别对中央磁铁和同极小磁铁得磁极强度和位置进行优化. 选择同极小磁铁磁极强度200 mT, 中央磁铁距靶后端面76 mm时, 靶面切向和法向磁感应强度随中央磁铁磁极强度的变化如图4(a)和图4(b)所示. 随着中央磁铁的磁极强度由0 mT增至400 mT, 靶面切向磁场强度B_z的峰值大幅上升, 由55 mT增至85 mT. 而红色虚线(B_z = 40 mT)与各切向磁场曲线的交点位置无明显变化, 坐标分别为z =7 和33 mm, 表明中央磁铁对有效磁场区域没有明显作用, 只是显著提升有效区域内切向磁场强度. 根据下式 ^[21]可知,
图 4 中央磁铁磁极强度对靶面磁感应强度的影响　(a) 对切向磁感应强度B_z的影响; (b) 对法向磁感应场B_r的影响
Figure4. Effects of central magnets strength on magnetic induction lines distribution of target surface: (a) Tangential magnetic field strength B_z; (b) longitudinal magnetic field strength B_r.

$ {D}_{{\rm Bohm}}=\frac{1}{\omega \tau }\frac{{T}_{{{\rm e}}}}{\overline{{B}_{z}}}. $

在电子温度T_e(V)和霍尔系数ωτ变化较小的条件下, 电子的扩散系数D_Bohm(m²/s)与靶面的平均切向磁感应强度$\overline {{{B}_z}} $成反比, 因此可以推断, 靶面电子密度随中央磁铁磁极强度上升, 放电强度显著增强. 在中央磁铁强度由0 mT增至400 mT的过程中, 法向磁感应强度B_r也上升, 由85 mT增至100 mT, 表明电子从靶面两侧逃逸靶面难度增大, 但其峰值位置不变, 均出现在坐标z = 2和38 mm处, 说明放电宽度未发生明显变化. 为了保证较高的靶面磁场感应强度, 将中央磁铁磁极强度取为400 mT.
固定中央磁极强度400 mT, 其距靶后端面76 mm时, 同极小磁铁磁极强度对靶面磁场的影响如图5所示. 随着同极小磁铁磁极强度由0 mT增至400 mT, 靶面切向磁感应强度B_z的峰值由78 mT增至92 mT. 此外, 红色虚线(B_z = 40 mT)与各切向磁场曲线的交点位置分别向两侧移动, 其间距逐渐由24 mm拓宽至31 mm, 表明切向磁感应B_z的有效宽度明显增大, 意味着等离子体放电区域增大, 并伴随着靶面的放电面积拓宽. 图5(b)所示为同极小磁铁磁极强度对靶面法向磁感应强度B_r的影响, 随着同极小磁铁强度由0 mT增至400 mT, 靶面边缘的法向磁感应强度B_r也进一步增强, 其峰值强度由89 mT增加至112 mT. 同时, 法向磁感应强度B_r峰值位置向靶面的边缘移动, 坐标分别由z = 4 mm和z = 36 mm外移至2 mm和38 mm, 峰值间距宽度的增幅占靶面总宽度的8%, 意味着靶面可利用的放电面积将进一步增大. 值得注意的是, 此时靶面中央的法向磁感应强度基本不变, 即同极小磁铁对靶面有效区域的磁感线弧度几乎没有影响, 说明随着同极小磁铁磁极强度增强, 同极小磁铁与电磁系统之间形成的磁感线联系逐渐增强, 从而抑制了电磁系统对阴极磁铁的拉伸作用, 有效地保证了靶面的磁场强度. 为了保证切向磁感应B_z有效区域的宽度, 将同极小磁铁磁极强度定为400 mT.
图 5 同极小磁铁磁极强度对靶面磁感应强度的影响　(a) 对切向磁感应强度Bz的影响; (b) 对法向磁感应场B_r的影响
Figure5. Effects of dipole magnets strength on magnetic induction lines distribution of target surface: (a) Effects on tangential magnetic field strength B_z; (b) effects on longitudinal magnetic field strength B_r.

在添加中央磁铁和同极小磁铁后, 靶面切向磁感应强度B_z和法向磁感应强度B_r分布均得到明显提高. 然而此时, 靶面切向磁感应强度B_z的峰值达到110 mT, 相对放电等离子体来说过高, 从而抑制了等离子体向外扩散, 降低沉积效率. 且磁感线形状呈圆滑的上凸状, 会降低等离子体分布均匀性, 并引起靶面局部刻蚀^[22,23]. 根据Qiu等^[24]的研究, 当切向磁感应强度B_z的曲线形状近似矩形时, 靶面刻蚀最均匀. 为调整靶面切向磁场形状, 研究了中央磁铁与靶面的距离对切向磁感应强度B_z的作用, 如图6所示. 随着中央磁铁到靶后端面距离由7.6 cm增加至8.4 cm, 切向磁感应强度B_z的磁感线形状逐渐由上凸变为下凹状, 其峰值位置由最初靶面中央(z = 20 mm)处向两侧(z = 10和30 mm)处转移, 最高磁场强度由110 mT减弱至62 mT, 与HiPIMS放电对应关系较好^[25]. 随着中央磁铁到靶面距离的增大, 红色虚线(B_z = 40 mT)与切向磁感应强度B_z交点之间的距离有微弱增加, 表明放电面积略有增大. 对比多组仿真数据后发现, 当中央磁铁距离靶后端面8.2 cm时, 切向磁感应强度B_z的磁感线形状最接近矩形, 因此将8.2 cm定为中央磁铁距靶后端面的距离.
图 6 中央磁铁与靶后端面距离对靶面磁场强度的影响　(a) 对切向磁感应强度B_z的影响; (b) 对法向磁感应场B_r的影响
Figure6. Effects of distance between the central magnets and the rear face of target on magnetic induction lines distribution of target surface: (a) Tangential magnetic field strength B_z; (b) longitudinal magnetic field strength B_r.

磁铁优化前后靶面切向磁感应强度B_z和法向磁感应强度B_r的分布如图7所示. 与原始情况相比, 优化后靶面的切向感应强度B_z明显增强, 其有效宽度由24 mm增至31 mm, 靶面占比由51%增至67%, 增幅为16%, 可显著增大等离子体的放电面积和放电强度. 同时, 靶面边缘的法向磁感应强度B_r的显著增强且其峰值外移, 不仅能够抑制电子从靶面两侧逃逸, 还有助于放电面积的进一步提高. 为验证磁场对放电的改进效果, 对优化前后的筒形阴极进行简单的气体放电仿真, 得到0.4 μs时等离子体密度(Ar⁺)分布情况分别如图7(e)和图7(f)所示, 可见优化仿真区域内Ar⁺离子的密度分布产生明显差异. 与原始情况相比, 优化后放电区域内Ar⁺的分布范围更广, 靶面的放电面积更宽, 从z = 10到40 mm, 总宽度为30 mm, 与磁场仿真结果中切向磁感应强度的有效区域一致. 同时, 由于靶面约束电子的能力增强, 减弱了电子的逃逸, 增加了电子的回旋运动, 使得电离碰撞概率大幅上升, 因此经过相同的时间, 优化后的筒形阴极可获得更高的等离子体密度和离化率^[24,26]. 这表明相同工艺条件下, 优化后的筒形阴极更容易发生放电, 且筒内的放电强度显著增大.
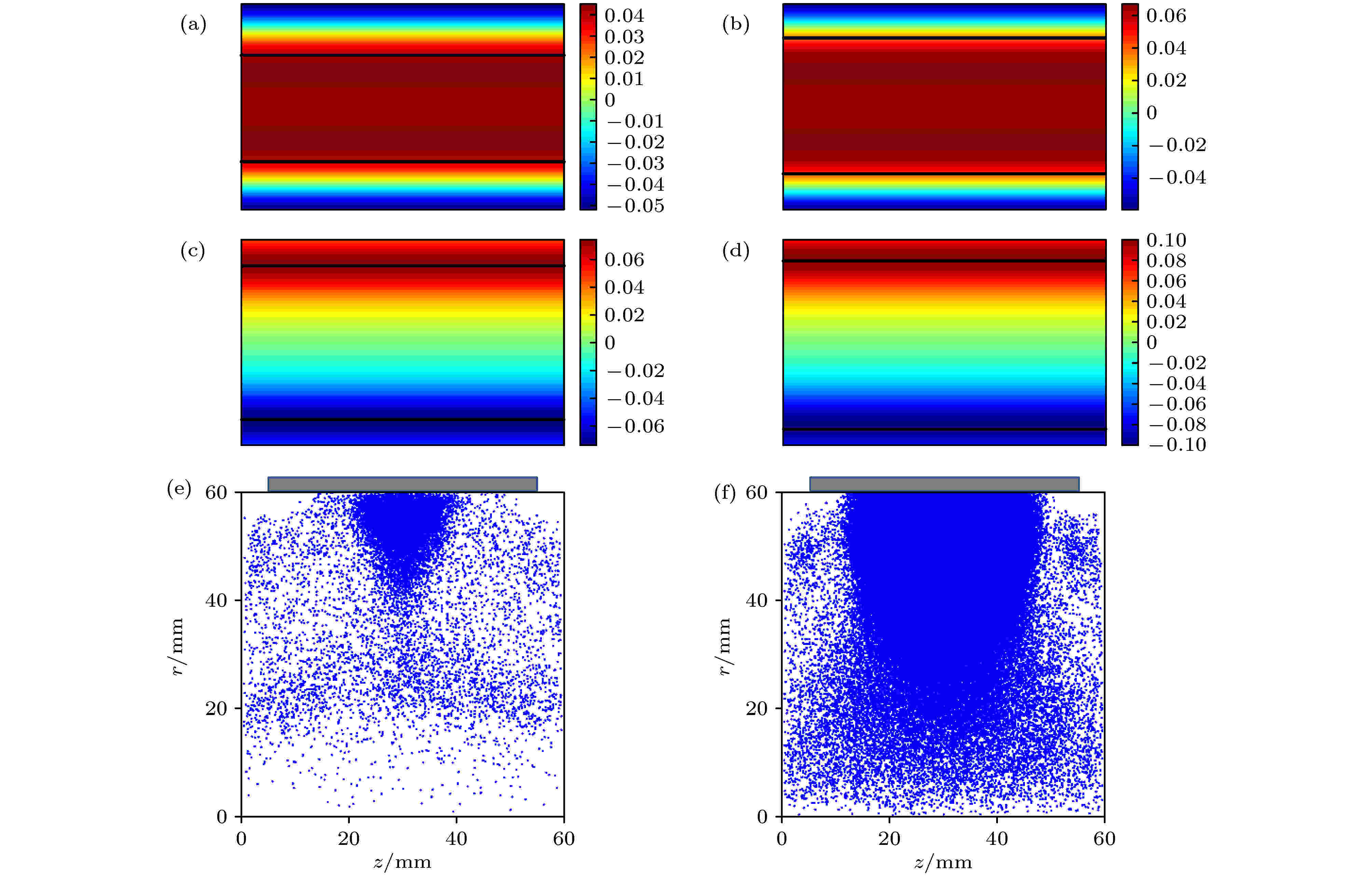图 7 优化前和优化后靶面磁场分布及放电预测　(a), (b) 切向磁场Bz分布; (c), (d) 法向磁场Br分布; (e), (f) 0.4 μs时放电Ar⁺离子密度分布
Figure7. The magnetic distribution of target surface and the discharge prediction before and after improvement: (a), (b) The tangential magnetic field strength B_z; (c), (d) the longitudinal magnetic field strength B_r; (e), (f) the distributions of Ar⁺ ions at 0.4 μs.

2 -->

3.2.高功率放电特性研究

对优化前后的筒形溅射阴极进行放电测试, 结果如图8所示. 可见相同实验参数条件下(–800 V, 1.0 Pa, 线圈电流–15 A), 优化后筒形阴极靶面的刻蚀区域显著增大, 由23 mm提升至28 mm, 相应的靶面占比由50%增至60.8%, 表明靶面放电面积得到明显拓宽. 图8(c)和图8(d)为辉光照片, 可见优化后辉光强度明显增强且输出等离子体束流宽度增大, 与仿真结果基本一致. 值得注意的是, 优化后筒形阴极辉光区域延伸的距离更大, 表明等离子输运距离更远, 这一方面是由于靶面切向磁场增强, 导致靶面放电强度增大, 从而产生更多的等离子体, 即增加了筒形阴极出口处输出离子密度; 另一方面, 靶面端口处法向磁感应强度增大抑制了电子从筒形阴极靶面边缘逃逸, 使得电子向中央轴处聚焦, 然后再由中央轴处向外扩散, 与此同时离子在电子的引导下沿中央轴向外输运, 从而减小了等离子体的损耗, 增大了输运距离.
图 8 靶面放电宽度及强度图　(a)优化前和(b)优化后放电宽度; (c)优化前和(d)优化后放电辉光图
Figure8. The etching width and plasma flow pictures: The etching width (a) before and (b) after the improvement; the plasma flow pictures (c) before and (d) after the improvement.

图9为优化前后筒形阴极的靶电流与离子电流放电电压的演化. 靶电流符合HiPIMS典型放电特征, 靶电压施加后, 靶电流缓慢上升到达峰值, 随后缓慢下降, 直到脉冲结束后降至为零^[27]. 电流达到峰值前主要是气体放电阶段, 电子与Ar原子发生电离碰撞造成电子雪崩, 产生的Ar⁺在靶面发生溅射并生成二次电子, 使得靶电流快速上升^[18]. 溅射产生的Cr原子生成了金属原子溅射风, 与Ar原子发生碰撞使其溢出放电区域, 产生气体稀薄效应^[28], 导致等离子体中的Cr元素成为放电区域的主要成分. 随着Cr原子进一步电离生成Cr⁺和Cr²⁺离子, 自溅射过程大部分代替了气体溅射过程^[18]. 由于相同电压下Ar⁺轰击靶面的溅射产额大于Cr⁺离子, 且靶面温度升高使得Cr各组分扩散损耗加剧, 放电区域内等离子体密度开始逐渐下降, 减弱了离子在靶面的溅射强度, 最终导致电流达到峰值后缓慢下降^[29]. 根据下面公式, 自溅射阶段靶电流主要由离子溅射通量Г_ion(m^–2·s^–1)和靶面刻蚀面积S_T(m²)决定^[18]:
图 9 不同电压下靶电压、靶电流及离子电流 优化前的　(a)靶电压、(c)靶电流及(e)离子电流曲线; 优化后的(b)靶电压、(d)靶电流及(f)离子电流曲线
Figure9. Target voltage, target current and ion current curves under different target voltages: (a), (c), (e) Before the improvement; (b), (d), (f) after the improvement.

$ {I}_{{\rm target}}={{\rm e}}{{\varGamma} }_{{\rm ion}}{S}_{{\rm T}}, $

$ {{\varGamma} }_{{\rm ion}}=0.4{n}_{{\rm ion}}{v}_{{\rm ion}}, $

其中n_ion(m^–3)为离子浓度; v_ion(m/s)为离子速度, 其中离子速度在相同电压下相差较小. 对比图9(c)和图9(d), 可见相同电压下, 优化后的靶电流得到显著增加, 这一方面归结于优化后靶面切向磁感应强度B_z得到增强且更为均匀, 使得靶面刻蚀面积S_T显著增大; 另一方面, 靶面边缘法向磁感应强度B_r显著增强, 大幅提高了靶面对电子约束作用, 使得等离子体密度上升, 最终导致离子溅射通量的增大. 优化后靶面电流到达峰值所需要的时间缩短, 这是由于优化后磁场对电子的约束能力增强, 使得电子能够更有效地在放电区域聚集, 靶面鞘层形成的速度更快, 从而使电流达到峰值所需时间变短.
图9(e)和图9(f)为优化前后离子电流随靶电压的变化情况, 表征沉积区域的离子数量. 离子电流先缓慢上升达到峰值后缓慢下降, 直至脉冲结束后缓慢下降为零, 与靶电流的变化趋势相同. 随着靶电压的升高, 离子回吸程度增大, 导致脉冲结束后离子电流下降的速度随电压的上升而同步增大. 通过对比优化前后的离子电流可以发现, 优化后离子电流增大, 达到峰值所需时间缩短, 这主要是由于优化后放电增强, 等离子体更快达到稳态, 从而离子可以更快地到达探针所在的区域. 此外, 优化后离子电流达到峰后下降形成了一个稳定的平台, 与靶电流相似, 此时靶面处于金属放电阶段^[30], 离子电流主要由金属离子组成, 其持续时间直接影响着薄膜的沉积速率及薄膜质量^[31]. 根据离子电流曲线, 由下式计算一个脉冲内到达探针的离子电荷量Q(C):

$ Q={\int }_{0}^{t}{I}_{{\rm i}{\rm o}{\rm n}}^{{\rm o}{\rm n}}{\rm d}t, $

$ {I}_{{\rm i}{\rm o}{\rm n}}^{{\rm o}{\rm n}} $(A)表示单位时间内离子电流的大小; t (300 μs)表示放电持续时间. 当靶电压为800 V时, 优化后的离子束流Q由1.12 × 10^–3 C增大至2.05 × 10^–3 C, 输出离子通量提高了近一倍.
为进一步验证辉光区域内等离子体的演变趋势, 利用等离子体整体模型^[20]对一个HiPIMS脉冲内的Ar/Cr放电过程进行了解析, 结果如图10所示, 其中虚线和实线分别表示优化前和优化后. 可见在一个脉冲时间内, Cr元素各组分以Cr, Cr⁺和Cr²⁺的顺序依次出现, 这是由各组分不同的生成机制决定的: 最初Cr原子由气体离子Ar⁺溅射靶材生成; 而Cr⁺需要由Cr原子与电子的电离碰撞生成; 而Cr²⁺最后出现是基于部分Cr⁺发生的二次电离^[18,28]. Cr原子密度随时间的演变曲线呈现三个拐点, 0—25 μs在Ar⁺溅射作用下快速上升并达到极大值, 此后由于大量的电离反应, Cr密度逐渐下降并在50 μs左右取得极小值. 此后, 放电进入金属放电阶段, 自溅射过程几乎取代了气体溅射, 使得Cr密度继续上升最终达到稳定^[23]. 注意到优化前后Cr原子密度在气体放电阶段的变化趋势几乎完全一致, 表明此时体系内Ar⁺离子的气体溅射强度基本相同. 随着电子的雪崩效应, 电子密度逐渐增加, 而优化后靶面两侧的法向磁感应强度B_r和靶面切向磁感应强度B_z均增强, 进而束缚了电子逸散. 因此, 优化后筒形阴极的电子密度大幅上升, 进而使Cr原子、Cr离子密度均成倍增加, 以Cr⁺离子为例, 其密度密度由1.2 × 10²⁰ m^–3增至2.6 × 10²⁰ m^–3, 增加了一倍有余.
图 10 (a) 金属粒子浓度; (b) 离化率及电子温度变化图
Figure10. (a) Metal particle concentration; (b) ionization rate and electron temperature before and after the improvement.

进一步处理得到放电区域内的金属离化率和平均电子温度, 其中金属的离化率根据下式进行计算:

$ {\alpha }_{{\rm C}{\rm r}}=\frac{{n}_{{{\rm C}{\rm r}}^+}+{n}_{{{\rm C}{\rm r}}^{2+}}}{{{n}_{{\rm C}{\rm r}}+n}_{{{\rm C}{\rm r}}^+}+{n}_{{{\rm C}{\rm r}}^{2+}}}, $

其中$ {\alpha }_{{\rm C}{\rm r}} $表示Cr的离化率$ ; {n}_{{\rm C}{\rm r}} $, $ {n}_{{{\rm C}{\rm r}}^{+}} $, $ {n}_{{{\rm C}{\rm r}}^{2+}} $分别表示等离子体体系中Cr原子、Cr⁺和Cr²⁺的空间数密度. 将图10(a)中对三种粒子密度计算结果代入(8)式, 结果如图10(b)所示. 由于电子密度和电离碰撞概率的增大, 优化后金属离子的离化率由优化前的90%进一步提升至92.1%. 优化前后平均电子温度在在气体放电阶段基本相同, 随后电子与Ar发生碰撞并发生电离生成Ar⁺, 从而平均电子温度下降, 随着Ar⁺溅射增强产生高能二次电子, 使得电子温度缓慢上升. 然而, 随HiPIMS放电过程由气体放电转移至金属放电, Cr原子大量的电离使得电子被迅速冷却, 最终达到平衡. 由于优化后筒形阴极内Cr原子和Cr离子的电离碰撞概率更高, 因此稳定后平均电子温度从原来的3.1 eV下降至优化后的2.7 eV.
图11为优化强化筒形阴极的放电光谱随靶电压的变化情况, 随着电压的增大, 金属离子光谱强度增大, 根据Schiebe - Lomakin方程^[32]:
图 11 中央轴处的原子发射光谱(OES)强度　(a) 优化前光谱强度; (b)优化后光谱强度
Figure11. The OES intensity at the center axis of cylindrical cathode: (a) Before the improvement; (b) after the improvement.

$ I=a{C}^{b}, $

I表示光谱强度; a和b为相关系数; C表示粒子密度. 光谱相对强度越高表明粒子密度越大, 与整体模型的仿真数据吻合. 随放电电压的增加, 等离子体中的金属粒子比例增加, 并逐渐取代气体粒子, 成为主导粒子. 优化后金属离子的光谱强度进一步增强, 说明金属的电离和碰撞更加强烈. 与Ar⁺光谱强度相比, 其比值增大, 表明优化后等离子体中的金属离子占比更高, 这与离子电流结果一致.

综上所述, 在耦合电磁场的情况下, 为同时增大靶面放电面积和增强放电强度, 本文针对筒形阴极与电磁系统, 研究了其靶面磁场与电磁场的相互作用, 并通过新型磁场设计分别对靶面切向磁场强度、磁力线形状及两侧法向磁场强度进行优化和加强, 既实现了放电强度和放电面积的有效增强, 又明显提高了等离子体的输运效果和沉积效率. 优化后放电区域内的切向磁感应强度B_z由41 mT增至62 mT, 有效区域宽度占比由51%增至67%, 法向磁感应强度B_r的峰值由73 mT增至96 mT. 对比磁场优化前后的筒形阴极高功率放电特性发现: 相同工艺条件下, 优化后的筒形溅射阴极, 靶面放电面积增大, 放电强度与等离子体输运特性均明显增强. 优化后的磁场主要影响金属放电阶段, 对气体放电阶段影响较小, 其中Cr离子密度由1.2 × 10²⁰ m^–3增至2.6 × 10²⁰ m^–3, 金属粒子离化率也由90%提升至92.1%.