全文HTML
--> --> -->通常光学谐振腔的传输谱具有对称Lorentzian线形, 是许多光子学应用的核心. 若将窄带Lorentzian响应叠加在宽带背景场上, 出现一种反对称共振线形光谱, 形成的光谱称为Fano共振光谱. 近年来, 纳米光子学[4,5]及其他研究分支如超晶格[6]、超材料[7,8]、等离子[9]及光子晶体(空间光及片上)都报道了Fano共振现象[10]. 在纳米光子学中, 最初引入Fano共振的是等离子体结构, 但其热损耗限制了光学器件的性能, 而在全介质波导引入Fano器件中, 就没有此类问题. 基于绝缘衬底上硅(silicon-on-insulator, SOI)的平面波导回路具有[11]体积小、与III-V 族有源光器件和互补金属氧化物半导体电路易实现单片/混合集成、驱动功耗低等优势. 硅及其扩展材料体系提供了非常强大的光子平台, 可实现片上光耦合、光传输、光调制及光探测. 硅光Fano共振的实现是通过谐振腔间的相互耦合, 谐振腔的强光子限制能力使其成为关键的通用器件, 它的优势来源于成熟微电子技术和光电子技术在微纳范畴内的有机结合. 目前部分硅光子谐振器件已发展较为成熟, 具体包括: 用于光通信的法布里-珀罗滤波器[12]及基于阵列波导光栅波分复用器[13], 用于微波光子链路的微环谐振腔调制器[14], 以及实现多功能生化传感的阵列微环谐振腔[15,16].
目前基于硅光器件的Fano共振现象受到广泛关注, 就理论研究而言, Fano公式最初来源于电子能量跃迁后产生的量子干涉, 对于通信波长, 单光子能量不足以引起硅原子的外层电子发生能级跃迁, 不能用量子干涉理论理解硅光子产生Fano共振机理. Bekelee等[17] 在2019年对二维光子晶体产生Fano共振现象进行了综述, 而利用硅光子器件包括微环谐振腔、光子晶体纳米梁腔及马赫-曾德尔干涉仪等其他片上结构产生的Fano共振的进展并未有综合性的总结及探讨, 仅Miroshnichenko等[4] 于2010年总结了部分关于硅光实现Fano共振的方法. 就应用层面而言, 目前基于Fano共振的光开关、光调制、光传感及光隔离等全光信号处理器件逐渐成熟, 针对不同的应用, Fano共振器件从结构设计、参数优化及其他物理现象的结合的层面都不同.
本文主要从4个方面综述了硅光子平台产生Fano共振相关研究进展. 首先, 本文对硅光器件产生此现象的机理及分析方法进行梳理, 现有研究对于器件的关键参数提取略有不同, 我们列举了不同表达方式并进行了归纳; 其次, 归类硅光子器件中产生Fano现象的方法; 再次, 介绍Fano器件的全光信号处理及应用; 最后, 对硅光子器件Fano共振存在的难点和问题、国际学术界研究趋势及后续的发展方向展开探讨.
2.1.Fano共振的一般特征
当离散的量子态于连续态发生耦合时会产生Fano共振现象, 其吸收光谱由著名的Fano公式描述[3], 考虑到整个系统除了吸收外, 还有非共振散射能量的分量[18,19], Fano共振吸收光谱σ(ε)的标准化形式为我们来简单讨论一下Fano共振吸收光谱随各参数的变化情况. 如图1(a)所示, 参量q随δ以π为周期变化, 当δ = nπ (n为整数)时, |q|→∞, 吸收谱中离散信号强度占主导地位, 光谱表现为Lorentzian线形, 因此Lorentzian是Fano共振的特例; δ = (n +1/2)π, q = 0, 在共振频率处对称下陷, 表明离散状态和连续状态之间发生相消干涉, 而在文献[4, 20]中它被称为逆Lorentzian或反Lorentzian共振, Fano线形演变成电磁诱导透明(electromagnetically induced transparency, EIT), 它表示传输光谱的共振受到抑制, EIT也是Fano共振的特例; q =–1和q = 1的传输谱分别是由图1(c)和图1(e)表示, 从传输谱形状可以看出离散状态和连续状态之间同时存在相长和相消干涉, q = –1 (+1)时, Fano 共振的光强最大值与最小值连线的斜率(这里用S 表示)为正(负). 如图1(g)中所示, Γ描述Fano光谱的线宽, 线宽越窄, Fano线形越陡峭. 吸收谱随共振频率的变化如图1(h)所示, 光谱形状保持不变, 对于实现可调谐Fano共振光谱具有重要意义.
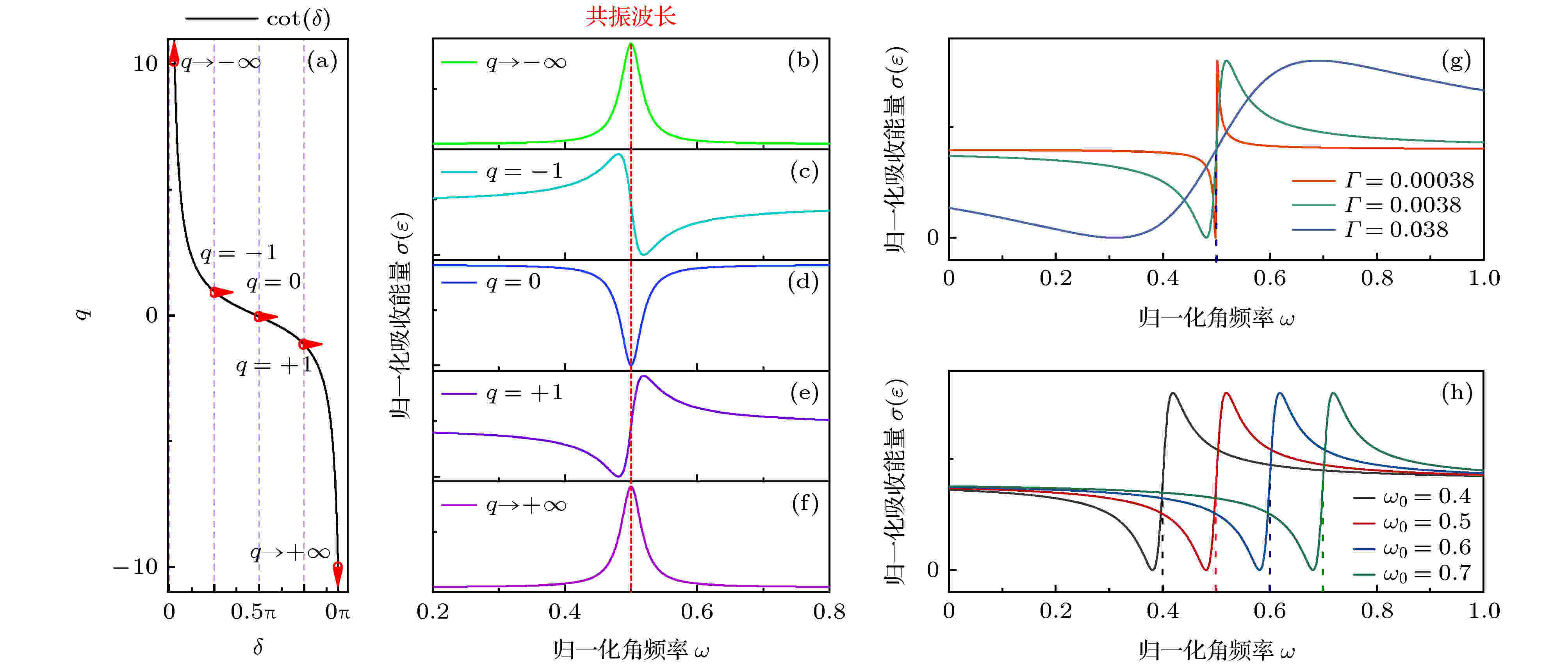图 1 (a) q与相移δ之间的关系曲线; (b)—(f) q → 
Figure1. (a) Relationship between q and the phase shift δ; (b)–(f) transmitted spectra corresponding to q →
2
2.2.硅光子平台中的Fano共振机理及理论描述方法
2002年Fan[21] 利用全介质硅基耦合腔首次在理论上实现了Fano共振光谱, 采用经典传输矩阵法进行传输谱分析, 由于传输矩阵法易于理解, 且每种硅光器件都有各自的传输矩阵, 因此此种分析方式至今沿用[22], 但是不适合直观地表示腔间耦合效应对Fano共振的影响; 有****采用直接类比法解释硅光谐振腔产生的Fano共振现象, 将量子干涉中的离散态与连续态各自的衰减因子类比为两个腔的光子寿命, 离散态与连续态的相互作用因子类比为两谐振腔的耦合系数, 得到谐振腔耦合的传输光谱的公式[23]. 到目前为止, 已报道的用于Fano共振的物理性质和主要特征的Fano-Anderson模型[4,24,25], 均采用类比法来描述Fano共振现象. 由于物理机制的不同, 采用类比法, 不利于理解硅光子产生Fano共振的机理; Limonov等[5]采用耦合模式微扰理论分析了硅光子Fano共振, 虽然Fano公式中q并未具体化且忽略了高Q腔的损耗, 但是通过建立理论模型, 能够使得器件的物理参数与Fano公式的参数建立解析关系.耦合模式微扰理论[26]法能够通过严格的电磁理论计算波导器件传输谱, 从而可以反映器件的耦合参数对传输谱的影响. 2003年Fan等[27]采用耦合模式理论结合时间反转对称性和耦合能量守恒推导出Fano共振光谱; 2010年Li等[28]研究表明由腔模式耦合引起的模式分裂可以形成不同的类型透射谱, 包括模式分裂、EIT和Fano共振等光谱; Du 等[29,30]证明波导耦合模式理论能够用来判断Fano共振与模式分裂产生的条件, 并建立了侧向耦合腔形成Fano共振传输光谱. 谐振腔间的耦合方式可归纳为如图2中所示的5种类型, 或者是这几种耦合形式的组合. 本文中所涉及的硅光器件耦合产生Fano共振的简化模型都可以采用上述模型来描述. 图2(a)—(c)对应两个谐振腔耦合后, 经低Q腔耦合回总线波导, 其中, 图2(a)为输入波导端面耦合低Q腔, 图2(b)为侧边耦合输入波导, 图2(c)为嵌入式波导结合侧边耦合输入波导. 图2(d)为经高Q腔端面耦合回总线波导, 图2(e)为两个谐振模式耦合后共同侧边耦合回总线波导.
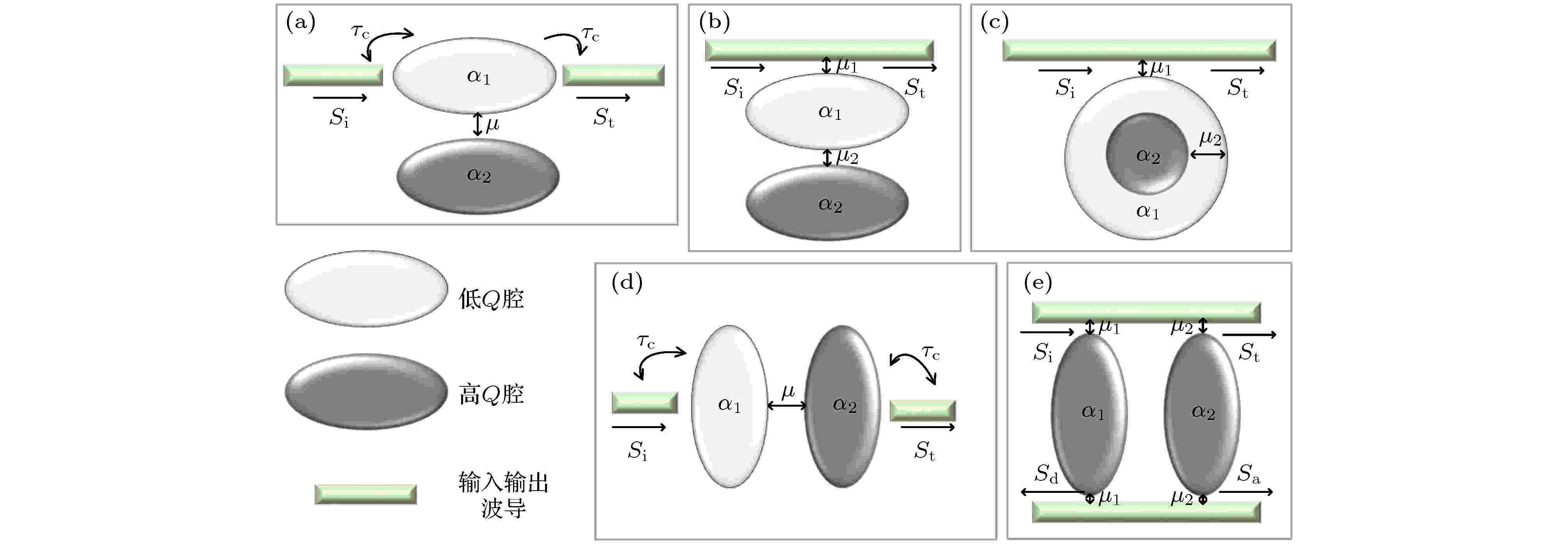图 2 硅基光子谐振腔不同耦合方式的简化模型 (a)—(c) 侧边直接耦合腔; (d) 端面耦合腔; (e)侧边间接耦合腔Figure2. A simplified model of different coupling modes of the silicon-based photonic resonator: (a)–(c) Directly side coupled cavities; (d) end-coupled cavities; (e) indirectly side coupled cavities.
图2(a)是侧边耦合的简化模型结构, 低Q腔与输入和输出波导相连, μ是高Q腔和低Q腔的耦合系数, 低Q腔波导因耦合引起的衰减为1/τc, τc为光子寿命. 低Q腔和高Q腔模式的振幅分别为α1和α2, 谐振频率为ω1 和ω2, 总损耗为1/τt1和1/τt2. 因此,
在Fano共振条件下, si和st表示输入和输出的波导模式振幅, si = Sieiωt, 耦合模方程可以表示为[26,29,30]
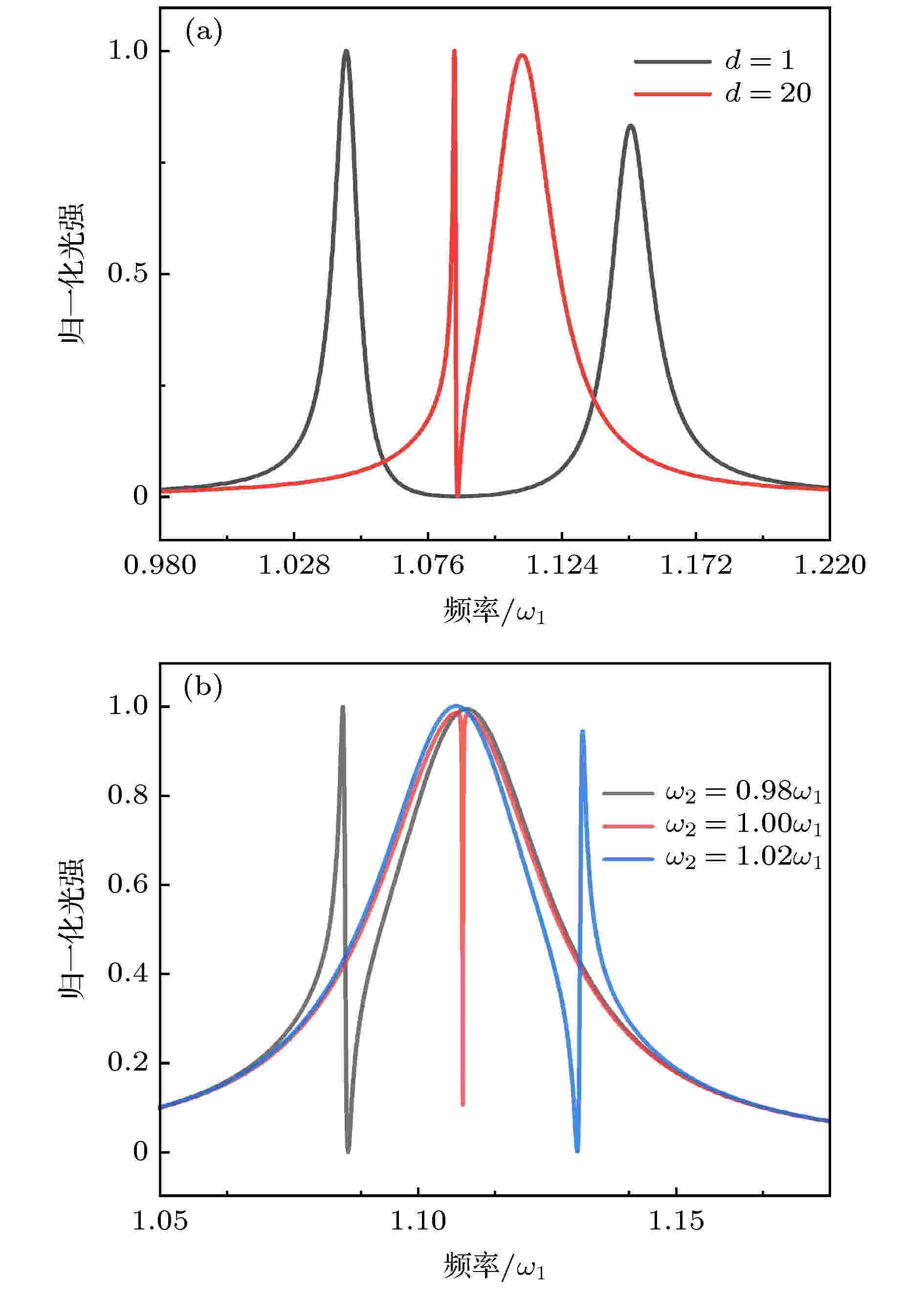图 3 (a) Fano共振形成条件; (b) ω2 – ω1的失谐量对Fano共振线形的影响Figure3. (a) Formation conditions for Fano resonance; (b) the effect of ω2 – ω1 on Fano resonance.
从图3及公式分析可以得出以下结论:
1) 两个谐振腔工作在弱耦合状态是形成Fano共振的前提. 如图3(a)所示, 耦合判定系数d < 4时, μ2 > Δ, 两个谐振腔处于强耦合状态, 输出光谱发生模式分裂. d远大于4时, Fano共振非常显著. 因为耦合系数减小, 其物理实现方法是增大谐振腔耦合间隙, 因此μ2不会无限制的减小.
2) 当ω1 > ω2, 即低Q值的谐振波长大于高Q值的谐振波长时, 斜率S为正, 反之为负. 因此, 在其他条件固定的情况下, Fano共振峰斜率的方向主要由两个腔的谐振频率差值决定. 因此Fano共振公式(1)中Fano谱形参数q共振线形部分取决于谐振腔谐振频率ω2 – ω1的失谐量, 与文献[5]中描述一致. 两个谐振腔的谐振频率相同时, 如图3(b)所示, 会形成EIT现象, 因此EIT是Fano共振特定条件下的一种现象. EIT可应用于光存储[35], 也可利用其慢光效应, 增强光的能量密度, 即增强光与被测物质的相互作用, 可提高微量物质能检测极限[36].
为了方便后续讨论及比较Fano共振现象的基本参数, 下面对Fano共振描述参数进行说明并纠正部分参数定义.
1)斜率: 也称光谱分辨率, 共振波长处的斜率定义为在Fano共振透射波谷和峰值之间光强相对于波长的变化率, 可表示为S = ΔI/Δλ.
2)消光比: 这部分与Lorentzian定义一样, 透射波谷和峰值之间的功率差值, 单位为dB.
3)共振波长: 对于共振波长很多文献定义不一样, 如文献[37]将Fano共振的谷底位置作为共振波长, 文献[20]将波谷对应波长与波峰对应波长的平均值作为共振波长. 如图1(c)和图1(e)所示, 共振波长位置可以描述为: 将波峰峰值功率降低一半的基准线定义为L1, 波峰与波谷构成的直线定义为L2, L1与L2的交叉点对应的波长即共振波长, 并非Fano线形的峰值或者谷值.
4)品质因子: Fano线形的峰值与谷值之间的波长间隔作为半高宽ωFWHM, 品质因子为共振波长除以半高宽, 即Q = ω0/ωFWHM.
3.1.光子晶体纳米梁
文献[10]和文献[17]全面地介绍了光子晶体Fano共振及面内光子晶体Fano共振. 与二维平板光子晶体和三维光子晶体不同, 线性周期性光波导中点缺陷称为光子晶体纳米梁腔(photonic crystal nanobeam cavity, PCNC), 其除了具备光子晶体的特性外, 且具有更小的加工尺寸, 因此本部分主要总结平面内一维PCNC结构产生Fano共振方法. 如图4所示, 利用PCNC结构对光子的限制作用, 使得光的离散模式与连续模式、准连续模式或者光子晶体带隙边缘模式发生侧向耦合, 可以获得不同性能参数的Fano共振光谱.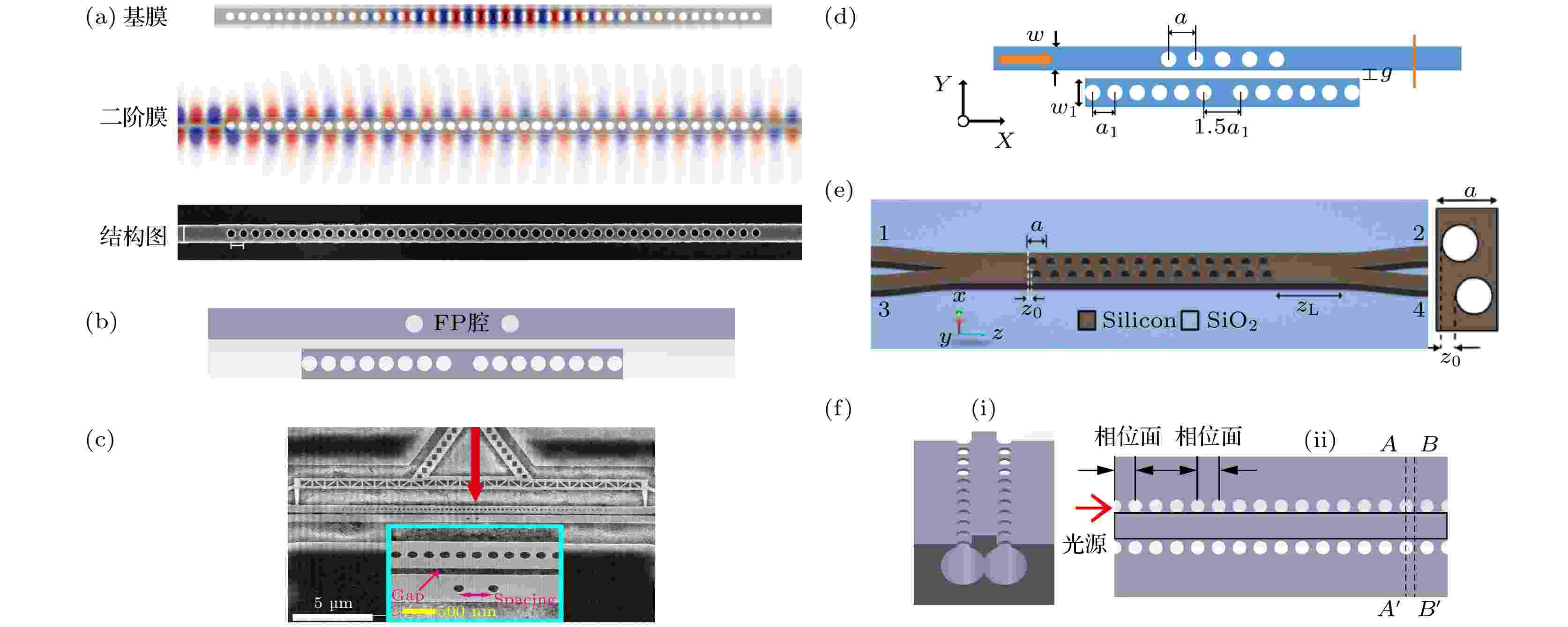
图 4 各种PCNC产生Fano共振的方法 (a)单PCNC[38]; (b) PCNC侧耦合F-P谐振器[39]; (c)纳米微机电结构动态控制Fano共振光谱[37]; (d) PCN的带隙边缘模式耦合PCNC[40]; (e)具有简并带隙边缘模式的双PCNC[43]; (f)双排PCN构建的布拉格反射结构的(i)整体结构图和(ii)俯视图[44]Figure4. Various PCNC structures for Fano resonance: (a) Single PCNC[38]; (b) PCNC side coupled F-P resonator[39]; (c) dynamic control of Fano resonance with a nanoelectromechanical structure[37]; (d) band edge mode of PCN couple with PCNC[40]; (e) double PCNCs with degenerate band edges mode[43]; (f) the overall structure (i) and top view (ii) Bragg reflection structure constructed with double-row PCN[44].
图4(a)是首次利用PCNC实现Fano共振的结构[38], 波导的基模能够被限制在中间部分空气孔内, 具有奇对称性的二阶准TE模式的40%的功率以泄漏模存在. 其中, 光引入/引出是通过衍射光栅进行实现, 当单模光纤位于光栅耦合器的中心时, 奇对称二阶模与光纤基模无重叠, 只有一阶波导模式被激发, 透射光谱为Lorentzian线形. 但是当输入和输出光纤都偏离中心时(微米量级), 光纤基模与二阶模式部分重叠, 此时二阶泄漏模与光子晶体腔基模进行耦合, 产生Fano共振.
上述方式通过调节光纤位置来获得Fano共振, 并不适合片上集成, 而图4(b)中的PCNC侧耦合F-P谐振腔的结构[39]有效地解决此问题, 在具有周期性空气孔的直波导引入缺陷构成了PCNC, 直波导中的两个孔用作部分反射单元, 形成F-P谐振腔. 由于纳米梁的两边各8个微孔反射镜, 使得PCNC的光子寿命较低, Q值仅为1720, 实验最终获得的Fano光谱的斜率仅为5.3 dB/nm, 消光比为7.5 dB.
由2.2节理论分析可知, 调节两个谐振腔的耦合系数可调控Fano共振光谱, 图4(c)所示结构为图4(b)结构的基础上增加了动态控制纳米微机电系统[37], PCNC两边各39个反射空气孔, 因此具有较高的Q值. 悬空波导F-P腔被固定, PCNC连接到双向梳齿驱动器, 当用电压驱动执行器时, PCNC以高位移分辨率双向平移, 实现两个腔之间的间隙调节(耦合系数), 从而控制Fano共振的形状, 此种方法需要波导结构悬空, 工艺复杂度高.
为了增大Fano器件的消光比及光谱斜率, Meng等[40]采用光子晶体纳米梁(photonic crystal nanobeam, PCN)的带隙边缘模式作为连续状态, 将PCNC模式作为离散状态, 结构如图4(d)所示, 通过改变光子晶体的光子带隙的位置, 利用高或低频带边缘模式, 进一步控制Fano传输曲线, 改变纳米梁腔的间距, 能够调整带隙边缘模式, 同时调整双腔的耦合系数, 可实现较高的性能Fano光谱. 此结构衍生出很多应用, 如高灵敏度的Fano共振折射率传感[41]及高对比度且低功耗Fano共振光开关[33,42].
图4(e)[43]结构同样利用光子晶体带隙边缘模式进行Fano共振光谱优化. 在硅波导上引入两排平行周期性的纳米孔, 两排孔沿横向(x轴)偏移距离为x0, 孔纵向(z轴)偏移z0 = 90 nm, 能够实现简并带隙边缘色散的设计. 常规能带边缘(z0 = 0)在相同频率下, 边缘共振腔模式与倏逝场模式电场的矢量不同, 偏移值z0 = 90 nm, 两种模式的能带边缘简并, 边缘共振腔模式与倏逝场模式的两个简并态耦合发生Fano共振.
上述PCN是基于SOI平台设计加工的, 而图4(f)中结构上是利用硅材料加工悬空结构形成双排周期性光子晶体结构[44], 实现布拉格反射, 而硅-空气界面的～55%的端面反射宽带光, 两反射光进行耦合, 通过改变两个反射的相对相位实现单结构反射式Fano共振, 光谱的消光比仅为3 dB, 器件的温度灵敏度为77 pm/℃.
PNCN产生Fano共振方案及其对应的性能指标如表1所列.
| 结构 | 尺寸/(μm × μm) | 消光比/dB | 斜率/(dB·nm–1) | 应用 | 文献 |
| PCNC结合光纤 | ～13.2 × 0.47 | 17 | [38] | ||
| F-P 侧边耦合 PCNC | ～6 × 0.45 | 7.3 | 5.3 | [39] | |
| F-P 侧边耦合 PCNC | ～18 × 0.72 | 14—18 | [37] | ||
| F-P 侧边耦合 PCNC | ～10.5 × 1.5 | 22 | [40] | ||
| F-P 侧边耦合狭缝 PCNC | ～10.5 × 1.5 | 24 | 折射率灵敏度778 nm/RIU | [41] | |
| 双 PCNs | ～5.18 × 0.74 | 20 | [43] | ||
| 交叉耦合四端口PCNC | ～4 | 16 | 光开关 | [45] |
表1不同PCNC产生Fano共振的参数表
Table1.Parameters for Fano resonance based on different PCNCs.
2
3.2.微环谐振腔
微环谐振腔(micro ring resonator, MRR)作为硅光器件中最基本的结构, 具有较高的光子寿命且结构紧凑. 这种结构共振模式通常作为离散模式, 通过与其他连续/准连续模式的硅光结构耦合, 可以实现种多种类的Fano共振. 从Fano共振实现方式来看, 主要可以分为两类, 一类是MRR的模式作为离散态, 总线波导直接引入连续态/准连续态模式. 此类结构不牺牲MRR的尺寸, 基本简化模型都可以用图2(a)表示; 另外一类是由多个微环相互耦合构成的, 此类结构易于其他材料体系结合, 形成性能较高的器件.3
3.2.1.紧凑型微环谐振腔产生Fano共振的方法
为了不牺牲MRR的紧凑性, 通常在总线波导中直接引入部分反射单元(如F-P腔). 首次实现的紧凑型微环Fano共振的结构如图5(a)所示, 总线波导中间部分与总线波导错位[46]连接(形成F-P腔), 形成的部分反射单元引入后向传播的光场, 这些光场干扰前向传输波的相位, 形成Fano共振.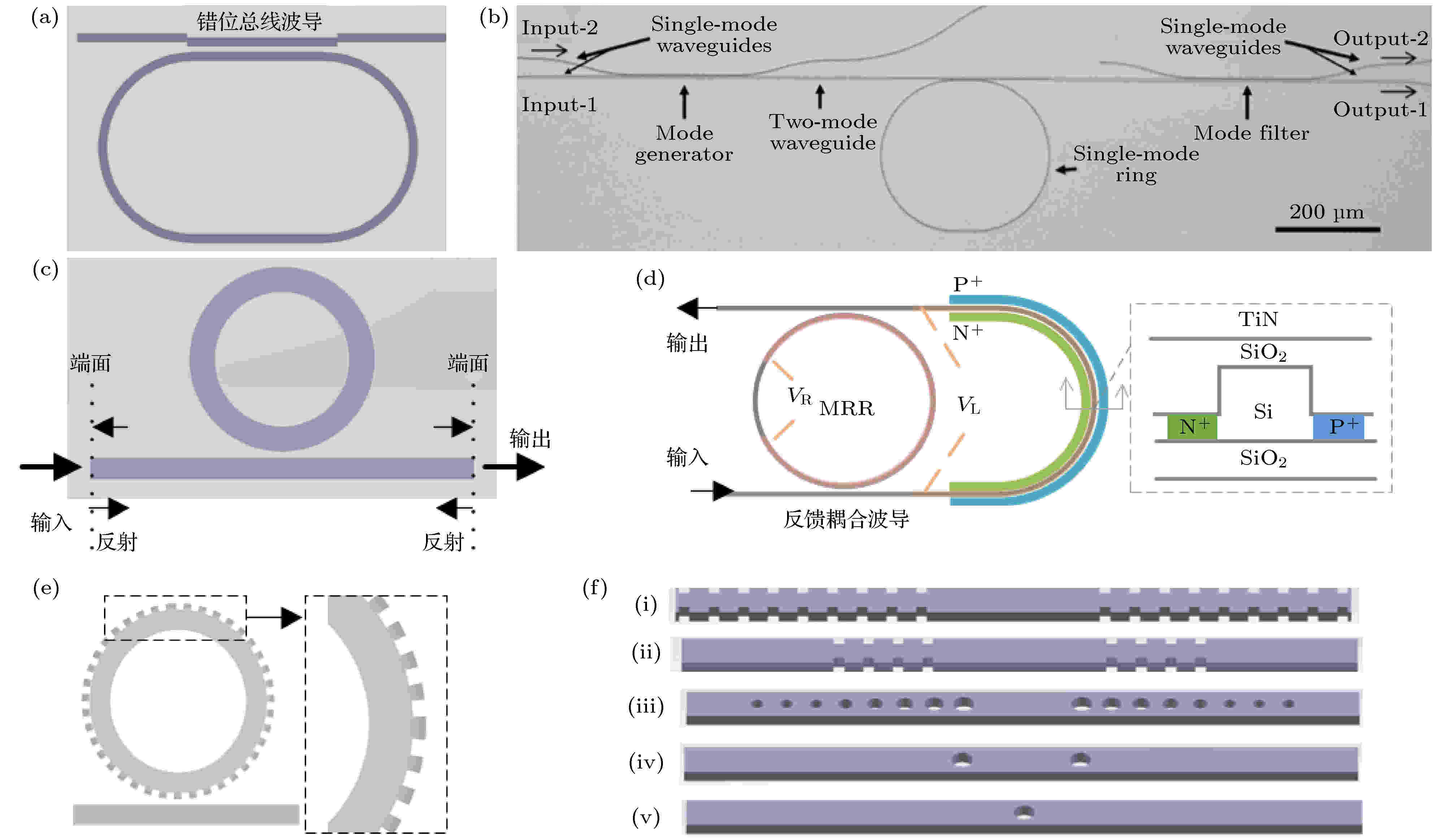
图 5 紧凑型MRR产生Fano共振的方法 (a)错位总线波导耦合MRR[46]; (b)双模式总线波导耦合MRR[47]; (c)直波导端面反射耦合MRR[48]; (d) 反馈直波导耦合MRR[50]; (e)直波导耦合带有相移布拉格光栅的MRR[51]; (f)总线波导结合光栅/空气孔/狭缝耦合MRR[20,34,54-56]Figure5. Various MRRs with compact footprint for Fano resonance: (a) Straight waveguide with misalignment[46]; (b) dual-mode bus waveguide[47]; (c) straight waveguide with end face reflection[48]; (d) straight waveguide with feedback[50]; (e) MRR with phase-shifted Bragg grating[51]; (f) bus waveguide combined Bragg grating/air holes/slits[20,34,54-56].
图5(b)为双模式Fano共振的结构图, 其由两个波导输入端、模式发生器、多模总线波导、单模环、模式滤波器及双输出端组成. 总线波导[47]同时激发基模TE0,0与二阶模式TE1,0, 单模MRR耦合双模总线波导, 输出的Fano光谱线形取决于两个输入模式的耦合系数、相对功率分布和相对相位差. “输入1”端口激发TE0,0模式, “输入2”端口激发TE1,0模式, 波导中双模模式的功率和相对相位由“输入1”和“输入2”独立控制. 模式滤波器在结构上类似模式发生器, 用于将两种不同模式进行分离, 最终两端口输出的Fano共振光谱斜率相反.
如图5(c)所示, 总线波导的端面反射形成F-P谐振腔[48], 跑道型MRR谐振器的离散模式与F-P谐振模式耦合产生Fano共振. 当F-P和MRR的共振具有π相位差时, 光谱斜率变得陡峭, 消光比达到30 dB, 折射率检测极限为～10–8 RIU (refractive index unit). 图5(d)给出了复合MRR产生Fano共振[49], add-drop环形谐振腔中drop端口和输入端口环路连接. 光的传播路径有两条: 一条是双耦合的环形谐振器, 另一条包含反馈回路, Fano共振线形可以通过调整反馈回路的长度来调整. Zhao等[50]对这种Fano共振的调谐特性及其反馈耦合波导的参数进行了详细研究, 在反馈波导加上电光调制及在MRR加上热调制, 获得了消光比为30.8 dB、光谱分辨率为226.5 dB/nm的Fano共振光谱. 由于MRR的drop与through端口的共振峰的位置一致, 因此每个共振峰处具有一致性较好的Fano线形.
图5(e)的结构是通过在MRR外圈引入布拉格光栅的方式实现Fano共振[51]. 布拉格光栅引入部分缺陷, 光栅缺陷的长度稍微偏离布拉格周期形成π相移, 得到具有相移光栅的MRR, 具有准连续状态的相移光栅与具有离散状态的MRR相互耦合形成Fano共振.
下面介绍在总线波导中引入部分反射结构(PCNC、相移光栅及F-P谐振腔)形成Fano共振的方法. 如图5(f)中(i)结构所示, MRR与由两个布拉格光栅形成的F-P谐振器耦合[52], 获得了消光比为22.54 dB、斜率为250.4 dB/nm 的Fano共振光谱. 利用其在共振波长处强双光子吸收引起的非线性热光效应, 可实现Fano共振波长的调谐[31]. 由于这种 Fano共振的频谱响应具有陡峭的边缘, 可用于将微波信号的频率信息转换为光功率变化信息, 使得器件在15 GHz的频率测量范围内, 分辨率优于 ±0.5 GHz. 调节MRR与由两个布拉格光栅形成的F-P谐振器之间的耦合强度[53], 结构如图5(f)中(ii), MRR谐振器中的模式突变π相移, 两个谐振器之间从相长干涉转换为相消干涉形成EIT. 在MRR谐振器从过耦合到欠耦合状态转变过程中, EIT传输谱到Fano共振传输谱演变具有连续性, 光谱的消光比可达43 dB.
总线波导引入空气孔/狭缝(三类结构)可提高Fano共振折射率灵敏度, 因此多用于生化检测. 亚波长周期的梯形硅MRR与矩形亚波长光栅总线波导进行耦合[54], MRR的光栅具有部分反射效果与MRR自身的离散模式相互作用, 在共振波长处形成尖锐的不对称Fano共振; 狭缝MRR与狭缝相移布拉格光栅总线波导进行耦合[55]; PCNC与MRR进行耦合(图5(f)中(iii))[56], 或者总线波导中两个气孔形成的F-P与MRR进行耦合(图5(f)中(iv))[34]. 带宽较窄的离散状态和带宽较宽的非离散状态, 两个腔室的共振波长不是每个都重合, 所以产生Fano共振的同时, 在相近的共振波长可能出现EIT或者Lorentzian光谱. 除了上述方案, 最简单的方法是在总线波导引入1个空气孔[20], 结构如图5(f)中(v), 单个空气孔的引入使连续传播模式的直波导与离散传播模式的MRR之间产生相移, 形成Fano共振, 且所有共振波长处都为Fano线形.
紧凑型MRR产生Fano共振方案及其对应的性能指标如表2所列.
| 结构 | 尺寸/(μm×μm) | 消光比/dB | 斜率 | 性能 | 文献 |
| 总线错位波导耦合MRR | ～20×30 | 30 | 葡萄糖灵敏度24 mg/dl | [46] | |
| 多模总线波导耦合MRR | ～1020×230 | 6 | 27.1/nm | [47] | |
| 端面反射总线波导耦合MRR | ～22×10000 | 30 | 折射率探测极限～10–8 RIU | [48] | |
| MRR耦合反馈总线波导 | ～20×350 | 30.8 | 226.5 dB/nm | [49,50] | |
| MRR耦合相移光栅 | ～60×60 | 20 | [51] | ||
| MRR耦合由两个布拉格 光栅形成的F-P腔 | ～17×140 | 22.54 | 250.4 dB/nm | [52] | |
| MRR耦合由光子晶体形成的F-P腔 | ～6×10 | 23 | 折射率灵敏度～1.76 × 10–4 | [56] | |
| 亚波长光栅耦合MRR | ～6×10 | 12 | 折射率灵敏度366 nm/RIU | [54] | |
| 狭缝F-P耦合狭缝MRR | ～4×10 | 20 | 折射率灵敏度297.13 nm/RIU | [55] | |
| PCNC侧耦合结合Kerr 非线性材料的PCN | ～16 | 关开关功耗0.76 pJ, 切换时间0.707 ps | [42] |
表2不同紧凑型MRR产生Fano共振的参数表
Table2.Parameters for Fano resonance based on different compact MRRs.
3
3.2.2.多微环谐振腔产生Fano共振的方法
多微环谐振腔产生Fano共振的理论分析方法主要有三种. 第一种采用耦合模式理论分析间接耦合腔(图6(a))[57], MRR之间通过总线波导间接耦合, 调整耦合强度和传播相位差, 能够获得Fano共振光谱; 第二种是将图2(a)总线波导上的F-P侧边耦合谐振腔等效为两个F-P腔[36](图6(b)), 形成单个Fano共振单元, 这种分析方式适合研究多单元级联结构, 如用于分析两个Fano单元级联形成频率可调的EIT; 第三种采用耦合模传输矩阵法分析以MRR为单元的级联谐振腔, 能够得出系统的色散及模式之间的相互作用对Fano共振的影响, 此方法可单独分析每个通道的Fano共振, 对多通道Fano滤波、传感及波分复用具有重要的指导意义[58].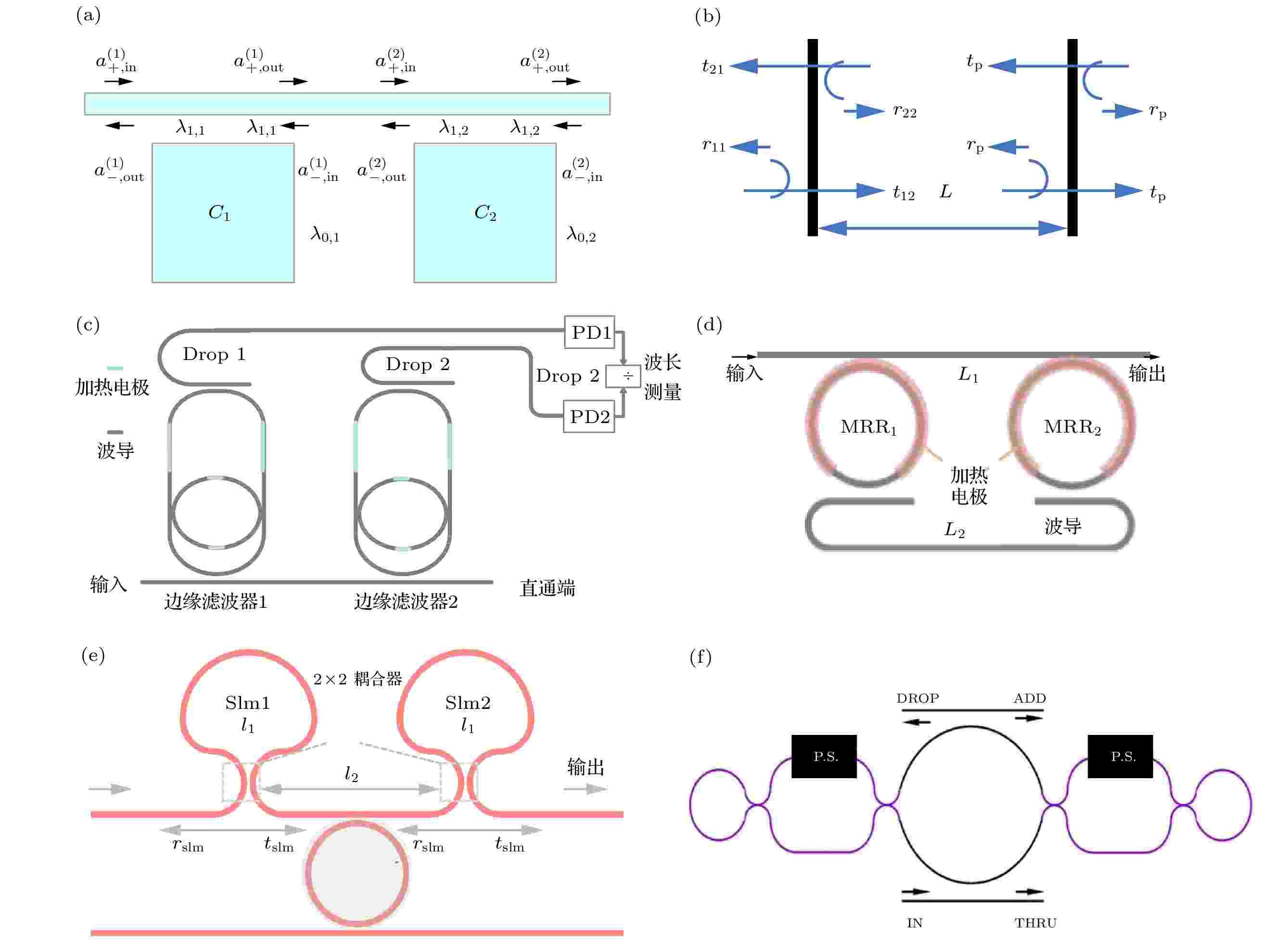
图 6 各种复合MRR产生Fano共振的方法 (a)耦合模式理论分析双MRR结构[57]; (b)等效F-P单元分析多环耦合结构[36]; (c)双环嵌套结构[59-64]; (d)双环反馈耦合结构[67,68]; (e) Sagnac形成F-P腔耦合MRR[75]; (f)等效双马赫-曾德尔干涉仪[35,76-78]Figure6. Various complex MRRs for Fano resonance: (a) Analysis of double MRR using coupling mode theory[57]; (b) analysis of multi-ring coupling with equivalent F-P unit[36]; (c) double-MRRs nested structure[59-64]; (d) double-MRRs with feedback configuration[67,68]; (e) Sagnac formed F-P cavity couples MRR[75]; (f) equivalent double Mach-Zehnder interferometer[35,76-78].
按照MRR的耦合方式来区分, 多MRR耦合产生Fano共振的结构主要分为两类: 一类是MRR嵌套结构, 另外一类是MRR串并联结构.
首先介绍MRR嵌套结构实现Fano共振的方案. 浙江大学Qiu等[59]设计跑道型MRR内部嵌入MRR, 结构见图6(c)(边缘滤波器1), 当两个MRR的相位比例接近整数时, 消光比比单跑道型MRR高3倍, 对应的增量为20 dB. 将中间MRR移到离输入总线波导较近的位置, 同时对MRR及跑道进行热光调制, 可获得斜率可调且消光比为40 dB的Fano共振光谱[60]. 两个嵌入式MRR形成的双边缘滤波器[61]在特定波长范围内能够实现“X型”光谱响应, 其在0.47 nm宽波长范围内具有0.8 pm的超高分辨率. 采用同样的结构, 天津大学团队采用氮化硅材料实现Fano共振, 通过调节两个MRR的相位差, 获得了EIT光谱, 并将此结构应用到液体及气体传感中[62-64]. 目前也有一些特殊嵌套结构在理论上可以实现Fano共振, 如双跑道结构嵌套、三维结构中上下微环耦合中间总线波导[65]或MRR嵌套U型结构[66].
下面介绍MRR串并联结构实现Fano共振方案. 兰州大学Xiao 等[67]设计图6(d)所示结构, 两个微环通过反馈的方式进行耦合, 得到Fano共振光谱. 为了提高折射率灵敏度, 东南大学Wen等[68]将该结构用亚波长光栅代替, 获得了500 nm/RIU的折射率灵敏度. 兰州大学Zhao 等[69]在图5(d)的结构基础上加上1个环, 使得器件的Fano共振光谱具有周期性且独立可调, 获得的光谱最高消光比为29.20 dB. 土耳其科奇大学Chaudhry 等[70]采用5个相同的定向耦合器组成5个MRR, 通过改变定向耦合器的耦合长度, 获得的Fano线形消光比大于26 dB, 光谱分辨率为368 dB/nm. 此种结构在每个共振点都形成了Fano共振.
MRR串并联结构中的1个MRR可由相变材料或者增益介质组成. 如图6(a)所示, 两个MRR侧耦合到总线波导, 其中1个MRR由相变材料VO2组成[71], 当VO2自感应加热到一定阈值时, 会发生从绝缘相到金属相的相变, 此时对光的吸收较强, 使得MRR的Q因子降低. 对于低入射光能量来说, 结构可双向产生Fano共振, 较高的光功率输入时, Fano共振是单向的, Fano共振传输谱的消光比高达45 dB. 宇称-时间对称(parity-time, PT)结构被认为是继光子晶体和电磁特异性材料之后又一种新型的人工合成结构[72], 改变增益损耗比时, PT结构能够发生相位突变. 将图6(a)的结构中谐振腔1侧边加入1个增益腔, 组成了PT对称的三腔阵列, 其折射率灵敏度比两个间接耦合腔高105倍以上[73]. 在PT辅助三腔阵列的基础上, 图6(a)无谐振腔2的结构[74]在理论上可实现非对称双 Fano共振光谱.
MRR和两个级联的Sagnac环形成的F-P组成的耦合系统如图6(e)所示[75], 两谐振腔过耦合时会形成EIT的传输谱, 欠耦合是会形成Fano共振传输谱. 利用热光效应动态地调整MRR的谐振波长, 能够获得最大消光比为23.22 dB, 最大斜率为252 dB/nm的可调谐Fano共振光谱. 将MRR用两个Sagnac环代替, 实验获得了Fano共振光谱最大斜率为770 dB/nm[30].
高消光比的MRR环谐振器在其顺时针和逆时针模式之间存在寄生耦合, 并且从输入到两种循环模式之间也存在寄生耦合, 可能造成响应失真. Ghent 大学Li 等[76-78]设计如图6(f)所示的结构, 1个单环谐振器内部集成两个可调反射器, 每个可调反射器本身是1个子光路(马赫-曾德尔干涉仪), 实现了最大斜率超过700 dB/nm的可调Fano共振、可调EIT在共振波长处延时超过1100 ps、光谱的自由光谱范围超过150 nm、调谐效率是传统MRR谐振器的11倍以上, 从根本上抑制了反向散射. 此结构还能实现在非线性共振情况下的光路的非互易性, 相对的传播方向具有超过30 dB的消光比, 插入损耗仅为1.5 dB[35].
多MRR产生Fano共振方法方案及其对应的性能指标如表3所列.
| 结构 | 尺寸/(μm×μm) | 消光比/dB | 斜率 | 性能 | 文献 |
| MRR嵌入跑道微环 | ～5×40 | 20 | [59] | ||
| 热调MRR嵌入跑道微环 | ～5 × 40 | 40 | 35—93 dB/nm | [60] | |
| 亚波长光栅式MRR嵌入跑道微环 | ～20×100 | 21.53 | 折射率灵敏度500 nm/RIU | [68] | |
| Sagnac形成的双F-P耦合 | ～100×300 | 20 | 770 dB/pm | [30] | |
| Sagnac形成的F-P耦合MRR | ～25×30 | 23.22 | 252 dB/nm | [75] |
表3多MRR产生Fano共振的参数表
Table3.Parameters for Fano resonance based on multiple MRRs.
2
3.3.马赫-曾德尔干涉仪
本部分解析MRR与各种等效马赫-曾德尔干涉仪(Mach-Zehnder interferometer, MZI)耦合产生Fano共振的方法, 结构可以简化成图7(a)所示模型. 模型中两个臂通过多模耦合器/方向耦合器进行耦合, MZI是由两个耦合器加上中间两个臂构成, 高Q值MRR耦合的上臂作为离散模式, 低Q值MRR耦合的下臂(单直波导臂)作为准连续(连续)模式, 两种模式通过合束器相互作用.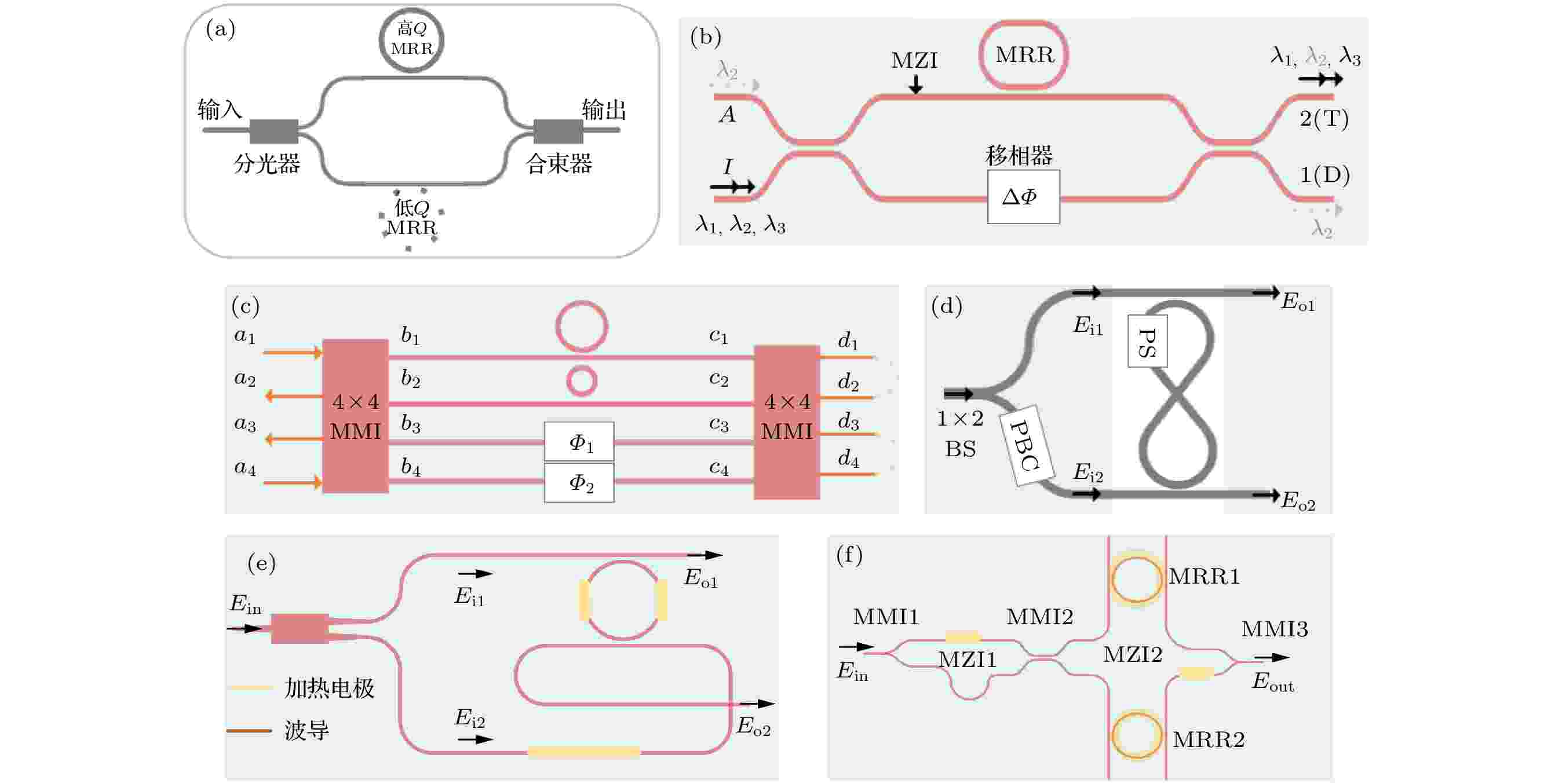
图 7 MRR与各种变异结构MZI耦合产生Fano共振的方法 (a) MZI耦合MRR模型[79]; (b) MZI侧边耦合MRR[83]; (c) 双4 × 4多模耦合器组成双MZI[85]; (d) MZI双臂耦合交叉环[86]; (e) MZI双臂耦合MRR及交叉波导[87]; (f)双MZI耦合双MRR[22]Figure7. MRR coupled with variant MZI for Fano resonance: (a) Model for MZI coupled MRR[79]; (b) MZI side coupled MRR[83]; (c) dual 4 × 4 multimode couplers form dual MZI[85]; (d) dual-arm of MZI coupled cross-loop waveguide[86]; (e) dual-arm of MZI coupled MRR and cross waveguide[87]; (f) dual MZI coupled dual MRR[22].
首先介绍MRR耦合MZI结构产生Fano共振的方法. 理论上图7(a)所示结构可以明显提高调制器的线性度[79] , Chen等[80]在实验上证明此结构可以有效地应用在硅基MZI调制器中, 另外, 该结构也可以在中红外波段3.8 μm范围实现Fano共振[81], 斜率比单个MRR共振的斜率高35.5%. Zheng等[82]采用多模波导组成MZI, 同时在输入端激发出多模, 可在输出端口同时获得基模及高阶模式Fano共振. 此状态的MRR与波导臂过耦合, 能够弱化MRR的作用, 仅用来实现可调波长的离散状态. 如图7(b)所示, Zhou和Poon[83]将分光器与合束器替换成2 × 2端口的分光器件, 调整下臂的有效折射率, 同时改变共振离散模式和背景连续模式之间的相对相位, 能够在实验上获得一对互补的Fano共振光谱, 但工艺误差引入的损耗较大, 最终获得的光谱消光较低. Lu等[84]在上臂侧耦合高Q值MRR (欠耦合), 同时在下臂中间嵌入1个低Q值MRR (过耦合), 当两个MRR的共振波长相同时, 理论上会在输出谱中同时发生EIT和电磁诱导透明吸收. 若MRR是具有Kerr效应的非线性材料, 在EIT共振波长处, 输出光谱会出现光双稳现象. 如图7(c)所示, Le和Cahill[85]采用两个4 × 4多模耦合器组成的双MZI, 两条通道分别耦合MRR, 另外两条通道控制相位差, 该结构可以产生两个独立的Fano线形, 若将输出端口反馈闭合, 可形成两路独立的EIT光谱.
接下来解析MRR耦合等效MZI结构的方法. 如图7(d)所示, 双总线耦合交叉MRR形成的等效MZI能够在光谱中产生Fano线形[86]. 器件作为光开关能够减少光开关切换所需的相变, 若设置合适相位偏置, 能够在两种开关状态下实现完全消光. 如图7(e)所示, 用单个MRR结合“十”交叉波导作为MZI的上下臂耦合点, 设置合适的相位条件, 能够获得较大的Fano共振斜率, 解决了不同Fano共振波长色散带来的消光比小的问题[87]. 双MRR作为MZI的上下臂耦合点, 可实现“X”型Fano共振光谱, 两个互补的输出和在–3 dB的传输点有两个固定的波长(自对准效应), 获得光谱斜率为127.4 dB/nm, 波长分辨率为1 pm[88]. 上述结构是将MZI的合束器进行等效, 也有研究者将MZI的分光器用复合结构代替. 如图7(e)所示, 将MRR的两个总线波导直通端口和drop端口组合起来形成MZI, 实现了消光比为30.2 dB, 斜率为41 dB/nm的Fano共振光谱. 采用热光调制, 能够将Fano参数q从–0.98调整为0.95, 且最大波长偏移为15.97 nm[89].
目前基于硅光平台实现的最优光谱参数的结构如图7(f)所示[22], 两个具有不同耦合间隙的MRR插入到MZI的上下臂, 小耦合间隙的MRR提供1个低Q值准连续背景模式, 大耦合间隙的MRR提供1个高Q值的离散模式, 两个可调谐的MZI用来调节两个模式的传输光的振幅和相位差. Fano共振光谱的消光比、斜率及共振波长能够独立调整, 实验上获得了消光比为 56.8 dB且最高斜率为 3388.1 dB/nm的光谱参数.
基于MZI单元产生Fano共振方案及其对应的性能指标如表4所列.
| 结构 | 尺寸/(μm×μm) | 消光比/dB | 斜率/(dB·nm–1) | 应用 | 文献 |
| 多模MZI耦合MRR | ～65×85 | 33 | 113 | 模式开关 | [82] |
| 双总线耦合交叉MRR形成的等效MZI | 光开关 | [86] | |||
| MRR结合“十”交叉波导作为MZI的干涉臂 | ～100×370 | 20 | [87] | ||
| MRR的两总线波导反馈形成MZI | ～390×850 | 30.2 | 41 | [88] | |
| 双MRR辅助双MZI | 56.8 | 3388.1 | [22] |
表4不同基于MZI 单元产生Fano共振的参数表
Table4.Parameters for Fano resonance based on MZI unit.
2
3.4.其他特殊硅光器件
除了常见的硅光子基本器件用来实现Fano共振外, 一些特殊的波导结构也能实现Fano共振, 主要包括自耦合波导和狭缝波导.自耦合波导结构如图8(a)所示, 输入和输出端口有两个定向耦合器, 理论上光在两个耦合器之间同时能够反向和正向谐振, 这两种谐振模式通过中央“桥”波导自耦合形成Fano共振光谱[90]. 若并联两个图8(a)中的结构, 在两个外部定向耦合器处于弱耦合状态而两个内部定向耦合器处于强耦合状态的特殊条件下, 结构内部形成了驻波共振模式, 获得的传输谱类似EIT共振模式[91].
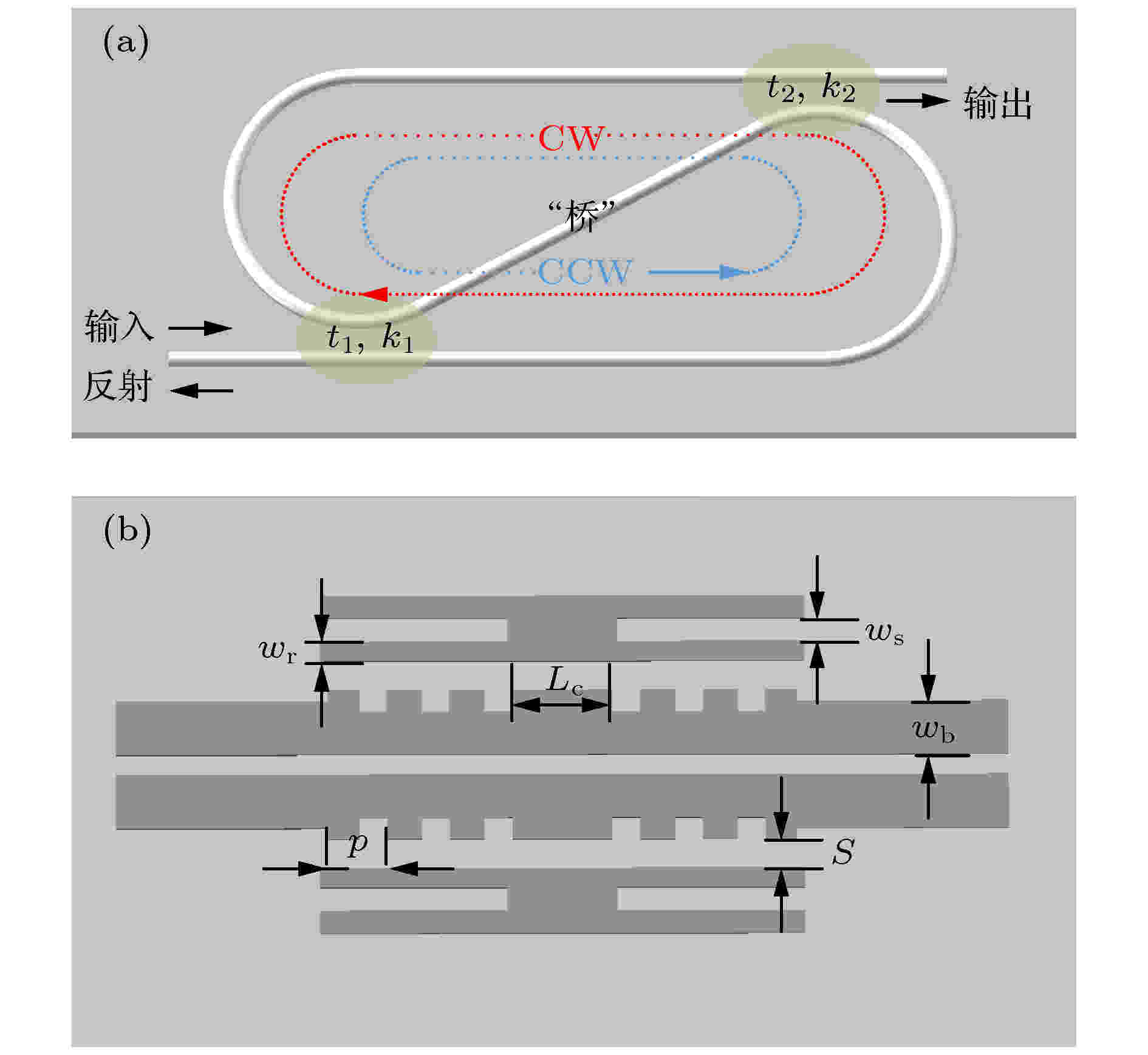图 8 (a)自耦合波导[90]; (b)狭缝波导耦合光栅式F-P[92]Figure8. (a) Self-coupling waveguide[90]; (b) slot waveguide coupling F-P composed by Bragg grating[92].
狭缝波导形成Fano共振结构如图8(b)所示[92], 其由3个平行的缝隙波导组成. 狭缝波导对低折射率介质(空气)具有光场限制能力, 光栅的相移量可以对Fano共振形状进行微调, 这种结构的器件灵敏度相对较低(92 nm/RIU), 总尺寸较小(61 μm × 1.3 μm).
2
3.5.比较各种产生Fano共振方法
通过前面对各种硅光子器件产生Fano共振方法的介绍, 我们了解了每种方法的具体实现过程, 在实际应用选择时, 每种方案存在优劣之分.PCNC是由线性周期性介电波导中产生的点缺陷组成, 能够提供高品质因数(Q > 105)和更小的模式体积(～(λ/n)3), 光与物质能够更有效地相互作用, 光能量密度也被提高, 从而实现能耗低的器件, 如低功耗光开关及调制器. 波导结构本身引入空气孔, 因此适合辅助其他类型的器件. 具有更加紧凑的尺寸(～μm3)适用于波导集成, 其中利用光子晶体带隙边缘作为准连续光的方式可以实现自由光谱范围较宽的Fano共振, 可以提高复用能力. 光子晶体结构是由空气孔阵列组成, 若将模式限制在空气孔内, 则传输模式易受外界液体的影响, 液体与光模式的重合面积较大, 能够实现高灵敏度生化传感. 但是由于其特征尺寸纳米孔阵列小于百纳米, 一般都采用电子束曝光工艺, 与其他类型的硅光器件相比, PCNC对加工工艺要求较高.
MRR作为硅光器件中最基本的结构, 具有较高的光子寿命及紧凑的尺寸, 共振模式通常作为离散模式, 与其他连续/准连续模式的光子结构耦合, 实现了硅光子中种类最多的Fano共振. MRR由总线波导与微环两部分组成, 因此特别适合在结构上引入相位差或者引入具有准连续模式的单元, 且易在总线波导中引入其他空气孔或者光栅结构, 尤其适合做生化传感, 但是不适合应用于对插入损耗要求较高的场合. MRR结构本身适合作为波分复用或者滤波器件, 以MRR为基础平台的Fano器件也具有相应的性质. MRR非常适合与其他物理效应/材料体系结合, 如非线性材料或增益介质, 可实现光双稳或者光非互易性传输.
由于MZI可调性较高, 通常在波导臂上耦合MRR结构, 能够实现性能较高的可调Fano光谱, 目前光谱参数最优的结构是MRR与MZI结合实现的[22]. 图6(f)由MRR组成的Fano光谱综合性能较优, 其结构本质上可以等效成两个MZI的级联耦合MRR. MZI能够作为基本单元, 可应用在消光比、共振波长、斜率及相位偏置可调的应用需求中, 又或者提高调制线性度的情况下.
我们归纳了各种硅光器件产生Fano共振方法的参数及使用场合, 如表5所列.
| 方法 | 尺寸 | 消光比 | 斜率 | 工艺要求 | 应用 |
| PCNC | 小 | 适中 | 小 | 高 | 光开关/传感 |
| MRR | 中 | 适中 | 大 | 一般 | 传感/滤波器 |
| MZI | 大 | 大 | 大 | 一般 | 调制器/隔离器 |
表5各种硅光器件产生Fano共振的方法对比
Table5.Comparation of diffrent silicon waveguide unit for Fano resonance.
2
4.1.Fano光开关器件
作为片上全光信号处理必不可少的组成部分, 全光开关一直备受关注, 近年来, 在实现高性能全光开关方面已经取得了广泛而显著的进步. 下面介绍Fano共振光谱应用于光开关的优势, 图9为Lorentzian线形(黑线)和Fano共振(红色)线形, 光强为“1”代表开关的开状态, 光强为“0.01”代表开关的关状态. 两者共振波长相同, 3 dB带宽相等, 因此Q因子相同. 此处的主要区别是Lorentzian共振需要具有比Fano共振更大的频谱偏移, 以实现同等的信号抑制水平, 即ΔλL > ΔλF. 这意味着Fano共振通过减少相同波长变化量所需的能量而具有显著优势, 适用于节能集成光开关.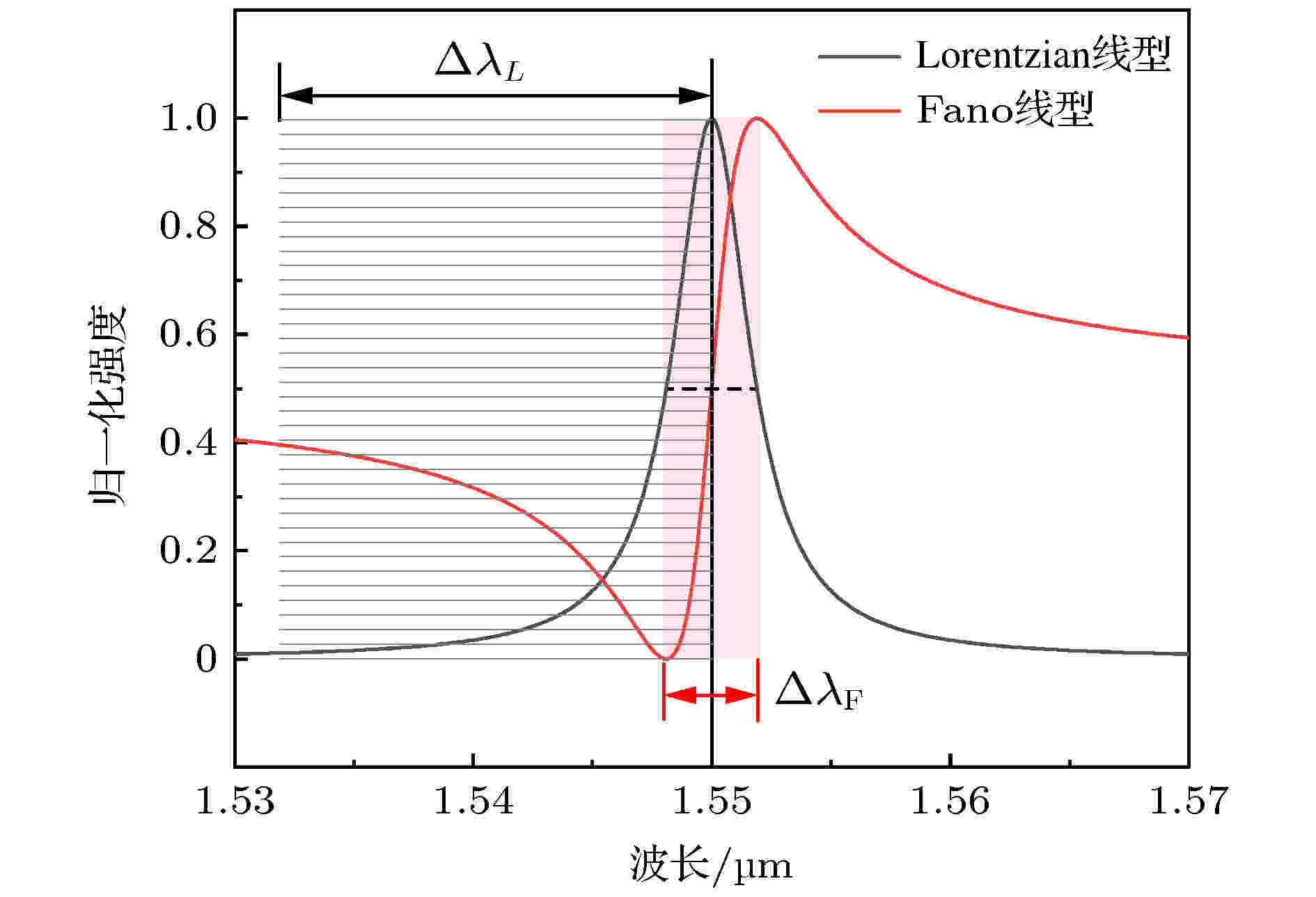
图 9 Fano共振与Lorentzian线形的开关性能Figure9. Switching performance of Fano resonance and Lorentzian lineshapes.
2009年的一项研究表明[86], 交叉微环作为MZI合束器的器件可显著减少开关切换所需的相变, 通过调节MZI的波导臂之间的相位差, 开关一端口处于“开”状态下, 另外一个端口能够在大范围波长内保持完全消光. 适当地调整环形波导中的相位变化, 可以控制谐振频率的偏移和透射光谱的不对称性, 从而最终在“开”状态下以高消光比甚至完全消光的方式实现光开关. 尽管Fano共振已成功应用于实现全光切换, 但切换时间仍在数百皮秒的范围内[93], 2018年的一项研究表明与典型的Lorentzian共振相比[33], 利用结构如图4(b)所示的PCNC侧耦合F-P得到的Fano共振光谱可以实现更大的消光比、更短的开关恢复时间和更低的功耗, 仅需亚皮焦耳的能量就能够获得亚皮秒量级的开关关断特性.
最新一项研究表明, Fano共振能够在亚皮秒级的切换时间内实现超快的全光切换, 结构见图10(a), 多项研究证明该结构可产生性能优越的Fano共振光谱[40,41]. SOI基的PCNC侧耦合PCN可实现双Fano共振[42] (图10(b)), 通过将具有Kerr非线性的有机共轭聚合物材料(聚苯乙烯)填充进光子晶体空气孔中, 构建硅聚合物复合非线性光子晶体. Fano共振光谱的陡峭斜率可以在中等抽运功率下实现高对比度切换, 并可抑制Lorentzian光谱拖尾效应. 与垂直抽运方案相比, 面内抽运方案(光开关的信号光与抽运光同时注入)具有更低的峰值功率. 主要是由于抽运光与PCNC模式之间的耦合效率被提高, 使得抽运峰值功率或能量大幅降低. 若引入高能量抽运光, 硅的双光子吸收效应显著增强, 同时由于硅的Kerr系数比聚苯乙烯低两个数量级, 将增加开关的能量消耗, 通过结构设计, 将能量主要限制在纳米孔内部, 即光主要与聚苯乙烯相互作用, 可以进一步降低开关能量, 避免了硅的非线性响应, 最终获得功耗为亚皮焦耳(0.76 pJ), 开关切换时间为亚皮秒(0.707 ps)的开关开断特性, 且封装尺寸仅为16 μm2.
图 10 Fano共振硅光开关[42] (a) PCNC耦合PCN; (b) PCNC耦合PCN的光谱Figure10. Silicon optical switch based on Fano resonant[42]: (a) PCNC couple PCN; (b) corresponding spectra.
上述纳米腔光开关基本上是双端口, 而不是通用的四端口纵横开关, 主要是由于多个端口与腔耦合时, 腔中具有无方向性驻波的功率会平均泄漏到每个端口, 从而降低传输效率[94]. Cheng等[45]提出单个交叉耦合PCNC结构的四端口光开关, 交叉状态下端口的插入损耗仅1.5 dB, 核心结构中尺寸为14 μm2.
2
4.2.Fano调制器
利用硅光Fano共振优化电光调制器目前有两种方式: 一种主要通过MRR辅助(miro ring resonator assistant, MRA) MZI结构实现, 基本结构如图7(a)所示; 另外一种是基于PCNC的新方案, 用于优化调制器带宽及功耗的平衡点.MZI调制器的非线性主要是由正弦调制曲线引起的, 可通过对MZI的臂施加超线性相位调制来提高线性度. 2003年Xie等[95]提出了基于MRR的全通滤波器可用于改善MZI调制器的线性度, 虽然没有分析光谱特性, 但从光谱上可知该器件工作在Fano共振波长处. 波导损耗在MRA-MZI强度调制器中的作用非常重要, 2004年Yang等[79]表明在低损耗情况下, MRA-MZI调制器能够保持较高的线性度, 但应当设置合适的相位偏置, 否则较大的损耗会使得MZI两臂之间的功率不平衡, 导致调制深度受限. 2005年Tazawa和Steier[96]研究超线性相位调制, 分析了线性化MRA-MZI电光调制器具有较好的动态范围和调制频率特性. 2013年Cardenas等[97]实验证明MRA-MZI的调制线性度被提高, 但是MRR具有固定的耦合系数, 因此缺乏灵活性, 难以达到最佳工作点.
最新研究表明[80], 在MZI的臂上加上光衰减器用于调节双臂的功率比值(图11(a)), 可灵活调节最佳工作点, 验证了Cardenas等[97]提高线性度的方法. 同时, 该团队专门研究了限制微波光子学系统的三阶互调失真(third-order intermodulation distortion, IMD3)的因素, 并通过载波失真比(carrier-to-distortion ratio, CDR)和无杂散动态范围(spurious-free dynamic range, SFDR)来评估线性度, 最终通过MRA-MZI调制器实现了在插入损耗5 dB的情况下, SFDRIMD3为111.3@1 GHz. 该器件可在两种情况下工作并获得高调制线性度, 第一种是在反Fano共振波长附近, 它具有较宽的线性调制间隔和较高的CDRIMD3, 第二种在Fano共振波长附近, 尽管线性范围较窄且CDRIMD3较低, 但调制效率较高, 使得SFDRIMD3较高. 与传统的硅MZI和MRR调制器相比, MRA-MZI调制线性度及SFDRIMD3得到了显著改善.
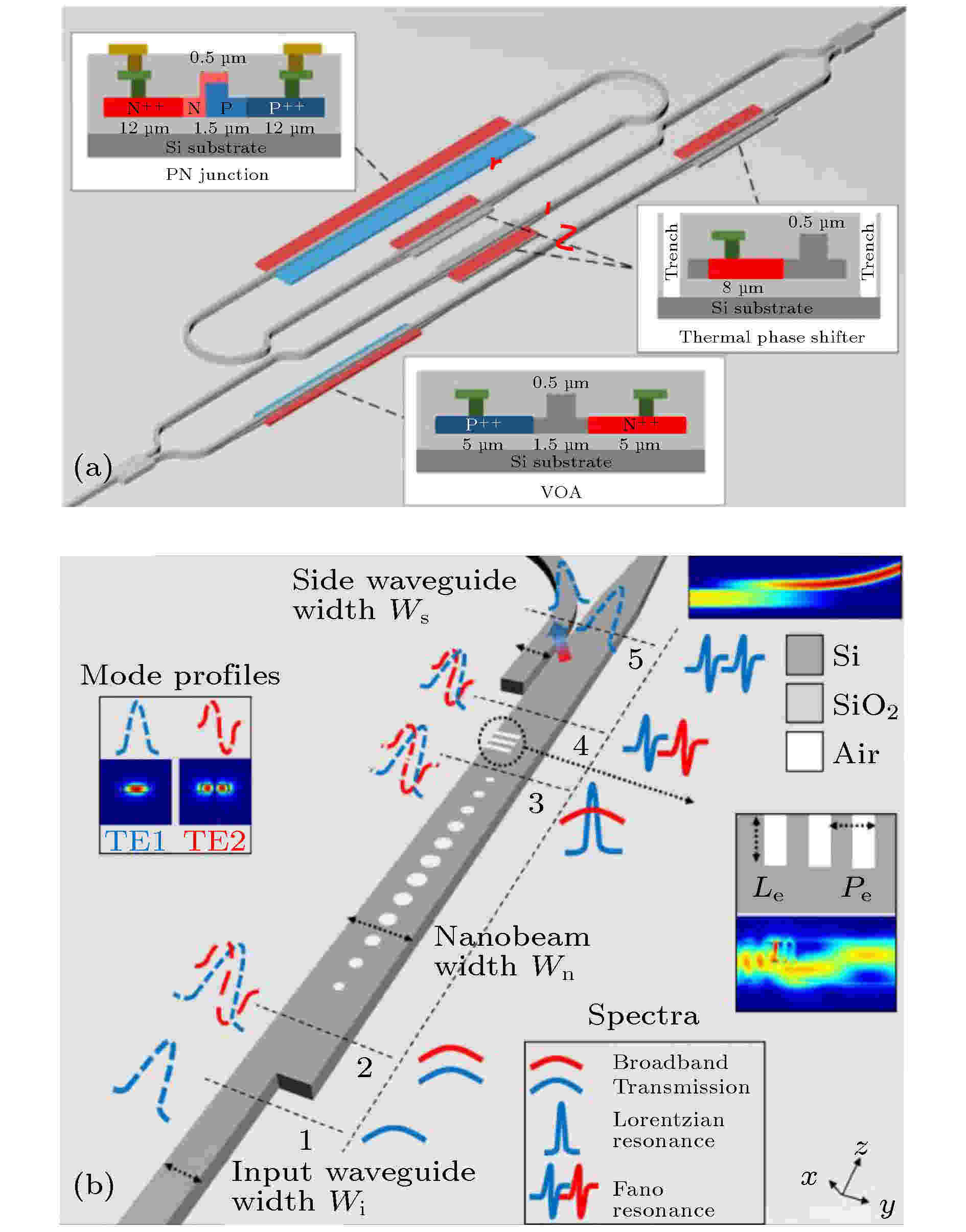图 11 Fano共振硅基电光调制器 (a) MZI耦合MRR[80]; (b)单波导PCNC[98]Figure11. Silicon electro-optic modulator based on Fano resonant: (a) MZI couple MRR[80]; (b) single waveguide PCNC[98].
单波导实现的Fano共振的电光调制器[98]结构如图11(b)所示, 单模输入波导连接到多模干涉结构(MMI), 同时激发零阶与一阶模, PCNC和亚波长光栅组成模式混频器. MMI的宽度使其激发的两种TE波导模式的有效折射率之间的差异较大, 从而使得零阶TE模式与PCNC发生强烈相互作用, 产生窄带离散模式, 而一阶TE模式对纳米梁的周期性波纹不敏感, 从而产生平坦的连续模式. 亚波长模式混频器使得离散和连续模式发生耦合, 形成了两个Fano共振(零阶及一阶TE模式). 最后定向耦合器将一阶TE模式耦合到单模输出波导. 此种方法产生双模式Fano共振与文献[82]有异曲同工之妙, 这对拓展于多模式Fano共振并增强通信复用能力具有重要意义. 该结构利用等离子体色散效应进行调制, 能量消耗小于几个fJ/bit, 为高数据比特率(
2
4.3.Fano传感器
虽然Fano共振适合应用于光开关、调制器, 以及传感应用, 但由于光开关、调制器和传感器的设计要求不同, 因此针对光开关及调制器进行的优化方案不适用于传感器件. 如MRA-MZI结构可应用实现光开关、调制器及传感器, 在应用到光开关时, 主要通过优化MZI两臂的相位差来实现输出端口的高消光比, 旨在降低开关恢复时间和功耗[86]; 调制器中MRR的损耗对线性调制深度影响较大, 同时需要优化MZI 两个臂功率比值, 旨在减小一阶及高阶失真度[82]; 应用到基于强度检测的光传感时, 目标是透射光谱的具有高的斜率. 因此, Fano共振在传感应用中参数优化具有特殊性.Terrel等[99]及Zhou等[63,64]研究了Fano共振用于检测物理量γ的灵敏度, 灵敏度可以表示为 Sp = S1S2S3, 其中, S1 = dPdiff/dλ表示光强度Pdiff相对于波长λ变化的光谱分辨率(Fano共振光谱的斜率); S2 = dλ/d?是波长λ相对于相位?变化率, 通常为常数; S3 = d?/dγ是波长相位?相对于被测量γ变化率, ? = Leffneff/λ (Leff代表谐振腔的长度, neff代表波导有效折射率). 被测对象通过影响谐振器相位实现传感, 对于生化传感器, 波导模式倏逝场与分析物的相互作用会改变波导模式的有效折射率neff, 从而改变?. 如果被测量是温度T, 波导的热膨胀系数(改变Leff)和热光系数(改变neff)随温度发生变化量决定灵敏度. 接下来介绍几种实现Fano共振的结构并优化增强灵敏度S1和S3的方法, 优化S1是为了获得高斜率光谱, 提高S3可以通过优化波导截面或者将波导模式限制在空气孔内, 增加物质与模式的有效重叠面积.
Chao和Guo等[46]在实现Fano共振时将截面设计如图12(a)所示, 实现了0.024%浓度的葡萄糖探测; Terrel等[99]将MRR与MRA-MZI折射率灵敏度进行了对比, S3是一个固定值, 因此灵敏度由S1决定, 调节MRA-MZI实现了高斜率Fano光谱, 能够使MRA-MZI灵敏度与传统MRR灵敏度相比提高30.5%; Zhou等[63,64]在理论上分析了图6(c)结构应用在液体及气体传感, 采用氮化硅作为波导芯区, 测量装置如图12(c)所示, 其液体探测极限达到3.24 × 10–8 RIU[63], 气体传感探测极限为6 × 10–8 RIU[64].
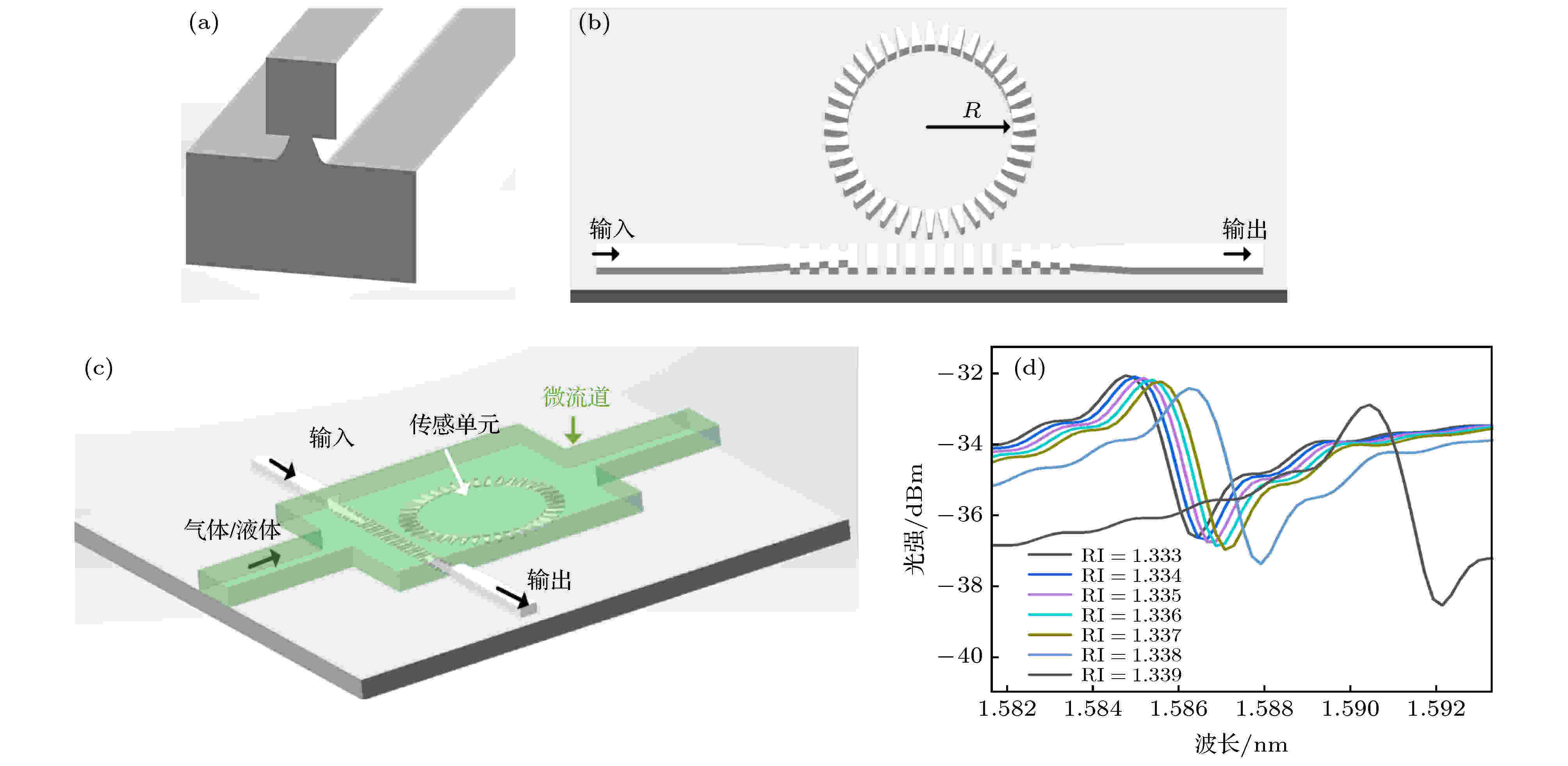图 12 Fano共振传感 (a)波导截面[46]; (b)光栅式MRR[68]; (c)传感测试装置[63,64]; (d) Fano共振光谱随折射率传感变化曲线, 图中RI (refractive index)代表折射率[56]Figure12. Fano resonance for sensing applications: (a) Cross section of waveguide[46]; (b) MRR composed of grating[68]; (c) setup for sensor[63,64]; (d) spectrum of Fano resonance versus refractive index (RI)[56].
在优化Fano共振的S1基础上, 优化S3的方法主要包括引入狭缝、光栅或空气孔. Meng 和Li[41]在图4(d)结构基础上优化S3, 通过在中间几个孔引入狭缝, 但是灵敏度的提高是有限的, 最大值为217 nm/RIU. 为了进一步提高灵敏度, 在PCNC加入单抛物线形缝隙, 同时在该腔的侧面添加了间距为0.1 μm的光子晶体. 由于大部分电场分布于细长的狭缝区域, 折射率灵敏度可以提高到778 nm/RIU; Tu等[54]采用亚波长光栅波导制作MRR以增强光-分析物的重叠量, 总线波导上的F-P与MRR共振态相互作用, 在1550 nm波长处形成了尖锐的不对称Fano共振, 实现了366 nm/RIU (实部折射率)和9700/RIU (虚部折射率)灵敏度; Zhao等[55]设计的狭缝MRR和狭缝相移布拉格光栅总线波导耦合结构的灵敏度为297.13 nm/RIU; Peng等[56]采用PCNC耦合MRR, 折射率灵敏度约为1.76 × 104 dB/RIU, 光谱随折射率变化示意曲线如图12(d)所示, 而单MRR的折射率灵敏度仅约为3.1 × 103 dB/RIU, 可以说明Fano共振能够有效提高传感灵敏度; Wen 等[68]用亚波长光栅替代图6(e)中的结构, 实现如图12(b)所示结构, 最终获得500 nm/RIU的折射率灵敏度.
2
4.4.基于光非互易性的Fano光器件
集成的纳米结构是实现具有不可逆光传输特性的理想基本单元, 非互易性传输可以实现隔离器的功能. Li和Bogaerts[35]在实验上验证了此种方法, 结构如图6(f)所示, 由MRR组成的双MZI结构在圆环处相互耦合, 测试方法如图13(a)所示. 该结构的关键之处在于, 利用腔增强材料的非线性特性, 结合空间对称性破坏和Fano共振, 实现超低功率和良好的波长可调效果, 达到了光不可逆传输传播效果. 器件的非线性取决于超快的载流子动力学特征, 而不是通常考虑的热效应[100], 最终获得以10 Gbit/s的比特率和4.5 fJ/bit低能耗的光非互易传输. 在Fano共振或EIT模式下, 由于腔内各模式之间的强度分布不对称所致, 该器件表现出非线性的不可逆行为. 具体来说, 在一个传输方向上, 非线性引起的共振失真可以消除EIT的传输谷, 形成高传输率的Lorentzian共振(图13(c)), 而在相反的方向上, EIT的传输谱形状不变(图13(d)). 从图13(b)可以看出, 该器件利用Fano共振效应, 实现了具有超过30 dB的超高消光比和1.5 dB的低插入损耗的光非互易性传输.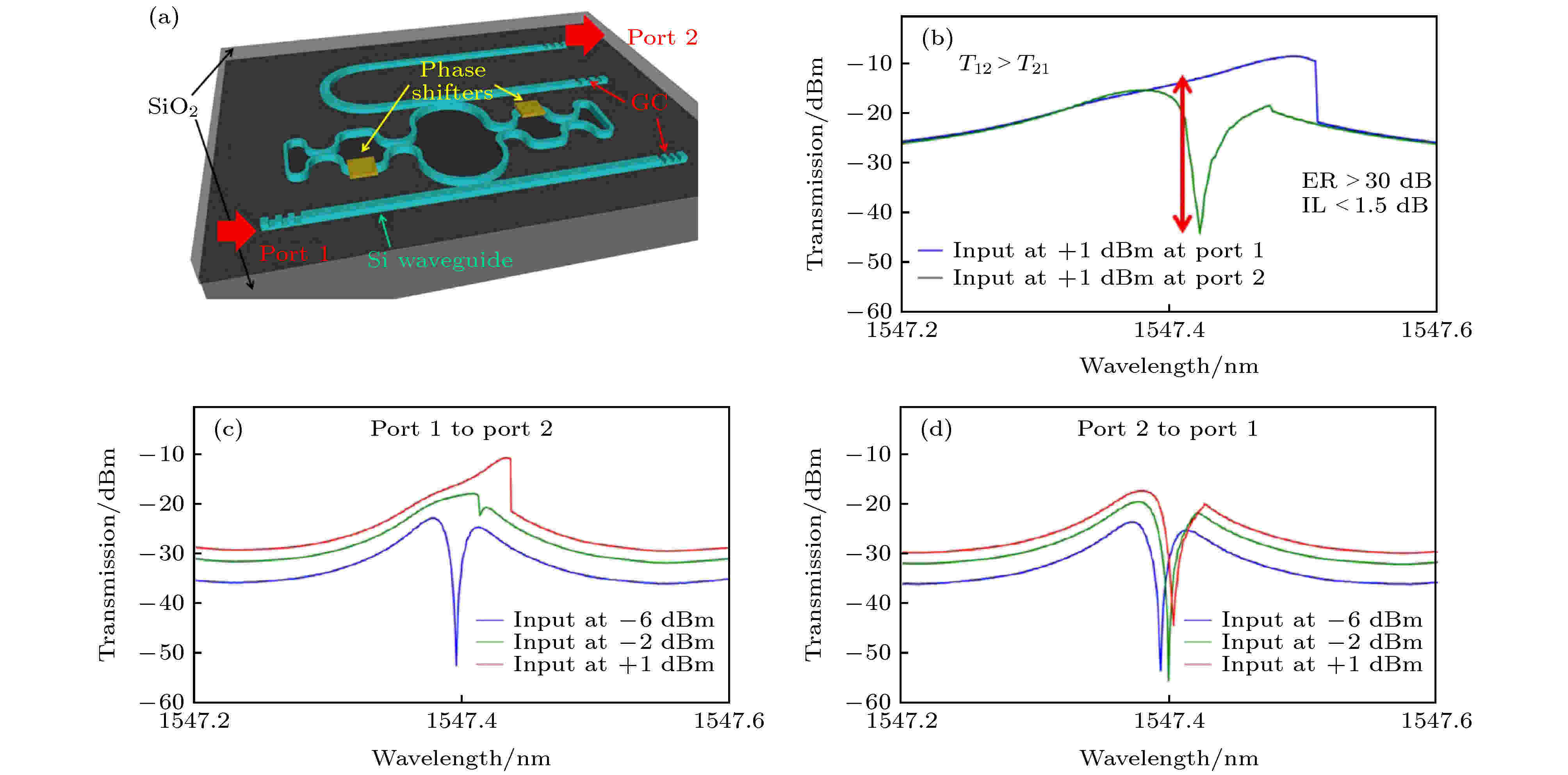
图 13 基于EIT的光非互易性传输 (a) 微环形成双MZI结构[35]; (b)非互易性光谱特征[35]; (c)端口1波长随输入功率变化曲线[35]; (d) 端口2波长随输入功率变化曲线[101]Figure13. EIT-based optical nonreciprocal transmission: (a) Microrings forming a dual MZIs[35]; (b) characteristics of optical nonreciprocity spectral[35]; (c) wavelength of port 1 versus input power[35]; (d) wavelength of port 2 versus input power[101].
Yang等[101]采用反向设计方法构造了MRR与空气孔缺陷形成部分反射单元相耦合的结构, 使得Fano共振光谱具有非互易性. 该器件利用谐振器的χ(3)非线性实现了全无源、低损耗(1.1 dB)、无偏置的非互易传输, 非常适合应用于集成光子雷达.
未来发展可以从Fano效应理论、器件性能参数及应用等方面进行研究. 在理论上建立硅光器件的物理描述参数(品质因子、耦合系数等)与Fano线形参数q之间的解析关系, 简化器件设计流程并加深对器件物理本质的理解; 在器件性能参数上, 需要进一步提高光谱分辨率(光谱的斜率). 可以结合其他物理分支, 如连续体束缚态概念[102], 如在光子晶体实际结构中引入各向异性[103], 使得Fano的品质因子Q达108以上, 从而有效地提高Fano器件光谱分辨率; 结合拓扑结构[104], 提高Fano共振结构的鲁棒性; 除了在通信波段实现Fano共振光谱, 还可以通过扩展材料体系来拓展Fano共振光谱的波段范围; 目前Fano共振最多实现双模式传输, 可以通过扩展多模式Fano共振来提高复用能力; 目前传输谱的所有共振模式里仅有部分共振波长是Fano线形, 考虑到应用, 可以研究全波长Fano共振光谱实现方法; 在应用方面, 目前实际应用都还处于开始研究阶段, 包括应用于微波光子链路的光开关及光调制器、用于光非互易性的集成光子雷达和芯片化的生化传感分析等, 尚未有商业产品. 同时, 也需要在硅光子Fano器件工艺实现上开展大量的研究工作, 为实际应用打下基础.
