摘要: 采用高精度的从头算方法研究了SeH
– 阴离子的基态(X
1 Σ
+ )和低激发(a
3 Π, A
1 Π, b
3 Σ
+ , 2
1 Σ
+ )的势能曲线、偶极矩和跃迁偶极矩. 在计算中考虑了价-芯(CV)电子关联、Davidson修正、标量相对论修正和自旋-轨道耦合效应(SOC). 考虑了SOC效应后,
$ {{\rm{b}}^3}\Sigma _{{0^ - }}^ + $ 和
$ {{\rm{b}}^3}\Sigma _{{1}}^ + $ 态变为了弱束缚态. 计算得到
$ {{\rm{a}}^3}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ ,
${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow $ ${{\rm{X}}^1}\Sigma _{{0^ + }}^ +$ 和
$ {{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁具有很大的跃迁偶极矩. 这三种跃迁都同时具有高对角分布的弗兰克-康登因子
f 00 及振动分支比
R 00 . 计算得到了
$ {{\rm{a}}^3}{\Pi _{{1}}}$ ,
$ {{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ 和
$ {{\rm{A}}^1}{\Pi _{{1}}}$ 激发态的自发辐射寿命都很短, 能够实现对SeH
– 阴离子的快速激光冷却.
$ {{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁为三能级跃迁, 中间态的存在对构建准闭合的循环能级的影响可以忽略. 驱动
$ {{\rm{a}}^3}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ ,
$ {{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 和
$ {{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁进行激光冷却SeH
– 阴离子的激光波长都在可见光范围内. 本文的结果为以后激光冷却SeH
– 阴离子的实验提供了部分理论参考.
关键词: 自旋-轨道耦合效应 /
振动分支比 /
自发辐射寿命 /
激光冷却 English Abstract Spectroscopic and transition properties of SeH– anion including spin-orbit coupling Wan Ming-Jie Liu Fu-Ti Huang Duo-Hui Faculty of Science, Yibin University, Yibin 644007, China Fund Project: Project supported by the Pre-Research Project of Yibin University, China (Grant No. 2019YY06) and the Open Research Fund of Computational Physics Key Laboratory of Sichuan Province, Yibin University, China (Grant No. YBXYJSWL-ZD-2020-001)Received Date: 26 August 2020Accepted Date: 21 September 2020Available Online: 26 January 2021Published Online: 05 February 2021Abstract: Potential energy curves (PECs), permanent dipole moments (PDMs) and transition dipole moments (TMDs) of five Λ-S states of SeH? anion are calculated by the MRCI + Q method with ACVQZ-DK basis set. The core-valence corrections, Davidson corrections, scalar relativistic corrections, and spin-orbit coupling (SOC) effects are also considered. In the CASSCF step, Se(1s2s2p3s3p) shells are put into the frozen orbitals, which are not optimized. Six molecular orbitals are chosen as active space, including H(1s) and Se(4s4p5s) shells, and eight electrons are distributed in a (4, 1, 1, 0) active space, which is referred to as CAS (8, 6), and the Se(3d) shell is selected as a closed-shell, which keeps doubly occupation. In the MRCI step, the remaining Se(3d) shell is used for core-valence calculations of SeH? anion. The SOC effects are taken into account in the one- and two- electron Breit-Pauli operators. The b3 Σ+ state is a repulsive state. Other excited states are bound, and all states possess two potential wells. The $ {{\rm{b}}^{{3}}}\Sigma _{{0^ - }}^ + $ and $ {{\rm{b}}^3}\Sigma _{{1}}^ + $ both turn into bound states when the SOC effect is considered. All spectroscopic parameters of Λ-S states and Ω states are reported for the first time. The TDMs of the $ {{\rm{A}}^{{1}}}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + $ , $ {{\rm{a}}^{{3}}}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , $ {{\rm{a}}^{{3}}}{\Pi _{{{{0}}^{{ + }}}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , $ {{\rm{A}}^{{1}}}{\Pi _{{1}}} \leftrightarrow {{\rm{a}}^{{3}}}{\Pi _{{1}}}$ , and $ {{\rm{A}}^{{1}}}{\Pi _{{1}}} \leftrightarrow {{\rm{a}}^{{3}}}{\Pi _{{{{0}}^{{ + }}}}}$ transitions are also calculated. The TDMs of the $ {{\rm{A}}^{{1}}}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + $ and $ {{\rm{a}}^{{3}}}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + $ transitions are large in the Franck-Condon region, which are about –2.05 Debye (D) and 1.45 D at R e . Notably, the TDMs of the $ {{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transition cannot be ignored. The value of TDM at R e equals –0.15 D. Based on the accurately PECs and PDMs, the values of Franck-Condon factor f υ ′υ ″R υ ′υ ″$ {{\rm{a}}^{{3}}}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + $ , $ {{\rm{a}}^{{3}}}{{{\Pi }}_{{{{0}}^{{ + }}}}} \leftrightarrow {{\rm{X}}^{{1}}}{{\Sigma }}_{{0^ + }}^ + $ , and $ {{\rm{A}}^{{1}}}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + $ transitions are also calculated. Highly diagonally distributed Franck-Condon factor f 00 and the values of vibrational branching ratio R 00 of the $ {{\rm{a}}^{{3}}}{\Pi _{{1}}}(\upsilon ') \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + (\upsilon '')$ , $ {{\rm{a}}^{{3}}}{\Pi _{{0^ + }}}(\upsilon ') \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + (\upsilon '')$ , and $ {{\rm{A}}^1}{\Pi _1}(\upsilon ') \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + (\upsilon '')$ transitions are obtained, respectively. Spontaneous radiation lifetimes of the $ {{\rm{a}}^3}{\Pi _{{1}}}$ , $ {{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ , and $ {{\rm{A}}^1}{\Pi _{{1}}}$ excited states are all short for rapid laser cooling. The influences of intervening states of the $ {{\rm{A}}^1}{\Pi _1}(\upsilon ') \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + (\upsilon '')$ transition can be ignored. The proposed cooling wavelengths using the $ {{\rm{a}}^3}{\Pi _{{1}}}(\upsilon ') \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + (\upsilon '')$ , $ {{\rm{a}}^{{3}}}{\Pi _{{0^ + }}}(\upsilon ') \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + (\upsilon '')$ , and $ {{\rm{A}}^1}{\Pi _1}(\upsilon ') \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + (\upsilon '')$ transitions are all in the visible region. Keywords: spin-orbit coupling effects /vibrational branching ratios /spontaneous radiative lifetimes /laser cooling 全文HTML --> --> --> 1.引 言 由于分子内部能级的复杂性, 首次激光冷却分子的实验于2010年实现, Shuman等[1 ] 采用横向激光冷却技术对SrF分子进行了冷却. 2013年, Hummon等[2 ] 采用同样的技术实现了YO分子的冷却. 这是1个三能级体系, 其存在1个中间态A′2 Δ3/2 . 2014年, Zhelyazkova等[3 ] 采用纵向激光冷却技术对CaF分子进行了冷却. 近十年, 有很多****对一系列的双原子分子进行了激光冷却的理论研究, 如MgH[4 ] , LiBe[5 ] , CH[6 ] , AlCl[7 ] , OH[8 ] , BaF[9 ] 等.[10 ] 才首次从理论上预测了激光冷却双原子分子阴离子的可能性. 随后激光冷却阴离子吸引了越来越多****的关注[11 -16 ] . 鲁东大学的杨传路教授等预测了激光冷却NH– [11 ] 和BH– [12 ] 阴离子的冷却途径. Zeid等[13 ] 在自旋无关水平下计算了X H– (X = Mg, Ca, Sr, Ba)体系的势能曲线和跃迁偶极矩. X H– 体系的11 Π $ \leftrightarrow $ X1 Σ+ 跃迁均具有很大的跃迁偶极矩和对角化的弗兰克-康登因子, 他们认为这些阴离子可能是激光冷却的潜在候选体系. 在我们前期的工作中, 研究了激光冷却VI簇氢化物的阴离子(OH– , SH– , TeH– )的可能性[14 -16 ] . SeH在实验上和理论上都是一种重要的自由基, 也是一种比较简单的重原子分子. 本文将主要研究在考虑自旋-轨道耦合效应(SOC)下SeH– 阴离子的光谱和跃迁性质, 并讨论其激光冷却的可行性.– 阴离子的光谱常数的实验和理论研究很少. 1987年, Stoneman和Larson[17 ] 在磁场中采用光致分离技术观察SeH– 阴离子, 他们得到了SeH– 基态的平衡核间距R e 是SeH分子基态1.0038(3)倍. 同时采用最小二乘法得到了转动常数B 为7.7289 cm–1 . 1982年, Brown和Fackerell[18 ] 采用CO激光磁共振观察了SeD和SeH分子的振转光谱, 得到了SeH分子基态X2 Π的平衡核间距为1.4640715(25) ?. 1987年, Balasubramanian等[19 ] 采用二阶组态相互作用方法计算了SeH和SeH+ 较低电子态的势能曲线, 并得到了SeH和SeH+ 基态的平衡核间距分别为1.467 ?和1.58 ?. 1990年, Binning Jr和Curtiss[20 ] 采用Hartree-Fock方法计算得到SeH基态的平衡核间距为1.463 ?. 到目前为止, 没有发现针对SeH– 阴离子的跃迁性质的理论或实验研究.– 阴离子的基态(X1 Σ+ )和低激发(a3 Π, A1 Π, b3 Σ+ , 21 Σ+ )的势能曲线和跃迁偶极矩, 拟合得到各束缚态的光谱常数, 预测其弗兰克-康登因子、振动分支比和自发辐射系数, 最后讨论其激光冷却的可能性, 并给出其冷却途径.2.计算细节 本文采用从头算方法计算了SeH– 阴离子4个Λ-S态(X1 Σ+ , a3 Π, 11 Π, b3 Σ+ )的电子结构. 在计算中增加了21 Σ+ 态, 以便比较11 Π和21 Σ+ 态的能级高低. 所有计算都在MOLPRO 2010程序包[21 ] 下完成. X1 Σ+ , a3 Π, 11 Π, b3 Σ+ 态对应于最低离解极限Se– (2 Pu )+H(2 Sg ), 第二离解极限为Se(3 Pg ) + H– (1 Sg ), 其对应的电子态只能是3重态, 所以第二个1 Σ+ 态对应于第三离解通道Se(1 Du ) + H– (1 Sg ). 首先, 采用限制性的Hartree-Fock方法对SeH– 阴离子进行波函数的初始猜测, 得到初始波函数; 然后, 采用完全活动空间自洽场方法(CASSCF)[22 ,23 ] 产生多参考的波函数; 最后, 采用多参考组态相互作用方法(MRCI)[24 ,25 ] 得到各Λ-S态的能量, 同时也考虑了Davidson修正[26 ] . 通过二阶Douglas-Kroll哈密顿量[27 ,28 ] 来考虑标量相对论效应.Q 水平下通过Breit-Pauli算符[29 ] 考虑了SOC效应. 在Λ-S和Ω态的所有计算中, Se原子选择了aug-cc-pCVQZ-DK (ACVQZ-DK)全电子基组[30 ] , H原子选择了aug-cc-pVQZ-DK(AVQZ-DK)全电子基组[31 ] .[32 ] , 通过求解径向薛定谔方程得到SeH– 阴离子低电子态的光谱常数、弗兰克-康登因子、自发辐射系数和自发辐射寿命.3.结果与讨论 23.1.势能曲线与光谱常数 3.1.势能曲线与光谱常数 计算了SeH– 阴离子X1 Σ+ , a3 Π, 11 Π和b3 Σ+ 态的势能曲线, 这4个电子态有1个共同的离解通道Se– (2 Pu ) + H(2 Sg ). 为了确定11 Π态的能级顺序, 同时计算了第二个1 Σ+ 态. 它对应于第三离解通道Se(1 Du ) + H– (1 Sg ). 所计算的电子态的势能曲线如图1 所示. 可以看出11 Π是单重态的第一激发态, 写为A1 Π.图 1 X1 Σ+ , a3 Π, A1 Π, b3 Σ+ 和21 Σ+ 电子态的势能曲线Figure1. Potential energy curves of the X1 Σ+ , a3 Π, A1 Π, b3 Σ+ , and 21 Σ+ states.– 阴离子的基态为X1 Σ+ , 具有1个很深的势阱, 其离解能D e 为3.729 eV. X1 Σ+ 态在平衡核间距R e 处的主要组态为(1σ2 2σ2 3σ2 1π4 4σ2 5σ2 1π4 6σ2 2π4 1δ4 )7σ2 8σ2 3π4 , 简写为(core)7σ2 8σ2 3π4 , 其权重为90.8%. Stoneman和Larson[17 ] 观察到SeH– 基态的平衡核间距R e (X1 Σ+ )是SeH分子R e (X2 Π)的1.0038倍. Brown和Larson[18 ] 测得SeH分子基态X2 Π的平衡核间距R e 为1.464 ?. 虽然Huber和Herzberg[33 ] 收集了SeH分子基态的实验值为1.475 ?, 但结果不准确. 本文的计算值为1.4694 ? (表1 ), 只比实验值[17 ,18 ] 小0.0002 ?, 相对误差仅为0.01%. 本文计算的转动常数B e 为7.8507 cm–1 , 比采用最小二乘法拟合得到的实验值[17 ] 大1.58%. 可以看出本文计算结果与已有的实验值符合很好. 同时基态的谐振频率(ω e )和非谐振频率(ω e χ e )也列于表1 中, 分别为2300.77和46.10 cm–1 . 同时在MRCI+Q /AVQZ-DK水平下计算了SeH– 阴离子低激发态的势能曲线, 在计算中没有考虑CV关联效应, 基态的光谱常数也列于表1 中, 可以看出考虑CV关联后, 基态的光谱常数(R e , B e )和已有实验值符合的更好.Λ-S态 来源 R e /?ω e /cm–1 ω e χ e /cm–1 B e /cm–1 D e /eVT e /cm–1 X1 Σ+ ACVQZ-DK 1.4694 2300.77 46.10 7.8507 3.487 0 AVQZ-DK 1.4614 2380.32 45.57 7.9326 3.711 实验[17 ] 1.4696 a 7.7289 c 1.4806 b a3 Π 本文工作 第一势阱 1.4778 2206.52 123.45 7.8428 0.519 20642.90 第二势阱 2.1787 839.87 49.66 3.44016 0.450 24549.11 A1 Π 本文工作 第一势阱 1.4726 2373.65 127.14 7.8391 0.734 21240.75 第二势阱 2.2780 437.62 44.07 3.0932 0.147 26997.57 b3 Σ+ 本文工作 repulsive 21 Σ+ 本文工作 第一势阱 1.6188 1336.45 — 6.1955 0.228 51684.73 第二势阱 4.0808 198.90 9.96 1.0190 0.135 46349.30 注: a 为SeH分子基态的平衡核间距的实验值来源于文献[18 ]; b 为SeH分子基态的平衡核间距的实验值来源于文献[33 ], 结果不准确; c 为采用最小二乘法得到转动惯量B .
表1 Λ-S的光谱常数Table1. Spectroscopic parameters of the Λ-S states.图1 可以看到b3 Σ+ 是1个排斥态. 其他3个激发态都是具有双势阱结构的束缚态. a3 Π, A1 Π和21 Σ+ 态的第一势阱分别位于比基态高20642.90, 21240.75, 51684.73 cm–1 处, 势阱深度分别为0.518, 0.737, 0.205 eV; 其平衡核间距R e 分别为1.4679, 1.4627, 1.6113 ?. 在平衡核间距位置处的主要组态分别为(core)7σ2 8σ2 9σα 3$\pi_x^{\text{α}}$ 3$\pi_y^{\text{αβ}}$ , (core)7σ2 8σ2 9σα 3$\pi_x^{\text{β}}$ 3$ \pi_y^{\text{αβ}} $ 和(core)7σ2 8σα 9σβ 3π4 , 权重分别为91.32%, 91.36%和88.28%. X1 Σ+ →A1 Π和X1 Σ+ → 21 Σ+ 跃迁主要是由3πx 3 Π, A1 Π和21 Σ+ 态电偶极矩的曲线非常平滑, 没有发生突变, 可以推测这3个电子态都可能由预解离所致. 从图1 可以看出这3个态分别约在1.98, 2.04, 2.12 ?处发生预解离. a3 Π, A1 Π和21 Σ+ 态的第二势阱的平衡核间距R e 分别为2.1787, 2.2780, 4.0808 ?. 其势阱深度分别为0.450, 0.147, 0.135 eV. 由于阴离子体系的光谱常数的实验值非常少, 本文对比了第VI主簇氢化物阴离子基态的光谱常数, 分别列于表2 中, 可以看出随着第VI主簇原子质量的增加, 其氢化物阴离子基态的平衡核间距R e 逐渐地增大, 但其氢化物阴离子基态的谐振频率ω e 、非谐振频率ω e χ e 和势阱深度D e 都逐渐地减小.阴离子 来源 R e /?ω e /cm–1 ω e χ e /cm–1 B e /cm–1 D e /eVOH– 文献[14 ] 0.9645 3722.10 87.93 19.1111 4.9857 SH– 文献[15 ] 1.3435 2622.04 46.66 9.5590 3.8793 SeH– 本文工作 1.4694 2300.77 46.10 7.8507 3.487 TeH– 文献[16 ] 1.6631 1973.73 36.8272 6.0996 3.0568
表2 第VI主簇氢化物阴离子基态的光谱常数Table2. Spectroscopic parameters of the ground state X1 Σ+ of the Group VI-hydride anions.– 离子的2 P原子态分裂为2 P1/2 和2 P3/2 态. ${{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^3}{\Pi _2}$ , ${{\rm{a}}^3}{\Pi _{{1}}}$ , ${{\rm{a}}^3}{\Pi _{{{{0}}^ - }}}$ 和${{\rm{A}}^{{1}}}{\Pi _{{1}}}$ 态对应于Se– (2 P3/2 ) + H(2 S1/2 )离解通道, ${{\rm{a}}^{{3}}}{\Pi _{{{{0}}^{{ + }}}}}, {{\rm{b}}^{{3}}}\Sigma _{{0^ - }}^ + , {{\rm{b}}^3}\Sigma _{{1}}^ + $ 态对应于Se– (2 P1/2 ) + H(2 S1/2 )离解通道. 本文预测了Se– (2 P)原子态的分裂常数, A SO (2 P1/2 – 2 P3/2 ) = 2303.77 cm–1 . 另外, ${2^1}\Sigma _{{0^ + }}^ + $ 对应于较高的离解通道Se(1 D2 ) + H– (1 S0 ), 其与最低离解通道的相对能量为20032.24 cm–1 , 比实验值[34 -36 ] 大241.36 cm–1 , 相对误差仅为1.22%, 本文计算值与已有实验值符合很好. Ω态之间的离解关系列于表3 . 表3 也同样可以看出考虑CV关联效应后, 第三离解极限与最低离解极限的相对能量和已有实验值符合得更好.离解通道 分子态(Ω) 相对能量/cm–1 ACVQZ-DK AVQZ-DK 实验[34 -36 ] Se– (2 P3/2 ) + H(2 S1/2 ) 2, 1, 1, 0+ , 0– 0 0 0 Se– (2 P1/2 ) + H(2 S1/2 ) 1, 0+ , 0– 2303.77 2192.98 — Se(1 D2 ) + H– (1 S0 ) 0+ 20032.24 19047.45 19790.88
表3 Ω态的离解关系Table3. Calculated dissociation relationships of the Ω states.图2 所示, 所计算的电子态都是束缚态, 各Ω态的光谱常数列于表4 . 对比表2 , 基态${{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 的势阱深度比X1 Σ+ 态的要小约0.1 eV. 从图2 可看出${{\rm{a}}^3}{\Pi _2}$ , ${{\rm{a}}^3}{\Pi _{{1}}}$ , ${{\rm{a}}^3}{\Pi _{{{{0}}^ - }}}$ , ${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ , ${{\rm{A}}^1}{\Pi _{{1}}}$ 和${{{2}}^1}\Sigma _{{0^ + }}^ + $ 态具有2个势阱. ${{\rm{a}}^{{3}}}{\Pi _2}$ 态是第一激发态, 其第一势阱到基态的垂直跃迁能为19787.17 cm–1 . a3 Π态的第一势阱的分裂常数为: A SO (${{\rm{a}}^3}{\Pi _{{1}}}$ – ${{\rm{a}}^3}{\Pi _2}$ ) = 249.1 cm–1 , A SO (${{\rm{a}}^3}{\Pi _{{{{0}}^ - }}}$ – ${{\rm{a}}^3}{\Pi _{{1}}}$ ) = 1436.25 cm–1 , A SO (${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ – ${{\rm{a}}^3}{\Pi _{{{{0}}^ - }}}$ ) = 4.60 cm–1 . 而a3 Π态的第二势阱具有更大的分裂常数, ${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ 和${{\rm{a}}^3}{\Pi _{{{{0}}^ - }}}$ 态之间的分裂常数达到了192.26 cm–1 . 从图2 还可以看出${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ 和${{\rm{A}}^1}{\Pi _{{1}}}$ 在2.89 ?处交叉. 考虑SOC效应后, b3 Σ+ 态的2个分裂态${{\rm{b}}^3}\Sigma _{{0^ - }}^ + $ 和${{\rm{b}}^3}\Sigma _{{1}}^ + $ 态都具有了1个很浅的势阱, 势阱深度分别为0.096和0.066 eV, 平衡核间距分别为3.1807和3.2046 ?, 这两个态都有较大的谐振频率, 均超过200 cm–1 , 说明这2个分裂态都是弱束缚态. 同时可以预测处b3 Σ+ 态的分裂常数A SO (${{\rm{b}}^3}\Sigma _{{1}}^ + $ –${{\rm{b}}^3}\Sigma _{{0^ - }}^ + $ )为239.22 cm–1 . 同样${{{2}}^1}\Sigma _{{0^ + }}^ + $ 态的第二势阱也是弱束缚态. 由于${{\rm{A}}^1}{\Pi _{{1}}}$ 的势阱太小, 可以认为其由弱束缚态变为排斥态. 由于a3 Π和b3 Σ+ 态的分裂常数很大, 可以看出SOC效应对SeH– 阴离子的势能曲线和光谱常数的影响很大.图 2 9个Ω电子态的势能曲线Figure2. Potential energy curves of nine Ω states.Ω态 R e /?ω e /cm–1 ω e χ e /cm–1 B e /cm–1 D e /eVT e /cm–1 ${{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 1.4694 2301.31 47.01 7.8499 3.395 0 ${{\rm{a}}^3}{\Pi _2}$ 第一势阱 1.4777 2207.22 122.39 7.8416 0.523 19787.17 第二势阱 2.1739 861.02 52.10 3.4081 0.454 23751.54 ${{\rm{a}}^3}{\Pi _{{1}}}$ 第一势阱 1.4759 2232.16 111.70 7.8434 0.560 20036.27 第二势阱 2.1822 818.11 55.64 3.3929 0.386 24301.10 ${{\rm{a}}^3}{\Pi _{{{{0}}^ - }}}$ 第一势阱 1.4778 2205.83 124.97 7.8485 0.513 21472.52 第二势阱 2.1986 778.28 73.70 3.4048 0.267 25261.96 ${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ 第一势阱 1.4777 2208.03 122.90 7.8422 0.522 21477.12 第二势阱 2.1619 904.15 49.02 3.4355 0.527 25454.22 ${{\rm{A}}^1}{\Pi _{{1}}}$ 第一势阱 1.4744 2368.50 144.22 7.8262 0.686 21821.04 第二势阱 排斥态 ${{\rm{b}}^3}\Sigma _{{0^ - }}^ + $ 第一势阱 3.1807 318.89 35.64 1.6988 0.096 28945.41 ${{\rm{b}}^3}\Sigma _{{1}}^ + $ 第二势阱 3.2046 239.13 30.94 1.6662 0.066 29184.63 ${2^1}\Sigma _{{0^ + }}^ + $ 第一势阱 1.6190 1332.50 — 6.1895 0.225 51714.58 第二势阱 4.0800 190.57 8.84 1.0190 0.135 46351.94
表4 Ω电子态的光谱常数Table4. Spectroscopic parameters of the Ω states.3.2.Ω态的跃迁偶极矩 -->3.2.Ω态的跃迁偶极矩 考虑SOC效应后, ${{\rm{a}}^3}{\Pi _{{2}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 和${{\rm{a}}^3}{\Pi _{{{{0}}^ - }}} \leftrightarrow $ ${{\rm{X}}^1}\Sigma _{{0^ + }}^ +$ 跃迁不被允许. 本文计算了${{\rm{A}}^{{1}}}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^3}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{A}}^1}{\Pi _{{1}}} \leftrightarrow {{\rm{a}}^3}{\Pi _{{1}}}$ 和${{\rm{A}}^1}{\Pi _{{1}}} \leftrightarrow {{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ 跃迁的跃迁偶极矩, 其与核间距的函数关系如图3 所示. 可以看出${{\rm{A}}^{{1}}}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + $ 和${{\rm{a}}^3}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁在弗兰克-康登区域具有很大的跃迁偶极矩, 在平衡核间距处分别达到了–2.05 Debye (D)和1.45 D. 值得注意的是, ${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}} \leftrightarrow$ $ {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁也具有较大的偶极矩, 在平衡核间距处为–0.15 D. 在讨论激光冷却SeH– 阴离子的过程中必须要考虑${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}} \!\leftrightarrow \!{{\rm{X}}^1}\Sigma _{{0^ + }}^ +$ 跃迁. 由于${{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^3}{\Pi _{{1}}}$ 和${{\rm{A}}^{{1}}}{\Pi _{{1}}}$ 来源于同一离解通道, 故当核间距大于6 ?后${{\rm{A}}^{{1}}}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^3}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 和${{\rm{A}}^1}{\Pi _{{1}}} \leftrightarrow {{\rm{a}}^3}{\Pi _{{1}}}$ 跃迁的跃迁偶极矩均趋于零. ${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 和${{\rm{A}}^1}{\Pi _{{1}}} \leftrightarrow {{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ 跃迁在核间距趋于无穷大时源于Se– 离子的2 P3/2 $ \leftrightarrow $ 2 P1/2 跃迁. 由于其跃迁强度很小, 故核间距大于8 ?后${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}} \!\leftrightarrow\! {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ +$ 和${{\rm{A}}^{{1}}}{\Pi _{{1}}} \!\leftrightarrow$ ${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ 跃迁的跃迁偶极矩也趋于零.图 3 ${{\rm{a}}^3}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{A}}^{{1}}}{\Pi _1} \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + $ , ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^{{3}}}{\Pi _1}$ 和${{\rm{A}}^{{1}}}{\Pi _1} \leftrightarrow {{\rm{a}}^{{3}}}{\Pi _{{{{0}}^{{ + }}}}}$ 跃迁的跃迁偶极矩Figure3. Transition dipole moments of the ${{\rm{a}}^3}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{A}}^{{1}}}{\Pi _1} \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + $ , ${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{a}}^{{3}}}{\Pi _1}$ , and ${{\rm{A}}^{{1}}}{\Pi _1} \leftrightarrow {{\rm{a}}^{{3}}}{\Pi _{{{{0}}^{{ + }}}}}$ transition.3.3.振动分支比及激光冷却SeH– 阴离子的可能性 -->3.3.振动分支比及激光冷却SeH– 阴离子的可能性 基于精确的势能曲线和跃迁偶极矩, 本文计算了${{\rm{A}}^1}{\Pi _{{1}}} \!\leftrightarrow\! {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ +$ , ${{\rm{a}}^{{3}}}{\Pi _{{1}}} \!\leftrightarrow\! {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ +$ 和${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}} \!\leftrightarrow\! {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ +$ 跃迁的弗兰克-康登因子${f_{\upsilon '\upsilon ''}}$ 和自发辐射系数${A_{\upsilon '\upsilon ''}}$ . 由于在激光冷却循环过程中光子损失路径的相对强度与振动分支比${R_{\upsilon '\upsilon ''}}$ 有直接关系[37 ] . 振动分支比可以表示为${A_{\upsilon '\upsilon ''}}$ 表示${{\rm{A}}^{{1}}}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^{{3}}}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 和${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁的自发辐射系数. 表5 列出了以上3种跃迁的弗兰克-康登因子、自发辐射系数和振动分支比. 本文分别讨论自旋阻禁和直接跃迁2种情况来进行激光冷却SeH– 阴离子的可能性.Index ${{\rm{a}}^3}{\Pi _{{1}}} \leftrightarrow $ ${{\rm{a}}^{{3}}}{\Pi _{{0^ + }}} \leftrightarrow $ ${{\rm{A}}^1}{\Pi _1} \leftrightarrow$ ${f_{\upsilon '\upsilon ''}}$ f 00 0.9949 0.9922 0.9974 f 01 0.0047 0.0072 0.0025 f 02 0.0004 0.0006 0.0001 f 10 0.0051 0.0079 0.0026 f 11 0.9541 0.9324 0.9792 f 12 0.0337 0.0486 0.0159 ${A_{\upsilon '\upsilon ''}}\rm /s$ A 00 5.02 ×106 8.02 ×104 1.36 ×107 A 01 1.88×102 4.28×103 1.87×104 A 02 2.81×101 7.48×101 2.00×103 A 10 1.10×105 6.50×102 5.79×104 A 11 4.13 ×106 9.13 ×104 1.32 ×107 A 12 1.32×104 1.57×104 1.45×105 ${R_{\upsilon '\upsilon ''}}$ R 00 0.99996 0.9484 0.9985 R 01 3.7×10–5 0.0506 0.0014 R 02 5.6×10–6 0.0009 0.0001 R 10 0.02592 0.0060 0.0043 R 11 0.9707 0.8394 0.9836 R 12 0.0031 0.1446 0.0108
表5 ${{\rm{a}}^3}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^{{3}}}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + $ 和${{\rm{A}}^1}{\Pi _1} \leftrightarrow $ ${{\rm{X}}^1}\Sigma _{{0^ + }}^ +$ 跃迁的辐射系数${A_{\upsilon '\upsilon ''}}$ 、弗兰克-康登因子${f_{\upsilon '\upsilon ''}}$ 和振动分支比${R_{\upsilon '\upsilon ''}}$ Table5. Emission rates ${A_{\upsilon '\upsilon ''}}$ , Franck-Condon Factors ${f_{\upsilon '\upsilon ''}}$ , branching ratios ${R_{\upsilon '\upsilon ''}}$ of the ${{\rm{a}}^3}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ , ${{\rm{a}}^{{3}}}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^{{1}}}\Sigma _{{0^ + }}^ + $ , and ${{\rm{A}}^1}{\Pi _1} \leftrightarrow $ ${{\rm{X}}^1}\Sigma _{{0^ + }}^ +$ transitions.3.3.1.自旋阻禁跃迁 -->3.3.1.自旋阻禁跃迁 ${\rm{a}}^{3}{\Pi }_{1}(\upsilon') \!\leftrightarrow\! {\rm X}^1\Sigma_{0^+}^+(\upsilon'')$ , ${\rm a}^3\Pi_{0^+}(\upsilon') \!\leftrightarrow\! {\rm X}^1\Sigma_{0^+}^+ (\upsilon'') $ 阻禁跃迁都有高对角分布的弗兰克-康登因子f 00 , 分别为0.9949和0.9922, 相应的振动分支比R 00 分别为0.99996和0.9484. 高对角分布的f 00 和R 00 使SeH– 阴离子满足了激光冷却的首要条件. 同时本文也计算了两种跃迁的非对角项振动分支比. 对于两种跃迁, R 00 , R 01 和R 02 的代数和非常接近1, 这可以保证在激光冷却SeH– 阴离子过程中的准循环跃迁. ${\rm{a}}^{3}{\Pi }_{1}(\upsilon')\leftrightarrow {\rm{X}}^{1}{\Sigma }_{{0}^{+}}^{+}(\upsilon'')$ 和${\rm{a}}^{3}{\Pi }_{{{0}}^{{+}}}(\upsilon')\leftrightarrow$ ${\rm X}^1 \!\Sigma_{0^+}^{+}\!(\upsilon'')$ 跃迁也有很大的自发辐射系数, 当υ ′ = 0时, 这两种跃迁总的自发辐射系数分别为5.18 × 106 和8.45 × 104 s–1 , 因此${{\rm{a}}^3}{\Pi _{{1}}}$ 和${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ 态的自发辐射寿命分别为0.199和11.8 μs. ${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ 态的辐射寿命比杨传路教授等[38 ] 预测的LiRb分子的辐射寿命(τ = 10.26 μs)要略大. 说明这两种跃迁构建的准闭合循环都能快速的冷却SeH– 阴离子.${\rm{a}}^{3}{\Pi }_{1}(\upsilon')\!\leftrightarrow\! {\rm{X}}^{1}{\Sigma }_{{0}^{+}}^{+}(\upsilon'')$ 跃迁具有非常大的振动分支比R 00 , 和TeH– 阴离子一样, 采用${\rm{a}}^{{3}}{\Pi }_{1} (\upsilon ') \leftrightarrow$ $ {\rm{X}}^{1}{\Sigma }_{{0}^{+}}^{+}(\upsilon'') $ 阻禁跃迁对SeH– 阴离子进行激光冷却时只需要选取一束主激光来驱动就可以保证跃迁循环的准闭合性, 其散射的光子数目为N scat = 1/R 01+ , 理论上可以散射光子数大于2×104 个. 所需的主激光波长为501.01 nm. 而${\rm a}^3 \Pi_{0^+} (\upsilon') \leftrightarrow$ $ {\rm X}^1\Sigma_{0^+}^+ (\upsilon '') $ 跃迁的振动分支比R 00 只有0.9484, 故在一束主激光的基础上增加了两束抽运激光来保证其跃迁循环的准闭合性, 其理论上散射光子数可以达到2.5 × 104 个. 所需的主激光波长为λ 00 = 467.59 nm, 抽运激光波长分别为λ 10 = 521.91和λ 21 = 526.15 nm. 其冷却方案绘于图4(a) 和图4(b) 中. 图中的实线表示驱动激光的波长, 虚线表示自发辐射.图 4 激光冷却SeH– 阴离子的方案 (a)${{\rm{a}}^3}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁; (b) ${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁Figure4. Proposed laser cooling scheme: (a) Using the ${{\rm{a}}^3}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transition; (b) using the ${{\rm{a}}^3}{\Pi _{{0^ + }}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transition.3.3.2.三能级跃迁 -->3.3.2.三能级跃迁 本文计算得到${\rm{A}}^{1}{\Pi }_{1}\left({\upsilon }{'}\right)\leftrightarrow {\rm{X}}^{1}{\Sigma }_{{0}^{+}}^{+}\left({\upsilon }{''}\right)$ 跃迁的f 00 和R 00 分别为0.9974和0.9985, 同样其具有很大的自发辐射系数, 为1.36 × 107 s–1 , 因此${{\rm{A}}^1}{\Pi _{{1}}}$ 态的自发辐射寿命为73.5 ns, 其比${{\rm{a}}^{{3}}}{\Pi _{{1}}}$ 和${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ 态的辐射寿命要短得多. 采用${\rm{A}}^{1}{\Pi }_{1}\left({\upsilon }{'}\right)\leftrightarrow {\rm{X}}^{{1}}{\Sigma }_{{0}^{+}}^{+}\left({\upsilon }{''}\right)$ 跃迁能更快速地冷却SeH– 阴离子. 在构建${\rm{A}}^{1}{\Pi }_{1}\left({\upsilon }{'}\right)\leftrightarrow {\rm{X}}^{1}{\Sigma }_{{0}^{+}}^{+}\left({\upsilon }{''}\right)$ 准闭合的循环跃迁时存在中间态${{\rm{a}}^3}{\Pi _{{1}}}$ 和${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ , 必须考虑中间态是否对跃迁循环准闭合性有影响. 本文采用振动分支损失比(η )来评估. 振动分支损失比可以表示为– 阴离子, γ 1 和γ 2 分别表示${{\rm{A}}^1}{\Pi _{{1}}} \leftrightarrow {{\rm{a}}^3}{\Pi _{{1}}}$ 和${{\rm{A}}^1}{\Pi _{{1}}} \leftrightarrow {{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ 跃迁的自发辐射系数. 本文的计算值分别为2.31和1.21 × 10–2 s–1 . γ Σ 表示${{\rm{A}}^1}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 态的自发辐射速率. 这样可以得到η 1 = γ 1 /γ Σ < 2.0 × 10–7 , η 2 = γ 2 /γ Σ < 9.0 × 10–10 , 本文的计算结果远远小于YO分子的振动分支损失比(< 4 × 10–4 )[2 ] . 结果表明中间态的存在对激光冷却SeH– 阴离子几乎没有影响. 可以选取一束主激光来驱动${{\rm{A}}^1}{\Pi _{{1}}} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁时, 理论上散射光子数仅为600个. 其主激光波长为459.52 nm. 为了提高冷却效率, 增加了两束抽运激光λ 10 = 511.88和λ 21 = 512.83 nm, 其理论上散射光子数可达到3.3 × 105 个. 相应的三能级跃迁进行激光冷却SeH– 阴离子的冷却途径如图5 所示.图 5 采用${{\rm{A}}^1}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ 跃迁进行激光冷却SeH– 阴离子的方案Figure5. Proposed laser cooling scheme by using the ${{\rm{A}}^{{1}}}{\Pi _1} \leftrightarrow {{\rm{X}}^1}\Sigma _{{0^ + }}^ + $ transition.4.结 论 在MRCI+Q /AVQZ-DK水平下, 本文计算了SeH– 阴离子5个Λ-S态和9个Ω态的势能曲线. 计算中考虑了标量相对论效应和CV关联效应. 考虑SOC效应后b3 Σ+ 态的2个分裂态变为了弱束缚态. 所有电子态的光谱常数都是首次报道. ${\rm{a}}^{3}{\Pi }_{1} \left({\upsilon }{'}\right) \!\leftrightarrow\! {\rm{X}}^{1}{\Sigma }_{{0}^{+}}^{+}\left({\upsilon }{''}\right)$ , ${\rm{a}}^{{3}}{\Pi }_{{{0}}^{{+}}}\left({\upsilon }{'}\right)\!\leftrightarrow\! {\rm{X}}^{1}{\Sigma }_{{0}^{+}}^{+}\left({\upsilon }{''}\right)$ 阻禁跃迁和${\rm{A}}^{1}{\Pi }_{1}\left({\upsilon }{'}\right)\leftrightarrow {\rm{X}}^{1}{\Sigma }_{{0}^{+}}^{+}\left({\upsilon }{''}\right)$ 三能级跃迁都具有高对角分布的弗兰克-康登因子和振动分支比. 并且${{\rm{a}}^{{3}}}{\Pi _{{1}}}$ , ${{\rm{a}}^{{3}}}{\Pi _{{{{0}}^{{ + }}}}}$ 和${{\rm{A}}^{{1}}}{\Pi _{{1}}}$ 态的自发辐射寿命都很短, 能快速地冷却SeH– 阴离子. 中间态${{\rm{a}}^3}{\Pi _{{1}}}$ 和${{\rm{a}}^3}{\Pi _{{{{0}}^{{ + }}}}}$ 的存在不影响构造${\rm{A}}^{1}{\Pi }_{1}\left({\upsilon }{'}\right)\leftrightarrow {\rm{X}}^{{1}}{\Sigma }_{{0}^{+}}^{+}\left({\upsilon }{''}\right)$ 准闭合的循环跃迁. 驱动${\rm{a}}^{3}{\Pi }_{1}\left({\upsilon }{'}\right)\leftrightarrow {\rm{X}}^{{1}}{\Sigma }_{{0}^{+}}^{+}\left({\upsilon }{''}\right)$ 跃迁只需要一束主激光, 由于振动分支比不够大, 驱动$ {\rm{a}}^{{3}}{\Pi }_{{{0}}^{{+}}} \left({\upsilon }{'}\right) $ $\leftrightarrow {\rm{X}}^{{1}}{\Sigma }_{{0}^{+}}^{+}\left({\upsilon }{''}\right)$ 和${\rm{A}}^{{1}}{\Pi }_{1}\left({\upsilon }{'}\right)\leftrightarrow$ $ {\rm{X}}^{{1}}{\Sigma }_{{0}^{+}}^{+}\left({\upsilon }{''}\right) $ 跃迁需要增加两束抽运激光. 所有的激光波长都在可见光的范围内. 本文预测SeH– 阴离子是适合激光冷却的潜在体系. 
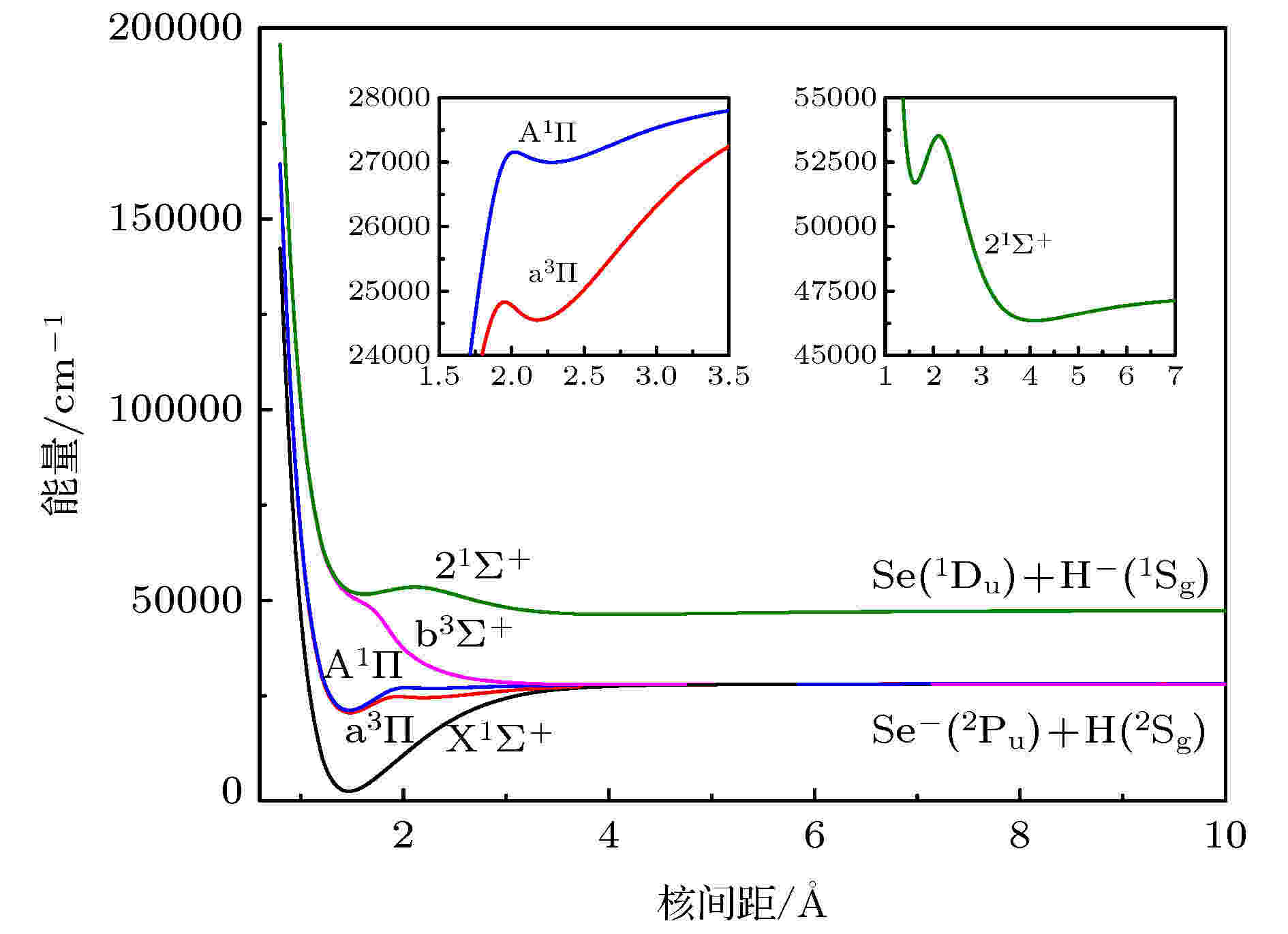 图 1 X1Σ+, a3Π, A1Π, b3Σ+和21Σ+电子态的势能曲线
图 1 X1Σ+, a3Π, A1Π, b3Σ+和21Σ+电子态的势能曲线














































































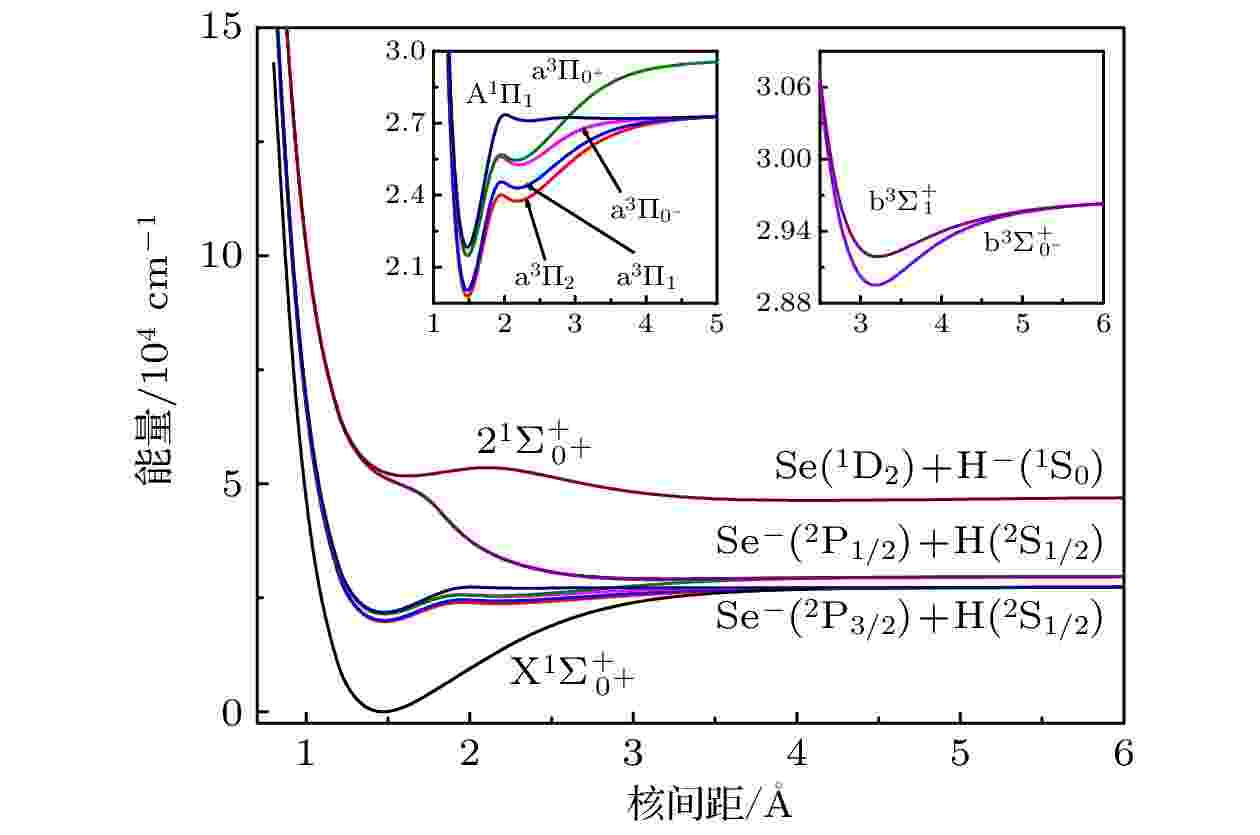 图 2 9个Ω电子态的势能曲线
图 2 9个Ω电子态的势能曲线










































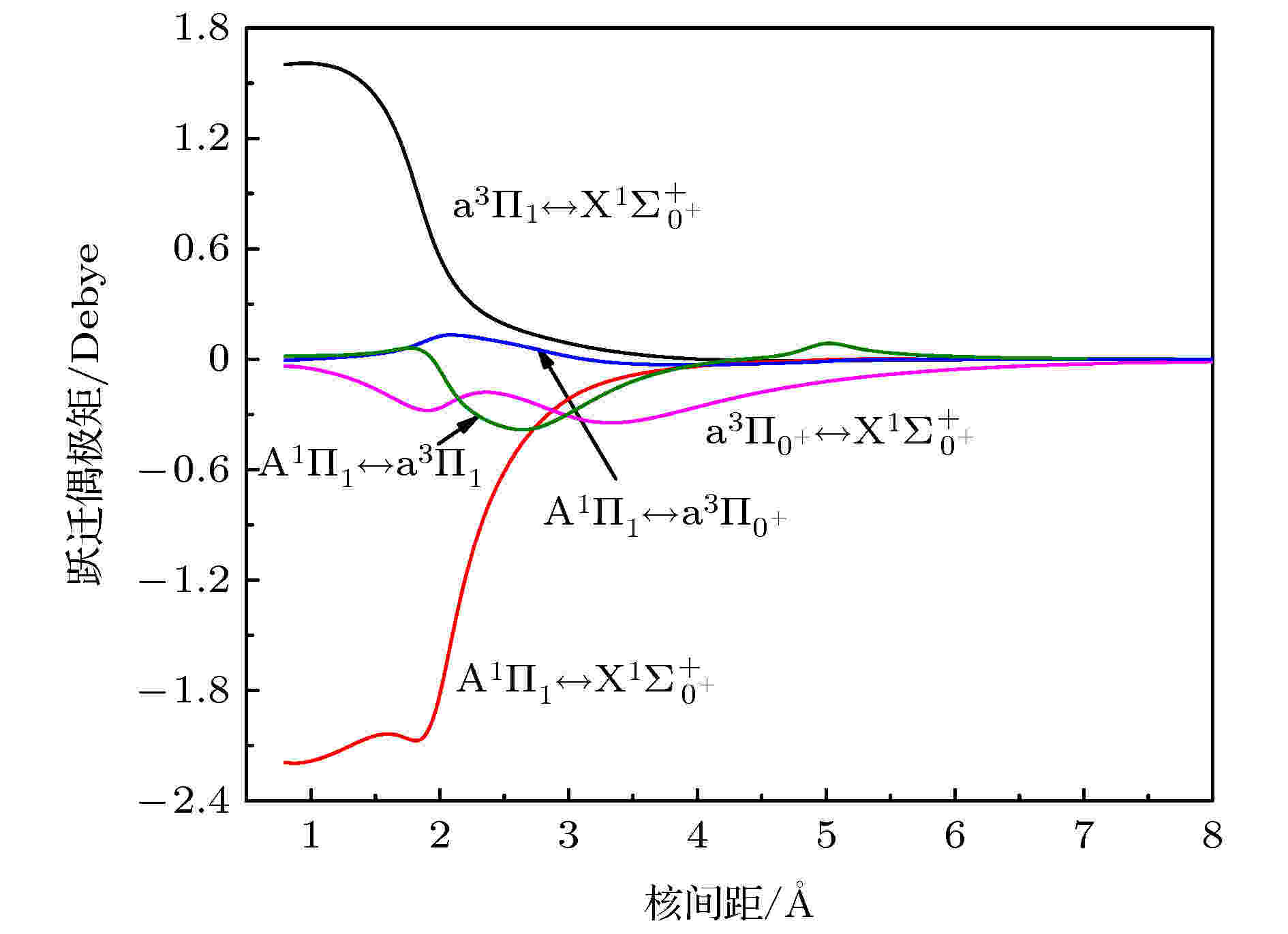 图 3
图 3 
















































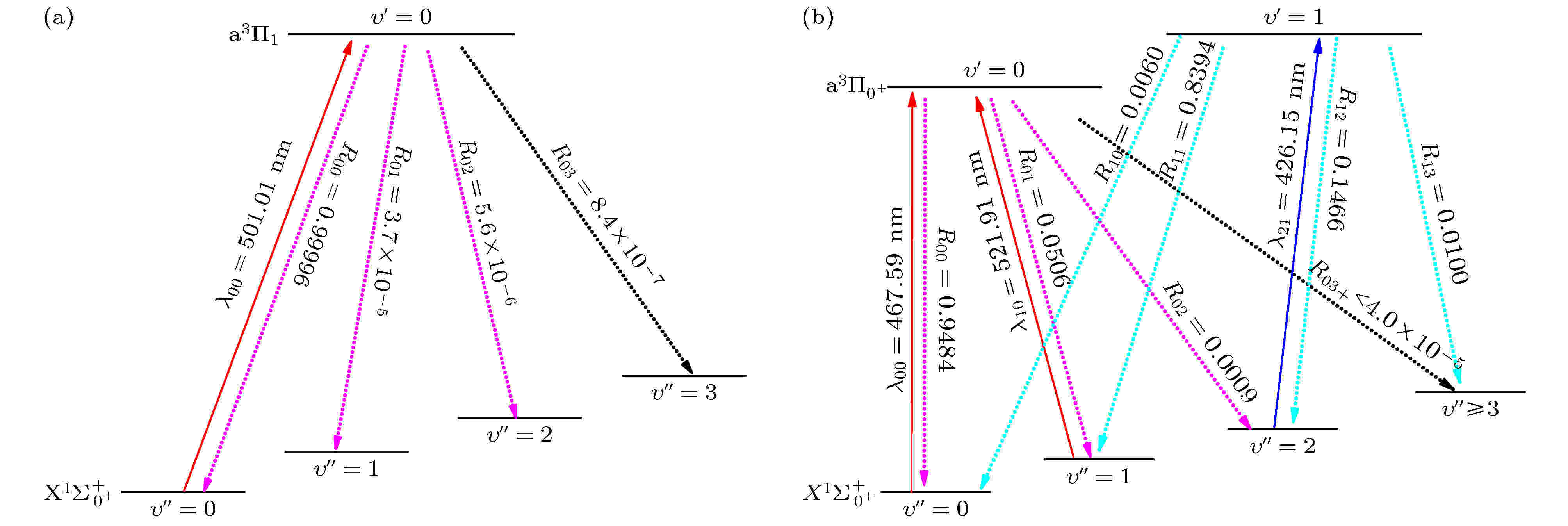 图 4 激光冷却SeH–阴离子的方案 (a)
图 4 激光冷却SeH–阴离子的方案 (a)





















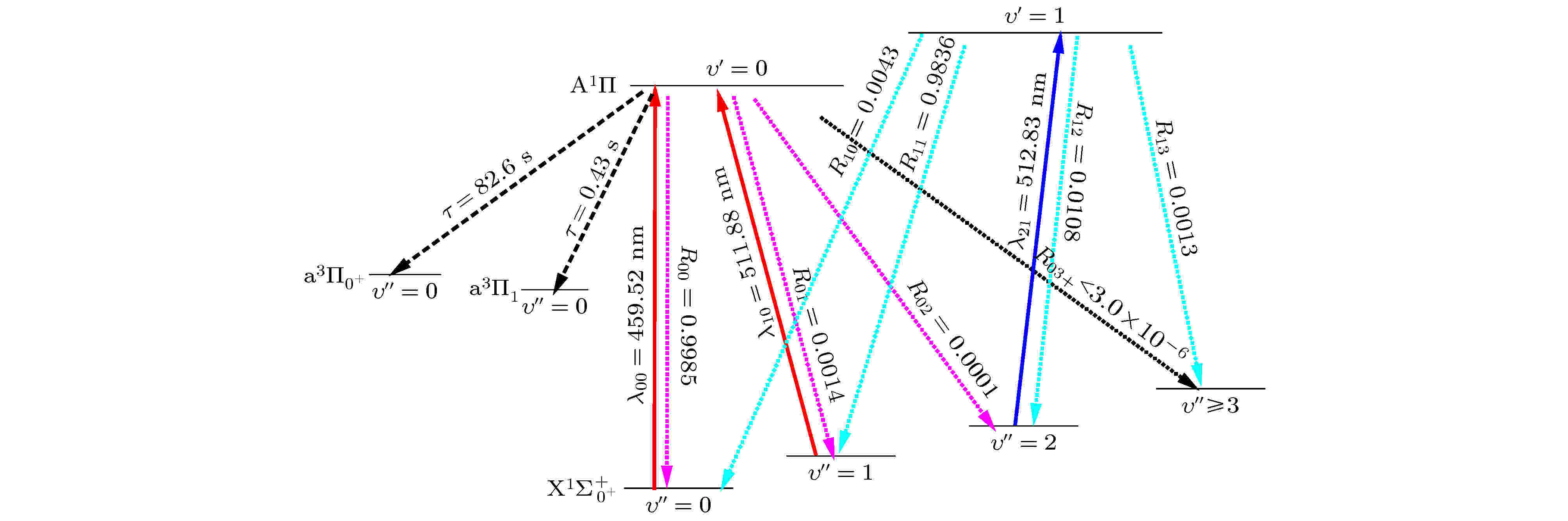 图 5 采用
图 5 采用










































