全文HTML
--> --> -->然而, 当前大能量脉冲激光器的重复频率只能达到10 Hz量级, 难以满足很多实际应用场景对更高重复频率的需求[10,11], 因此迫切需要研制百赫兹量级的重频大能量激光器[12]. 在高泵浦功率密度下, 重复频率的提升将进一步加剧激光系统热效应的累积, 采用高效的冷却结构、准确评估激光介质内的温度分布是高重频大能量激光器突破热效应瓶颈, 实现稳定可靠运行的重要途径. 在冷却结构的设计和介质温度评估中, 大部分研究常采用对流换热系数来简化模型, 而忽视了冷却过程中冷却液温升和流场特性对介质温度分布的影响[12-17]. 针对这一问题, 李策等[18]通过解析表达, 分析了流体直接冷却板条激光器中对流换热系数和冷却液温升与流速的关系, 以及介质的温度和应力分布. 采用标准k-ε或RNG k-ε湍流模型, 文献[19-22]先后建立了热-流-固多物理场耦合模型, 对低温气冷叠片激光器、流体直接冷却板条激光器、薄片激光器的流道结构和激光介质的温度分布进行了研究. 但上述湍流模型对黏性作用较强的固壁区采用壁面函数法作近似处理, 并未细致评估壁面区的流动, 且对流动分离过大或近壁面处于高压下的流动也具有一定的局限性, 因而会影响介质温度分布的评估. 低雷诺数k-ε湍流模型能适应不同的雷诺数区域, 对湍流区和近壁区均采用一套公式计算, 具有较高的计算精度[23]. 目前, 基于低雷诺数k-ε湍流模型, 对背面水冷Nd:YAG激活镜放大器进行热管理的分析尚未报道, 有必要进行深入研究, 为高重频水冷Nd:YAG激活镜放大器的优化设计和稳定运行提供指导.
本文主要研究了高重频大能量背面水冷Nd:YAG激活镜放大器的温度分布特性. 基于低雷诺数k-ε湍流模型, 建立了激活镜放大器流-固共轭传热多物理场耦合分析模型, 利用COMSOL Multiphysics有限元软件对比分析了标准k-ε和低雷诺数k-ε湍流模型近壁面处理方法对流体流动、对流扩散和热传导过程及温度分布的影响, 分析研究了不同流量和泵浦参数下冷却液的流场特性、激光介质温度和波前分布, 并开展了相关实验研究, 实验结果与数值模拟符合较好.
2.1.水冷Nd:YAG激活镜放大器结构模型
二极管泵浦水冷Nd:YAG激活镜放大器的结构如图1(a)所示, 激光介质的背面沉浸在冷却液去离子水中, 侧面和前表面由不锈钢支撑固定; 高功率二极管阵列从Nd:YAG背面泵浦, 种子激光由其前表面注入经背面反射后双程放大输出. 增益介质Nd:YAG口径为52 mm × 32 mm, 厚度为7 mm, 掺杂浓度为1% (原子百分比), 对泵浦光的吸收系数为3.0 cm–1, 一面镀1064 nm高反膜和808 nm增透膜, 另一面镀1064 nm增透膜和808 nm高反膜; 同时介质四周采用紫外固化胶粘合吸收系数为2.5 cm–1、宽为4.5 mm的Cr4+:YAG包边, 以便抑制放大自发辐射和寄生振荡. 假定二极管阵列压缩整形后输出50 mm × 32 mm的平顶光束, 最大泵浦强度为3 kW/cm2, 并以90%的效率耦合进Nd:YAG中被完全吸收. 被吸收的泵浦光一部分直接转化成热, 另一部分以反转粒子数的形式存储在激光上能级, 然后又会以荧光或放大的荧光被包边吸收而产热[24]. 根据前期建立的泵浦和放大过程物理模型[25], 假定Nd:YAG的产热率为37%, 紫外固化胶的厚度为0.5 mm, 考虑Cr4+:YAG的吸收后, 可得放大器激光介质内的热源分布. 为了简化计算模型, 忽略介质前表面的空气对流冷却及不锈钢的传导冷却, 其流道结构如图1(b)所示, 且以Nd:YAG的背面中心为坐标原点; 介质背面与玻璃窗口之间的流道间隔为1.5 mm, 冷却液的初始温度为20 ℃, 其进入流道后先经过导流板, 再流经Nd:YAG背面进行冷却. 计算过程中的物性参数如表1所列[14,26].
图 1 水冷Nd:YAG激活镜放大器的模型 (a) 激活镜放大器结构; (b) 流道结构Figure1. Simulational model of water-cooled Nd:YAG active mirror amplifeir: (a) Configuration of the active mirror amplifier; (b) configuration of cooling channel.
| 物性参数 | Nd:YAG | Optical adhesive | H2O |
| 密度 ρ/(kg·m–3) | 4560 | 1160 | 997 |
| 热导率 k/(W·m–1·K–1) | 15.09(T/164.17)–0.75 | 2.11 × 10–3T + 1.81 | 0.6 |
| 比热 Cp/(J·kg–1·K–1) | 125.4T 0.4005 – 626.4 | 1.48 – 9.72 × 10–3T + 1.79 × 10–5T 2 | 4182 |
| 动力黏度 μ/(kg·m–1·s–1) | — | — | 1.0 × 10–3 |
| 折射率 n0 | 1.82 | 1.65 | — |
| 热光系数(dn/dT )/(10–6 K–1) | –3.946 + 0.053T – 4.5 × 10–5T 2 | — | — |
| 热膨胀系数 α/(10–6 K–1) | –1.850 + 0.044T – 5.7 × 10–5T 2 | 58 | — |
| 杨氏模量 υ/GPa | 308 | 1 | — |
| 泊松比 | 0.232 | 0.38 | — |
表1计算过程中的物性参数
Table1.Physical parameters used in the simulation.
2
2.2.流-固共轭传热理论模型
在激光器泵浦和冷却过程中, 涉及流体流动、对流扩散和热传导等过程, 其中流体的冷却效果与流动状态密切相关. 一般认为湍流比层流的冷却效果更好, 其流动状态可由雷诺数Re确定[23]:用于冷却的去离子水一般可视为不可压缩黏性流体, 其内部的流动状态、对流扩散和热传导可通过连续方程、动量方程和能量方程来描述:
在流-固耦合边界上热耦合条件为
对于固壁区内的流动, 由于分子黏性作用, 流体速度将逐渐降低, 此时Re数较低, 湍流发展并不充分. 然而, 目前常用的标准k-ε模型和RNG k-ε模型等都是针对充分发展的湍流才有效; 为了求解这一区域内的流动, 这些模型引入了壁面函数法, 采用一组半经验的公式将壁面上的物理量与湍流核心区的相应物理量联系起来, 而不对黏性影响比较严重的区域进行有效地计算, 因而并不能细致地评估壁面区的流动, 从而也会影响流-固边界层内的换热[23]. 为此, 本文采用低雷诺数k-ε模型, 使数值模型能适应不同的雷诺数区域, 并结合流-固边界层热耦合条件, 分析流体内的流动状态及与固体之间的传热.
3.1.温度与流场分布
根据图1所示的泵浦方式, 在泵浦光传输方向上, 泵浦光能量按吸收定律呈指数分布. 假设放大器以50 Hz的重复频率运行, 泵浦强度和脉宽分别为1.90 kW/cm2和240 μs, 此时激光介质中横向热沉积分布如图2(a)所示. 从图2(a)可知, 激光介质横向热沉积分布呈中心对称, Cr4+:YAG吸收放大自发辐射光线后产生的热量主要集中在边界中心部分而在四个角上较少, 且在边界处的平均热功率最大可达2.33 × 107 W/m3, 远大于Nd:YAG中平均热功率1.08 × 107 W/m3. 假设冷却液在流道入口处初始温度为20 ℃, 入口总流量为10 L/min, 出口参考静压为0, 基于标准k-ε模型和低雷诺数k-ε模型计算所得的流道中心截面 (x = 0)流速分布、激光介质及中心截面固液边界层中的温度分布, 如图2(b)—(d)所示. 从图2(b)可以看出: 由于导流板的水流匀化作用, 冷却液经过导流板后流速达到最大值, 然后立即降速混合均匀, 在流道末端, 导流板也可减少湍流区域; 然而, 当冷却液进入激光介质背面转接口时, 流速变化较快, 为了消除其对介质冷却的影响, 设计中延长了介质与两端转接口之间的流道距离以便介质背面水流更加均匀. 对比标准k-ε模型和低雷诺数k-ε模型, 两种模型流道内的流速形貌基本一致, 然而介质背面固液边界层内标准k-ε模型中流速相对更大, 界面处甚至达到1.27 m/s, 这主要是由于标准k-ε模型忽视了黏性作用对边界层的影响, 壁面函数法也无法像低雷诺数k-ε模型那样细致地评估壁面区内的速度分布. 由图2(c)和图2(d)可知: 在两种模型中, 激光介质内的最大温升均位于介质表面包边与Nd:YAG边界处, 冷却液流经激光介质吸热后温度会逐渐升高, 从而导致介质内温度分布与热沉积分布不再一致, 沿水流方向不再对称; 然而由于边界层内的黏性作用, 在低雷诺数k-ε模型中固液边界层及介质内的温升表现得更加明显, 标准k-ε模型中由于边界层内的流速较大从而导致纵向热扩散很少, 水流中的纵向温升几乎不存在. 在低雷诺数k-ε模型中, 与Nd:YAG相比包边内的产热更高且横向热传导明显, 因而Nd:YAG前表面的温度分布沿水流方向将稍微降低、然后逐渐升高, 其平均温度达到49.62 ℃, 温差约为3.27 ℃; 而在后表面, 由于水流换热更加显著, Nd:YAG中的温度将随水温升高而一直升高; 当水流经激光介质时, 固液边界层内的温升主要发生在100 μm范围内, 其中界面的温升主要来源于激光介质的传热, 最大温升可达10.85 ℃, 此后热扩散起主要作用, 温升降到1.2 ℃.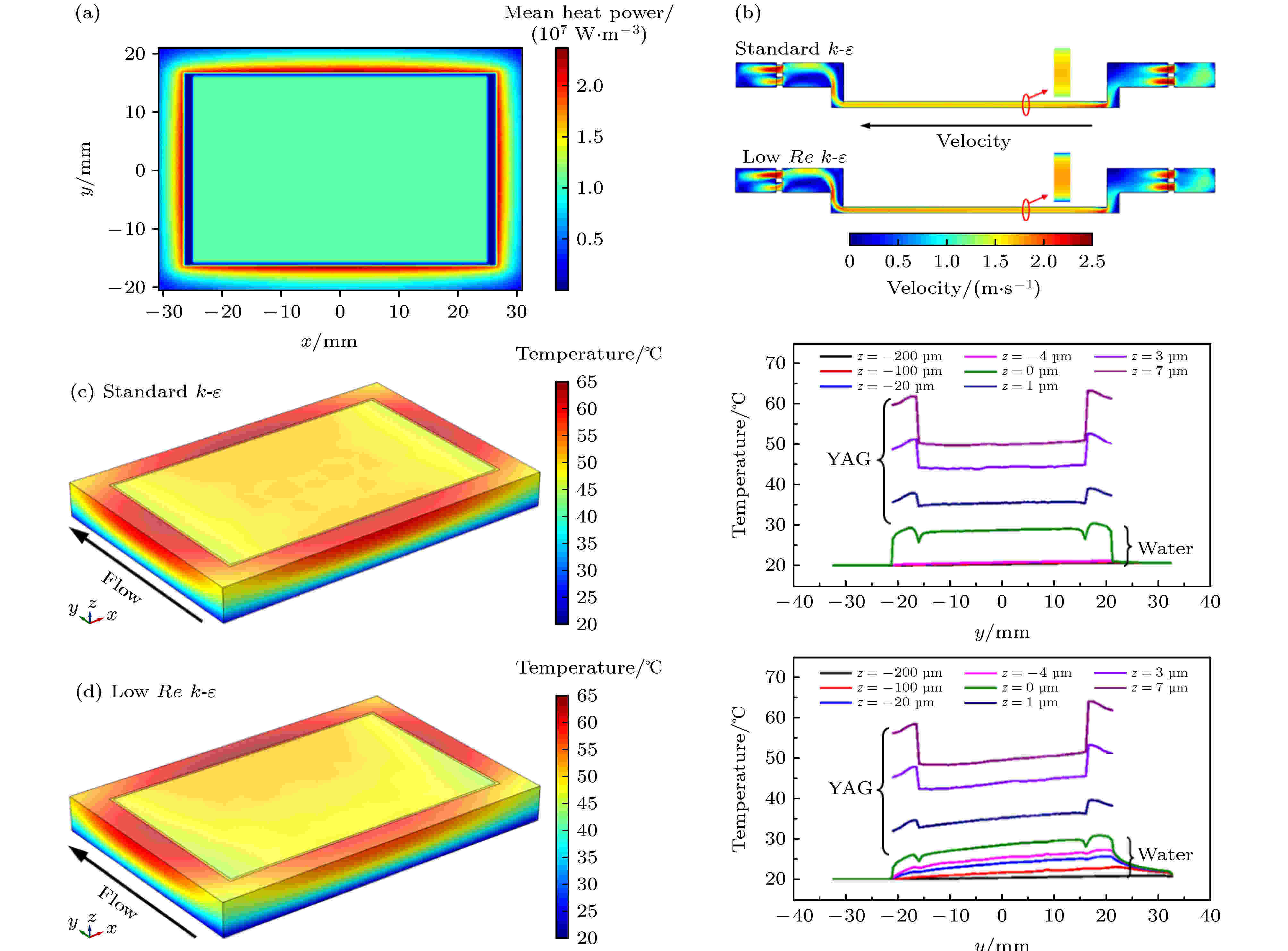
图 2 (a) 激光介质中横向热沉积分布; (b) 流道中心截面流速分布比较; (c) 标准k-ε模型和(d) 低雷诺数k-ε模型中激光介质及固液边界层中的温度分布Figure2. (a) Transverse heat density distribution in the laser medium. (b) Comparison of flow velocity distribution across the center of the cooling channel. Temperature profiles in the laser medium and the solid and liquid boundary layers obtained by (c) the standard k-ε model and (d) low Re k-ε model.
2
3.2.应力应变及波前分布
激光器运行时, 激光介质内的温度梯度将使介质在高温区域产生的热膨胀受到低温区域的制约, 形成不均匀的位移, 从而产生热应力. 根据上述研究, 将低雷诺数k-ε模型获得的激光介质温度分布与固体力学进行耦合, 可得激光介质的热应力和形变分布, 如图3所示. 图3(a)—(c)分别为激光介质沿x, y, z方向的热应力分布, 可以看出, 由于包边内温度梯度较大且前表面形变被约束, 应力主要存在于包边内, 其中最大应力达到361 MPa, 且沿x, y方向的应力分布与温度分布相似. 从图3(d)可以看出, 由于紫外固化胶的膨胀系数较大且弹性模量较小, 因而沿z方向的形变略大于激光介质, 最大达到3.37 μm; Nd:YAG介质内沿z方向的形变中心区域较为均匀, 边缘梯度较大, Nd:YAG介质内最大形变量位于后表面, 达到为3.27 μm.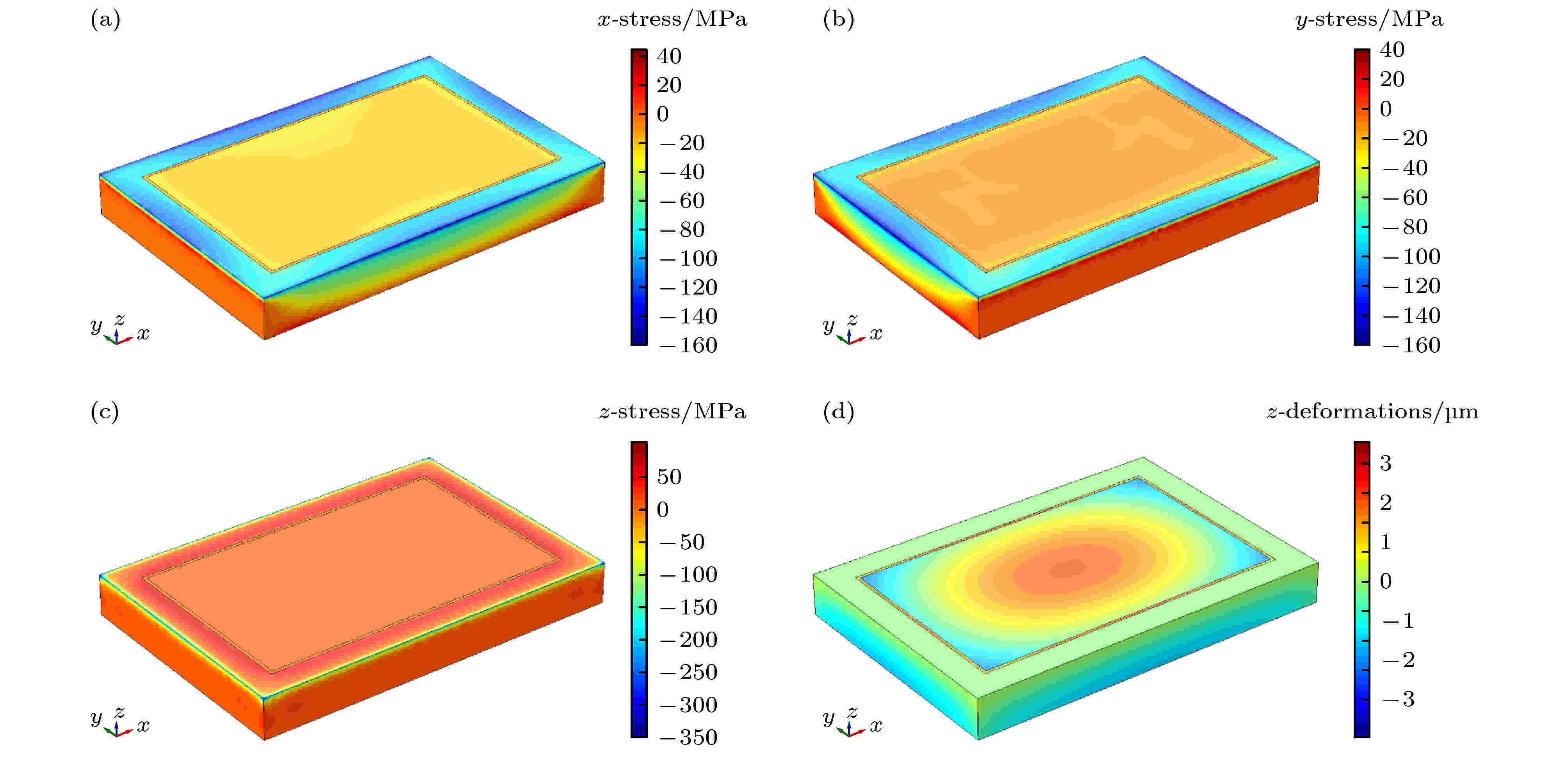
图 3 激光介质沿 (a) x方向、(b) y方向、(c) z方向的应力分布; (d) 激光介质沿z方向的形变分布Figure3. Thermal stress distributions in the laser medium along (a) x direction, (b) y direction, (c) z direction; (d) z-deformation of the laser medium.
此外, 介质内的温度梯度也将导致光束通过放大器后光程差发生变化, 从而引起波前畸变. 对于激活镜放大器, 热致波前畸变主要来源于四方面: 1)激光介质由于热膨胀产生的形变; 2)热光效应导致介质折射率发生变化; 3)热应力引起的弹光效应对折射率的影响; 4)激发态反转粒子引起的电子作用对折射率的影响, 其中后两项的作用相对较小[13]. 根据上述所得的温度、热应力和形变分布可得光束通过Nd:YAG介质后的热致波前畸变, 如图4所示. 从图4可知, 热光效应引起的波前畸变与温度分布基本一致, 波前PV (peak-to-valley)值为0.78λ; 形变引起的畸变与热光效应引起的畸变相反, 对总波前具有较大的影响, 且中心低、边缘高, 四周顶角热畸变较大, 约7.45λ; 由于热光效应对形变的补偿, Nd:YAG中总波前畸变PV值降到7.27λ, RMS (root mean square, RMS)值约为2.88λ.
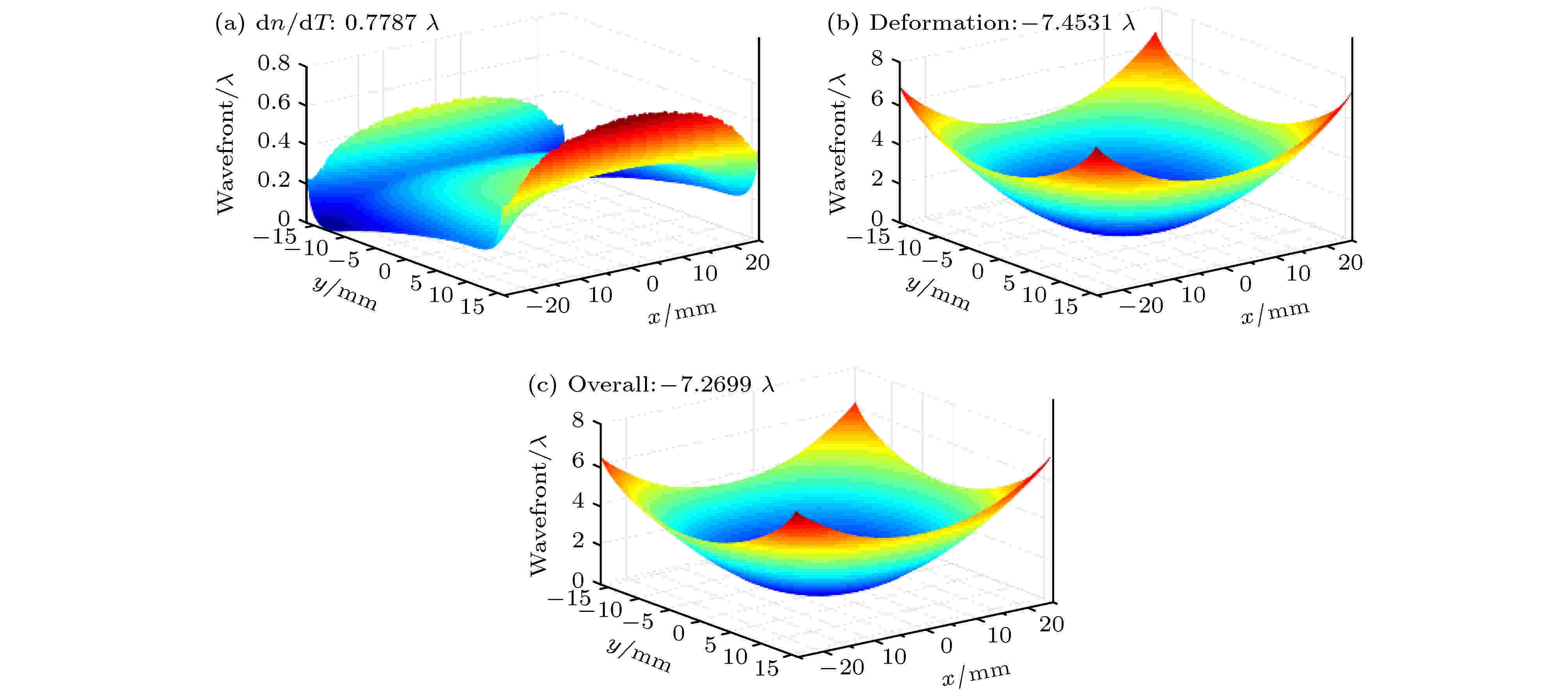图 4 Nd:YAG中热致波前畸变(λ = 1064 nm) (a) 热光效应引起的畸变; (b) 形变引起的畸变; (c) 总波前畸变Figure4. Thermally induced wavefront distortions in the Nd:YAG slab: (a) Thermal-optical effect induced wavefront distortion; (b) the deformation induced wavefront distortion; (c) the overall wavefront distortion.
2
3.3.流量对激光介质温度和波前分布的影响
在散热过程中, 激光介质表面的对流换热与流道的设计, 流体的物性参数以及受热条件等密切相关, 其中流体流量是影响换热的一个关键因素. 在上述研究的基础上, 基于低雷诺数k-ε模型, 模拟分析了不同流量下激光介质的温度和波前分布. 假定冷却液在流道入口处总流量从2.5 L/min增加至22.5 L/min (间隔为2.5 L/min), 放大器的运行条件保持不变, 其计算结果如图5所示. 从图5可知, 随着流速增加, Nd:YAG前表面的平均温度和温差都将逐渐降低, 但增益介质中最高温度点始终保持不变, 且当流量超过12.5 L/min后, 温度变化逐渐平缓, 温度分布总体形貌基本一致; 同时, 由于温度梯度降低, 波前畸变也相应减少, 其PV值由7.92λ降低到7.13λ, 最后趋于稳定.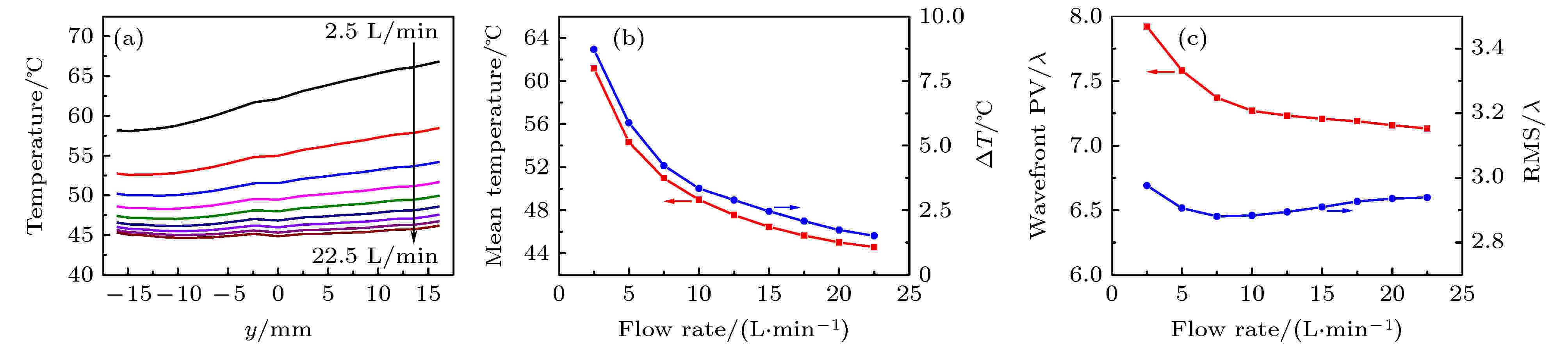
图 5 流量对Nd:YAG前表面温度分布和介质波前的影响 (a) 中心截面(x = 0)处温度分布曲线; (b) 平均温度和沿水流温差分布; (c) 波前分布Figure5. Temperature field distributions and wavefront distortions of gain medium at different flow rates: (a) Temperature profiles across the center of gain medium; (b) mean temperature and temperature difference distributions; (c) wavefront distortions.
2
3.4.泵浦参数对激光介质温度和波前分布的影响
在放大器运行过程中, 泵浦参数, 如泵浦光强度和重复频率等, 将直接影响介质中的热负载, 从而影响放大器的热效应. 假定放大器以50 Hz重频运行, 泵浦脉宽为240 μs, 将泵浦电流从100 A增加到390 A, 相应的泵浦强度从0.63 kW/cm2递增到2.95 kW/cm2, 流量为10 L/min, 则泵浦强度对Nd:YAG温度和波前的影响如图6(a)和图6(c)所示. 随着泵浦强度的增加, Nd:YAG介质前表面平均温度和温差、波前PV和RMS值均线性增加, 当泵浦强度达到2.95 kW/cm2时, 平均温度和温差分别达到67.89 ℃和3.54 ℃, 波前PV和RMS值分别为12.17λ和4.80λ. 此外, 假定放大器泵浦强度和脉宽分别为1.90 kW/cm2和240 μs, 流量保持不变, 改变放大器的运行频率, 则激光介质的温度变化和波前分布如图6(b)和图6(d)所示. 随着运行频率从10 Hz增加到60 Hz, 增益介质前表面的平均温度和温差、波前PV和RMS值也近似线性增加, 当重复频率低于35 Hz时, Nd:YAG前表面平均温度和温差分别在41 ℃和1.5 ℃以内, 波前PV和RMS值分别在4.93λ和1.95λ以内.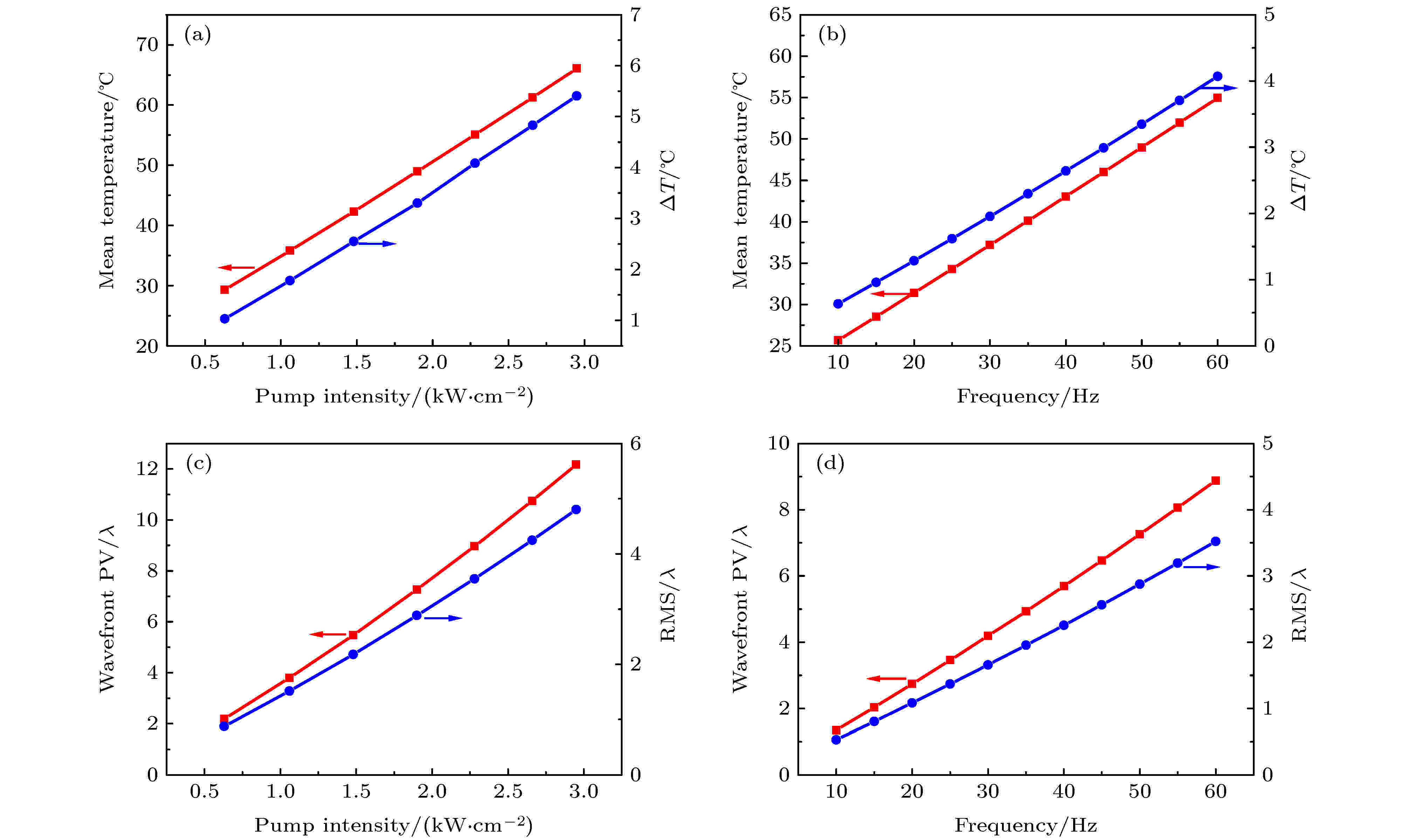
图 6 Nd:YAG前表面平均温度、温差及介质波前随(a), (c)泵浦功率和(b), (d)重复频率的变化Figure6. Average temperature and temperature difference on the front surface of Nd:YAG and the wavefront distortions of the gain medium at different (a), (c) pump intensities and (b), (d) repetition rates.
2
3.5.实验验证
为了验证理论分析模型, 采用红外热像仪对Nd:YAG激活镜放大器的表面温度分布进行了测量, 并与低雷诺数k-ε模型的分析结果进行比较. 放大器运行时, 二极管泵浦电流为250 A, 泵浦脉宽为240 μs, 相应的泵浦强度为1.9 kW/cm2, 通过观察前表面的荧光分布来保证泵浦沉积的对称性, 同时为了避免种子激光对测量结果的影响, 测量时放大器没有通光. 放大器在50 Hz重复频率下运行时, Nd:YAG介质前表面实验测得的温度分布与数值模拟结果整体形貌基本符合; 但实验测得的最高温度点位于顶端右侧, 这主要是由于压缩整形后泵浦源左右不对称或二极管阵列巴条的泵浦强度不一致所致, 如图7所示. 此外, 调节泵浦源的重复频率, 测量了放大器10—60 Hz运行下Nd:YAG前表面的温度分布, 其最高温度点处沿水流方向的温度分布曲线, 前表面的平均温度和温差, 如图8所示. 从图8可知: 随着热负载的增加, Nd:YAG前表面的温度逐渐升高, 且最高温度点位置保持不变; 对于Nd:YAG前表面的平均温度, 实验测量和数值模拟的结果基本符合, 且两者之间的差异与频率无关; 当频率小于25 Hz时, 实验测量与数值模拟的温差基本一致, 此后随频率的增加, 两者之间的差异逐渐变大, 这主要是由于数值模型忽略了Nd:YAG背面介质膜层的热阻和不锈钢支撑件的热传导所致.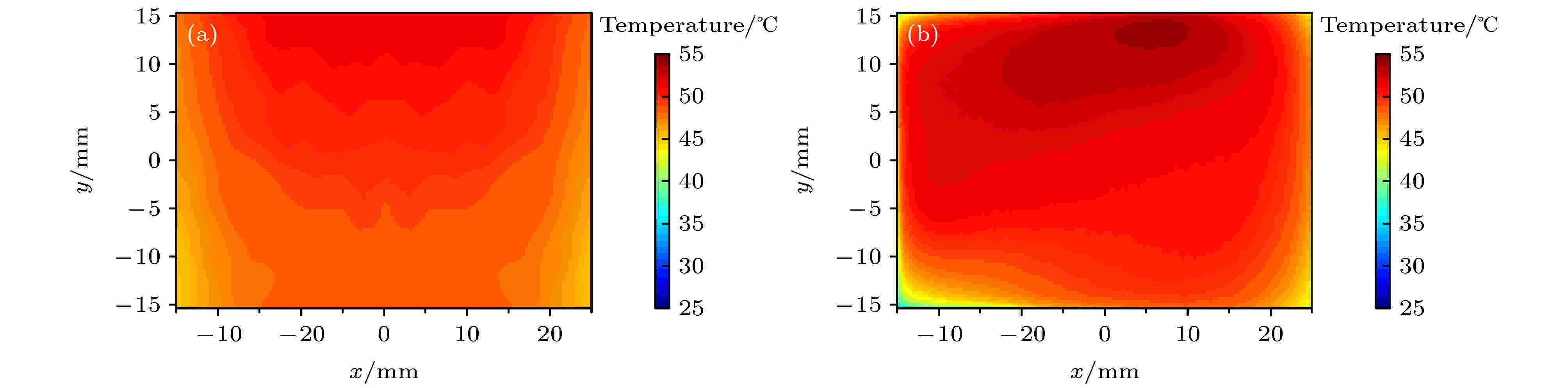
图 7 50 Hz重复频率下Nd:YAG前表面的温度分布 (a) 数值模拟值; (b) 实验测量值Figure7. Temperature field distributions on the front surface of Nd:YAG operating at the repetition rate of 50 Hz: (a) Numerical simulation results; (b) experimental results.
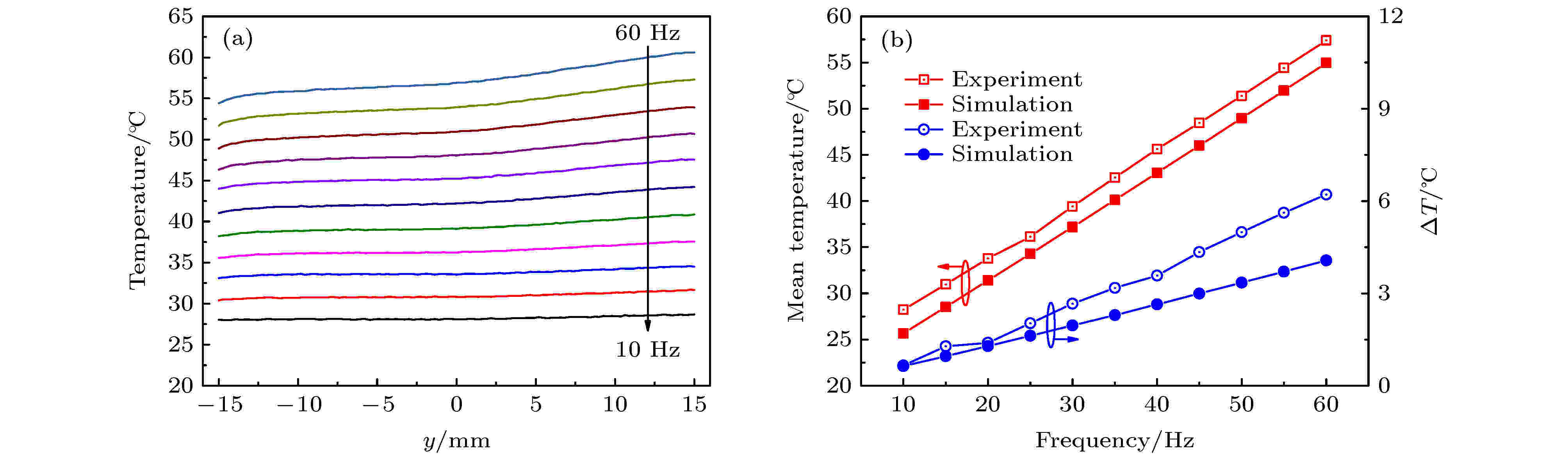图 8 (a) 实验测量的Nd:YAG最高温度点处沿水流方向的温度分布曲线; (b) Nd:YAG前表面平均温度和温差的理论与实验对比Figure8. (a) Measured longitudinal temperature profiles through the peak temperature of Nd:YAG; (b) theoretical and experimental comparison of the average temperature and temperature difference on the front surface of Nd:YAG.
