摘要:比例积分调节单相H桥光伏逆变器存在复杂的分岔与混沌等非线性行为, 这些非线性行为会大大增加输出电流的谐波含量, 降低系统运行的稳定性与供电可靠性. 现有的混沌控制方法存在建模复杂、控制系数难以确定等问题. 针对于此, 本文提出了一种改进指数延迟反馈控制方法. 该方法首先利用系统输出电流与其自身延迟的差值形成反馈信号, 然后将该反馈信号通过指数环节、作差环节和比例环节得到控制信号, 并将该控制信号以反馈的形式施加于被控系统, 同时建立系统的离散映射模型并求取系统雅克比矩阵表达式; 最后基于稳定判据推导出该控制信号的反馈控制系数的限定条件并实施对系统的控制. 为了验证该方法的控制效果, 进行了大量的仿真实验. 结果表明, 该方法能有效抑制系统中的混沌行为, 大大扩展系统稳定运行域.
关键词: 比例积分调节/
单相H桥光伏逆变器/
混沌控制/
改进指数延迟反馈控制

English Abstract

全文HTML

--> --> -->

通常电力电子装置中都含有各种各样的开关器件和非线性负载等, 呈现出丰富的非线性行为^[1-5]. H桥逆变器作为一种常见的电力电子装置, 已经广泛应用于分布式发电系统、微网系统、不间断供电系统及各种电力电子系统中^[6,7], 是新能源并网的关键接口部分^[8-10]. 同时, H桥逆变器作为一种时变非线性系统, 其表现出的非线性行为, 诸如倍周期分岔、Hopf分岔等会大大增加开关应力与谐波含量, 降低并网系统的供电可靠性与运行稳定性^[11-13], 严重劣化系统的整体性能. 因此, 探索一种能有效抑制分岔与混沌行为的控制方法具有重要理论和实践意义.
近年来, 已有****对H桥逆变器的分岔与混沌行为进行了研究, 并取得了一些成果. 文献[14,15]研究了脉冲宽度调制(pulse width modulation, PWM)控制的单相H桥逆变器的边界碰撞分岔现象, 给出了系统分段离散映射模型与状态变量边界解析式, 指出发生边界碰撞现象的本质原因是占空比的有界性; 文献[16,17]研究了电压型单相H桥逆变器的快尺度不稳定现象, 发现这种现象的本质是局部的倍周期分岔. 文献[18]分别基于平均状态模型和离散映射模型研究了两个单相H桥逆变器在并联模式下运行时慢尺度不稳定现象和快尺度不稳定现象, 给出了参数的稳定运行域. 文献[19]采用时域图、分岔图及李亚普诺夫指数谱对基于周期性扩频的单相H桥逆变器中的非线性现象进行了研究, 发现扩频调制下的单相H桥逆变器更容易进入非线性区域. 文献[20]采用分岔图对比例控制下单相H桥逆变器中多个系统参数变化时的非线性行为进行了研究. 这些研究对揭示单相H桥逆变器的分岔与混沌等非线性行为的产生机理具有重要意义, 同时也为深刻认识这种非线性行为的本质奠定了理论基础. 然而, 这些研究都没有进一步考虑如何对这些非线性行为进行有效的控制来提升系统性能. 文献[21]将时间延迟反馈控制应用于工作在DC-DC模式下的单相H桥变换器. 文献[22]将扩展的时间延迟反馈控制应用于单相H桥逆变器, 控制器采用比例控制, 控制效果差, 对实际工程的意义不大. 文献[23]采用基于滤波器的混沌控制法对单相H桥逆变器中的非线性行为进行控制, 但没有给出控制系数的选择依据, 只能通过试凑法来确定, 实用性有限.
本文针对目前比例积分(proportional integral, PI)调节单相H桥逆变器混沌控制方面存在的不足, 提出了一种改进指数延迟反馈控制方法(improved exponential delayed feedback control, IEDFC). 该方法首先构建系统离散映射模型; 然后, 通过取输出电流与自身延迟一定时间的参量之差经过相关指数环节、作差环节和比例环节获得控制所需的反馈信号; 最后, 基于稳定判据推出反馈系数的限定条件, 并将该方法应用于单相H桥光伏逆变器的混沌控制中. 结果表明, 该方法能有效抑制系统中的分岔与混沌行为, 有效拓展系统的稳定工作范围.

2

-->

2.1.离散模型

PI调节光伏逆变器原理如图1(a)和图1(b)实线所示. 光伏阵列的输出接至具有最大功率点跟踪功能的Boost升压变换器的输入端, 与升压电路并联的稳压电容C提供H桥逆变器直流侧电压E, 桥臂上2对开关管(S₁S₃)和(S₂S₄)(带反并联二极管)采用双极性正弦脉宽方式进行调制, 输出端是电感L和电阻R组成的阻感性负载. 输出电流i经过电流传感器采样后与参考电流i_ref相比较, 经过PI控制器得到调制信号i_con.
图 1 PI调节单相H桥光伏逆变器控制系统　(a)引入EDFC系统原理图; (b) 引入IEDFC系统原理图
Figure1. PI regulating single-phase H-bridge photovoltaic inverter control system: (a) System schematic diagram with EDFC applied; (b) system schematic diagram with IEDFC applied

以输出电流i为状态变量, S₁S₃和S₂S₄按互补方式工作, 变换器存在2种工作模态, 在第n个开关周期T内系统的状态方程可表示为:

$ {T}_{1}\!:\left\{ \begin{array}{l}{\rm{S}}_{\rm{1}}{\rm{S}}_{\rm{3}}:\rm{on};\;{\rm{S}}_{\rm{2}}{\rm{S}}_{4}:\rm{off,}\\ \dfrac{{{\rm{d}}}{i}\left(t\right)}{{{\rm{d}}}t}=-\dfrac{R}{L}i\left(t\right)+\dfrac{E}{L}, \end{array} \rm{ }\begin{array}{c}nT \!<\! t\leqslant \left(n+{d}_{n}\right)T,\end{array} \right.$

${T}_{2}\!:\left\{ \begin{aligned}&{\rm{S}}_{\rm{1}}{\rm{S}}_{3}:\rm{off};\;{\rm{S}}_{\rm{2}}{\rm{S}}_{4}:\rm{on,}\\ &\dfrac{{{\rm{d}}}i(t)}{{{\rm{d}}}t}\!=\!-\dfrac{R}{L}i(t)\!-\!\dfrac{E}{L},\end{aligned} \rm{ }\begin{array}{c}(n\!+\!{d}_{n})T \!<\! t\!\leqslant \! (n\!+\!1)T,\end{array} \right. $

其中, 占空比d_n表示第n个开关周期中S₁, S₃导通时间在整个开关周期T内所占比例. 以开关周期T为采样间隔, 采用频闪映射法得到主电路离散模型:

$\begin{split}{i_{n + 1}} \!=\;& {{\rm{e}}^{ - \tfrac{R}{L}T}}{i_n} \!+\! \bigg[ {\frac{2}{R}{{\rm{e}}^{ - \tfrac{{\left( {1 - {d_n}} \right)RT}}{L}}} \!-\! \frac{1}{R}\Big( {1 \!+\! {{\rm{e}}^{ - \tfrac{R}{L}T}}} \Big)} \bigg]E \\& \left( {0 \leqslant {d_n} \leqslant 1} \right).\\[-10pt]\end{split}$

对PI调节电流控制部分, 采用先频域分析, 再拉氏反变换得到调制信号的状态方程式:

$\frac{{{\rm{d}}{i_{{\rm{con}}}}(t)}}{{{\rm{d}}t}} = {k_{\rm{p}}}\frac{{{\rm{d}}{i_{\rm{e}}}\left( t \right)}}{{{\rm{d}}t}} + {k_{\rm{i}}}{i_{\rm{e}}}\left( t \right),$

式中k_p, k_i分别为比例、积分系数,$ i_{\rm e}(t)=i_{\rm ref}(t)–i(t) $, 令$u(t)=k_p [{\rm d}i_{\rm ref} (t)/{\rm d}t]+k_{\rm i}i_{\rm ref}(t),$则有

$\frac{{{\rm{d}}{i_{{\rm{con}}}}\left( t \right)}}{{{\rm{d}}t}} = - {k_{\rm{p}}}\frac{{{\rm{d}}i\left( t \right)}}{{{\rm{d}}t}} - {k_{\rm{i}}}i\left( t \right) + u\left( t \right).$

基于准静态的思想, 令$ i_{\rm ref}(t)=i_{\rm refm}\sin(\omega nT) $. 结合(1)式—(3)式以及(5)式得到PI调节电流控制部分的离散模型:

${i_{{\rm{con}}}}(n) = {p_1}{i_{n - 1}} + {i_{{\rm{con}}}}(n - 1) + {p_2}E + T{U_{n - 1}},$

式中

$\begin{split} &{p_1} = \left( {{k_{\rm{i}}}\frac{L}{R} - {k_{\rm{p}}}} \right)\Big( {{{\rm{e}}^{ - \tfrac{R}{L}T}} - 1} \Big),\\ &{p}_{2}=\left({k}_{\rm{i}}\frac{L}{R}\!-\!{k}_{\rm{p}}\right)\left(\frac{2}{R}{\rm{e}}^{-\tfrac{\left(1-{d}_{n-1}\right)RT}{L}}\!-\!\frac{1}{R}\!-\!\frac{1}{R}{\rm{e}}^{-\tfrac{R}{L}T}\right)\!\!\\&\quad\quad+ \frac{{k}_{\rm{i}}T}{R}\left(1-2{d}_{n-1}\right), \\ &U{}_{n-1}={k}_{\rm{p}}{I}_{\rm{m}}\omega \mathrm{cos}\left(\omega (n-1)T\right)\!+\!{k}_{\rm{i}}{I}_{\rm{m}}\mathrm{sin}\left(\omega (n-1)T\right). \end{split}$

综上, 逆变器的离散映射模型方程可表示为:

$ \left\{ \begin{split}&{i}_{n+1}={\rm{e}}^{-\tfrac{R}{L}T}{i}_{n}\!\!+\!\!\left[\frac{2}{R}{\rm{e}}^{-\tfrac{\left(1-{d}_{n}\right)RT}{L}}\!\!-\!\!\frac{1}{R}\Big(1\!+\!{\rm{e}}^{-\tfrac{R}{L}T}\Big)\right]E, \\ &{i}_{\rm{con}}\left(n\right)={p}_{1}{i}_{n-1}+{i}_{\rm{con}}(n-1)+{p}_{2}E+T{U}_{n-1}, \\&{d}_{n}=\frac{1}{2}\left(1+{i}_{\rm{con}}(n)\right),\;\;\;\; 0 \leqslant {d}_{n}\leqslant 1.\end{split} \right.$

2 -->

2.2.PI调节光伏逆变器的混沌现象

PI调节器的比例增益是逆变器设计的关键参数. 另外, 由于光伏系统的随机性和间歇性, 系统的输入电压存在一定的波动, 可能导致系统运行处于不稳定状态. 为此, 分别深入分析了比例控制系数k_p、系统直流侧输入电压E与系统稳定性的关系. 当取k_p为分岔参数时, E = 250 V; 当取E为分岔参数时, k_p = 1. 利用(7)式, 分别以k_p, E为分岔参数, 以调制信号周期T_s为采样周期, 其他电路参数按表1配置, 考查了系统状态的演化过程, 得到峰值处电感电流的分岔图如图2(a)和图2(b)所示.

电路参数	取值	电路参数	取值
直流侧输入电压E/V	250	载波itri的最大值	1
电感L/mH	7	载波itri的最小值	–1
电阻R/Ω	20	积分控制系数ki	180
给定参考电流幅值 irefm/A	5	开关频率fs/kHz	20
载波itri的周期T/μs	50	调制信号icon的 周期Ts/s	0.02

表1电路参数设定值
Table1.Set values of circuit parameters.

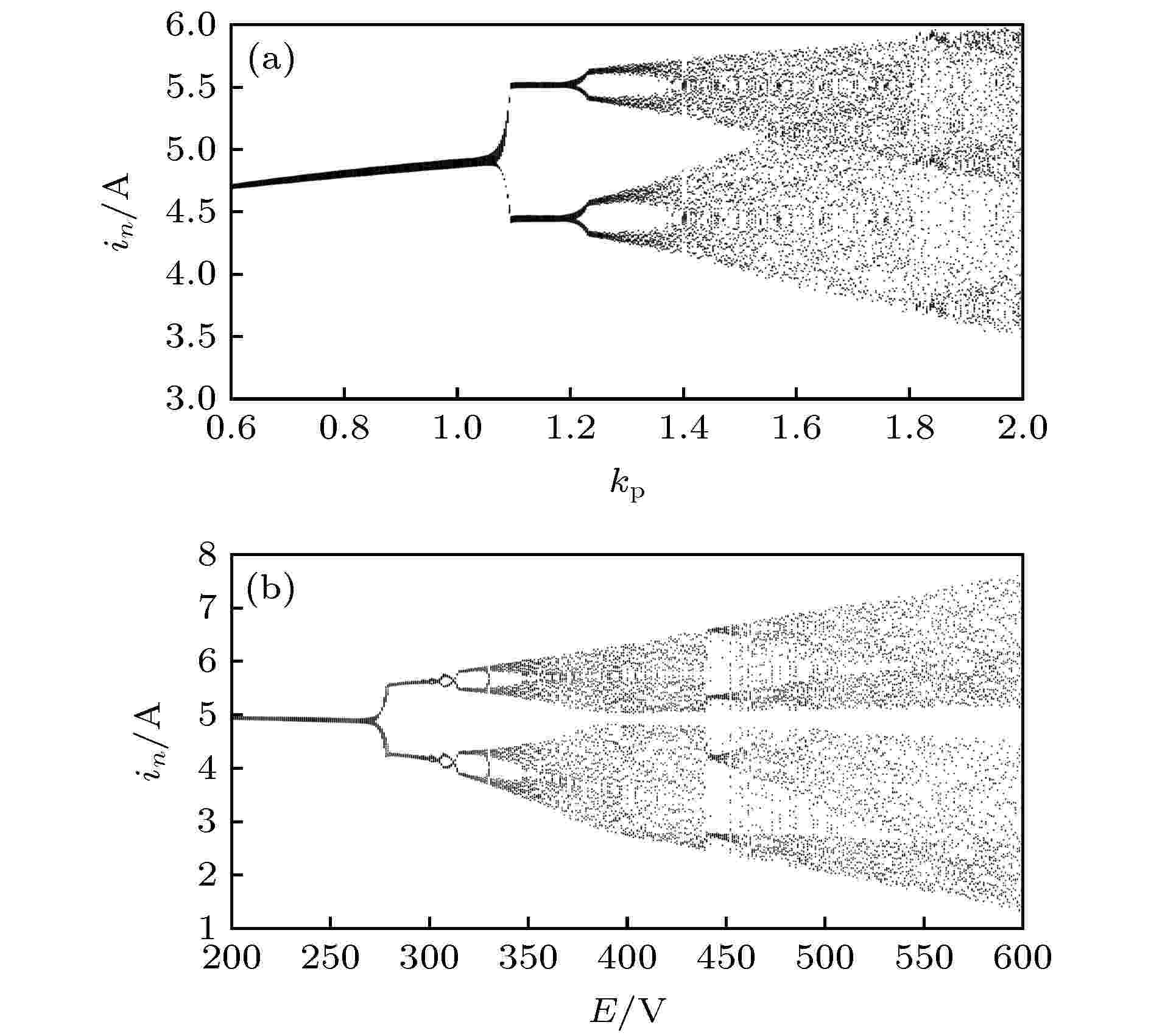图 2 未引入混沌控制时电感电流峰值处分岔图(n = 100+400k, k = 1, 2, 3, ···)　(a) k_p为分岔参数时分岔图; (b) E为分岔参数时分岔图
Figure2. Bifurcation diagram with inductance current at peak value without chaos control (n = 100+ 400k, k = 1, 2, 3, ···): (a) Bifurcation diagram with k_p as bifurcation parameter; (b) bifurcation diagram with E as bifurcation parameter.

由图2(a)和图2(b)可以看出, 随着分岔参数k_p, E的增大, 系统从1-周期态变化进入2-周期态, 之后逐渐过渡到混沌态.
由(7)式可得系统输出电流i_n、调制信号i_con(n)、占空比d_n对应的平衡点I_Q, I_conQ, D_Q:

$\begin{split} &{I_{\rm{Q}}} = \dfrac{{\left[ {\dfrac{2}{R}{{\rm{e}}^{ - \tfrac{{\left( {1 - {D_{\rm{Q}}}} \right)RT}}{L}}} - \dfrac{1}{R}\left( {1 + {{\rm{e}}^{ - \tfrac{{RT}}{L}}}} \right)} \right]E}}{{1 - {{\rm{e}}^{ - \tfrac{{RT}}{L}}}}},\\ &{I_{{\rm{conQ}}}} = \frac{{{U_{n - 1}}R}}{{{k_{\rm{i}}}E}},\;{D_{\rm{Q}}} = \frac{1}{2}\left( {\frac{{{U_{n - 1}}R}}{{{k_{\rm{i}}}E}} + 1} \right). \end{split}$

取系统状态变量为$ X_n=[i_n~~ i_{n-1}~~ i_{\rm con}(n-1)]^{\rm T},$令

$\begin{split}& A = \frac{{ET}}{L}{{\rm{e}}^{ - \tfrac{{(1 - {D_{\rm{Q}}})RT}}{L}}},\\& B = {k_{\rm{i}}}\frac{L}{R} - {k_{\rm{p}}},~~C = {{\rm{e}}^{ - \tfrac{{RT}}{L}}} - 1.\end{split}$

可得平衡点处的雅克比矩阵:

${{J}}({{{X}}_{\rm{Q}}}) \!=\! \left[\! \begin{array}{*{20}{c}} {{{\rm{e}}^{ - \tfrac{{RT}}{L}}}}&{ABC}&{A\Big( {1 \!+\! AB \!-\! \dfrac{{{k_{\rm{i}}}TE}}{R}} \Big)} \\ 1&0&0 \\ 0&{BC}&{1 \!+\! AB - \dfrac{{{k_{\rm{i}}}TE}}{R}} \end{array}\! \right].$

由特征方程式$ {\rm det} [\lambda I - J( X_Q)]=0 $可求得其特征值λ₁, λ₂, λ₃. 分别绘制k_p从0.6增大到2.0、E从200 V增大到600 V时, 特征值λ₁, λ₂, λ₃的轨迹图如图3(a)和图3(b)所示. 根据平衡点处雅克比矩阵稳定性判断准则, 由图3(a)和图3(b) 可知, 当k_p = 1.0928, E = 275 V时, 特征值λ₃ = –1, 而特征值λ₁, λ₂均在单位圆内. 可知此时系统发生倍周期分岔. 随着k_p, E的继续增大, 系统逐渐过渡到不稳定态. 由此可知, 系统是因为发生倍周期分岔后进入混沌态, 图2与图3相符合.
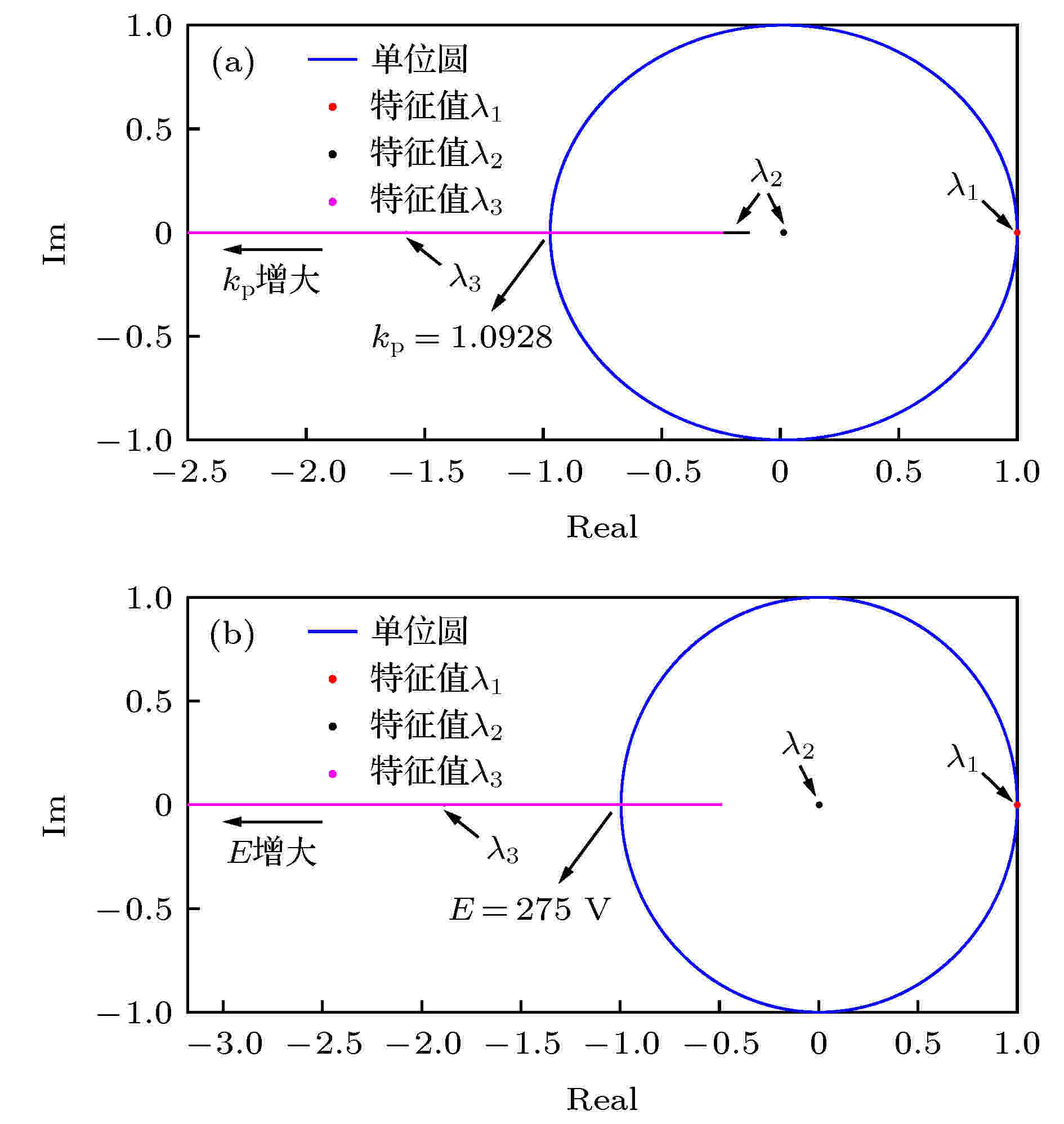图 3 未引入混沌控制时特征值轨迹图　(a) k_p从0.6增大到2; (b) E从200 V增大到600 V
Figure3. Eigenvalue trajectory without chaos control: (a) k_p increasing from 0.6 to 2; (b) E increasing from 200 V to 600 V.

2

-->

3.1.直接引入指数延迟反馈控制

指数延迟反馈控制(exponential delayed feedback control, EDFC)^[24]的基本原理是利用系统输出与自身延迟一定时间的参量之差, 以指数函数的形式反馈给混沌系统, 实现系统由混沌态到稳定态的转变.
将EDFC应用于PI调节下单相H桥光伏逆变器中, 如图1(a)中虚线部分所示. 由上述分析可知, 要控制系统的混沌行为实质上就是控制系统的倍周期分岔. 因此重点分析引入EDFC后系统平衡点处雅克比矩阵特征值的变化轨迹. 本文延迟时间取τ = T. 此时调制信号i_con的离散模型为

$\begin{split} {i}_{\rm{con}}(n)=\;&\left[{p}_{1}{i}_{n-1}+{i}_{\rm{con}}(n-1)+{p}_{2}E+T{U}_{n-1}\right] \\&\times {\rm{e}}^{\left({i}_{n}-{i}_{n-1}\right)}, \\[-10pt]\end{split}$

系统平衡点处雅克比矩阵为

${{J}}({{{X}}_{\rm{Q}}}) = \left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{ - \tfrac{{RT}}{L}}} + A{I_{{\rm{conQ}}}}}&{A\left( {BC - {I_{{\rm{conQ}}}}} \right)}&{A\left(1 + AB - \dfrac{{{k_{\rm{i}}}TE}}{R}\right)} \\ 1&0&0 \\ {{I_{{\rm{conQ}}}}}&{BC - {I_{{\rm{conQ}}}}}&{1 + AB - \dfrac{{{k_{\rm{i}}}TE}}{R}} \end{array}} \right].$

结合(3)式和(9)式, 分别以k_p, E为分岔参数, 以T_s为采样周期, 得到系统引入EDFC后电感电流峰值处分岔图如图4(a)和图4(b)所示. 引入EDFC后, k_p从0.6增大到2.0、E从200 V增大到600 V时, 特征值λ₁, λ₂, λ₃的轨迹图如图5(a)和图5(b)所示.
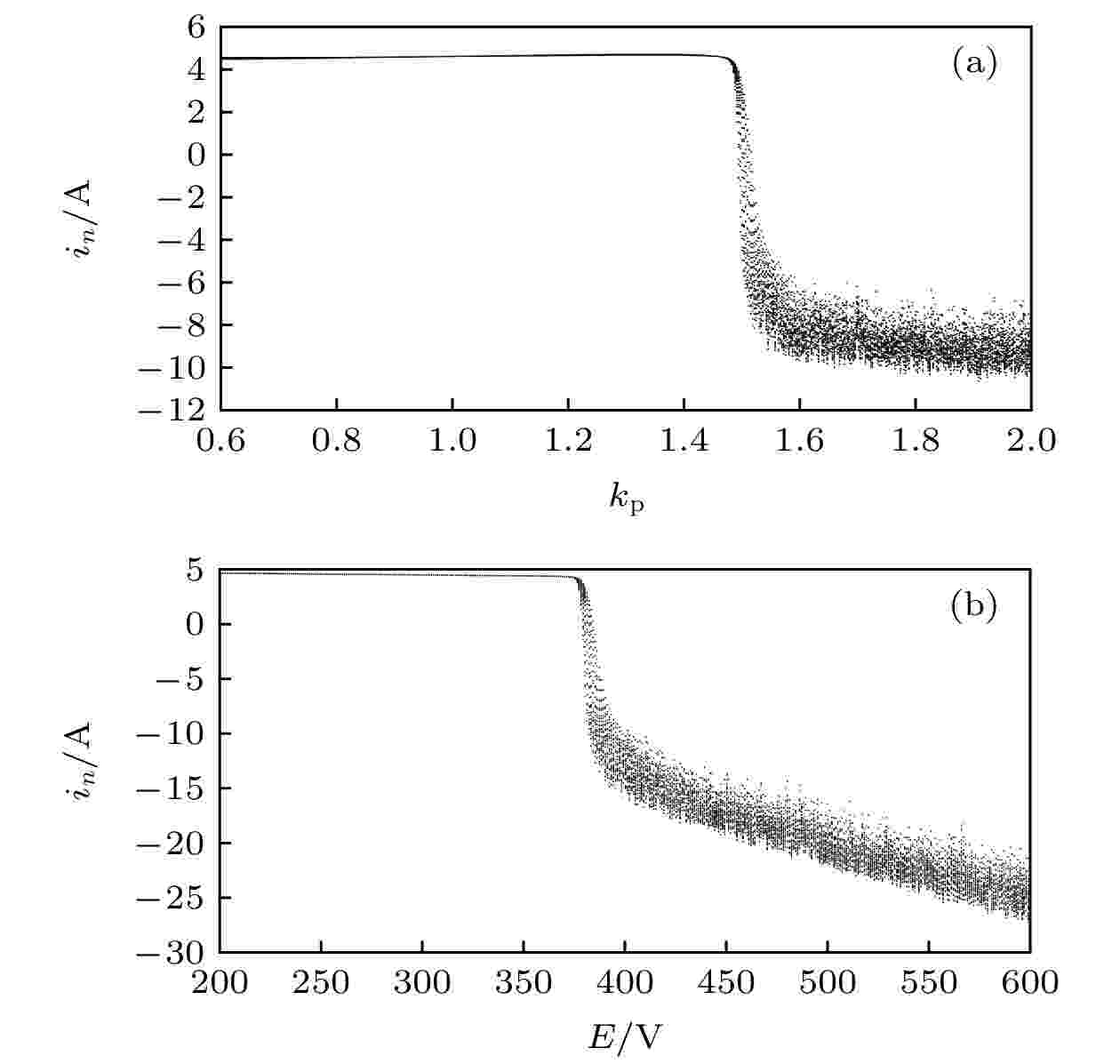图 4 引入EDFC后电感电流峰值处分岔图 (n = 100+400k, k = 1, 2, 3, ···)　(a) k_p为分岔参数时分岔图; (b) E为分岔参数时分岔图
Figure4. Bifurcation diagram with inductance current at peak value with EDFC applied (n = 100+ 400k, k = 1, 2, 3···): (a) Bifurcation diagram with k_p as bifurcation parameter; (b) bifurcation diagram with E as bifurcation parameter

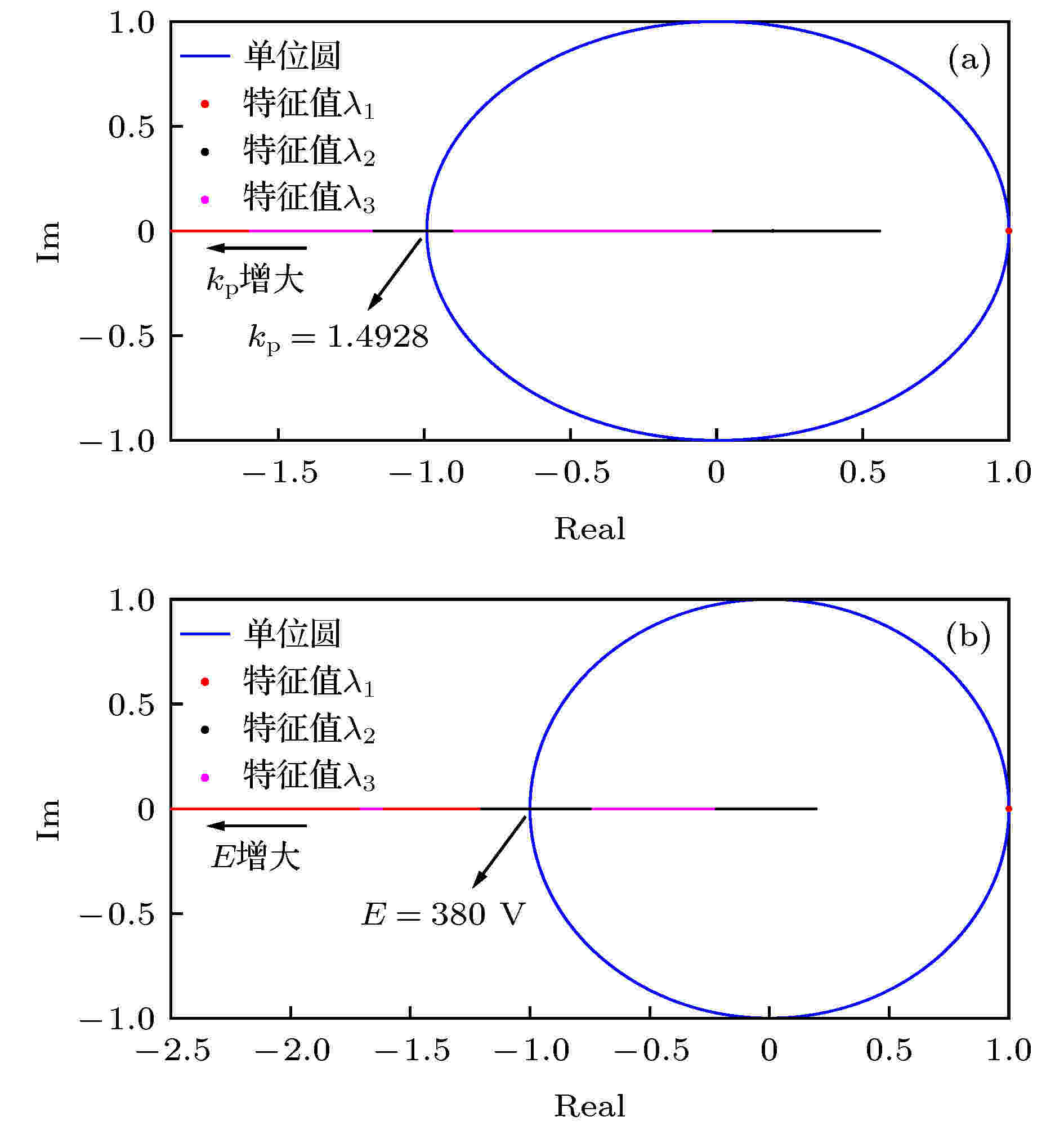图 5 引入EDFC后特征值轨迹图　(a) k_p从0.6增大到2.0; (b) E从200 V增大到600 V
Figure5. Eigenvalue trajectory with EDFC applied: (a) with k_p increasing from 0.6 to 2.0; (b) with E increasing from 200 V to 600 V.

由图4、图5可知, 系统引入EDFC后, 在分岔参数k_p, E分别增大至1.4928, 380 V时发生倍周期分岔, 随后系统进入混沌态. 由此可知, 当分岔参数k_p, E变化较小时, EDFC能有效地控制倍周期分岔, 保持系统稳定运行, 但当分岔参数k_p, E变化较大时, EDFC无法控制系统中的混沌行为. 原因是逆变系统是时变的, i_n与i_n-1并不相等, EDFC产生的控制信号一直存在, 而当分岔参数变化进一步增大时, i_n与i_n–1差值也可能增大, 将其差值作为e指数函数的幂得到的反馈信号也会增大, 若直接引入EDFC无法控制反馈强度, 将EDFC的反馈信号与原PI调节信号以直接相乘的形式得到新的控制信号会给系统带来过大扰动, 导致无法进行有效控制.
2 -->

3.2.引入IEDFC

针对系统分岔参数变化较大时, 直接引入EDFC会带来过大扰动, 无法有效控制混沌行为的问题, 提出一种IEDFC方法. 先利用系统输出电流与自身延迟一个开关周期T后的差值乘以反馈系数k₁, 得到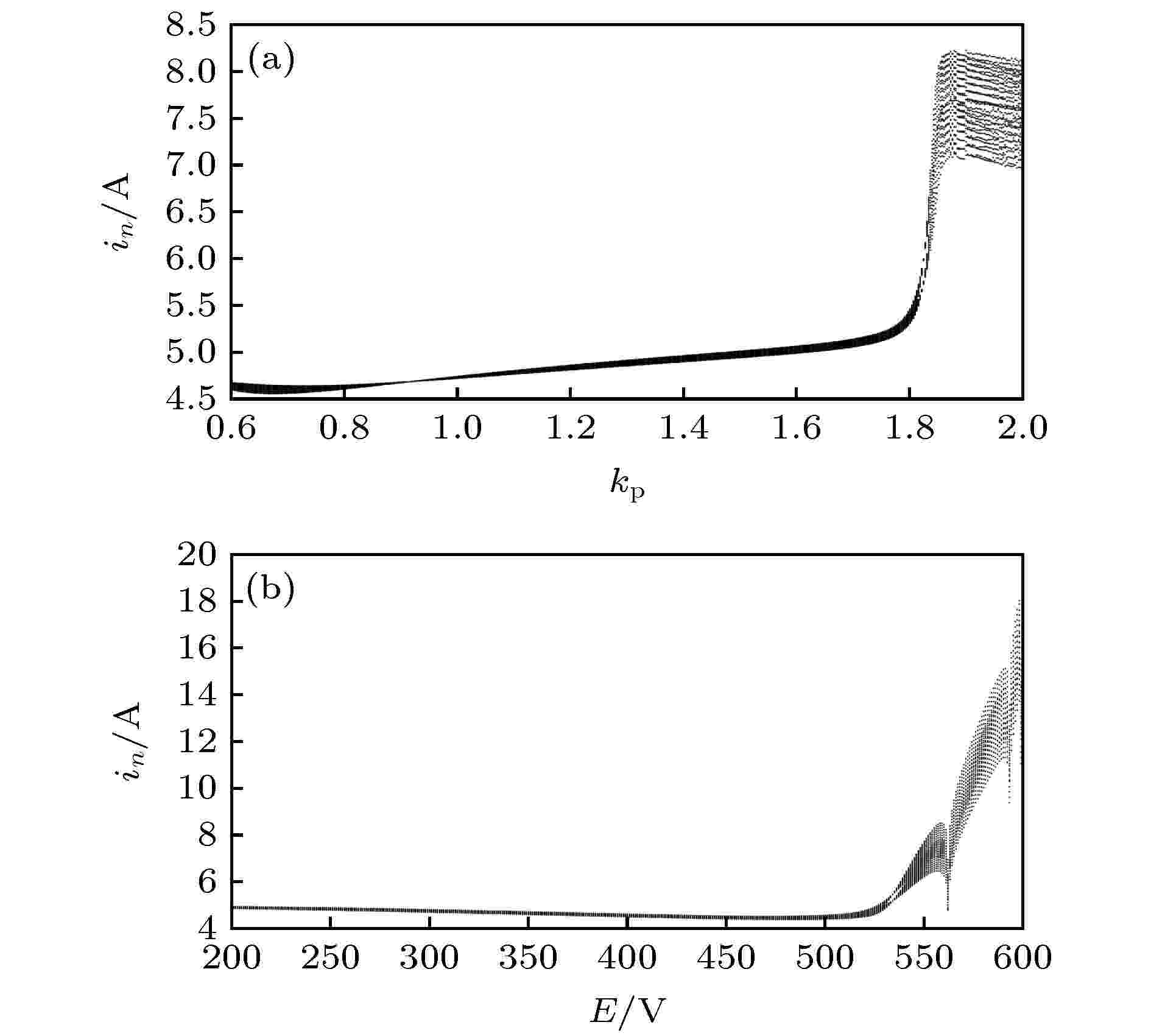

${k_{\rm{1}}}\left( {i\left( t \right) - i\left( {t - T} \right)} \right),$

再将(11)式作为e指数函数的幂, 与常数1做差得:

${{\rm{e}}^{{k_{\rm{1}}}\left( {i\left( t \right) - i\left( {t - T} \right)} \right)}} - 1,$

再将(12)式乘以反馈系数k₂, 得到

${k_{\rm{2}}}\left( {{{\rm{e}}^{{k_{\rm{1}}}\left( {i\left( t \right) - i\left( {t - T} \right)} \right)}} - 1} \right),$

最后将(13)式与经过PI调节的信号叠加作为调制信号与载波信号比较产生控制逆变器开关器件的正弦脉冲宽度调制信号. 具体的实现过程如图1(b)虚线部分所示. IEDFC将反馈控制信号与原有的经PI调节控制信号以相加的形式形成新的调制信号, 减小了对系统的扰动, 同时当系统稳定运行时, i_n与i_n–1的差值较小, 将差值作为e指数函数的幂得到的值接近1, 与1做差的差值接近0. 也就是说当系统稳定运行时IEDFC所起的控制作用对系统影响很小, 有利于系统保持稳定. 另外, 通过调整k₁, k₂两个反馈系数, 能很好地调整反馈强度, 获得较好的控制效果. 系统引入IEDFC后, 调制信号i_con的离散模型为

$\begin{split}{i_{{\rm{con}}}}(n) =\; & {p_1}{i_{n - 1}} + {i_{{\rm{con}}}}(n - 1) + {p_2}E + \\&T{U_{n - 1}} + {k_{\rm{2}}}\left( {{{\rm{e}}^{{k_{\rm{1}}}\left( {{i_n} - {i_{n - 1}}} \right)}} - 1} \right).\end{split}$

引入IEDFC后, 系统在平衡点处的雅克比矩阵为

${{J}}\left( {{{{X}}_{\rm{Q}}}} \right) = \left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{ - \tfrac{{RT}}{L}}} + A{k_{\rm{1}}}{k_{\rm{2}}}}&{A\left( {BC - {k_{\rm{1}}}{k_{\rm{2}}}} \right)}&{A\left(1 + AB - \dfrac{{{k_{\rm{i}}}TE}}{R}\right)} \\ 1&0&0 \\ {{k_{\rm{1}}}{k_{\rm{2}}}}&{BC - {k_{\rm{1}}}{k_{\rm{2}}}}&{1 + AB - \dfrac{{{k_{\rm{i}}}TE}}{R}} \end{array}} \right].$

由特征方程式det[λI – J(X_Q)] = 0得:

$\lambda \left[ {{\lambda ^2} + \left( {\frac{{{k_{\rm{i}}}TE}}{R} - 1 - AB - {{\rm{e}}^{ - \frac{{RT}}{L}}} - A{k_{\rm{1}}}{k_{\rm{2}}}} \right)\lambda + {{\rm{e}}^{ - \frac{{RT}}{L}}}\left( {1 + AB - \frac{{{k_{\rm{i}}}TE}}{R}} \right) + A\left( {{k_{\rm{1}}}{k_{\rm{2}}} - BC} \right)} \right] = 0.$

反馈控制系数k₁, k₂对控制效果有重要影响. 本文将基于稳定性判据给出两个反馈系数k₁, k₂的限定条件. 在(16)式中, 设λ₁恒为0, 只研究λ₂, λ₃随分岔参数k_p变化的情况. 假设λ₂ = a+bj, λ₃ = c+dj (j为虚数单位). 令:

$\begin{split}&{J_{\rm{1}}} = \frac{{{k_{\rm{i}}}TE}}{R} - 1 - AB - {{\rm{e}}^{ - \tfrac{{RT}}{L}}} - A{k_{\rm{1}}}{k_{\rm{2}}},\\&{J_{\rm{2}}} = {{\rm{e}}^{ - \tfrac{{RT}}{L}}}\left( {1 + AB - \frac{{{k_{\rm{i}}}TE}}{R}} \right) + A\left( {{k_{\rm{1}}}{k_{\rm{2}}} - BC} \right).\end{split}$

根据韦达定理, 有λ₂+λ₃ = –J₁ = a + c, λ₂λ₃ = J₂ = ac – bd. 易得a = c, b = –d. 假设b, d都不为0, 若要满足特征值都在复数平面的单位圆内, 得到第一个稳定条件:

${J_{\rm{2}}}{\rm{ = }}{a^2} + {b^2} = {c^2} + {d^2} < 1;$

若–J₁ < 0, 则–1 < a = c < 0, 有a+c = 2a > –1–a²–b², 得到第二个稳定条件:

$ - {J_{\rm{1}}} > - 1 - {J_{\rm{2}}};$

若–J₁ > 0, 则0 < a = c < 1, 有a+c = 2a < 1+a²+b², 得到第三个稳定条件:

$ - {J_{\rm{1}}} < 1 + {J_{\rm{2}}};$

若b, d都为0, λ₂+λ₃ = –J₁ = a+c, λ₂λ₃ = J₂ = ac. 若要满足特征值都在复数平面的单位圆内, 得到第四个稳定条件:

$\left\{ {\begin{array}{*{20}{c}} { - 2 < - {J_{\rm{1}}} < 2,} \\ { - 1 < {J_{\rm{2}}} < 1.} \end{array}} \right.$

综合稳定条件(17)式—(20)式, 可得两个反馈系数k₁, k₂需满足的限定条件:

$ \left\{ \begin{split}&{k}_{\rm{1}}{k}_{\rm{2}} > \dfrac{\left(\dfrac{{k}_{\rm{i}}TE}{R}-2\right)\cdot \left({\rm{e}}^{-\tfrac{RT}{L}}+1\right)+\left(AC-{\rm{e}}^{-\tfrac{RT}{L}}A-A\right)B}{2A}, \\ & {k}_{\rm{1}}{k}_{\rm{2}} < \dfrac1{A}\bigg[{1+\left(\dfrac{{k}_{\rm{i}}TE}{R}-1\right){\rm{e}}^{-\tfrac{RT}{L}}+\left(AC-{\rm{e}}^{-\tfrac{RT}{L}}A\right)B}\bigg]. \end{split} \right.$

由上述分析可知, 当k_p = 1.8或E = 500 V时, 系统进入混沌态, 为使其恢复至稳定态, 引入IEDFC. 根据(21)式, 当k_p = 1.8时, 令k₁ = k₂ = 0.707, 当E = 500 V时, 令k₁ = 0.45, k₂ = 0.5. 结合(3)式和(14)式, 分别以k_p, E为分岔参数, 以T_s为采样周期, 得到电感电流峰值处的分岔图如图6(a)和图6(b)所示.
图 6 引入IEDFC后电感电流峰值处分岔图 (n = 100+400k, k = 1, 2, 3, ···)　(a) 以k_p为分岔参数时分岔图; (b) 以E为分岔参数时分岔图
Figure6. Bifurcation diagram with inductance current at peak value with IEDFC applied (n = 100+400k, k = 1, 2, 3, ···): (a) Bifurcation diagram with k_p as bifurcation parameter; (b) bifurcation diagram with E as bifurcation parameter

在引入IEDFC后, k_p从0.6增大至2.0或E从200 V增大至600 V时特征值λ₂, λ₃的轨迹图如图7所示. 可以看出, 即使k_p增大至1.8或E增大至500 V时系统也没有出现分岔与混沌现象, 特征值λ₂, λ₃均在单位圆内. 这说明当分岔参数变化较大时, IEDFC能有效抑制系统的非线性行为, 使系统保持稳定运行, 有效地解决了系统直接引入EDFC带来过大扰动的问题.
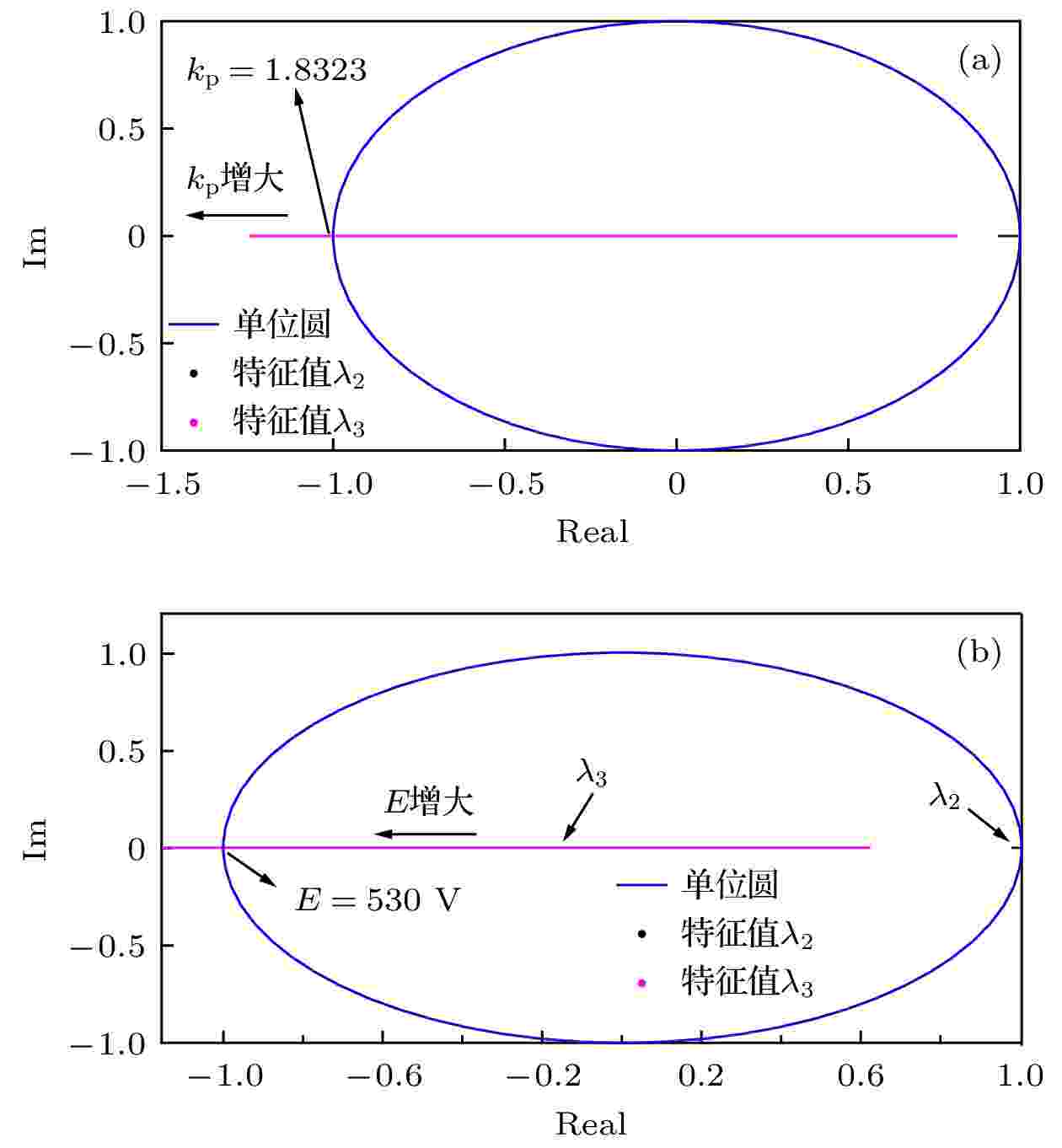图 7 引入IEDFC后特征值轨迹图　(a) k_p从0.6增大至2.0; (b) E从200 V增大至600 V
Figure7. Eigenvalue trajectory with IEDFC applied: (a) with k_p increasing from 0.6 to 2.0; (b) with E increasing from 200 V to 600 V.

2

-->

4.1.k_p为分岔参数时的仿真结果

图8—图10分别给出了k_p = 1.8时未引入混沌控制、引入EDFC、引入IEDFC电感电流的仿真结果. 可以看出, 未引入混沌控制时系统处于混沌态, 电感电流波形严重失真, 其总谐波失真(total harmonic distortion, THD)高达15.54%, 无法满足电力行业的需求. 当t = 0.08 s时, 引入EDFC, 电感电流THD增加至16.31%, 系统失真更严重. 而引入IEDFC后, 电感电流THD下降至2.80%, 谐波含量大大减小, 失真现象得到明显改善, 波形趋于光滑. 这说明当分岔参数变化较大时, 未引入混沌控制时, 系统处于混沌态; 直接引入EDFC会给系统会带来过大扰动, EDFC不但不能使系统恢复稳定, 而且还会增加谐波含量; 而引入IEDFC后, 分岔、混沌等非线性行为得到有效抑制.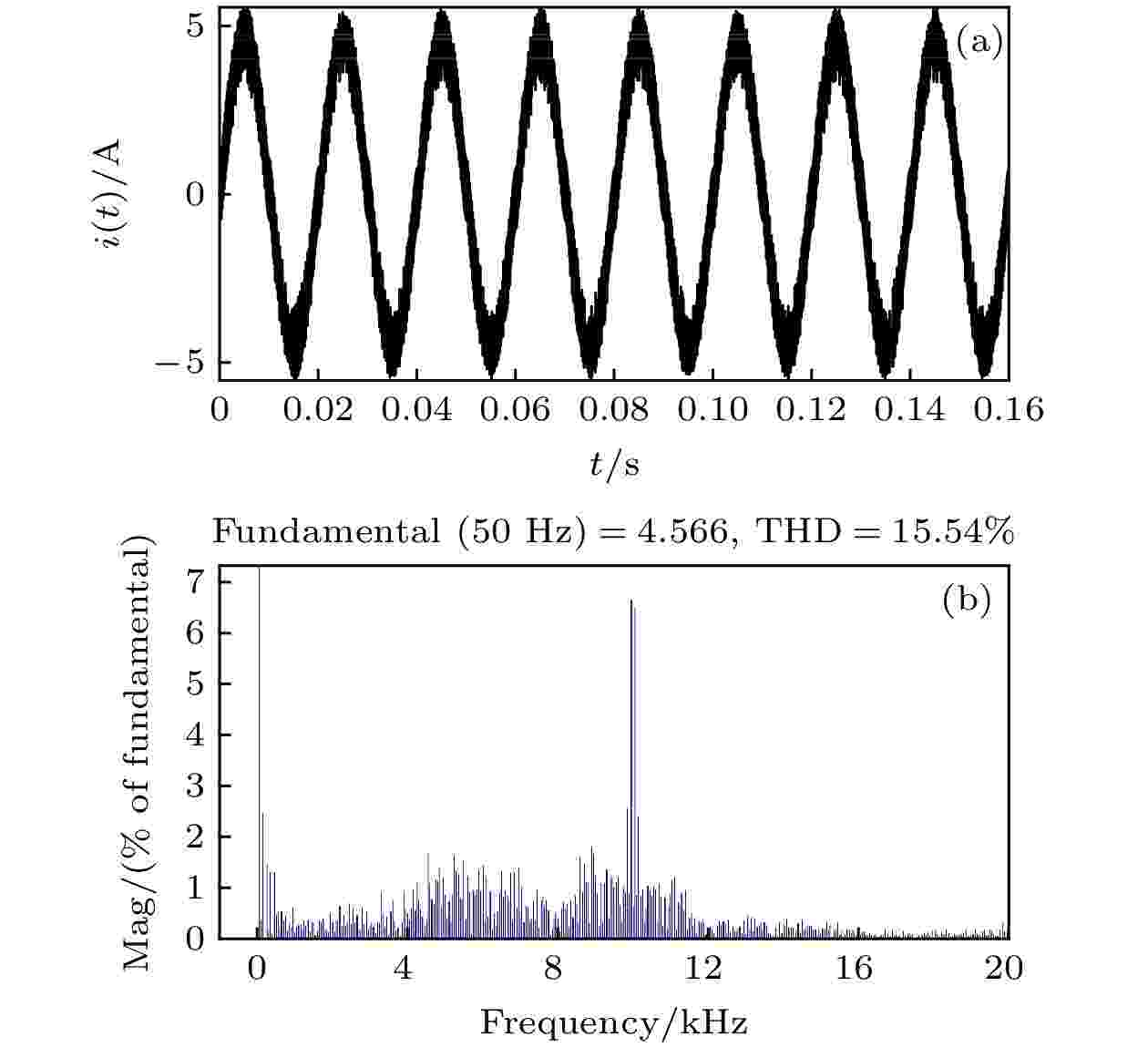
图 8 未引入混沌控制时的电感电流　(a) 时域波形图; (b) 非线性失真系数
Figure8. Inductor current without chaos control: (a) Time domain waveform; (b) THD obtained by FFT.

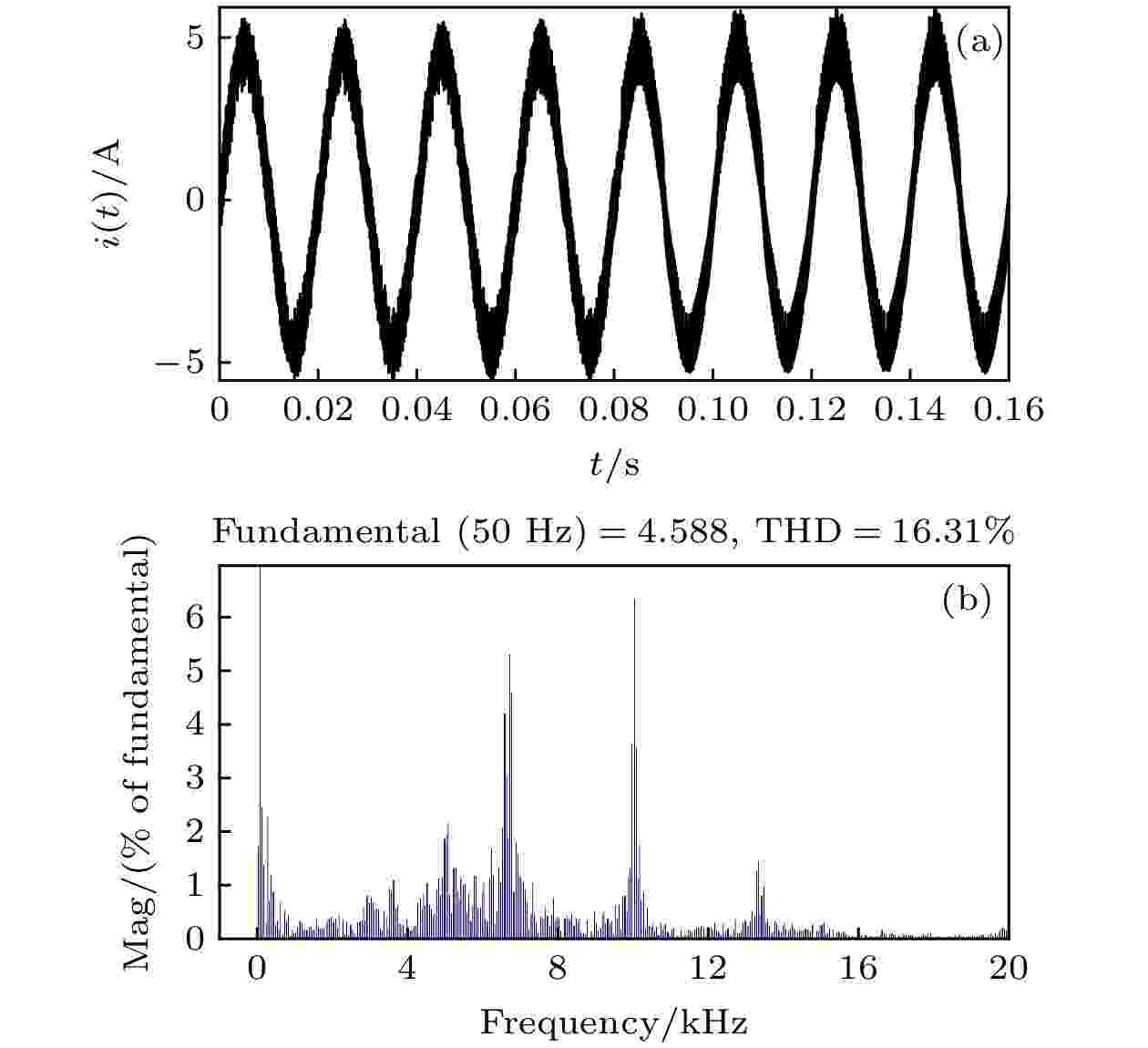图 9 引入EDFC后的电感电流　(a) 时域波形图; (b) 非线性失真系数
Figure9. Inductor current with EDFC applied: (a) Time domain waveform; (b) THD obtained by FFT.

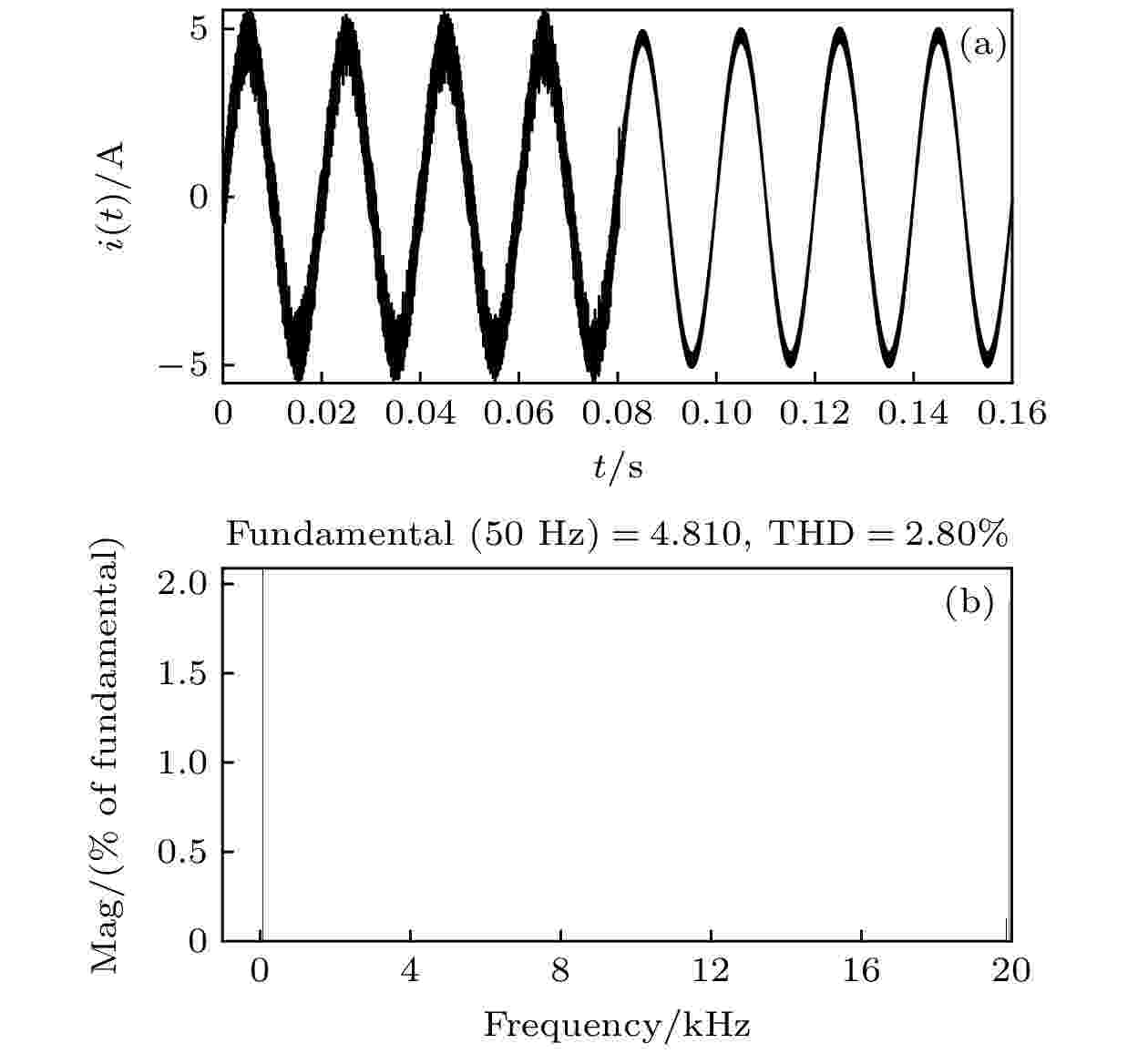图 10 引入IEDFC后的电感电流　(a) 时域波形图; (b) 非线性失真系数
Figure10. Inductor current with IEDFC applied: (a) Time domain waveform; (b) THD obtained by FFT.

图11、图12分别示出了当k_p = 1.400, 其他参数配置同表1, 在t = 0.06 s时对系统施加EDFC和IEDFC, 并在t = 0.14 s时对系统直流侧电压E施加扰动ΔE = 50 V后电感电流的仿真结果. 当k_p = 1.400, 根据（21）式令k₁ = 0.707, k₂ = 0.630, 对系统施加IEDFC. 可以看出, 引入EDFC和IEDFC系统都能由混沌态恢复至稳定态. 但对系统施加EDFC后需要约0.01 s, 电流波形才能从不规则态恢复至规则态, 而施加IEDFC, 仅需约0.0017 s即可恢复至规则态. 此外, 当对直流侧电压E施加扰动后, EDFC完全失去控制作用, 系统由稳定态转变成混沌态, 而IEDFC仍能控制系统稳定运行. 这表明当k_p = 1.400时, 虽然EDFC和IEDFC都能控制系统稳定运行, 但IEDFC相对于EDFC具有更快的响应速度和更好的鲁棒性.
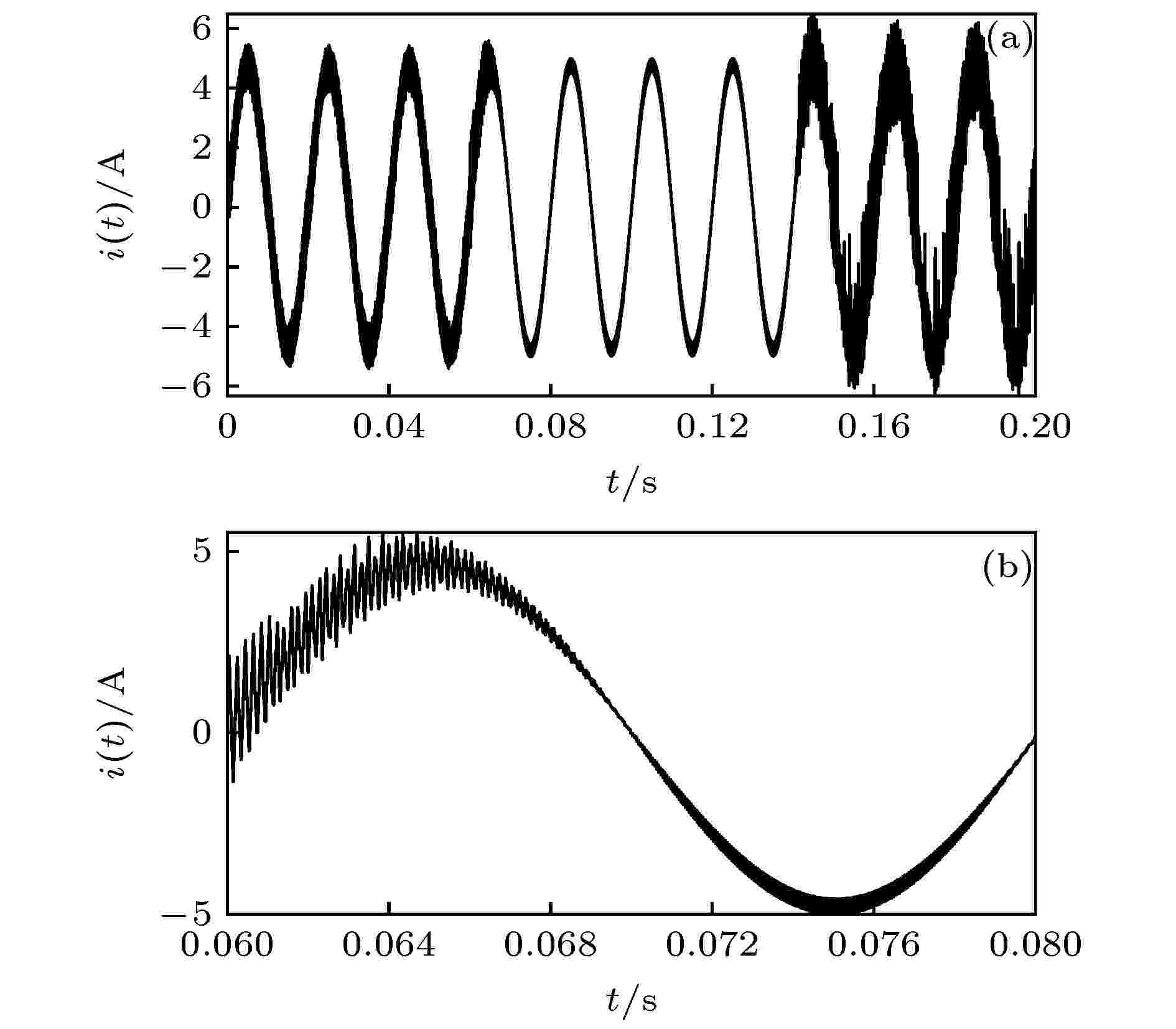图 11 k_p = 1.400时, 引入EDFC后电感电流　(a) 时域波形图; (b) 时域波形局部放大图
Figure11. Inductor current with EDFC applied for k_p = 1.400: (a) Time domain waveform; (b) local magnification diagram of time-domain waveform.

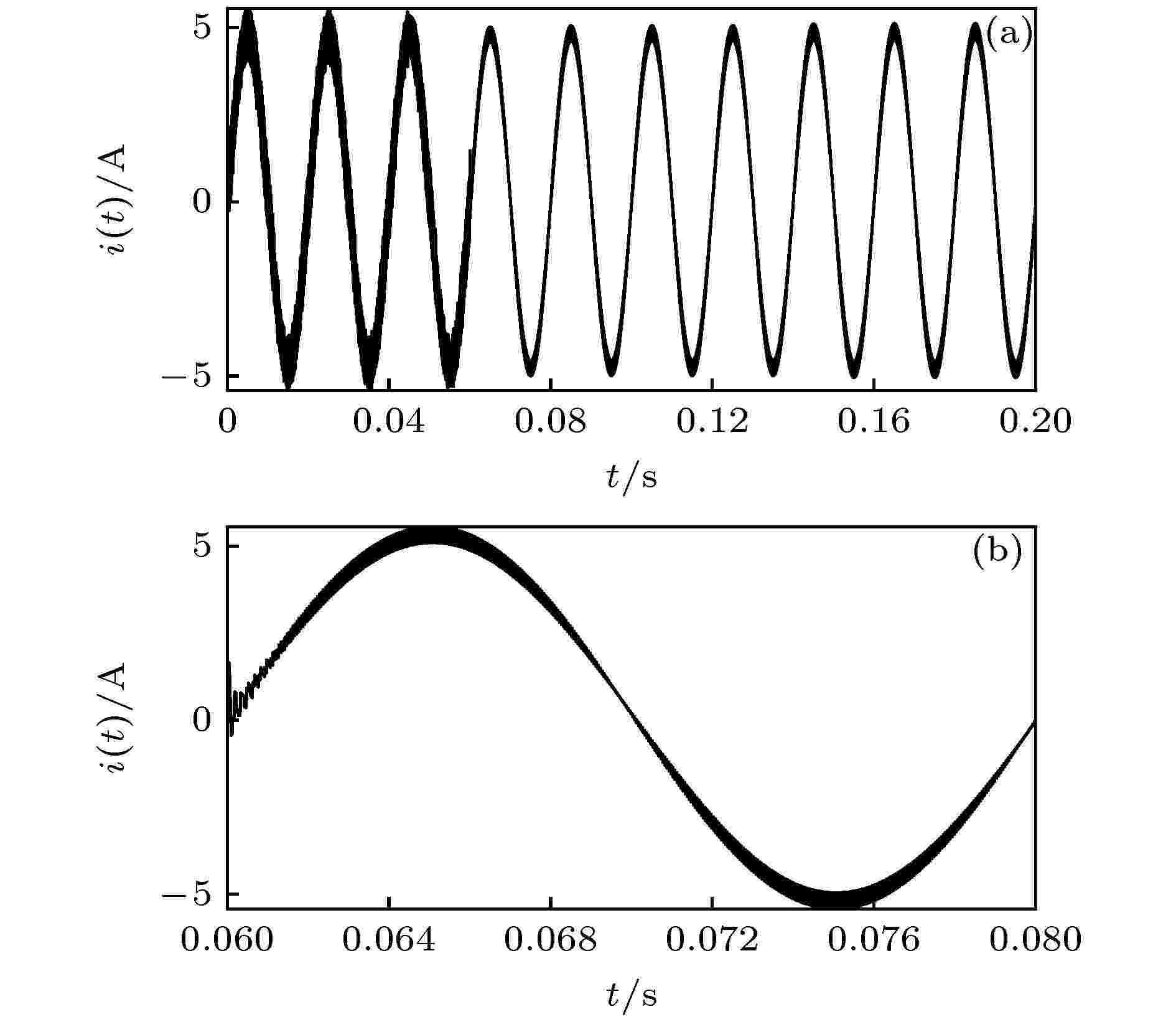图 12 k_p = 1.400, k₁ = 0.707, k₂ = 0.630时, 引入IEDFC后电感电流　(a) 时域波形图; (b) 时域波形局部放大图
Figure12. Inductor current with IEDFC applied for k_p = 1.400, k₁ = 0.707, k₂ = 0.630: (a) Time domain waveform; (b) local magnification diagram of time-domain waveform.

图13(a)—图13(c)分别示出了当k_p = 1.4, t = 0.06 s时对系统施加时间延迟反馈法^[21]、扩展时间延迟反馈法^[22]、基于滤波器的混沌控制法^[23], 且在t = 0.14 s时对系统直流侧电压E施加ΔE = 50 V扰动后电感电流的仿真结果. 对比图12(a)与图13(a)—图13(c)可以看出, 引入IEDFC与这三种方法后系统都能由混沌态恢复至稳定态. 但当对系统直流侧电压施加扰动后, 这三种混沌控制方法都无法控制系统继续稳定运行, 而本文提出的IEDFC法仍能有效地控制系统, 使系统继续保持稳定运行. 这表明IEDFC比这三种混沌控制方法鲁棒性更强.
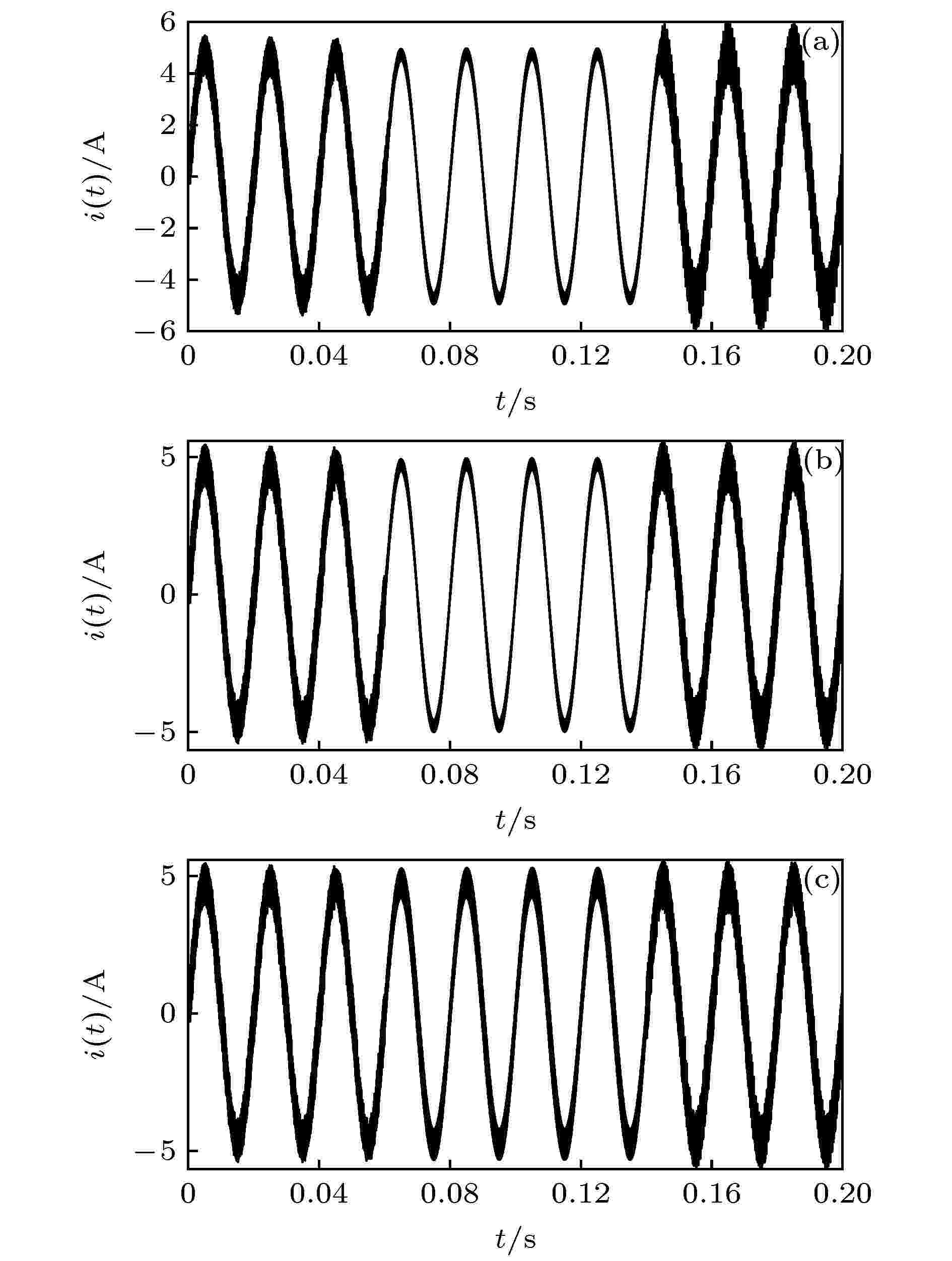图 13 k_p = 1.4, t = 0.06 s时, 引入其他混沌控制后电感电流　(a) 引入时间延迟反馈控制后; (b) 引入扩展时间延迟反馈控制后; (c) 引入基于滤波器的混沌控制后
Figure13. Inductor current with other chaos control applied for k_p = 1.4, t = 0.06 s: (a) With time-delay feedback control applied; (b) with extended time-delay feedback control applied; (c) with chaos control based on filter applied.

2 -->

4.2.E为分岔参数时的仿真结果

图14、图15分别示出了当E = 500 V, k_p = 1, 在t = 0.08 s时对系统施加EDFC和IEDFC后电感电流的仿真结果(其中t = 0—0.08 s之间未施加任何混沌控制). 可以看出未引入混沌控制时系统处于混沌态, 电感电流波形严重失真. 引入EDFC后, 不仅不能使系统恢复到稳定态, 反而给系统带来更大的扰动, 同时波形失真比引入前更严重; 而引入IEDFC后, 电流波形失真现象得到明显改善, 波形趋于光滑. 这说明系统输入参数E变化较大时, 直接引入EDFC无法对系统实施有效控制, 而引入IEDFC能对系统实施有效控制, 使系统由混沌态恢复至稳定态, 大大扩展系统稳定运行域.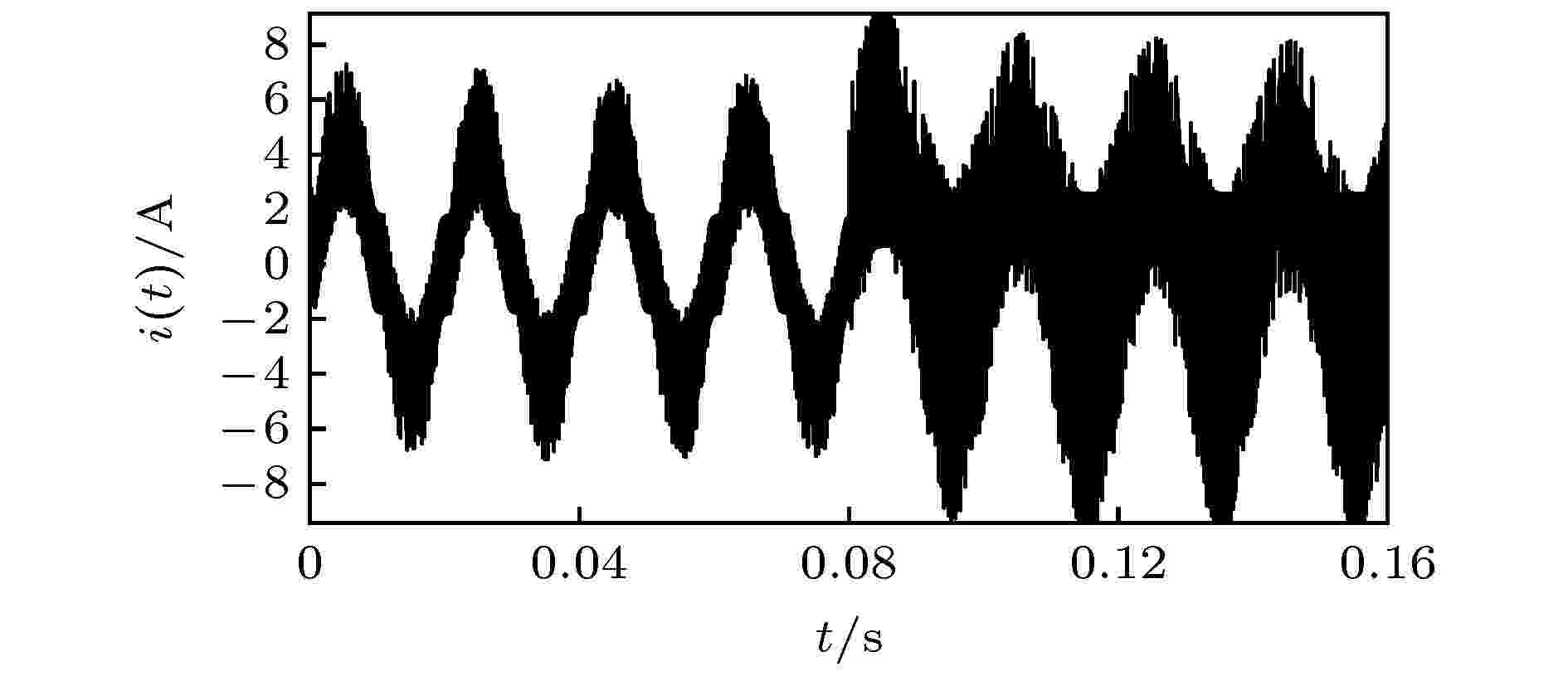
图 14 引入EDFC后电感电流时域波形图
Figure14. Time domain waveform with EDFC applied.

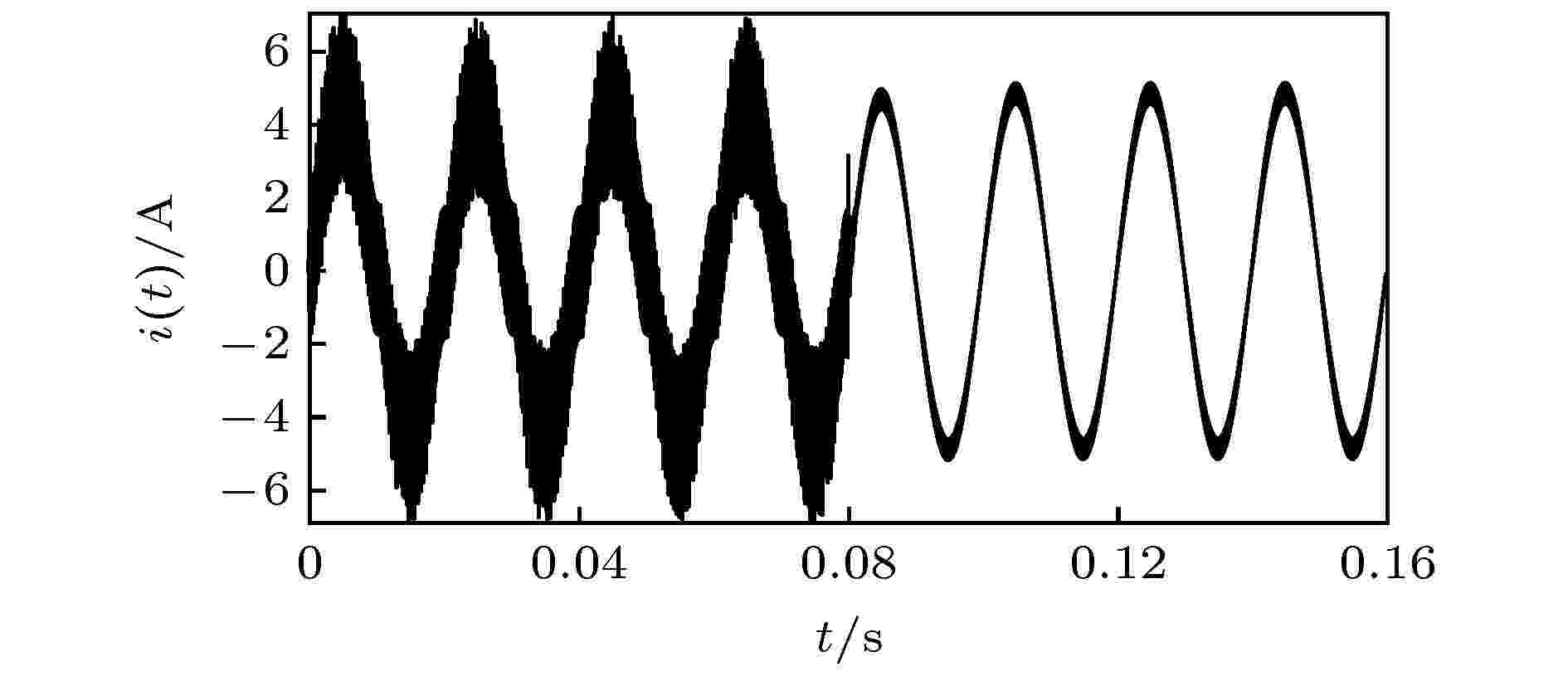图 15 引入IEDFC后电感电流时域波形图
Figure15. Time domain waveform with IEDFC applied.

本文针对PI调节单相H桥光伏逆变器的分岔与混沌现象, 提出了一种改进指数延迟反馈控制(IEDFC)方法. 详细阐述了该方法的原理, 并与其他多种混沌控制方法进行了对比仿真实验和分析. 结果表明, 本文提出的IEDFC能有效抑制系统的非线性行为, 大大扩大系统的稳定运行域, 显著降低电流的谐波含量, 显著改善供电质量. 相比于其他混沌控制方法, 该方法具有更快的响应速度和更好的鲁棒性.