摘要: 高密度物质环境内可能存在多种相互竞争的粒子相. 利用包含
ω 2 ρ 2 相互作用项的相对论平均场理论中FSUGold参数组描述强子相物质, 夸克质量密度相关的有效质量口袋模型描述夸克相物质, 再通过Gibbs相平衡条件构建强子-夸克混合相物质, 研究了处于
β 平衡的混合中子星性质. 计算口袋常数
B 对混合中子星性质的影响, 结果表明
B 对混合中子星内强子-夸克退禁闭相变始末点、粒子分布均有较大影响, 且相较于相变开始点, 相变结束点受
B 的影响会更加明显. 随着
B 的增大, 混合中子星物质状态方程变硬, 质量-半径关系曲线上升, 极限质量在1.3—1.4倍太阳质量(
M ☉ )范围内, 半径在9—12 km之间. 此外, 还研究了吸引和排斥的
Σ 势对混合中子星性质的影响, 结果表明不同
Σ 势对混合中子星内的粒子种类影响较大, 且相较于
Σ 引力势, 混合中子星在
Σ 斥力势下拥有更大的极限质量. 计算得到吸引和排斥的
Σ 势下混合中子星的极限质量分别为1.38
M ☉ 和1.41
M ☉ .
关键词: 致密核物质 /
相对论平均场 /
有效质量口袋模型 /
核天体物理 English Abstract Hadron-quark deconfinement phase transition in hybrid stars Gong Wu-Kun Guo Wen-Jun College of Science, University of Shanghai for Science and Technology, Shanghai 200093, China Received Date: 16 June 2020Accepted Date: 17 August 2020Available Online: 05 December 2020Published Online: 20 December 2020Abstract: Astronomical statistics shows that the mass of neutron star is of the order of the solar mass, but the radius is only about ten kilometers. Therefore, the neutron star is highly condensed and there may be a variety of competing material phases inside the compact star. Hadron-quark deconfinement phase transition that is poorly understood at high density can be studied by the matter properties of hybrid star. The hybrid star contains many kinds of material phases, which cannot be described uniformly by one theory. So, different material phases are described by different theories. The hadronic phase is described by the relativistic mean-field theory with parameter set FSUGold including ω 2 ρ 2 interaction term, and the quark phase is described by an effective mass bag model in which the quark mass is density-dependent. The hadron-quark mixed phase is constructed by the Gibbs phase transition, and the properties of hybrid star in β equilibrium is studied in this model. It is found that the bag constant B has a great influence on the starting point and ending point of the hadron-quark deconfinement phase transition and the particle composition in the hybrid star. Comparing with the starting point of phase transition, the influence of B on the ending point of phase transition is very obvious. For the hybrid star, the equation of state of matter becomes stiffer at low density and softer at high density as B increases. The overall effect is that the slope of the mass-radius curve increases with B increasing. The calculated results show that the maximum mass of hybrid star is between 1.3 solar mass and 1.4 solar mass (M ☉ ), and the radius is between 9 km and 12 km. In addition, the influence of attractive and repulsive Σ potential on the properties of hybrid stars are studied. The results show that the Σ potential has a great influence on the particle composition in the hybrid star. We also find that the repulsive Σ potential makes the hybrid star have a greater maximum mass then an attractive Σ potential. For the attractive Σ potential, the maximum mass of hybrid star is 1.38M ☉ , while for the repulsive Σ potential, the maximum mass of hybrid stars is 1.41M ☉ .Keywords: dense nuclear matter /relativistic mean field /effective mass bag model /nuclear astrophysics 全文HTML --> --> --> 1.引 言 中子星作为超新星爆发的产物, 拥有极高的物质密度, 其内部可能存在多种相互竞争的新物质形态. 特别是在核心处, 高密度环境可能导致强子-夸克退禁闭相变的发生[1 –5 ] , 这无疑为科研工作者提供了一个天然的高密度物理实验室. 因此, 对中子星物质性质的研究一直是核天体物理学关注的热点之一.β 衰变形成超子, 构成了包含重子八重态和轻子物质的超子星[6 –9 ] . 同时, 也可能发生K 介子或ρ 介子的玻色-爱因斯坦凝聚[10 –13 ] . 超子的出现, 让人们意识到中子星内部可能存在更加复杂的物质形式. 天文学数据统计发现, 中子星质量期望值在1.4M ☉ 左右[14 ] , 半径在11 km左右[15 ] , 推测其核心处甚至能达到10倍饱和核密度, 极有可能发生强子-夸克退禁闭相变, 形成具有夸克核心而外层包裹着强子物质的混合星[16 –21 ] . 此外, 在强磁场中子星[22 ,23 ] 、热前中子星[24 ,25 ] 、奇异星[26 –28 ] 、夸克星[29 ,30 ] 等方面也有很多的研究成果.[31 –33 ] 、多体微扰理论模型[34 –36 ] 、相对论平均场模型[37 ,38 ] 等来描述, 夸克相可通过MIT口袋模型[39 –41 ] 、Nambu-Jona-Lasinio模型[42 ] 等进行描述. 对于强子与夸克的混合物质相, 需要通过Gibbs相平衡条件[43 ] , 将强子相和夸克相构建在一起以达到描述混合相的目的.44 ]中, 利用相对论平均场(relativistic mean field, RMF)理论中FSUGold参数组计算了超子星性质, 但没有考虑夸克物质存在的可能性. 研究表明, FSUGold参数组描述的超子星核心密度可高达10倍核物质密度, 而在这种高密度物质环境下, 强子相到夸克相的退禁闭相变已经发生. 在本文中, 加入了有效质量口袋模型(effective mass bag model, EMBM)描述的夸克相, 并通过Gibbs相平衡条件连接, 研究了混合星相关性质. 研究发现, 在2—3倍核物质密度处, 强子物质开始转变为夸克物质. 夸克物质的出现, 使中子星状态方程(equation of state, EOS)软化. 此外, 还研究了Σ 粒子与核子之间的相互作用势(以下简称Σ 势)对混合星的影响, 发现Σ 势对粒子分布有较大影响.2.混合星理论模型 本文通过RMF理论描述混合星内强子物质, 通过EMBM描述夸克物质, 通过Gibbs相平衡条件构建混合相, 以下将进行相关介绍.2.1.强子相RMF理论 2.1.强子相RMF理论 自从Glendenning[45 ] 指出致密星中超子(Λ , Σ , Ξ )的重要性以后, 中子星组分逐渐从中子和质子拓展到超子层面, 形成了超子星理论. 在超子星内, 强子间的相互作用通过交换介子进行, 主要包括σ 介子、ω 介子、ρ 介子. 引入介子交互作用项ω 2 ρ 2 [44 ,46 ] , 处于β 平衡的强子物质在RMF理论下的拉格朗日密度为B 表示重子八重态($ {n} $ , $ {p} $ , Λ , Σ – , Σ + , Σ 0 , Ξ 0 , Ξ – ), 符号l 表示轻子(e – , μ – ). 符号σ , ω , ρ 分别表示三种介子, 符号${\varLambda_\nu} $ 用于修正密度依赖的对称能. 符号$ {{m}}_{{B}} $ , m σ m ω m ρ g Σb g ωB g ρB σ , ω , ρ 介子与重子之间的耦合常数. 各物质β 平衡条件如(2 )式—(5 )式所示:μ 表示粒子化学势.$m_B^* = {m_B} - {g_{\sigma B}}\sigma $ 表示重子有效质量[44 ] , 符号k F 表示粒子费米能.[44 ,46 ] 为: m σ m ω m ρ g σN g ωN g ρN κ = 1.42, λ = 0.0238, ζ = 0.06, Λ ν SU (6)对称性选取:σ 介子与超子间的耦合常数由拟合超子势$U_Y^{(N)} = {g_{\omega Y}}{\omega _0} - {g_{\sigma Y}}{\sigma _0}$ [6 ,44 ] 确定. $\varLambda \text{-}N$ 势和$\varXi \text{-}N$ 势分别取$U_\varLambda^{(N)} $ = –28 MeV[47 ] 和$U_\varXi^{(N)} $ = –18 MeV[48 ] , 相应的耦合常数g σΛ g σΞ $\varSigma\text{-}N$ 势可能存在不同的取值, 斥力势$U_\varSigma^{(N)} $ = 30 MeV[48 ] , 耦合常数g σΣ $U_\varSigma^{(N)} $ = –30 MeV[49 ] , 耦合常数g σΣ 2.2.夸克相EMBM理论 -->2.2.夸克相EMBM理论 MIT口袋模型把夸克物质看作零温自由费米气体. 进一步在夸克间加入强相互作用, 使夸克获得与密度相关的有效质量, 得到EMBM[50 ,51 ] . 处于β 平衡的零温热力学势函数密度为i 表示电子e 及夸克u , d , s 四种粒子; g i β 平衡条件为${\mu _d} = {\mu _s} = {\mu _u} + {\mu _e}$ . 粒子数密度n i ε 以及压强P 的表达式为表示夸克有效质量n i u , d , s , e 四种粒子数密度; 符号B 表示口袋常数; 符号f 表示u , d , s 三味夸克; 符号$ {{m}}_{{f}}^{{*}} $ 表示夸克有效质量, 具体表达式为g 为夸克间强耦合常数, 根据文献[50 —52 ], 可取g = 1; $ {{m}}_{{f}} $ 为流夸克静止质量, 分别取m u 0m d 0m s 02.3.混合相Gibbs构建 -->2.3.混合相Gibbs构建 强子相和夸克相组成的二分量系统中, 守恒荷包括电荷量和重子数, 是多守恒荷相变体系. 对多守恒荷体系, 混合相通过Gibbs相平衡条件构建[43 ] . 处于平衡态的混合相物质, 两相的压强满足p H = p Q , 其中p H , p Q 分别表示强子相和夸克相的压强. 定义夸克相在混合相中体积占比为χ , 即$\chi = {V_q}/V$ , 其只V q V 表示总体积. 由此, 总重子数密度、整体电荷密度, 以及整体能量密度分别为ρ , q , ε 分别表示粒子数密度、电荷密度, 以及能量密度; 符号M, H, Q分别表示混合相、强子相、以及夸克相. 混合相β 平衡条件为${\mu _n} = {\mu _u} + 2{\mu _d}, {\mu _p} = 2{\mu _u} + {\mu _d}$ .[43 ] ,G 表示引力常数, C 表示光速. 通过对(1 )式—(17 )式求解, 得到混合星EOS曲线, 再对(18 )式和(19 )式进行数值积分, 得到混合星质量-半径关系.图1 展示了强子相、混合相、夸克相的每核子能量及压强随物质密度的变化曲线. 图像表明, 强子相到夸克相的退禁闭相变过程中, 每核子能量和压强都是连续渐变的, 这与在引力系统中的中子星物质性质相符.图 1 强子相(划线)、混合相(实线)、夸克相(点线)中, 每核子能量与物质密度的关系(a)以及压强与物质密度的关系(b), 取$ {{B}}^{{1/4}} $ = 195 MeV, $U_\varSigma^{(N)} $ = –30 MeVFigure1. Relationships of each nucleon (a) and pressure (b) with matter density in hadron phase (dashed line), mixed phase (solid line) and quark phase (dotted line), respectively, with $ {{B}}^{{1/4}} $ = 195 MeV, $U_\varSigma^{(N)} $ = –30 MeV.3.混合星性质及计算结果 图2 给出$U_\varSigma^{(N)}$ = –30 MeV情况下, 强子-夸克退禁闭过程中, 夸克相在混合星内的占比变化. 随着B 的增大, 相变始末点均推迟出现, 且相较于开始点, 结束点的推迟更加明显. $ {{B}}^{{1/4}} $ 由185 MeV增大到195 MeV时, 相变开始点由0.32 fm–3 推迟到0.54 fm–3 , 相变结束点由1.24 fm–3 推迟到1.58 fm–3 . 口袋常数在EMBM中, 表示袋内和袋外的压强差. 物质密度相同时, B 越大, 夸克相产生的压强越小, 导致Gibbs相平衡的满足条件推迟出现, 相变始末点随之推迟. 从图2 还可以看出, 相变开始时, 一部分中子和质子衰变为超子, 另一部分退禁闭产生夸克, 且逐渐趋于平衡. 当密度进一步增大时, 图像显示在0.8 fm–3 附近, 强子-夸克退禁闭相变将突破平衡临界值, 超子物质开始被大量压碎, 夸克物质增长趋势急剧上升.图 2 $U_\varSigma^{(N)} $ = –30 MeV下$ {{B}}^{{1/4}} $ = 185 MeV (实线)、190 MeV (划线)、195 MeV (点线)时夸克相在混合星内的占比χ Figure2. Proportion of quark phase χ in hybrid stars when $ {{B}}^{{1/4}} $ taking 185 MeV (solid line), 190 MeV (dashed line) and 195 MeV (dotted line), respectively, with $U_\varSigma^{(N)} $ = –30 MeV.图3 为不同B 及Σ 势下混合星内的粒子分布. 随着B 的增大, 相变结束点推迟, 导致混合相在混合星结构中的比例增大, 强子在混合相中的竞争优势增强, 超子出现的种类随之增多. 如图3(a) —图3(c) , 当$U_\varSigma^{(N)} $ = 30 MeV时, $ {{B}}^{{1/4}} $ 从185 MeV增大到195 MeV时, 超子出现的种类由Λ , Ξ 0 增大到Λ , Ξ 0 , Ξ – . 此外, Σ 势也会影响超子产生的种类, 如图3(c) 和图3(f) , $ {{B}}^{{1/4}} $ = 195 MeV时, $U_\varSigma^{(N)} $ 分别取30 MeV和 –30 MeV时超子产生的种类分别是Λ , Ξ – , Ξ 0 和Λ , Σ – , Σ + , Σ 0 . 计算过程中, 不同的$U_\varSigma^{(N)} $ 对应不同的耦合常数g σΣ $U_\varSigma^{(N)} $ = 30 MeV时g σΣ $U_\varSigma^{(N)} $ = –30 MeV时g σΣ g σΣ g σΣ Σ 粒子, 而抑制Ξ 粒子的产生.图 3 混合星粒子分布图($ {{B}}^{{1/4}} $ 分别取185, 190, 195 MeV) (a), (b), (c) $U_\varSigma^{(N)} $ = 30 MeV; (d), (e), (f) $U_\varSigma^{(N)} $ = –30 MeVFigure3. Particle composition in the hybrid star: (a), (b), (c) $U_\varSigma^{(N)} $ = 30 MeV; (d), (e), (f) $U_\varSigma^{(N)} $ = –30 MeV. $ {{B}}^{{1/4}} $ taking 185, 190, and 195 MeV.图4 给出不同B 下混合星的EOS曲线. 低密度时, 随着B 的增大, EOS变硬; 高密度时, 情况相反, 随着B 的增大EOS变软. 这是因为, 在能量密度较低时, B 越大强子相竞争优势越明显, 导致EOS偏硬; 随着能量密度的增大, 强子-夸克退禁闭相变不断发生, 夸克相在竞争中优势越来越强, 使EOS逐渐变软. 从整体上看, B 越大混合星EOS整体上更硬, 即质量-半径关系曲线上升, 如图5(a) 所示.图 4 $U_\varSigma^{(N)} $ = –30 MeV下$ {{B}}^{{1/4}} $ = 185 MeV (实线)、190 MeV (划线)、195 MeV (点线)时的EOS曲线Figure4. EOS when $ {{B}}^{{1/4}} $ taking 185 MeV (solid line), 190 MeV (dashed line) and 195 MeV (dotted line), respectively, with $U_\varSigma^{(N)} $ = –30 MeV.图 5 不同口袋常数下, 混合星质量-半径关系 (a)和质量-能量密度关系(b)Figure5. Mass-radius (a) and mass-energy density (b) curves of hybrid stars, respectively, with different bag constant.图5 展示的是根据图4 的EOS曲线计算的不同B 下混合星的质量-半径关系曲线和质量-能量密度关系曲线. 可以看出, 随着B 的增大, 质量-半径关系曲线上升, 同质量下半径越大, 能量密度越小. 混合星极限质量在1.3M ☉ —1.4M ☉ , 半径在9—12 km之间, 这些结果与天文学中子星实验观测数据相符[14 ,15 ] .Σ 势对混合星性质的影响. 如图6 所示, $ {{B}}^{{1/4}} $ = 195 MeV时, 分别给出了$U_\varSigma^{(N)} $ = –30 MeV和$U_\varSigma^{(N)} $ = 30 MeV情况下夸克相在混合星内占比的分布曲线. 结果表明, 不同Σ 势对相变开始点几乎没有影响, 对相变结束点, 斥力势相较于引力势明显推迟. $U_\varSigma^{(N)} $ 取值的不同, 影响粒子产生的种类, 结果表明$U_\varSigma^{(N)} $ = –30 MeV时, 耦合常数g σΣ Σ – , Σ + , Σ 0 , 粒子在高密度时更容易被压碎, 导致退禁闭相变结束点提前.图 6 $ {{B}}^{{1/4}} $ = 195 MeV下混合星内夸克相比份χ 分布, 其中实线表示$U_\varSigma^{(N)} $ = –30 MeV的情况; 虚线表示$U_\varSigma^{(N)} $ = 30 MeV的情况Figure6. Proportion of quark phase χ in hybrid stars when $U_\varSigma^{(N)} $ taking –30 MeV (solid line) and 30 MeV (dashed line) at $ {{B}}^{{1/4}} $ = 195 MeV, respectively.图7 给出了吸引和排斥的Σ 势下混合星质量-半径关系曲线和质量-能量密度关系曲线. 结果表明, $U_\varSigma^{(N)} $ = –30 MeV时, 极限质量为1.38M ☉ , $U_\varSigma^{(N)} $ = 30 MeV时, 极限质量为1.41M ☉ , 半径均在9—12.5 km范围内. 结合图3 的粒子分布图, 表明Σ 势对粒子产生种类, 强子-夸克相变始末点及混合星极限质量等性质均有影响. 根据现阶段的天文观测数据, Σ 势取引力势或斥力势都是有可能的, 对中子星极限质量的计算结果都在观测数据范围之内[14 ,15 ] .图 7 $ {{B}}^{{1/4}} $ = 195 MeV下混合星的质量-半径关系(a)和质量-能量密度关系(b), 其中实线表示$U_\varSigma^{(N)} $ = –30 MeV, 虚线表示$U_\varSigma^{(N)} $ = 30 MeVFigure7. Mass-radius (a) and mass-energy density (b) curves of hybrid stars, respectively, with $U_\varSigma^{(N)} $ taking –30 MeV (solid line) and 30 MeV (dashed line) at $ {{B}}^{{1/4}} $ = 195 MeV.4.总结与讨论 本文研究了混合星内可能发生的强子-夸克退禁闭相变. 描述强子相采用了RMF理论中FSUGold参数组, 自动满足了因果律, 并使夸克物质在高密度下渐进自由. 描述夸克相采用了EMBM, 引入了密度相关的夸克有效质量. 混合相通过强子-夸克的Gibbs相平衡条件构建, 由此计算了混合星的整体性质.B 的增大, 会导致强子-夸克退禁闭相变始末点推迟. 在低密度时, B 的增大使EOS方程变硬, 高密度时, 情况相反. 从整体上看, B 的增大导致EOS方程整体变硬, 混合星极限质量上升. 计算得到的混合星极限质量在1.3M ☉ —1.4M ☉ , 半径在9—12 km之间. 此外, Σ 势对混合星内粒子产生的种类和极限质量均有影响, 引力势$U_\varSigma^{(N)} $ = –30 MeV, 对应的极限质量为1.38M ☉ , 斥力势$U_\varSigma^{(N)} $ = 30 MeV对应的极限质量为1.41M ☉ . 本文的计算结果能为今后夸克退禁闭性质的研究提供有益的参考. 



















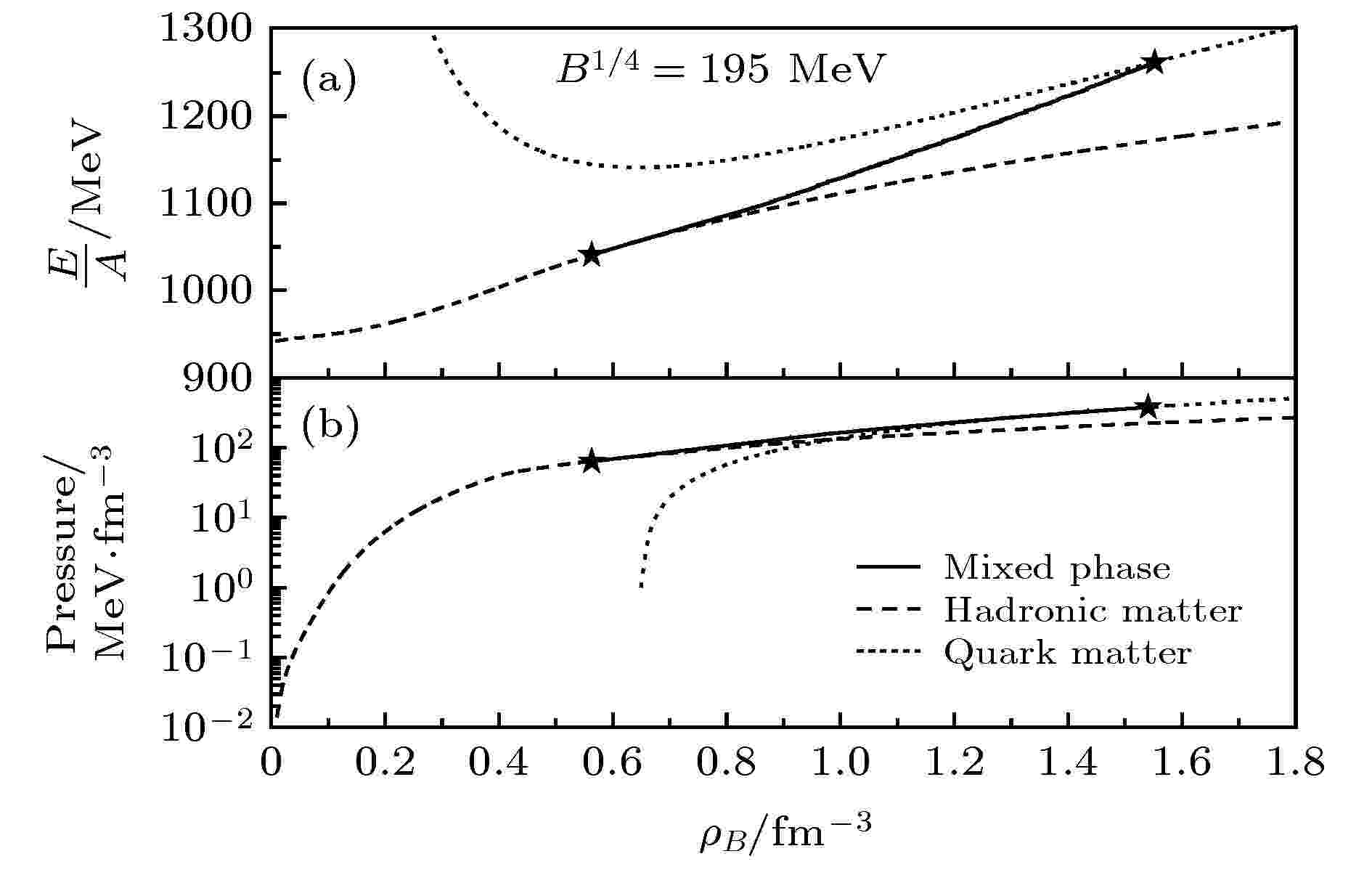 图 1 强子相(划线)、混合相(实线)、夸克相(点线)中, 每核子能量与物质密度的关系(a)以及压强与物质密度的关系(b), 取
图 1 强子相(划线)、混合相(实线)、夸克相(点线)中, 每核子能量与物质密度的关系(a)以及压强与物质密度的关系(b), 取





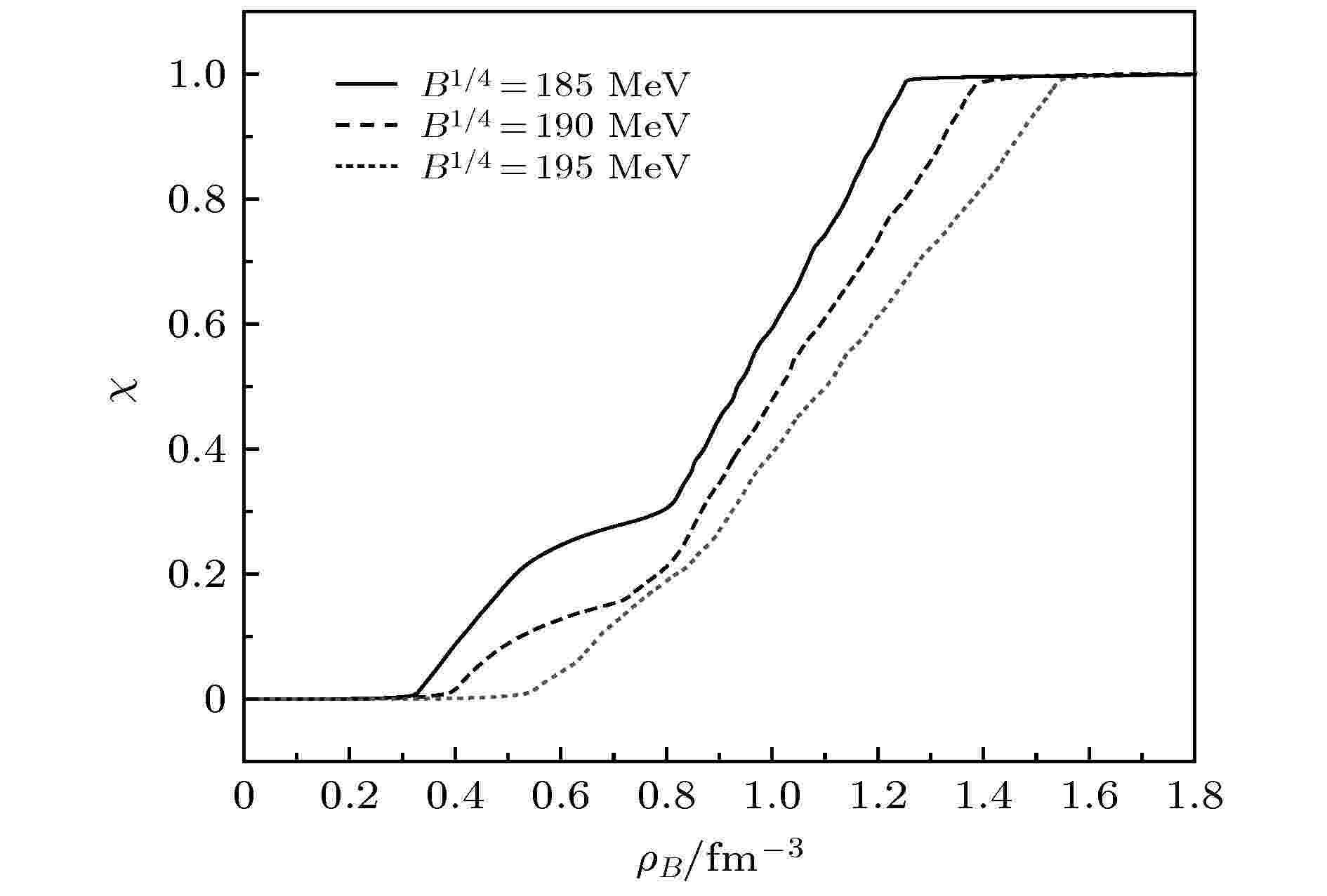 图 2
图 2 
































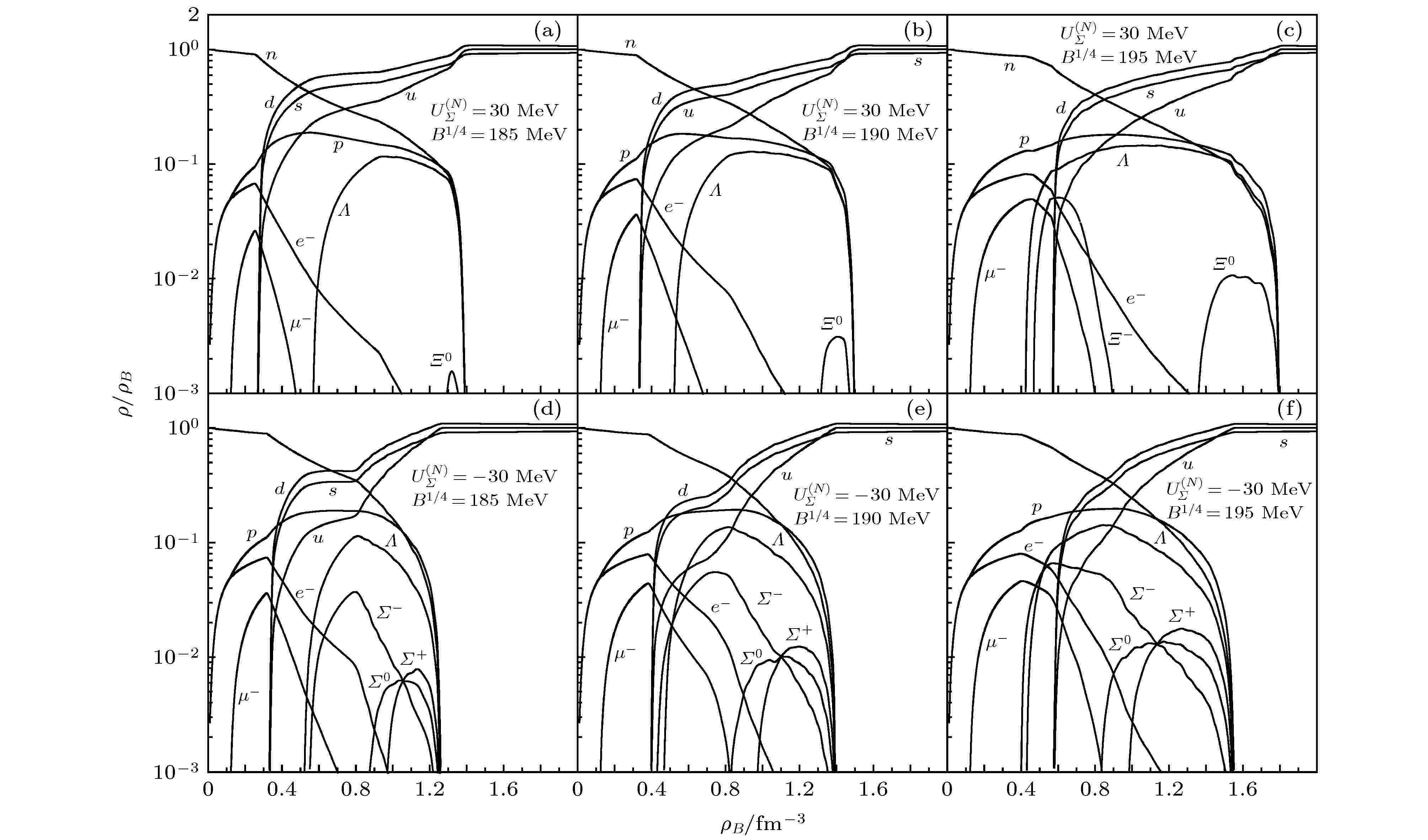 图 3 混合星粒子分布图(
图 3 混合星粒子分布图(









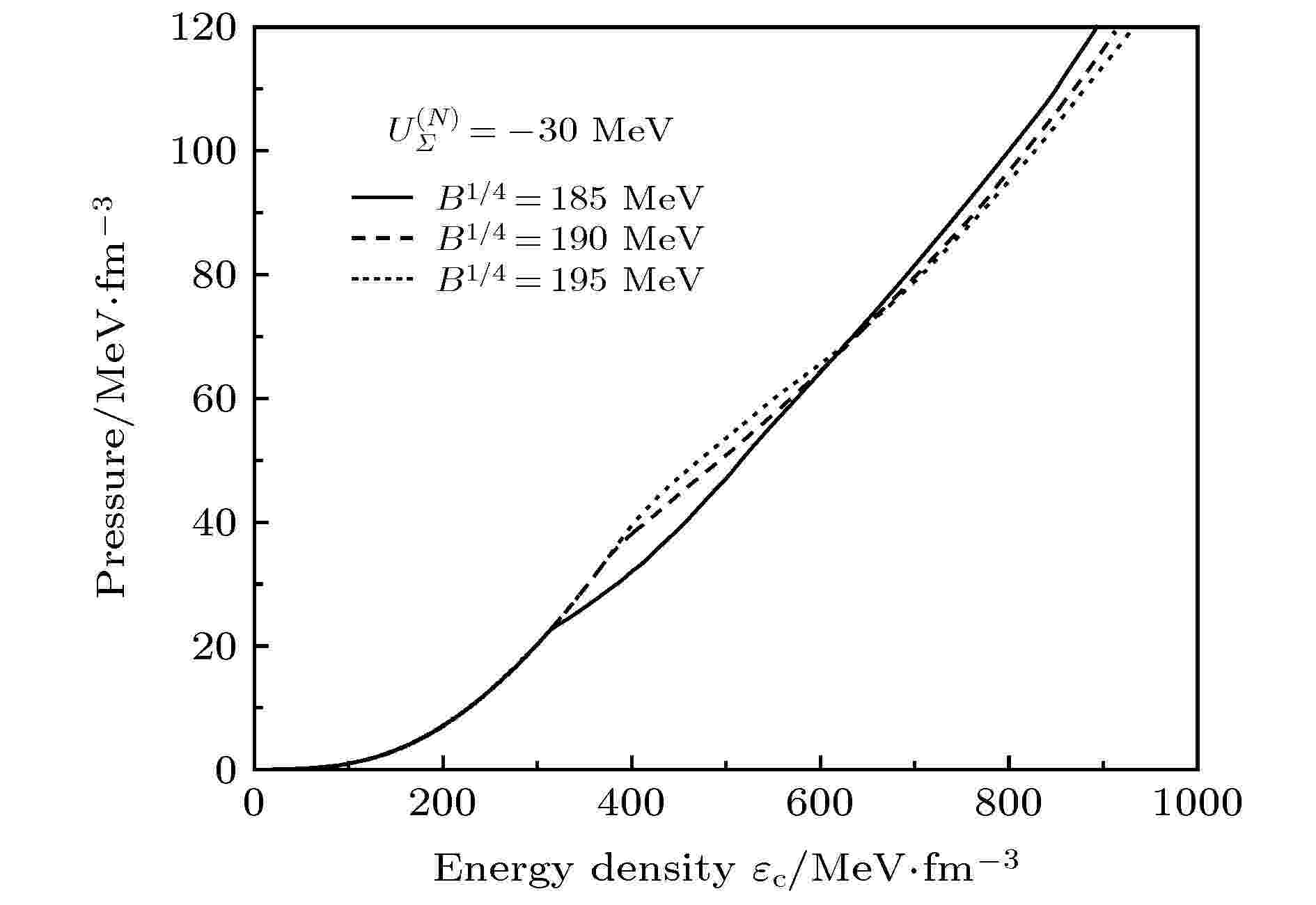 图 4
图 4 



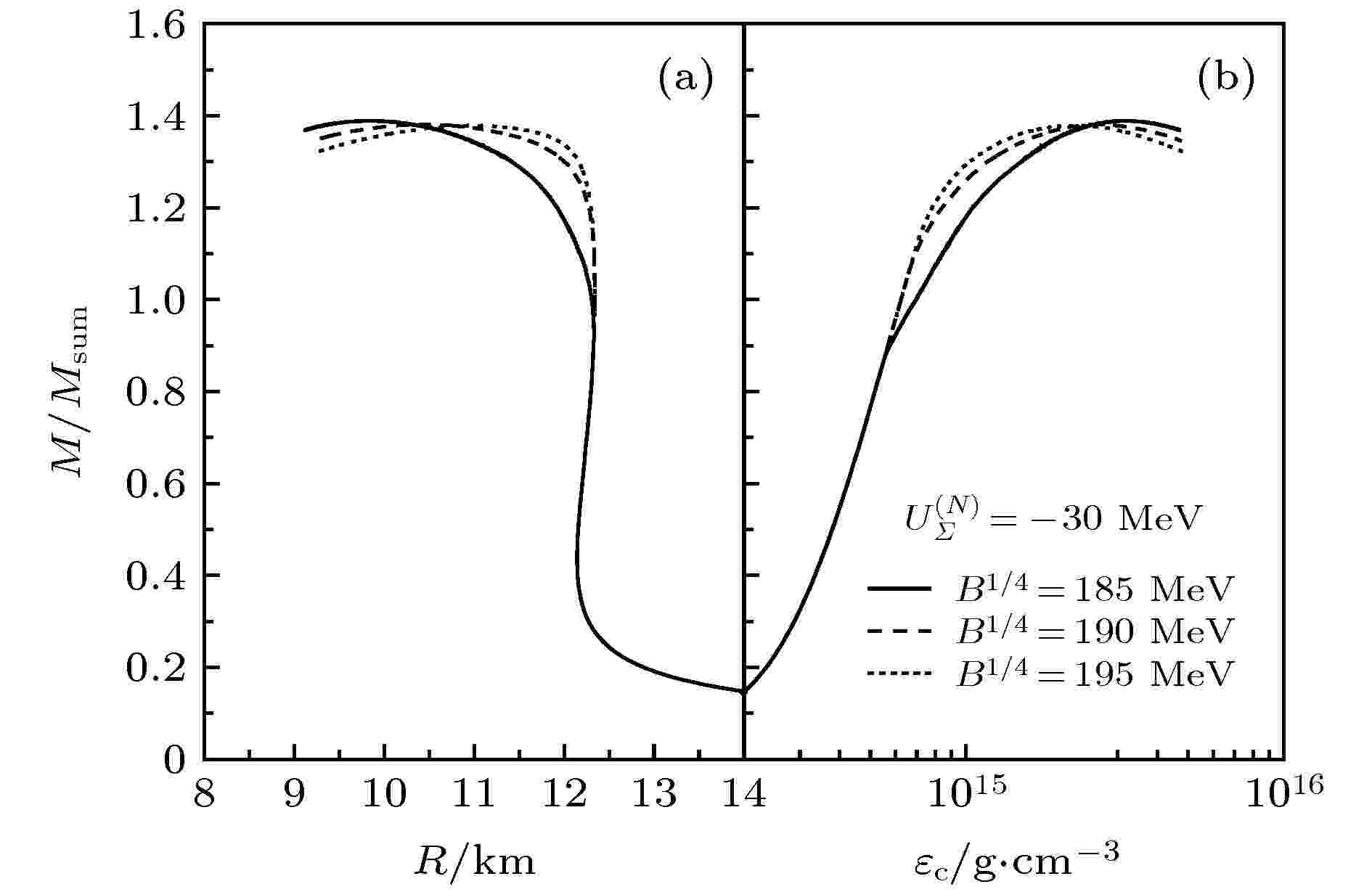 图 5 不同口袋常数下, 混合星质量-半径关系 (a)和质量-能量密度关系(b)
图 5 不同口袋常数下, 混合星质量-半径关系 (a)和质量-能量密度关系(b)
















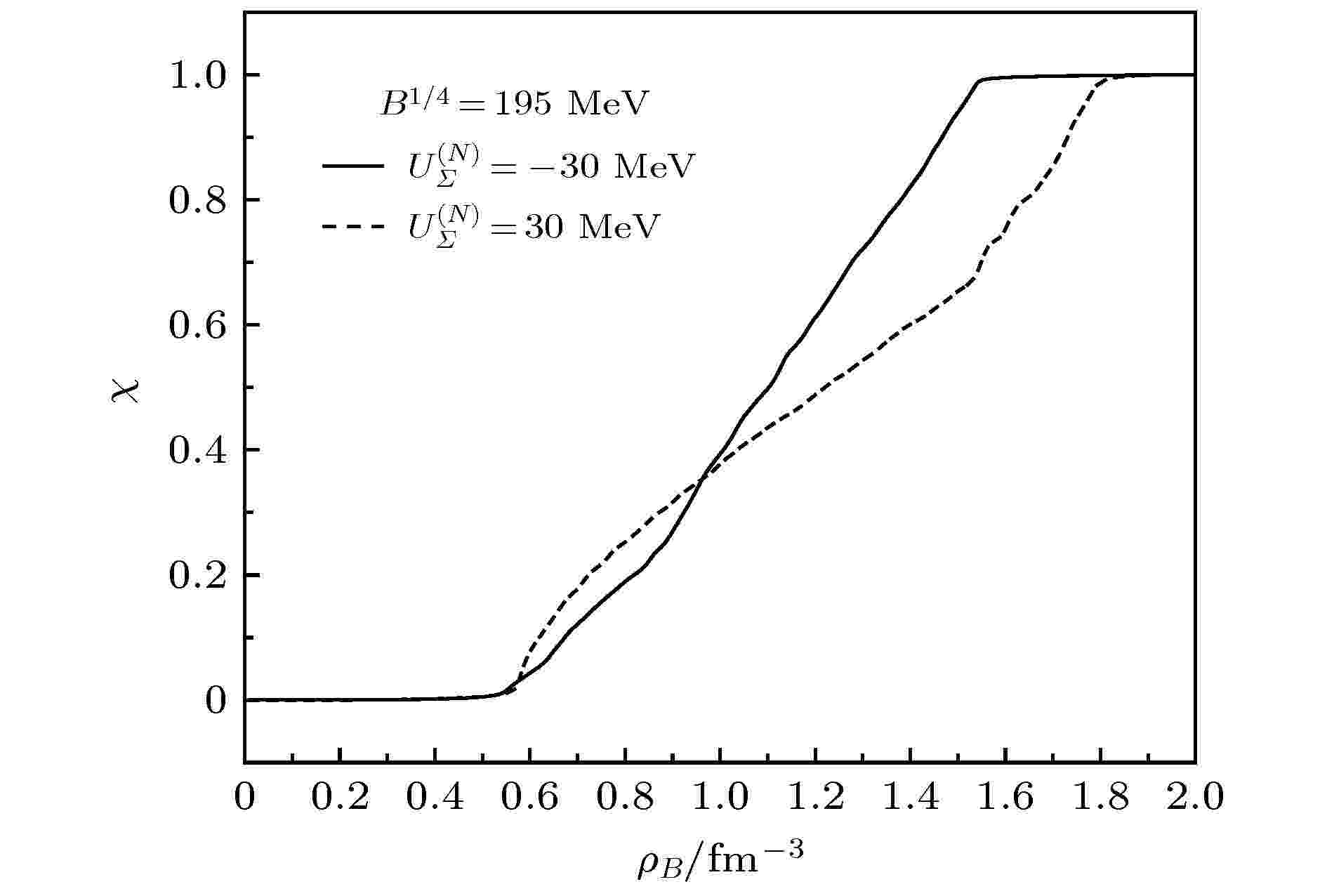 图 6
图 6 










 图 7
图 7 










