摘要:由于受电子器件尺寸和加工技术的限制, 在太赫兹波段很少有主动调控的编码超表面. 为了提高太赫兹编码超表面的灵活性, 本文选择相变材料二氧化钒进行主动调控. 分析了二氧化钒相变前(绝缘态)和相变后(金属态)两种态对单元结构幅值和相位的影响, 设计出一种能够主动调控的基于二氧化钒的1 bit太赫兹编码超表面, 该结构由二氧化钒、聚酰亚胺和铝构成, 不仅可以实现编码超表面调节电磁波波束的基本功能, 而且对于同一编码序列还能通过温控二氧化钒在1.1 THz实现两种远场波束的切换, 同样对于同一编码序列也能通过温控在1.1 THz实现两种近场聚焦焦点的切换. 这种基于二氧化钒对相位的影响而设计的编码超表面为灵活调控太赫兹波提供一种新的途径, 将在太赫兹传输、成像和通信等方面有着重大的应用前景.
关键词: 二氧化钒/
太赫兹/
编码超表面

English Abstract

全文HTML

--> --> -->

太赫兹一般是指频率在0.1—10 THz(波长为30—3000 μm)范围内的电磁波, 具有非电离、穿透性、吸水性和高分辨率等特性^[1-3], 在诸多领域例如无损检测^[4,5]、成像^[6,7]和通信^[8,9]方面展示了重要的应用前景. 但是由于太赫兹属于多学科交叉领域, 长期以来的发展受到很多限制, 尤其是没有有效的太赫兹产生和检测方法, 形成了电磁波中的“太赫兹间隙”. 近年来, 随着太赫兹量子级联^[10]和太赫兹时域光谱^[11]等技术的完善, 极大地促进了太赫兹的发展, 对太赫兹相位^[12]和偏振^[13]等性质的调控也渐渐地引起了广大研究人员的兴趣.
由于超表面有许多自然材料不具备的性质, 所以利用超表面调控太赫兹是目前常用的一种方式^[14-19]. 2011年, Capasso课题组^[20]提出广义斯涅耳定律, 将相位进行了离散化, 大大提高了超表面调控电磁波的能力, 涌现了很多结构新颖、功能强大的超表面^[21-24], 如能实现矢量全息的超表面^[22,23]和实现光传输到光衍射转化的多功能超表面^[24]. 2014年, 东南大学崔铁军院士进一步扩展了相位离散的思想, 在微波波段提出了数字超表面, 即编码超表面^[25]. 此后, 该思想被扩展到太赫兹领域, 涌现了一系列新颖的超表面, 如双频双功能编码超表面能实现两个频点不同功能^[26]、P–B编码超表面用于太赫兹波段自旋波和涡旋束的动态振幅调制^[27]. 但是这些编码超表面结构单一, 一旦结构固定, 功能就无法改变, 很少有主动调控的太赫兹编码超表面, 这极大地限制了编码超表面在太赫兹领域的发展.
本文选择相变材料二氧化钒作为主动调控的材料. 二氧化钒的相变温度大约68 ℃, 相变前可视作绝缘态, 而相变后视作金属态, 并且可以被温度、电场和光场等多种方式激励, 是一种相对理想的材料^[28-32]. 通过结合二氧化钒和编码超表面, 能大大地提高编码超表面调节太赫兹的灵活性, 为编码超表面的实际应用奠定基础.

编码超表面的设计思路主要是将相位进行数字化, 是相位梯度概念的进一步发展. 对于正常入射的平面波, 整个超表面的远场散射函数可以表示为^[25]

$ \begin{split} & f(\theta,\varphi ) = {f_{\rm{e}}}(\theta,\varphi ) \sum\limits_{m = 1}^N \sum\limits_{n = 1}^N \exp {\{} - {\rm i} {\{} \varphi (m,n) \\ &~~ +kD\sin \theta [(m \!-\! 1/2)\cos \varphi \!+\! (n \!\!- 1/2)\sin \varphi ]{\}} {\}}, \end{split} $

其中f_e(θ, φ)代表单个单元的远场函数; D是单元尺寸; θ, φ是任意方向的仰角和方向角; φ(m, n)表示位置(m, n)的单个单元的相位.
方向图函数可表示为

$Dir(\theta,\varphi ) = \frac{{4\pi | {f{{(\theta,\varphi )}^2}} |}}{{\displaystyle\int_0^{2\pi } {| {f{{(\theta,\varphi )}^2}} |} }}\sin \theta {\rm{d}}\theta {\rm{d}}\varphi .$

对于1 bit编码超表面来说, φ(m, n)只有0或π, 当单元“0”和“1”的幅度相同时, 两单元的散射特性相消, f_e(θ, φ)的辐射特性基本为0. 对于2 bit编码超表面来说, φ(m, n)有0, π/2, π和3π/2, 以此类推. 从(1)式和(2)式可以看出, 远场散射的方向和超表面单元的相位相关, 对于1 bit编码超表面, 设计单元时只需在保证单元幅度相同的情况下, 相位相差为π, 这样通过人为设计不同的相位排列方式(编码序列)就可以实现不同形式的远场波束^[25].
首先设计了一个简单的1 bit的编码超表面结构, 利用CST microwave studio(CST)的floquet模式进行仿真, 如图1所示. 超表面由三层组成, 周期d = 120 μm, 顶层和底层都为铝, 厚度t = 0.2 μm, 中间基底为聚酰亚胺, 介电常数ε = 3, 正切损耗tanδ = 0.03, 厚度h = 20 μm. 对于单元“0”, 圆环外半径r₁ = 35 μm, 内半径r₂ = 29 μm. 对于单元“1”, s₁ = 70 μm. 单元“0”和“1”的共极化反射振幅和相位如图1(c)和图1(d)所示, 在1.1 THz, 单元“0”和“1”的幅值相近, 都大于0.8, 而相位差约180°(参考平面的选择不改变相位差), 满足1 bit编码超表面条件.
图 1 1 bit编码超表面示意图　(a) 单元“0”的结构示意图; (b) 单元“1”的结构示意图; (c) 单元“0”和“1”的反射振幅; (d) 单元“0”和“1”的反射相位
Figure1. Schematic diagram of 1 bit coding metasurface: (a) Schematic diagram of unit “0”; (b) schematic diagram of unit “1”; (c) reflection amplitude of units “0” and “1”; (d) reflection phase of units “0” and “1”.

然后验证了频率为1.1 THz时不同编码序列下的远场方向图, 如图2所示. 当编码序列为1010/1010周期排列时, 在平面波垂直(偏振方向为x方向)入射下, 反射波被均匀地反射到两个不同的方向; 当编码序列为0101/1010周期排列时, 入射波主要被反射到四个不同的方向, 这里的超级子单元选择4 × 4, 以降低相邻单元之间的反射相位恶化.
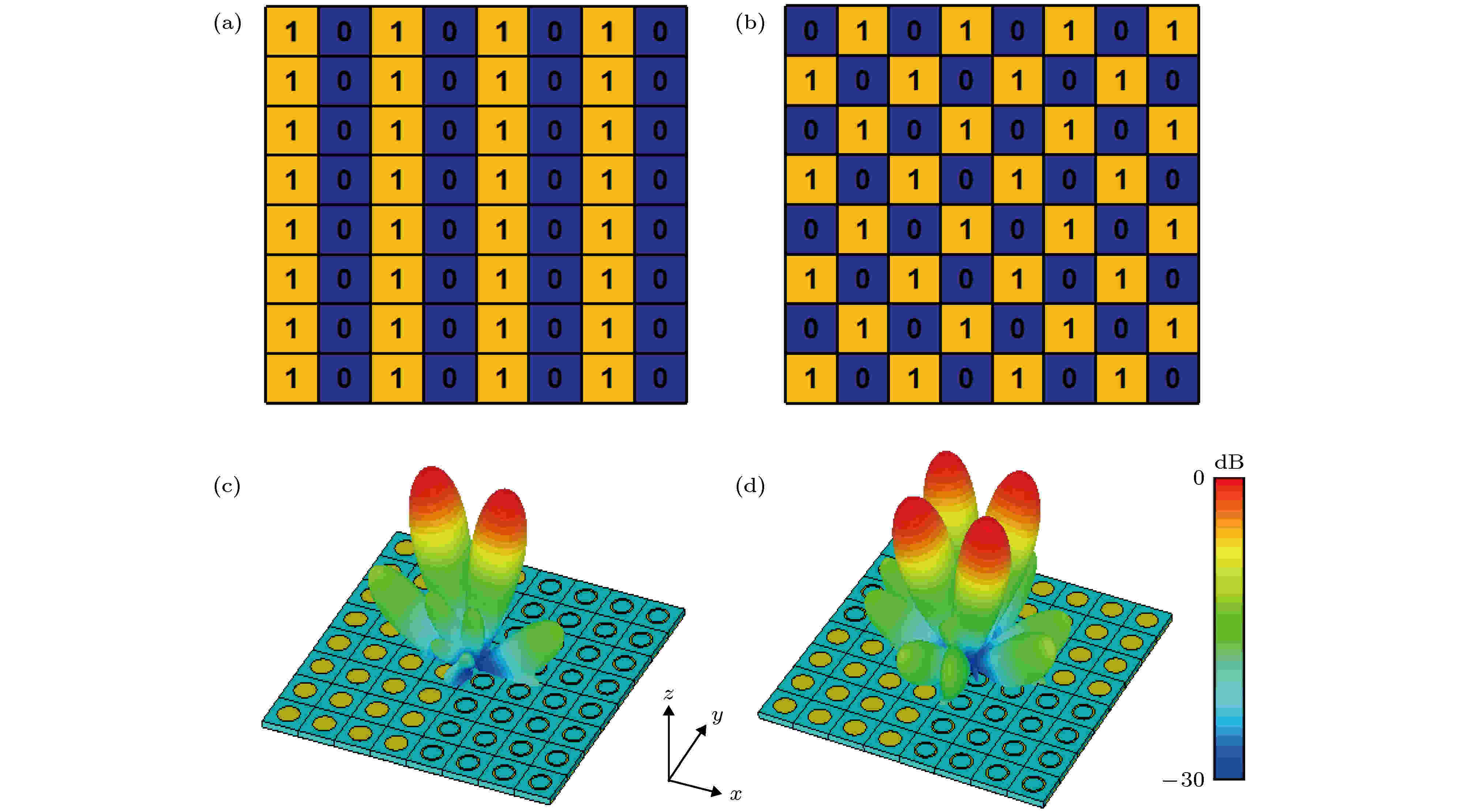图 2 1 bit编码超表面不同编码序列示意图　(a) 编码序列1010/1010; (b) 编码序列0101/1010; 在1.1 THz(c) 编码序列1010/1010的远场方向图; (d) 编码序列0101/1010的远场方向图
Figure2. Schematic diagram of different coding sequences on coding metasurface: (a) Coding sequence 1010/1010; (b) coding sequence 0101/1010; At 1.1 THz (c) far-field pattern of coding sequence 1010/1010; (d) far-field pattern of coding sequence 0101/1010.

而二氧化钒作为一种相变材料, 在这里只考虑两种情况, 常温下(相变前)可以看成绝缘态, 介电常数ε_i = 9, 电导率σ = 200 S/m^[28], 然后用加热台加热基于二氧化钒的编码超表面并用温度传感器监测温度^[30,33], 当温度超过68 ℃时, 二氧化钒转化了金属态, 复介电常数进而可以用Drude模型进行表示^[32]:

$ \varepsilon (\omega )=\varepsilon '+\varepsilon'' ={\varepsilon }_{\infty }-\dfrac{{\omega }_{{\rm{p}}}^{2}(\sigma )}{{\omega }^{2}+{\rm{i}}\gamma \omega }, $

其中ε_∞ = 12, 碰撞频率γ = 5.75 × 10¹³ rad/s.

$\omega _{\rm{p}}^2(\sigma ) = \sigma \omega _{\rm{p}}^2({\sigma _0})/{\sigma _0}.$

σ₀ = 3 × 10⁵ S/m, ω_p(σ₀) = 1.4 × 10¹⁵ rad/s, 当二氧化钒为金属态时, 实际电导率σ = 2 × 10⁵ S/m. 这样就可以将二氧化钒相变前后的两种情况的介电常数表示出来, 再结合编码超表面的理论, 可以用仿真软件进行仿真.

为了实现主动调控, 将编码超表面和二氧化钒相结合, 如图3所示. 除了顶层外, 其余部分和图1的结构相同, 单元“0”顶层圆环内半径c₂ = 27 μm, 外半径c₁ = 34.5 μm, 其余部分全部为二氧化钒, 而对于单元“1”, 顶层铝的直径s₂ = 68 μm, 其余部分为二氧化钒. 单元“0”和“1”的幅值相位图如图2(c)和图2(d). 当二氧化钒为绝缘态时, 单元“0”和“1”在1.1 THz的幅值相差无几, 均在0.7以上, 而相位相差约为180°, 满足编码超表面的条件. 而当单元“0”和“1”的二氧化钒转化为金属态时, 幅值均大于0.85, 相位基本相同. 这样通过改变二氧化钒, 可以实现反射波束的变化, 如图4所示. 当平面波垂直入射时(偏振方向为x方向), 二氧化钒为绝缘态时, 棋盘序列(0101/1010)的反射波束为四波束, 和基本的编码超表面相同; 当二氧化钒转化为金属态时, 反射波束为垂直的波束. 这样通过温控二氧化钒等方式就能够实现反射波束的动态变化.
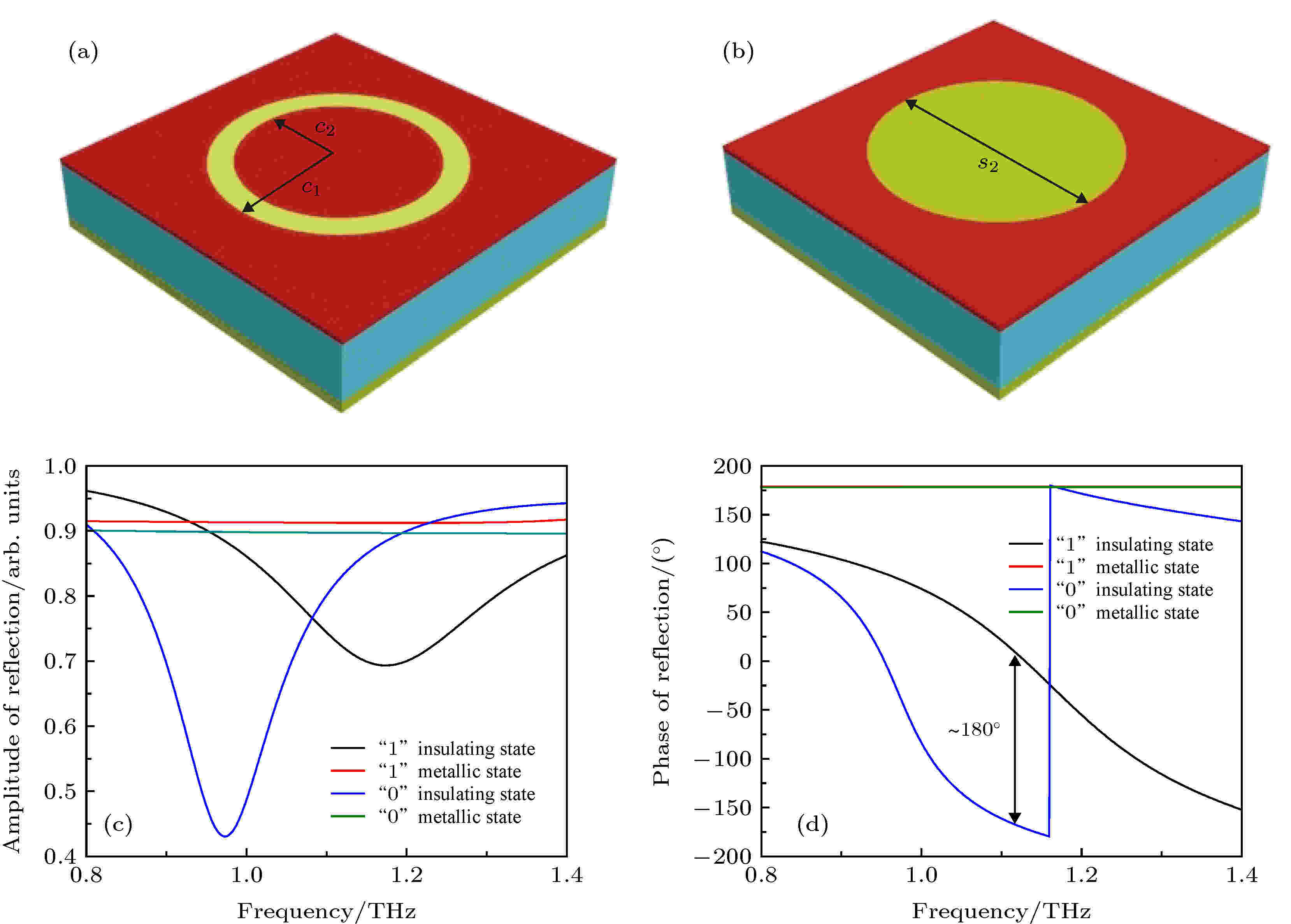图 3 1 bit编码超表面示意图　(a) 单元“0”的结构示意图; (b) 单元“1”的结构示意图; (c) 单元“0”和“1”在二氧化钒不同态时的反射振幅; (d) 单元“0”和“1”在二氧化钒不同态时的反射相位
Figure3. Schematic diagram of 1-bit coding metasurface: (a) Schematic diagram of unit “0”; (b) schematic diagram of unit “1”; (c) reflection amplitude of units “0” and “1” in different vanadium dioxide states; (d) reflection phase of units “0” and “1” in different vanadium dioxide states.

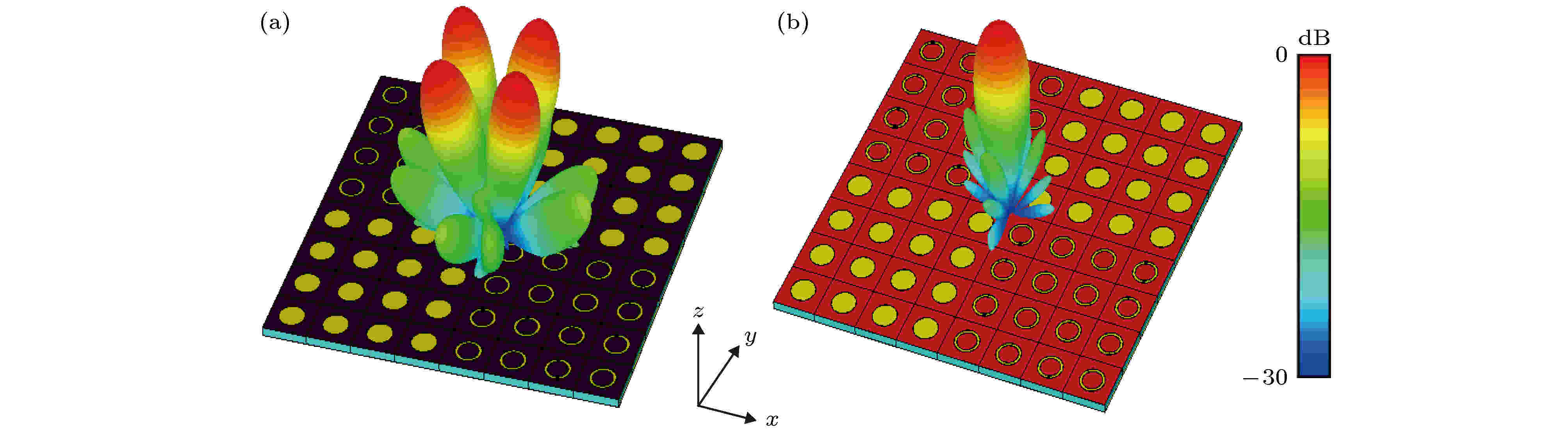图 4 棋盘序列(0101/1010)在1.1 THz的远场示意图　(a) 二氧化钒为绝缘态时的远场示意图; (b) 二氧化钒为金属态时的远场示意图
Figure4. Far-field diagram of chessboard sequence (0101/1010) at 1.1 THz: (a) Far-field diagram when vanadium dioxide is in insulating state; (b) far-field diagram when vanadium dioxide is in metallic state.

值得一提的是, 图3所展示的二氧化钒的变化, 只是将单元“0”和“1”的相位转变为相同的相位, 从而让任意编码序列的反射波束转变为垂直波束, 无法实现各种波束间的转化. 为此设计了新的二氧化钒-金属结构如图5所示, 单元“0”中q₁ = 8 μm, w = 31 μm, b = 71 μm, 单元“1”中q₂ = 14 μm, e = 80 μm, a = 108 μm, 红色部分为二氧化钒. 幅值和相位如图5(c)和图5(d)所示, 在1.1 THz处, 当二氧化钒都为绝缘态时, 单元“0”和“1”的幅值相差不大, 相位相差约180°, 当二氧化钒转化为金属态时, 单元“0”和“1”的幅值同样在0.7以上, 相位差也相差180°, 即相当于单元“0”变成了单元“1”, 单元“1”变成了单元“0”. 图6展示了在1.1 THz时, 棋盘序列的远场方向图, 可以看出, 无论二氧化钒是金属态还是绝缘态, 入射波都被反射到了四个方向, 不同的是编码序列由0101/1010序列转换成了1010/0101序列.
图 5 1 bit编码超表面示意图　(a) 单元“0”的结构示意图; (b) 单元“1”的结构示意图; (c) 单元“0”和“1”在二氧化钒不同态时的反射振幅; (d)单元“0”和“1”在二氧化钒不同态时的反射相位
Figure5. Schematic diagram of 1 bit coding metasurface: (a) Schematic diagram of unit "0"; (b) schematic diagram of unit "1"; (c) reflection amplitude of units "0" and "1" in differ rent vanadium dioxide states; (d) reflection phase of units "0" and "1" in different vanadium dioxide states.

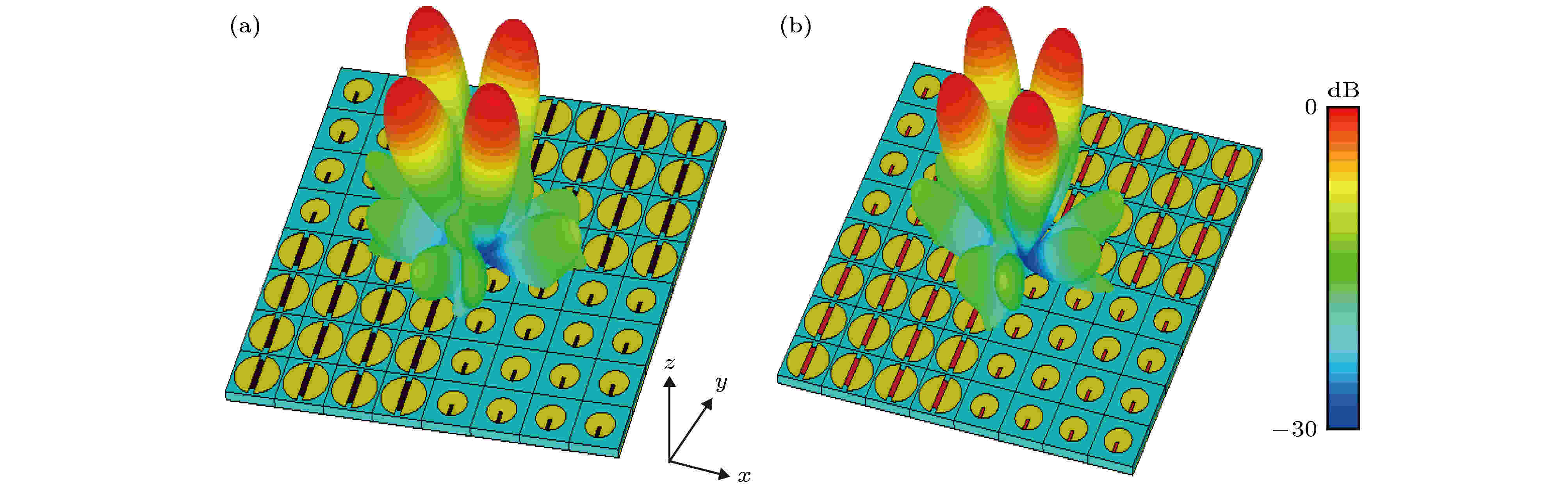图 6 1.1 THz棋盘序列的远场方向图　(a) 二氧化钒为绝缘态; (b) 二氧化钒为金属态
Figure6. Far-field pattern of chessboard sequence at 1.1 THz: (a) Vanadium dioxide is in insulating state; (b) vanadium dioxide is in metallic state.

这样, 通过将图5的二氧化钒-金属结构和图1中的1 bit基本结构相结合, 能进一步提高主动调控的灵活性, 具体如图7所示. 图1中基本的编码超表面结构不变, 通过配置图5中的基本结构, 可以将1010/1010周期序列转化成0000/1111周期序列, 这样在垂直的平面波(偏振方向为x方向)入射下, 绝缘态的二氧化钒可以将入射波反射到沿x轴的两个方向, 金属态的二氧化钒可以将入射波反射到沿y轴的两个方向. 通过这种方式, 可以实现两种不同编码序列间的动态转化, 在远场上表现为不同波束的转换, 大大提高了主动调控的灵活性.
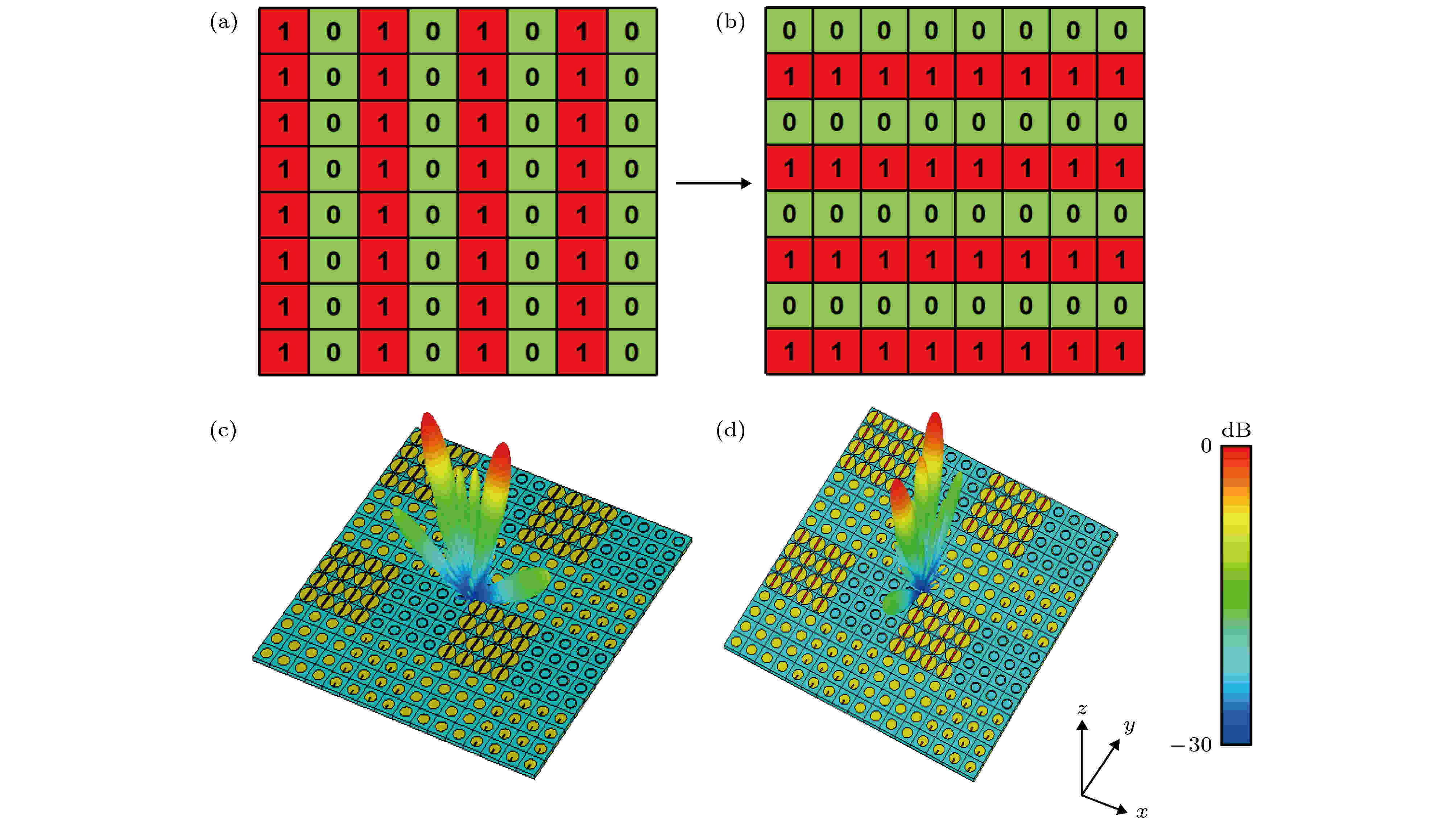图 7 不同编码序列示意图　(a) 编码序列1010/1010; (b) 编码序列0000/1111; 在1.1 THz(c) 编码序列1010/1010的远场方向图; (d) 编码序列0000/1111的远场方向图
Figure7. Schematic diagram of different coding sequences: (a) Coding sequence 1010/1010; (b) coding sequence 0000/1111; At 1.1 THz, (c) far-field pattern of coding sequence 1010/1010; (d) far-field pattern of coding sequence 0000/1111.

同时, 利用二氧化钒的相变性质也可以实现近场聚焦的转化. 根据相位补偿原理, 位于平面(z = 0)的超表面实现聚焦的相位分布满足公式:

$\phi \!=\! \frac{{2\pi }}{\lambda }\Big(\sqrt {{{(x - {x_f})}^2} + {{(y \!-\! {y_f})}^2} \!+\! {{(z \!-\! {z_f})}^2}} \!-\! {z_f}\Big), $

其中λ为设计的波长, (x_f, y_f, z_f)表示焦点的坐标, (x, y, z)为单元的中心坐标.
这样通过将相位数字化, 转化为1 bit编码超表面的基本单元, 就可以用编码超表面实现焦点的转移, 如图8所示. 选择18 × 18基本单元的编码超表面, 对于焦点(0, 0, 900)代入(5)式得到相位再将其转化为相近的1 bit编码单元, 同样对于焦点(600, 600, 800)也能得到相应的编码和相位图. 比较不同焦点的编码序列, 将不同的编码单元用二氧化钒-金属结构的基本单元替代, 通过改变二氧化钒的相变属性, 就能够转移焦点的位置. CST仿真结果如图9所示, 二氧化钒为金属态时, 从z = 900 μm平面可以看出中心(x = 0 μm, y = 0 μm)的归一的电场x分量明显大于其他位置, 而当二氧化钒是绝缘态时, 从z = 800 μm平面可以看出, 最大的电场x分量在x = 600 μm, y = 600 μm附近, 符合我的预期.
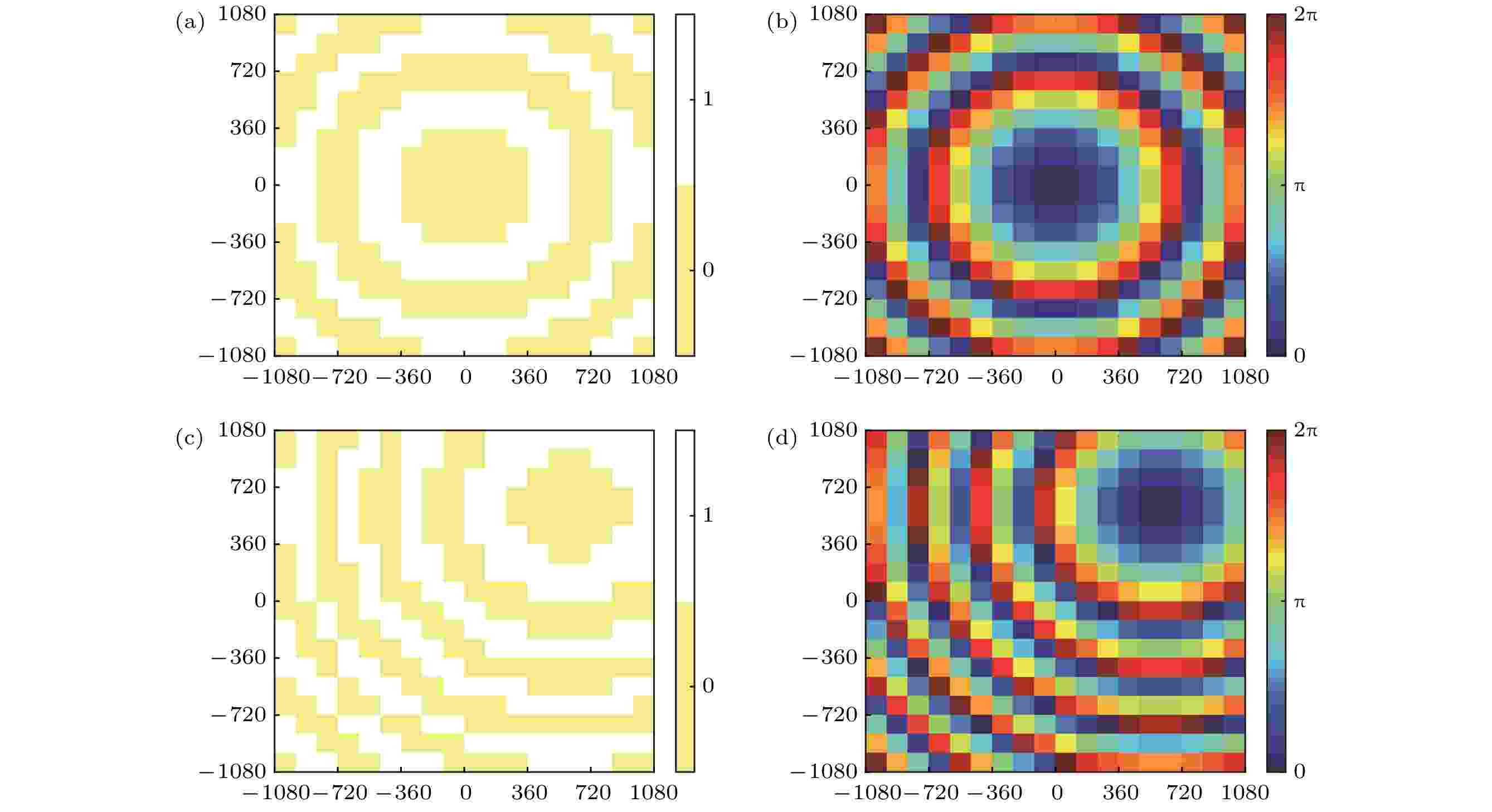图 8 聚焦的编码和相位示意图　(a) 焦点(x_f = 0 μm, y_f = 0 μm, z_f = 900 μm)的编码图; (b) 焦点(x_f = 0 μm, y_f = 0 μm, z_f = 900 μm)的相位图; (c) 焦点(x_f = 600 μm, y_f = 600 μm, z_f = 800 μm)的编码图; (d) 焦点(x_f = 600 μm, y_f = 600 μm, z_f = 800 μm)的相位图
Figure8. Coding and phase diagram of focus: (a) Coding diagram of focus (x_f = 0 μm, y_f = 0 μm, z_f = 900 μm); (b) phase diagram of focus (x_f = 0 μm, y_f = 0 μm, z_f = 900 μm); (c) coding diagram of focus (x_f = 600 μm, y_f = 600 μm, z_f = 800 μm); (d) phase diagram of focus (x_f = 600 μm, y_f = 600 μm, z_f = 800 μm).

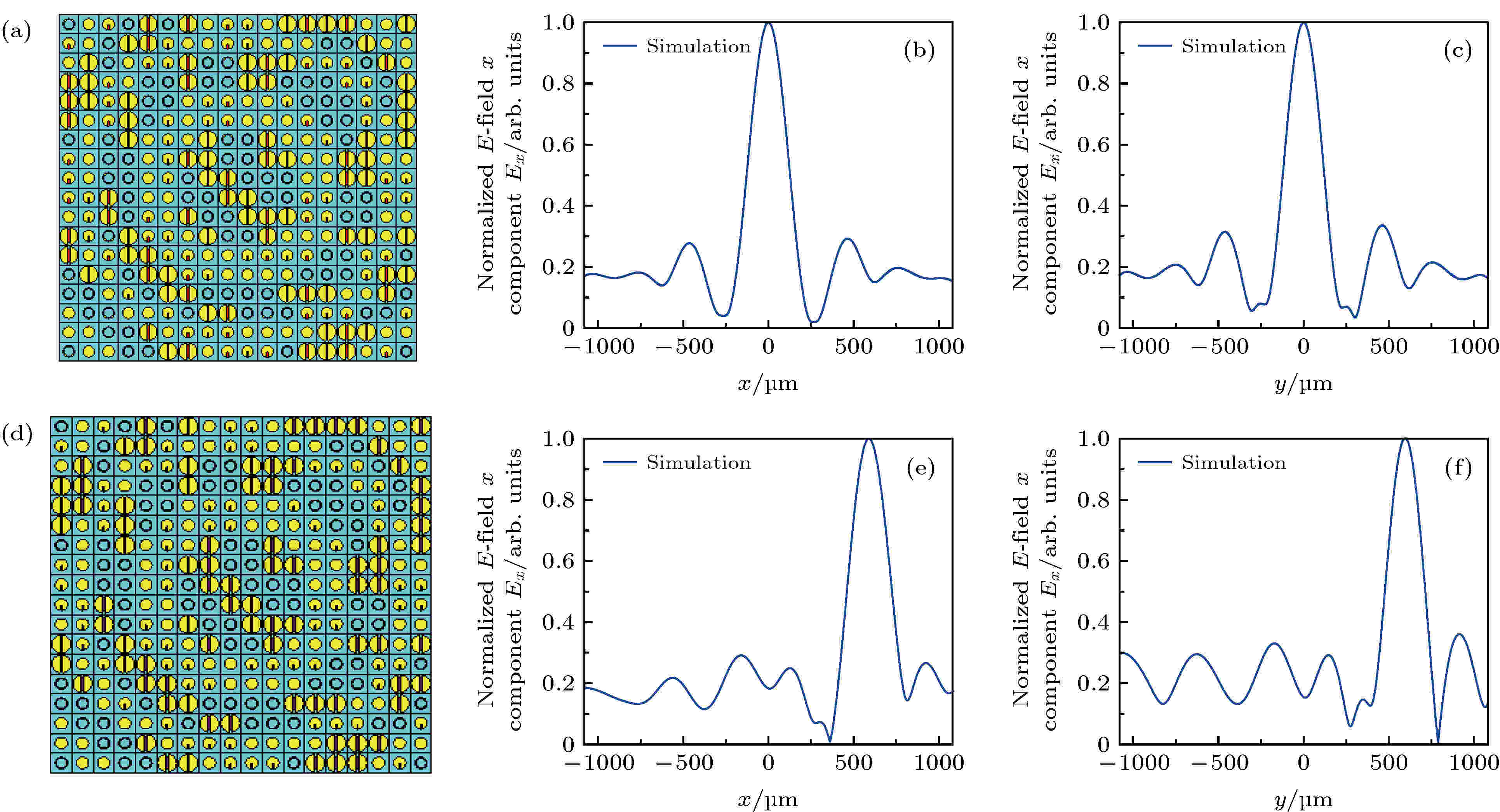图 9 整体结构和电场图 二氧化钒为金属态时　(a) 超表面结构; (b)在z = 900 μm平面的x方向的归一化电场的x分量图; (c)在z = 900 μm平面的y方向的归一化电场的x分量图. 二氧化钒为绝缘时 (d) 超表面结构; (e) 在z = 800 μm平面的x方向的归一化电场的x分量图; (f) 在z = 800 μm平面的y方向的归一化电场的x分量图
Figure9. Overall structure and electric field diagram. When vanadium dioxide is metallic state: (a) Metasurface structure; (b) x component diagram of normalized electric field in X direction of z = 900 μm plane; (c) x component diagram of normalized electric field in Y direction of z = 900 μm plane. When vanadium dioxide is insulating state (d) metasurface structure; (E) x component diagram of normalized electric field in X direction of z = 800 μm plane; (f) x component diagram of normalized electric field in Y direction of z = 800 μm plane.

传统的太赫兹编码超表面只能实现单一功能, 无法主动调控, 通过讨论二氧化钒和编码超表面相结合的方式, 设计了太赫兹频段的二氧化钒-金属编码超表面结构. 通过温控等方式控制二氧化钒的相变, 使结构能在1.1 THz实现两种远场波束间的切换, 基于同样的思路, 设计合理的编码超表面序列, 也能在1.1 THz实现近场聚焦焦点的转化. 设计的主动调控的太赫兹编码超表面在太赫兹通信、太赫兹聚焦成像领域都有着巨大的应用前景.