摘要:利用自研的磁场下太赫兹时域光谱(terahertz time-domain spectroscopy, THz-TDS), 系统研究了磁场与非磁性Y³⁺离子掺杂对HoFeO₃单晶中自旋态以及自旋重取向的影响. 结果表明Y³⁺掺杂可以在不改变自旋重取向类型情况下, 有效降低自旋重取向温区, 而且还能降低Ho_1–xY_xFeO₃单晶中低温区准铁磁模式(q-FM, quasi-ferromagnetic mode)自旋共振频率以及提升高温区的准反铁磁模式(q-AFM, quasi-antiferromagnetic mode)自旋共振频率. 在沿(110)方向施加外加磁场( H _DC)的情况下, 一方面, 发现磁场不仅能有效调控Ho_1–xY_xFeO₃单晶中的q-FM共振频率, 而且还能诱导出自旋重取向; 另一方面, 发现温度越接近自旋重取向温区时, 磁诱导自旋重取向的发生越容易, 而且磁诱导效应的临界磁场强度随Y³⁺离子掺杂浓度而增加. 研究表明, THz光谱数据可以用于检测HoFeO₃中Y³⁺离子的掺杂浓度, 而且Y³⁺掺杂可以使HoFeO₃晶体中的自旋态更加稳定, 不容易受外界磁场的影响. 这一自旋重取向的掺杂效应、磁控效应的研究将有助于理解稀土正铁氧体中的自旋交换作用及其外场调控机制.
关键词: 太赫兹时域光谱/
稀土正铁氧体/
自旋重取向/
自旋共振

English Abstract

全文HTML

--> --> -->

因具有磁光效应、超快磁翻转、多铁性和自旋重取向相变等新奇的物理特性, 稀土正铁氧体RFeO₃(R表示Y或稀土元素)已经成为凝聚态物理的热点研究对象之一^[1-8]. RFeO₃材料中有两种磁性离子: R³⁺和Fe³⁺离子. 它们之间存在三种磁相互作用, 分别存在于Fe³⁺-Fe³⁺, R³⁺-Fe³⁺ 以及R³⁺-R³⁺之间^[9-13]. 这三种作用相互竞争, 产生了丰富的磁相变. 其中一种常见而又有趣的磁相变就是自旋重取向, 也就是RFeO₃材料中的自旋矢量会随着温度等外场变化而出现重新排布的现象^[8,14-20]. 这一现象一般认为是铁离子(Fe³⁺)和稀土离子(R³⁺)之间的弱相互作用, 以及它们各自子格子磁性行为的不一致造成的^[8,17]. 自旋重取向代表着自旋态的转变, 不仅可以作为自旋电子学器件中信息的载体, 而且其衍生效应可以为深入挖掘磁性物理机制提供基础. 为此, 自旋重取向相变成为了RFeO₃研究中的重要内容, 吸引了广泛的关注^{[1,3,14,21-23]}.
一方面, 人们不断探索不同RFeO₃体系中自旋重取向相变的不同特征; 另一方面, 人们希望通过各种手段实现对自旋重取向相变的调控, 比如元素掺杂、外场调控等, 以期获取调控规律与潜在应用基础. 已有研究表明, R位的元素掺杂能有效改变R³⁺-Fe³⁺交换作用能量, 从而可以调控RFeO₃的自旋重取向温区^{[9,19,21,24-26]}. 元素掺杂一般分为磁性离子掺杂和非磁性离子掺杂. RFeO₃体系的磁性离子掺杂中最为典型是Sm³⁺离子. SmFeO₃本身也在RFeO₃体系中具有最高的自旋重取向温度(T_SR约为480 K). 目前, 人们认为Sm_xR_1-xFeO₃是实现室温的自旋重取向的最佳材料^[9,11,24,26]. 例如, Wang等^[11]生长了高质量的Sm_0.7Tb_0.3FeO₃单晶, 自旋重取向的温区为330—360 K. 随后, Liu等^[24]发现在Sm³⁺离子掺杂的DyFeO₃单晶样品中, 样品的自旋重取向温区随着Sm³⁺离子掺杂浓度上升而线性上升. 对于非磁性离子掺杂, 新掺入的离子不会与Fe³⁺产生新的交换作用. 因此在非磁性离子掺杂的RFeO₃中, 能更方便地分析Fe³⁺-R³⁺交换作用对于自旋重取向相变的影响. 在掺杂的非磁性离子中, Y³⁺是常见的一种^[13,25]. 例如2018年, Li等^[25]系统研究了不同浓度Y³⁺掺杂的ErFeO₃单晶样品中不同温度磁场下的太赫兹(terahertz, THz)吸收谱, 证明了样品中存在着迪克协作耦合效应.
除了掺杂(化学压力), 磁场是另一种常见的、用于调控RFeO₃中自旋重取向相变的手段^[27-30]. 例如, Jiang等^[28]利用太赫兹光谱发现, 外加磁场诱导下的NdFeO₃单晶中的自旋重取向转变具有强烈的各向异性, 这取决于外加磁场的方向. Guo等^[27]研究了TmFeO₃单晶中外加磁场分别沿a或c轴施加时, 准铁磁模式(q-FM, quasi-ferromagnetic mode)的共振频率上升或下降, 而准反铁磁模式(q-AFM, quasi-antiferromagnetic mode)的共振频率几乎不变. Amelin等^[23]研究了YFeO₃单晶中低温磁场下的太赫兹吸收谱, 在3 K的温度下沿a轴施加到6.2 T的磁场可以诱导自旋重取向转变发生. 值得注意的是由于Y³⁺是非磁性离子, YFeO₃中没有产生温度诱导的Fe³⁺离子的自旋重取向过程.
既然元素掺杂与外加磁场都能有效地调控RFeO₃体系中的自旋重取向相变, 那么探索两种方法的差异与其共同作用效果是非常有意义的. 据我们所知, 这一思路还未有人提出. 本文采用太赫兹光谱, 系统研究了变温条件下磁场、非磁性Y³⁺离子掺杂对HoFeO₃单晶中q-FM和q-AFM的共振频率以及自旋重取向的影响. 研究表明非磁性Y³⁺离子的掺入不仅能改变q-FM和q-AFM的共振频率, 而且能移动自旋重取向发生的温区. 另外, 我们还发现外加磁场不仅能有效地调控Ho_1–xY_xFeO₃单晶中的q-FM共振频率, 而且还能诱导出自旋重取向.

实验中用到的单晶HoFeO₃, Ho_0.8Y_0.2FeO₃和Ho_0.6Y_0.4FeO₃采用助溶剂法^[31]生长获得. 为了有效地获得这些单晶样品中自旋波及其自旋重取向过程, 本文选择了太赫兹时域光谱(terahertz time-domain spectroscopy, THz-TDS)技术. 该技术是研究磁性材料的自旋共振和自旋重取向最有效的方法之一, 并且由于THz脉冲具有非常小的光子能量 (1 THz, 约为4.1 meV), 其热效应可以被忽略^[14,32-35].
本文的THz-TDS光谱实验是在中国科学院强磁场科学中心自主研制的变温磁场下THz-TDS测试系统中完成的. 该系统的温度变化范围为5—350 K; 磁场变化范围为0—8 T. 系统所用的光源是Menlo Systems公司的飞秒光纤激光器, 输出的中心波长为780 nm, 脉冲宽度为120 fs, 重复频率为80 MHz. 激光被分为两束, 一束作为THz脉冲产生光, 聚焦到光电导天线上产生宽谱THz脉冲. 透射的THz光通过离轴抛物镜改变方向和第二束激光同时聚焦到厚度为2 mm, (110)取向的ZnTe晶体上, 利用电光取样技术探测THz信号. 有效的光谱范围为0.1—1.5 THz. 在测量过程中, THz脉冲垂直入射到样品上, 并且所有的样品都固定到一个直径为2.5 mm的金属孔上.
选取了(110)取向的HoFeO₃, Ho_0.8Y_0.2FeO₃和Ho_0.6Y_0.4FeO₃单晶用于THz-TDS光谱测量, 厚度分别为0.5, 0.8和0.8 mm, 所有的样品都进行了双面抛光.

HoFeO₃具有扭曲的钙钛矿结构, 可以用空间群${D}_{2 h}^{16}\text-Pbnm$来描述^[16]. 其中Fe³⁺自旋在奈尔温度(T_N = 647 K)以下反铁磁有序, 由于Dzyaloshinskii–Moriya (DM) 相互作用导致两套磁亚晶格的磁化S₁和S₂具有约0.5°的相对倾斜角度, 并且晶体中具有两种自旋共振模式: 准反铁磁模式(q-AFM, quasi-antiferromagnetic mode)和准铁磁模式(q-FM, quasi-ferromagnetic mode)^[36]. 这两种共振模式的频率都在THz范围内, 因此采用THz吸收谱可以有效地探测出q-FM和q-AFM的共振频率及其变化规律, 从而分析出样品中的自旋状态.
HoFeO₃中倾斜的反铁磁结构导致了非零的铁磁净磁矩M = S₁ + S₂和G型反铁磁磁矩L = S₁ – S₂. 在自旋重取向转变的温度范围内, HoFeO₃单晶具有多个磁相变, 其中T₃, T₂和T₁(T₃ < T₂ < T₁)分别对应Γ₂→Γ₁₂, Γ₁₂→Γ₂₄, 和Γ₂₄→Γ₄磁相变的特征温度点^[16,20,36]. 当温度T < T₃时, 晶体处于Γ₂相, L平行于晶体的c轴, M平行于a轴. 当THz脉冲的磁场分量与c轴平行(H_THz//c), 晶体中的Γ₂相对应q-FM共振模将被太赫兹谱观察到(见图1(a)中的红色虚线). 从变温的结果可以看到, 该q-FM共振模的频率随着温度的上升而下降. 当样品温度上升到T₃ < T < T₂温区时, L向(100)面逐渐旋转, 最终与c轴夹角θ约为30°, 此时晶体处于Γ₁₂相. 当T = T₂时, 晶体发生一阶相变, 反铁磁磁矩矢量突然转向(010)面并且保持与c轴的夹角 θ, 这种转变导致M从a轴转向c轴, 沿c轴方向出现了非零的净磁矩^[20,36]. 由于在Γ₂→Γ₁₂相变过程中, q-FM共振频率一直随着温度上升而下降, 并没有明显转变点. 因此, 我们无法确定Γ₂→Γ₁₂相变的转变点^[16,20]. 随着样品温度继续上升至T₂ < T < T₁时, L从(010)面逐渐转向a轴, 此时晶体处于Γ₂₄相. 当温度T₁ < T < T_N时, 晶体处于Γ₄相, L平行于晶体的a轴, M平行于c轴. 当H_THz//c轴, 样品中Γ₄相对应q-AFM共振模将被太赫兹谱观察到(见图1(a)中的蓝色虚线). 从变温的结果可以看到, 该q-AFM共振模的频率随着温度的上升而上升. 这一结果充分表明, THz光谱能有效的探测RFeO₃体系中的自旋共振与自旋重取向行为.
图 1 (a)?(c) 不同温度下(110)取向的HoFeO₃, Ho_0.8Y_0.2FeO₃和Ho_0.6Y_0.4FeO₃单晶的THz透射谱, 入射的太赫兹磁场分量(H_THz)平行于晶体的c轴, 图中红色和蓝色虚线分别帮助识别准铁磁模式(q-FM)共振峰和准反铁磁模式(q-AFM)共振峰; (d)?(f) 不同Y³⁺掺杂浓度单晶中的自旋波共振吸收谱随温度的关系. 图中的红色和蓝色的虚线分别代表低温下q-FM共振峰和高温下q-AFM共振峰随温度的变化
Figure1. (a)?(c) THz transmission spectra of the (110) HoFeO₃, Ho_0.8Y_0.2FeO₃, and Ho_0.6Y_0.4FeO₃ single crystals measured at different temperatures, the incident THz magnetic component (H_THz) is aligned along c-axis of the crystal. The dashed red and blue lines are guides to the eye for identifying the quasi-ferromagnetic mode (q-FM) and quasi-antiferromagnetic mode (q-AFM) resonant peaks, respectively; (d)?(f) temperature dependence of THz spin wave resonance absorption spectra of single crystals with different Y³⁺ doping levels. The red dotted lines in the figures represent q-FM resonant absorption peaks change with temperature at low temperature, and the blue dotted lines represent q-AFM resonant absorption peaks change with temperature at high temperature.

伴随着Y³⁺的掺入, HoFeO₃晶体中自旋态的行为略有变化. 由于Y³⁺具有满壳层的电子而不显示磁性, Y³⁺的掺杂可以在不引入新的磁结构的情况下降低Ho³⁺-Fe³⁺交换作用的整体强度, 从而会降低自旋重取向转变的温区^[13,23,29]. 我们采用THz-TDS透射谱详细研究了不同Y³⁺掺杂浓度下的Ho_1–xY_xFeO₃中的q-AFM和q-FM共振峰随温度的变化关系(图1). 与未掺杂样品的测试条件一致, 太赫兹脉冲的磁场分量与c轴平行(H_THz//c轴), 在Γ₂和Γ₁₂相中激发和探测的是q-FM共振峰, 而在Γ₄相中激发和探测的是q-AFM共振峰. 为了方便, 在这里定义q-FM共振峰频率的最低点为Γ₁₂→Γ₂₄相变的转变点T₂, q-AFM共振峰频率的最低点为Γ₂₄→Γ₄相变的转变点T₁.
通过三个样品的太赫兹光谱测量, 观察到了Y³⁺掺杂对HoFeO₃晶体中自旋共振频率与自旋重取向温区的影响. 为了更好地呈现出不同掺杂浓度样品的自旋共振、自旋重取向随温度变化规律, 需要提取样品中自旋波吸收谱. 由于样品在不同温度下的吸收率可以通过THz波穿过样品的THz幅值E_S与自由空间的THz幅值E_R得出, (E_S/E_R)² = (1–R)²exp(–αd)^[23], 其中R为反射系数, α为吸收系数, d为样品厚度. 因此样品的吸收率A_S = αd = –2 ln{E_S/[E_R(1–R)]}. 若样品在不同温度下的反射率不变, 可以计算出自旋波的共振吸收谱A_SW = A_S–A₀ ∝ 1–(E_S/E₀), 其中为E₀基线. 在Y³⁺掺杂为0, 0.2, 0.4的样品中分别在60, 45和40 K时, 自旋共振吸收消失, 因此选择这些数据作为基线. 最后基线的吸收率A₀可以通过去除 (E_S/E₀)–1中的负数值来得出. 样品中自旋波共振吸收峰随温度变化关系详见图1(d)—(f). 从图1(d)—(f)中可以清晰看到低温区(Γ₂相)的q-FM共振峰频率随着温度的上升而下降; 高温区(Γ₄相)的q-AFM共振峰频率随着温度的上升而上升. 这一特征对于不同掺杂浓度的样品都是适用的.
通过进一步观察, 发现Y³⁺掺杂对HoFeO₃晶体中自旋态的影响体现在两个方面. 第一个方面是对共振频率的影响. 在10 K时, Y³⁺掺杂浓度为0, 0.2和0.4的共振峰分别出现在0.63, 0.61和0.50 THz, 对应激发的是Ho_1–xY_xFeO₃中q-FM模. 这表明Γ₂相q-FM的自旋共振频率随着Y³⁺掺杂浓度上升而下降. 当温度上升到80 K时, Y³⁺掺杂浓度为0, 0.2和0.4的共振峰分别出现在0.34, 0.37和0.42 THz, 对应激发的是Ho_1–xY_xFeO₃中的q-AFM模. 这表明Γ₄相q-AFM的自旋共振频率随着Y³⁺掺杂浓度上升而上升. 当温度80 K上升至300 K时, q-AFM共振峰频率分别从0.34, 0.37和0.42 THz上升至0.56, 0.57和0.56 THz, 并且吸收率上升, 所有单晶都稳定在Γ₄相, 且它们的共振频率基本相同.
第二个方面是对自旋重取向温区的影响. 当温度从10 K上升至30 K时, q-FM共振峰频率下降, 吸收率基本保持不变, 样品处于Γ₂相. 对于Y³⁺掺杂浓度为0, 0.2和0.4的单晶, q-FM共振峰分别在温度大于50, 40和30 K时消失, 对应单晶中发生了Γ₁₂→Γ₂₄相转变. 当温度继续上升至80, 55和45 K时, Y³⁺掺杂浓度为0, 0.2和0.4的q-AFM共振峰出现, 对应单晶中发生了Γ₂₄→Γ₄相转变. 这一结果表明, 0, 0.2和0.4的Y³⁺掺杂浓度分别可以使单晶的自旋重取向温区从50—80 K下降至40—55 K再下降至30—45 K. 为了进一步对比Y³⁺掺杂对样品自旋态的影响, 提取了HoFeO₃, Ho_0.8Y_0.2FeO₃和Ho_0.6Y_0.4FeO₃中q-AFM和q-FM共振频率随温度的变化关系, 如图2所示. 可以清晰地看到, Y³⁺掺杂不仅可以降低低温下q-FM共振峰频率以及提升高温下q-AFM共振峰频率, 而且可以使得自旋重取向温区向低温移动.
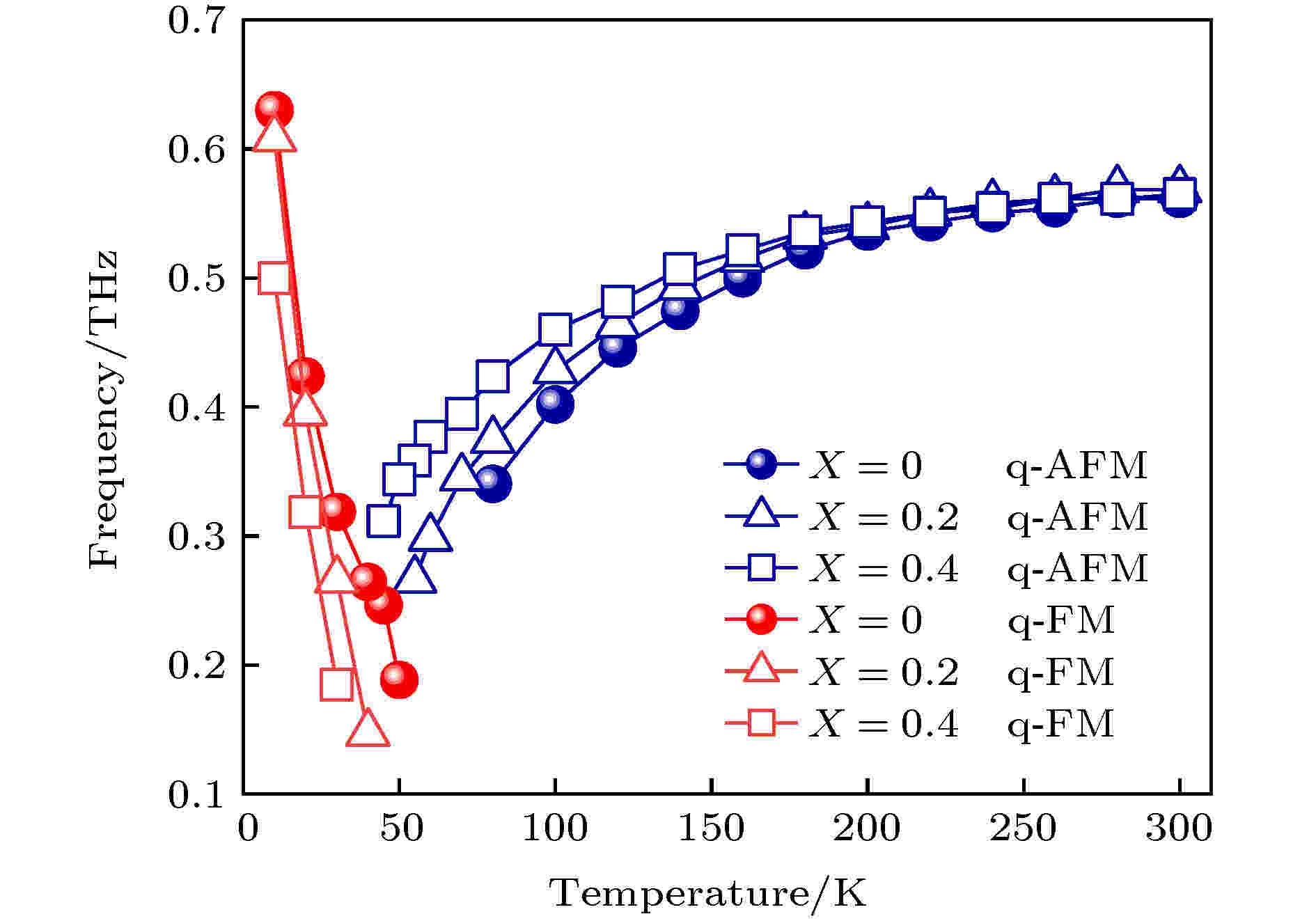图 2 Ho_1–xY_xFeO₃中q-AFM和q-FM共振频率随温度的变化关系, 圆圈、三角和正方形标记分别代表Y³⁺离子掺杂浓度为0, 0.2和0.4的(110)取向的单晶中的共振频率
Figure2. The temperature dependence of q-AFM and q-FM resonant frequencies in Ho_1–xY_xFeO₃. Circle, triangle and square markers show resonant frequencies in single crystals with Y³⁺ dopant concentration of 0, 0.2 and 0.4.

q-AFM和q-FM共振频率随温度的变化趋势可以用各向异性能机制解释^[16]:

$\begin{split}{\varGamma _4}:\left\{ {\begin{array}{*{20}{c}}{{\omega _{{\rm{FM}}}} = \dfrac{\gamma }{{2{\text{π}}}}{{\left( {2{H_{\rm{E}}}{K_{ac}}/{M_0}} \right)}^{1/2}},}\\{{\omega _{{\rm{AFM}}}} = \dfrac{\gamma }{{2{\text{π}}}}{{\left( {2{H_{\rm{E}}}{K_{ab}}/{M_0}} \right)}^{1/2}},}\end{array}} \right.\end{split}$

$\begin{split}{\varGamma _2}:\left\{ {\begin{array}{*{20}{c}}{{\omega _{{\rm{FM}}}} = \dfrac{\gamma }{{2{\text{π}}}}{{\left( {2{H_{\rm{E}}}{K_{ca}}/{M_0}} \right)}^{1/2}},}\\{{\omega _{{\rm{AFM}}}} = \dfrac{\gamma }{{2{\text{π}}}}{{\left( {2{H_{\rm{E}}}{K_{cb}}/{M_0}} \right)}^{1/2}},}\end{array}} \right.\end{split}$

其中γ为旋磁比; H_E为交换场; M₀为饱和磁矩; K_ac, K_ab, K_ca, 和K_cb为各向异性常数. 当温度从T₂ > T > 10 K时, K_ca逐渐下降, q-FM频率逐渐软化. 当T > T₂时, K_ca接近0, q-FM模式共振峰消失, 单晶发生Γ₁₂→Γ₂₄转变. 当温度T = T₁时, q-AFM共振峰出现, 单晶发生Γ₂₄→Γ₄转变, 当样品温度继续上升300 K > T > T₁时, K_ab增加, q-AFM频率硬化, 样品稳定在Γ₄相. 由于Y³⁺是无磁性的, 与Fe³⁺间无交换作用, Y³⁺掺杂只会降低Ho³⁺-Fe³⁺交换作用能而不会改变HoFeO₃中自旋重取向类型. 因此在升温过程中, Y³⁺掺杂浓度越高的单晶中的Ho³⁺-Fe³⁺交换作用能会在越低温度就降低到与Fe³⁺-Fe³⁺各向异性能相近从而发生自旋重取向. 如果采用其他离子掺杂也可能会有效改变自旋重取向温区, 例如稀土离子Sm³⁺掺杂, 由于在高温下Sm³⁺-Fe³⁺交换作用能远高于Ho³⁺-Fe³⁺交换作用能^[9,26], 因此可能会提升HoFeO₃中自旋重取向温区; 如果采用稀土离子Dy³⁺掺杂, 可能会改变HoFeO₃的自旋重取向类型, 如 Dy_0.5Pr_0.5FeO₃发生了Γ₄→Γ₁→Γ₂转变, 而DyFeO₃或PrFeO₃只能分别发生Γ₄→Γ₁转变或Γ₄→Γ₂转变^[10]. 而当Y³⁺掺杂后, HoFeO₃的自旋重取向温区下降而自旋重取向类型不变, 这种现象与Er_1–xY_xFeO₃中一致^[13]. 而且在温度小于30 K时, Ho³⁺-Fe³⁺的交换作用能与Fe³⁺-Fe³⁺各向异性能间的差值会随着Y³⁺掺杂浓度上升而减小, 从而导致了K_ca的降低, 此时Y³⁺掺杂浓度越大, q-FM共振频率越低; 但是在温度大于80 K后, 由于Ho³⁺-Fe³⁺的交换作用能大于Fe³⁺-Fe³⁺各向异性能, Ho³⁺-Fe³⁺的交换作用能与Fe³⁺-Fe³⁺各向异性能间的差值会增加, 从而导致了K_ab的增加, 因此相同温度下, Y³⁺掺杂浓度越大, q-AFM共振频率越高; 但是随着温度的继续上升至远高于自旋重取向温区(T = 300 K)时, Ho³⁺-Fe³⁺的交换作用能降低至接近零, K_ab完全取决于Fe³⁺-Fe³⁺各向异性能, 由于Fe³⁺-Fe³⁺各向异性能几乎不随掺杂浓度变化导致300 K时, 不同Y³⁺掺杂浓度的q-AFM共振频率几乎相等. Y³⁺掺杂有效降低了Ho³⁺-Fe³⁺的交换作用能导致高温下K_ab降低和低温下K_ca增加, 从而不仅使HoFeO₃的自旋重取向温区下降, 而且使低温(T ≤ 30 K)下q-FM共振频率降低以及高温(80 K ≤ T < 300 K)下q-AFM共振频率提升.
在讨论了Y³⁺掺杂浓度对Ho_1–xY_xFeO₃单晶中自旋共振模式、自旋重取向的影响之后, 接下来探索磁场对该体系自旋态的作用. 我们关注的重点是利用磁场诱导Ho_1–xY_xFeO₃单晶发生自旋重取向, 以及发生自旋重取向过程中磁场强度对不同Y³⁺掺杂浓度单晶中的q-AFM模式和q-FM模式共振峰的影响. 在RFeO₃单晶中, 沿反铁磁矢量L方向施加磁场通常会诱导自旋重取向的发生^[23,27]. 在低温Γ₂相时(L//c), 沿c轴施加一定大小的磁场会抵消沿c轴方向的各向异性能, 从而在K_ca和K_cb不为0的情况下诱导样品发生Γ₂→Γ₄转变, 此时q-FM频率降至到最低点后消失, q-AFM出现; 沿b轴施加磁场对样品几乎无影响; 在高温Γ₄相时(L//a); 沿a轴施加一定磁场同样会在K_ac和K_ab不为0的情况下诱导样品发生Γ₄→Γ₂转变, 此时q-AFM消失, q-FM出现并且频率上升. 由于临近自旋重取向温区时, q-AFM共振峰吸收率较弱, 而q-FM具有较强的吸收峰, 因此在Γ₄相沿c轴施加磁场, 发生自旋重取向后Γ₂相的q-FM模式比较容易观察到, 因此选择沿a轴有投影分量的(110)方向施加磁场.
如图3(a), (e), (i)所示, 当温度T = 20 K时, 不同Y³⁺掺杂浓度的Ho_1–xY_xFeO₃单晶均处于Γ₂相, q-FM共振峰频率随着磁场增强而线性上升, 铁磁矢量M//a且不发生翻转. 这一特征与相关文献中TmFeO₃和YFeO₃随磁场的变化一致^[23,27]. 当样品处于高温下(约100 K), Ho_1–xY_xFeO₃单晶均处于Γ₄相, 0—2.5 T的磁场范围内, 虽然q-AFM的共振强度略有下降, 但其共振频率基本保持不变(如图3(d), (h), (l)所示). 这是Ho_1–xY_xFeO₃分别处于稳定的Γ₂相和Γ₄相的情况. 当Ho_1–xY_xFeO₃单晶处于或接近自旋重取向温区时, 磁场的作用则更为有趣. 我们发现在这一温区磁场不仅能有效调控自旋共振频率, 还能诱导自旋重取向. 如图3(b)所示, 当未掺杂的HoFeO₃单晶在45 K时, 随着磁场强度增加, Γ₁₂相对应的q-FM共振频率缓慢减小. 当磁场增加到1 T时, 发生磁场诱导的自旋重取向(Γ₁₂→Γ₂)相变. 伴随着磁场强度的进一步增加, Γ₂对应的q-FM共振频率增加, 这与低温(20 K)下Γ₂相的行为一致. 对于Y³⁺掺杂的Ho_1–xY_xFeO₃单晶, 在小磁场和45 K条件下的THz谱测量不到自旋共振模(图3(f), (j)). 当磁场增加到1 T时, Γ₂相对应的q-FM共振模开始出现. 这一现象表明, 1 T的磁场诱导出了自旋重取向. 随着磁场进一步增加, Γ₂对应的q-FM共振频率增加. 从以上实验结果可以看出温度越接近自旋重取向温区, 磁场越容易诱导自旋重取向的发生. 这是由于温度越接近自旋重取向温区, Ho³⁺-Fe³⁺交换作用能就越接近Fe³⁺-Fe³⁺各向异性能, 导致各项异性常数K_ac和K_ab更接近0, 因此只需要很小的磁场就能诱导自旋重取向的发生.
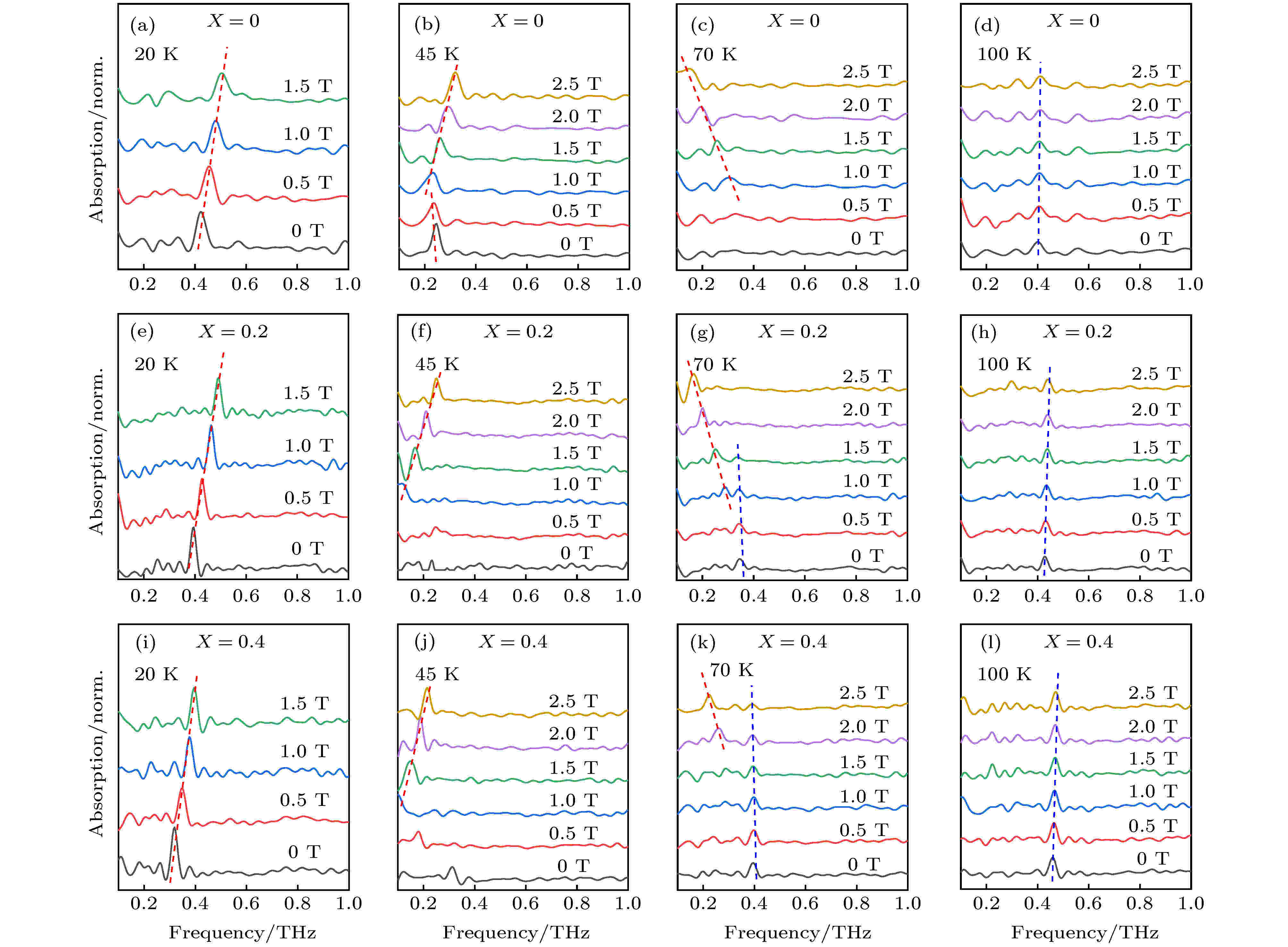图 3 (a)?(l) Ho_1–xY_xFeO₃单晶中在不同温度下随磁场变化的自旋波共振吸收谱, 入射的太赫兹磁场分量(H_THz)平行于晶体的c轴, 外加磁场H_DC沿晶体的[110]方向, 蓝色和红色的虚线分别表示q-AFM共振峰和q-FM共振峰随磁场的变化
Figure3. (a)?(l) Magnetic field dependence of THz spin wave resonance absorption spectra of Ho_1–xY_xFeO₃ single crystals measured at different temperatures. The incident THz magnetic component (H_THz) is aligned along c-axis of crystals, and the external magnetic field H_DC is applied along [110] axis of crystals. The blue and red dotted lines are q-AFM and q-FM resonant absorption peaks change with the applied magnetic field, respectively.

在讨论完低温相变区(T = 45 K)附近的磁场效应之后, 接下来让我们探索Ho_1–xY_xFeO₃单晶在高温相变区的磁控现象. 在70 K这一特征温度下, 未掺杂的HoFeO₃单晶处于自旋重取向(Γ₄→Γ₂₄)相变的临界状态附近. 虽然自旋基态为Γ₄相, 但其对应的q-AFM自旋波强度很弱. 如图3(c)所示, HoFeO₃单晶在小磁场THz谱中不能观察到明显的自旋共振模. 当磁场增加到1 T时, Γ₂₄相对应的q-FM共振模开始出现. 这表明, 1 T的磁场诱导出了自旋重取向(Γ₄→Γ₂₄)相变. 随着磁场强度进一步增加, Γ₂₄对应的q-FM共振频率线性降低. 对于Y³⁺掺杂的Ho_1–xY_xFeO₃单晶, 情况略有不同. 如图2所示, 在Y³⁺掺杂浓度为0.2和0.4的Ho_1–xY_xFeO₃单晶中, 相变温度T₁(Γ₂₄→Γ₄)分别为55, 45 K. 因此, 70 K温度(>T₁)下的Ho_1–xY_xFeO₃单晶的自旋基态为稳定的Γ₄相. 如图3(g), (k)所示, 零场和小磁场条件下的THz谱可以探测到的明显的Γ₄相对应的q-AFM共振模. 随着磁场增加, 该q-AFM共振模的频率基本不变. 这与100 K条件下的磁控行为一致. 当磁场强度增加到1 T时, Ho_0.8Y_0.2FeO₃单晶的THz频谱中出现了Γ₂₄对应的q-FM共振. 这表明, 磁场诱导出了自旋重取向(Γ₄→Γ₂₄)相变. 此时铁磁矢量由M//c轴旋转至M与c轴和a轴成一定夹角. 更为有趣的是, 在1.0—1.5 T磁场范围内, Γ₄相对应的q-AFM共振模和Γ₂₄相对应的q-FM共振模共存(图3(g)). 这表明磁场诱导的相变是一个渐进过程, 在1.0—1.5 T磁场范围内, 并不是所有自旋都发生了转向. 随着磁场进一步增加(> 2 T), 磁场诱导的自旋重取向相变完成, 体系自旋完全处于Γ₂₄相. 这一过程中, 磁场诱导出的Γ₂₄相所对应的q-FM共振模的频率随磁场强度增加而降低. 当Y³⁺掺杂浓度从0.2提升至0.4, 磁场效应的趋势基本一致. 不同之处在于Y³⁺掺杂浓度为0.4的单晶中发生自旋重取向(Γ₄→Γ₂₄)的临界磁场强度(2 T)比掺杂浓度为0.2的情况(1 T)要大. 这是由于Y³⁺离子掺杂浓度越大, 单晶中的Ho³⁺-Fe³⁺交换能越小, 各项异性常数K_ac和K_ab也越大, 这导致了单晶越难发生自旋重取向.

本文利用变温变场下的THz-TDS, 系统研究了非磁性Y³⁺离子掺杂与外加磁场对HoFeO₃单晶中自旋态以及自旋重取向的影响. 变温THz谱表明Ho_1–xY_xFeO₃单晶中低温区q-FM共振频率随着温度的上升而下降; 而高温区的q-AFM共振频率随着温度的上升而上升. 随着非磁性Y³⁺离子的掺入, 一方面低温q-FM共振频率降低而高温q-AFM共振频率得到提升; 另一方面自旋重取向的温区整体向低温移动. 另外, 实验表明磁场不仅能够有效地调控Ho_1–xY_xFeO₃单晶中的q-FM共振频率, 而且还能诱导出自旋重取向. 这一磁场诱导的自旋重取向效应在晶体的本征自旋重取向温区最为明显, 其磁诱导效应的临界磁场强度随Y³⁺离子掺杂浓度而增加. 这一掺杂效应、磁控效应的研究将有助于理解稀土正铁氧体中的自旋交换作用机制, 并为场控器件的研发提供了相关实验基础.