摘要:利用小型脉冲功率装置CQ-4, 实现了RDX单晶(210), (100)两种晶向15 GPa内的斜波压缩加载. 利用激光干涉测速技术, 实验获得了RDX单晶样品与LiF界面的速度历史曲线. 速度曲线表现出明显的三波结构, 表明出现了弹塑性转变和α-γ相变. 分别计算了两种晶向的应力屈服极限和屈服强度, 不同晶向的RDX单晶的屈服极限表现出明显的差别. 并对斜波加载下的α-γ相变特征进行了分析, 两种晶向的相转变起始压力基本相同, α-γ相变起始压力在3.5—4.0 GPa之间, 相变起始压力至5 GPa内均为相转变区, 5—15 GPa为稳定新相.
关键词: 含能材料/
弹-黏塑性/
电磁驱动/
斜波压缩

English Abstract

全文HTML

--> --> -->

含能材料的高压物性与含能材料的反应机理和化爆安全性问题紧密相关, 是国防科研工作中的重要问题, 长期以来受到广泛关注. 含能材料不同于惰性材料, 在高压下容易发生化学反应, 采用传统的冲击加载办法, 往往由于发生化学反应, 给实验的设计和测量带来困难. 因此, 在理论模拟研究方面, 特别是单质高能炸药如HMX, RDX的分子动力学模拟计算的研究工作, 会对实验的设计和测量起到促进作用, 理论模拟计算与静压加载实验的结合, 可以帮助研究人员对单晶含能材料的高压物性有全面的认识. 但是, 动载下炸药单晶的动力学响应特性依然由于炸药的高感度, 很难获得较高压力下的实验结果, 冲击下的实验数据十分有限.
近年发展起来斜波压缩加载实验技术^[1], 由于加载过程中样品中保持斜波加载, 样品中熵增小, 在获得高压状态的同时, 依然可以保持样品材料中较低的温升, 使含能材料不易发生化学反应. 目前相关研究工作已取得了一定的研究结果^[2-5], 为获得高能炸药的高压物性和细观尺度模拟计算提供了重要的高压物性参数^[6].
RDX作为重要的高能炸药, 其高压物性一直受到关注, 特别是其相变问题, 与其化学反应机理紧密相关. 分子动力学模拟和静高压实验结果表明^[7], RDX存在α, β, γ, δ和ε五相. 其中α相在常温常压下稳定, 在4 GPa附近出现α-γ相变, 并伴随1.6%的体积减小. 由于该相变条件为RDX冲击反应阈值(10—13 GPa)前出现的第一个相变, 且伴随显著的体积变化, 因此格外引起关注. 利用光谱探测技术在静压实验和冲击加载实验中^[8-10], 通过光谱的非连续变化, 均发现了明显的相变迹象. 冲击加载速度剖面测量^[11-14], 尚未见有发现该相变的报道.
本研究利用磁驱动斜波压缩加载实验技术, 开展了斜波加载下RDX单晶(100)和(210)两个晶向在10 GPa内的动力学响应研究, 目的在于, 通过全光纤测速系统(PDV)测量单晶的速度响应曲线, 获得RDX单晶不同晶向的弹塑性转变特性. 试图获得斜波加载条件下4 GPa附近α-γ相变信息, 从速度剖面获得相变的直接证据.

实验工作在中国工程物理研究院流体物理研究所建立的小型脉冲功率装置CQ-4^[15]上开展. CQ-4装置是一种基于低电感电容器储能的直板传输线的小型装置, 装置放电上升沿为450—600 ns, 峰值电流可达4 MA. 装置如图1所示, 负载区域安装条片对称电极, 保证单发实验中上下样品加载压力的一致性, 负载区加载示意图如图2所示. 装置放电时, 电流流经负载区条形对称电极, 产生洛伦兹排斥力, 对不同厚度样品产生对称且一致的加载压力. 实现实验样品的斜波加载过程. 利用VISAR测试探头, 对样品/窗口界面的速度剖面进行连续测量, 获得材料响应的速度历史曲线. 罗斌强等^[16]对磁驱动斜波加载实验结果的不确定度开展了分析研究, 指出现阶段实验界面速度测量的相对不确定度为1.0%, 声速、应力、应变和比容的相对不确定度分别为1.4%, 2.3%, 2.3%和0.3%, 说明磁驱动斜波加载是一种可靠的精密物理实验技术.
图 1 CQ-4 装置
Figure1. CQ-4 device.

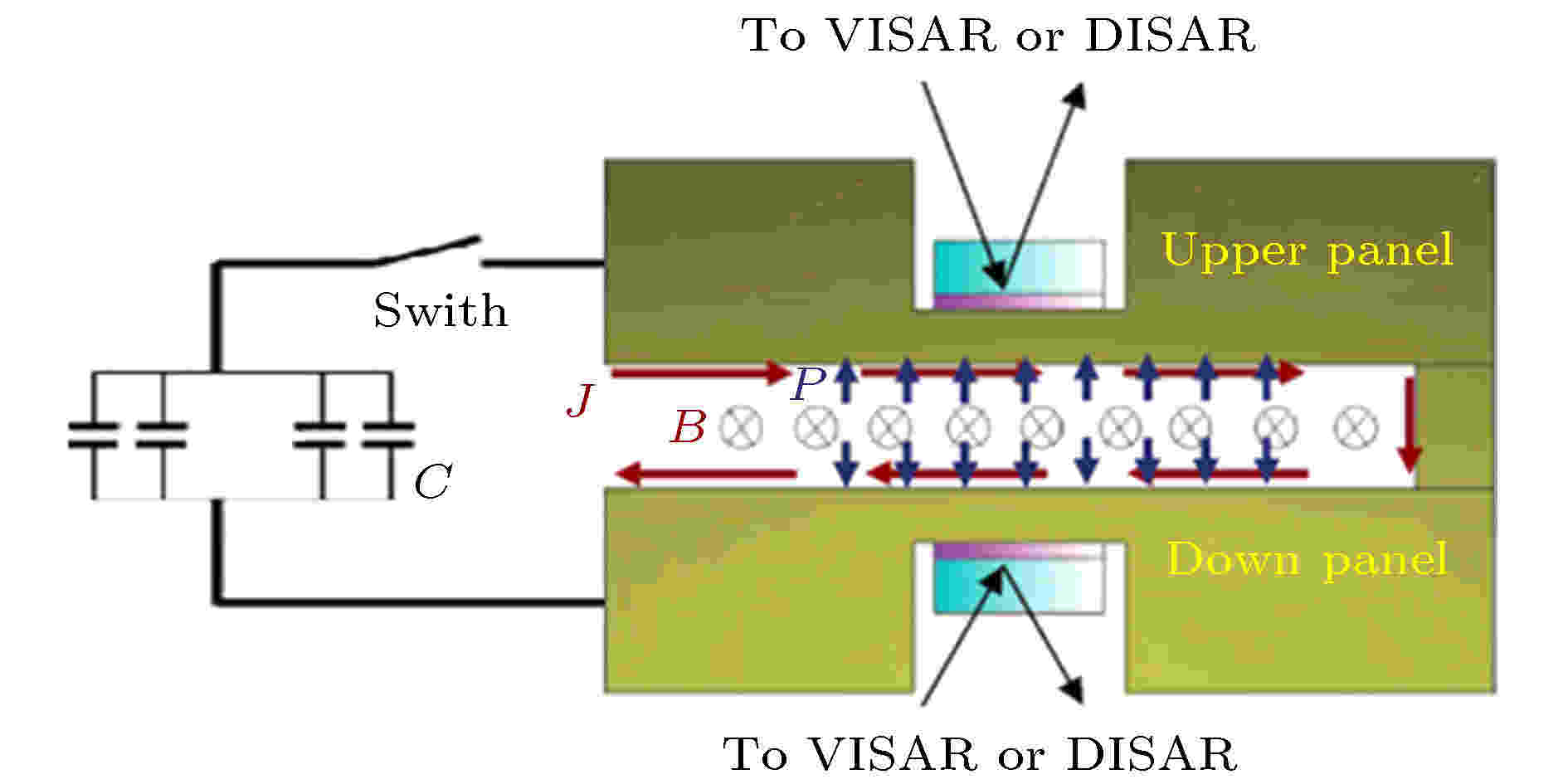图 2 负载区示意图
Figure2. Schematic diagram of load area.

实验样品为大块单晶RDX, 由中北大学提供. 利用水冷的线切割工具将RDX单晶沿不同晶向切割后研磨, 以获得满足实验要求的样品尺寸. 对切割研磨后的单晶样品进行XRD分析, 确定切片的晶向, 保证加载样品的加载面与晶向偏差小于0.5°. 图3为大块RDX单晶晶相与晶体晶面对应情况.
图 3 RDX单晶炸药
Figure3. RDX single crystal explosive.

实验中, 不同厚度RDX单晶对称安装于铝驱动电极上, 铝驱动电极宽度为10 mm, 厚度为1 mm, 测试窗口选择光学性能稳定的LiF(100), 厚度为4 mm, 实验条件如表1所示. 实验中样品厚度控制在小于1 mm, 避免由于RDX单晶弹塑性转变点处的速度弛豫导致的冲击.

实验发次	样品晶向	样品厚度/mm	充电电压/kV
Shot-1	RDX(210)	0.763	70
		0.697
Shot-2	RDX(100)	0.835	70
		0.746

表1实验条件
Table1.Experimental condition.

实验获得了RDX(210)和RDX(100)两种不同晶向的不同厚度实验样品与窗口界面的速度响应曲线, 结果见图4和图5所示. 两种晶向速度响应曲线均表现出明显的多波结构, 出现两个明显速度拐点. 其中RDX(210)晶向在50 —55 m/s附近出现明显弹塑性转变导致的速度弛豫, (100)晶向则在75—80 m/s附近出现弹塑性转变导致的速度弛豫, 与Baer等^[17]在Z机器上获得的实验结果一致, 他们的实验结果中, 弹性波经过应力弛豫, 转变为塑性波, 且不同厚度样品弹塑性转变点略有差异, 速度弛豫过程类似于HMX单晶的弹-黏塑性行为. 上述斜波加载实验结果显示, 弹塑性转变速度在两个晶向上均高于冲击加载下Hook的实验结果, 特别是在(100)晶向, 冲击加载下的弹塑性转变速度约为60 m/s, 远低于斜波加载下的弹塑性转变速度.
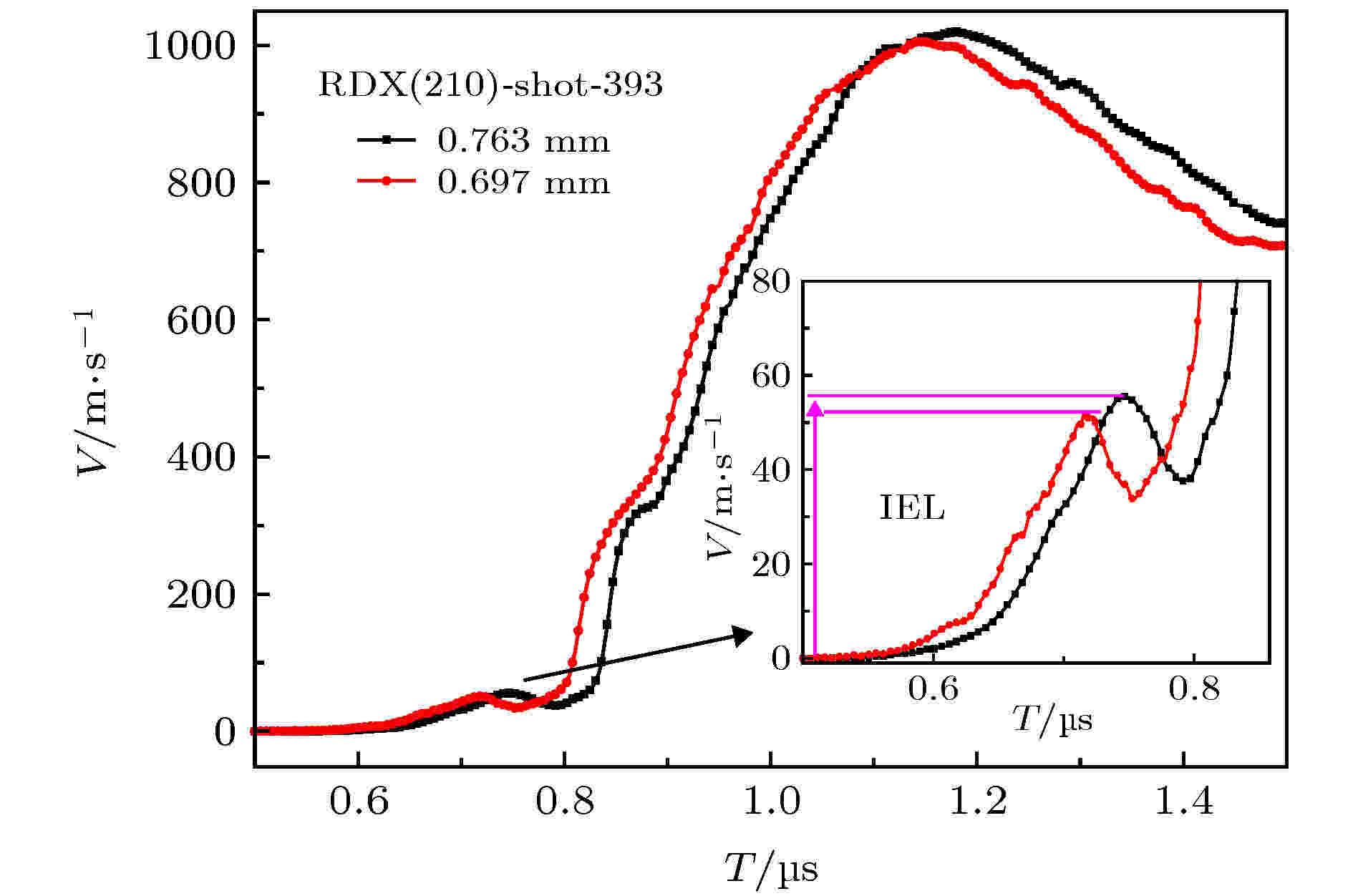图 4 RDX单晶(210)晶向实验速度曲线
Figure4. Experimental velocity curve of (210) RDX single crystal explosive.

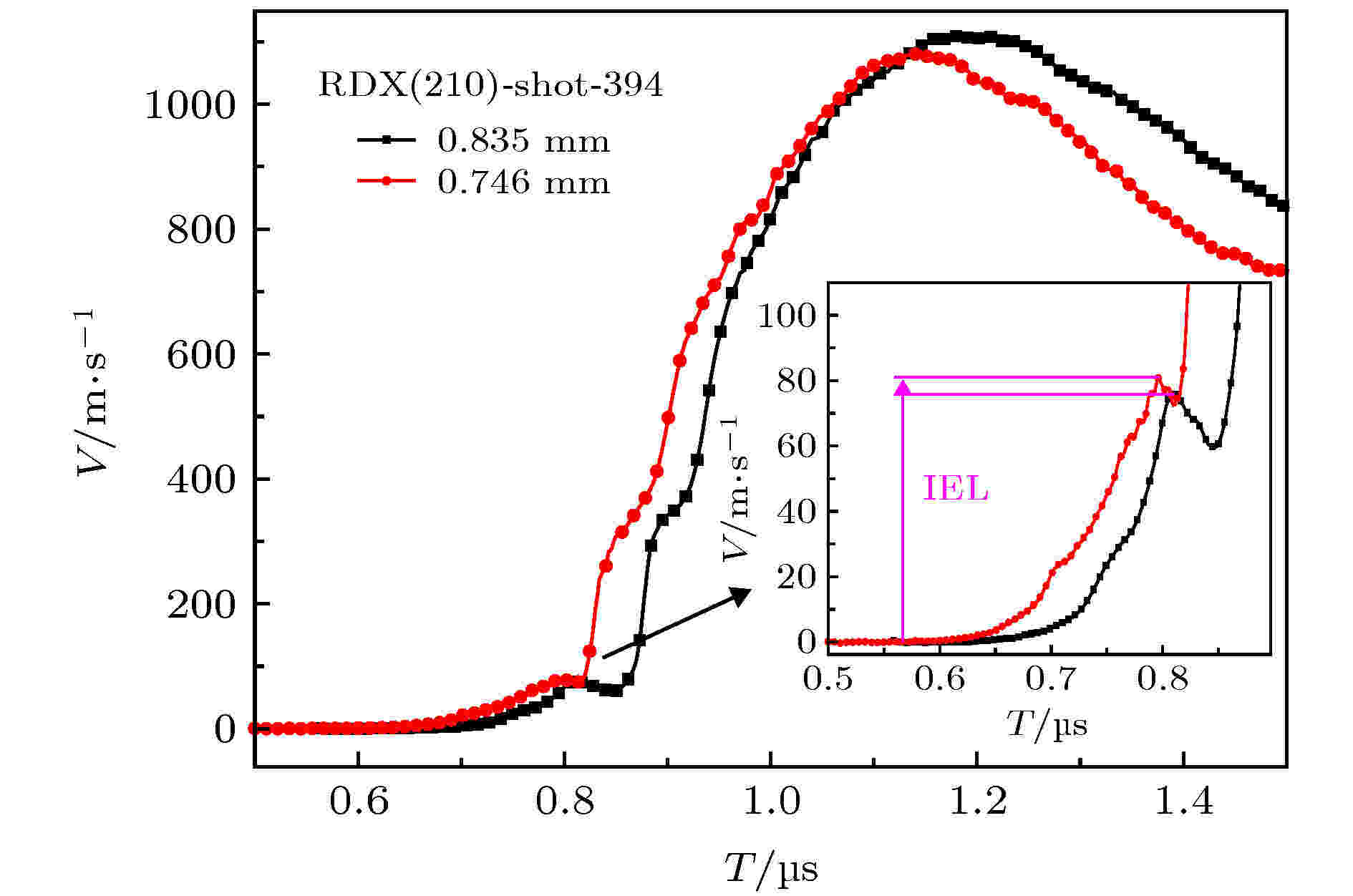图 5 RDX单晶(100)晶向实验速度曲线
Figure5. Experimental velocity curve of (100) RDX single crystal explosive.

考虑RDX单晶/LiF界面处的速度历史, 由于应力平衡, 弹塑性转变时对应的窗口材料处的应力即为斜波压缩加载下的RDX的应力屈服极限σ_IEL. 取LiF单晶的动力学参数分别为: 密度ρ₀ = 2.638 g/cm³, C₀ = 5.15 km/s, s₁ = 1.35, 计算得到RDX(210)晶向的σ_IEL为0.688—0.758 GPa, RDX(100)晶向的σ_IEL为1.039—1.110 GPa.
对于线弹塑性模型, 应力屈服极限为

${\sigma _{{\rm{IEL}}}} = Y(1 - \nu )/(1 - 2\nu ), $

其中, Y为屈服强度, ν为泊松比. 假设对于晶体RDX, 泊松比取0.25, 则RDX(210)晶向屈服强度Y为0.459—0.506 GPa, RDX(100)晶向屈服强度Y为0.693—0.740 GPa.
在300—400 m/s之间, 上述实验速度曲线出现速度拐折, 两种不同晶向的不同厚度样品速度响应表现出明显的一致性, 该拐折预示着RDX单晶出现了相变, 与分子动力学模拟^[18]、静压加载^[8-10]、冲击加载结果^[11-14]所示的α-γ相变压力条件一致. 将两发实验结果放置于同一坐标系中, 后移RDX(210)实验结果150 ns, 如图6所示, 两个晶向速度曲线拐折出现在同一速度区域, 可见该相变过程在这两个晶向上的压力阈值无明显差别, 且在斜波加载下, 该相变过程为渐进过程.
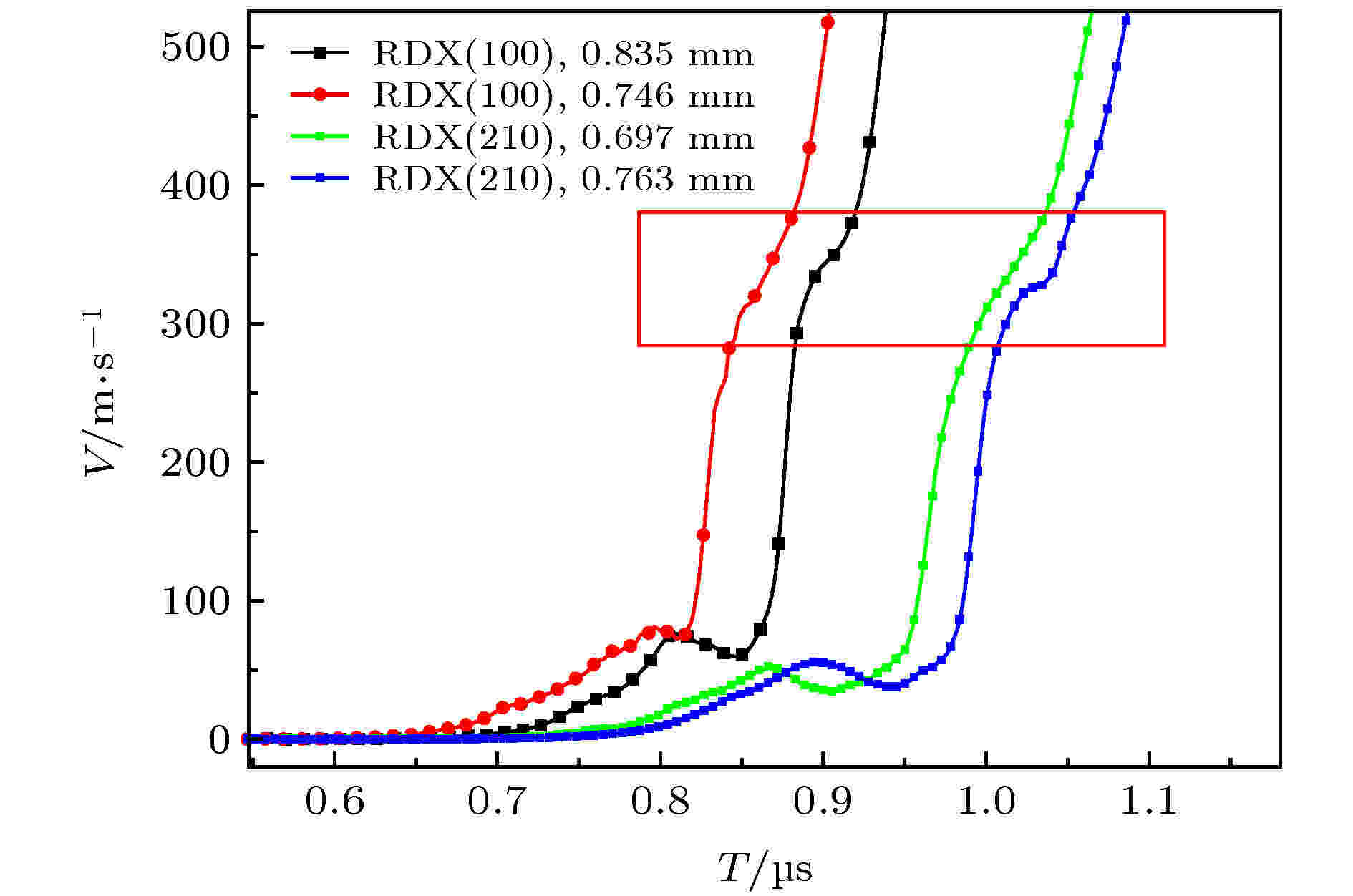图 6 RDX/LiF界面速度波形
Figure6. RDX/LiF interface velocity waveforms.

分别计算RDX(100)和(210)两个晶向样品与窗口处的压力历史曲线, 如图7所示, 相变起始压力在3.5—4.0 GPa之间, 约5 GPa后, RDX进入稳定新相γ, 5—15 GPa压力区间, γ相为稳定新相.
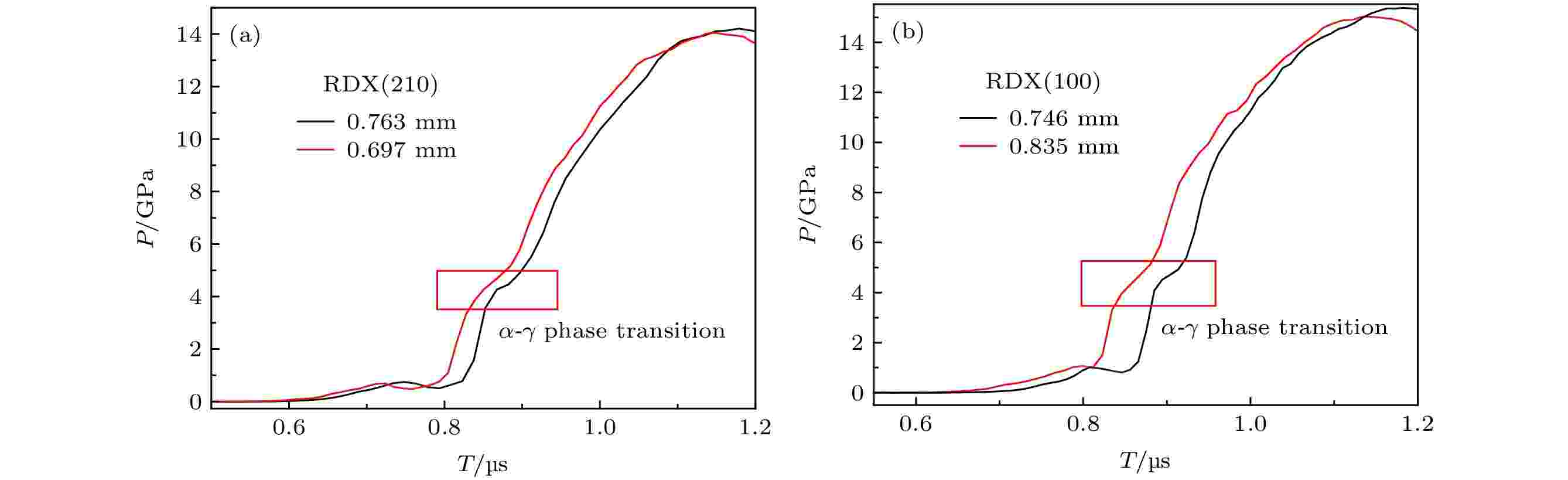图 7 RDX与LiF窗口之间界面处的压力历史曲线　(a) (210)晶向; (b) (100) 晶向
Figure7. Pressure history curves at the interface between RDX single crystal explosive and LiF:　(a) (210) crystal orientation; (b) (100) crystal orientation.

RDX单晶在实验中表现出明显的三波结构, 且在弹-塑性转变过程中出现明显的速度弛豫, 给模拟计算模型的确定带来一定困难. 弹塑性转变阶段, HMX单晶也表现出相似的力学特性, Ralph Menikoff团队^[19] 利用弹-黏塑性模型模拟冲击下HMX单晶弹塑性转变阶段的速度弛豫现象, 可从一定程度上较好地反映真实的实验结果, 因此, 本项目采用Hobenemser-Prager弹-黏塑性本构关系处理RDX单晶的弹塑性转变过程.
对于有机大分子单晶材料, 由于其相变的复杂性, 为从宏观上实现对实验结果的模拟, 采用经典的Murnaghan-Hayes多相状态方程, 相变过程则采用KJMA相变速率模型, 相变压力阈值作为相变判据, 具体的模型见(2)式—(4)式.
Hobenemser-Prager弹-黏塑性本构关系为

$\left\{ \begin{aligned}&{{\dot e}_{ji}} = \frac{1}{{2G}}{S_{ij}} + \frac{{1 - \dfrac{k}{{\sqrt {{J_2}} }}}}{{2\eta }}{S_{ij}}, \quad \sqrt{{J_2}} > k,\\&{{\dot e}_{ji}} = \frac{1}{{2G}}{S_{ij}},\qquad\quad \;\;\sqrt {{J_2}} < k,\end{aligned} \right.$

其中, ${{\dot e}_{ij}}$为应变率, S_ij为应力偏量, η为材料黏性系数, G为弹性剪切模量, J₂为应力偏量第二不变量.
Murnaghan-Hayes多相物态方程为:

$\left\{ \begin{aligned}&\dot p = ({K_{\bf{\xi }}} + K_\xi ' \cdot p)({{\dot \varepsilon }^V} - \Delta {\varepsilon ^V} \cdot \dot {\bf{\xi}} - {\alpha _{\bf{\xi }}}\dot T),\\&\dot T = - \frac{{T\Delta S \cdot \dot {\bf{\xi}} + A{s_{ij}}\dot \gamma _{ij}^C}}{{{C_{p{,_{\bf{\xi }}}}}}},\end{aligned} \right.$

其中RDX单晶的α相和γ相均用该物态方程表示, 体模量K_ξ修正^[20]为${K_\xi } + K_\xi ' \cdot p$, 温度项分为两部分, 前面部分为塑性功引起的温度升高, 后部分为相变引起的温度的增加.
KJMA相变速率模型为

$\xi = 1 - \exp [- {({t}/{\tau })^n}], $

其中, τ为相变特征时间, n为与成核模式相关的常数.
利用上述模型对实验结果进行了模拟计算分析, 模型参数如表2所示. 对于相变, 采用压力阈值作为判据, 对于(210)晶向, 相变阈值为4.0 GPa, 对于(100)晶向, 相变阈值为4.2 GPa.

晶向	形核时间/ns	n	屈服强度/GPa	Kξ/GPa	$K_\xi '$	Remarks
(210)	60	1.3	0.5	10.10	8.20	α
				9.56	5.03	γ
(100)	60	1.3	0.7	13.00	10.20	α
				10.56	8.53	γ

表2数值模拟的模型参数
Table2.Parameters for numerical simulation.

计算模型为与图2一样的三明治结构, 其中纯铝电极和LiF单晶为标准材料. 在本文实验温度(温升小于30 ℃)、压力(小于20 GPa)范围内, 纯铝和LiF单晶物理性质单一、动力学参数基本不变, 对实验速度波形和数值模拟结果影响可以忽略. 利用多相物态方程模拟计算结果如图8和图9所示, 模拟计算能较好地再现实验结果的三波结构. 在相变部分, 模拟计算结果与实验结果吻合较好, 在速度拐折区域及相变完成方面计算结果与实验结果匹配较好. 弹塑性转变部分, 计算结果能反映出实验结果的基本特征, 但是不能较好再现弹塑性区域的速度弛豫过程, 这与有机大分子材料弹塑性转变过程的复杂性有关.
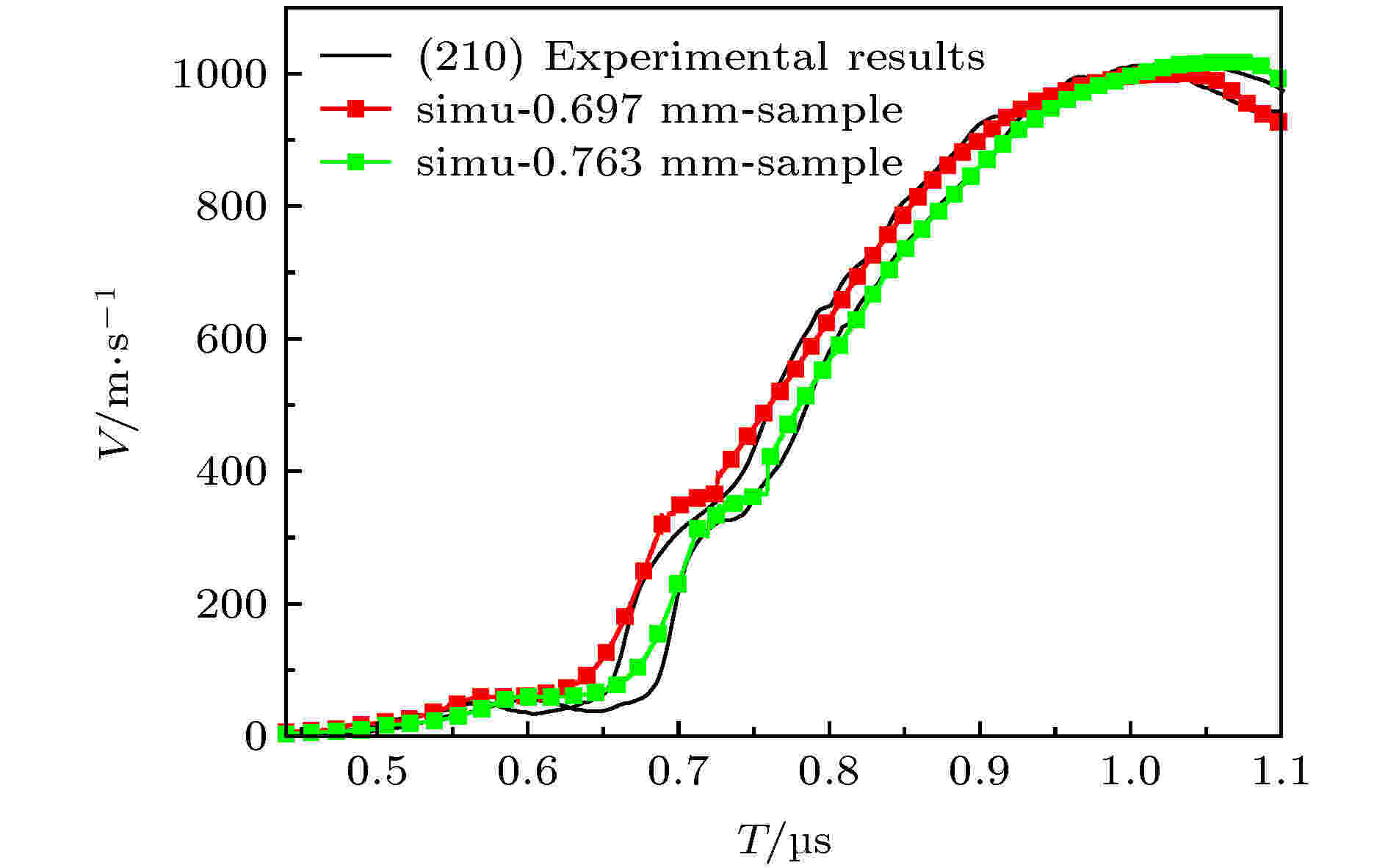图 8 (210)晶向模拟计算结果与实验结果对比
Figure8. Calculated and experimental data of (210) RDX single crystal explosive.

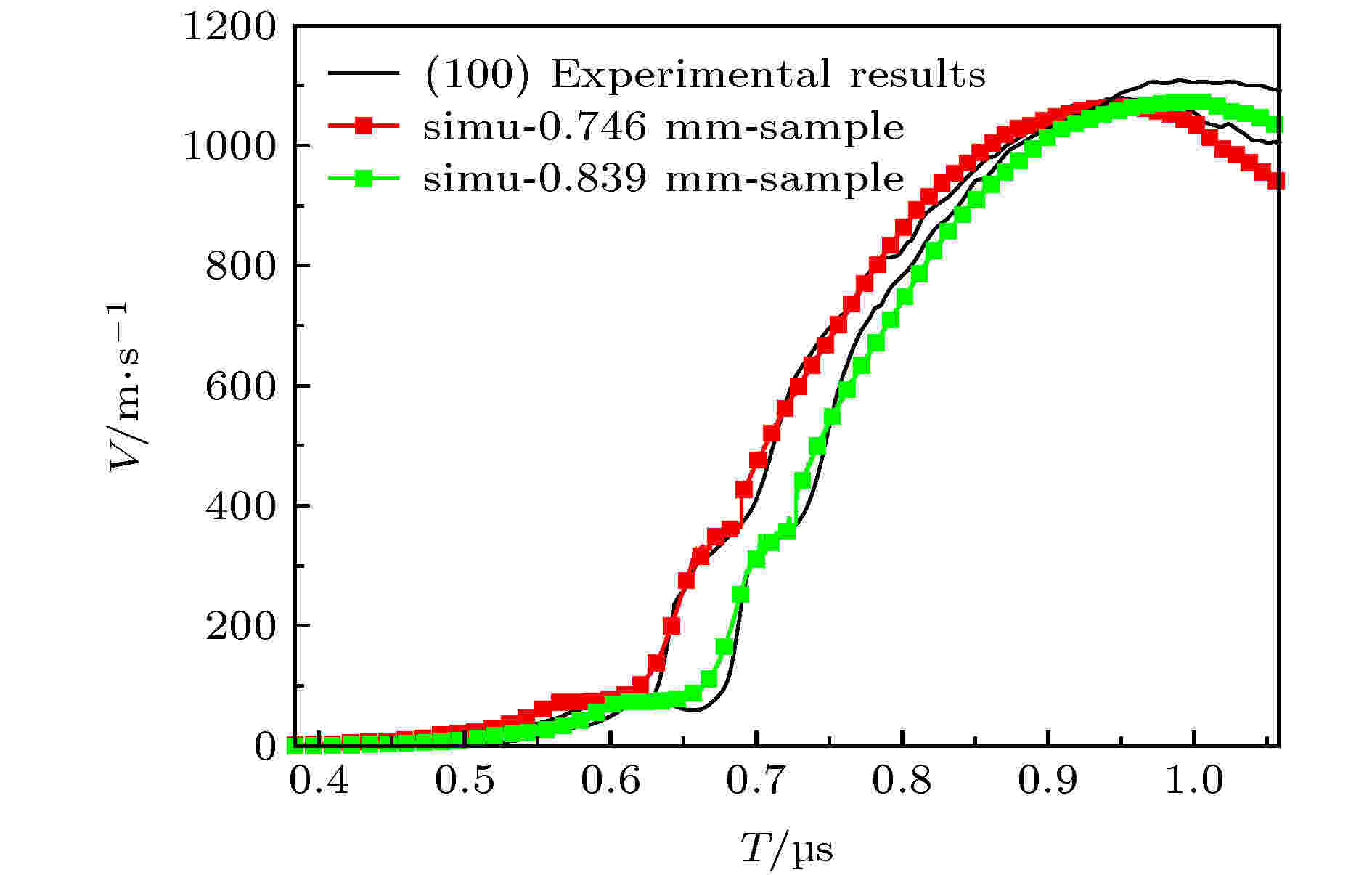图 9 (100)晶向模拟计算结果与实验结果对比
Figure9. Calculated and experimental data of (100) RDX single crystal explosive.

利用磁驱动装置CQ-4, 开展了15 GPa压力内RDX单晶(210), (100)两种晶向斜波加载实验. 通过激光干涉测速技术, 首次在动加载过程中, 获得了包含弹塑性信息和α-γ相变信息的三波结构, 其中α-γ相变的速度剖面信息, 在冲击加载实验中未见报导.
两种晶向RDX的弹塑性转变速度有明显差异, 计算结果表明, (100)晶向的应力屈服极限和屈服强度更高. 通过与文献中静压加载和模拟计算结果对比, 在300—400 m/s处出现的速度拐折为α-γ相变, 对斜波加载下该相变特征进行分析, 发现两种晶向的相转变起始压力相同, 相变过程与晶向方向无关, 相变过程为渐变过程, α-γ相变起始压力在3.5—4.0 GPa之间, 相变起始压力至5 GPa内均为相转变区, 5—15 GPa为稳定新相.