摘要: 提出了一种基于BSIM4的屏蔽栅沟槽MOSFET紧凑型模型. 在直流模型中使用两端电势建立JFET区等效电阻模型, 并引入电子扩散区等效电阻, 解决了因忽视JFET区源端电势导致的电流存在误差的问题. 在电容模型中, 漏源电容模型在BSIM4的基础上添加了屏蔽栅-漏等效电容模型, 栅漏电容模型将栅漏偏置电压修改为栅极同栅-漂移区重叠区末端节点的电势差. 使用泊松方程求解该节点电势, 并引入栅氧厚度因子
k 1 、屏蔽栅氧化层厚度因子
k 2 、等效栅-漂移区重叠长度
L ovequ 和等效屏蔽栅长
L SHequ 对栅和屏蔽栅的结构进行等效, 以简化泊松方程的计算并确保该节点电势曲线的光滑性. 使用Verilog-A编写模型程序, 搭建实验平台测试屏蔽栅沟槽MOSFET的直流特性、电容特性和开关特性, 模型仿真结果与测试数据有较好的拟合, 验证了所建模型的有效性.
关键词: 屏蔽栅沟槽MOSFET /
紧凑型模型 /
BSIM4 /
Verilog-A English Abstract A compact model of shield-gate trench MOSFET based on BSIM4 Jiang Yi-Xun 1 ,Qiao Ming 1 ,Gao Wen-Ming 2 ,He Xiao-Dong 2 ,Feng Jun-Bo 1 ,Zhang Sen 2 ,Zhang Bo 1 1.State Key Laboratory of Electronic Thin Film and Integrated Devices, University of Electronic Science and Technology of China, Chendu 610054, China Received Date: 11 March 2020Accepted Date: 29 May 2020Available Online: 29 May 2020Published Online: 05 September 2020Abstract: Shield-gate trench MOSFET in a low-to-medium voltage range (12－250 V) plays a key role in the power conversion market due to its low power loss caused by the sheild-gate structure. In order to eliminate the faults resulting from the parasitic effects of the device and improve the conversion efficiency, the device model is indispensable in designing a circuit system. In this paper, a compact model of shield-gate trench MOSFET based on BSIM4 is proposed, including the DC model and the capacitance model. In the DC model, the basic MOSFET structure uses BSIM4, and the equivalent resistances of the basic MOSFET in series are divided into three parts. The equivalent resistance model of JFET region is established by using the electric potential difference between both ends for the first time, and the equivalent resistance model of electron diffusion region is also introduced, in order to solve the problem of current error caused by neglecting the source potential of JFET region. The equivalent resistance between drain and JFET region and the equivalent resistance of electron diffusion region both prove to be constant. In the capacitance model based on BSIM4, the model of shield-gate to drain capacitance is added to the model of drain to source capacitance, and the voltage bias between drain and gate in the model of gate to drain capacitance is modified into the potential difference between the node at the end of the gate-drift overlap region and the gate. Poisson equations are used to solve the electric potential of this node. Furthermore, the gate oxide thickness factor k 1 , the shield-gate oxide thickness factor k 2 , the equivalent length of gate-drift overlap L ovequ and the equivalent length of shield-gate L SHequ are introduced to redefine the position of gate and shield-gate, thereby simplifying the Poisson equations and ensuring the smoothness of the potential curve of the node. Comparison of the data from the simulation by using Verilog-A program with the test results from the experimental platform shows that the model simulation results fit well with the test data, Therefore, the proposed model is verified.Keywords: shield-gate trench MOSFET /compact model /BSIM4 /Verilog-A 全文HTML --> --> --> 1.引 言 屏蔽栅沟槽MOSFET (shield-gate trench MOSFET, SGT MOS)在中低压(12—250 V)范围内被广泛地应用[1 -3 ] , 具有重要的市场价值. SGT MOS在利用屏蔽栅降低器件导通电阻, 减小器件静态损耗的同时, 缩短了控制栅与漂移区的交叠长度, 从而降低了栅漏电容, 使得器件具有较低的栅电荷(Q g ), 降低了其动态损耗[4 -6 ] . 屏蔽栅技术从成本和性能两个方面提高了功率器件的竞争力.[7 -10 ] . SGT MOS作为一种新型功率器件, 屏蔽栅的引入在降低导通电阻和栅漏电容的同时, 使漂移区特性随外加电压的关系变得更加复杂, 器件建模的难度显著增加. 目前, 仅有少数关于SGT MOS模型的报道, 包括建立基于SPICE的等效电路模型[11 ] , 以及Coner和统计模型的开发[12 ] . 但是这些报道的模型并不完全基于实际的物理结构, 且在模型尤其是电容模型建立的叙述上过于简略, 难以作为进一步研究的参考.2.屏蔽栅沟槽MOSFET结构与模型 SGT MOS紧凑型模型分为直流模型和电容模型. 其中直流模型将器件分为本征MOS区(intrinsic MOS)和非本征MOS区(non-intrinsic MOS), 本征MOS区等效为一个基本MOS管, 非本征MOS区等效为多个串联的电阻. 基于此, 本章采用基本MOS管串联多个等效电阻的方法建立SGT MOS的直流模型, 其中基本MOS管使用BSIM4的直流模型, 包含轻掺杂漏极区(light-doped drain region, LDD区)的电阻模型[13 ] . 电容模型分为栅源电容模型、漏源电容模型和栅漏电容模型. 本节通过分析屏蔽栅对电容的影响, 采用了保持BSIM4栅源电容模型不变、在BSIM4的基础上对漏源电容模型进行扩展, 以及修改栅漏电容模型的偏置的方法来建立和完善SGT MOS的电容模型.2.1.屏蔽栅沟槽MOSFET直流模型 2.1.屏蔽栅沟槽MOSFET直流模型 图1(a) 所示为SGT MOS的结构, 其中非本征MOS区由漂移区(drift)和N型衬底(N-sub)组成, 可等效为与基本MOS管串联的电阻. JFET区是漂移区中最为重要的一部分, 受到屏蔽栅的影响. JFET区和LDD区之间还存在一个电子扩散区(electron diffusion region), 电子流从LDD区以α 角度扩散至该区域. 对于JFET区的建模, 常用的做法是直接引入JFET器件模型或在子电路中使用JFET元件, 并忽略JFET区和LDD区之间的电子扩散区[11 ] . 由于JFET器件的模型是在源极为零电位的基础上推导的, 而实际SGT MOS的JFET区的源端电位V S1 并不为零, 因此传统模型会在该区域引入误差. 为解决这一问题, 本文采用以JFET区两端电势V S1 和V D2 为自变量的电阻R JFET 来模拟JFET区的IV特性. 此外, 当栅与屏蔽栅的间距L DT 与屏蔽栅长L SH 接近时, 忽略电子扩散区会导致JFET区源端电势V S1 过低, 因此本文在本征MOS区与电阻R JFET 之间引入电阻R DT 来提升JFET区源端电势V S1 .图 1 SGT MOS的等效电阻分布(a)和直流等效电路(b)Figure1. (a) Distribution of equivalent resistance of SGT MOS; (b) equivalent DC circuit of SGT MOS.图1(b) 所示的SGT MOS的直流等效电路, 其中本征MOS区等效的基本MOS管采用了BSIM4模型, R DT 为电子扩散区等效电阻, R JFET 为JFET区等效电阻, R DB 为JFET区下方漂移区和N型衬底的等效电阻, 等于图1(a) 中R DB1 , R DB2 , R SUB 之和. 为了简化模型, 对电子的流动路径进行了如下处理. LDD区积累层的厚度是关于栅电压的弱函数, 可近似为定值t ch . 忽略JFET区底部电子流的扩散, R DB1 简化为宽度恒定为t s 的电阻. R DB2 所在区域电子流以β 角度扩散至槽下方的漂移区. 可获得R DT 和R DB 表达式为[14 ] Z 为SGT MOS的元胞宽度, q 为元电荷电荷量, μ n 为电子迁移率, N d 为漂移区掺杂浓度, t DB 为屏蔽栅底部与漂移区的距离, L DB 为槽下方漂移区长度, L SUB 为N型衬底长度, W cell 为元胞宽度. 根据(1 )式、(2 )式可知R DT 和R DB 为仅与尺寸相关的定值电阻, 与偏置电压无关.2 组成的MOS结构控制电子流通道的开启和关断, 漂移区表面电势ψ sh 决定了耗尽区宽度W D 的大小, 可表示为[15 ] Vx 为JFET区域内x 方向上任意一点的电势, V FBsh 为漂移区与屏蔽栅间的平带电压, t i 为屏蔽栅与漂移区间氧化层厚度, ε si 为硅的介电常数, ε ox 为SiO2 的介电常数, V PS 为屏蔽栅与源极间的电压, 由于两者短接, V PS 为0. 则耗尽区宽度[16 ] 表示为I D 可由以下积分式得到:W D (V D2 ) = t s 时, I D 饱和. 根据TCAD仿真, 在SGT MOS的工作区间内, W D (V D2 )始终小于t s , 其原因是电阻R DB1 , R DB2 , R SUB 分担了大部分的电压降, V D2 不足以使该处漂移区完全耗尽, 因此(5 )式适用于SGT MOS的所有静态工作区间. 根据(5 )式求解得到的I D 表达式, JFET区电阻R JFET 可表示为beta , P 1 , P 2 , P 3 仅与尺寸相关, 可表示为R DT , R JFET 和R DB 则通过代入以下经验公式中的R ex 来表示温度的影响[17 ] :T NOM 为常温, T CRD1 和T CRD2 分别为一次项和二次项的拟合系数.2.2.屏蔽栅沟槽MOSFET电容模型 -->2.2.屏蔽栅沟槽MOSFET电容模型 如图2(a) 所示, 与传统的功率MOSFET器件相比[18 ,19 ] , SGT MOS引入了电容C GH , C GSH1 , C GSH2 , 其中栅-屏蔽栅电容C GH 属于栅源电容C GS , 屏蔽栅-漏电容C GSH1 和C GSH2 属于漏源电容C DS , 此外栅-漂移区重叠区域(即LDD区)的减少降低了栅漏电容C GD , C GD 其中一端也从漏极收缩至栅-漂移区重叠区末端的节点B 处. 本文以BSIM4为基础, 对漏源电容模型进行扩展, 并将栅漏电容模型中的栅漏偏置V GD 修改为栅极同栅-漂移区重叠区末端节点B 的电势差V GB , 其电容等效电路如图2(b) 所示, 其中B 点下方为受V DS 控制的压控电压源, 表示B 点电势V B 为关于V DS 的函数.图 2 SGT MOS的电容和电荷的分布(a)及电容等效电路(b)Figure2. (a) Distribution of capacitance and charge of SGT MOS; (b) equivalent capacitance circuit of SGT MOS.C GS 等于栅-体区电容C GI 、栅-屏蔽栅电容C GH 、栅源重叠电容C GO 之和. 由于栅-体区电容C GI 为典型的MOS电容, 栅-屏蔽栅电容C GH 与栅源重叠电容C GO 均为与电压无关的定值电容, 因而可分别使用BSIM4栅源电容模型中的栅体电容模型和栅源重叠电容模型表示.C J 采用耗尽公式推导得到[20 ] :C J0 为单位宽度零偏结电容, v i 为结电势, m 为分级系数. C GSH1 和C GSH2 是关于V DS 的函数, 为简化模型使用屏蔽栅-漏等效电容C GSH 表示C GSH1 和C GSH2 之和, 使用屏蔽栅-漏等效电荷Q GSH 表示Q GSH1 和Q GSH2 之和:m sh 为屏蔽栅电容修正因子. 则扩展后的漏源电容可表示为C GD 从所处的位置上看更接近于LDMOS的栅漏电容. 文献[21 ]使用漂移区等效电阻与基本MOS管之间的节点与栅极之间的电压差来表示LDMOS的栅漏电容, 漂移区等效电阻与基本MOS管之间的节点电压可直接取自直流模型. 本文SGT MOS直流模型中使用的漂移区和衬底的等效电阻公式是在静态工作条件下推导的, 因此无法准确模拟等效电阻R DT 与基本MOS管之间节点D1在开关过程中的电压. 为准确预测开关过程中C GD 的值, 本文选用图2(a) 中栅-漂移区重叠区域的末端节点B 的电势作为C GD 其中一端的偏置, 使用泊松方程求解节点B 电势V B 关于V DS 的表达式, 模拟开关过程中漂移区的耗尽区域承受器件的大部分压降.V GB (V GS –V B )大于漂移区与栅之间平带电压V FBd 时, 电子在漂移区表面累积, 栅漏电荷Q GD 表示为C GDL 为单位宽度的等效栅漏电容.V GB 小于V FBd 时, 漂移区处于耗尽状态, 栅漏电荷表达式为[13 ] ,C GD 曲线的连续性和光滑性, 对(15 )式和(16 )式进行如下处理, 得到Q GD 对V GB 整个区间的表达式:V GB, overlap 为对 (V GB –V FBd ) 的光滑处理[13 ] , 表示为B 点电势V B 关于漏源偏置V DS 的表达式使用泊松方程求解. 如图3(a) 所示, 漂移区分为I, Ⅱ, Ⅲ三个区域, 虚线箭头为漂移区指向栅和屏蔽栅的电场线, 相当于在栅与屏蔽栅之间存在一个虚拟栅(virtual gate)和一个虚拟屏蔽栅(virtual shield-gate), 如图3(a) 阴影区所示. 由于栅与屏蔽栅最左边电场线的路径超过了图中槽的宽度, 因此虚拟栅与虚拟屏蔽栅会超出图示槽的左边界. 上文在推导C GSH 对V DS 的表达式时忽略了虚拟屏蔽栅影响, 这是由于虚拟屏蔽栅的长度远小于屏蔽栅长L SH , 且与漂移区的距离非常大, 对屏蔽栅-漏等效电容的影响非常小.图 3 SGT MOS栅和屏蔽栅 (a) 等效前的结构示意图和 (b) 等效后的结构示意图Figure3. Schematic diagrams of structure before equivalence (a) and after equivalence (b).V B 曲线, 将虚拟栅与栅整合成一个等效栅, 将虚拟屏蔽栅和屏蔽栅整合成一个等效屏蔽栅, 同时Ⅲ区被并入I区和Ⅱ区中, B 点因此下移至I区和Ⅱ区的边界. 整合后器件漂移区受栅和屏蔽栅的影响与整合前一致. 如图3(b) 所示, SGT MOS等效栅-漂移区重叠长度为L ovequ , 等效栅氧厚度为k 1 ·t ox , 等效屏蔽栅长度为L SHequ , 等效屏蔽栅氧化层厚度为k 2 ·t i , 其中k 1 为栅氧厚度因子, 代表栅对漂移区影响的程度, k 2 为屏蔽栅氧化层厚度因子, 代表屏蔽栅对漂移区影响的程度, 且L ovequ 与L SHequ 之和等于L ov , L DT 与L SH 之和. 随着栅氧厚度的变化, 整合之后(17 )式中的栅-漂移区重叠区域的漂移区偏置系数γ 修改为V B 的影响不大; SGT MOS进入工作区之前, 尽管电流大, 但漏源两端工作电压小, V B 的变化非常小. 同理, SGT MOS关断过程电流对V B 的影响也很小, 因此忽略电流影响的泊松方程解得的V B 的表达式能够较为准确地反映B 点的电压变化. V B 的表达式为T 3eff 是关于V DS 的函数, T 1 , T 2 , N 1eff , N 2eff 为V B 表达式的常系数, V db2 为V B 表达式中V DS 的边界值, 对应漂移区恰好耗尽完Ⅱ区. 以上函数关系和常系数表达式以及V B 表达式的推导过程见附录 .3.模型直流特性和动态特性的验证 本文使用Verilog-A对华润上华某45V SGT MOS器件建立直流模型和电容模型, 并搭建实验平台测试数据, 进行模型验证. SGT MOS器件的尺寸如表1 所示, 其中L DT 超过L SH 的一半, 因此电子扩散区对直流特性的影响不可忽略.参数名 含义 大小/μm t ox 栅氧厚度 0.07 t i 屏蔽栅与漂移区间氧化层厚度 0.18 t s 槽右侧漂移区宽度 0.30 t DB 屏蔽栅底部与漂移区的距离 0.07 L ch 沟道长度 0.53 L ov 栅与漂移区重叠部分的长度 0.10 L DT 栅与屏蔽栅间距 0.52 L SH 屏蔽栅长度 0.87 W cell 元胞宽度 1.20
表1 SGT MOS的尺寸Table1. The size of SGT MOS.3.1.屏蔽栅沟槽MOSFET直流特性验证 3.1.屏蔽栅沟槽MOSFET直流特性验证 使用Verilog-A编写直流模型程序, 直流模型中等效电阻的相关参数为: R DT = 125.2 Ω, R DB = 465.8 Ω, beta = 8.84, P 1 = 1.232 × 10–4 cm, P 2 = 1.1 × 10–5 cm·V–0.5 , P 3 = 13 V. 电阻随温度变化的参数为: T NOM = 298.15 K, T CRD1 = –0.1809 K–1 , T CRD2 = 1.505 K–2 .图4 和图5 分别为25 ℃和150 ℃下的器件转移特性及其跨导G m 和输出特性及其输出电导G DS 的仿真曲线和测试曲线. 受限于测试仪器的功率, SGT MOS的输出特性曲线仅测试了V DS 在0—6 V的范围. 在该范围内, 本文建立的直流模型能够很好地拟合实际测试值, 且能够有效反映温度对直流特性的影响. 例如, 从图4(a) 可知25 ℃下器件的阈值电压V th 在2.68 V左右, 从图5(a) 可知150 ℃下器件的阈值电压V th 在2.45 V左右, 阈值电压随着温度的升高发生偏移, 从图4(c) 和图5(c) 可知器件的饱和电压V Dsat 随着温度的升高而增大.图 4 25 ℃下的 (a) 转移特性曲线, (b) 跨导G m 曲线, (c) 输出特性曲线和 (d) 输出电导G DS 曲线Figure4. The curves of (a) transfer characteristic, (b) transconductance G m , (c) output characteristic and (d) output conductance G DS at 25 ℃.图 5 150 ℃下的 (a) 转移特性曲线, (b) 跨导G m 曲线, (c) 输出特性曲线和 (d) 输出电导G DS 曲线Figure5. The curves of (a) transfer characteristic, (b) transconductance G m , (c) output characteristic and (d) output conductance G DS at 150 ℃.3.2.屏蔽栅沟槽MOSFET电容特性验证 -->3.2.屏蔽栅沟槽MOSFET电容特性验证 动态电容C GS , C GD , C DS 通常不是直接测量得到, 产品手册中只提供输入电容C iss 、输出电容C oss 和反馈电容C rss , 它们的关系如下所示:C iss , C oss 和C rss 的数据, 并通过(22 )式得到动态电容C GS , C GD , C DS 的数据. 使用Verilog-A编写电容模型程序, 电容模型的相关参数设置为: m = 0.5, m sh = 0.065 4, k 1 = 6, k 2 = 1.7, L ovequ = 0.35 μm, L SHequ = 1.14 μm.图6 为SGT MOS寄生电容的仿真曲线和测试曲线, 从图中可知, 仿真数据与测试数据有较好的拟合, 且电容模型能够很好地解释测试数据所包含的电学现象. 例如, 图6(a) 中C GD 在V DS = 25 V时下降速率突然变缓, 图6(b) 中C GS 在V DS = 25 V时不再增大, V DS = 25 V这个电压值对应(21 )式中V DS 的边界值V db2 , 此时耗尽区恰好覆盖图3(b) 中整个Ⅱ区.图 6 电容-偏压变化曲线 (a) C GD -V DS 曲线; (b) C GS -V DS 曲线; (c) C DS -V DS 曲线; (d) C iss , C oss , C rss 关于V DS 的曲线Figure6. Capacitance curves on bias voltage: (a) Curve of C GD on V DS ; (b) curve of C GS on V DS ; (c) curve of C DS on V DS ; (d) curves of C iss , C oss and C rss on V DS .3.3.屏蔽栅沟槽MOSFET开关特性验证 -->3.3.屏蔽栅沟槽MOSFET开关特性验证 屏蔽栅沟槽MOSFET的开关特性与电容C GS 和C GD 及其直流特性相关, 因此直流模型和电容模型的准确度决定了模型开关特性的精度. 为评估SGT MOS的开关特性, 本文采用图7(a) 所示的测试电路, 其中电流源I G 为1 mA, 电压源E 为30 V, 外电阻R o 为3 Ω, SGT MOS开启时的工作电流I on 为10 A.图 7 开关特性验证 (a) 测试电路; (b) 工作电流I on = 10 A下的开关特性曲线Figure7. Verification of switching characteristic: (a) Switching characteristic test circuit; (b) switching characteristic curve at I on = 10 A图7(b) 所示为SGT MOS工作电流I on 为10 A下开关特性的仿真曲线和测试曲线. 从图中可以看到, 开启过程中SGT MOS模型模拟的V GS 与V DS 的变化趋势与实际测试数据拟合较好. 图7(b) 中V GS 平台区的前端与测试数据有略微差距, 这是因为在该处V DS 从电压源E 开始下降, V B 处于变化最大的阶段, 而流过漂移区的电流等于I on , 处于电流最大的阶段, 此时电流对V B 的影响不可忽略, 从而导致平台区前端模型仿真与测试数据存在一定的偏差.4.结 论 本文基于BSIM4建立了屏蔽栅沟槽MOSFET的直流模型和电容模型. 直流模型采用以BSIM4为模型的本征MOS区串联多个等效电阻的方法, 将漂移区和N型衬底等效为R DT , R JFET 和R DB 三个电阻, 使用两端电势V S1 和V D2 推导了JFET区等效电阻R JFET 的表达式, 引入R DT 解决JFET区源端电势V S1 过低的问题, 并验证了电阻R DT 和R DB 与偏置电压无关. 电容模型中, 栅源电容直接采用BSIM4模型, 漏源电容在BSIM4基础上添加屏蔽栅- 漏等效电容的公式, 栅漏电容以栅极同栅-漂移区重叠区末端节点B 的电势差V GB 为偏置. 使用泊松方程求解B 点电势V B 的表达式, 通过对栅和屏蔽栅结构进行等效来简化泊松方程, 并保证V B 曲线的光滑性. 使用Verilog-A和电路仿真工具对本文所提模型进行仿真分析, 并搭建电路获取测试数据. 结果表明, 本文所提出的模型与实际测试数据能够较好地拟合, 在科研及生产中具有较高的研究价值和应用价值.附录 如图3(b) 所示漂移区分为Ⅰ区和Ⅱ区, Ⅰ区的电势分布φ 1 和Ⅱ区的电势分布φ 2 可由如下泊松方程所示:φ 1 的边界条件为A3 )式和(A1 )式化简得到Ⅰ区的电势分布的方程为[22 ] $\small {t_1} = \sqrt {{{{t_{\rm{s}}}^2}}/{2} + {{{k_1}{\varepsilon _{\rm{s}}}{t_{\rm ox}}{t_{\rm{s}}}}}/{{{\varepsilon _{\rm ox}}}}}.$ φ 2 的边界条件为A5 )式和(A2 )式化简得到漂移区电势分布的方程为$ \small{t_2} = \sqrt { {{{t_{\rm{s}}}^2}}/{2} + {{{k_2}{\varepsilon _{\rm{s}}}{t_{\rm{i}}}{t_{\rm{s}}}}}/{{{\varepsilon _{\rm ox}}}}}. $ V DS 的增大, 漂移区耗尽区先覆盖整个I区, 后覆盖整个Ⅱ区, 这两个时刻的漏源电压为V DS 的边界电压, 分别为V db1 和V db2 . V DS 超过V db2 后, 耗尽区的覆盖范围将超过Ⅱ区.V DS < V db1 时, I区部分耗尽, 电压降主要由耗尽区承受, 因此V B 等于耗尽区边界的电势, 即V B = V DS .V db1 ≤ V DS ≤ V db2 时, I区完全耗尽, Ⅱ区部分耗尽, 此时方程(A4 )的边界条件为A6 )的边界条件为W D2 表示耗尽区末端位于x 方向的坐标值. 根据边界条件(A7 )和(A8 )求解得到V B 表达式为V DS > V db2 时, 耗尽区的覆盖范围将超过Ⅱ区, 此时I, Ⅱ区的电场分布近似为抛物线, 漏源电压主要降在I, Ⅱ区内, 因此Ⅱ区边界C点处电势可近似等于V DS . 该情况下方程(A4 )的边界条件依旧为(A7 )式, 方程(A6 )的边界条件为A7 )式和(A10 )式求解得到V B 的表达式为V db1 和V db2 的表达式为V B 作如下处理.V DS ≤ V db2 时, V B 表示为d 0 为平滑系数, 取值为0.5.V DS > V db2 时, V B 表示为M 2 , T 3 M 的表达式为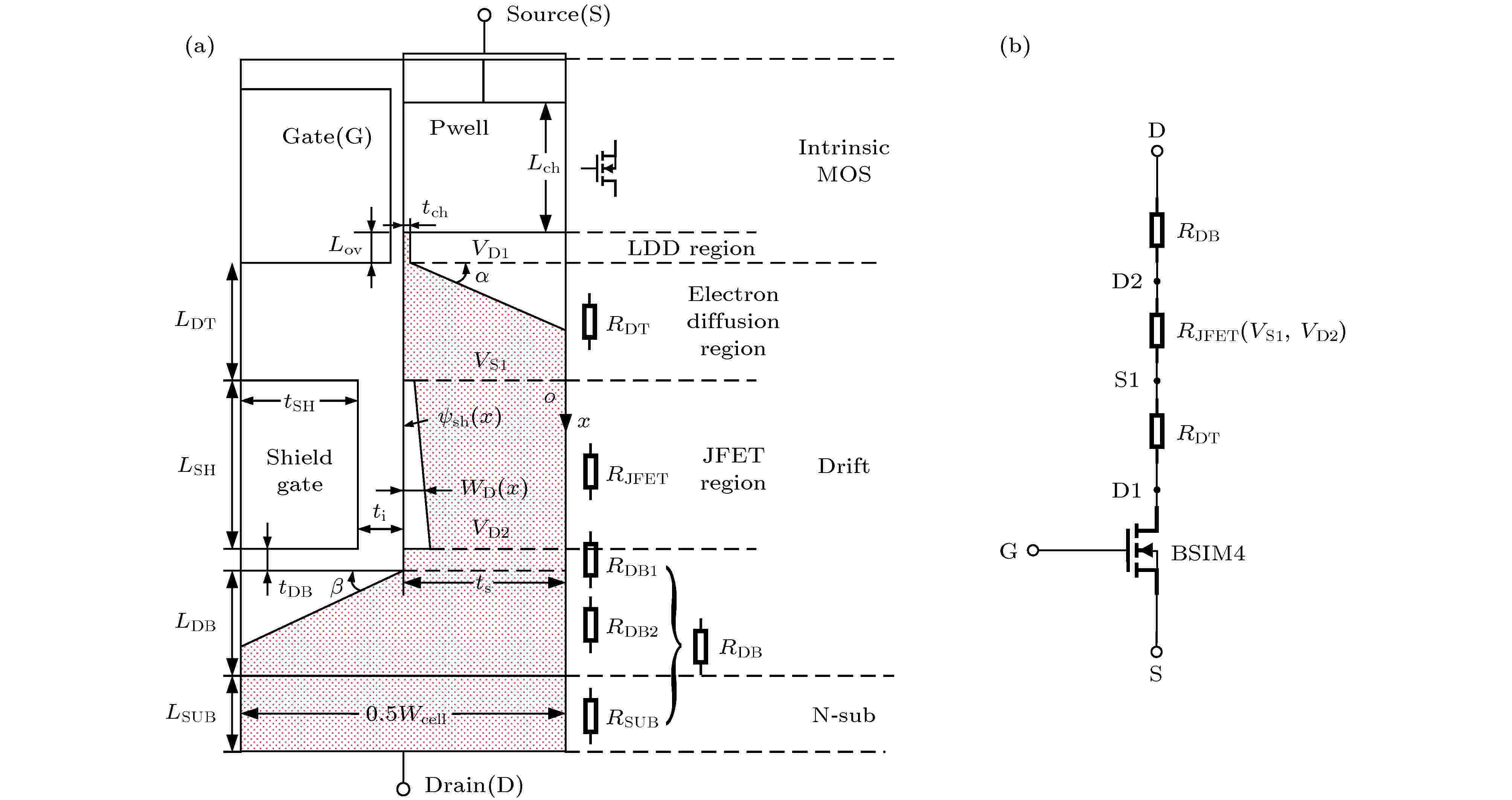 
图 1 SGT MOS的等效电阻分布(a)和直流等效电路(b)
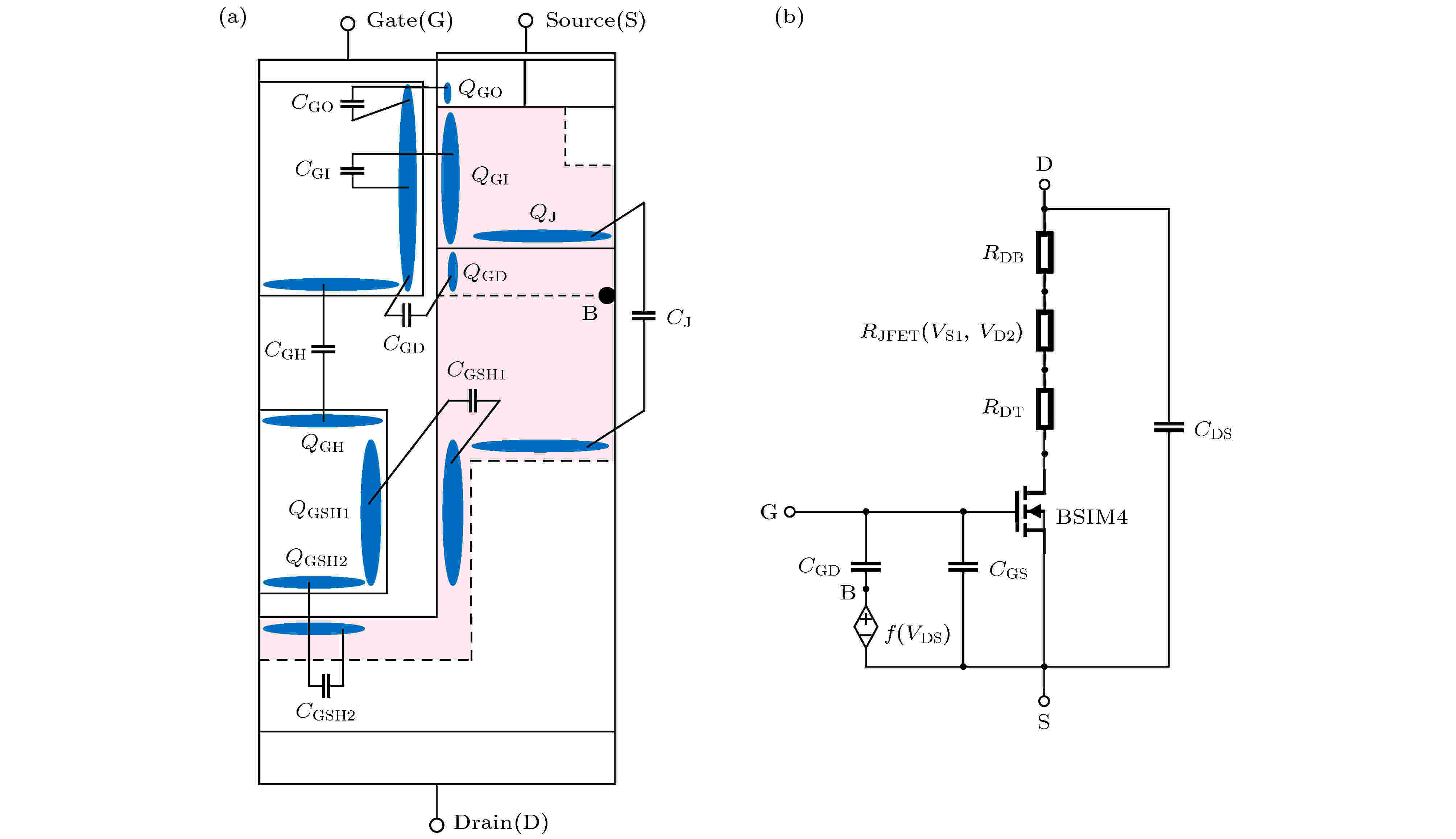图 2 SGT MOS的电容和电荷的分布(a)及电容等效电路(b)
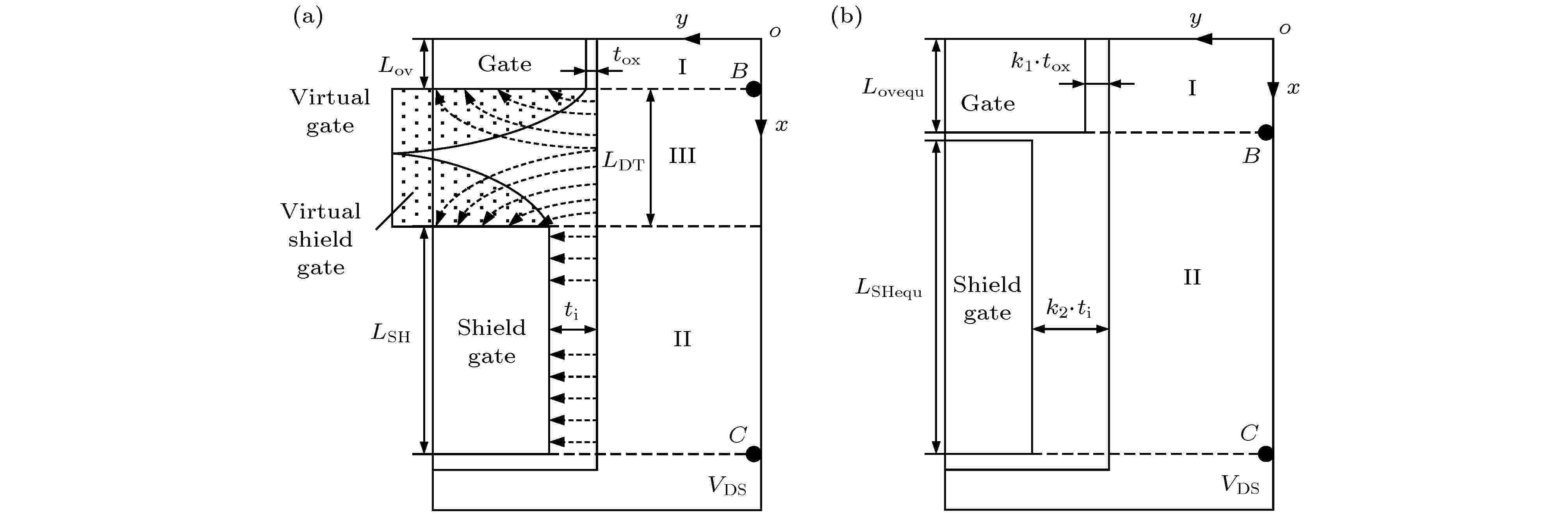图 3 SGT MOS栅和屏蔽栅 (a) 等效前的结构示意图和 (b) 等效后的结构示意图
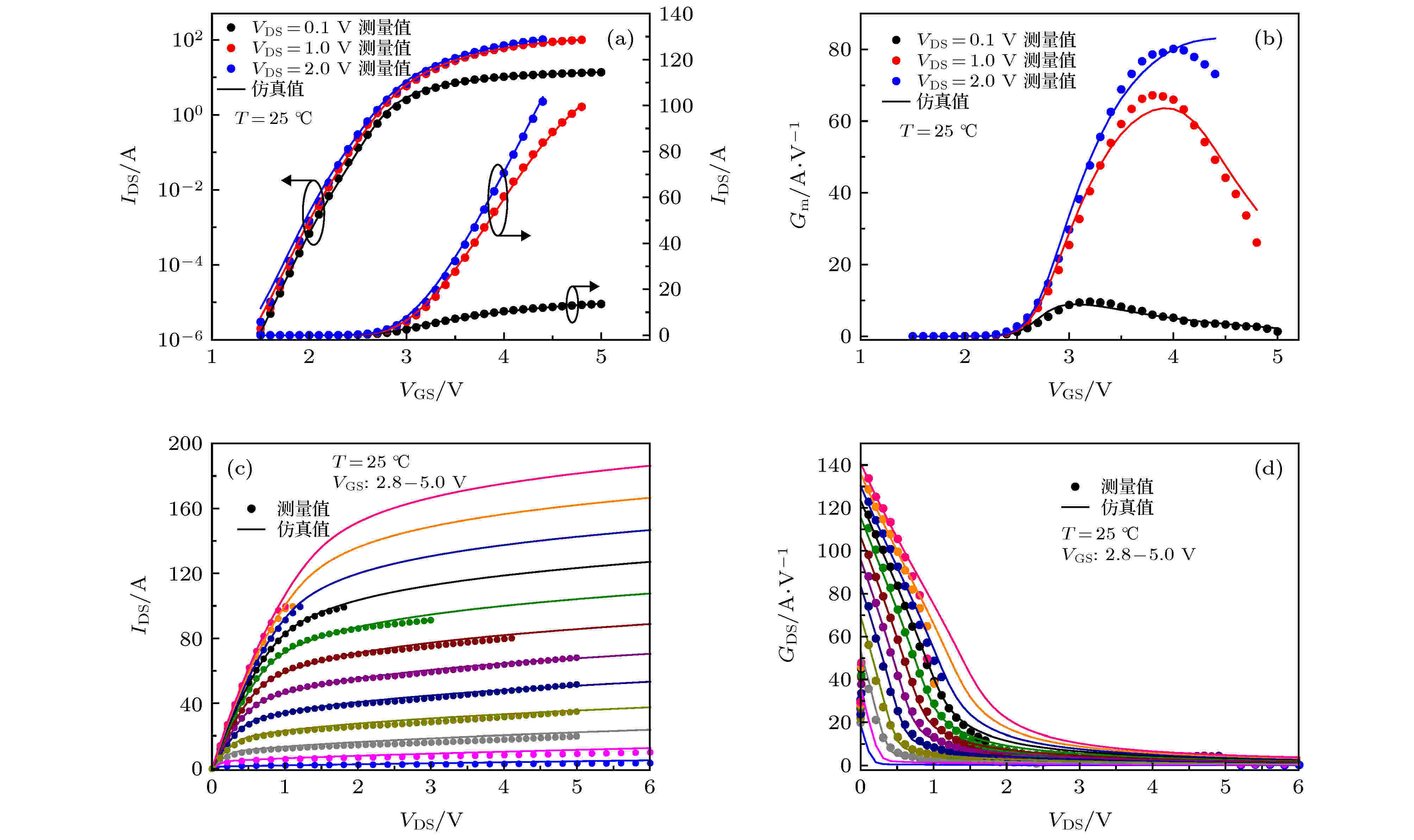图 4 25 ℃下的 (a) 转移特性曲线, (b) 跨导Gm曲线, (c) 输出特性曲线和 (d) 输出电导GDS曲线
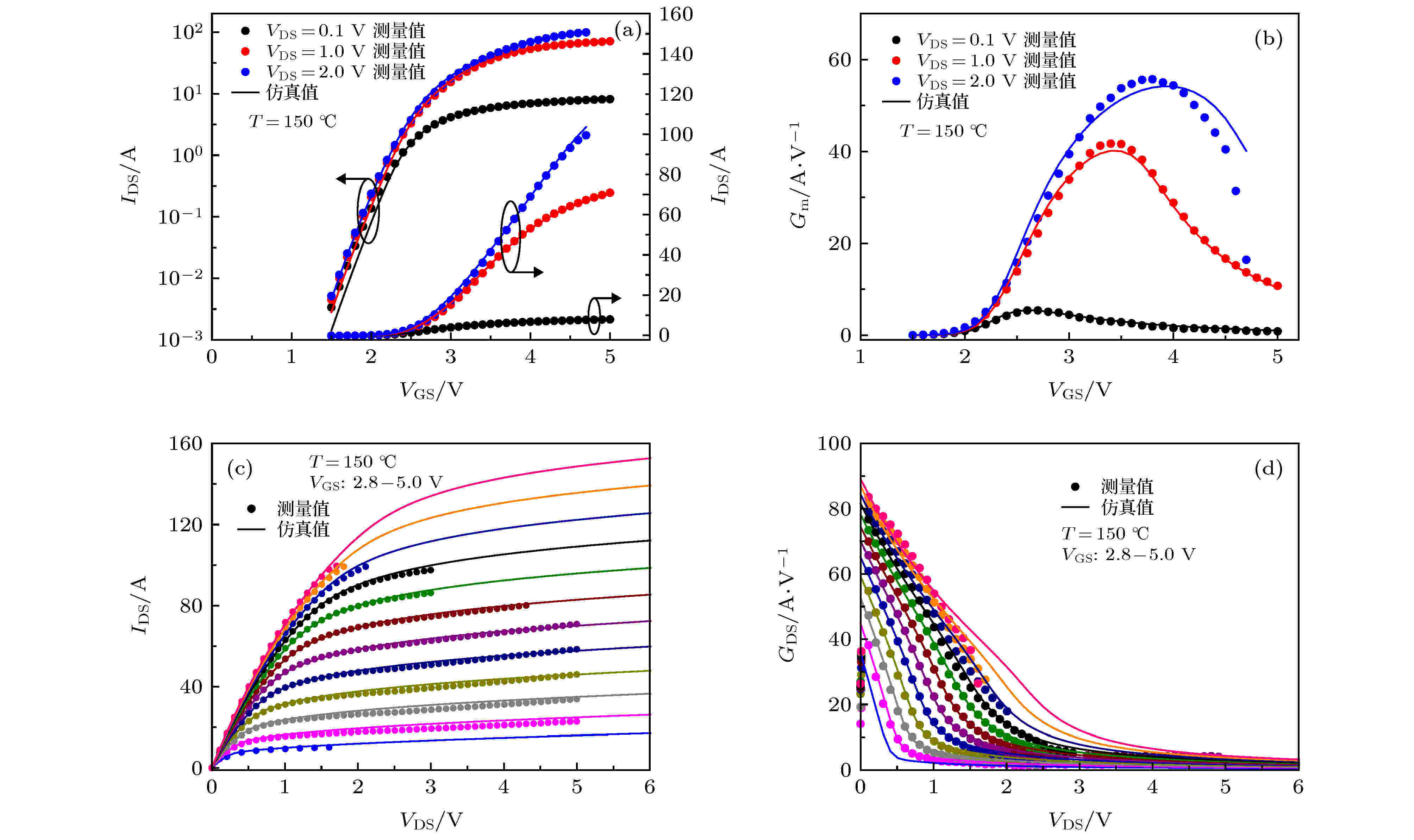图 5 150 ℃下的 (a) 转移特性曲线, (b) 跨导Gm曲线, (c) 输出特性曲线和 (d) 输出电导GDS曲线
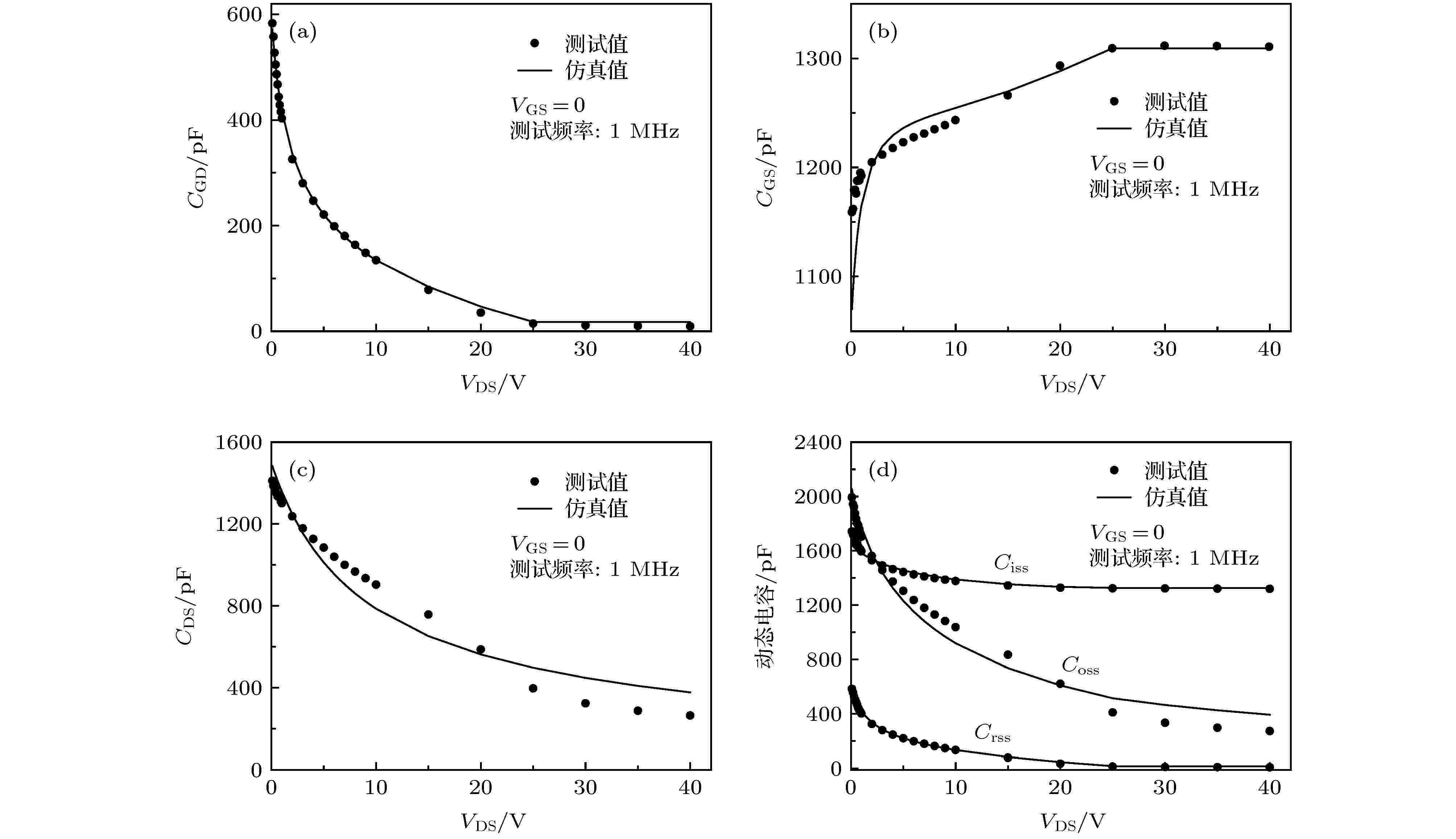图 6 电容-偏压变化曲线 (a) CGD-VDS曲线; (b) CGS-VDS曲线; (c) CDS-VDS曲线; (d) Ciss, Coss, Crss关于VDS的曲线
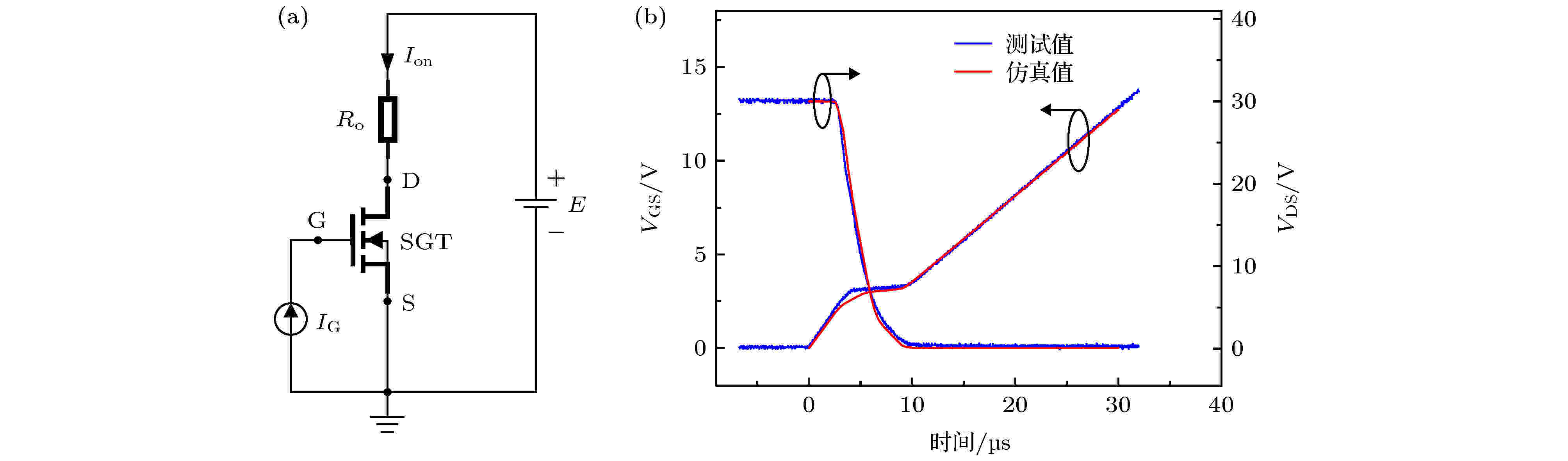图 7 开关特性验证 (a) 测试电路; (b) 工作电流Ion = 10 A下的开关特性曲线
