摘要:本文对一种高效率速调型RBWO进行了理论分析和实验研究. 通过理论分析, 给出两个预调制腔间距的选择依据; 提出一种高功率容量的椭圆形提取腔, 可使得提取腔内表面场强降低约25%; 分析了磁场分布对效率的影响, 结果表明: 使用特殊设计的引导磁场, 可克服器件转换效率对收集位置的强烈依赖; 分析了阴阳极间距对效率的影响, 结果表明: 随着阴阳极间距增大, 器件的最优工作电压降低, 并且效率有所提升. 在实验中获得X波段微波功率为2.15 GW, 脉宽达到25 ns, 转换效率为50%(± 5%). 实验结果与理论和数值模拟结果吻合.
关键词: 高效率/
速调型/
相对论返波管/
高功率微波

English Abstract

全文HTML

--> --> -->

相对论返波管^[1-4] (relativistic backward wave oscillator, RBWO)是具有潜力的高功率微波(high power microwave, HPM)产生器件之一, 其具有输出功率高、转换效率高、适合高重复频率工作, 以及设计方法具有良好的频率可拓展性等特点^[4-10]. 一般而言, 相对论返波管由无箔二极管、高频结构、电子束收集极以及引导磁体组成. 其中: 无箔二极管产生强流相对论电子束(intense relativistic electron beam, IREB); 高频结构主要由慢波结构(slow wave structure, SWS)和经过特殊设计的谐振腔等组成, 是发生波束互作用的主要位置; 电子束收集极收集强流相对论电子束; 引导磁体产生磁场, 引导相对论电子束沿磁力线运动.
相对论返波管的研究始于19世纪70年代, 当时转换效率仅有0.05%, 输出功率为100 MW^[1]. 自此, 高转换效率是研究人员追求的主要目标之一. 基于截止颈型相对论返波管, 国外已有研究表明, 在不考虑空间电荷效应时, 理论上相对论返波管的转换效率可达到60%, 在实验中采用非均匀慢波结构的相对论返波管在实验中获得40%的转换效率^[11].
然而, 对于数GW更高效率微波产生器件的研制还需要突破诸多限制, 如: 恰当调制相对论电子束, 充分提取电子束的动能, 抑制高频结构中的射频击穿等. 对束流强度为数kA、束流密度为数十kA/cm²的相对论电子束进行调制, 并使其形成良好的群聚以及充分提取束流动能是困难的. 对于效率接近50%的相对论返波管, 高频结构表面的电场强度往往较高, 通常超过1 MV/cm, 容易造成射频击穿, 进而对波束互作用产生不良的影响^[10,12,13].
为了进一步提高相对论返波管的效率, 国内外研究人员开展了大量研究. 在数值模拟中, 转换效率可以达到70%^[5,6]. 在实验中, 数GW微波输出时, C波段、X波段和Ku的转换效率分别达到了47%^[6], 45%^[10,14]和42%^[15]. 特别地, 我们提出的速调型相对论返波管(klystron-like RBWO)^[5], 是一种混合波束作用机理的高功率微波产生器件, 结合了切伦柯夫辐射和渡越辐射机制. 与一般相对论返波管不同的是, 在慢波结构中间引入漂移段改善束流预调制, 在慢波结构末端连接提取腔, 利用渡越辐射机制可进一步提取束流动能, 达到大幅提高效率的目的.
近来, 我们报道了一种高频结构由预调制腔、带脊的谐振腔反射器和带漂移段的慢波结构以及提取腔组成的X波段速调型相对论返波管(如图1所示). 在实验中微波功率为2 GW、转换效率为45%^[10,16]. 在此基础上, 对该器件开展了进一步研究, 本文将介绍相关的研究进展.
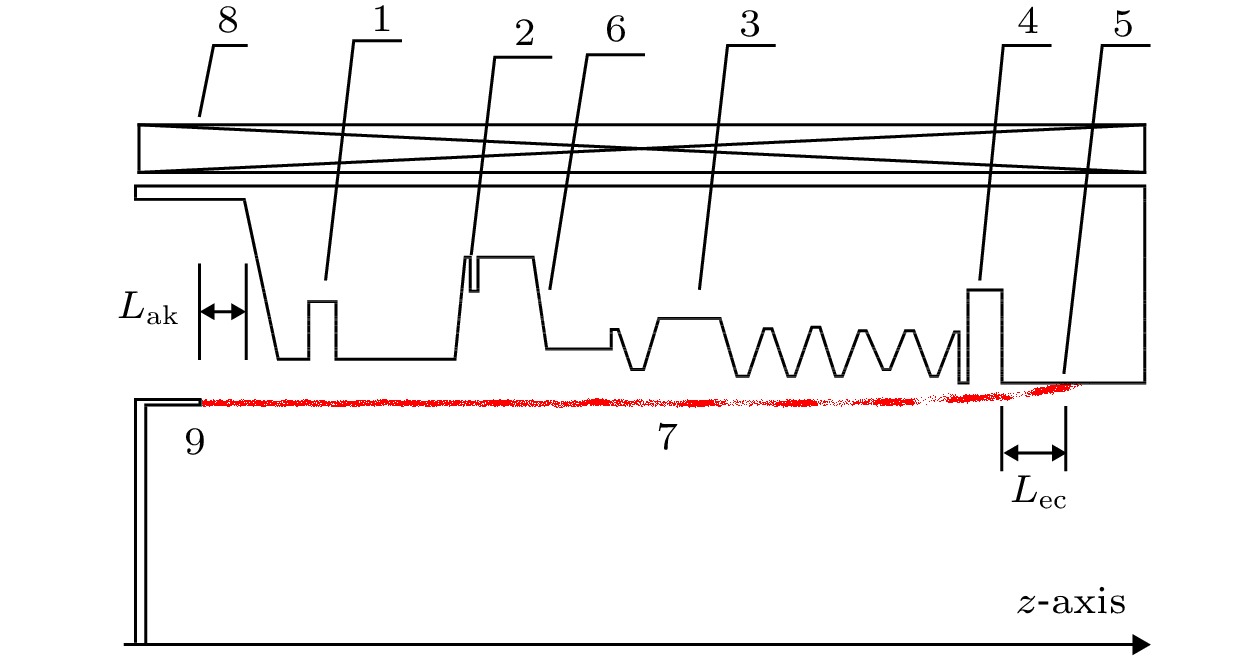图 1 一种高效率速调型相对论返波管结构图　(1 预调制腔; 2调制脊; 3 慢波结构; 4 提取腔; 5 电子束收集极; 6谐振腔反射器; 7电子束; 8 引导磁体; 9 阴极)
Figure1. Schematic of a high efficiency klystron-like RBWO. (1 pre-modulation cavity; 2 modulation ridge; 3 slow wave structure; 4 extraction cavity; 5 electron beam collector; 6 resonant reflector; 7 electron beam; 8 guiding magnet; 9 cathode)

2

-->

2.1.束流预调制

为了实现RBWO高效率输出, 良好调制的束流是必要条件之一. 研究发现, 在RBWO中采用多级预调制结构, 通过多级调制场之间的配合, 可以有效改善束流的调制状态, 达到提升转换效率的目的. 一般情况下, 预调制腔采用TM₀₂₀的谐振腔, 利用其中的纵向电场对束流进行预调制.
考虑如图2所示的预调制结构. 束流电子在预调制腔A中电场的作用下, 产生速度调制. 经过漂移后形成密度调制. 为了改善束团的群聚状态, 预调制腔B中电场需与A中的电场反相. 设t₁时刻、z₁位置的电场为
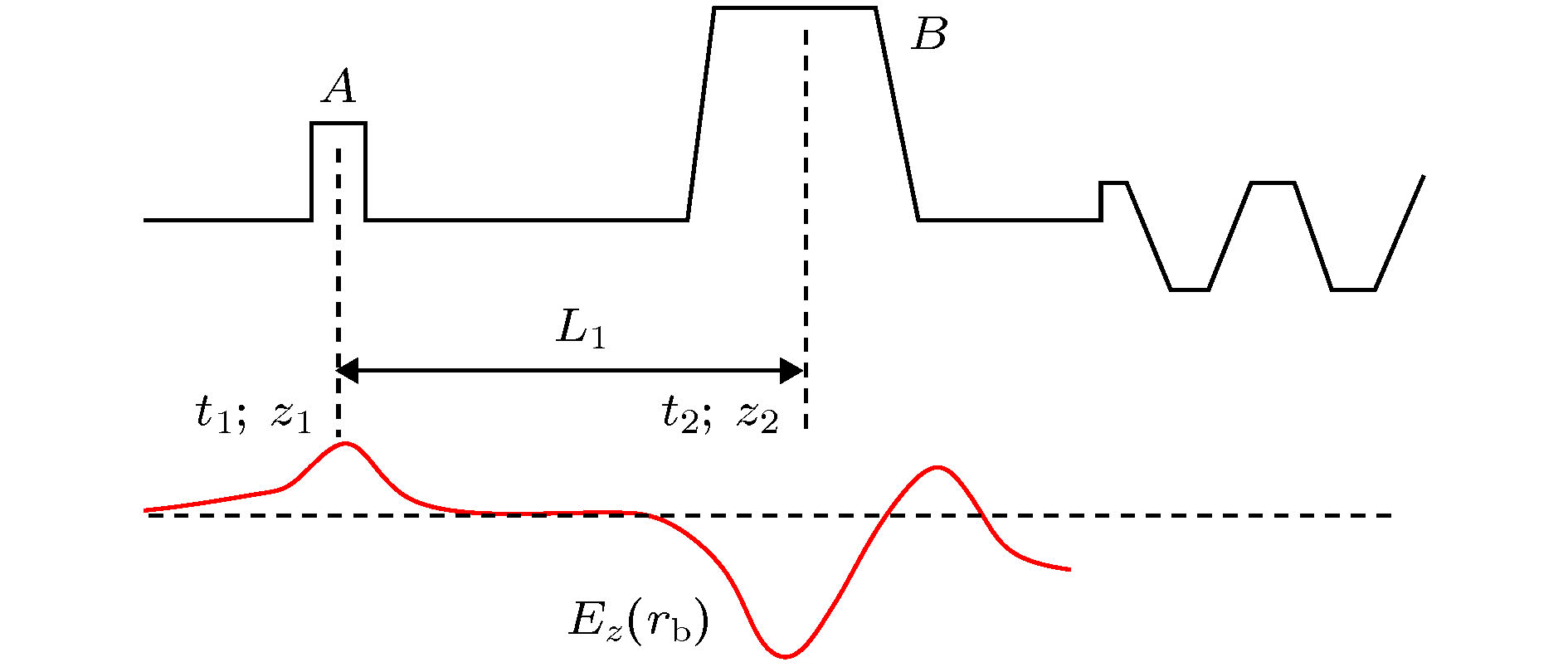图 2 含两个预调制腔的预调制结构
Figure2. Pre-modulation structure with two cavities.

${E_z}({t_1},{z_1}) = {E_1}\cos \left({\omega {t_1} + {\beta _z}{z_1} + {\phi _0}} \right),$

式中, t₂时刻, z₂位置的电场为

${E_z}({t_2},{z_2}) = {E_2}\cos \left({\omega {t_2} + {\beta _z}{z_2} + {\phi _0}} \right),$

式中E₁和E₂分别为两个位置调制电场幅值.
电子经过z₁、z₁两个位置时的电场反相, 即

$\Delta \phi = (2n + 1){\rm{\pi }} = \omega \left({{t_2} - {t_1}} \right) + {\beta _z}\left({{z_2} - {z_1}} \right).$

考虑到电子的平均漂移速度为v_d, 则

$\frac{{{z_2} - {z_1}}}{{{t_2} - {t_1}}} = \frac{{{L_1}}}{{{t_2} - {t_1}}} = {v_d},$

式中L₁为两个调制腔间距. 于是L₁需满足

${L_1} = \frac{{(2n + 1){\rm{\pi }}}}{{{\omega / {{v_{\rm{d}}}}} + {\beta _z}}}.$

即${L_1}\left({{\omega / {{v_{\rm{d}}}}} + {\beta _z}} \right) = (2 n + 1){\text{π}}$, 式中n为整数.
对于图1所示RBWO, 图3给出了数值模拟中两个调制腔间距L₁对效率的影响, 并且依据(5)式给出了调制电场相位差随L₁的变化. 理论表明, 当两个调制腔中的电场反相, 即${{L_1}\left({{\omega / {{v_{\rm{d}}}}} + {\beta _z}} \right)} / {\text{π}} = (2 n + 1)$时, 有利于束流调制, 器件效率较高, 如L₁为 39 mm和56 mm的情形; 当调制电场同相, 即${{{L_1}\left({{\omega / {{v_{\rm{d}}}}} + {\beta _z}} \right)} / {\text{π}}} = 2 n$时, 不利于束流调制, 器件效率较低, 如L₁ = 47 mm的情形. 结果表明, 理论结果与PIC数值模拟吻合较好.
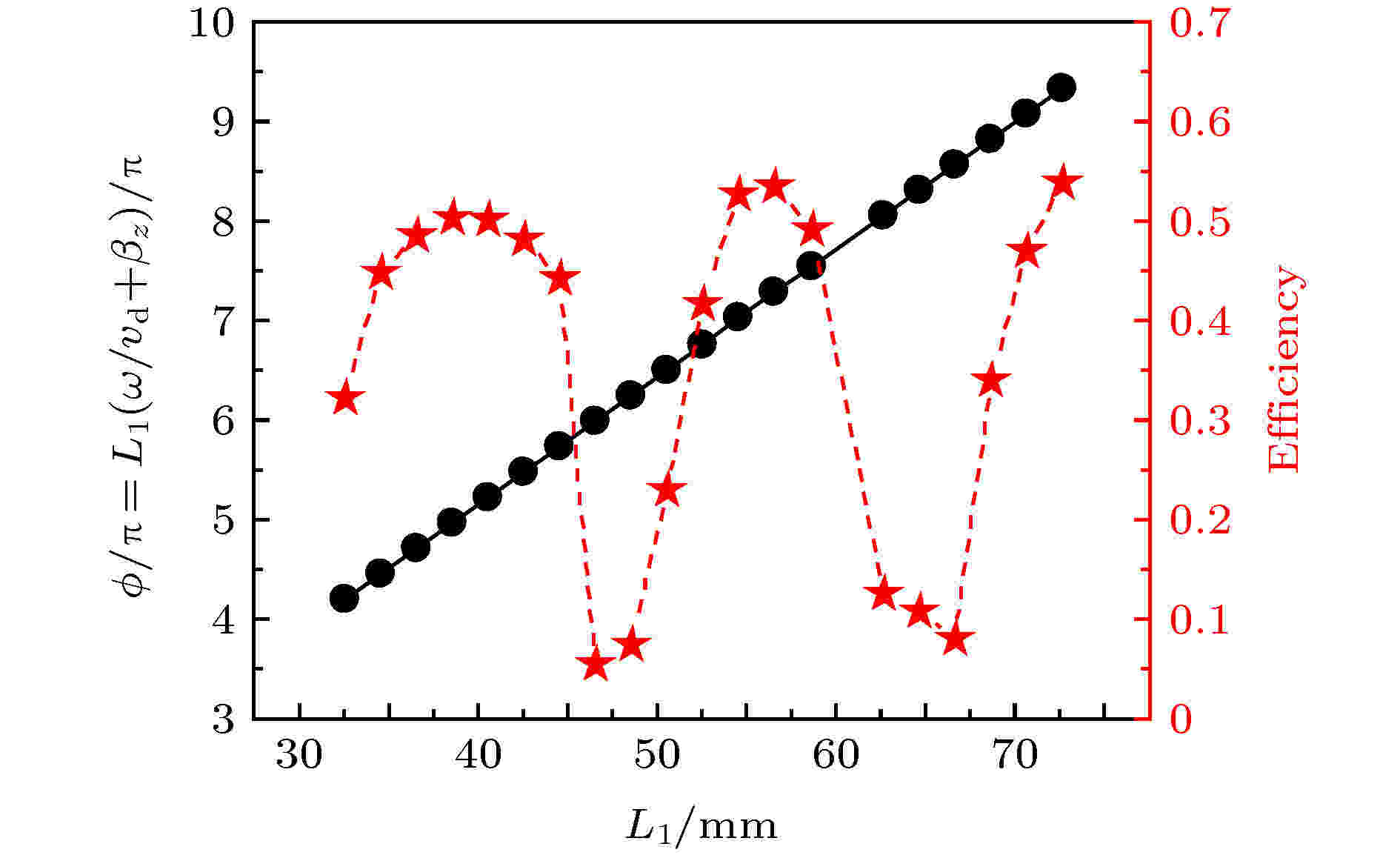图 3 两个调制腔间距L₁对效率的影响
Figure3. Effect of the two modulation cavity spacing L₁ on efficiency.

2 -->

2.2.束流能量提取

高频结构中的电场对束流作用的功率为^[17]

$P = \int_V {J \cdot {E_z}({r_{\rm{b}}}){\rm{d}}V} ,$

式中, J为束流密度, E_z(r_b)为束流半径r_b位置的纵向电场. 为了提升转换效率, 一方面可以增强局部电场(如提取腔等), 集中提取束流动能; 另一方面, 可以优化束流与慢波结构中电场的匹配关系, 增强束流位置的电场, 使得束流动能被更有效提取.
在增强局部电场方面, 提取腔是速调型RBWO提取束流动能、提高转换效率的关键部件, 通常为工作在TM₀₂₀模式的矩形腔, 如图4(a)所示. 对于提取束团能量的时刻, 其中的电场分布大致如图4所示. 但随着场强的提高, 提取腔表面的场强也随着增加, 击穿风险增加. 在实验中, 也发现提取腔击穿限制了效率提升^[10].
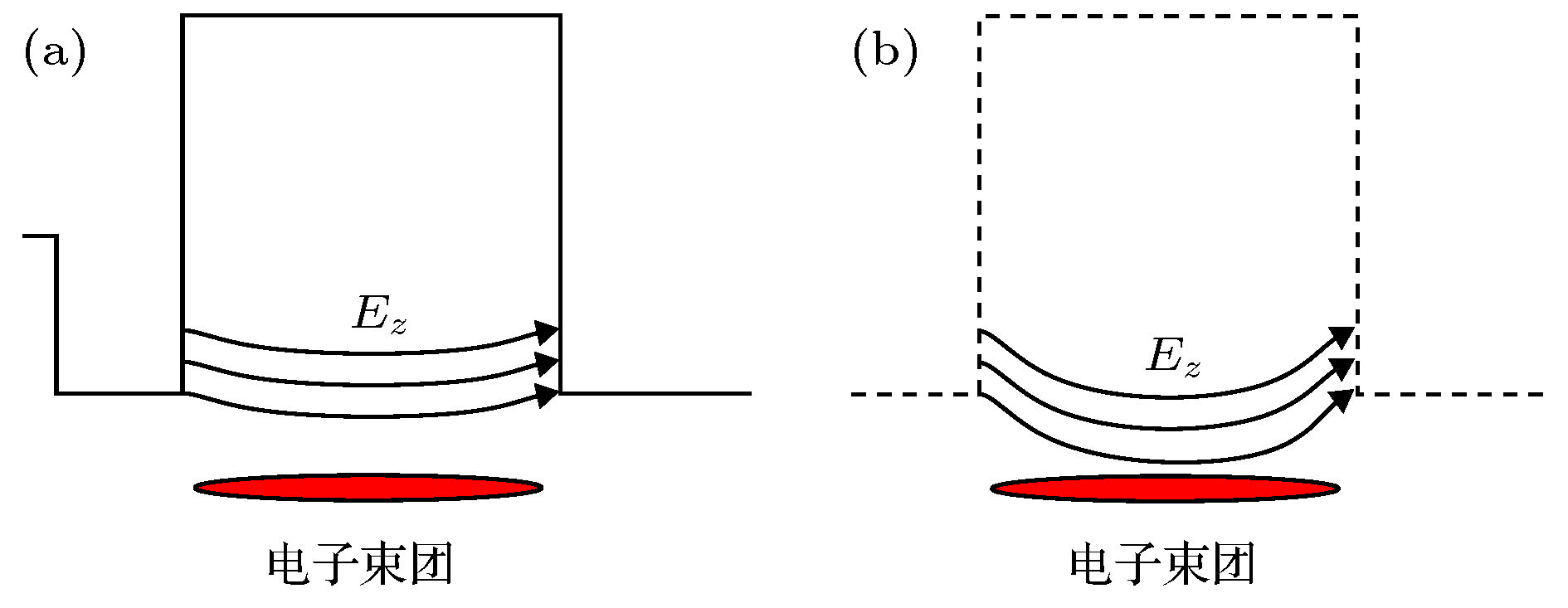图 4 提取腔改进的示意图　(a)矩形提取腔; (b)“理想”提取腔
Figure4. Schematic of enhanced extraction cavity: (a) Rectangular extraction cavity; (b) perfect extraction cavity.

为了提高提取腔的功率容量, 现有的方法包括对提取腔倒圆角、采用双TM₀₂₀提取腔^[18]、采用分布式能量提取结构^[13]以及TM₀₂₁模式提取腔^[12]等. 其中, 对提取腔进行倒角, 能够在一定程度上缓解由于内表面尖角造成的场增强, 但是改善功率容量的效果有限. 双TM₀₂₀提取腔能够在一定程度上降低提取腔内表面场强, 但是每个单独的腔体仍然工作于TM₀₂₀模式, 单个腔体内表面的场强依然较高. 对于分布式能量提取结构, 可使得提取腔的场强显著减小. 但是, 该方法在器件末端引入同轴结构, 使得提取结构复杂. 另外, 耦合结构输出结构中的场强较大, 存在较大击穿风险. 对于工作在TM₀₂₁模式提取腔, 在效率接近50%的条件下, 可以将提取腔的场强减低48%, 但是进一步提高效率困难.
为了缓解高效率与提取腔表面强场的矛盾, 一个物理思路是将有效减速场向束流位置“聚焦”, 使得提取腔表面电场减弱, 同时有效减速电场依然较大, 原理图如图4(b)所示.
为了达到图4(b)所示的“理想”场分布, 需要寻找一种特殊形状的提取腔. 众所周知, 对于理想导体, 表面电场垂直与导体表面. 因此, 可以通过提取腔形状(或纵切面曲线的曲率)控制局部电场分布. 我们发现, 提取腔纵剖面为1/4椭圆和1/4圆弧配合时, 能够近似实现图4(b)所示的物理设计. 图5给出了矩形提取腔和椭圆提取强的结构示意图. 其中, 椭圆曲线满足方程${{{{(r - {r_{{\rm{ec}}}})}^2}}}/{{R_0^2}} + {{{{(z - {z_{{\rm{ec}}}})}^2}}}/{{Z_0^2}} = 1$.
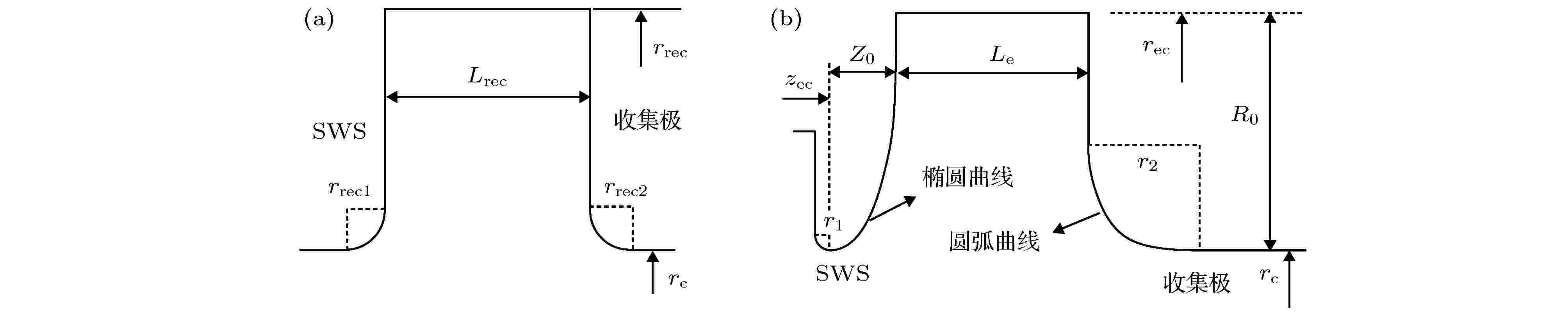图 5 两种提取腔结构示意图　(a)矩形提取腔; (b)椭圆形提取腔
Figure5. Schematic of two extraction cavities: (a) Rectangular extraction cavity; (b) ellipse extraction cavity.

下面比较两种提取腔的功率容量. 基于图1所示的RBWO, 在相同的输出频率、输出功率和转换效率时, 两种提取腔的结构参数如表1和表2所示.

参数	rrec/mm	Lrec/mm	rrec1/mm	rrec2/mm	rc/mm
取值	31.00	7.00	2.25	2.00	23.00

表1矩形提取腔各参数
Table1.Parameters of rectangular extraction cavity.

参数	R0/mm	Z0/mm	rec/mm	zec/mm	r1/mm	r2/mm	Le/mm	rc/mm
取值	8.50	2.25	32.00	243.00	0.75	4.00	6.75	23.00

表2椭圆形提取腔各参数
Table2.Parameters of ellipse extraction cavity.

在PIC数值模拟中, 当输出功率为2.8 GW时, 矩形提取腔慢波结构侧(如图6所示A侧)导致电子发射的最大纵向电场$E_{z{\rm{max}}}^{{\rm{sws}}} = - 1.1\;{\rm{MV/cm}}$, 收集极侧(如图6所示B侧)导致电子发射的最大纵向电场$E_{z{\rm{max}}}^{{\rm{col}}} = {\rm{51}}0\;{\rm{ kV/cm}}$. 提取腔A侧的最大纵向电场超过一般金属材料的发射阈值, 容易发生射频击穿. 需说明, 我们认为在良导体表面, 电场只有法向分量, 当电场指向导体内部时, 可导致电子从表面发射; 反之, 不能导致电子从表面发射. 因此, 分析功率容量时, 重点关注指向导体内部的电场强度.
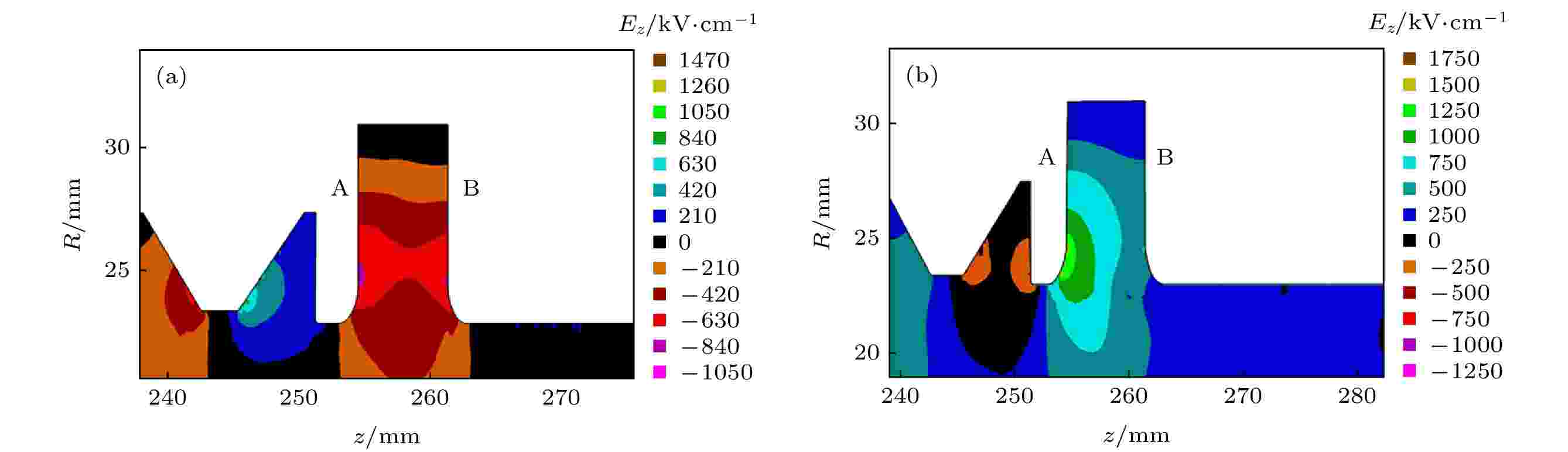图 6 PIC仿真中矩形提取腔中的场强分布　(a)电场分量E_z朝–z方向的情形; (b)电场分量Ez朝+z方向的情形
Figure6. Field distribution in rectangular extraction cavity in PIC simulation: (a) E_z orients –z direction; (b) E_z orients +z direction.

椭圆形提取腔慢波结构侧(如图7所示A侧)导致电子发射的最大纵向电场$E_{z{\rm{max}}}^{{\rm{sws}}} = - 810\;{\rm{kV/cm}}$, 收集极侧(如图7所示B侧)导致电子发射的最大纵向电场$E_{z{\rm{max}}}^{{\rm{col}}} = 420 \;{\rm{ kV/cm}}$. 相比于矩形提取腔, 椭圆形提取腔A、B两侧导致电子发射的电场分别降低26%和18%, 提取腔的功率容量显著提升.
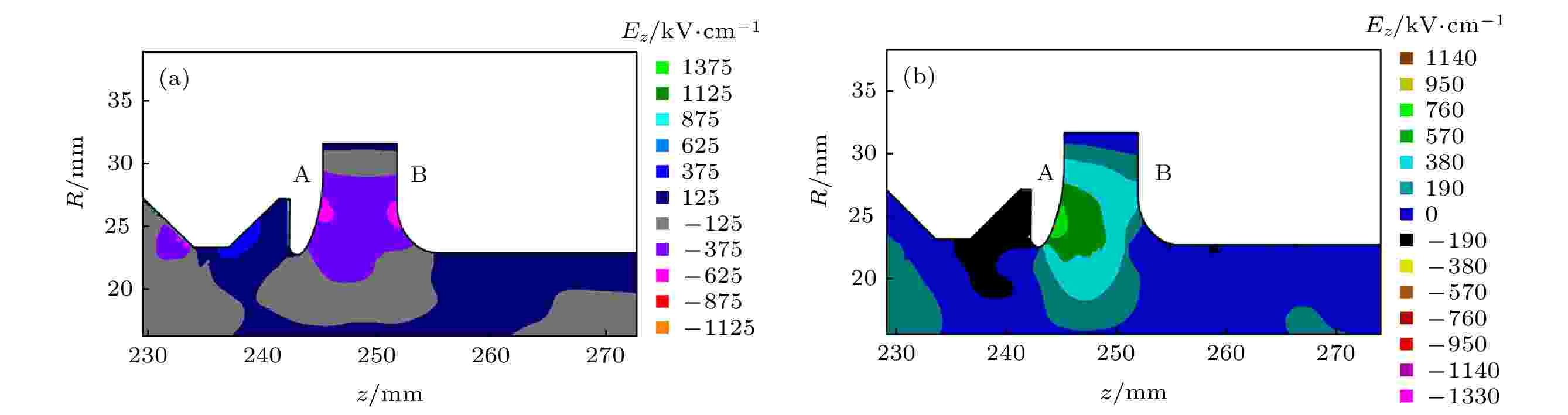图 7 PIC仿真中椭圆形提取腔中的纵向电场分布　(a)纵向电场E_z朝–z方向的情形; (b)纵向电场E_z朝+z方向的情形
Figure7. Longitudinal electric field distribution in ellipse extraction cavity in PIC simulation: (a) E_z orients –z direction; (b) E_z orients +z direction.

综上, 使用椭圆形提取腔达到了既减小提取腔内表面电场强度又维持较高转换效率的目的.
在束流与慢波结构中电场的匹配关系方面, 我们发现引导磁场的磁场分布对器件工作状态有显著的影响. 采用了均匀区的磁场强度均为4.5 T的两种磁场分布对器件的影响进行了分析. 一种是由(7)式近似表达的螺线管产生的磁场分布, 取B₀ = 4.5 T, z_a = 2.0 cm. 通过改变z_b改变束流的收集位置L_ec(如图1所示).

$\left\{ \begin{aligned}& {B_z}(z,r) = \frac{{{B_0}}}{{1 + \;{\rm{exp}}\left({\dfrac{{z - {z_b}}}{{{z_a}}}} \right)}}, \\& {B_r}(z,r) = \frac{{{B_0}}}{2}\frac{r}{{{z_a}}}\frac{{{\rm{exp}}\left({\dfrac{{z - {z_b}}}{{{z_a}}}} \right)}}{{{{\left[{1 + \;{\rm{exp}}\left({\dfrac{{z - {z_b}}}{{{z_a}}}} \right)} \right]}^2}}}, \end{aligned} \right.$

另一种是某型超导磁体的磁场分布, 轴向磁场分量B_z和径向次场分量B_r随纵坐标的变化如图8所示.
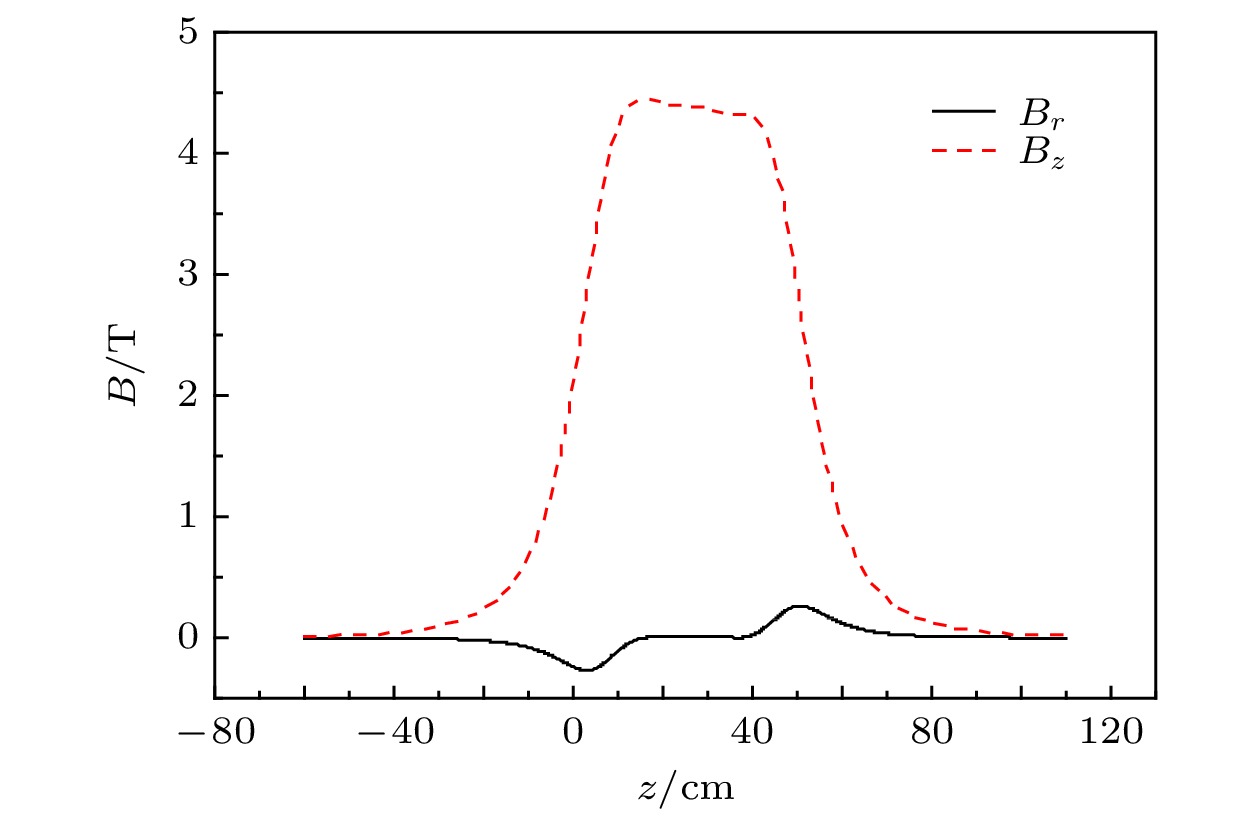图 8 超导磁体的磁场
Figure8. Magnetic field of superconductor magnet.

在两种磁场分布下, 束流收集在L_ec = 1.5 cm附近的相空间图分别如图9(a)和图9(b)所示. 可见, 两种引导磁场的主要不同是超导磁体的磁力线在慢波结构后端处于非均匀区域, 磁力线向大半径扩张, 使得束流在收集前更加靠近慢波结构表面.
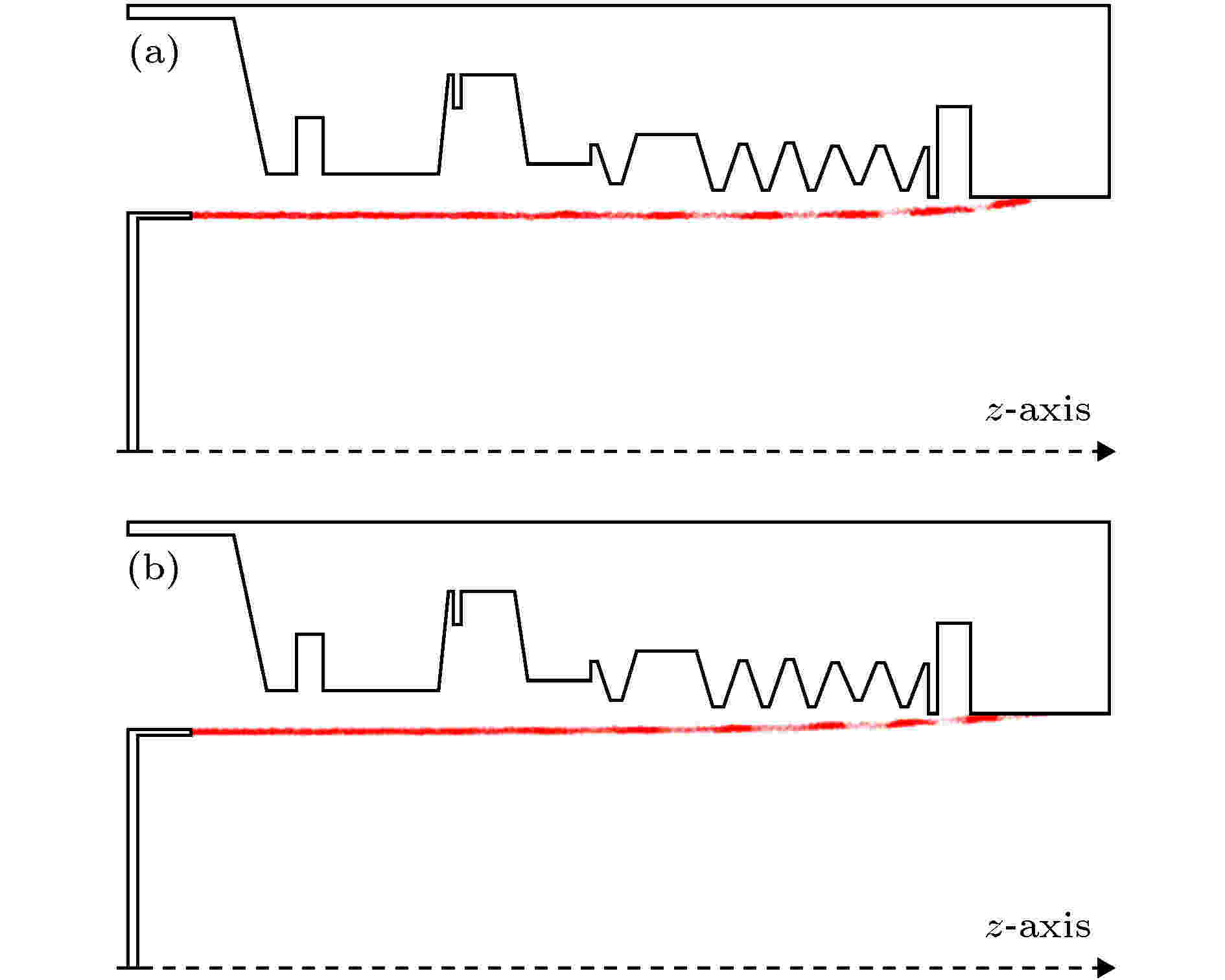图 9 螺线管磁场和超导磁场下的相空间图　(a)螺线管磁体的情形; (b)超导磁场的情形
Figure9. Phasespace of electron beam under solenoid and superconductor magnet: (a) Case with solenoid magnet; (b) case with superconductor magnet.

图10给出了阴阳极间距L_ak = 10 mm时, 螺线管磁场和超导磁场下器件的转换效率随L_ec的变化. 可见, 在螺线管磁场分布下, 效率强烈依赖于束流的收集位置, 当收集位置从L_ec = 0变化到L_ec = 50 mm时, 效率降低约10个百分点; 在超导磁场分布下, 效率随L_ec变化并不显著, 当L_ec从0增加到35 mm时, 效率仅下降了约1个百分点. 在超导磁体条件下, 束流更加靠近高频结构, 具有更小的势能, 所受有效作用电场更强, 束流收集位置的改变对势能和电场的影响较小, 因而转换效率对束流收集位置变化不敏感, 即使在较远的位置收集, 也具有较高的效率; 反之, 在螺线管磁体条件下, 束流收集位置的改变对其影响较大, 转换效率强烈依赖束流收集位置. 可见, 通过磁场分布的改善, 使得束流在波束互作用区后端更加靠近慢波结构, 可以在一定程度上克服器件转换效率对收集位置的强烈依赖.
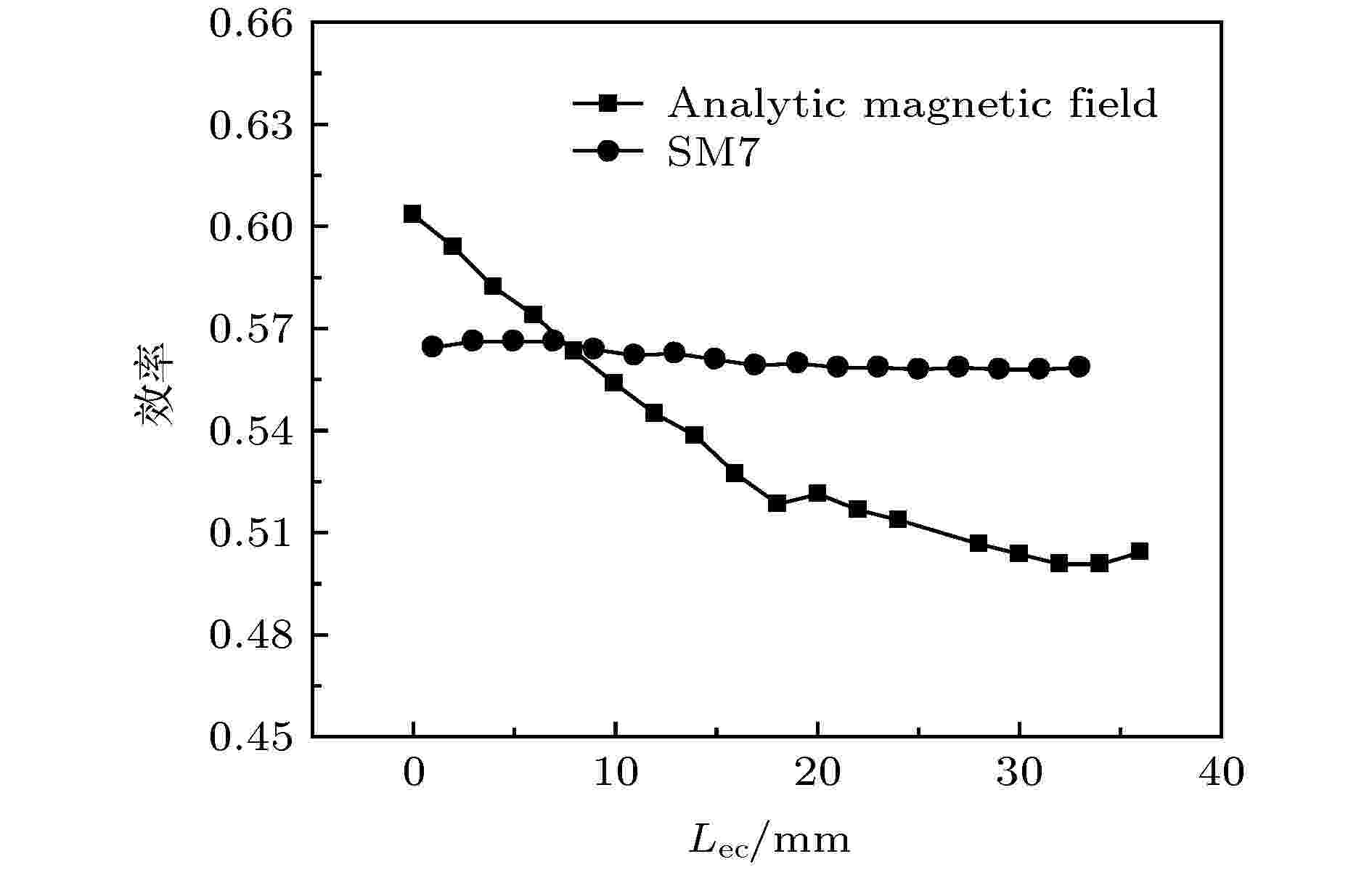图 10 螺线管磁场和超导磁场下的效率随L_ec的变化
Figure10. Variation of efficiency with L_ec under solenoid and superconductor magnet.

采用超导磁体, 并使用椭圆形提取腔时, 当L_ak = 30 mm, 二极管电压607 kV、电流5.86 kA时, 输出微波功率为2.12 GW, 频率为9.55 GHz, 转换效率为60%, 输出功率和频谱如图11所示.
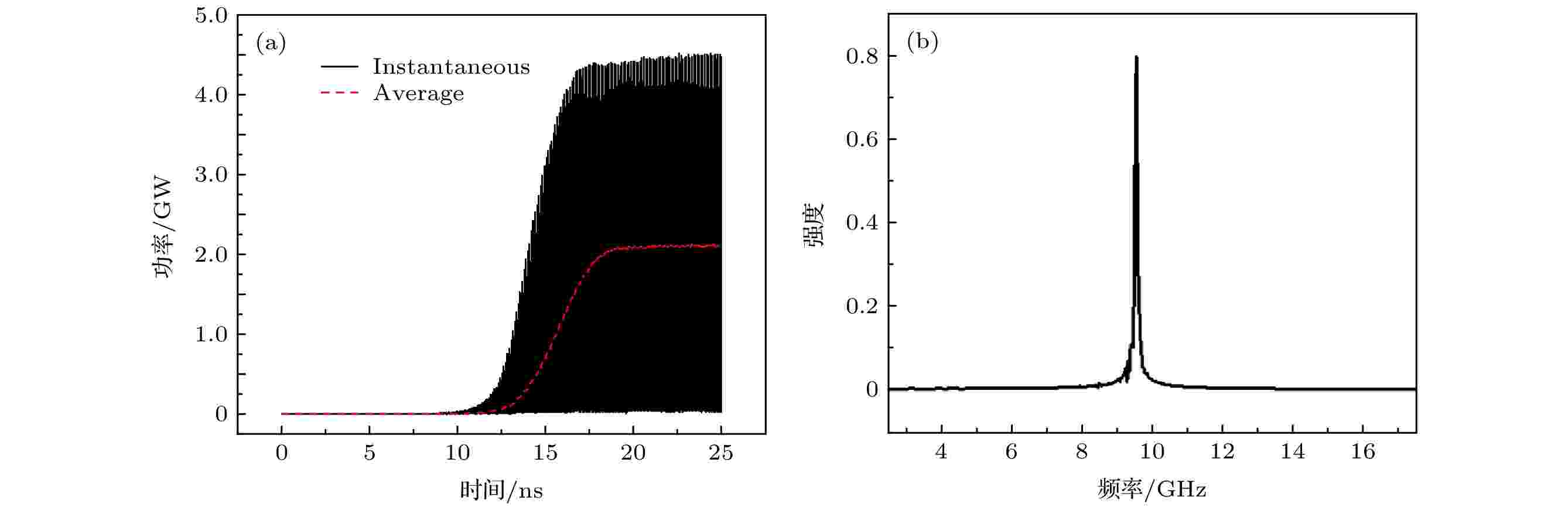图 11 PIC数值模拟中的典型结果　(a)输出功率; (b)频谱
Figure11. Typical results in PIC simulation: (a) Microwave power; (b) frequency spectrum.

2 -->

2.3.阴阳极间距的影响

阴阳极间距对器件的影响规律如图12所示. 图12(a)给出了效率随电压的变化关系. 可见, 随着阴阳极间距增大, 最优电压减小, 并且效率有所增加. 如L_ak = 10 mm, 二极管电压为640 kV时, 效率57%; 当L_ak = 20 mm, 二极管电压为615 kV时, 效率59%. 图12(b)给出了频率随电压的变化关系, 随着电压的升高频率逐渐增加, 二极管电压每升高50 kV, 输出频率升高约25 MHz.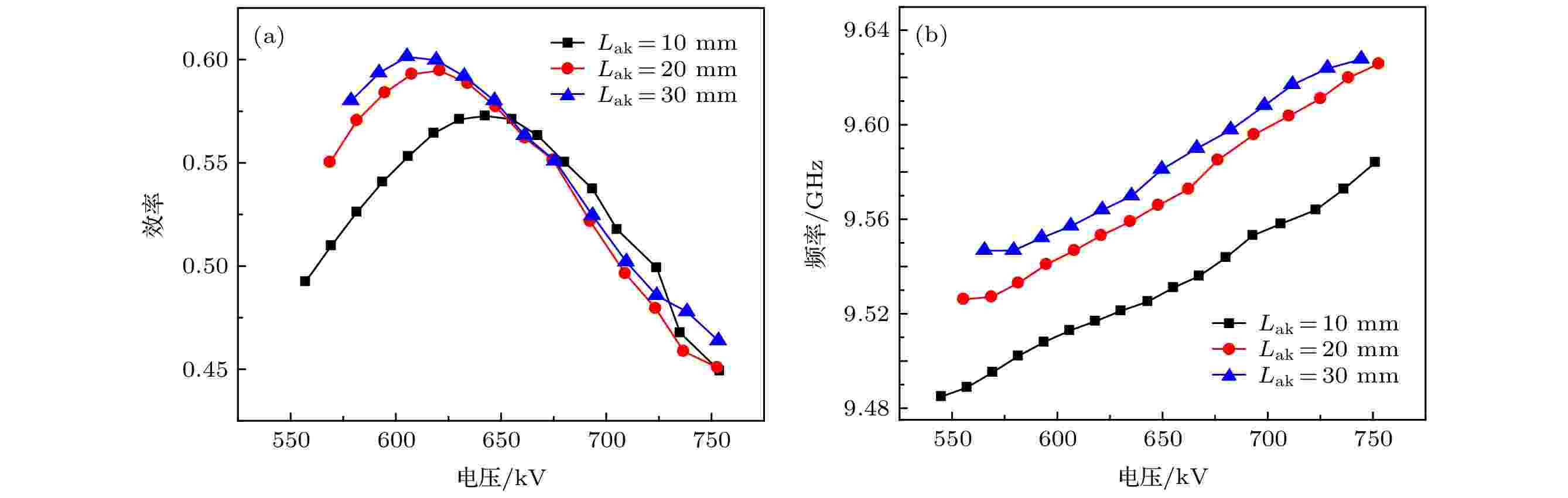
图 12 不同阴阳极间距L_ak的电压规律　(a)效率随电压的变化; (b)频率随电压的变化
Figure12. Effect of diode voltage under different L_ak: (a) Variation of efficiency with diode voltage; (b) variation of frequency with diode voltage.

一方面, 阴阳极间距增大, 导致二极管阻抗升高. 在相同束流功率下, 束流较小, 进而束流密度较小, 在一定程度上抑制了空间电荷效应对束流调制的不利影响, 使得器件效率提升. 另一方面, 根据同步条件^[19], 当电压升高时, 电子束线与慢波结构色散曲线的交点上移, 使得器件工作频率升高. 另一方面, 当阴阳极间距较小时, 二极管电压对束流电子的加速不充分, 导致有效的加速电压较小, 进而使得器件的工作频率较低. 随着阴阳极间距的增大, 有效的加速电压逐渐升高并趋于稳定, 使得器件工作频率逐渐升高并趋于稳定. 由于高频结构的谐振特性, 器件工作在特定频率下(如9.55 GHz)效率较高, 阴阳极间距增大导致的频率上升需要通过降低电压弥补, 因此最优电压随着阴阳极间距增大有所减小.

2

-->

3.1.实验装置

利用Tesla型脉冲功率源TPG1000开展了高功率微波产生实验, 实验系统示意图如图13所示. 采用超导磁体产生4 T的引导磁场, 使用石墨阴极发射环形电子束, 产生的TM₀₁模式通过模式转换器转换为TE₁₁模式辐射, 馈源口径为680 mm, 介质板外敷充满SF₆和N₂混合气体的气球. 实验中二极管区域的真空度优于10^–3 Pa, 馈源侧的真空度优于10^–2 Pa. 高频结构主要使用钛合金和不锈钢材料, 实验前进行超声清洗并烘干. 图14给出了器件的外观照片.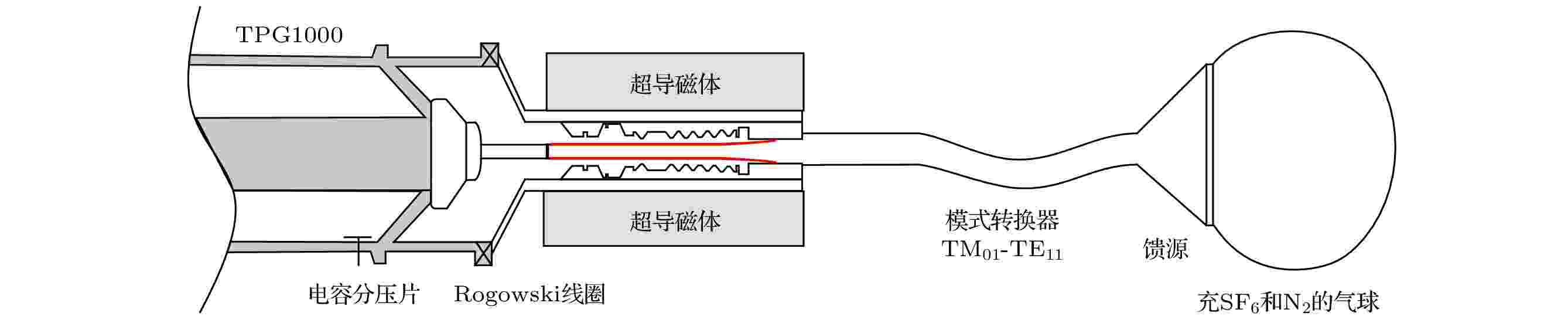
图 13 实验系统示意图
Figure13. Schematic of experiment system.

图 14 速调型相对论返波管外观
Figure14. Picture of the Klystron-like RBWO.

微波功率采用辐射场方向图积分获得, 接收天线采用角锥喇叭天线, 测量通路的示意图如图15所示. 对各元件标定的结果如表3所示. 所用检波器标定曲线如图16所示.

部件	衰减值/dB
衰减器	26.256
5 m微波缆	5.165
定向耦合器和波同转换器	30.05

表3测量元件的衰减标定值
Table3.Calibration result of measurement element.

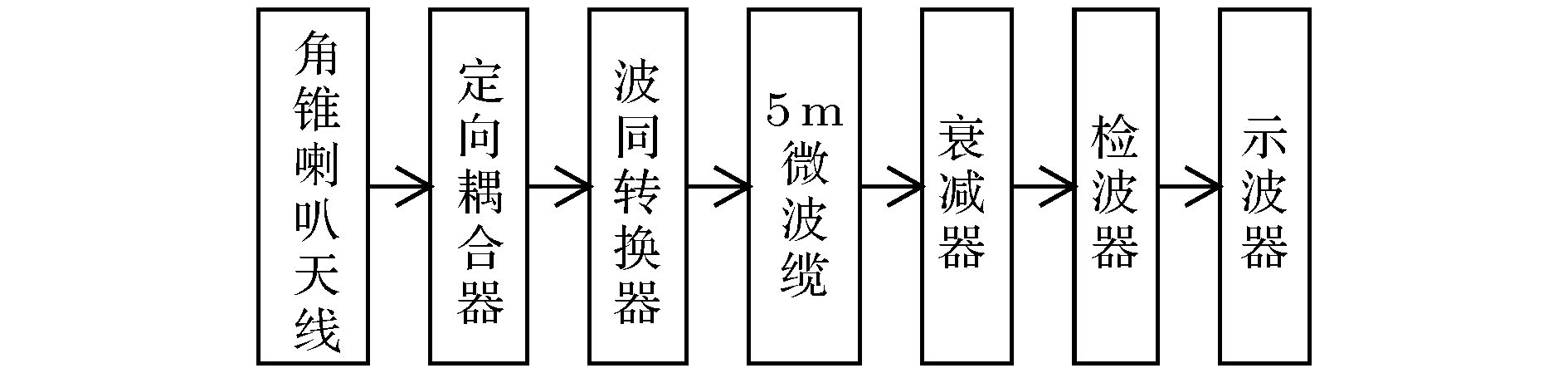图 15 辐射场测量系统示意图
Figure15. Schematic of measurement system.

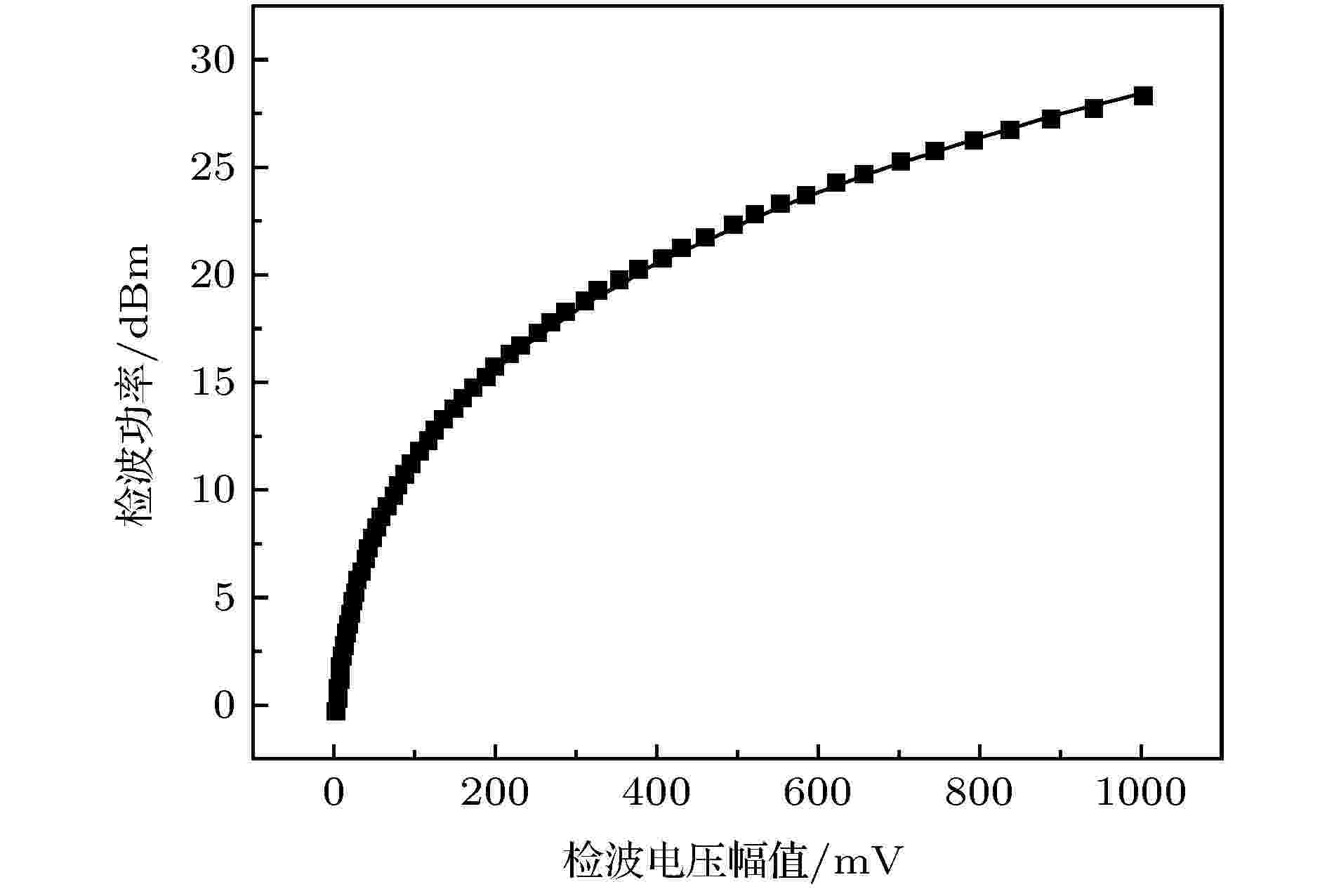图 16 检波器的标定曲线
Figure16. Calibration result of envelope detector.

2 -->

3.2.实验中的击穿与抑制

3 -->

3.2.1.矩形提取腔的情形

提取腔内表面的粗糙度对功率容量有显著的影响. 图17给出了两种不同粗糙度的表面照片, 粗糙度分别为Ra = 0.4 μm和Ra = 0.05 μm. 图18给出了两种粗糙度提取腔对应的微波波形. 当粗糙度Ra = 0.4 μm时, 微波脉宽仅有15 ns, 此时微波幅值较低; 当粗糙度减小到Ra = 0.05 μm时, 微波脉宽增加到25 ns, 幅值显著增大. 图19给出了120个脉冲后提取腔B侧的表面痕迹, Ra = 0.05 μm的提取腔, 表面痕迹显著减少, 表面损伤减弱. 可见, 随着高频结构粗糙度减小到Ra = 0.05 μm, 器件效率提升约10个百分点(即由40%提升到50%), 且输出微波脉宽增加7 ns. 提高器件表面的光洁度, 使得器件表面的场致增强因子显著减小, 进而提升了器件的发射阈值^[20].
图 17 不同粗糙度的表面　(a)粗糙度Ra = 0.4; (b)粗糙度Ra = 0.05
Figure17. Surface with different roughness: (a) Roughness Ra = 0.4; (b) roughness Ra = 0.05.

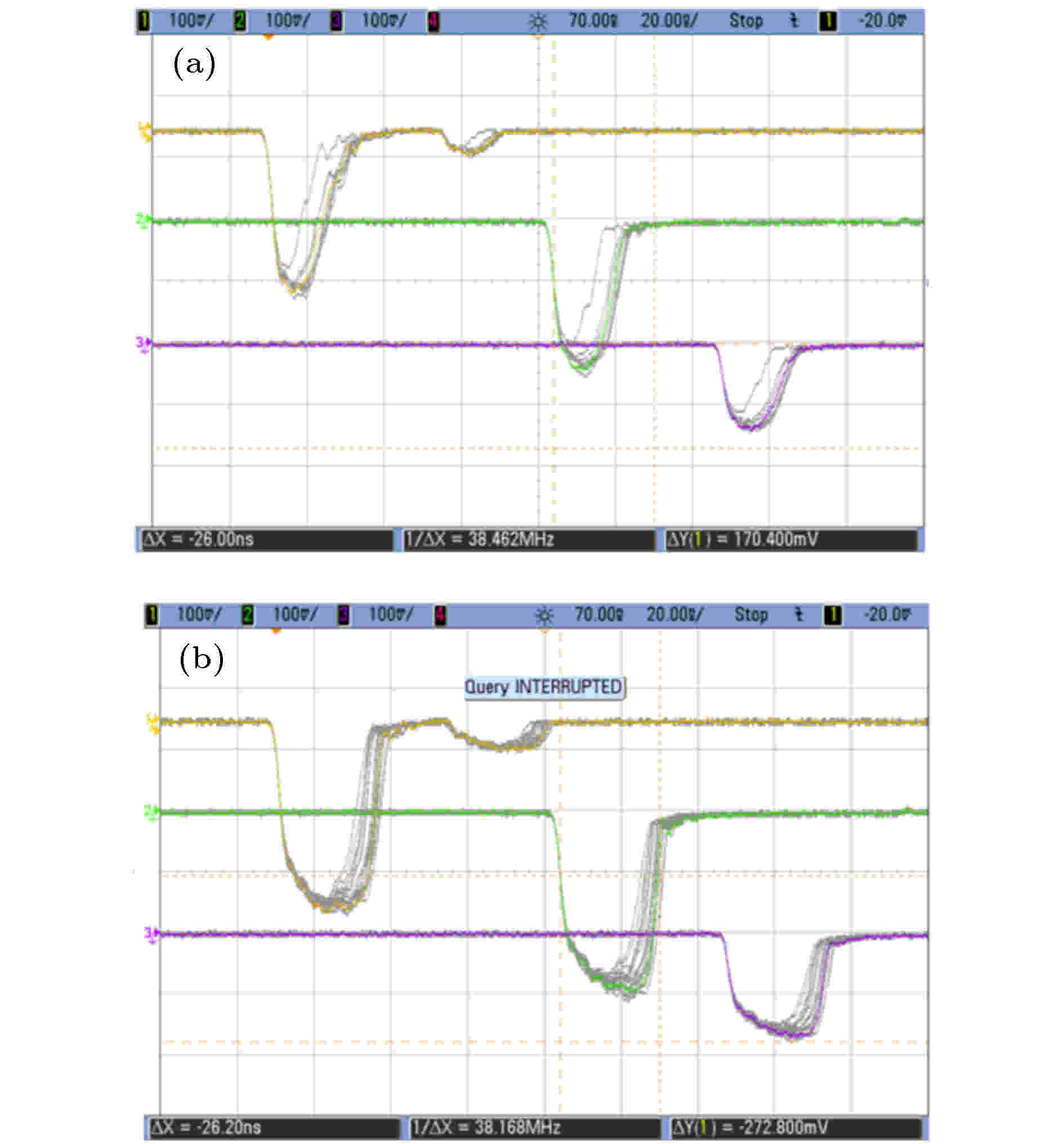图 18 不同粗糙度时的输出波形　(a)粗糙度Ra = 0.4; (b)粗糙度Ra = 0.05. (通道1: 在线微波波形; 通道2, 3: 辐射场微波波形)
Figure18. Output waveform for different roughness: (a) Roughness Ra = 0.4; (b) Roughness Ra = 0.05. (channel 1, online microwave; channel 2 and 3, radiation field)

图 19 不同粗糙度120个微波脉冲后的表面痕迹　(a)粗糙度Ra = 0.4; (b)粗糙度Ra = 0.05
Figure19. Breakdown traces after 120 pulses for different roughness: (a) Roughness Ra = 0.4; (b) roughness Ra = 0.05.

但是, 在实验中发现钛材料的提取腔存在寿命不足的限制. 某个Ra = 0.05 μm的提取腔, 在100～105个脉冲的微波波形如图20(a)所示, 此时微波波形相对饱满, 脉宽可达到约28 ns. 但是在130个脉冲之后, 微波波形如图20(b)所示, 此时微波出现明显尾蚀, 幅值显著降低, 器件效率显著下降, 脉宽减小到23 ns. 在实验中, 可以排除收集极损坏、阴极以及慢波结构击穿等其他因素的影响. 说明高频结构经过精细抛光, 即使光洁度达到Ra = 0.05 μm, 在一定程度上缓解了强场击穿, 但是随着击穿痕迹的积累, 击穿阈值将突然下降, 使得强场击穿加剧.
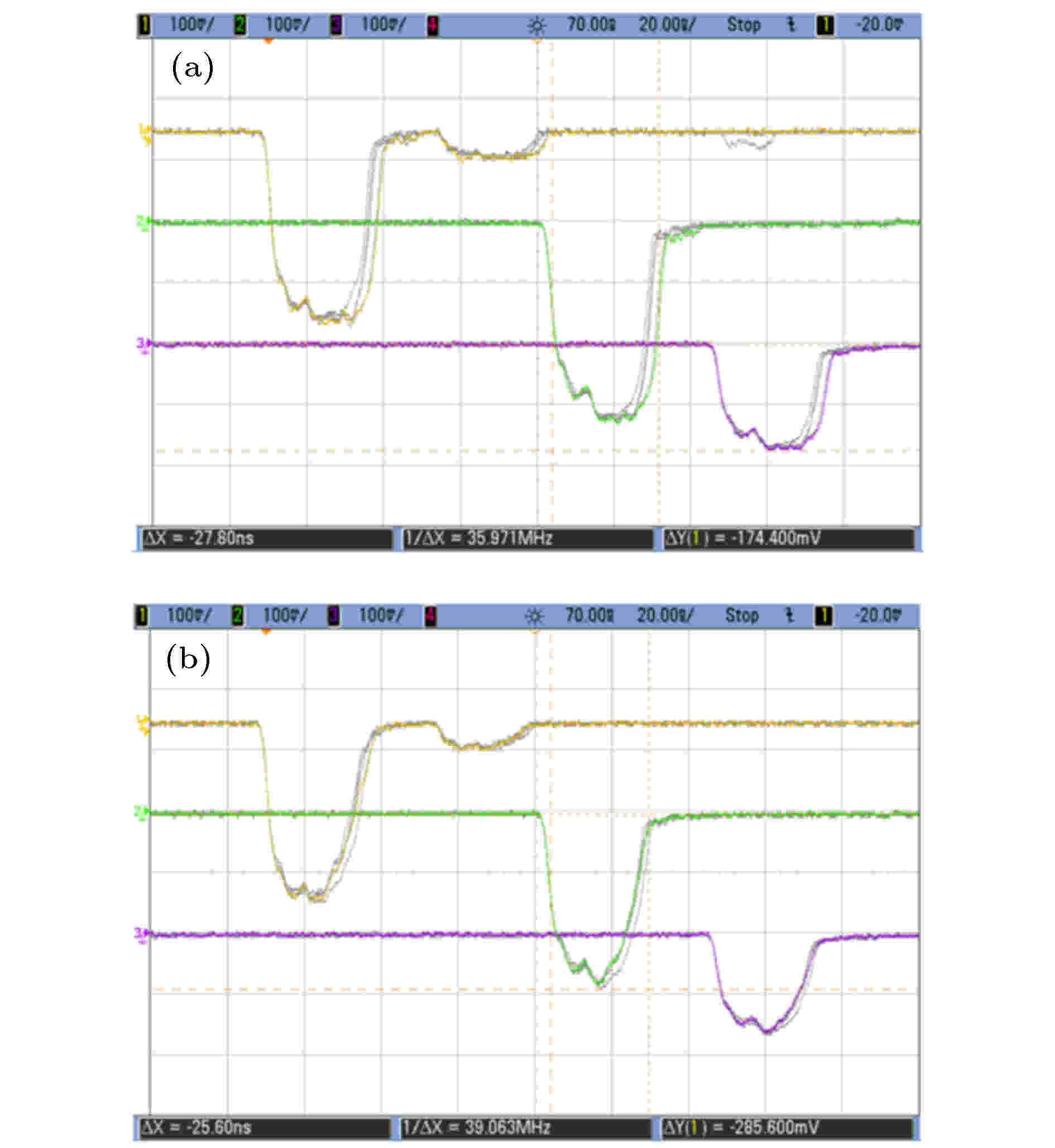图 20 提取腔的寿命现象　(a) 100个脉冲后; (b) 130个脉冲后. (通道1: 在线微波波形; 通道2, 3: 辐射场微波波形)
Figure20. Lifetime of extraction cavity: (a) After 100 pulses; (b) after 130 pulses. (channel 1, online microwave; channel 2 and 3, radiation field)

3 -->

3.2.2.椭圆形提取腔

显然, 矩形提取腔无法满足需求. 在实验中, 在其他实验条件保持不变时, 对矩形提取腔和椭圆形提取腔进行了对比实验. 两种提取腔的材料均为不锈钢304 L, 表面光洁度均为Ra 0.05 μm, 实验前均进行超声波清洗和烘干处理, 并密封保存.
图21给出了两种提取腔输出波形, 可见器件使用椭圆形提取腔后, 输出微波由三角波变为方波, 而且微波场幅值也有所升高. 图22给出了40个微波脉冲后提取腔内表面的击穿痕迹. 可见, 椭圆形提取腔内表面的击穿痕迹显著减少.
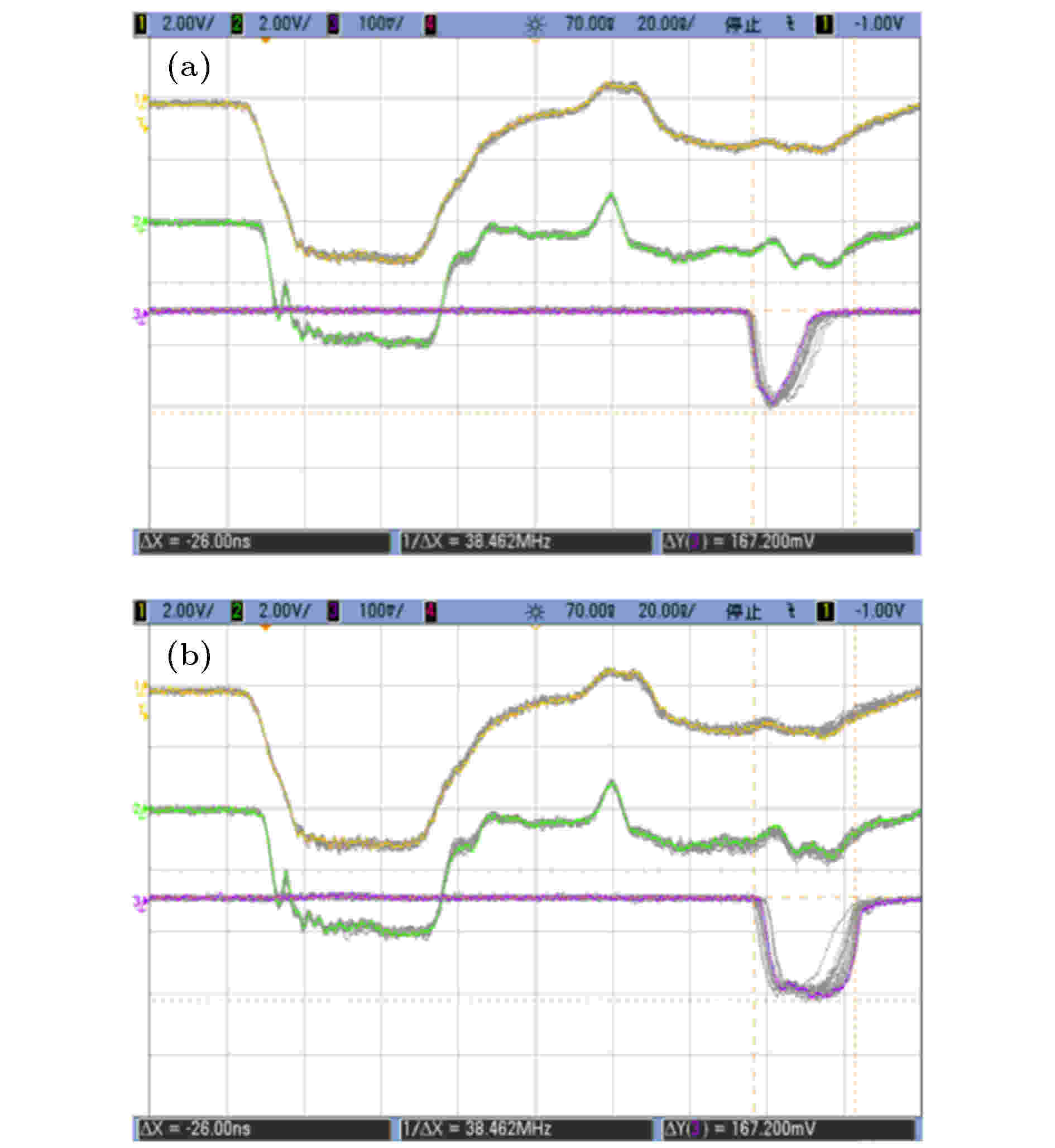图 21 矩形提取腔和椭圆形提取腔时的波形　(a)矩形提取腔; (b)椭圆形提取腔. (通道1: 二极管电压波形; 通道2: 二极管电流波形; 3: 辐射场波形)
Figure21. Waveform under rectangular and ellipse extraction cavity: (a) Rectangular extraction cavity; (b) ellipse extraction cavity. (channel 1, diode voltage; channel 2, diode current; channel 3, radiation field)

图 22 40个微波脉冲后的击穿痕迹　(a)矩形提取腔; (b)椭圆形提取腔
Figure22. Breakdown trace after 40 pulses: (a) Rectangular extraction cavity; (b) ellipse extraction cavity.

在对比实验后, 使用钛合金材料的椭圆形提取腔, 经过数千个微波脉冲, 输出微波仍为方波, 而且微波幅值稳定, 没有出现矩形提取腔的寿命不足的现象. 可见, 椭圆形提取腔具有较高的功率容量, 具有较大的应用潜力.
2 -->

3.3.典型的实验结果

在实验中, 典型的辐射场功率密度分布如图23所示, 输出微波波形和频谱如图24所示. 当阴阳极间距L_ak = 18 mm、二极管电压为601 kV、二极管电流为7.1 kA时, 辐射场积分功率为2.15 GW, 频率为9.55 GHz, 所得转换效率为50% (±5%). 所得结果与PIC数值模拟接近, 效率的差异可能来源于高频结构内表面的射频击穿和传输通路的功率损耗等.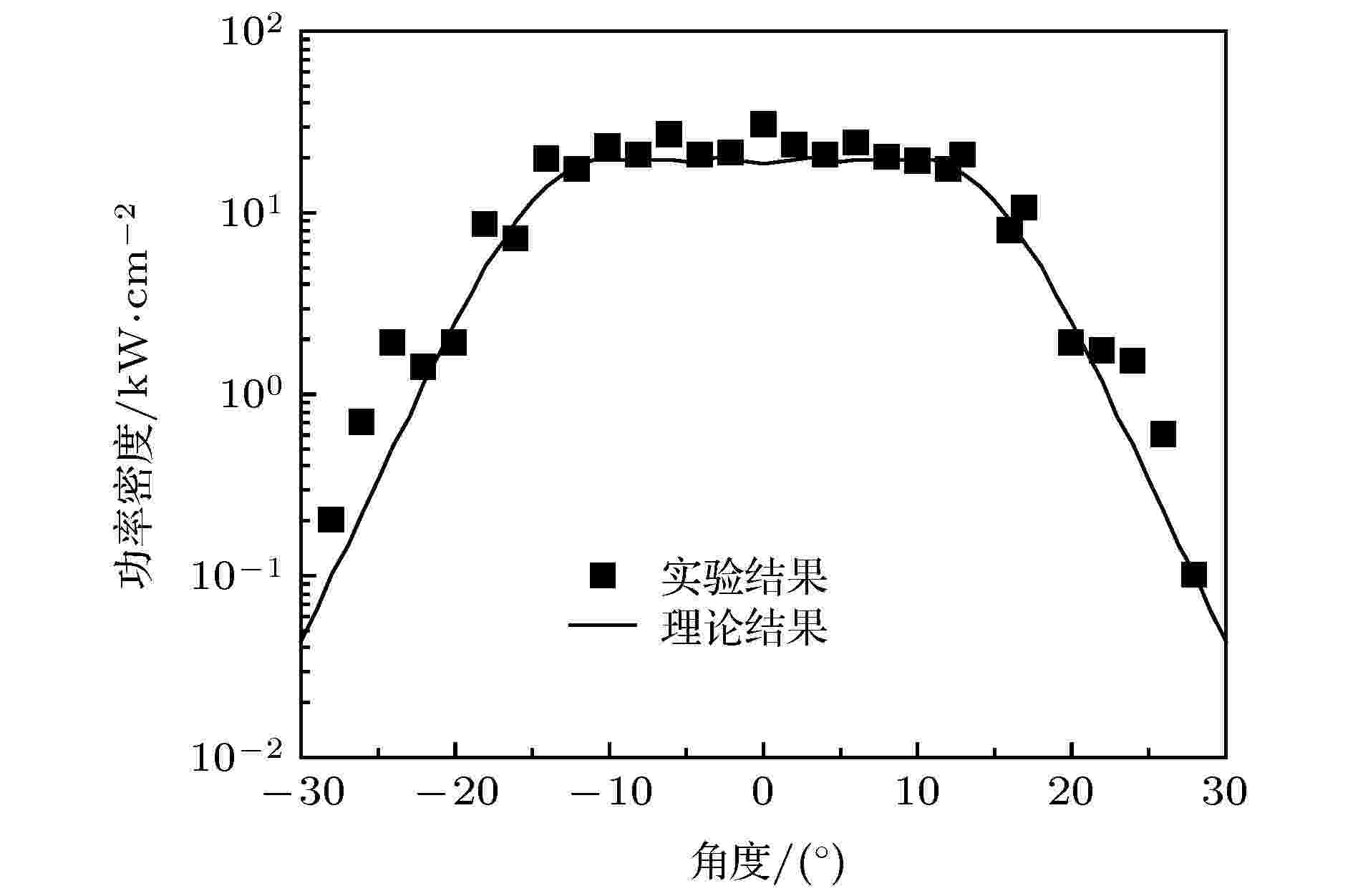
图 23 辐射场功率密度分布
Figure23. Power density distribution of radiation field.

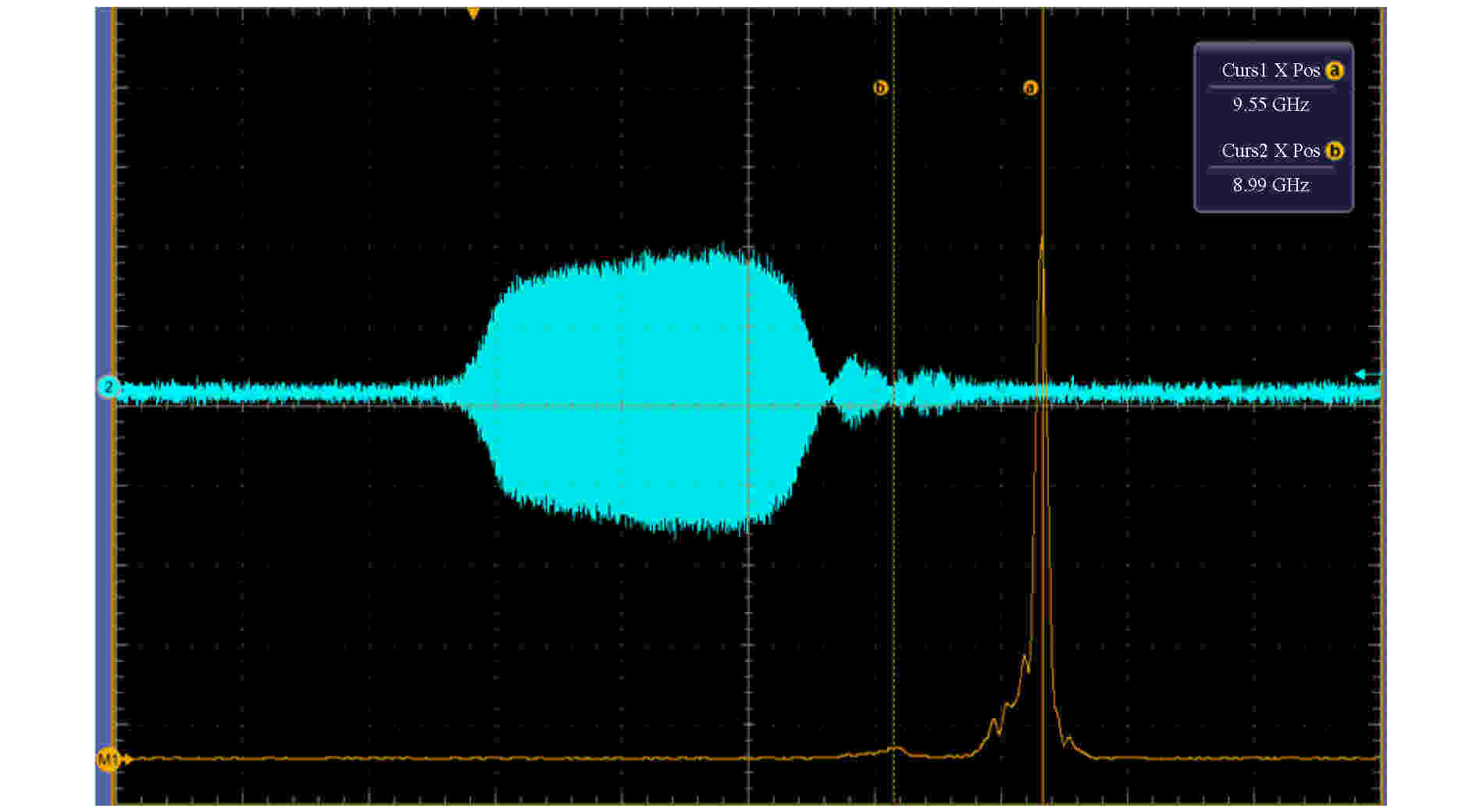图 24 微波波形和频谱
Figure24. Microwave waveform and frequency spectrum.

本文对一种高效率速调型RBWO进行了理论分析和实验研究. 在PIC数值模拟中, 该速调型相对论返波管, 输出功率为2.12 GW, 转换效率为60%. 通过理论分析, 给出了两个预调制腔间距的选择依据; 提出了一种高功率容量的提取腔, 可使得提取腔内表面场强降低约25%; 分析了磁场分布对效率的影响, 通过优化磁场分布, 使得波束互作用区后端束流更加靠近慢波结构, 可以在一定程度上克服器件转换效率对收集位置的强烈依赖; 分析了阴阳极间距对效率的影响, 随着阴阳极间距增大, 器件的最优工作电压降低, 并且效率有所提升. 在实验中, 该器件输出微波频率为9.55 GHz, 辐射场积分功率为2.15 GW, 脉宽可达到25 ns, 所得转换效率为50% (±5%). 实验结果与理论和数值模拟结果基本吻合.
感谢潘亚峰、朱晓欣博士在实验中提供的帮助, 感谢曹亦兵、吴平、刘胜、李爽、邓昱群博士和王东阳的有益讨论. 感谢武向国、郭海洋、程攀伦和袁华标在实验中的支持.